Конформизм — что это такое | Определение конформности
Наверняка, вы замечали, что практически в любой компании есть люди, которые стараются быть как все, а есть и такие, кто с точностью до наоборот, старается делать все наперекор большинству. Это связано с понятием конформизма, как его называют в психологии, и в этой статье мы рассмотрим, почему люди себя ведут тем или иным образом, хорошо это или плохо, и как избавиться от конформности, если она стала мешать.
Что такое конформизм в психологии?
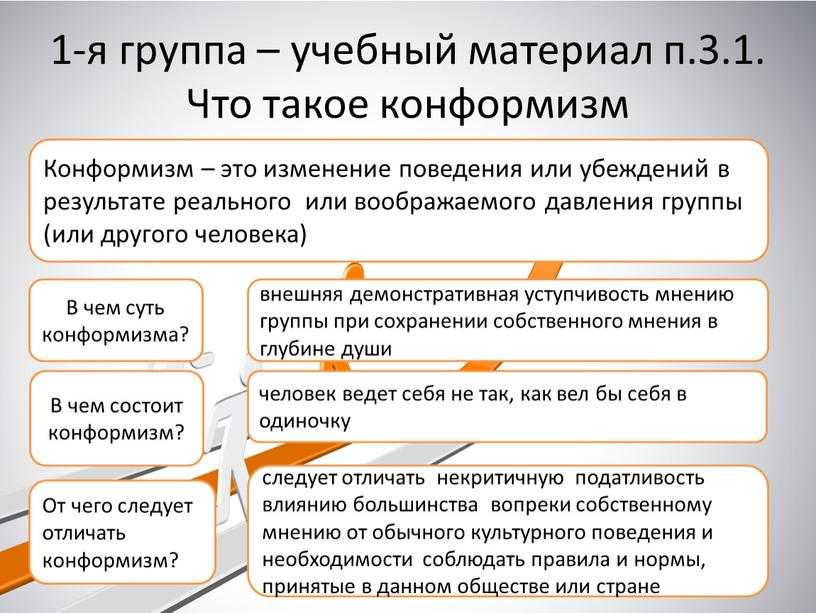
Конформизм — это изменение человека в поведении и мыслях, которое произошло в результате влияние извне (другим человеком, группой людей и т. д.). То есть, если другой человек может повлиять на то, что мы делаем, и мы подсознательно «доверяемся» его позиции и не анализируем сами, это можно описать, как конформность.
Кто такой конформист, характеристика личности
Конформист — это человек, занимающий подчиненное положение в обществе, согласен с большинством, способен изменить свои мысли и действия под влиянием другого человека. За счет удобности такой позиции конформистов в мире гораздо больше, чем нонконформистов.
За счет удобности такой позиции конформистов в мире гораздо больше, чем нонконформистов.
Что такое конформное поведение?
При такой форме поведения, человек подавляет свои истинные мысли и интересы, и действует так же, как большинство. Люди, привыкшие к конформному поведению, слабовольные, легко внушаемые.
Достоинства и недостатки конформности
Польза от конформизма в том, что это своеобразная экономия ресурсов и психологический блок на часть бытовых решений. Конформизм позволяет сохранять энергию и тесно общаться с другими людьми как с единомышленниками. Конформизм в компаниях помогает руководителям успешно управлять группами людей, а также способствует соблюдению законов, например, ПДД.
Недостатками конформного поведения являются утрата своей индивидуальности, консервативные взгляды, мешающие изобретению новых решений, неспособность нести ответственность за собственную жизнь и снижение самооценки.
Виды конформизма
Даже конформное поведение, с которым, казалось бы, все понятно, может быть разным, в зависимости от действий и целей.
I work!
Внешний конформизм
Часто это можно назвать своего рода лицемерием. Человек внешне соблюдает правила и согласен с большинством, но его истинные мысли, планы и цели могут быть совершенно другими.
Внутренний конформизм
При внутреннем конформизме человек даже не отличает мнение большинства от своего, поступает так, как действует большинство, потому что искренне считает, что он согласен.
Социальный конформизм в психологии
Конформизм в психологии давно стал обыденностью: на них основана мода, политические программы, искусство в разное время. Зная предпочтения большинства, можно разработать идею, у которой будет миллионная аудитория.
Причины конформизма
Конформность с нами уже много тысяч лет, она проявлялась с эволюцией человека и была тесно связана с инстинктом самосохранения. также конформные люди часто предпочитают быть такими, чтобы добиться успех, но здесь, скорее всего, имеет место быть внешний конформизм.
Факторы влияния
На предрасположенность к конформному поведению могут влиять следующие факторы.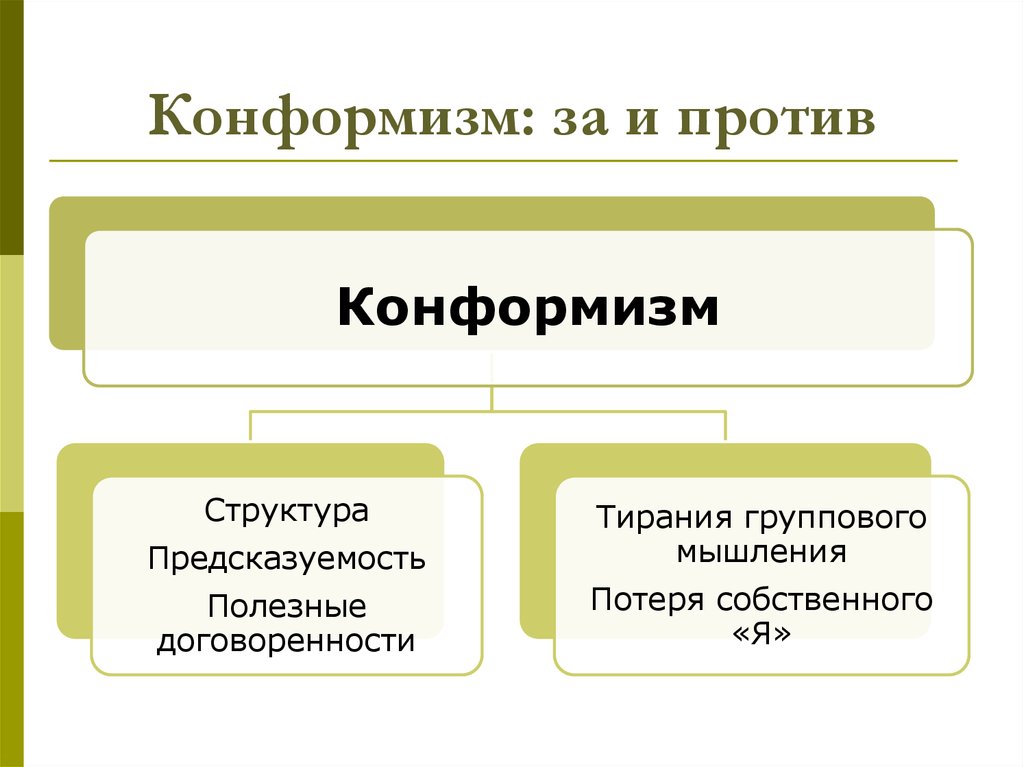
- 1. Особенности характера: некоторые с рождения отличаются высокой степенью внушаемости и мягкохарактерности;
- 2. Осведомленность проблемы: чем меньше человек разбирается в предмете дискуссии, тем охотнее он займет позицию большинства;
- 3. Уровень культурности: конформное поведение часто продиктовано желанием мирного сосуществования.
Этапы развития
Развитие конформного поведения можно разделить на 3 основных этапа.
- 1. Вхождение в группу и подчинение. Человек старается понравится окружающим и не провоцировать конфликтов, чтобы пользоваться благами этого сообщества;
- 2. Этап перестройки. Человек анализирует свои прежние мысли и идеи и находит их неправильными, так как люди из новой группы ему уже пояснили, «как правильно». Человек начинает перестраиваться даже мысленно.
- 3. Этап деятельности. Персона хочет получать высокое положение в данной группе, поэтому, даже несмотря на то, что она не со всем из сказанного соратниками согласна, человек продолжает поступать по модели социального одобрения.

Как не допустить развития конформности?
- 1. Всегда думайте и не забывайте о своих истинных целях;
- 2. Работайте над уверенностью в себе и вашей самооценкой;
- 3. Уделяйте внимание развитию творческого и критического мышления;
- 4. Работайте над осознанностью, анализируйте все, что с вами происходит;
- 5. Больше читайте. Как мы помним, одна из причин конформного поведения — неосведомленность в вопросе дискуссии;
- 6. Знакомьтесь с новыми разными людьми, дискутируйте.
Примеры конформности в жизни
К проявлениям конформности относятся некоторые стереотипы, например, человек в очках — умный, человек в галстуке — деловой. Также дети и подростки часто группами сбегают с уроков, собираются с разными целями после занятий — это тоже проявление конформизма. Также вышеупомянутая мода возможна также благодаря конформизму — люди начинают носить одежду одного фасона, цветов, слушать одну и ту же музыку, смотреть одинаковые фильмы и т. д..
Источник: https://astro7. ru/online-journal/luchshie-stati/chem-opasen-konformizm.html
ru/online-journal/luchshie-stati/chem-opasen-konformizm.html
Конформность — это не хорошо, и не плохо, это просто явление, которое остается с нами со времен эволюции. Учитесь пользоваться преимуществами такой модели поведения и избегать недостатков. Если вас беспокоит ваша конформность и вы не можете справиться самостоятельно, пишите на astro7.ru — наши эксперты будут рады помочь вам стать увереннее.
Занятие с элементами тренинга «Конформное поведение»
Классы: 6, 7, 8, 9, 10
Ключевые слова: профилактика аддиктивного поведения, конформное поведение, профилактика употребления психоактивных веществ
Цель: отработка методов
противостояния внешнему воздействию ровесников
и взрослых.
Время: 2 академических часа.
Форма зала: круг.
Материалы: магнитофон, бумага формата А 4, ватман, белый картон, английские булавки, ножницы, цветные карандаши, фломастеры, ручки, клей, газета, бланки к тестовым заданиям, упражнениям, три кольца диаметром 7-15 см (например, моток неширокого скотча), нитки, бейджики.
ХОД ЗАНЯТИЯ
1. Упражнение «Экран настроения»
Цель: выразить свое настроение.
Время: 5 минут.
Техника проведения: перед началом занятий на стене крепится «Экран», на котором участники группы могут выразить свое настроение.
Материал: лист ватмана, карандаши.
Инструкция: Ребята, это у нас своеобразный
«Экран настроения». На нем можно выразить свое
настроение. Перед вами восемь карандашей
(красный, желтый, синий, зеленый, фиолетовый,
коричневый, серый и черный) различных цветов и
оттенков. Каждый из вас пусть возьмет тот цвет,
который соответствует вашему сегодняшнему
настроению и отметит его в виде круга на
«Экране». Ребята, это упражнение будет являться
своеобразным ритуалом наших тренинговых занятий
и оно будет выполняться в начале и в конце
последующих встреч.
Каждый из вас пусть возьмет тот цвет,
который соответствует вашему сегодняшнему
настроению и отметит его в виде круга на
«Экране». Ребята, это упражнение будет являться
своеобразным ритуалом наших тренинговых занятий
и оно будет выполняться в начале и в конце
последующих встреч.
2. Упражнение «Приветственное движение»
Цель: создать положительный настрой на день, поднять настроение, развить групповую сплоченность.
Время: 5 минут.
Техника проведения: участники стоят в кругу, показывают приветственное движение, обращенное ко всем остальным. Движение повторяется всеми участниками.
Материал: магнитофон.
Инструкция: ребята, давайте встанем в круг. Сейчас, каждый по-очереди будет показывать под музыку приветственное движение, а вся группа за ним повторит.
Анализ:
– Понравилась ли вам игра?
– Какое у вас настроение?
– Готовы ли вы продолжать работу?
3.
Цель: развитие эмпатии, расширение представлений участников группы друг о друге, повышение эмоционального фона настроения.
Время: 5 минут.
Техника проведения: участники группы по очереди должны вспомнить всех знаменитых своих тезок.
Инструкция: Ребята, подумайте и вспомните в уме всех знаменитых тезок: царей, князей, певцов, артистов, политических деятелей, святых и т. д. А теперь каждый из вас представиться от имени знаменитости. Например, Александр – Александр Македонский, Константин – Константин Эрнст.
Анализ:
– С какими трудностями вы столкнулись в этом
упражнении?
– Что вы испытывали, когда представлялись от
имени знаменитого человека?
– Какие эмоции у вас вызвало это упражнение?
4. Упражнение «Мое настроение»
Цель: развитие групповой сплоченности,
навыков группового взаимодействия, творческого
самовыражения, снятие психоэмоционального
напряжения.
Время: 5 минут.
Техника проведения: участникам группы предлагается слепить из бумаги свое настроение, по хлопку передать модель настроения соседу слева и т. д., в результате бумага будет изорвана. В центре круга устроить салют. После выполнения задания провести конкурс «Кто больше салютов соберет».
Инструкция: Вам необходимо слепить из бумаги свое настроение в виде какой-либо модели, по хлопку передать модель настроения соседу слева и т. д. Посмотрите, наше настроение превратилось в маленькие кусочки бумаги. Возьмем наше настроение в руки и устроим салют. А теперь – конкурс «Кто больше салютов соберет». Молодцы!
Анализ:
– На что похоже ваше настроение, в виде чего вы
хотели его изобразить?
– Расскажите о своем состоянии до и после
упражнения.
– Какое у вас настроение?
5. Упражнение «Властелины кольца» (модификация
авторская).
Цель: развитие групповой сплоченности, обучение координации совместных действий, поиску способов коллективного решения необычной проблемы, обмен информацией при ограниченности средств, снятие психоэмоциональное напряжение.
Время: 10 минут.
Техника проведения: участники разбиваются на две малые группы. Три участника каждой подгруппы становятся по кругу на расстоянии примерно 1,5 м друг от друга, и каждый из них берет в руки по одной нитке. Действуя синхронно, опустить кольцо точно на мишень — например, лежащую на полу монетку. Упражнение выполняется в нескольких вариантах: с открытыми глазами, с закрытыми глазами, с посторонней помощью, всеми участниками группы.
Материал: два кольца диаметром 7-15 см
(например, моток неширокого скотча), к которому
привязаны на равном расстоянии друг от друга 3
нитки длиной 1,5-2 м каждая. кольцо диаметром 7-15 см,
к которому привязаны на равном расстоянии друг
от друга 6 ниток длиной 1,5-2 м каждая.
Инструкция: Вам необходимо разбиться на две малые группы по принципу «первый, второй». Три участника каждой подгруппы встаньте по кругу на расстоянии примерно 1,5 м друг от друга, и каждый из вас возьмите в руки по одной нитке. Ваша задача – действуя синхронно, опустить кольцо точно на мишень — например, лежащую на полу монетку.
Упражнение выполняется в нескольких, вариантах. Поэтому вы должны быть внимательными и следовать моим инструкциям:
1. Опустите кольцо точно на мишень, при этом у
вас открыты глаза и можете переговариваться
между собой.
2. Опустите кольцо точно на мишень, при этом у вас
открыты глаза, но переговариваться не можете.
3. Опустите кольцо точно на мишень, при этом у вас
закрыты глаза. За спиной каждого из вас встанет
еще по одному участнику, которые будут смотреть
на происходящее и подсказывать своему
подопечному, как двигать нитку, чтобы кольцо
опустилось в нужном месте.
4. Перед вами кольцо с 6 нитками. Участвуют все
члены группы. Задание аналогично третьему
варианту, но переговариваться нельзя.
Анализ:
– Понравилось ли вам упражнение?
– С какими трудностями столкнулись?
– Нашли ли вы обще групповую тактику?
– Какие психологические качества важнее всего
для успешного выполнения этого упражнения?
– Какие для себя вы сделали выводы?
– Какое у вас настроение?
6. Мини-лекция «Конформное поведение»
Цель: повышение представлений участников о понятиях конформность, конформное поведение и как научиться отстаивать свою точку зрения.
Время: 10 минут.
7. Упражнение «Коленочки – колечки – ракета».
Цель: снятие утомляемости, повышение эмоционального фона настроения.
Время: 5 минут.
Техника проведения: все стоят в кругу. Под
музыкальное сопровождение по команде ведущего
«направо» участники должны повернуться и
пробежаться по кругу, по команде «коленочки»
участники должны сесть друг другу на колени и
перемещаться в тесном кругу, по команде
«колечки» надеть виртуальные кольца на каждый из
пальцев рук, по команде «ракета», взявшись за
руки, участники должны сделать ракету, то есть
произнося «Ух» поднять руки вверх, образовав при
этом тесный круг.
Инструкция: Ребята, а теперь я предлагаю подвигаться под музыку. Встаньте в круг. Под музыкальное сопровождение по моей команде «направо» вы должны повернуться и пробежаться по кругу, по команде «коленочки» вы должны тесно встать друг за другом по кругу и сесть друг другу на колени и друг за другом, как змейка, перемещаться в тесном кругу. По команде «колечки», надеть виртуальные кольца на каждый из пальцев рук, затем на руку, накрутить на ноги. По команде «ракета», встанем в круг и, взявшись за руки, вы должны произнести «Ух!», при этом поднять руки вверх, образовав тесный круг.
Анализ:
– Понравилось ли упражнение?
– Какое у вас настроение?
– Готовы ли вы продолжать дальнейшую работу?
8. Дискуссия в малых группах на тему: «Портрет подростка с зависимым поведением»
Цель: научить участников проводить анализ
и адекватно реагировать в проблемных ситуациях,
обучение навыкам ведения дискуссии.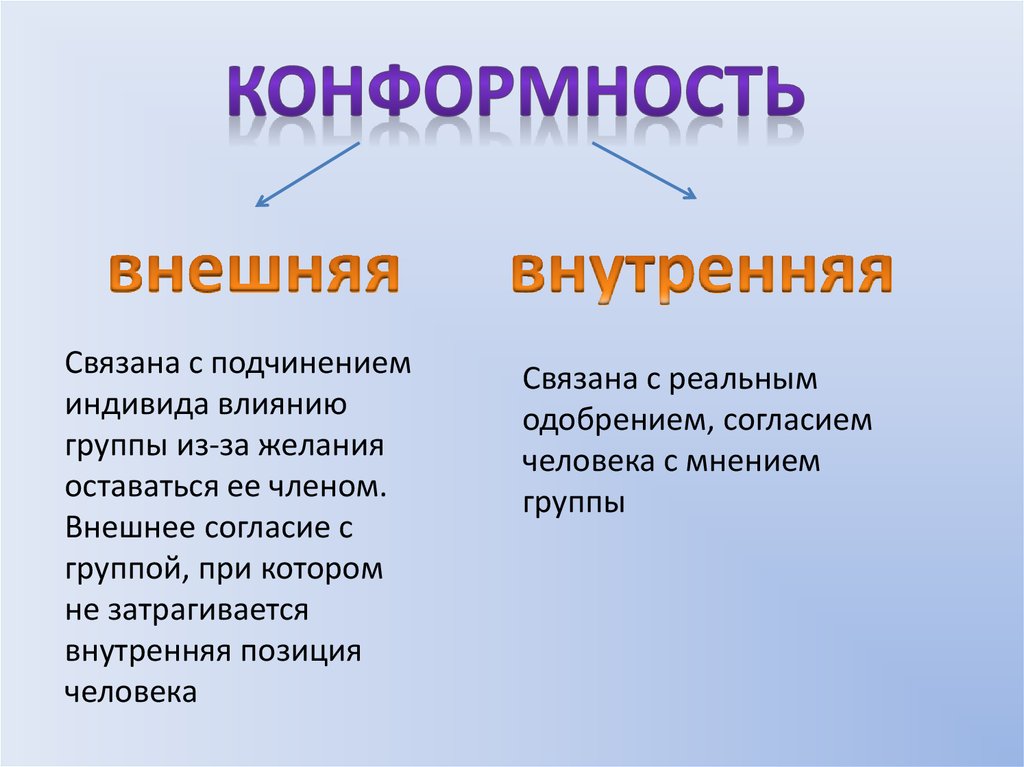
Время: 15 минут.
Техника проведения: участники группы разбиваются на 3 малые группы, выбирают председателя, таймера, спикера, секретаря. Каждой группе дается задание, которое надо будет сначала обсудить, затем записать на листе бумаги. После этого, группа садится в круг и один из представителей каждой малой группы зачитывает качества. Остальные добавляют, соглашаются, либо возражают, предлагая свои варианты.
Материал: 3 листа ватмана, маркеры, список качеств личности.
Инструкция: яприветствую вас в нашем
дискуссионном клубе! Для работы предлагаю
разделиться на 3 малые группы. При формировании
групп будем использовать следующую технику
деления: я на ухо каждому из вас скажу одно слово.
Это будет животное (медведь, лиса, заяц).
Задача: найти своих, т. е. тех, кому это животное
было сказано. Найти тихо, без слов, используя
только жесты и мимику.
Для работы каждая малая группа избирает:
председателя, таймера, спикера, секретаря.
Сейчас я вам раздам вопросы для обсуждения.
Используйте при обсуждении принципы мозгового
штурма и соблюдайте правила работы группы.
На работу вам дается 5 минут.
Задание 1 группе.
- Отметьте положительные стороны подростка с зависимым поведением.
- Напишите качества, какими он должен обладать.
Задание 2 группе.
- Отметьте отрицательные стороны подростка с зависимым поведением.
- Напишите качества, какими он должен обладать.
Задание 3 группе.
- Составьте портрет подростка с зависимым поведением.
- Напишите качества, какими он должен обладать.
– Просим спикеров прикрепить лист ватмана к
стене и доложить выработанные групповые идеи по
обсуждаемым вопросам.
– Поаплодируем за хорошую продуктивную работу.
Анализ:
– Кто хочет что-либо добавить или с чем не
согласен?
– Все ли выдвинутые идеи принимаются? Если да, то
выносим на обще групповое голосование.
– Что меня удивило?
– Какие для себя вы сделали выводы?
– Не хотели бы Вы что-либо изменить в себе, в
своем поведении?
9. Упражнение «Дождь в летний день»
Цель: снять эмоциональное напряжение, разрядка.
Время: 5 минут.
Техника проведения: все участники группы стоят в кругу, друг за другом по часовой стрелке. Под инструкцию ведущего участники на спине впереди стоящего изображают природное явление – дождь в летний день, тихий ветер, ветер усилился, начался ураган, мелкий дождь, усиливается дождь, льет крупный дождь, град, затем дождь успокаивается, ветер стихает.
Инструкция: Ребята, встаньте в круг, друг
за другом по часовой стрелке. Под мое
сопровождение мы на спине впереди стоящего
участника с помощью рук будем изображать дождь в
летний день. И так: «дует тихий ветер, ветер
усиливается, пошел мелкий дождь, дождик
усиливается, льет крупный дождь, затем пошел
град, дождик успокаивается, ветер стихает».
Под мое
сопровождение мы на спине впереди стоящего
участника с помощью рук будем изображать дождь в
летний день. И так: «дует тихий ветер, ветер
усиливается, пошел мелкий дождь, дождик
усиливается, льет крупный дождь, затем пошел
град, дождик успокаивается, ветер стихает».
Анализ:
– Ваше настроение?
– Что вы почувствовали?
10. Игровое моделирование реальных ситуаций.
Цель: обучение навыкам выхода из сложных жизненных психотравмирующих ситуаций.
Время: 15 минут.
Техника проведения: участники группы разбиваются на 3 малые группы. Каждой группе дается своя ситуация. Они должны представить вариант ее завершения в виде театрализованной сценки.
Инструкция: Ребята, яприветствую вас на
театрализованной сцене! Для работы предлагаю
разделиться на 3 малые группы. При формировании
групп будем использовать следующую технику
деления: белый, мягкий, пушистый.
Каждой группе дается своя ситуация. Вы должны представить вариант ее завершения в виде театрализованной сценки.
– Итак, на обсуждение задания 3 минуты.
1) Вы с компанией сверстников гуляете по улице и встречаете ребенка 9 лет. Один из лидеров вашей компании предлагает вам отобрать у мальчика сотовый телефон. Ваши действия?
2) Одноклассники идут по улице и распивают алкогольный коктейль. Вы спортсмен. По дороге на тренировку встречаетесь со своими одноклассниками, которые предлагают выпить. Ваши действия?
3) Действие происходит в школе. Основная часть одноклассников не выучили уроки по предмету «химия». Все решили уйти с урока, т. е. прогулять. Ваши действия?
Анализ:
– Какая роль тебе досталась?
– Было ли тебе комфортно играть эту роль?
– Знакомы ли тебе проигрываемые ситуации?
Сталкивался ли ты с ними или твои друзья?
– Что было легким в проблемной ситуации?
– Что было самым трудным в проблемной ситуации?
– Что ты вынес для себя из этой ролевой игры?
– Что можно добавить в игру?
11. Обратная связь
Обратная связь
Цель: узнать мнение участников о тренинговом занятии.
Время: 5 минут.
Анализ:
– Самое интересное упражнение?
– Что вам понравилось больше всего?
– С какими трудностями вы столкнулись?
– Довольны ли вы собой и своим поведением?
– О чем вы задумались и что полезного вы взяли
для себя и будете использовать?
– Оцените в процентах ваше участие в тренинговом
занятии.
12. Упражнение «Фотография на память»
Цель: повысить уровень самопринятия.
Время: 5 минут.
Техника проведения: участникам предлагается изобразить фотографию на память в любом образе.
Инструкция: Ребята, вам предлагается изобразить фотографию на память в любом образе.
В конце упражнения – аплодисменты за совместную работу.
13. Упражнение «Экран настроения»
Цель: подвести итоги дня, выразить свое
настроение.
Время: 5 минут.
Техника проведения: перед началом занятий на стене крепится «Экран», на котором участники группы могут выразить свое настроение.
Материал: лист ватмана, карандаши.
Инструкция: Ребята, это у нас своеобразный «Экран настроения». На нем можно выразить свое настроение. Перед вами восемь карандашей (красный, желтый, синий, зеленый, фиолетовый, коричневый, серый и черный) различных цветов и оттенков. Каждый из вас пусть возьмет тот цвет, который соответствует вашему сегодняшнему настроению и отметит его в виде круга на «Экране». Это упражнение будет являться своеобразным ритуалом наших тренинговых занятий и оно будет выполняться в начале и в конце последующих встреч.
Конформное поведение — неизбежное зло или благо для общества? :: SYL.ru
Любовь на автопилоте: дарите внимание и другие способы отключить «прибор»
Всего 3 ингредиента: как быстро приготовить суп из помидоров
Хрустящий салат с витаминами. Готовим брокколи правильно
Готовим брокколи правильно
Чтобы куст 100% прижился и плодоносил: как высаживать крыжовник осенью
Рисование, танцы — обязательно! Что на корню разрушает женскую энергию
Что добавить в воду для полива, чтобы заставить цвести кактус, алоэ и толстянку
Нужно ли очищать газон от опавших листьев? Мнения разделились
Фрукты, специи, румяна: чем заменить стойкую помаду для губ
На закуску и не только. Готовим ароматные хлебные палочки
Метод Сахо: содержит двойную гидратацию и систему двойного очищения кожи лица
Автор Ольга Иванова
Наши действия и поступки во многом предопределяются обществом в целом и окружающими нас людьми в частности. Поведение человека — это не только простая формула «стимул — реакция», но сложная модель со многими составляющими, которые находятся во взаимной обусловленности и зависимости. К примеру, дома с родителями индивид может противопоставлять себя семье и принятым в ней ценностям, а в классе или дворовой компании у него способно наблюдаться конформное поведение. Все зависит и от той социальной группы, с которой субъект себя идентифицирует, и от его личностных качеств, и от сиюминутных обстоятельств.
Поведение человека — это не только простая формула «стимул — реакция», но сложная модель со многими составляющими, которые находятся во взаимной обусловленности и зависимости. К примеру, дома с родителями индивид может противопоставлять себя семье и принятым в ней ценностям, а в классе или дворовой компании у него способно наблюдаться конформное поведение. Все зависит и от той социальной группы, с которой субъект себя идентифицирует, и от его личностных качеств, и от сиюминутных обстоятельств.
Следование нормам и социальный контроль
Любая группа так или иначе подчиняет себе личность. Если государство и все его институты оказывают формальный контроль при помощи законов, постановлений, распоряжений органов власти, то семья или объединения людей по интересам пытаются руководить индивидом неформально: путем моральных установок, ценностей, похвалы или порицания. Конформное поведение — это ориентация на соблюдение принятых в данной группе норм, «встраивание» в сообщество. Без него нет социального развития. Независимо от того, подчиняется ли индивид общим нормам добровольно и убежденно или делает это неосознанно, конформное поведение обеспечивает приверженность большинства определенным ценностям и правилам. Простейший пример: дорожное движение. Бунт и вождение «вопреки всему» тут не только запрещены, но и опасны. Следовательно, все водители должны соблюдать определенную культуру поведения на дороге. На этом же принципе основаны и законы.
Независимо от того, подчиняется ли индивид общим нормам добровольно и убежденно или делает это неосознанно, конформное поведение обеспечивает приверженность большинства определенным ценностям и правилам. Простейший пример: дорожное движение. Бунт и вождение «вопреки всему» тут не только запрещены, но и опасны. Следовательно, все водители должны соблюдать определенную культуру поведения на дороге. На этом же принципе основаны и законы.
Стадный инстинкт
В формализованной сфере конформное поведение не только желательно, но и необходимо. Подчиняясь общепринятым нормам, человек упрощает жизнь себе и не осложняет ее другим. Но как быть, когда конформное поведение оказывается «со знаком минус»? Зачастую давление неформальных групп на личность намного сильнее, чем стремление быть законопослушным. Следовательно, в страхе оказаться изгоем и кроется опасность. Вспомним хотя бы такие организации, как СС или нацистская партия. Если определенные принципы, даже идущие вразрез с общечеловеческими ценностями, приняты в группе, принадлежность к которой важна для индивида, в нем срабатывает стадный инстинкт. В любом сообществе можно наблюдать различные виды поведения человека, которые зависят от распределения ролей. Нонконформисты — это, как правило, идейные вдохновители, бунтари, революционеры. Они способны сконцентрировать вокруг себя «серую массу» — последователей, исполнителей. Среди последних также можно выделить различные типы: подражатели, подчиненные, равнодушные, робкие. То есть одни выполняют чужую волю (большинства или руководителей) из идейных соображений, а другие — из страха. Третьи вообще не участвуют в группах, стараются держаться подальше от любых объединений. Яркий пример такой жизненной установки — отшельники, философы.
В любом сообществе можно наблюдать различные виды поведения человека, которые зависят от распределения ролей. Нонконформисты — это, как правило, идейные вдохновители, бунтари, революционеры. Они способны сконцентрировать вокруг себя «серую массу» — последователей, исполнителей. Среди последних также можно выделить различные типы: подражатели, подчиненные, равнодушные, робкие. То есть одни выполняют чужую волю (большинства или руководителей) из идейных соображений, а другие — из страха. Третьи вообще не участвуют в группах, стараются держаться подальше от любых объединений. Яркий пример такой жизненной установки — отшельники, философы.
Нужно ли бороться с конформизмом?
Однозначного ответа на этот вопрос нет. Конформное поведение — естественный механизм приспособляемости человека к окружающей его среде. Однако в неформальных группах оно зачастую приводит к отрицательным последствиям как для самой личности, так и для общества. Яркий пример — преступные формирования или партии и объединения, пропагандирующие насилие и ненависть. Личностные установки закладываются с детства. Следовательно, именно задачей воспитателей и родителей должно быть формирование внутреннего стержня в человеке, который позволит ему отличать добро от зла.
Личностные установки закладываются с детства. Следовательно, именно задачей воспитателей и родителей должно быть формирование внутреннего стержня в человеке, который позволит ему отличать добро от зла.
Похожие статьи
- Конформизм — это… Понятие и черты конформизма
- Конформистское поведение – соглашательство или разумный компромисс
- Что такое поведение: понятие, виды. Правила поведения. Нормы поведения человека в обществе. Психология поведения
- Что такое конфронтация? Это мир или война?
- Социальное поведение: в сетях общества
- Социальная фасилитация: описание феномена, примеры
- Компромисс — это лучший выход из положения? Что такое компромисс?
Также читайте
Неконформное поведение голографических мер запутанности
Дж. М. Малдасена, Большой предел N суперконформных теорий поля и супергравитации , Adv. Теор. Мат. физ. 2 (1998) 231 [hep-th/9711200] [INSPIRE].
М. Малдасена, Большой предел N суперконформных теорий поля и супергравитации , Adv. Теор. Мат. физ. 2 (1998) 231 [hep-th/9711200] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
E. Witten, Пространство анти-де Ситтера и голография , Adv. Теор. Мат. физ. 2 (1998) 253 [hep-th/9802150] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
M. Natsuume, Руководство пользователя AdS/CFT Duality , Lect. Примечания физ. 903 (2015) 1 [arXiv:1409.3575] [ВДОХНОВЕНИЕ].
MathSciNet МАТЕМАТИКА Статья Google ученый
Дж. Касалдеррей-Солана, Х. Лю, Д. Матеос, К. Раджагопал и У.А. Видеманн, Gauge/String Duality, Hot QCD and Heavy Ion Collision , Cambridge University Press, Кембридж, Великобритания (2014) [arXiv:1101. 0618] [INSPIRE].
0618] [INSPIRE].
Г. Камило, Расширяющаяся плазма черных дыр Анти де Ситтера , Евро. физ. J. C 76 (2016) 682 [arXiv:1609.07116] [INSPIRE].
ОБЪЯВЛЕНИЕ Статья Google ученый
S.A. Hartnoll, Лекции по голографическим методам физики конденсированного состояния , Класс. Квант. Грав. 26 (2009) 224002 [arXiv:0903.3246] [INSPIRE].
М. Аттемс и др., Термодинамика, перенос и релаксация в неконформных теориях , JHEP 10 (2016) 155 [arXiv:1603.01254] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Д.-В. Панг, Угловые вклады в голографическую энтропию запутанности в неконформных фонах , JHEP 09 (2015) 133 [arXiv:1506.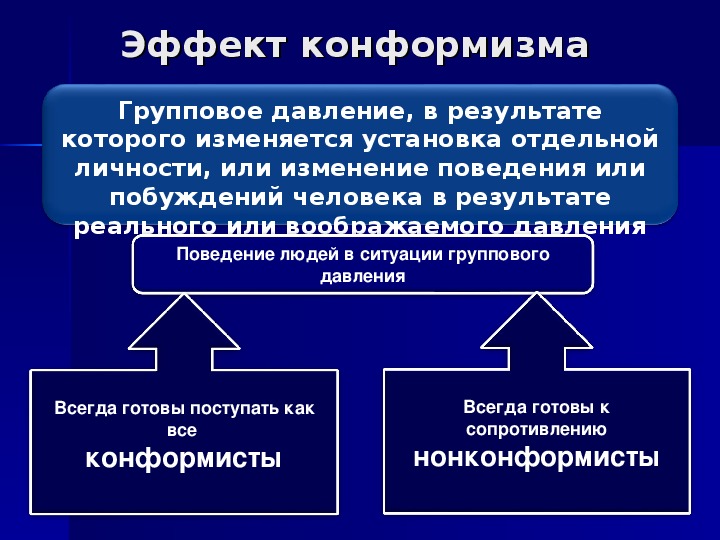 07979] [INSPIRE].
07979] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
М. Рахими, М. Али-Акбари и М. Лезги, Энтропия запутывания в неконформном фоне , Phys. лат. B 771 (2017) 583 [arXiv:1610.01835] [INSPIRE].
ОБЪЯВЛЕНИЕ МАТЕМАТИКА Статья Google ученый
Л. Бомбелли, Р.К. Коул, Дж. Ли и Р.Д. Соркин, Квантовый источник энтропии для черных дыр , Phys. Ред. D 34 (1986) 373 [INSPIRE].
М. Среднецкий, Энтропия и площадь , Физ. Преподобный Летт. 71 (1993) 666 [hep-th/9303048] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
К. Хольцей, Ф. Ларсен и Ф. Вильчек, Геометрическая и перенормированная энтропия в конформной теории поля , Nucl. физ. B 424 (1994) 443 [hep-th/9403108] [INSPIRE].
физ. B 424 (1994) 443 [hep-th/9403108] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
П. Калабрезе и Дж. Л. Карди, Энтропия запутанности и квантовая теория поля , J. Stat. мех. 0406 (2004) P06002 [hep-th/0405152] [INSPIRE].
МАТЕМАТИКА Google ученый
H. Casini and M. Huerta, Энтропия запутанности в свободной квантовой теории поля , J. Phys. A 42 (2009) 504007 [arXiv:0905.2562] [INSPIRE].
М.П. Hertzberg, Энтропия запутанности в скалярной теории поля , J. Phys. A 46 (2013) 015402 [arXiv:1209.4646] [INSPIRE].
В. Розенхаус и М. Смолькин, Энтропия запутанности, плоские поверхности и спектральные функции , JHEP 09 (2014) 119 [arXiv:1407. 2891] [INSPIRE].
2891] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
В. Розенхаус и М. Смолькин, Энтропия запутанности для релевантных и геометрических возмущений , JHEP 02 (2015) 015 [arXiv:1410.6530] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
С. Исо, Т. Мори и К. Сакаи, Энтропия запутанности в скалярной теории поля и ℤ M калибровочная теория на диаграммах Фейнмана , Phys. Ред. D 103 (2021) 105010 [arXiv:2103.05303] [INSPIRE].
С. Исо, Т. Мори и К. Сакаи, Уилсоновское эффективное действие и энтропия запутывания , Симметрия 13 (2021) 1221 [arXiv:2105.14834] [INSPIRE].
Артикул Google ученый
Р. Д. Соркин, Выражение энтропии глобально через (4D) полевые корреляции , J. Phys. конф. сер. 484 (2014) 012004 [arXiv:1205.2953] [INSPIRE].
Д. Соркин, Выражение энтропии глобально через (4D) полевые корреляции , J. Phys. конф. сер. 484 (2014) 012004 [arXiv:1205.2953] [INSPIRE].
Ю. Чен, Л. Хакл, Р. Кунджвал, Х. Моради, Ю.К. Yazdi and M. Zilhão, К энтропии пространственно-временной запутанности для взаимодействующих теорий , JHEP 11 (2020) 114 [arXiv:2002.00966] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
С. Рю и Т. Такаянаги, Голографический вывод энтропии запутанности из AdS/CFT , Phys. Преподобный Летт. 96 (2006) 181602 [hep-th/0603001] [INSPIRE].
С. Рю и Т. Такаянаги, Аспекты голографической запутанной энтропии , JHEP 08 (2006) 045 [hep-th/0605073] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Х. Казини, М. Уэрта и Р.К. Myers, К выводу голографической энтропии запутанности , JHEP 05 (2011) 036 [arXiv:1102.0440] [INSPIRE].
Казини, М. Уэрта и Р.К. Myers, К выводу голографической энтропии запутанности , JHEP 05 (2011) 036 [arXiv:1102.0440] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Р.К. Майерс и А. Сингх, Комментарии к энтропии голографической запутанности и потокам RG , JHEP 04 (2012) 122 [arXiv:1202.2068] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
С.Ф. Локханде, Г.В.Дж. Олинг и Дж. Ф. Педраса, Линейный отклик энтропии запутывания из голографии , JHEP 10 (2017) 104 [arXiv:1705.10324] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
М. Рахими и М. Али-Акбари, Энтропийное разложение голографической запутанности в анизотропной калибровочной теории , Phys. Ред. D 98 (2018) 026004 [arXiv:1803.01754] [INSPIRE].
Ред. D 98 (2018) 026004 [arXiv:1803.01754] [INSPIRE].
В. Фишлер и С. Кунду, Калибровочные теории с сильной связью: поведение нелокальных наблюдаемых при высоких и низких температурах , JHEP 05 (2013) 098 [arXiv:14312.INS].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
О. Бен-Ами, Д. Карми и Дж. Зонненшайн, Голографическая энтропия запутывания нескольких полос , JHEP 11 (2014) 144 [arXiv:1409.6305] [INSPI].
ОБЪЯВЛЕНИЕ Статья Google ученый
Д.-В. Pang, Голографическая энтропия запутанности нелокальных теорий поля , Phys. Ред. D 89 (2014) 126005 [arXiv:1404.5419] [INSPIRE].
С. Кунду и Дж. Ф. Педраза, Аспекты голографической запутанности при конечной температуре и химическом потенциале , JHEP 08 (2016) 177 [arXiv:1602. 07353].
07353].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Х. Эбрахим и Г.-М. Nafisi, Голографическая взаимная информация и критические показатели сильно связанной плазмы , Phys. Версия D 102 (2020) 106007 [arXiv:2002.09993] [INSPIRE].
Р.В. Буний и С.Д.Х. Хсу, Энтропия запутывания, черные дыры и голография , Phys. лат. B 644 (2007) 72 [hep-th/0510021] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Х. Казини и М. Уэрта, A Конечная энтропия запутанности и c-теорема , Физ. лат. B 600 (2004) 142 [hep-th/0405111] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
М. М. Вольф, Ф. Верстрате, М.Б. Гастингс и Дж.И. Cirac, Законы площади в квантовых системах: взаимная информация и корреляции , Phys. Преподобный Летт. 100 (2008) 070502 [arXiv:0704.3906] [ВДОХНОВЕНИЕ].
М. Вольф, Ф. Верстрате, М.Б. Гастингс и Дж.И. Cirac, Законы площади в квантовых системах: взаимная информация и корреляции , Phys. Преподобный Летт. 100 (2008) 070502 [arXiv:0704.3906] [ВДОХНОВЕНИЕ].
В. Фишлер, А. Кунду и С. Кунду, Голографическая взаимная информация при конечной температуре , Phys. Ред. D 87 (2013) 126012 [arXiv:1212.4764] [INSPIRE].
А. Алле и Э. Тонни, Голографическая эволюция взаимной информации , JHEP 01 (2012) 102 [arXiv:1110.1607] [INSPIRE].
ОБЪЯВЛЕНИЕ МАТЕМАТИКА Статья Google ученый
П. Хейден, М. Хедрик и А. Малони, Голографическая взаимная информация моногамна , Phys. Ред. D 87 (2013) 046003 [arXiv:1107.2940] [INSPIRE].
М. Р. Мохаммади Мозаффар, А. Моллабаши и Ф. Омиди, Голографическая взаимная информация для особых поверхностей , JHEP 12 (2015) 082 [arXiv:12411.0INSPI].
Моллабаши и Ф. Омиди, Голографическая взаимная информация для особых поверхностей , JHEP 12 (2015) 082 [arXiv:12411.0INSPI].
М. Асади и М. Али-Акбари, Голографическая взаимная и трехчастная информация в подавлении нарушения симметрии , Физ. лат. B 785 (2018) 409 [arXiv:1804.05604] [INSPIRE].
ОБЪЯВЛЕНИЕ Статья Google ученый
М. Али-Акбари, М. Рахими и М. Асади, Голографическая взаимная и трехсторонняя информация в неконформном фоне , Nucl. физ. B 964 (2021) 115329 [arXiv:1907.08917] [INSPIRE].
Б.М. Терхал, М. Городецкий, Д.В. Люнг и Д.П. Ди Винченцо, Запутанность очищения , J. Math. физ. 43 (2002) 4286 [квант-ph/0202044].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
С. Багчи и А.К. Пати, Моногамия, полигамия и другие свойства запутанности очищения , Phys. Ред. A 91 (2015) 042323 [arXiv:1502.01272].
Багчи и А.К. Пати, Моногамия, полигамия и другие свойства запутанности очищения , Phys. Ред. A 91 (2015) 042323 [arXiv:1502.01272].
А. Бхаттачарья, Т. Такаянаги и К. Умемото, Запутанность очистки в теориях свободного скалярного поля , JHEP 04 (2018) 132 [arXiv:1802.09545] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
П. Капута, М. Мияджи, Т. Такаянаги и К. Умемото, Голографическая запутанность очищения от теорий конформного поля , Phys. Преподобный Летт. 122 (2019) 111601 [arXiv:1812.05268] [INSPIRE].
Х.А. Камарго, Л. Хакл, М.П. Хеллер, А. Ян, Т. Такаянаги и Б. Виндт, Запутанность и сложность очистки в (1 + 1) -мерных свободных конформных теориях поля , Phys. Преподобный Рез. 3 (2021) 013248 [arXiv:2009. 11881] [INSPIRE].
11881] [INSPIRE].
Т. Такаянаги и К. Умемото, Запутанность очищения посредством голографической двойственности , Nature Phys. 14 (2018) 573 [arXiv:1708.09393] [ВДОХНОВЕНИЕ].
ОБЪЯВЛЕНИЕ Статья Google ученый
П. Нгуен, Т. Девакул, М.Г. Хальбаш, М.П. Zaletel and B. Swingle, Entanglement of Purification: from Spin Chains to holography , JHEP 01 (2018) 098 [arXiv:1709.07424] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
С. Датта и Т. Фолкнер, Каноническая очистка поперечного сечения клина запутывания , JHEP 03 (2021) 178 [arXiv:1905.00577] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
К. Тамаока, Поперечное сечение клина запутывания из матрицы двойной плотности , Phys. Преподобный Летт. 122 (2019) 141601 [arXiv:1809.09109] [INSPIRE].
Тамаока, Поперечное сечение клина запутывания из матрицы двойной плотности , Phys. Преподобный Летт. 122 (2019) 141601 [arXiv:1809.09109] [INSPIRE].
Дж. Кудлер-Флам и С. Рю, Негативность запутанности и минимальное сечение клина запутанности в голографических теориях , Phys. Ред. D 99 (2019) 106014 [arXiv:1808.00446] [INSPIRE].
Р.-К. Ян, С.-Ю. Чжан и В.-М. Li, Голографическая запутанность очистки для двойных состояний термополя и термического подавления , JHEP 01 (2019) 114 [arXiv:1810.00420] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
R. Espíndola, A. Guijosa и J.F. Pedraza, Реконструкция клина запутывания и очищение запутывания , Eur. физ. J. C 78 (2018) 646 [arXiv:1804.05855] [INSPIRE].
ОБЪЯВЛЕНИЕ Статья Google ученый
Н. Бао и И.Ф. Халперн, Голографические неравенства и запутанность очистки , JHEP 03 (2018) 006 [arXiv:1710.07643] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
K. Umemoto and Y. Zhou, Entanglement of Purification for Multipartite State and its Holographic Dual , JHEP 10 (2018) 152 [arXiv:1805.02625] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Н. Бао и И.Ф. Халперн, Условные и многочастные запутывания очищения и голографии , Phys. Ред. D 99 (2019) 046010 [arXiv:1805.00476] [INSPIRE].
Н. Бао, А. Чатвин-Дэвис и Г. Н. Реммен, Запутанность очистки и многограничные геометрии червоточин , JHEP 02 (2019) 110 [arXiv:1811.01983] [INSPIRE].
Н. Реммен, Запутанность очистки и многограничные геометрии червоточин , JHEP 02 (2019) 110 [arXiv:1811.01983] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
A. Bhattacharyya, A. Jahn, T. Takayanagi and K. Umemoto, Запутанность очищения во многих системах тела и нарушение симметрии , Phys. Преподобный Летт. 122 (2019) 201601 [arXiv:1902.02369] [INSPIRE].
П. Лю, Ю. Линг, К. Ниу и Ж.-П. Ву, Запутанность очистки в голографических системах , JHEP 09 (2019) 071 [arXiv:1902.02243] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Google ученый
N. Jokela and A. Pönni, Примечания к поперечным сечениям клина запутывания , JHEP 07 (2019) 087 [arXiv:1904. 09582] [INSPIRE].
09582] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
К. Бабаи Велни, М.Р. Мохаммади Мозаффар и М.Х. Vahidinia, Some Aspects of Entanglement Wedge Cross Section , JHEP 05 (2019) 200 [arXiv:1903.08490] [ВДОХНОВЕНИЕ].
К. Бабаи Велни, М.Р. Мохаммади Мозаффар и М.Х. Vahidinia, Эволюция поперечного сечения клина зацепления после глобального гашения , JHEP 08 (2020) 129 [arXiv:2005.05673] [INSPIRE].
Б. Амрахи, М. Али-Акбари и М. Асади, Голографическая запутанность очищения вблизи критической точки , Евро. физ. J. C 80 (2020) 1152 [arXiv:2004.02856] [INSPIRE].
ОБЪЯВЛЕНИЕ Статья Google ученый
Б. Амрахи, М. Али-Акбари и М. Асади, Температурная зависимость запутанности очистки в присутствии химического потенциала , Физ. Ред. D 103 (2021) 086019 [arXiv:2101.03994] [INSPIRE].
Ред. D 103 (2021) 086019 [arXiv:2101.03994] [INSPIRE].
М. Сахраи, М. Дж. Васли, М. Р. М. Мозаффар и К.Б. Velni, Сечение клина запутывания в голографических возбужденных состояниях , JHEP 08 (2021) 038 [arXiv:2105.12476] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
W.-Z. Guo, Запутанность операторов очистки и проектирования в конформных теориях поля , Phys. лат. B 797 (2019) 134934 [arXiv:1901.00330] [INSPIRE].
М. Годрати, Х.-М. Куанг, Б. Ван, К.-Ю. Чжан и Ю.-Т. Чжоу, Связь между голографической запутанностью и сложностью очистки , JHEP 09 (2019) 009 [arXiv:1902.02475] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Д. -Х. Ду, С.-Б. Чен и Ф.-В. Shu, Битовые нити и голографическая запутанность очистки , JHEP 08 (2019) 140 [arXiv:1904.06871] [INSPIRE].
-Х. Ду, С.-Б. Чен и Ф.-В. Shu, Битовые нити и голографическая запутанность очистки , JHEP 08 (2019) 140 [arXiv:1904.06871] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
W.-Z. Guo, Запутанность очистки и распутывания в CFT , JHEP 09 (2019) 080 [arXiv:1904.12124] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Н. Бао, А. Чатвин-Дэвис, Дж. Поллак и Г.Н. Реммен, К битовым нитям Вывод голографической запутанности очищения , JHEP 07 (2019) 152 [arXiv:1905.04317] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Google ученый
Дж. Харпер и М. Хедрик, Битовые нити и голографическая запутанность очистки , JHEP 08 (2019) 101 [arXiv:1906. 05970] [INSPIRE].
05970] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
Х.А. Камарго, Л. Хакл, М.П. Хеллер, А. Ян и Б. Виндт, Запутанность на больших расстояниях очистки и отраженной энтропии в конформной теории поля , Phys. Преподобный Летт. 127 (2021) 141604 [arXiv:2102.00013] [INSPIRE].
Б.С. DiNunno, N. Jokela, J.F. Pedraza and A. Pönni, Квантово-информационные исследования фракционирования заряда в калибровочных теориях с большим N , JHEP 05 (2021) 149[arXiv:2101.11636] [ВДОХНОВЕНИЕ].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
А. Саха и С. Гангопадхьяй, Голографическое исследование запутанности и сложности для смешанных состояний , Phys. Ред. D 103 (2021) 086002 [arXiv:2101. 00887] [INSPIRE].
00887] [INSPIRE].
Ю.-Ю. Лин, Дж.-Р. Sun and Y. Sun, Битовая нить, перегонка запутывания и очищение запутанности , Физ. Ред. D 103 (2021) 126002 [arXiv:2012.05737] [INSPIRE].
П. Лю и Ж.-П. Wu, Запутанность в смешанном состоянии и тепловые фазовые переходы , Phys. Ред. D 104 (2021) 046017 [arXiv:2009.01529] [INSPIRE].
Г. Фу, П. Лю, Х. Гонг, Х.-М. Куанг и Ж.-П. Wu, Голографические информационные свойства для конкретной теории гравитации Эйнштейна-Максвелла-дилатона , Phys. Версия D 104 (2021) 026016 [arXiv:2007.06001] [INSPIRE].
Ю.-ф. Хуанг, З.-Дж. Ши, К. Ниу, К.-у. Чжан и П. Лю, Смешанная запутанность состояний для голографической модели Аксион , евро. физ. J. C 80 (2020) 426 [arXiv:1911.10977] [INSPIRE].
P. Jain and S. Mahapatra, Меры запутывания в смешанном состоянии как проба для заключения , Phys. Ред. D 102 (2020) 126022 [arXiv:2010.07702] [INSPIRE].
Jain and S. Mahapatra, Меры запутывания в смешанном состоянии как проба для заключения , Phys. Ред. D 102 (2020) 126022 [arXiv:2010.07702] [INSPIRE].
М. Годрати, Корреляции смешанных систем в ограничивающих фонах , arXiv:2110.12970 [INSPIRE].
О. Андреев и В.И. Захаров, Потенциалы тяжелых кварков и AdS/КХД , Phys. Ред. D 74 (2006) 025023 [hep-ph/0604204] [INSPIRE].
О. Андреев и В.И. Захаров, Пространственное натяжение струны, тепловой фазовый переход и AdS/КХД , Phys. лат. Б 645 (2007) 437 [hep-ph/0607026] [INSPIRE].
М. Лезги, М. Али-Акбари и М. Асади, Неконформность, сложность подобластей и связывание мезонов , Phys. Ред. D 104 (2021) 026001 [arXiv:2011.11625] [INSPIRE].
Р. Городецкий, П. Городецкий, М. Городецкий и К. Городецкий, Квантовая запутанность , Rev. Mod. физ. 81 (2009) 865 [quant-ph/0702225] [INSPIRE].
Городецкий, М. Городецкий и К. Городецкий, Квантовая запутанность , Rev. Mod. физ. 81 (2009) 865 [quant-ph/0702225] [INSPIRE].
М. Хедрик и Т. Такаянаги, Голографическое доказательство сильной субаддитивности энтропии запутанности , Phys. Ред. D 76 (2007) 106013 [arXiv:0704.3719] [INSPIRE].
T. Nishioka and T. Takayanagi, AdS Bubbles, Entropy and Closed String Tachyons , JHEP 01 (2007) 090 [hep-th/0611035] [INSPI].
И.Р. Клебанов, Д. Кутасов и А. Муруган, Запутанность как проба конфайнмента , Нукл. физ. B 796 (2008) 274 [arXiv:0709.2140] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Статья Google ученый
А. Пакман и А. Парначев, Топологическая запутанность, энтропия и голография , JHEP 07 (2008) 097 [arXiv:0805.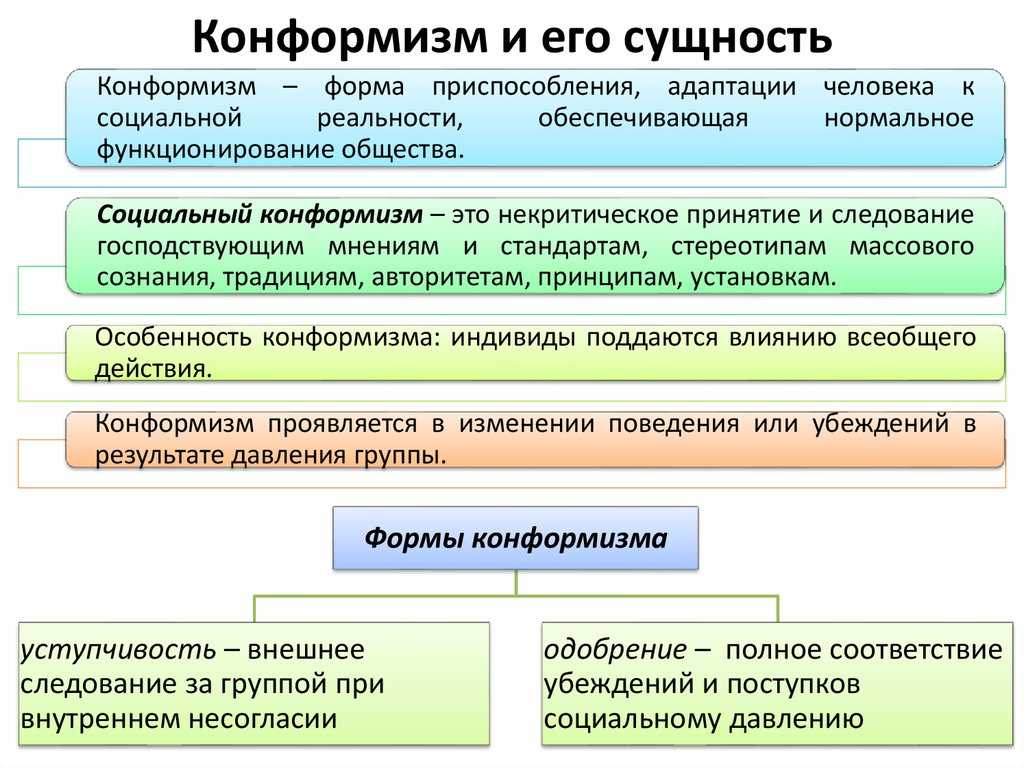 1891] [INSPIRE].
1891] [INSPIRE].
ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
E. Chitambar and G. Gour, Теории квантовых ресурсов , Rev. Mod. физ. 91 (2019) 025001 [arXiv:1806.06107].
Ф.Г.С.Л. Brandão and G. Gour, Обратимая структура для теорий квантовых ресурсов , Phys. Преподобный Летт. 115 (2015) 070503 [arXiv:1502.03149].
шт. Техада, К. Паласуэлос и Х.И. де Висенте, Ресурсная теория запутанности с уникальным многочастным максимально запутанным состоянием , Физ. Преподобный Летт. 122 (2019) 120503 [arXiv:1807.11395].
Б. Гройсман, С. Попеску и А. Винтер, Квантовые, классические и суммарные корреляции в квантовом состоянии , Phys. Ред. A 72 (2005) 032317 [quant-ph/0410091].
H. Bernigau, M.J. Kastoryano and J. Eisert, Законы области взаимной информации для тепловых свободных фермионов , J. Stat. мех. 2015 (2015) P02008 [архив: 1301.5646].
Bernigau, M.J. Kastoryano and J. Eisert, Законы области взаимной информации для тепловых свободных фермионов , J. Stat. мех. 2015 (2015) P02008 [архив: 1301.5646].
MathSciNet МАТЕМАТИКА Статья Google ученый
[PDF] Исследования конформного поведения в сильно взаимодействующих квантовых теориях поля title={Исследования конформного поведения в сильно взаимодействующих квантовых теориях поля}, автор = {Эндрю Д. Гасбарро}, journal={arXiv: Физика высоких энергий — Решетка}, год = {2019} }
- А. Гасбарро
- Опубликовано 1 ноября 2019 г.
- Физика
- arXiv: Физика высоких энергий — решетки
Автор(ы): Гасбарро, Эндрю | Аннотация: В этой диссертации мы представляем работу по непертурбативному описанию различных конформных и почти конформных квантовых теорий поля с использованием комбинации численных и аналитических методов. Ключевой областью интереса является конформное окно четырехмерных калибровочных теорий с фермионами Дирака и его потенциальная применимость за пределами физики стандартной модели. В первой главе мы рассмотрим некоторые моменты истории создания моделей составного бозона бозона Хиггса… 94 $…
В первой главе мы рассмотрим некоторые моменты истории создания моделей составного бозона бозона Хиггса… 94 $…
Бозон Голдстоун рассеяние со светлым составным скалярным скалярным лакомством
- T. Appelquist, R. Brower, O. Witzel
Physics, Education
Physical Review D
- 2022
T.P. Р. К. Брауэр2, К. К. Кушман1, Г. Т. Флеминг1, А. Гасбарро3, ∗ А. Хазенфратц4, Дж. Инголдби5, † С. И. Джин,6 Э. Т. Нил,4 Дж. К. Осборн,6 К. Ребби,2 Э. Rinaldi,7, 8, 9 D. Schaich,10 P.…
ПОКАЗАНЫ 1-10 ИЗ 183 ССЫЛОК
Сорт Byrelevancemost Lintaventupent Recemercesservency
CAN LINEAR SIGMA ОПИСАНИЕ Теории калибровки ходьбы при низких энергиях
- A. Gasbarro
Физика
- 2017
В последних годах. края конформного окна были выполнены с использованием решетчатых методов. Эти исследования показали, что…
Линейная сигма ТЭС для почти конформных калибровочных теорий
- T.
 Appelquist, R. Brower, O. Witzel
Appelquist, R. Brower, O. Witzel Physics
Physical Review D
- 2018
теории при низких энергиях. Работа мотивирована недавними исследованиями решетки калибровочных…
Моделирование решетки с восемью разновидностями фермионов доменных стенок в калибровочной теории SU(3)
- Т. Аппельквист, Р. Брауэр, О. Витцель
Физика
- 2014
Мы изучаем SU(3) калибровочную теорию с Nf=8 вырожденными ароматами легких фермионов в фундаментальном представлении. Используя формулировку фермиона доменной стенки, мы исследуем спектр легких адронов,…
Исследование конформной области калибровочной теории SU(3) с фермионами доменной стенки
- Дж. Ноаки, Г. Коссу, К. Исикава, Ю. Ивасаки, Т. Йоши
Физика
- 2015
Мы исследуем фазовую структуру калибровочной теории SU(3) с $N_f=8$ путем численного моделирования с использованием безмассовых фермионов доменных стенок. неподвижная точка с двенадцатью безмассовыми фермионами и калибровочной группой SU(3)
неподвижная точка с двенадцатью безмассовыми фермионами и калибровочной группой SU(3)
- З. Фодор, К. Холланд, Дж. Кути, С. Мондал, Д. Ногради, К. Вонг
Физика
- 2016
Физический спектр конформных SU(N) калибровочных теорий
- Т. Аппельквист, Франческо Саннино
Физика
- 1999
связь близка, но выше критического значения для конформного фазового перехода. Мы используем дисперсионные соотношения,…
На пути к минимальной реализации легкого композита Хиггса
- З. Фодор, К. Холланд, Дж. Кути, С. Мондал, Д. Ногради, К. Вонг
Физика. Расширение предыдущих…
Монте-Карло Исследование квантованной SU(2) Калибровочной теории
- М.
 Кройтца
Кройтца Физика
- 1980
Используя методы Монте-Карло для калибровочных полей2, мы оцениваем интегралы по траекториям2 . Процедура регуляризации Вильсона на решетке до 10/sup 4/ узлов контролирует ультрафиолетовые расходимости. Наши…
Фазовая диаграмма SU(2) с двумя ароматами динамически сопряженных кварков
- С. Каттералл, Дж. Гидт, Франческо Саннино, Дж. Шнайбл
Физика
- 2008 9003 Отчет о численном моделировании 9103 9103 Калибровочная теория решетки SU(2) с двумя ароматами легких динамических кварков в сопряженной калибровочной группе. Динамика этой теории считается очень…1051
- З. Фодор, К. Холланд, Дж. Кути, С. Мондал, Д. Ногради, К. Вонг
Физика
- 2015
Аннотация. теория, связанная с Nf = 2 ароматами безмассовых фермионов Дирака в 2-индексно-симметричном (секстетном) представлении. Эта модель состоит из…
Континуальные и решетчатые подходы к инфракрасному поведению конформных и квазиконформных калибровочных теорий: 8–12 января 2018 г.

Автор: Джанелл Роджерс, 8 мая 2017 г. в мастерских
Организаторы Томас Рыттов и Роберт Шрок
Список участниковРасписаниеПросмотр видео
Эволюция асимптотически свободной калибровочной теории от больших евклидовых импульсов в ультрафиолетовом (УФ) диапазоне к малым масштабам импульсов в инфракрасном (ИК) диапазоне имеет фундаментальное теоретико-полевое значение. Эволюция калибровочной связи описывается бета-функцией ренормализационной группы. Особый интерес представляют свойства теории в ИК-нуле этой бета-функции, где теория масштабно-инвариантна и считается конформно-инвариантной. Рассмотрим векторную калибровочную теорию с калибровочной группой G и набором Nf безмассовых фермионов, преобразующихся в соответствии с представлением R группы G. Существует диапазон Nf такой, что теория течет из UV в деконфинированную кирально-симметричную конформную неабелеву кулоновскую фаза (NACP), связанная с IR-нулем бета-функции, которая является IR-неподвижной точкой (IRFP) ренормализационной группы.
 Напротив, для малых Nf теория демонстрирует конфайнмент со спонтанным нарушением киральной симметрии в ИК. Хотя для суперсимметричных калибровочных теорий был получен ряд точных результатов, многие вопросы все еще остаются без ответа и исследуются в настоящее время для несуперсимметричных калибровочных теорий; например, (i) каково минимальное значение Nf (в теории с заданными G и R), при котором теория эволюционирует к NACP в инфракрасном диапазоне? (ii) каковы размеры масштабирования различных физических операторов в IRFP?
Напротив, для малых Nf теория демонстрирует конфайнмент со спонтанным нарушением киральной симметрии в ИК. Хотя для суперсимметричных калибровочных теорий был получен ряд точных результатов, многие вопросы все еще остаются без ответа и исследуются в настоящее время для несуперсимметричных калибровочных теорий; например, (i) каково минимальное значение Nf (в теории с заданными G и R), при котором теория эволюционирует к NACP в инфракрасном диапазоне? (ii) каковы размеры масштабирования различных физических операторов в IRFP?В последние несколько лет проводилась интенсивная программа исследований, чтобы лучше понять свойства этой эволюции и результирующую конформную теорию поля. Эта программа включала в себя как континуальные подходы (например, разложение в ряд и методы конформного бутстрапа), так и моделирование калибровочной теории решетки. Также интересно исследовать теории, демонстрирующие медленно текущую связь, связанную с приближенным IRFP и, следовательно, квазиконформным поведением.
 Цель этой конференции — собрать вместе экспертов, работающих над всеми этими подходами к конформной и квазиконформной теориям поля, чтобы они могли представить свои новые результаты, узнать о работе других групп, обменяться идеями и, надеюсь, получить новые результаты. .
Цель этой конференции — собрать вместе экспертов, работающих над всеми этими подходами к конформной и квазиконформной теориям поля, чтобы они могли представить свои новые результаты, узнать о работе других групп, обменяться идеями и, надеюсь, получить новые результаты. .- Понедельник, 8 января
- вторник, 9 января
- Среда, 10 января
- Четверг, 11 января
- Пятница, 12 января
Время Титул Ведущий Местоположение 9:00 Приветствие от организаторов Приветственные речи SCGP 102 9:30 Световые дилатоны, самозванцы и связь между масштабной и конформной инвариантностью Бенджамин Гринштейн SCGP 102 10:30 Перерыв на кофе н/д Кафе 11:00 Легкий составной скаляр в калибровочной теории решетки SU(3) с Nf = 8 фермионами в фундаментальном представлении Итан Нил SCGP 102 12:00 Обед н/д Кафе 13:30 Нарушение универсальности фермионов в конформной неподвижной точке Анна Хазенфрац SCGP 102 14:30 Перерыв на кофе н/д кафе 15:00 Изучение сигналов конформности в теориях со многими ароматами: отчет LatKMI
.
Энрико Ринальди SCGP 102 Время Титул Ведущий Местоположение 9:00 Графики фундаментальных взаимодействий: гарантированная безопасность и фундаментальная композитная динамика Франческо Саннино SCGP 102 10:00 Перерыв на кофе н/д кафе 10:30 Сигма Частица или Дилатон? Юлий Кути SCGP 102 11:30 Обед н/д кафе 13:00 Еженедельное обсуждение SCGP: Прогресс в исследованиях конформных и квазиконформных калибровочных теорий Джордж Флеминг SCGP 102 14:00 Решетчатые модели составного Хиггса Dynamics Клаудио Пика SCGP 102 15:00 Перерыв на кофе н/д Кафе 15:30 Вычисления высшего порядка в инфракрасных фиксированных точках в калибровочных теориях Роберт Шрок SCGP 102 Время Титул Ведущий Местоположение 9:00 CMS ищет резонансы, затухающие до WW/WZ Минакши Нараин SCGP 102 10:00 Перерыв на кофе н/д Кафе 10:30 ATLAS ищет резонансы, затухающие до WW/WZ Инес Очоа SCGP 102 11:30 Феноменология составного бозона Хиггса – векторные дибозонные резонансы Кеннет Лейн SCGP 102 12:30 Обед н/д Кафе 14:00 Независимые от схемы расчеты конформного инфракрасного поведения в несуперсимметричных и суперсимметричных калибровочных теориях Томас Рыттов SCGP 102 15:00 Перерыв на кофе н/д Кафе 15:30 Инфракрасное поведение калибровочной теории SU(2) с фермионами Кимо Туоминен SCGP 102 18:00 Конференц-банкет Кафе Время Титул Ведущий Местоположение 9:00 Перенормируемая и асимптотически свободная квантовая гравитация Д.  Р. Т. Джонс
Р. Т. ДжонсSCGP 102 10:00 Перерыв на кофе н/д Кафе 10:30 Анализ с фиксированной точкой для критического анализа Бэнкса-Закса и моделей графена Джон Грейси SCGP 102 11:30 Построение решетки для конформной теории поля на криволинейных римановых многообразиях Ричард Брауэр SCGP 102 12:30 Обед н/д Кафе 14:00 Проект экзафлопсных вычислений в США и решетчатый поиск конформности Мэйфэн Линь SCGP 102 15:00 Перерыв на кофе н/д н/д 15:30 Максимально суперсимметричные теории на решетке Дэвид Шайх SCGP 102 16:30 Анализ теории эффективного поля Дилатона для данных решетки Джеймс Инголдби SCGP 102 Время Титул Ведущий Местоположение 9:00 Инфракрасное излучение (2 + 1)-мерной КХД: конфайнмент, конформность и нарушение симметрии Зоар Комаргодски SCGP 102 10:00 Перерыв на кофе н/д Кафе 10:30 Цепочки квантовых спинов и теория чисел Владимир Корепин SCGP 102 11:30 Конформная теория поля, методы начальной загрузки и приложения Далимил Мазак SCGP 102 12:30 Обед н/д Кафе 14:00 Новые результаты в конформных теориях поля Синань Чжоу SCGP 102 15:00 Заключительные замечания SCGP 102 15:30 Чаепитие н/д 515 Количественная симплектическая геометрия: 8–12 мая 2017 г.

- М.
 Appelquist, R. Brower, O. Witzel
Appelquist, R. Brower, O. Witzel Кройтца
Кройтца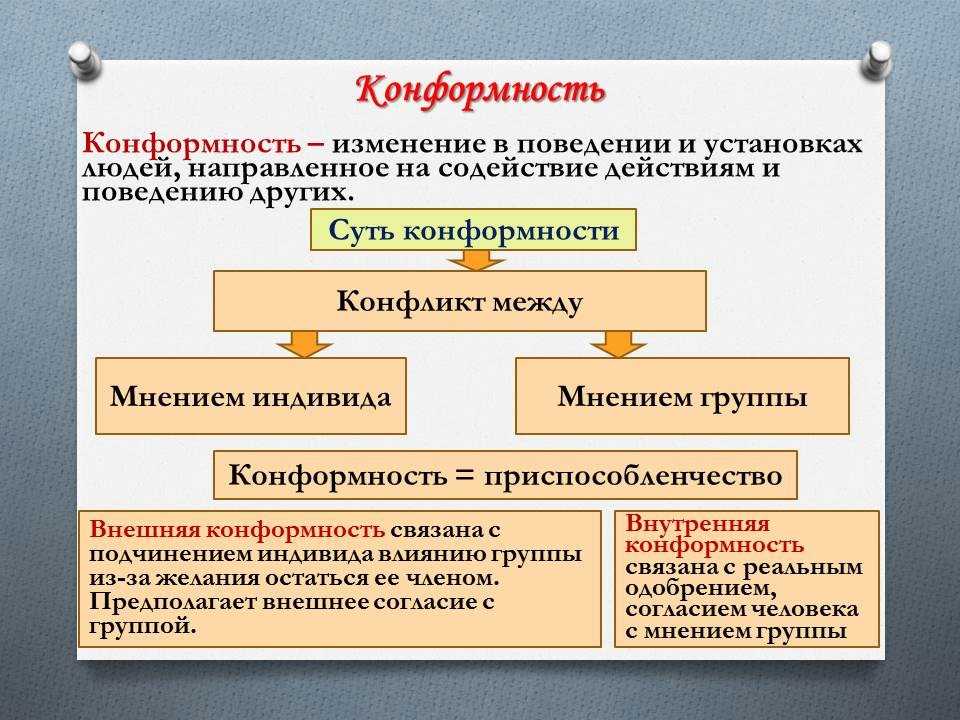
 Напротив, для малых Nf теория демонстрирует конфайнмент со спонтанным нарушением киральной симметрии в ИК. Хотя для суперсимметричных калибровочных теорий был получен ряд точных результатов, многие вопросы все еще остаются без ответа и исследуются в настоящее время для несуперсимметричных калибровочных теорий; например, (i) каково минимальное значение Nf (в теории с заданными G и R), при котором теория эволюционирует к NACP в инфракрасном диапазоне? (ii) каковы размеры масштабирования различных физических операторов в IRFP?
Напротив, для малых Nf теория демонстрирует конфайнмент со спонтанным нарушением киральной симметрии в ИК. Хотя для суперсимметричных калибровочных теорий был получен ряд точных результатов, многие вопросы все еще остаются без ответа и исследуются в настоящее время для несуперсимметричных калибровочных теорий; например, (i) каково минимальное значение Nf (в теории с заданными G и R), при котором теория эволюционирует к NACP в инфракрасном диапазоне? (ii) каковы размеры масштабирования различных физических операторов в IRFP? Цель этой конференции — собрать вместе экспертов, работающих над всеми этими подходами к конформной и квазиконформной теориям поля, чтобы они могли представить свои новые результаты, узнать о работе других групп, обменяться идеями и, надеюсь, получить новые результаты. .
Цель этой конференции — собрать вместе экспертов, работающих над всеми этими подходами к конформной и квазиконформной теориям поля, чтобы они могли представить свои новые результаты, узнать о работе других групп, обменяться идеями и, надеюсь, получить новые результаты. .
 Р. Т. Джонс
Р. Т. Джонс