Математическая логика : Формальная логика
Формальная логика — это конструирование и исследование правил преобразования высказываний, которые сохраняют истинное значение вне зависимости от содержания входящих в эти высказывания понятий.
В конце XIX-начала XX века формальная логика была обособленным разделом философии, отдельным направлением логики конца. В настоящее время термин формальная логика выступает в качестве синонимии символической или математической логики.
Иммануил Кант
Термин «формальная логика» появился в глубокой древности. Был введен Аристотелем. Позднее, Кант в «Критике чистого разума» определял главным направлением формальной логики — форму понятий, а не их содержание. Область интересов формальной логики — это наука, предельно точно и строго излагающая и доказывающая только формальные правила всякого мышления.
В противовес формальной логике Кант выдвигал содержательную, так называемую трансцендентальную логику, которая положила начало учению о категориях.
Представители так называемой «логистики» в конце XIX-начале XX века сформировали общество формалистов конца, которые тесно связывали формальность логики с выделением значений истинности высказываний при переносе их из естественного языка в символические обозначения. Основной целью исследований логистиков было обоснование математических знаний с помощью формальной логики. Весомый вклад в это направление внесли такие выдающиеся математики, как Д. Гильберт, Кутюр, Б. Рассел.
По представлению логистиков, под формой понималось выражение, в котором по крайней мере одна переменная входит таким образом, что это выражение превращается в истинное или ложное высказывание после того, как на место этой переменной подставляется нечто.
В этом заключалось главное отличие формальной логики от других дисциплин, которые также занимались изучением формы, будь-то лингвистика, арифметика, геометрия или алгебра. Таким образом, к формальной логике были отнесены все разделы логики, которые стало возможным формализовать в символические знаки. Эти символы были разработаны известными математиками и логиками О. де Морганом, Дж. Булем, Дж. Пеано, Г. Фреге, Расселом и другими.
Эти символы были разработаны известными математиками и логиками О. де Морганом, Дж. Булем, Дж. Пеано, Г. Фреге, Расселом и другими.
Благодаря реконструкции, было определено, что логика имеет дело с языковым мышлением, в котором группы знаков, связанные между собой определенным образом и определенными законами, замещают реальные объекты, а также и друг друга в отношении к действиям. Это выглядит следующим образом:
объективное содержание ────────────── знаки языка
связь значения
Формальная логика возможна лишь в том случае, когда в качестве замещаемого содержания выступают не объекты действия, а знаки, которые образуют замкнутые оперативные системы. Основной целью методов формальной логики является определение параллели формы и содержания мышления.
Символизация формальной логики сделала неизбежным превращение ее в одну из важнейших математических дисциплин.
Поделиться ссылкой
Тест по логике, 25 вопросов с ответами
administrator
?Логика — это…
!наука об умозаключениях и доказательствах
!наука о правилах мышления
!наука о формах и законах правильного познания
*наука о формах и законах правильного мышления
?Формальная логика появилась…
*в античности
!в Средние века
!в Новое время
!в эпоху Возрождения
?Традиционная логика является…
*аристотелевской
!математической
!символической
!современной
?Создателем логики считается древнегреческий философ…
!Аркесилай
!Пифагор
*Аристотель
!Анаксимен
!Антисфен
!Анаксагор
!Аристипп
?С точки зрения формальной логики высказывание <b>«Все Снегурочки — это геометрические фигуры»</b>…
!представляет собой абсурд
!лишено всякого смысла
!является фантастическим
!выражает пример классической нелепости
?Математическая или символическая логика появилась…
!в XVII в
!в Средние века
*в XIX в
!тогда же, когда и традиционная логика
!в середине XX в
!в начале нашей эры
?Интуитивная логика — это…
!теоретические знания, оставшиеся у человека после изучения курса логики в школе или вузе
!полное искажение теоретической логики
*стихийно сформированное в процессе жизненного опыта знание форм и принципов правильного мышления
!ничто из перечисленного
!совершенное незнание законов правильного мышления, приводящее любое рассуждение к многочисленным ошибкам и ложным выводам
?Древнегреческие философы, которые изобретали разнообразные приемы нарушения логических законов с целью доказать все, что угодно, — это…
!киники
!стоики
!пифагорейцы
*софисты
!милетцы
!эпикурейцы
?Понятие — это…
!некий предмет
!истинный тезис
!слово или словосочетание
*форма мышления
?Любое понятие имеет…
*объем
!фигуру
!размер
!величину
?Любое понятие выражается в форме…
!простого предложения
*слова или словосочетания
!связного текста
!сложного предложения
?Содержание понятия — это…
!совокупность всех объектов, которые оно охватывает
!слово или словосочетание, в котором оно выражается
!объект, который оно обозначает
!то суждение, в котором оно может употребляться
*наиболее важные признаки того объекта, который оно выражает
?Объем понятия — это совокупность…
*объектов, охватываемых этим понятием
!всех рассуждений, в которых оно употребляется
!всех значений, которые могут в него вкладываться
!наиболее важных признаков того объекта, который оно обозначает
!всех слов или словосочетаний, которые могут его выражать
!всех людей, которым известно это понятие
*единичное
!нулевое
!физическое
!общее
!астрономическое
?<b>«Глупость»</b> — это понятие…
*абстрактное
!отвлеченное
!конкретное
!отрицательное
!психологическое
?<b>«Неряха»</b> — это понятие…
!нейтральное
!пустое
*положительное
!собирательное
!отрицательное
?Понятию <b>«Созвездие Ориона»</b> соответствует логическая характеристика…
*ни одна из перечисленных
!единичное, несобирательное, конкретное, положительное
!общее, собирательное, конкретное, положительное
!единичное, собирательное, абстрактное, положительное
!единичное, собирательное, конкретное, отрицательное
!нулевое, собирательное, абстрактное, положительное
?Логической характеристике <b>«общее, собирательное, конкретное, положительное»</b> соответствует понятие…
!музыкальный коллектив
!семья
*все перечисленные
!набор цветных карандашей
!ни одно из перечисленных
!10 класс «А»
!букет роз
!сборная России
?Понятие <b>«умный человек»</b> является…
!не имеющим ни объема, ни содержания
*неясным по содержанию и нерезким по объему
!ясным по содержанию и нерезким по объему
!неясным по содержанию и резким по объему
!ясным по содержанию и резким по объему
?Понятие, большее по объему называется…
!видовым
!нулевым
*родовым
!общим
!широким
?Понятия <b>«звезда»</b> и <b>«созвездие»</b> находятся в отношениях…
!деления
!подчинения
!исключения
!пересечения
*соподчинения
!определения
?Отношения между понятиями изображаются…
!круговыми схемами Бойлера
*круговыми схемами Эйлера
!круговыми схемами Аристотеля
!круговыми схемами Пейджера
?Отношения между понятиями <b>«точка»</b>, <b>«прямая»</b>, <b>«плоскость»</b>, <b>«пространство»</b> изображаются следующей схемой: <a name=»i03560″></a><img class=»иллюстрация» src=».

!3)
!1)
*4)
!5)
!2)
?Данной схеме <a name=»i03575″></a><img class=»иллюстрация» src=»../../files/Ris_TK-1_2.gif» border=»0″> соответствует следующая группа понятий:
!известный футболист; известный хоккеист; молодой человек; старый человек
*известный футболист; футболист; негр; китаец
!известный спортсмен; человек; известный человек; спортсмен
!футболист; баскетболист; спортсмен; человек
?Данной схеме <a name=»i03588″></a><img class=»иллюстрация» src=»../../files/Ris_TK-1_3.gif» border=»0″> не соответствует следующая группа понятий:
*растение; дерево; сосна
!рыба; хищник; акула
!млекопитающее; хищник; тигр
!русский писатель;знаменитый человек; Лев Толстой Учебные тесты с ответами
Рекомендуемые посты
Тест по педагогической психологии Тест по конфликтологии Тест по экономике Тест по правовым основам государственной службы
Формальная логика | Определение, примеры, символы и факты
Альфред Норт Уайтхед
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См. весь связанный контент →
весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины.
Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (вывод) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что утверждение было бы непоследовательным или внутренне противоречивым. предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно различных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-то специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны ли посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода состоят в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он повлечет за собой логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-то специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны ли посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода состоят в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он повлечет за собой логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every
Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее.
Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее.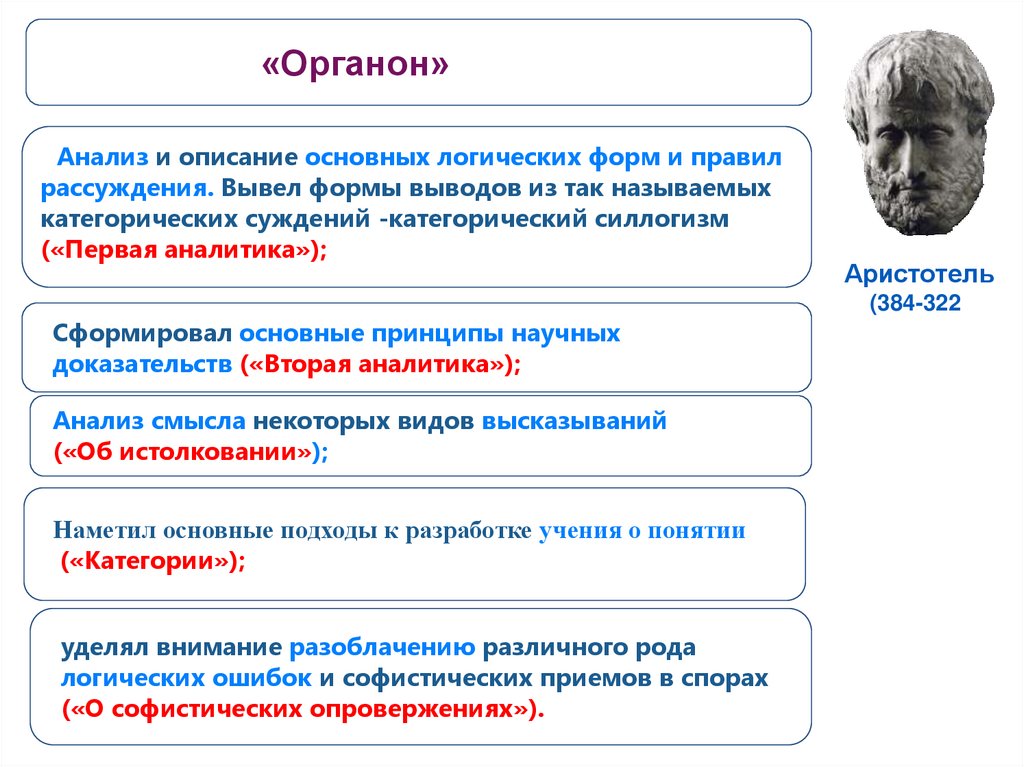 Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что системы логики оказываются обладающими определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны.
Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что системы логики оказываются обладающими определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.
В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.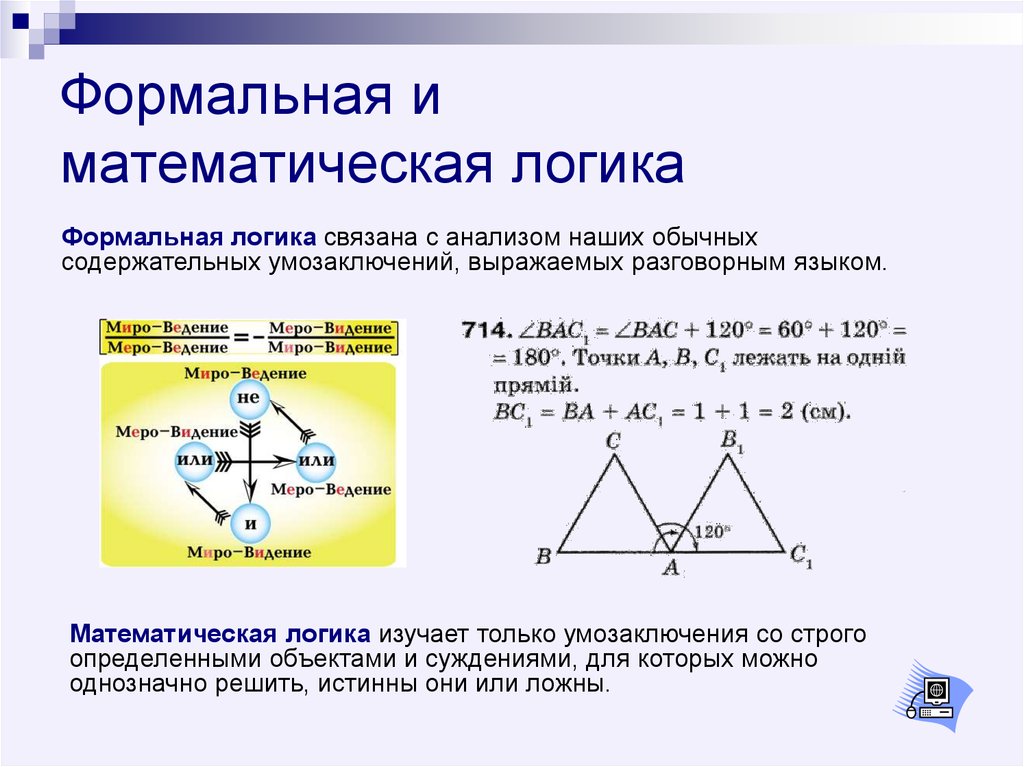 мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.
мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или умственными построениями?
Формальная логика | Определение, примеры, символы и факты
Альфред Норт Уайтхед
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См. весь связанный контент →
весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивный. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (вывод) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что утверждение было бы непоследовательным или внутренне противоречивым. предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно различных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-то специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны ли посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода состоят в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он повлечет за собой логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-то специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны ли посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода состоят в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он повлечет за собой логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее.
Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что системы логики оказываются обладающими определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны.
Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что системы логики оказываются обладающими определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.
В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.