как найти общий знаменатель
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
Скопировать ссылку
Что такое общий знаменатель?
Кроме понятия «общий знаменатель«, есть еще такое понятие как — «Наименьший общий знаменатель (НОЗ)» — это… тоже самое, что и «НОК». Поэтому, мы не будем это разбирать здесь второй раз.Но что такое общий знаменатель простыми словами?
Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗПример общего знаменателя :
Для того, чтобы понять, «что такое общий знаменатель» нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение — «+».
Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.
1*32*3 + 1*23*2 =
36 + 26 =
3 + 2 6 =
5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос — «в каком случае ноз двух дробей будет являться произведением знаменателей? «, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Скопировать ссылку
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
AB + CD =A*DB*D + C*BD*B =
A*D + C*B DB
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.

Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный «НОК» — только может называться по другому…смайлы
Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»
Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:
8 = 2 * 2 * 2Ниже раскладываем меньший знаменатель :
6 = 2 * 3Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
8 * 3 = 24Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
10 = 2 * 5Раскладываем меньший знаменатель :
4 = 2 * 2Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
10 * 2 = 20Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Скопировать ссылку
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находить общий знаменатель дробей онлайн!Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
20 = 2 * 2 * 5Раскладываем на множители второй знаменатель :
8 = 2 * 2 * 2Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
20 * 2 = 40Итого получаем их общий знаменатель 40.
Переходим к нахождению общего знаменателя онлайн
Открываем наш калькулятор.Вводим первый знаменатель 20.
Нажимаем кнопку «НОК»
Набираем второй знаменатель 8.
Нажимаем равно — «=»
Получаем результат нахождения общего знаменателя онлайн :
Далее вы можете сравнить два результата нахождения общего знаменателя.Скопировать ссылку
Что такое
наименьший общий знаменатель? Разница между «общим знаменателем«(1) и «наименьшим общим знаменателем«(2) в том, что первое может быть бесконечное количество… а второе «НОЗ», только один!Но, что же такое «наименьший общий знаменатель»
НОЗ — это абсолютно тоже самое, что и «НОК».Определение, что же такое «наименьший общий знаменатель»
Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Скопировать ссылку
Формула наименьшего общего кратного
Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
10 = 2 * 5Разложим второй знаменатель на множители :
6 = 2 * 3Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
10 * 3 = 30 Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Скопировать ссылку
Как найти
наименьший общий знаменатель на калькуляторе Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12Прежде чем приступать к нахождению «нок» двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
18 = 2 * 3 * 3Раскладываем меньшее число на множители :
12 = 2 * 2 * 3Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.
Умножаем большее число на 2.
18 * 2 = 36 Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
Теперь проверим правильность нахождения «нок» на калькуляторе.
Открываем калькулятор.
Набираем первое число – пусть это будет число 12
Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.
И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
Скопировать ссылку
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса — давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать… перебором…, а потом подтвердим наше решение через «НОК».
5 — не подходит — не делится на 3.
10 — не подходит — не делится на 3.
15 — не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 — не подходит, не делится на 2.
30 — подходит, делится на все без остатка.
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель — 2.
Нажимаем кнопку — «НОК».
Набираем второй знаменатель — 3.
Нажимаем равно — «=».
Далее опять нажимаем — «НОК».
Набираем третий знаменатель — 6.
Нажимаем равно — «=».
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
Скопировать ссылку
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.
Выше были рассмотрены варианты нахождения общего знаменателя дробей с разными знаменателями.Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.
Теги :
как найти общий знаменатель
как найти наименьший общий знаменатель
как найти общий знаменатель дробей с разными
как найти общий знаменатель у дробей
как найти наименьший общий знаменатель дробей
найдите общий знаменатель дробей
найти общий знаменатель онлайн
найти общий знаменатель чисел
найдите наименьшее общее кратное знаменателей
как быстро найти общий знаменатель
как найти общий знаменатель дробей класс
как найти наибольший общий знаменатель
найти общее кратное знаменателей дробей
найдите наименьший общий знаменатель дробей
найти общий знаменатель дробей онлайн
найдите наименьший общий знаменатель дробей
как найти общий знаменатель при сложении
калькулятор найти общий знаменатель
как найти общий знаменатель двух дробей
как быстро найти общий знаменатель у дроби с большим знаменателем
общий знаменатель дробей это такое простыми словами
общий знаменатель трех дробей онлайн
решение общего знаменателя
Общий знаменатель дробей онлайн | umath.
 ru
ruКалькулятор приводит несколько дробей к общему знаменателю. Просто введите дроби и получите подробное решение и ответ. Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.
Как привести дроби к общему знаменателю?
Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к общему знаменателю.
Рассмотрим алгоритм приведения дробей к общему знаменателю. Пусть даны две дроби и Чтобы привести их к общему знаменателю, надо:
- Найти наименьшее общее кратное знаменателей дробей. Пусть оно равно .
- Числитель и знаменатель первой дроби умножить на число
- Числитель и знаменатель второй дроби умножить на число
В результате мы получим две дроби со знаменателем, равным
Пример. Привести к общему знаменателю дроби и
Привести к общему знаменателю дроби и
Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым знаменателем.
Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 = 24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.
Приводим к общему знаменателю первую дробь:
Приводим к общему знаменателю вторую дробь:
Общий знаменатель трёх дробей
Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен алгоритму для двух дробей.
- Находим наименьшее число , которое делится на знаменатели всех дробей (наименьшее общее кратное знаменателей всех дробей). Найденное число будет новым знаменателем.
- Домножаем числитель и знаменатель каждой дроби на частное
В результате знаменатели всех дробей будут равны .
Чтобы разобраться лучше, рассмотрим пример.
Пример. Привести к общему знаменателю три дроби и
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12. Число 12 будет новым знаменателем.
Чтобы знаменатели дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби — на 3 = 12:4, а числитель и знаменатель третьей дроби — на 2 = 12:6.
Приводим дроби к общему знаменателю и получаем:
Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число, которое будет новым знаменателем.
Как найти общие кратные числа
В этой статье мы рассмотрим мир кратных. Однако основное внимание уделяется наименьшему общему кратному. Вся информация, необходимая для понимания этой концепции, содержится в этой статье. Мы также приводим примеры, которые помогут вам быстро освоить арифметику!
Однако основное внимание уделяется наименьшему общему кратному. Вся информация, необходимая для понимания этой концепции, содержится в этой статье. Мы также приводим примеры, которые помогут вам быстро освоить арифметику!
Что такое кратность?
, кратное , — это число, которое можно разделить на две части без остатка. Детям может быть полезно думать об этом как о числе в расписании другого числа. Например, 24 кратно 12, а также 1, 2, 3, 4, 6, 8 и 24. Множители и кратные связаны. Например, 4 — это коэффициент 12, а 12 — кратное 4.
Что такое общее кратное?
Наименьшее общее кратное (НОК) также известно как наименьший общий делитель (НОД). НОК — это наименьшее положительное целое число , которое делится без остатка как на a, так и на b для двух целых чисел, сокращенно НОК (a,b). Например, НОК(2,3) равно 6, а НОК(6,10) равно 30.
Наименьшее общее кратное (НОК) двух или более чисел — это наименьшее число, которое делится на все числа в равной степени. набор.
набор.
В чем смысл LCM?
Наименьшие общие кратные полезны при сложении или вычитании дробей или при сравнении дробей одного номинала . Например, чтобы вычислить 3/5 + 1/6, вам нужно вычислить наименьшее общее кратное 5 и 6, чтобы определить общий знаменатель (30). Затем дроби можно преобразовать в 18/30 + 5/30 = 23/30.
Как проще всего найти общие кратные?
Чтобы определить общие кратные группы чисел, вы должны сначала перечислить все кратные числа, а затем начать выбирать общие кратные .
Перечислив их кратные, вы можете быстро найти частые кратные двух чисел. Вы можете указать или обвести кратные, которые являются общими для обоих чисел, после перечисления кратных указанных целых чисел. Это общие кратные двух чисел.
В качестве примера найдем типичные числа, кратные 2 и 5:
- 2, 4, 6, 8, 10 , 12, 14, 16, 18, 20 и так далее кратны двум.
- 5, 10 , 15, 20 , 25, 30,… все кратны пяти.

В результате популярные числа, кратные 2 и 5, включают: 10, 20,… и так далее. Стоит отметить, что все общие кратные делятся на 2 или 5.
НОК множества
Вы можете определить общие кратные трех чисел, используя тот же метод, который вы использовали для нахождения общие кратные двух чисел. Общие кратные — это кратные, которые являются общими для трех чисел.
Давайте посмотрим, каковы наиболее распространенные числа, кратные 10, 20 и 30. Есть несколько кратных, которые преобладают в кратных 10 и 20, но не в кратных 30. В результате они не могут рассматриваться как кратные всем трем числам. Вы должны выбрать кратные, которые являются общими для всех трех значений.
Чтобы найти их общие кратные, составьте список кратных 10, 20 и 30.
- 10, 20, 30, 40, 50, 600007 120 и т. д. кратны десяти.
- 20, 40, 60 , 80, 100, 120 , 140, 160, 180 и т. д. кратны 20.
- 30, 60 , 90, 120 , 150, 180, 210 и т.
 д. — все числа кратны 30.
д. — все числа кратны 30.
60 и 120 обычно кратны 10, 20 и 30 и т. д.
Каковы свойства наименьшего общего кратного (НОК)?
Наименьшее общее кратное — это наименьшее число, которое можно разделить на указанные числа. Различные подходы, такие как метод перечисления, метод простой факторизации и метод деления, могут использоваться для вычисления наименьшего общего кратного (НОК) чисел.
Вот свойств НОК :
- Наименьшее общее кратное (НОК) двух или более чисел не может быть меньше одного из них. НОК 3, 8 и 12 равен 24, что не меньше любого из заданных значений.
- НОК числа — это большее число, если оно является множителем другого числа. НОК 8 и 16 — это, например, само число 16.
Как найти наименьшее общее кратное числа?
Метод общих кратных
Для этого метода перечисляйте кратные каждого числа, пока хотя бы одно из них не появится во всех списках. Затем во всех списках найдите наименьшее общее число. Это ЛКМ!
Это ЛКМ!
Например: LCM(6,7,21)
- Давайте сначала перечислим числа, кратные 6:
6, 12, 18, 24, 30, 36, 42 , 48, 54, 60, 72,
- Далее, давайте проделаем то же самое для 7:
7, 14, 21, 28, 35, 42 , 56, 63
- Наконец, нам нужно перечислить кратные 21:
21, 42 , 62…
Найдите наименьшее число из каждого списка. Он выделен жирным шрифтом выше.
В результате НОК(6, 7, 21) равно 42.
Вот еще один пример. Давайте воспользуемся методом листинга, чтобы найти LCM 3 и 7.
- 3, 6, 9, 12, 15, 18, 21 , 24, 27, 30, 33, 36, 39, 42 ,… все кратны трем.
- 7, 14, 21 , 28, 35, 42 , 49 и т. д. кратны семи.
Типичные числа, кратные 3 и 7, равны 21, 42 и т. д., как видно. Наименьшее кратное среди этих общих кратных равно 21. Поскольку это наименьшее из всех общих кратных, НОК 3 и 7 равен 21. В результате НОК 3 и 7 равен 21.
Факторизация простых чисел
Для этого метода необходимо определить все простые множители числа. Перечислите все найденные простые числа в том порядке, в котором они встречаются чаще всего для каждого заданного числа. Чтобы найти наименьшее общее кратное, напишите список простых множителей и перемножьте их.
Нахождение простой факторизации как a, так и b дает LCM(a,b). Используйте ту же процедуру, чтобы найти LCM для более чем двух чисел.
Например, для LCM(12,30) мы находим:
- Простые множители 12 = 2, 2, 3
- Простые множители 30 = 2, 3, 5
Возьмем сумму всех простых чисел, найденных в том порядке, в котором они встречаются чаще всего: 2 × 2 × 3 × 5 = 60
Следовательно, НОК(12,30) = 60
Наибольший общий делитель
Для этого метода мы используем метод наибольшего общего фактора. Во-первых, что такое коэффициент? Множитель — это число, которое получается при делении двух чисел без остатка. В этом контексте множитель также известен как делитель. Наибольшее число, разделяемое всеми факторами, является наибольшим общим делителем двух или более чисел.
В этом контексте множитель также известен как делитель. Наибольшее число, разделяемое всеми факторами, является наибольшим общим делителем двух или более чисел.
Формула для расчета НОК набора чисел с использованием наибольшего общего делителя (НОК): НОК(a,b) = (a×b)/НОК(a,b)
Вот пример . Найти LCM(6,10)
- Факторы 6: 1, 2 , 3, 6
- Факторы 10: 1, 2 , 5, 10
GCF(6,10) = 2
Рассчитайте (6×10)/2 = 60/2 = 30, используя НОК по алгоритму GCF.
В результате НОК(6,10) = 30.
Метод пирога
Другим методом является метод пирога, который использует деление для нахождения НОК. Поскольку это простое деление, люди считают подход с использованием торта или лестницы самым быстрым и простым способом найти LCM.
Метод пирога также известен как метод лестницы, метод умножения, метод ящика, метод факторного ящика или метод ярлыков сетки. Блоки и сетки могут отличаться по внешнему виду, но они всегда используют простое деление для нахождения НОК.
Найдите LCM (10, 12, 15, 75)
- Сделайте слой торта со своими номерами (строка)
10 12 15 75
- Разделите номера слоев на простое число, которое делится без остатка на два или более номеров слоев, затем перенесите результат на следующий слой.
2: 10 12 15 75
5 6 – –
- Если какое-либо целое число в слое не делится на равные части, просто опустите его.
2: 10 12 15 75
5 6 15 75
- Продолжайте разбивать слои торта на простые числа. Вы закончите, когда больше не останется простых чисел, которые можно поровну разделить на два или более числа.
2: 10 12 15 75
3 5 6 15 75 07 5: 5 2 5 25
1 2 1 5
НОК представляет собой произведение простых чисел в левом столбце и нижней строке (жирный шрифт)
НОК = 2 x 3 x 5 x 2 x 5 9 0003
= 300
Самый низкий общее кратное 10, 12, 15 и 75 равно 300!
Нужна помощь по математике?
Репетиторские услуги Tutorax на дому и онлайн могут быть полезны учащимся начальной, средней, старшей школы и даже университета. Ряд предметов, в том числе математика, английский язык, география, химия и французский язык, доступны для репетиторства. Наши преподаватели могут помочь вам с домашними заданиями, подготовкой к экзаменам и поддержкой в классе, среди прочего.
Ряд предметов, в том числе математика, английский язык, география, химия и французский язык, доступны для репетиторства. Наши преподаватели могут помочь вам с домашними заданиями, подготовкой к экзаменам и поддержкой в классе, среди прочего.
Найти репетитора
Что такое наибольший общий делитель и наименьшее общее кратное?
TranscriptFAQsFact SheetPractice
Привет! Добро пожаловать в это видео, посвященное наименьшему общему кратному и наибольшему общему множителю!
Как вы знаете, бывают случаи, когда нам приходится алгебраически «настраивать» то, как выглядит число или уравнение, чтобы продолжить нашу математическую работу. Для этого мы можем использовать наибольший общий делитель и наименьшее общее кратное. наибольший общий делитель (НОК) — это наибольшее число, являющееся делителем двух или более чисел, а наименьшее общее кратное (НОК) — это наименьшее число, кратное двум или более числам.
Чтобы понять, насколько полезны эти понятия, давайте рассмотрим сложение дробей. Прежде чем мы сможем складывать дроби, мы должны убедиться, что знаменатели одинаковы, создав эквивалентную дробь:
\(\frac{2}{3}+\frac{1}{6} \rightarrow \frac{2 }{3} \times \frac{2}{2}\)\(+\frac{1}{6} \rightarrow \frac{4}{6} +\frac{1}{6}=\frac{ 5}{6}\)
В этом примере необходимо определить наименьшее общее кратное 3 и 6. Другими словами, «Каково наименьшее число, на которое можно разделить без остатка и 3, и 6?» Немного подумав, мы понимаем, что 6 является наименьшим общим кратным, потому что 6, деленное на 3, равно 2, а 6, деленное на 6, равно 1. Затем дробь \(\frac{2}{3}\) приводится к эквиваленту дробь \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2. Теперь можно сложить две дроби с общими знаменателями, чтобы получить окончательное значение \(\frac{5}{6}\) .
Найдите наименьшее общее кратное
В контексте сложения или вычитания дробей наименьшее общее кратное называется наименьшим общим знаменателем .
Как правило, вам нужно определить число, большее или равное двум или более числам, чтобы найти их наименьшее общее кратное.
Важно отметить, что существует несколько способов определения наименьшего общего кратного. Один из способов — просто перечислить все кратные рассматриваемых значений и выбрать наименьшее общее значение, как показано здесь:
Наименьшее общее кратное 8, 4, 6
\(8\стрелка вправо 8,16,24,32,40,48\)
\(4\стрелка вправо 4,8,12,16,20,24, 28,32\)
\(6\стрелка вправо 6,12,18,24,30,36\)
Это показывает, что наименьшее общее кратное чисел 8, 4 и 6 равно 24, поскольку оно является наименьшим число, на которое можно поровну разделить 8, 4 и 6.
Другой распространенный метод включает простую факторизацию каждого значения. Помните, что простое число делится только на 1 и само на себя.
После определения простых множителей перечислите общие множители один раз, а затем умножьте их на остальные оставшиеся простые множители. Результатом является наименьшее общее кратное:
Результатом является наименьшее общее кратное:
\(30=2\умножить на 2\умножить на 3\умножить на 3\)
\(90=2\умножить на 3\умножить на 3\умножить на 5\)\(\text {НОК}=2\умножить на 3\умножить на 3\умножить на 2\умножить на 5\)
Наименьшее общее кратное можно также найти путем общего (или повторного) деления. Этот метод иногда считают более быстрым и эффективным, чем листинг 9.0299 умножить на и найти простые множители. Вот пример нахождения наименьшего общего кратного чисел 3, 6 и 9 с помощью этого метода:
Разделите числа на множители любого из трех чисел. 6 имеет коэффициент 2, поэтому давайте использовать 2. Девять и 3 не могут делиться на 2, поэтому мы просто перепишем здесь 9 и 3. Повторяйте этот процесс, пока все числа не будут уменьшены до 1. Затем перемножьте все множители вместе, чтобы получить наименьшее общее кратное.
| 2 | 3 | 6 | 9 |
| 3 | 3 | 3 | 9 |
| 3 | 1 | 1 | 3 |
| 1 | 1 | 1 |
НОК \(=2\умножить на 3\умножить на 3=18\)
Теперь, когда были введены методы нахождения наименьших общих кратных, нам нужно изменить свое мышление, чтобы найти наибольший общий множитель двух или более числа. Мы будем определять значение, меньшее или равное рассматриваемым числам. Другими словами, спросите себя: «Какое наибольшее число делит оба этих числа?» Понимание этой концепции необходимо для деления и факторизации многочленов.
Мы будем определять значение, меньшее или равное рассматриваемым числам. Другими словами, спросите себя: «Какое наибольшее число делит оба этих числа?» Понимание этой концепции необходимо для деления и факторизации многочленов.
Какой наибольший общий делитель?
Разложение на простые множители также можно использовать для определения наибольшего общего делителя. Однако вместо того, чтобы умножать все простые множители, как мы это делали для наименьшего общего кратного, мы будем умножать только те простые множители, которые являются общими для чисел. Полученное произведение является наибольшим общим множителем.
Обзор
Давайте завершим парой вопросов, верных или неверных:
1. Наименьшее общее кратное 45 и 60 равно 15.
2. Наименьшим общим кратным является число, большее или равное рассматриваемым числам.
Спасибо за просмотр и приятного изучения!
Часто задаваемые вопросы
Q
Как найти LCM и GCF?
A
Существует множество методов определения LCM и GCF. Две наиболее распространенные стратегии включают составление списка или использование простой факторизации.
Две наиболее распространенные стратегии включают составление списка или использование простой факторизации.
Например, НОК 5 и 6 можно найти, просто перечислив кратные \(5\) и \(6\), а затем указав наименьшее кратное, общее для обоих чисел.
\(5, 10, 15, 20, 25, \mathbf{30}, 35…\)
\(6, 12, 18, 24, \mathbf{30}, 36…\)
\(\mathbf{ 30}\) — LCM.
Аналогичным образом, GCF можно найти, перечислив факторы каждого числа, а затем указав наибольший общий фактор. Например, GCF для \(40\) и \(32\) можно найти, перечислив множители каждого числа.
\(40\): \(1, 2, 4, 5, \mathbf8, 10, 20, 40\)
\(32\): \(1, 2, 4, \mathbf8, 16, 32\ )
\(\mathbf8\) — это GCF.
Для больших чисел будет нереально составить список факторов или множителей для определения GCF или LCM. Для больших чисел наиболее эффективно использовать метод простой факторизации.
Например, при нахождении НОК начните с нахождения разложения каждого числа на простые множители (это можно сделать, создав дерево факторов). Простая факторизация \(20\) равна \(2\times2\times5\), а простая факторизация \(32\) — это \(2\times2\times2\times2\times2\). Обведите общие факторы и посчитайте эти только один раз .
Простая факторизация \(20\) равна \(2\times2\times5\), а простая факторизация \(32\) — это \(2\times2\times2\times2\times2\). Обведите общие факторы и посчитайте эти только один раз .
Теперь умножьте все множители (помните, что не нужно дважды считать обведенные \(2\)). Это становится \(2\times2\times5\times2\times2\times2\), что равняется \(160\). LCM \(20\) и \(32\) равен \(160\).
Находя GCF, начните с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Например, простая факторизация \(45\) равна \(5\times3\times3\), а простая факторизация \(120\) равна \(5\times3\times2\times2\times2\). Теперь просто умножьте все факторы, которые являются общими для обоих чисел. В этом случае мы умножим \(5\times3\), что равно \(15\). GCF \(45\) и \(120\) равен \(15\).
Подход с простой факторизацией может показаться довольно длительным процессом, но при работе с большими числами он гарантированно сэкономит время.
Q
Как найти GCF?
A
Существует две основные стратегии нахождения GCF: перечисление факторов или использование простой факторизации.
Первая стратегия состоит в том, чтобы просто перечислить множители каждого числа, а затем найти наибольший множитель, общий для обоих чисел. Например, если мы ищем GCF для \(36\) и \(45\), мы можем перечислить множители обоих чисел и определить наибольшее общее число.
\(36\): \(1,2,3,4,6,\mathbf9,12,18,36\)
\(45\): \(1,3,5,\mathbf9,15,45 \)
GCF для \(36\) и \(45\) равен \(\mathbf9\).
Составление списка множителей каждого числа с последующим определением наибольшего общего множителя хорошо работает для небольших чисел. Однако при нахождении GCF очень больших чисел более эффективно использовать метод простой факторизации.
Например, при нахождении GCF чисел \(180\) и \(162\) мы начинаем с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Простая факторизация \(180\) равна \(2\times2\times3\times3\times5\), а простая факторизация \(162\) — это \(2\times3\times3\times3\times3\). Теперь найдите факторы, которые являются общими для обоих чисел. В этом случае оба числа имеют одну общую \(2\) и две \(3\)s, или \(2\times3\times3\). Результатом \(2\times3\times3\) является \(18\), что является GCF! Эта стратегия часто более эффективна при нахождении GCF действительно больших чисел.
В этом случае оба числа имеют одну общую \(2\) и две \(3\)s, или \(2\times3\times3\). Результатом \(2\times3\times3\) является \(18\), что является GCF! Эта стратегия часто более эффективна при нахождении GCF действительно больших чисел.
Q
Что означает GCF?
A
GCF означает «наибольший общий делитель». GCF определяется как наибольшее число, являющееся множителем двух или более чисел. Например, GCF для \(24\) и \(36\) равен \(12\), потому что наибольший делитель, общий для \(24\) и \(36\), равен \(12\). \(24\) и \(36\) имеют другие общие факторы, но \(12\) является самым большим.
Q
Как найти наименьшее общее кратное?
A
Существует множество методов нахождения наименьшего общего кратного. Двумя распространенными подходами являются перечисление кратных и использование простой факторизации. Список кратных так же, как это звучит, просто перечислите кратные каждого числа, а затем найдите наименьшее кратное, общее для обоих чисел. Например, при нахождении наименьшего общего кратного чисел \(3\) и \(4\) перечислите кратные:
Например, при нахождении наименьшего общего кратного чисел \(3\) и \(4\) перечислите кратные:
\(3\): \(3,6,9,\mathbf{12},15,18 …\)
\(4\): \(4,8,\mathbf{12},16,20…\)
\(\mathbf{12}\) — наименьшее кратное, общее для \(3\) и \(4\).
Список кратных — отличная стратегия, когда числа довольно малы. Когда числа большие, такие как \(38\) и \(42\), мы должны использовать метод простой факторизации. Начните с перечисления простой факторизации каждого числа (это можно сделать с помощью факторного дерева).
\(38\): \(2\times19\)
\(42\): \(2\times3\times7\)
Теперь обведите общие множители (считайте эти только один раз ).
Теперь умножьте все множители (не забудьте подсчитать \(2\) только один раз). Это становится \(2\times19\times3\times7\), что равняется \(798\). LCM \(38\) и \(42\) равен \(798\).
Q
Как вынуть LCM?
A
Извлечение НОК полезно при сложении или вычитании дробей. При определении наименьшего общего кратного получается знаменатель, одинаковый для обеих дробей. Например, общий знаменатель для \(\frac{2}{7}+\frac{3}{5}\) будет равен \(35\), потому что \(35\) является НОК для \(7\ ) и \(5\). Новые дроби становятся \(\frac{10}{35}+\frac{21}{35}\), что равняется \(\frac{31}{35}\).
Например, общий знаменатель для \(\frac{2}{7}+\frac{3}{5}\) будет равен \(35\), потому что \(35\) является НОК для \(7\ ) и \(5\). Новые дроби становятся \(\frac{10}{35}+\frac{21}{35}\), что равняется \(\frac{31}{35}\).
Факты
Скачать Информационный бюллетень
Загрузить информационные бюллетени
Практические вопросы
Вопрос № 1:
Что является наибольшим общим фактором 16 и 42? Используйте его, чтобы уменьшить дробь \(\frac{16}{42}\).
GCF равно 8, и мы уменьшаем его до \(\frac{2}{5}\).
GCF равен 1, и мы не можем больше уменьшать.
GCF равно 4, и мы уменьшаем его до \(\frac{4}{11}\).
GCF равен 2, и мы уменьшаем его до \(\frac{8}{21}\).
Показать ответ
Ответ:
Правильный ответ D: GCF равен 2, и мы уменьшаем до \(\frac{8}{21}\).
Давайте подойдем к этой проблеме, перечислив простые множители как числителя, так и знаменателя.
\(16=2×2×2×2\)
\(42=2×3×7\)
Здесь мы видим, что 2 — единственный общий делитель чисел 16 и 42 и, следовательно, их наибольший общий делитель. Затем мы можем разделить оба числа на 2, чтобы уменьшить дробь:
\(\frac{16\div2}{42\div2}=\frac{8}{21}\)
Скрыть ответ
Вопрос №2:
Найдите наименьшее общее кратное 2, 6 и 8.
16
18
2 4
48
Показать Ответ
Ответ:
Правильный ответ C: 24.
Для этой задачи давайте перечислим простые множители каждого числа.
\(2=2\) (обратите внимание, что мы могли написать \(2\times1\), но 1 понимается или подразумевается, и обычно его не нужно писать)
\(6=2\times3\)
\(8=2\times2\times2\)
Помните, что при вычислении НОК двух или более чисел мы перечисляем каждый простой множитель один раз, который является общим для всех чисел.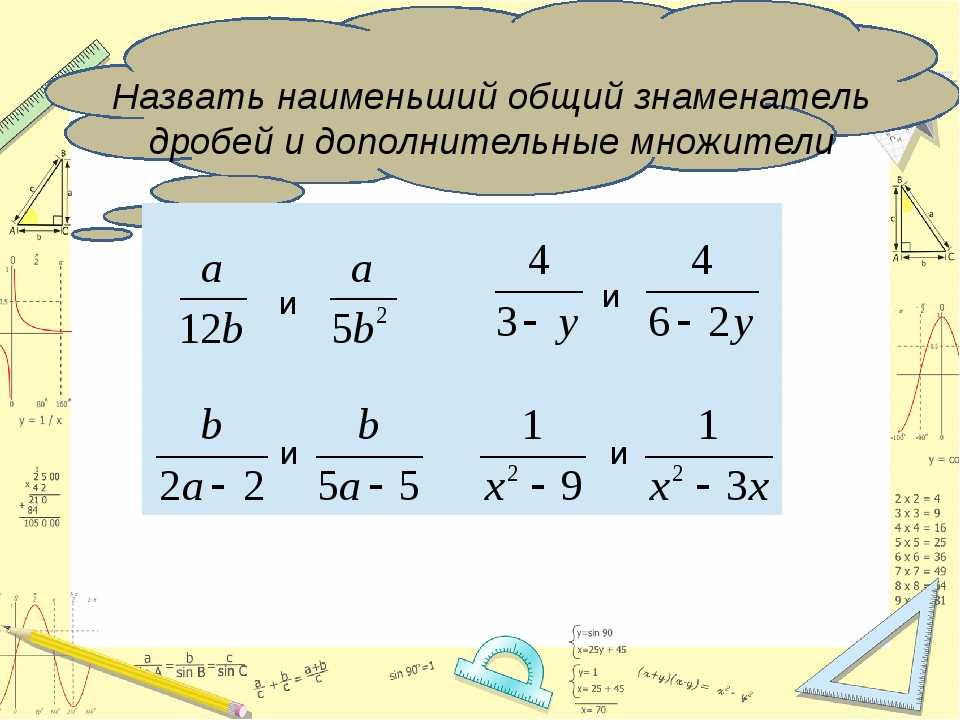 Поскольку каждое из наших чисел имеет 2 в качестве простого множителя, наш LCM также будет иметь 2 в качестве одного из своих простых множителей.
Поскольку каждое из наших чисел имеет 2 в качестве простого множителя, наш LCM также будет иметь 2 в качестве одного из своих простых множителей.
LCM \(=2\times\) _______
Теперь из 6 у нас осталась 3, а из 8 осталось две двойки. Мы умножаем их, чтобы получить
LCM \(=2\times3\times2\times2=24\)
Обратите внимание, что хотя 2, 6 и 8 являются делителями 48, решение не D, потому что 48 не наименьшее общее кратное.
Скрыть ответ
Вопрос № 3:
Перечислите первые несколько чисел, кратных 3, 5 и 6, чтобы найти наименьшее общее кратное.
LCM равно 15
LCM равно 30
LCM равно 18
LCM равно 75
Показать ответ
Ответ:
900 02 Правильный ответ: B: LCM равно 30.Первые несколько чисел, кратных 3, : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
Первые несколько кратных 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Первые несколько кратных 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Как мы см. выше, 30 — это первое (наименьшее) число, общее для чисел 3, 5 и 6 среди своих кратных, поэтому наименьшее общее кратное равно 30.
выше, 30 — это первое (наименьшее) число, общее для чисел 3, 5 и 6 среди своих кратных, поэтому наименьшее общее кратное равно 30.
Скрыть ответ
54 конфеты, а у Триш 36. Они хотят приготовить мешочки с конфетами на день рождения своей подруги Ким, но в каждом мешочке должно быть равное количество конфет. Чтобы в каждом пакете было как можно больше конфет, когда Кортни и Триш работают отдельно, сколько пакетов они могут сделать и сколько конфет будет в каждом пакете?
10 пакетов по 9 конфет
9 пакетов по 10 конфет
15 пакетов по 6 конфет
5 пакетов по 18 конфет
Показать ответ
Ответ:
Правильный ответ D: 5 пакетов по 18 конфет в каждом.
Для начала перечислите простые множители чисел 54 и 36:
\(54=2\times3\times3\times3\)
\(36=2\times2\times3\times3\)
Обратите внимание, что они оба разделяют двойка и две тройки. Произведение этих общих простых множителей равно \(2\times3\times3=18\). Теперь мы знаем, что GCF равен 18, а это значит, что в каждом пакете будет 18 конфет. Из 54 частей Кортни получится 3 сумки, а из 36 частей Триш получится 2 сумки. Вместе они сделают 5 пакетов по 18 конфет в каждом.
Произведение этих общих простых множителей равно \(2\times3\times3=18\). Теперь мы знаем, что GCF равен 18, а это значит, что в каждом пакете будет 18 конфет. Из 54 частей Кортни получится 3 сумки, а из 36 частей Триш получится 2 сумки. Вместе они сделают 5 пакетов по 18 конфет в каждом.
Скрыть ответ
Вопрос № 5:
Сара покупает фрукты для обеда в офисе, и ей нужно равное количество яблок и бананов. Однако яблоки продаются в мешках по 4 штуки, а бананы — в связках по 6 штук. Какое наименьшее количество яблок и бананов может купить Сара?
24 яблока и 24 банана
18 яблок и 18 бананов
12 яблок и 12 бананов
16 яблок и 16 бананов
Показать ответ
Ответ:
Правильный ответ C: 12 яблок и 12 бананов.
В этой задаче мы хотим узнать наименьшее общее кратное 4 и 6.
 д. — все числа кратны 30.
д. — все числа кратны 30.