Тест по теме: Контрольно — измерительные материалы
Контрольная работа
по теме «Множества и операции над ними».
Вариант 1.
1. Выполните операции над множествами:
А = a, b, c, d, m, k, p, h
В = d, m, k, p
С = a, b, c, d, m
а) (А \ В) ∩ С
б) В U А ∩ С
Принадлежат ли получающимся множествам числа 2, 16, 15 20?
2. Изобразить отношения между множествами на кругах Эйлера.
А: «цветы на клумбе»
В: « астры на клумбе»
С: «циннии на клумбе»
3. На какие классы можно разбить множество многоугольников при помощи свойств:
«быть четырехугольником»
«быть прямоугольником»
Изобрази на кругах Эйлера, запиши классы, начерти по 2 фигуры каждого класса.
4. Найди произведения множеств А и В, используя любой способ:
а) А = 2, 4, 6, 8 В = R
б) А = a, b, c В = 10; 20
5. Реши задачу (дополнительное задание).
Из 40 студентов 32 изучают английский язык, 21 – немецкий, 15 – английский и немецкий. Сколько студентов не изучает ни английский, ни немецкий язык? (используй круги Эйлера и формулы)
Вариант 2.
1. Выполните операции над множествами:
А: «множество натуральных чисел»
B: «множество натуральных чисел, кратных 4»
С: «множество натуральных чисел, кратных 5»
а) А\ (В U С)
б) С U А ∩ В
Принадлежат ли получающимся множествам числа 2, 16, 15 20?
2. Изобразить отношения между множествами на кругах Эйлера.
А: «двузначные натуральные числа»
В: « двузначные натуральные числа, кратные 11»
С: « натуральные числа»
3. На какие классы можно разбить множество многоугольников при помощи свойств:
«быть треугольником»
«быть равносторонним треугольником»
Изобрази на кругах Эйлера, запиши классы, начерти по 2 фигуры каждого класса.
4. Найди произведения множеств А и В, используя любой способ:
а) А = R В = — 3; 0; 3
б) А = 3, 4, 5 В = 15; 20
5. Реши задачу (дополнительное задание).
В костюмерной танцевального кружка имеются белые и розовые кофты, а также синие, черные и коричневые юбки. Сколько можно из них составлять различные костюмы?
nsportal.ru
Методическая разработка по алгебре (6 класс) на тему: Проверочная работа по теме: «Множества»
Проверочная работа по теме : «Множества».
1 вариант
- Что такое множество?
- Виды множеств? Приведите пример к каждому виду.
- Задайте множества цифр , с помощью которых записывают число 3254.
- Пусть множество А-множество натуральных чисел. Из чисел 0;3; -5; 576,6; ; -49;8900 принадлежат данному множеству.
- Даны множества: А{3, 67, 78,560} и В{ 1,3,67, 78, 456, 500, 560}
поставьте вместо ….. знак А…В.
- Пусть А={ п,я,т,е,р,к,а}, В= {ч,е,т,в,е,р,к,а}. Запишите пересечение и объединение множеств.
- В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?
2 вариант.
- Что такое подмножество?
- Операции над множествами. Приведите примеры.
- Задайте множество цифр, с помощью которых записывается слово «отличник».
- Пусть множество А-множество целых чисел. Из чисел 3; -5,6; 576,6; ; -49;8900 принадлежат данному множеству.
- Даны множества: А{о,с,а} и В{ о,с,о,к,а} поставьте вместо ….. знак А…В.
- Пусть А={ ч,е,р,е,п,а,х,а}, В= {ч,е,т,в,р,е,к,а}. Запишите пересечение и объединение множеств.
- Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
Проверочная работа по теме : «Множества».
1 вариант
- Что такое множество?
- Виды множеств? Приведите пример к каждому виду.
- Задайте множества цифр , с помощью которых записывают число 3254.
- Пусть множество А-множество натуральных чисел. Из чисел 0;3; -5; 576,6; ; -49;8900 принадлежат данному множеству.
- Даны множества: А{3, 67, 78,560} и В{ 1,3,67, 78, 456, 500, 560}
поставьте вместо ….. знак А…В.
- Пусть А={ п,я,т,е,р,к,а}, В= {ч,е,т,в,е,р,к,а}. Запишите пересечение и объединение множеств.
- В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?
2 вариант.
- Что такое подмножество?
- Операции над множествами. Приведите примеры.
- Задайте множество цифр, с помощью которых записывается слово «отличник».
- Пусть множество А-множество целых чисел. Из чисел 3; -5,6; 576,6; ; -49;8900 принадлежат данному множеству.
- Даны множества: А{о,с,а} и В{ о,с,о,к,а} поставьте вместо ….. знак А…В.
- Пусть А={ ч,е,р,е,п,а,х,а}, В= {ч,е,т,в,р,е,к,а}. Запишите пересечение и объединение множеств.
- Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
nsportal.ru
Домашняя контрольная работа по теме «Множества» — Мегаобучалка
Домашняя контрольная работа по теме «Множества»
В — 1
1. Укажите множество действительных чисел, соответствующее записи .
2. Дано множество .
а) Приведите три примера элементов множества .
б) Укажите, какие из чисел 3, 4, 5, 13, 25, , , принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, , , не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество . Какие из элементов этого множества являются множествами? Верна ли запись ?
4. На множестве U всех букв русского алфавита заданы множества А, В: ; . Найдите множество и изобразите его кругами Эйлера.
5. Даны отрезки . Найдите множество и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов любят ходить в театр?
Домашняя контрольная работа по теме «Множества»
В — 2
1. Укажите множество действительных чисел, соответствующее записи .
2. Дано множество .
а) Приведите три примера элементов множества .
б) Укажите, какие из чисел 3, 4, 5, 13, 25, , , принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, , , не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество . Какие из элементов этого множества являются множествами? Верна ли запись ?
4. На множестве U всех букв русского алфавита заданы множества А, В: ; . Найдите множество и изобразите его кругами Эйлера.
5. Даны отрезки . Найдите множество и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов читают книги, посещают театр, но не дискотеки?
Домашняя контрольная работа по теме «Множества»
В — 3
1. Укажите множество действительных чисел, соответствующее записи .
2. Дано множество .
а) Приведите три примера элементов множества .
б) Укажите, какие из чисел 3, 4, 5, 13, 25, , , принадлежат этому множеству.
в) Укажите, какие из чисел 3, 4, 5, 13, 25, , , не принадлежат этому множеству.
Запишите эти утверждения символически.
3. Дано множество . Какие из элементов этого множества являются множествами? Верна ли запись ?
4. На множестве U всех букв русского алфавита заданы множества А, В: ; ; Найдите множество и изобразите его кругами Эйлера.
5. Даны отрезки . Найдите множество и изобразите его кругами Эйлера.
6.В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек:
18 – любят только читать книги;
24 – читают книги, но не ходят в театр;
7 – читают книги и посещают театр;
38 – читают книги;
47 – ходят на дискотеки;
9 – посещают театр и дискотеки;
13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Сколько студентов посещают либо дискотеки, либо театр?
megaobuchalka.ru
Контрольно-измерительные материалы по теме «Множества»
Самостоятельная работа по теме «Множества»
Вариант 1
Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) цифры, которые больше 7;
б) первые пять букв русского алфавита;
в) целые отрицательные числа от -7 до -1 включительно.
Найдите пересечение множеств А и В, если А={5; 9; -4; 0; 8} и В={8; 0; -1; 4}.
Найдите объединение множеств А и В, если А={-1; -2; -3; -4} и В={-3; -4; -6; -5}.
Верно ли, что: а) -7
 N; б) -7
N; б) -7
 R?
R?Найдите пересечение заданных множеств А и В, если А={x|x-2<4}, B={x|18+2x<0}.
Самостоятельная работа по теме «Множества»
Вариант 2
Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) положительные целые числа, кратные 2, меньше 10;
б) три последние буквы русского алфавита;
в) натуральные числа от 1 до 7 включительно.
Найдите пересечение множеств А и В, если А={6; -2; 0; 4; 9} и В={10; -2; 7; 6; 8}.
Найдите объединение множеств А и В, если А={-9; 4; -7; 2} и В={-8; -9 -10}.
Верно ли, что: а) 4
 Z; б) — 4
Z; б) — 4 N; в)
N; в) 
 Z?
Z?Найдите пересечение заданных множеств А и В, если А={x|2x+4>8}, B={x|x+7>0}.
Самостоятельная работа по теме «Множества»
Вариант 1
Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) цифры, которые больше 7;
б) первые пять букв русского алфавита;
в) целые отрицательные числа от -7 до -1 включительно.
Найдите пересечение множеств А и В, если А={5; 9; -4; 0; 8} и В={8; 0; -1; 4}.
Найдите объединение множеств А и В, если А={-1; -2; -3; -4} и В={-3; -4; -6; -5}.
Верно ли, что: а) -7
 N; б) -7
N; б) -7
 R?
R?Найдите пересечение заданных множеств А и В, если А={x|x-2<4}, B={x|18+2x<0}.
Самостоятельная работа по теме «Множества»
Вариант 2
Множество задано словесным описанием. Задайте это множество, перечислив его элементы:
а) положительные целые числа, кратные 2, меньше 10;
б) три последние буквы русского алфавита;
в) натуральные числа от 1 до 7 включительно.
Найдите пересечение множеств А и В, если А={6; -2; 0; 4; 9} и В={10; -2; 7; 6; 8}.
Найдите объединение множеств А и В, если А={-9; 4; -7; 2} и В={-8; -9 -10}.
Верно ли, что: а) 4
 Z; б) — 4
Z; б) — 4 N; в)
N; в) 
 Z?
Z?Найдите пересечение заданных множеств А и В, если А={x|2x+4>8}, B={x|x+7>0}.
infourok.ru
Элементы теории множеств. Контрольные вопросы.
Министерство образования Российской Федерации
Вологодский государственный педагогический университет
Методические материалы
к практическим занятиям по математике
для студентов-гуманитариев
Вологда
“Русь”
2008
УДК Печатается по решению Ученого Совета ВГПУ от
В работе приведена подборка задач для практических занятий по математике со студентами гуманитарных факультетов (иностранных языков, исторического, отделения культурологии). Для каждого занятия составлены также контрольные вопросы и задачи для самостоятельного решения. Приведены примерные варианты контрольных работ.
Составители: и. о. доцента, кандидат технических наук А.Ю. Белянина,
доцент, кандидат физико-математических наук Т.В. Васильева,
ст. преподаватель М. А.Доброва
Рецензент: доцент, кандидат физико-математических наук Н. Г. Чернышева.
Ответственный за выпуск:
профессор, доктор пед. наук В.А. Тестов.
Вологодский государственный
педагогический университет,
издательство “Русь”, 2008 г.
Выписка из государственного стандарта.
Математика. Аксиоматический метод, основные математические структуры, вероятность и статистика, математические модели.
Выписка из учебного плана:
Факультет иностранных языков: лекции – 34 часа, практические занятия – 16 часов.
Исторический факультет: лекции – 12 часов, практические занятия – 18 часов.
Занятие 1.
1. Приведите примеры конечных и бесконечных множеств.
Перечислите способы задания множеств.
Назовите несколько подмножеств
а) множества натуральных чисел; б) множества геометрических фигур.
4. Какие множества называются равными? Какие из следующих множеств геометрических фигур на плоскости равны между собой:
A – множество всех квадратов;
B — множество всех прямоугольников;
C — множество всех четырехугольников с прямыми углами;
F — множество всех ромбов с прямыми углами?
5. Перечислите основные операции над множествами. Для каждой операции сформулируйте определение и приведите простые примеры.
Упражнения.
1. Запишите множество A, элементами которого являются натуральные делители числа 24, используя перечисление элементов множеств.
2. Даны множества: A={а, и, о, у, э, ы}, B={111, 222, 333, 444, 555, 666, 777, 888, 999}, C={0, 2, 4, 6, 8}. Задайте каждое из них описанием характеристического свойства.
Даны числа: 19;
 ;
0; -27; 5,4
;
0; -27; 5,4 . Какие из них принадлежат множеству: а)
целых чисел; б) целых неотрицательных
чисел; в) рациональных чисел; г)
действительных чисел?
. Какие из них принадлежат множеству: а)
целых чисел; б) целых неотрицательных
чисел; в) рациональных чисел; г)
действительных чисел?Изобразите на координатной прямой множество Х, если
Х = {xxR, -2 x 7};
Х = {xxZ, -1 x 3};
Х = {xxN, -2 x 3}.
Изобразите на координатной прямой множество решений неравенства:
 .
.Найдите множество решений уравнения, используя формулу для расстояния между двумя точками координатной прямой: а)
 ;
б)
;
б)  .
.Дано множество A={72, 56, 513, 117, 324}. Составьте подмножества данного множества, состоящие из чисел, которые:
а) делятся на 4;
б) делятся на 9;
в) делятся на 5;
г) не делятся на 10.
Изобразите при помощи кругов Эйлера множества P и Qi, если P – множество равнобедренных треугольников,
а) Q1 – множество остроугольных треугольников;
б) Q2 – множество прямоугольных треугольников;
в) Q3 – множество равносторонних треугольников.
Изобразите все четыре множества на одном чертеже.
Пусть A— множество натуральных чисел, запись которых оканчивается 0, B — множество натуральных чисел, кратных 10. Докажите, что множества A и B равны.
Известно, что N множество натуральных чисел, Z – множество целых чисел. Докажите, что высказывание Z N ложно.
11. Изобразите при помощи кругов Эйлера множества A, B и C, если:
а) А множество четных целых чисел,
B множество целых чисел, кратных 4;
b) А множество четных целых чисел,
В множество целых чисел, кратных 2;
с) А множество нечетных целых чисел,
В множество целых чисел, кратных 3,
С множество чисел, кратных 5.
Отношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.
А D
F
Рис. 1
Установите, в каком отношении находятся множества А и В, если А = {a, b, c, d}, а множество В:
а) {k, l, m}; b) {b, c, o, f, k}; с) {b, d}.
Задания для самостоятельной работы.
I. Повторите теоретический материал по теме Множества. Операции над множествами. Попытайтесь ответить на контрольные вопросы к занятию 2.
II. Решите задачи:
1. Для каждого из слов “сосна“, “осколок“, “насос“, “колосс“, “сокол“ составьте множество его различных букв. Имеются ли среди полученных множеств равные?
2. Найдите
все подмножества множества М = 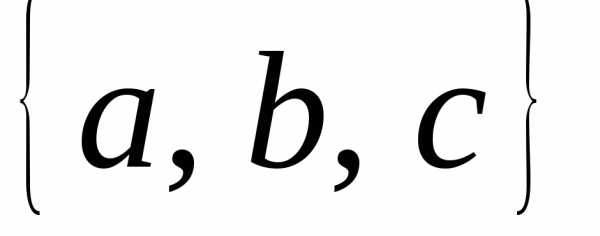 .
Сколько подмножеств получилось?
.
Сколько подмножеств получилось?
3. В каких отношениях находятся множества решений неравенств:
а) ; б) ?
4. А – множество двузначных чисел, В – множество четных натуральных чисел, С – множество чисел, кратных числу 4. В каком из случаев изображены данные множества? Приведите примеры множеств для двух других случаев.
а) б) в)
5. Задайте множество D, элементами которого являются натуральные числа, меньшие семи.
studfiles.net
Контрольная работа по теме «Теоретико-множественный смысл суммы»
Контрольная работа по теме
«Теоретико—множественный смысл суммы»
1. Дайте определение понятию «сумма натуральных чисел а и b» с теоретико-множественных позиций.
2. Что означает понятие «конечное множество»?
Множество, количество элементов которого конечно.
Множество, не являющееся конечным.
Множество, равномощное отрезку натурального ряда, а также пустое множество.
3. Дайте определения операциям «пересечение» и «объединение» над множествами.
4. Установите соответствие между коммутативностью, ассоциативностью сложения и их равенством
А. Коммутативность сложения1. (А ⋃ В) ⋃ С=А ⋃ (В ⋃ С)
Б. Ассоциативность сложения
2. А ⋃ В = В ⋃ А
5. Дайте определение понятию «сложение».
6. Каков теоретико-множественный смысл суммы:
А)9+1
Б)6+0
7. Объясните, почему нижеприведённые задачи решается сложением
А) В ателье работали 23 портнихи, потом на работу приняли еще 12 портних. Сколько портних теперь работает в ателье?
Б) Ваня купил 35 карандашей и 12 тетрадей. Сколько всего предметов купил Ваня?
8. Найдите рациональным способом значение выражения 1755+8993+555+1607. Укажите, какие свойства использовались.
9. Составьте задачу, которая решалась бы так: 6+8, указав какой теоретико-множественный смысл суммы.
Ключ:
1. С теоретико – множественных позиций сумма натуральных чисел а и b представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а = n (А), b=n (B).
2. А, С
3. Пересечение множеств — это множество, которому принадлежат те, и только те элементы, которые одновременно принадлежат всем данным множествам.
Объединение множеств — множество, содержащее в себе все элементы исходных множеств.
4. А-2,Б-1
5. Сложение — арифметическое действие, которым находится сумма.
6. А) 9+1=10; п (А)=9, п (В)=1; А∩В= ; п(А⋃ В)= п (А)+ п (В)=9+1=10;
Б)6+0=6; п (А)=6, п (В)=0; А∩В= ; п(А⋃ )= п (А)+ п ()=6+0=6.
7. А) В данной задаче рассматривается три множества: множество А портнихи, которые работали в ателье с самого начала, множество В портнихи, которых только что приняли на работу и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как п (А)=23, п (В)=12 и А∩В= , то п(А⋃ В)= п (А)+ п (В)=23+12 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи:23+12 = 35. Следовательно, теперь в ателье работает 35 портних.
Б) В данной задаче рассматривается три множества: множество А карандаши, множество В тетради и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как п (А)=35, п (В)=12 и А∩В= , то п(А⋃ В)= п (А)+ п (В)=35+12 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи:35+12 = 47. Следовательно, Ваня купил 47 предметов.
8. 1755+8993+555+1607=(1755+555)+(8993+1607)= 2310+10600=12910. Переместительный и сочетательный закон.
9. 6+8=14; п (А)=6, п (В)=8; А∩В= ; п(А⋃ В)= п (А)+ п (В)=6+8=14.
infourok.ru
Контрольная работа по теме:»Множества и логика»
Просмотр содержимого документа
«Контрольная работа по теме:»Множества и логика»»
Контрольная работа по теме: «Множества. Логика»
Вариант 1
1. Найти A⋂B и A⋃B, если:
1) A = , B =;
2) A = , B =.
2. Сформулировать высказывание , если высказывание таково: 29 ≥ 25. Определить, истинным или ложным является высказывание .
3. Записать уравнение окружности с центром в точке М и радиусом r, если М (2; 3), r =5.
4. Найти координаты середины отрезка AB , если: A(3; 8), B(5; 2).
5. Записать уравнение прямой, проходящей через точки M (6; 0) и N (0;).
6*. На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству
Контрольная работа по теме: «Множества. Логика»
Вариант 2
1. Найти A⋂B и A⋃B, если:
1) A = , B =;
2) A = , B =.
2. Сформулировать высказывание , если высказывание таково: 13 .
3. Записать уравнение окружности с центром в точке М и радиусом r, если М (5;1), r =3.
4. Найти координаты середины отрезка AB , если: A(4; 7), B(6; 5).
5. Записать уравнение прямой, проходящей через точки M (0; 5) и N(3; 0).
6*. На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству
multiurok.ru
 N; б) -7
N; б) -7
 ;
0; -27; 5,4
;
0; -27; 5,4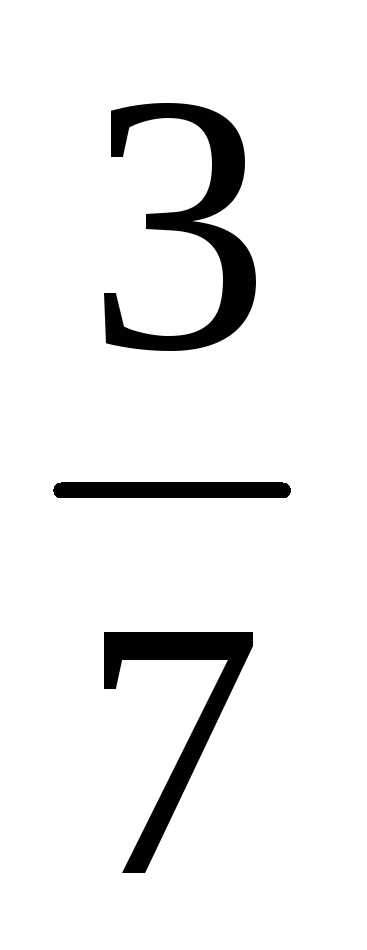 . Какие из них принадлежат множеству: а)
целых чисел; б) целых неотрицательных
чисел; в) рациональных чисел; г)
действительных чисел?
. Какие из них принадлежат множеству: а)
целых чисел; б) целых неотрицательных
чисел; в) рациональных чисел; г)
действительных чисел?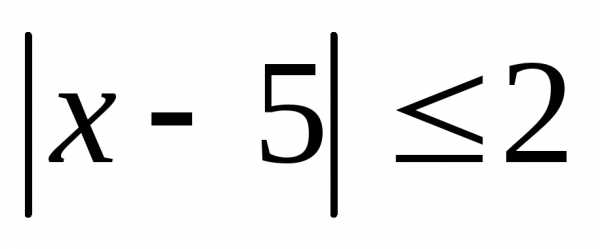 .
.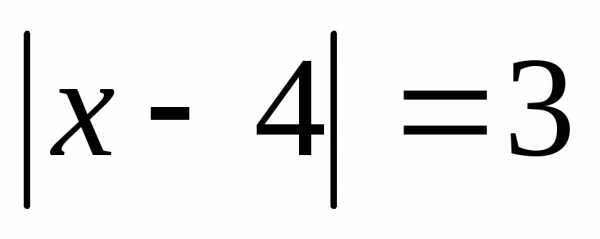 ;
б)
;
б) 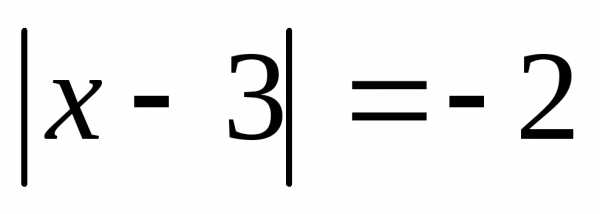 .
.