Корреляция в психологии это – Корреляции в психологии

Корреляции в психологии

Корреляционный анализ активно используется в психологических исследованиях для выявления взаимосвязи между психологическими параметрами. Практическая глава курсовых, дипломных и магистерских работ психологии чаще всего содержит корреляционный анализ.

Для того, чтобы написать диплом по психологии и успешно его защитить, необходимо не только знать, что такое корреляция, но и понимать специфику использования этого статистического метода в психологических исследования.

Признаком использования корреляций в дипломной работе по психологии является наличие в названии темы следующих слов: «Изучение взаимосвязи…», «Исследование влияния…», «Выявление факторов…».

В курсовых и дипломных по психологии чаще всего используются два корреляционных метода: коэффициенты ранговой корреляции Спирмена и корреляции Пирсона. Второй из них более строгий, то есть для его использования необходимо выполнения некоторых условий к данным. Чаще используется менее строгий коэффициент корреляции Спирмена. Но суть обоих коэффициентов корреляции применительно к психологическому исследованию одинакова.

 

Корреляции в психологическом исследовании

Корреляция – это степень взаимосвязи между какими-то показателями. В психологическом исследовании психологические показатели коррелируют, если в некоторой группе они изменяются согласованно. Например, от испытуемого к испытуемому с ростом одного показателя растет и другой – корреляция положительная или прямая. Или от испытуемого к испытуемому с ростом одного показателя второй снижается – корреляция отрицательная или обратная.

Например, мы измерили у 10 российских мужей два психологических показателя: 1) уровень удовлетворенности браком и 2) уровень интеллекта. Для простоты не будем привязываться к конкретным методикам, и показатели возьмем условные. В таблице приведены эти данные.

№ испытуемого	Уровень удовлетворённости браком	Уровень интеллекта
1	1	10
2	2	20
3	3	30
4	4	40
5	5	50
6	6	60
7	7	70
8	8	80
9	9	90
10	10	100

Посмотрим внимательно, как меняются показатели УБ и интеллекта от испытуемого к испытуемому. Видно, что УБ растет и уровень интеллекта тоже растет. Причем нет ни одного исключения в этой закономерности. Это пример положительной корреляции, причем это максимально возможная положительная (прямая) корреляция, равная 1.

Содержательно полученная корреляция означает, что чем выше уровень интеллекта у российских мужей, тем выше их удовлетворенность браком.

В следующей таблице данные, полученные на мужьях другой страны, например, Монголии.

№ испытуемого	Уровень удовлетворённости браком	Уровень интеллекта
1	10	10
2	20	9
3	30	8
4	40	7
5	50	6
6	60	5
7	70	4
8	80	3
9	90	2
10	100	1

Посмотрим внимательно, как меняются показатели УБ и интеллекта от испытуемого к испытуемому. Видно, что УБ растет, а уровень интеллекта строго снижается. Причем нет ни одного исключения в этой закономерности.

Это пример отрицательной корреляции, причем это максимально возможная отрицательная (обратная) корреляция, равная -1.

Содержательно полученная корреляция означает, что чем выше уровень интеллекта у монгольских мужей, тем ниже их удовлетворенность браком. Или, по-другому, чем ниже уровень интеллекта монгольских мужей, тем выше их удовлетворенность браком. Описание полученного результата может звучать примерно так.

«Как видим, мы получили совершенно различные результаты на выборках российских и монгольских мужей. Корреляционный анализ показал, что чем умнее российские мужчины, тем они более счастливы в браке.

А вот у монгольских мужчин ситуация совершенно иная — чем они глупее, тем более счастливы в браке.

Таким образом, у монгольских мужчин низкий интеллект выступает фактором роста удовлетворенности браком, а у российских – фактором снижения удовлетворенности браком.»

Мы рассмотрели два крайних случая – полных прямой и обратной корреляции применительно к эмпирическому психологическому исследованию. В реальности психологические данные в группе испытуемых расположены не так однозначно, и получаемые коэффициенты корреляции расположены в промежутке от -1 до 1.

В следующей таблице мы немного изменили показатели во втором столбце. 

№ испытуемого	Уровень удовлетворённости браком	Уровень интеллекта
1	1	20
2	2	10
3	3	40
4	4	30
5	5	50
6	6	60
7	7	70
8	8	80
9	9	90
10	10	100

Расчет показал, что теперь коэффициент корреляции равен 0,976.

Теперь еще больше перепутаем показатели во втором столбце.

№ испытуемого	Уровень удовлетворённости браком	Уровень интеллекта
1	10	9
2	20	1
3	30	8
4	40	3
5	50	5
6	60	7
7	70	6
8	80	10
9	90	2
10	100	4

Расчет показывает, что теперь коэффициент корреляции равен -0,103. Близость коэффициента корреляции к 0 означает очень низкое значение и низкую корреляцию, низкую взаимосвязь. И действительно, теперь трудно уловить какую-либо согласованность между вторым и третьим столбцами.

 

Корреляция в дипломной (курсовой) работе по психологии

Коэффициенты корреляции при анализе взаимосвязей между психологическими показателями могут принимать численные значения от -1 до 1.

Положительный коэффициент корреляции означает положительную (прямую) зависимость между двумя психологическими показателями в группе.

Отрицательный коэффициент корреляции означает отрицательную (обратную) зависимость между двумя психологическими показателями в группе.

Между двумя психологическими показателями, измеренными в группе испытуемых, всегда есть какая-то зависимость (корреляция) Она отражается числом от -1 до 1. Однако интерес представляют лишь статистически значимые коэффициенты корреляции.

Статистически значимые коэффициенты корреляции выявляются путем сравнения полученного нами эмпирического коэффициента корреляции с критическим значением.

Критическое значение коэффициента корреляции берется из специальных статистических таблиц, и его значение определяется объемом выборки. Чем больше человек в выборке, тем ниже критическое значение.

Чтобы определить, является ли статистически значимым полученный нами коэффициент корреляции, необходимо сравнить его значение по модулю (без учета знака) с критическим значением. Если наш эмпирический коэффициент корреляции без учета знака больше критического, то он статистически значим; если нет, — незначим.

Если расчет коэффициента корреляции проводится с помощью статистических программ, то она сама помечает значимые корреляции, и необходимость искать критические значения и сравнивать исчезает.

Пример.

В группе подростков из 30 человек с помощью тестов были измерены два показателя: уровень агрессивности и уровень тревожности.

С помощью статистической программы рассчитали коэффициент корреляции агрессивности и тревожности.

Коэффициент корреляции агрессивности и тревожности в группе подростков

	Агрессивность
Тревожность	0,58*

* — статистически значимая корреляция (р≤0,05)

Критическое значение коэффициента корреляции Спирмена для выборки из 30 человек при уровне значимости р=0,05 (см. ниже) равен 0,36.

Сравниваем и получаем, что наш эмпирический коэффициент корреляции больше по модулю, чем критический. Следовательно, корреляция статистически значима.

Вот как правильно должно выглядеть описание полученной корреляции:

«Анализ данных, приведенных в таблице, показывает, что выявлена статистически значимая положительная корреляция между уровнем агрессивности и уровнем тревожности в группе подростков. Это означает, что чем выше проявления агрессивности у подростков, тем выше их склонность проявлять тревожные реакции в ситуациях, угрожающих безопасности или самооценке».

Обычно описания корреляции достаточно. Однако лучше дополнительно привести интерпретацию полученного результата. Примерно вот так:

«С нашей точки зрения, полученный результат показывает, что рост тревоги подростка в связи с его физической безопасностью, а также в связи с угрозой самооценке может реализоваться в форме агрессивных реакций. Такой результат еще раз подтверждает мнение многих авторов о том, что подростковая агрессия выступает непродуктивным и архаичным способом адаптации. В этой связи развитие у подростков конструктивных способов преодоления негативных эмоциональных состояний, в том числе и тревожности, будет способствовать снижению их агрессивности».

 

Уровень статистической значимости — это таинственное «р»

В статистических расчетах «р» – это обозначение уровня статистической значимости.

 

Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи между агрессивностью и тревожностью.

То есть, выше приведенный коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?

Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.

 

Что отражает корреляция — взаимосвязь или влияние?

Корреляционный анализ выявляет взаимосвязь между психологическими показателями. При этом наличие корреляции, строго говоря, не дает нам оснований говорить о причинно-следственных связях между показателями.

Вернемся к примеру с агрессивностью и тревожностью. Корреляция между ними не дает оснований говорить, что тревожность является причиной, а агрессивность — следствием. Нельзя также говорить обратное, что агрессивность является причиной, а тревожность – следствием.

В то же время в реальных исследованиях на основании корреляций часто делаются выводы о причинно-следственных связях. В нашем случае можно было бы сказать, что наличие положительной статистически значимой корреляционной связи между агрессивностью и тревожностью позволяет говорить о том, что тревожность выступает одним из факторов (причин) роста агрессивности у подростков. В этом случае также можно сказать, что тревожность влияет на агрессивность.

Термин «влияние» как раз и предполагает наличие между показателями причинно-следственной связи. А термин «взаимосвязь» не предполагает.

В некоторых вузах требуют использовать только термин взаимосвязь, и это более правильно и строго. В других спокойно воспринимают термин «влияние», который ближе к жизни.

 

---

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать

dip-psi.ru

Корреляции в дипломных работах по психологии

Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.

Материалы по корреляциям в сети слишком научны. Неспециалисту трудно разобраться в формулах. В то же время понимание смысла корреляций необходимо маркетологу, социологу, медику, психологу – всем, кто проводит исследования на людях.

В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.

 

Содержание

 

Что такое корреляция
Численное выражение корреляционной связи

Корреляционный анализ в психологии
Коэффициенты корреляции Пирсона и Спирмена
Как рассчитать коэффициент корреляции

Использование корреляционного анализа в дипломных работах по психологии 

Что такое корреляция

Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.

Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».

Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).

Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?

Правильно,  между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.

В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.

 

Численное выражение корреляционной зависимости

Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.

Например, изучается роль чтения в жизни людей. Исследователи взяли группу из 40 человек и измерили у каждого испытуемого два показателя: 1) сколько времени он читает в неделю; 2) в какой мере он считает себя благополучным (по шкале от 1 до 10). Ученые занесли эти данные в два столбика и с помощью статистической программы рассчитали корреляцию между чтением и благополучием. Предположим, они получили следующий результат -0,76. Но что значит это число? Как его проинтерпретировать? Давайте разбираться.

Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:

1. Знак «+» или «-»  отражает направление зависимости.
2. Величина коэффициента отражает силу зависимости.

 

Прямая и обратная

Знак плюс перед коэффициентом указывает на то, что связь между явлениями или показателями прямая. То есть, чем больше один показатель, тем больше и другой. Выше оклад — выше продажи. Такая корреляция называется прямой, или положительной.

Если коэффициент имеет знак минус, значит, корреляция обратная, или отрицательная. В этом случае чем выше один показатель, тем ниже другой. В примере с чтением и благополучием мы получили -0,76, и это значит, что, чем больше люди читают, тем ниже уровень их благополучия.

 

Сильная и слабая

Корреляционная связь в численном выражении – это число в диапазоне от -1 до +1. Обозначается буквой «r». Чем выше число (без учета знака), тем корреляционная связь сильнее.

Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.

Максимально возможная сила зависимости  – это 1 или -1. Как это понять и представить?

Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.

Испытуемый	IQ	Успеваемость (баллы)
1	90	4,0
2	91	4,1
3	92	4,2
4	93	4,3
5	94	4,4
6	95	4,5
7	96	4,6
8	97	4,7
9	98	4,8
10	99	4,9

 

Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.

Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость  между интеллектом и успеваемостью равна 1.

Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).

Испытуемый	IQ	Успех в общении с противоположным полом (баллы)
1	90	10
2	91	9
3	92	8
4	93	7
5	94	6
6	95	5
7	96	4
8	97	3
9	98	2
10	99	1

 

Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.

Это пример полной согласованности изменения двух показателей в группе — максимально возможная отрицательная взаимосвязь. Корреляционная связь между IQ и успешностью общения с противоположным полом равна -1.

А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.

Испытуемый	IQ	Длина прыжка с места (м)
1	90	2,5
2	91	1,2
3	92	2,0
4	93	1,7
5	94	1,9
6	95	1,3
7	96	1,7
8	97	2,3
9	98	1,1
10	99	2,6

 

Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.

Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:

• если коэффициент больше 0,70 – связь между показателями сильная;
• от 0,30 до 0,70 – связь умеренная,
• меньше 0,30 – связь слабая.

Если оценить по этой шкале полученную нами выше корреляцию между чтением и благополучием, то окажется, что эта зависимость  сильная и отрицательная -0,76. То есть, наблюдается сильная отрицательная связь между начитанностью и благополучием. Что еще раз подтверждает библейскую мудрость о соотношении  мудрости и печали.

Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.

Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).

 

Корреляционный анализ в психологии

Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?

В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.

В психологии иная ситуация. Например, психологи публикуют данные о связи теплых отношений в детстве с родителями и уровня креативности во взрослом возрасте. Означает ли это, что любой из испытуемых с очень теплыми отношениями с родителями в детстве будет иметь очень высокие творческие способности? Ответ однозначный – нет. Здесь нет закона, подобного физическому. Нет механизма влияния детского опыта на креативность взрослых. Это наши фантазии! Есть согласованность данных (отношения – креативность), но за ними нет закона. А есть лишь корреляционная связь. Психологи часто называют выявляемые взаимосвязи психологическими закономерностями, подчеркивая их вероятностный характер — не жесткость.

Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:

1. Анализ взаимосвязи между психологическими показателями. В нашем примере IQ и успешность общения с противоположным полом – это психологические параметры. Выявление корреляции между ними расширяет представления о психической организации человека, о взаимосвязях между различными сторонами его личности – в данном случае между интеллектом и сферой общения.
2. Анализ взаимосвязей IQ с успеваемостью и прыжками – пример связи психологического параметра с непсихологическими. Полученные результаты раскрывают особенности влияния интеллекта на учебную и спортивную деятельность.

Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:

1. Выявлена значимая положительная зависимость интеллекта студентов и их успеваемости.
2. Существует отрицательная значимая взаимосвязь IQ с успешностью общения с противоположным полом.
3. Не выявлено связи IQ студентов с умением прыгать с места.

Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.

Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.

Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.

 

Коэффициенты Пирсона и Спирмена

Рассмотрим два метода расчета.

Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:

1. Берутся значения двух параметров в группе испытуемых (например, агрессии и перфекционизма).
2. Находятся средние значения каждого параметра в группе.
3. Находятся разности параметров каждого испытуемого и среднего значения.
4. Эти разности подставляются в специальную форму для расчета коэффициента Пирсона.

Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:

1. Берутся значения двух индикаторов в группе испытуемых.
2. Находятся ранги каждого фактора в группе, то есть место в списке по возрастанию.
3. Находятся разности рангов, возводятся в квадрат и суммируются.
4. Далее разности рангов подставляются в специальную форму для вычисления коэффициента Спирмена.

В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.

В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.

Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.

 

Как рассчитать коэффициент корреляции

Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.

Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.

 

Расчет с помощью электронных таблиц Microsoft Excel

Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.

Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».

Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.

 

Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему.

В таблицах Excel реализована формула расчета только коэффициента Пирсона.

 

Расчет с помощью программы STATISTICA

Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.

 

Как видно, расчет  дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.

 

Использование корреляционного анализа в дипломных работах по психологии (пример)

Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).

Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:

• «Взаимосвязь субъективного ощущения одиночества и самоактуализации у женщин зрелого возраста»;
• «Особенности влияния жизнестойкости менеджеров на успешность их взаимодействия с клиентами в конфликтных ситуациях»;
• «Личностные факторы стрессоустойчивости сотрудников МЧС».

Таким образом, слова «взаимосвязь», «влияние» и «факторы» — верные признаки того, что методом анализа данных в эмпирическом исследовании должен быть корреляционный анализ.

Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».

1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:

• каждая строка содержит данные на одного испытуемого;
• каждый столбец содержит показатели по одной шкале для всех испытуемых.

№ испытуемого	Личностная тревожность	Агрессивность
1	12	24
2	14	25
3	11	13
4	17	19
5	21	29
6	26	29
7	13	16
8	16	20
8	13	24
9	18	21
10	23	31

2. Необходимо решить, какой из двух типов коэффициентов — Пирсона или Спирмена — будет использоваться. Напоминаем, что Пирсон дает более точный результат, но он чувствителен к выбросам в данных Коэффициенты  Спирмена могут использоваться с любыми данными (кроме номинативной шкалы), поэтому именно они чаще всего используют в дипломах по психологии.

3. Заносим таблицу сырых данных в статистическую программу.

 

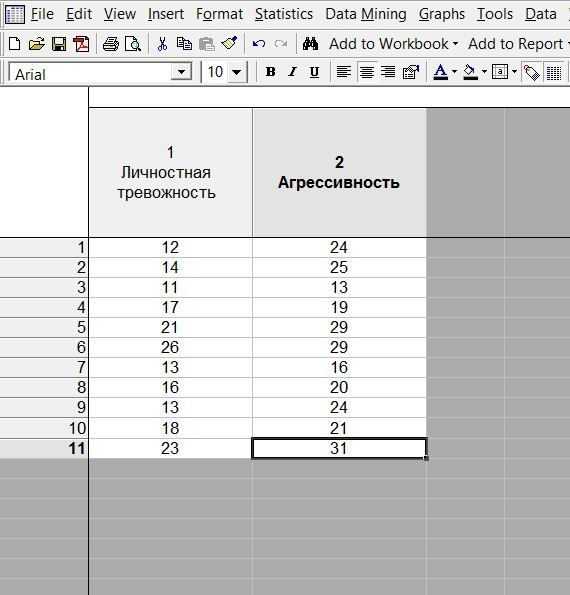
4. Рассчитываем значение.

5. На следующем этапе важно определить, значима ли взаимосвязь. Статистическая программа подсветила результаты красным, что означает, что корреляция статистически значимы при уровне значимости 0,05 (указано выше).

Однако полезно знать, как определить значимость вручную. Для этого понадобится таблица критических значений Спирмена.

Таблица критических значений коэффициентов Спирмена

	Уровень статистической значимости
Число испытуемых	р=0,05	р=0,01	р=0,001
5	0,88	0,96	0,99
6	0,81	0,92	0,97
7	0,75	0,88	0,95
8	0,71	0,83	0,93
9	0,67	0,8	0,9
10	0,63	0,77	0,87
11	0,6	0,74	0,85
12	0,58	0,71	0,82
13	0,55	0,68	0,8
14	0,53	0,66	0,78
15	0,51	0,64	0,76

Нас интересует уровень значимости 0,05 и объем нашей выборки 10 человек. На пересечении этих данных находим значение критического Спирмена: Rкр=0,63.

Правило такое: если полученное эмпирическое значение Спирмена больше либо равно критическому, то он статистически значим. В нашем случае: Rэмп (0,66) > Rкр (0,63), следовательно, взаимосвязь между агрессивностью и тревожностью в группе подростков статистически значима.

5. В текст дипломной нужно вставлять данные в таблице формата word, а не таблицу из статистической программы. Под таблицей описываем полученный результат и интерпретируем его.

Таблица 1

Коэффициенты Спирмена агрессивности и тревожности в группе подростков

	Агрессивность
Личностная тревожность	0,665*

* — статистически достоверна (р≤0,05)

Анализ данных, приведенных в таблице 1, показывает, что существует статистически значимая положительная связьмежду агрессивностью и тревожностью подростков. Это означает, что чем выше личностная тревожность подростков, тем выше уровень их агрессивности. Такой результат дает основание предположить, что агрессия для подростков выступает одним из способов купирования тревожности. Испытывая неуверенность в себе, тревогу в связи с угрозами самооценке, особенно чувствительной в подростковом возрасте, подросток часто использует агрессивное поведение, таким непродуктивным способом снижая тревогу.

6. Можно ли при интерпретации связей говорить о влиянии? Можно ли сказать, что тревожность влияет на агрессивность? Строго говоря, нет. Выше мы показали, что корреляционная связь между явлениями носит вероятностный характер и отражает лишь согласованность изменений признаков в группе. При этом мы не можем сказать, что эта согласованность вызвана тем, что одно из явлений является причиной другого, влияет на него. То есть, наличие корреляции между психологическими параметрами не дает оснований говорить о существовании между ними причинно-следственной связи. Однако практика показывает, что термин «влияние» часто используется при анализе результатов корреляционного анализа.

© СтудентуПсихологу.рф

xn--c1abdmpkibfqehdkeh3a.xn--p1ai

Корреляция — Википедия

Материал из Википедии — свободной энциклопедии

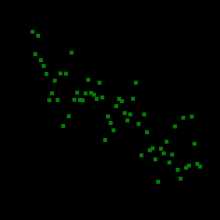Для графического представления корреляционной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определённого символа. Такой график называется диаграммой рассеяния.

Корреля́ция (от лат. correlatio «соотношение, взаимосвязь»), или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1]

Математической мерой корреляции двух случайных величин служит корреляционное отношение η{\displaystyle \mathbf {\eta } }^[2] либо коэффициент корреляции R{\displaystyle \mathbf {R} } (или r{\displaystyle \mathbf {r} })^[1]. В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.^[4]

ru.wikipedia.org

Корреляция как показатель взаимосвязи между параметрами.

Научные термины пугают и притягивают одновременно. Термин «корреляция» все чаще можно встретить на страницах газет, по радио, на телевидении. Им козыряют экономисты, политологи, аналитики. Но, похоже, частота использования этого термина в СМИ отрицательно коррелирует с уровнем его понимания потребителями.

В переводе на простой язык, сказанная фраза означает следующее: «Чем чаще используется термин «корреляция», тем менее точным становится содержание этого понятия в сознании людей». В реальности, возможно, это и не так – исследования не проводились. Но важно другое – корреляция в обыденном понимании отражает взаимосвязь между явлениями.

 

Взаимосвязи вокруг нас

В человеке живет интуитивное ощущение взаимосвязи всех явлений. В фантастическом рассказе Рэя Брэдбери герой попадает в далекое прошлое и, нарушая запрет, сходит с тропы. Он лишь раздавил бабочку. Но вернулся в другой мир, с другим языком и даже президентом. Все связано вокруг…

При чем здесь корреляция? А при том, что пытливое сознание человека пытается выявлять корреляции. Зная взаимосвязи между явлениями, на них можно влиять, ими можно управлять.

Я не буду «грузить» вас математической терминологией, сложными формулами. Давайте разберемся в сути этого понятия; уясним что значит отрицательная и положительная корреляция; значимая и незначимая.

 

Понятие корреляции

Слово «корреляция» происходит от латинского «correlatio», что означает «соотношение» или «взаимосвязь».

Взаимосвязь присуща многим явлениям. Например, кепка, надетая на голову, связана с ней – куда голова, туда и кепка. Или палочка в руке дирижёра – они взаимосвязаны, и она послушна руке хозяина, полету его вдохновения. Но можно ли говорить, что их движения коррелируют между собой? Нет, и вот почему.

 

Функциональная связь

Палочка и рука взаимосвязаны и эта связь – функциональная. Она детерминирующая – жестко связывает между собой объекты. Если дирижёр сосредоточен и крепко держит палочку, то в их согласованном движении не будет моментов, когда которых рука движется в одну сторону, а палочку – в другую. Корреляционная связь совсем иной природы.

Посмотрим за спину нашего дирижёра. В зале сидят слушатели, любители музыки. Они испытывают какие-то эмоции. Их переживания, возможно, как-то связаны с уровнем их музыкального образования. Чем больше они знают про музыку, тем выше их эмоциональный отклик. Эта связь — корреляционная.

 

Корреляционная связь

В отличие от функциональной связи, корреляция отражает не жесткую зависимость между явлениями. Кто-то очень подкован теоретически, но эмоциональный отклик на музыку слабый. Другой мало образован, но его «пробило» на эмоции. Такая связь называется случайной, стохастической. И это сфера статистики – науки, занимающейся не отдельными явлениями, а массовыми.

Итак, корреляция отражает не функциональную, а статистическую случайную связь между явлениями (переменными). Почему случайную? Потому что заранее не известно, кто и как из слушателей будет реагировать на музыку. Но если статистический (массовый) расчет показал положительную корреляцию между образованностью и эмоциональным откликом, то это дает основания для важных выводов. Знание корреляционной связи позволяет предсказывать.

В данном примере мы с большой долей вероятности сможем утверждать, что из двух слушателей более эмоционально слушал тот, кто более образован. Это не будет однозначный вывод, ведь связь у нас не функциональная. Это будет вывод статистический, вероятностный – мы всегда можем ошибиться. Но вероятность этой ошибки не велика и заранее известна. Она называется «уровень статистической значимости». Как видим, без математики в этом вопросе все-таки не обойтись.

 

Коэффициент корреляции

В повседневной жизни, говоря о корреляции, например, успеха и затраченных усилий или ощущения счастья и материального достатка, мы опираемся на мифы, интуицию или досужие домыслы. Эти величины трудно измерить, перевести на язык цифр потом строго доказать их взаимосвязи. Но если мы имеем дело с явлениями, которые можно измерить, то здесь корреляцию можно рассчитать и получить коэффициент, который будет отражать силу и направление взаимосвязи.

Например, мы взяли группу из 20-ти человек и определили для каждого два параметра: возраст (посмотрели паспорт) и уровень оптимизма (провели психологический тестирование). Эти данные нужно занести в так называемую таблицу исходных данных и загрузить в статистическую программу. В итоге получим значение коэффициента корреляции. Не стоит пугаться этого числа, разгадать его тайны не так сложно.

Коэффициент корреляции может принимать численные значения в диапазоне от -1 до +1. Для анализа важны два показателя:

• Знак коэффициента корреляции (положительный или отрицательный).
• Абсолютное значение коэффициента корреляции (то есть, без учета знака, «по модулю»).

 

Отрицательная связь не значит плохая, положительная не значит хорошая

Если расчет корреляции между возрастом и оптимизмом среди испытуемых дал отрицательный показатель, это значит следующее: с годами растет оптимизм. То есть, чем выше возраст испытуемого, тем более оптимистично он смотрит на жизнь (мудрецы).

Но мы могли получить и обратный результат – отрицательную корреляцию между возрастом и оптимизмом. То есть, чем больше прожитых лет, тем меньше хорошего видится вокруг (скептики).

Если выборка подобрана правильно (репрезентативна), то она отражает ключевые особенности всех людей (или почти, например, живущих в большом городе). Тогда, полученные коэффициенты корреляции, дают важную информацию. Ее можно использовать, например, при приеме на работу. В случае положительной корреляции на должность менеджеров по продажам стоит брать людей постарше – они будут оптимистичны и доброжелательны.

 

Сила взаимосвязи – большая сила

Вы, наверное, уже догадались, что величина коэффициента корреляции отражает силу взаимосвязи между показателями. Чем больше численное значение по абсолютной величине (без учета знака), тем сила взаимосвязи больше.

Представим, что в нашей группе корреляция между возрастом и оптимизмом равна +1. Это значит, что, взяв любых двух человек из этой группы и узнав их возраст, мы точно сможем предсказать, кто из них более оптимистичен? Кстати, вы уже поняли кто? … Правильно, тот, кто старше.

А если корреляция равна -1, то в этой группе тот, кто моложе, более позитивно смотрит на мир. И это без всяких исключений! А вот если корреляция будет -0,9, значит в закономерности есть сбой — один или два человека в преклонных годах имеют высокий оптимизм. Они и нарушают общую закономерность и «снижают» коэффициент корреляции.

А теперь попробуйте сами объяснить, что значит, если коэффициент корреляции равен 0? Правильно, в этом случае никакой связи между переменными нет. Невозможно, зная возраст, предсказать позитивность взгляда на мир. И, наоборот, нельзя, зная оптимизм двоих испытуемых, сказать, кто старше. Но и эту информацию можно использовать. При поиске оптимистов для работы в «отделе бесперспективных проектов» не стоит смотреть на возраст.

 

Вывод

Надеюсь, теперь термин «корреляция» вас не пугает. Уверен, что вы сможете отличить функциональную связь (движение мышки и курсора) и корреляционную (время тренировок и высота прыжка). Имейте в виду, что, когда в обыденной речи просто говорят о корреляции, то имеют в виду положительную и значимую (достаточно высокую) взаимосвязь.

Этих знаний вполне хватит, чтобы понимать других и самому к месту ввернуть этот термин. Для более глубокого изучения необходимо разобраться, какие бывают коэффициенты корреляции, как их рассчитывать, как интерпретировать результаты. Это может быть полезно студентам, при проведении эмпирических исследований по психологии или социологии; при написании дипломных и курсовых.

 

Корреляции в дипломах по психологии

Коэффициент корреляции Пирсона

Коэффициент корреляции Спирмена

 

 

---

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать

dip-psi.ru

корреляция — это… Что такое корреляция?

   КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio — соотношение) — термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений.

   Большинство психологических опытов — как исследовательских, так и диагностических — ставится с целью обнаружения корреляции психических явлений и свойств друг с другом либо с явлениями биологическими, социальными и прочими. Правильнее было бы сказать, что целью почти всякого опыта является выяснение взаимосвязи и взаимозависимости явлений. Это и понятно: установление такой взаимосвязи впоследствии позволяет по одному какому-то явлению судить и о многих других. Например, установив взаимосвязь такого внепсихологического фактора, как цвет глаз или волос, с некими психическими особенностями — скажем, со свойствами темперамента, — можно значительно облегчить визуальную экспресс-диагностику и судить о темпераменте человека, едва окинув взглядом конкретного индивида. Такой подход таит немалый соблазн, и многие энтузиасты ему безоглядно поддаются. Увы, в том конкретном случае, когда речь заходит о связи внешних черт и психологических свойств (а на этом зиждятся все физиогномические построения), большинство взаимозависимостей усмотрены весьма произвольно. Более того — во всех подобных случаях речь идет именно о корреляции, да и то довольно спорной. Этим и определяется Уязвимость физиогномики. Впрочем, как показывает практика, не только физиогномики, но и многих научных и практических выводов, претендующих на психологичность.

   Наряду со многими иноязычными словами понятие «корреляция» прочно утвердилось в лексиконе отечественных психологов. Многие, однако, не вполне отдают себе отчет в его буквальном значении и используют этот термин просто как более изысканную замену знакомому понятию «взаимосвязь», подобно тому как стало немодно говорить о самосознании, зато у всех на устах «Я-концепция». Но если в последнем случае синонимичность терминов могла бы стать предметом пространной научной дискуссии, то в случае с корреляцией и взаимосвязью и дискутировать не о чем. Говоря о взаимосвязи явлений, мы подразумеваем, что эти явления определенным образом влияют друг на друга. Корреляция означает лишь сочетание этих явлений, сопутствие одного другому, но вовсе необязательно — их взаимовлияние. Коррелирующие явления и свойства могут быть взаимосвязаны. А могут и не быть; то есть наличие корреляции — еще не достаточный повод для утверждения о взаимозависимости. Если же взаимосвязь существует, то факт корреляции сам по себе ничего не проясняет в причинно-следственной зависимости, то есть направленности влияния.

   Для наглядности обратимся к наиболее показательным примерам из педагогической практики. Как известно, первые тесты интеллекта еще в начале XX в. были созданы для того, чтобы из массы учащихся отсеять неспособных к освоению школьной программы. Впоследствии они были усовершенствованы, с тем чтобы ранжировать учащихся по степени их способности успешно учиться. В основе этих построений лежал постулат о том, что интеллект и школьная успеваемость — явления тесно взаимосвязанные, причем второе однозначно зависит от первого. Многие практики придерживаются этого постулата и поныне, полагая, что оценка интеллекта посредством тестирования — надежное основание для педагогического прогноза.

   Соответственно, критерием валидности теста должна служить высокая степень корреляции тестового балла со школьной успеваемостью. Действительно, такая корреляция имеет место, и это, казалось бы, позволяет без колебаний интерпретировать тестовые баллы. Однако многолетние исследования этой проблемы заставили усомниться в однозначности таких толкований.

   Установлено: низкий (ниже определенного уровня) интеллект практически не оставляет надежды на высокие учебные достижения. То есть до определенного уровня (который, вероятно, можно обозначить конкретным тестовым баллом) корреляция однозначно подразумевает прямую взаимосвязь интеллекта и успеваемости. Однако превышение этого уровня уже не позволяет делать выводы о прямой зависимости. В действие вступает такой принципиальный фактор, как мотивация учебной деятельности. Нельзя сказать, что на более низком уровне интеллекта он незначим. Высокая мотивация малоспособного ученика позволяет ему достичь максимальных для его уровня успехов, которые, увы, не могут быть очень высокими. Для успешного освоения школьной программы необходим некий базовый уровень интеллекта, на котором мотивация приобретает решающее значение. Без учета этого фактора мы никогда не сможем понять, почему из двух равно способных учеников один превосходит другого по параметру успеваемости. Слепое доверие к корреляции заведет нас в тупик и не позволит объективно оценить реальную педагогическую проблему.

   Еще один пример наглядно иллюстрирует, как переоценка корреляционного сочетания приводит к заблуждению. В ряде исследований была выявлена корреляция (впрочем, и без того эмпирически очевидная) самооценки и успеваемости. Это дало повод для далекоидущих выводов о необходимости коренной перестройки педагогической стратегии. В качестве важнейшей задачи учебно-воспитательного процесса было выдвинуто формирование у школьников высокой самооценки, позитивного самосознания, уверенности в себе. Гуманистический по своему пафосу, такой подход, однако, оказался вовсе не столь эффективен, как ожидалось. Выяснилось, что стимулирование самооценки, не подкрепленное объективными основаниями, оказывает скорее тормозящее влияние, ибо позволяет человеку испытывать удовлетворение и уверенность в себе даже при очень невысоком уровне реальных достижений. Массированным «поглаживанием» сформировать у человека высокую самооценку не так уж сложно, но при этом исчезает всякая ее корреляция с достижениями (в частности — с учебными). А это заставляет переосмыслить характер и направленность взаимозависимости. Очевидно, что высокие достижения порождают высокую самооценку. Обратное влияние спорно. То есть и тут, вероятно, существует некий барьер, за которым сочетание факторов приобретает совершенно особый характер. Успешность учебной деятельности требует определенного уровня самооценки: если самооценка ниже этого уровня, мотивация сильно страдает. Поэтому стимулирование целесообразно лишь до достижения данного уровня, а впоследствии может даже оказать обратное действие. Ведь известно, например, что высокий уровень благосостояния семьи нередко порождает у ребенка необоснованно завышенную самооценку, а это, в свою очередь, искажает учебную мотивацию.

   Таким образом, психологу в практической работе недопустимо ограничиваться установлением корреляций, поскольку пока не установлен факт объективной взаимосвязи и ее направленности. Поспешный вывод чреват серьезными ошибками. Знание одной переменной позволяет нам делать вывод о существовании другой, но это справедливо лишь для определенной степени выраженности переменной; при изменении этой степени сочетание может осложниться дополнительными факторами и даже кардинально изменить свой характер. К тому же само по себе наличие сочетания, как правило, ничего не говорит о причинно-следственном отношении.

   Психолог, столкнувшийся с конкретными поведенческими проблемами человека, легко может установить их сочетание с его психологическими качествами. Но констатация такого сочетания не только ничего не объясняет по сути, но и может увести в противоположном направлении. Избежать заблуждения можно лишь при многостороннем анализе разнообразных факторов с опорой на не вызывающие сомнения причинно-следственные взаимосвязи.

Популярная психологическая энциклопедия. — М.: Эксмо. С.С. Степанов. 2005.

psychology.academic.ru

Понятие о корреляции и корреляционном анализе в психологии

Московский государственный социальный университет

Филиал в г. Минске

ПОНЯТИЕ О КОРРЕЛЯЦИИ И КОРРЕЛЯЦИОННОМ АНАЛИЗЕ В ПСИХОЛОГИИ. ВИДЫ КОРРЕЛЯЦИЙ.

Контрольная работа №3 по предмету

«Основы психологического экспериментирования»

студентки 5 курса з/о

Минск 2005

СОДЕРЖАНИЕ

Введение

1. Понятие корреляции

2. Виды корреляций

3. Корреляционный анализ

3.1 Коэффициент корреляции рангов Спирмена

3.2 Коэффициент корреляции Пирсона

3.3 Случай одинаковых (равных) рангов

3.4 Расчет уровней значимости коэффициентов корреляции

3.5 Коэффициент корреляции «φ»

3.6 Коэффициент корреляции «τ» Кендалла

3.7 Бисериальный коэффициент корреляции

3.8 Рангово-бисериальный коэффициент корреляции

3.9 Корреляционное отношение Пирсона η

3.10 Множественная корреляция

3.11 Частная корреляция

Заключение

Список использованной литературы

ВВЕДЕНИЕ

Усиление интереса в психологической науке к потенциалу корреляционного анализа обусловлено целым рядом причин. Во-первых, становится допустимым изучение широкого круга переменных, экспериментальная проверка которых затруднена или невозможна. Ведь по этическим соображениям, к примеру, нельзя провести экспериментальные исследования самоубийств, наркомании, деструктивных родительских воздействий, влияния авторитарных сект. Во-вторых, возможно получение за короткое время ценных обобщений данных о больших количествах исследуемых лиц. В-третьих, известно, что многие феномены изменяют свою специфику во время строгих лабораторных экспериментов. А корреляционный анализ предоставляет исследователю возможность оперировать информацией, полученной в условиях, максимально приближенных к реальным. В-четвертых, осуществление статистического изучения динамики той или иной зависимости нередко создает предпосылки к достоверному прогнозированию психологических процессов и явлений.

Однако следует иметь в виду, что применение корреляционного метода связано и с весьма существенными принципиальными ограничениями.

Так, известно, что переменные вполне могут коррелировать и при отсутствии причинно-следственной связи между собой.

Это иногда возможно в силу действия случайных причин, при неоднородности выборки, из-за неадекватности исследовательского инструментария поставленным задачам. Такая ложная корреляция способна стать, скажем, «доказательством» того, что женщины дисциплинированнее мужчин, подростки из неполных семей более склонны к правонарушениям, экстраверты агрессивнее интровертов и т. п.

Необходимо запомнить: наличие корреляций не является показателем выраженности и направленности причинно-следственных отношений.

Другими словами, установив корреляцию переменных мы можем судить не о детерминантах и производных, а лишь о том, насколько тесно взаимосвязаны изменения переменных и каким образом одна из них реагирует на динамику другой (2).

1. ПОНЯТИЕ КОРРЕЛЯЦИИ.

Термин «корреляция» впервые применил французский палеонтолог Ж. Кювье, который вывел «закон корреляции частей и органов животных» (этот закон позволяет восстанавливать по найденным частям тела облик всего животного). В статистику указанный термин ввел в 1886 году английский биолог и статистик Френсис Гальтон (не просто связь – relation, а «как бы связь» – co-relation). Однако точную формулу для подсчёта коэффициента корреляции разработал его ученик – математик и биолог — Карл Пирсон (1857 – 1936).(7).

Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными. В психологии переменными могут выступать психические свойства, процессы, состояния и др.

«Корреляция» в прямом переводе означает «соотношение». Если изменение одной переменной сопровождается изменением другой, то можно говорить о корреляции этих переменных. Наличие корреляции двух переменных ничего не говорит о причинно-следственных зависимостях между ними, но дает возможность выдвинуть такую гипотезу. Отсутствие же корреляции позволяет отвергнуть гипотезу о причинно-следственной связи переменных. Различают несколько интерпретаций наличия корреляционной связи между двумя измерениями:

1. Прямая корреляционная связь. Уровень одной переменной непосредственно соответствует уровню другой. Примером является закон Хика: скорость переработки информации пропорциональна логарифму от числа альтернатив. Другой пример: корреляция высокой личностной пластичности и склонности к смене социальных установок.

2. Корреляция, обусловленная третьей переменной. Две переменные (а, с) связаны одна с другой через третью (в), не измеренную в ходе исследования. По правилу транзитивности, если есть R (а, Ь) и R (Ь, с), то R (а, с). Примером подобной корреляции является установленный психологами США факт связи уровня интеллекта с уровнем доходов. Если бы такое исследование проводилось в сегодняшней России, то результаты были бы иными. Очевидно, все дело в структуре общества. Скорость опознания изображения при быстром предъявлении и словарный запас испытуемых также положительно коррелируют. Скрытой переменной, обусловливающей эту корреляцию, является общий интеллект.

3. Случайная корреляция, не обусловленная никакой переменной.

4. Корреляция, обусловленная неоднородностью выборки. Представим себе, что выборка, которую мы будем обследовать, состоит из двух однородных групп. Например, мы хотим выяснить, связана ли принадлежность к полу с уровнем экстраверсии. Считаем, что «измерение» пола трудностей не вызывает, экстраверсию же измеряем с помощью опросником Айзенка ETI-1. У нас две группы: мужчины-математики и женщины-журналистки. Не удивительно, если мы получим линейную зависимость между полом и уровнем экстраверсии — интроверсии: большинство мужчин будут интровертами, большинство женщин — экстравертами (3, 4).

2. ВИДЫ КОРРЕЛЯЦИЙ

Виды корреляционной связи между измеренными переменными могут быть различны: так корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна, если с увеличением или уменьшением одной переменной, вторая переменная также растёт, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами (полиномиальная, гиперболическая). (5).

Если повышение уровня одной переменной сопровождается повышением уровня другой, то речь идет о положительной корреляции. Чем выше личностная тревожность, тем больше риск заболеть язвой желудка. Возрастание громкости звука сопровождается ощущением повышения его тона.

Если рост уровня одной переменной сопровождается снижением уровня другой, то мы имеем дело с отрицательной корреляцией. По данным Зайонца, число детей в семье отрицательно коррелирует с уровнем их интеллекта. Чем боязливей особь, тем меньше у нее шансов занять доминирующее положение в группе.

Нулевой называется корреляция при отсутствии связи переменных. (2).

В психологии практически нет примеров строго линейных связей (положительных или отрицательных). Большинство связей — нелинейные. Классический пример нелинейной зависимости — закон Йеркса—Додсона:. возрастание мотивации первоначально повышает эффективность научения, а затем наступает снижение продуктивности (эффект «перемотивации»). Другим примером является связь между уровнем мотивации достижений и выбором задач различной трудности. Лица, мотивированные надеждой на успех, предпочитают задания среднего диапазона трудности — частота выборов на шкале трудности описывается колоколообразной кривой.

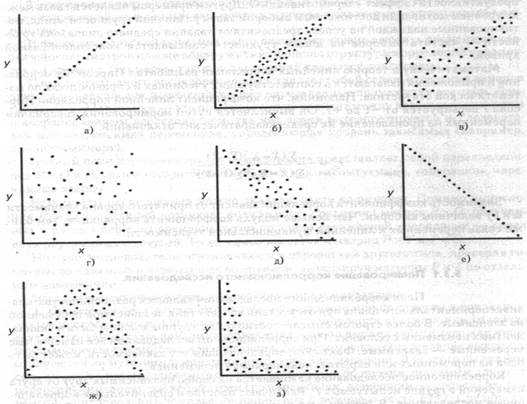
Примеры распределений испытуемых в пространстве двух признаков.

а) строгая положительная корреляция, б) сильная положительная корреляция, в) слабая положительная корреляция, г) нулевая корреляция, д) отрицательная корреляция, е) строгая отрицательная корреляция, ж) нелинейная корреляция, з) нелинейная корреляция.

3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Корреляционный анализ (от лат. «соотношение», «связь») применяется для проверки гипотезы о статистической зависимости значений двух или нескольких переменных в том случае, если исследователь может их регистрировать (измерять), но не контролировать (изменять).(2). Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.

Графики корреляционных зависимостей строят по уравнениям следующих функций:

Y

mirznanii.com

Корреляционный анализ — это… Что такое Корреляционный анализ?

Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.

Коэффициент корреляции

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.

Коэффициент корреляции Пирсона

Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:

Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

,

где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,

,

где символ обозначает математическое ожидание.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).

Коэффициент корреляции Кенделла

Используется для измерения взаимной неупорядоченности.

Коэффициент корреляции Спирмена

Свойства коэффициента корреляции

если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:

.

• Коэффициент корреляции равен тогда и только тогда, когда X и Y линейно зависимы:

,

где . Более того в этом случае знаки и k совпадают:

.

• Если X,Y независимые случайные величины, то . Обратное в общем случае неверно.

Корреляционный анализ

Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.

Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.

Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin²(x) + cos²(x) = 1.

Ограничения корреляционного анализа

Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).

1. Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
2. Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
3. Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.

Область применения

Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Ложная корреляция

Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.

В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

No related posts.