Математические методы в психологии: Математические методы в психологии

Математические методы в психологии

Примеры решенийПоказатели вариацииДоверительный интервал Расчет моды и медианы Группировка данныхДецили Проверка гипотез по Пирсону Корреляционная таблица Квартили

Данный раздел представлен следующими онлайн-калькуляторами.

Методы описательной статистики

1. Построение вариационных рядов. Пример. Сгруппировать данные, классифицируя оценки по распределения частот.
2. Построение доверительных интервалов для математического ожидания и среднего квадратического отклонения нормально распределенной случайной величины. Пример. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0.95, зная выборочную среднюю x, объем выборки n и среднее квадратическое отклонение σ.
3. Показатели вариации. Пример. Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. Требуется: 1) Упорядочить данные (по убыванию) в каждой выборке; 2) Рассчитать моду, медиану и среднее; 3) Сделать сравнительный анализ полученных результатов; 4) Посчитать дисперсию, стандартное отклонение; 5) Посчитать коэффициент вариации; 6) Рассчитать асимметрию и эксцесс; 7) Сделать интерпретацию результатов.

Меры связи между признаками

1. Расчет коэффициента Фехнера;
2. Расчет коэффициента Спирмена;
3. Расчет коэффициента Кендэла;
4. Коэффициент конкордации.
5. Коэффициент контингенции.

Методы проверки статистических гипотез

1. Проверка статистических гипотез
2. Ранжирование данных
3. Критерий Манна-Уитни
4. Критерий Вилкоксона
5. Проверка гипотезы о равенстве дисперсий и генеральных средних.
6. Проверка статистических гипотез о виде распределения

Многомерный анализ данных

1. Методом одномерного дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта.
2. Двумерный анализ может использоваться для проверки воздействия двух независимых переменных и возможного эффекта взаимодействия на зависимую переменную.
3. Метод средних оценок.
4. Метод медиан рангов.

Какие критерии следует использовать в случаях, когда выборки независимы и когда зависимы.

1. Выборки независимы (например, выборка населения из городской и сельской местности).
   • Q–критерий Розенбаума, используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного
   • U–критерий Манна-Уитни
   • F–критерий Фишера, используется для установления сходства-различия дисперсий в двух независимых выборках
   • t–критерий Стьюдента, используется для установления сходства-различия средних арифметических значений в двух выборках или в более общем виде, для установления сходства-различия двух эмпирических распределений
2. Выборки зависимы (например, одна и та же выборка испытуемых, но замеры делаются до и после эксперимента).
   • T–критерий Вилкоксона, применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить направленность изменений, и их выраженность.
   • t–критерий Стьюдента.
   • t–критерий Спирмена.
   • Cs–критерий Ман-Мемара.

Функции Excel

Критические точки распределения Стьюдента: СТЬЮДРАСПОБР(вероятность; степени_свободы).
Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента.
Степени_свободы — число степеней свободы, характеризующее распределение.

При решении задач для проверки надежности показателей используются статистические таблицы:

• Распределение Стьюдента (t-распределение)
• Распределение Фишера (F-распределение)
• Таблица значений функции Лапласа
• Статистические таблицы Дарбина-Уотсона
• Распределение ХИ квадрат (X2). Используется для определения доверительного интервала дисперсии.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

что это и основные виды

Содержание

• Суть и задачи
• Этапы развития и формирования
• Основные виды
• Стратегии обработки данных при работе с гипотезами
• Преимущества и недостатки
• Принципы применения в исследованиях

Психология — гуманитарная дисциплина. Поэтому у студентов начальных курсов возникает много вопросов, когда им приходится изучать высшую математику. Многие не знают, что такое математические методы в психологии — обязательный инструмент для анализа или усложненный прием, который можно заменить. Ответ можно получить только на практике, изучив особенности работы методики.

Суть и задачи

Математическая психология применяется для оценки полученных результатов и моделирования абстрактных ситуаций, требующих проверки.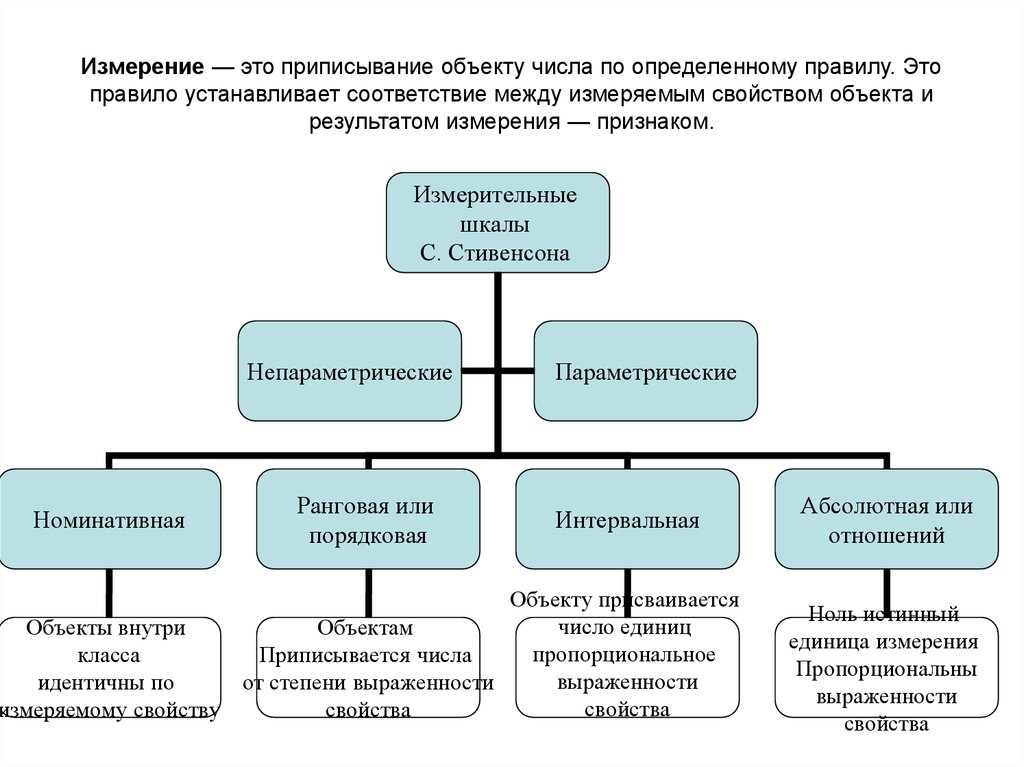 Аналитическое исследование не используется для изучения конкретного явления. Оно рассматривает психическую деятельность совокупно.

Объект исследований — естественная структура, имеющая психические свойства, модель, теоретическую базу. Предмет — создание и применение алгоритма для моделирования подобной структуры.

Математические методы нужны для обработки данных, собранных путем наблюдения или эксперимента. С их помощью решают задачи:

• на установление сходства или различия;
• на группировку, классификацию информации;
• на оценку, анализ источников данных;
• на составление прогноза на основе полученной информации.

Сущность матметодов — описание психологических явлений с помощью количественных показателей. Применение алгоритмов при подсчете результатов снижает риск появления ошибки. Информацию можно собирать, обрабатывать и классифицировать одновременно.

Этапы развития и формирования

Сейчас математика занимает отдельное место в психологии. Ее выделение в самостоятельную дисциплину шло постепенно. В этом процессе есть отдельные этапы, подробно рассмотренные в книге Первитской А. М. «Математические методы в психологии»:

1. Первый — конец 19 – начало 20 века. Результаты эксперимента впервые обрабатываются заданным алгоритмом. Сформировались первые законы и дисциплины.
2. Второй — 40–50 г. Появилась первая модель психических процессов, разработанная с использованием матанализа. Проведение практических испытаний.
3. Третий — с 60 годов по настоящее время. Официальное признание самостоятельности отрасли. Включение в список обязательных для изучения дисциплин.
4. Четвертый — время наступления неизвестно. Этот этап будет переходом математической психологии в теоретическую.

Математическую психологию часто воспринимают как совокупность матметодов, но на самом деле они — только часть дисциплины, как эксперимент — часть исследования.

Основные виды

Шкала измерений — удобный способ обработки данных. В первую очередь используют количественную шкалу. С ее помощью данные ранжируют — распределяют по показателям. Данные размещаются в порядке убывания или возрастания. Каждому значению добавляют ранг, определяющий минимальный и максимальный показатель. Сравнение рангов необходимо для распределения данных по группам.

Корреляционный анализ — установление связи между явлениями. Корреляцию оценивают по силе, направлению. Показатели могут возрастать и убывать, из-за чего меняется тип зависимости данных. Он бывает линейным (показатели равноудалены), но чаще выражен в форме кривой.

Факторный анализ — прогнозирование результатов. Изначально данные расцениваются как равные показатели, для получения результатов их табулируют (заносят в таблицу) или используют графическое построение.

Стратегии обработки данных при работе с гипотезами

Гипотеза — предположение, требующее проверки. Чтобы использование методов математической обработки в психологии давало достоверный результат, исследователи должны соблюдать правила выбора, проверки гипотезы:

1. Статистические гипотезы бывают нулевыми и альтернативными. Они несовместимы и взаимоисключающие.
2. Проверять гипотезу нужно с помощью статистических критериев — правил, по которым принимают истинную и отклоняют ложную гипотезу.
3. Критерии бывают параметрическими (данные распределены по шкале) и непараметрическими (распределение данных не учитывается).
4. Порядок проверки критериев включает выбор критерия, определение зависимости или независимости выборки, количество выборок.
5. Гипотезу оценивают по числовым характеристикам. Точечно, выбрав одно число на оси, или интервально, используя измерение отрезка данных на оси.

Выбор способа проверки гипотезы зависит от поставленной задачи.

Преимущества и недостатки

С помощью алгоритмов можно оперировать большим объемом данных и получать достоверные результаты. Недостатки:

1. Результаты моделирования необходимо подтверждать экспериментом в реальных условиях.
2. Моделирование не дает заглянуть дальше исследуемой области данных.
3. При выборе эксперимента повышается риск «подгонки» реальных данных под моделируемый процесс.

Принципы применения в исследованиях

Принципы применения математических методов — положения, которые используют в психологии. Они определяют применение и стратегии дальнейшего развития науки. К ним относятся:

1. Принцип детерминизма. Требует объяснения изучаемых феноменов через общепринятые факты (под общепринятыми понимаются факты, официально признанные учеными и опубликованные в соответствующей литературе).
2. Деятельность, личность и сознание едины. Личность — носитель сознания, а сознание неотделимо от личности. Деятельность — форма взаимодействия личности с миром, определяемая причинно-следственной связью.
3. Личностный и системный подход. Требует рассматривать объекты как отдельные, присущие одному человеку и группе.
4. Обусловленность рефлекторной и социальной составляющей. Объективный мир влияет на психику, поэтому психические явления — отражение окружающей действительности.
5. Принцип совокупности. Требует исследования явления как единого целого.
6. Принцип развития. Явления необходимо рассматривать во время развития, с учетом причин появления и возможных вариантов объединения.
7. Принцип иерархии. Предполагается рассматривать психологические явления как лестницу, с подчинением низших ступеней высшим.
8. Единство теории, эксперимента и практики. Теория проверяется практическим экспериментом, необходимым для поиска решения.

Чтобы получать достоверные результаты, психолог должен соблюдать все принципы.

Несмотря на все недостатки, матметоды все же остаются подходящим инструментом проверки гипотез, снижающими вероятность погрешности. Точность результатов в большей степени зависит от навыков исследователя, чем от выбранного способа оценки.

Рейтинг автора

Написано статей

Об авторе

Математическая психология — Психология — Оксфордские библиографии

Введение

Математическая психология — это отрасль психологии, занимающаяся использованием математических и вычислительных моделей для объяснения и прогнозирования человеческого поведения. Типичными областями интереса являются память, внимание, решение проблем, восприятие, принятие решений и двигательный контроль. Область возникла из проблем измерения, с которыми сталкивается психофизика, с упором на поведенческие реакции. Он развивался с развитием технологий, таких как передовые компьютерные системы и системы визуализации мозга, которые стимулировали рост нейронауки. По мере роста числа инструментов для исследований в этой области росла сложность и сложность моделей. Однако уникальной характеристикой математической психологии является ее потенциальная роль во всех областях психологии. Все «содержательные» области психологии (например, клиническая, социальная и связанная с развитием) могут иметь как эмпирическую, так и математическую основу. По мере роста сложности и нюансов эта область вносит все больший вклад в эти более широкие области.

Учебники и основные тексты

Существует ряд важных учебников, которые, хотя и устарели, все еще используются в начале 21 века для преподавания математической психологии на уровне выпускников и до сих пор используются в качестве важных справочных материалов. Более новые тексты включают исторические обзоры и современные вычислительные подходы, которых не было на практике, когда математическая психология была признана отдельной дисциплиной. Батчелдер и др. Обновления 2016 г. Люс и др. 1963. Люс и др. 1963 год был первой классической попыткой сделать обзор литературы по математической психологии и представить математическую психологию как единую дисциплину. Батчелдер и др. В 2016 г. представлен исчерпывающий обзор современной математической психологии. Буземейер и др. 2015 дает еще один всесторонний обзор современной математической психологии. Ламинг 1973 представляет собой обзор математической психологии, узко сфокусированный на вопросах, возникающих при моделировании памяти, но обеспечивающий всестороннее представление проблемы накопления информации при простом выборе, проблемы, которая лежит в основе многих современных исследований в области познания. Restle and Greeno 1970 — менее известный учебник, в котором изложение материалов сильно зависит от бихевиоризма и математической теории обучения. Кумбс и др. 1970 — это первый учебник, доступный для студентов, который остается важным историческим справочником, включающим ряд важных основополагающих тем.

• Батчелдер, У. Х., Х. Колониус, Э. Джафаров и Дж. И. Мьюнг, ред. 2016. Новый справочник по математической психологии . тт. 1–2. Кембридж, Великобритания: Кембриджский унив. Нажимать.

  Обновленное издание классического справочника по математической психологии Luce et al. 1963 года , в котором дисциплина математической психологии представлена ​​в современном контексте.

• Busemeyer, J. R., and A. Diederich. 2010. Когнитивное моделирование . Лос-Анджелес: SAGE.

  Вводный учебник, посвященный конкретным вопросам построения и оценки моделей для когнитивной психологии.

• Busemeyer, J. R., Z. Wang, J. T. Townsend и A. Eidels. 2015. Оксфордский справочник по вычислительной и математической психологии . Нью-Йорк: Оксфордский ун-т. Нажимать.

  Еще один всеобъемлющий обзор современной математической психологии.

• Кумбс, С. Х., Р. М. Доус и А. Тверски. 1970. Математическая психология: Элементарное введение . Оксфорд: Прентис-Холл.

  Первый учебник по математической психологии, важный исторический справочник, включающий ряд важных основополагающих тем.

• Laming, D. R. J. 1973. Математическая психология . Лондон: Академическая пресса.

  Еще одна основополагающая ссылка, не такая широкая, как другие тексты того времени, но с большим вниманием к темам накопления информации и проблемам, связанным с моделированием памяти.

• Люс, Р. Д., Р. Р. Буш и Э. Галантер, ред. 1963. Справочник по математической психологии . Том. 1. Оксфорд: Джон Уайли.

  Первая классическая попытка сделать обзор литературы по математической психологии и представить математическую психологию как единую дисциплину.

• Рестл Ф. и Дж. Г. Грино. 1970. Введение в математическую психологию . Оксфорд: Аддисон-Уэсли.

  Менее известный учебник, в котором на изложение материалов сильно повлияли бихевиоризм и математическая теория обучения.

наверх

Пользователи без подписки не могут видеть весь контент на эта страница. Пожалуйста, подпишитесь или войдите.

Как подписаться

Oxford Bibliographies Online доступен по подписке и с бессрочным доступом к учреждениям. Чтобы получить дополнительную информацию или связаться с торговым представителем Oxford, нажмите здесь.

Значение математики и статистики в области психологии

Опубликовано 9 августачт, 2021 г. в Соискатели

Вы выбрали специализацию в области психологии, но не ожидали всей математики, которая с этим связана. Честно говоря, математика вам не по душе, поэтому вы не понимаете, зачем вам нужно ходить на такие курсы, как статистика. Конечно, эти классы не были бы необходимы, если бы они не служили очень хорошей цели.

Математика может помочь психологам лучше понять мозг и интерпретировать данные. Поэтому важно иметь эти навыки, чтобы вы могли быть максимально эффективными в своей работе. Вот несколько примеров того, как математика и статистика имеют решающее значение для области психологии.

Лучшее понимание исследований в области психологии  

Если вы будете в курсе последних исследований в области психологии, это поможет вам обеспечить наилучший уход за пациентами. Однако вы не сможете сделать это, не разбираясь в математике и статистике. Как вы, возможно, уже знаете, опубликованные исследования часто содержат таблицы, графики и статистические анализы, которые человеку без этих знаний может быть трудно интерпретировать. Если вы не понимаете этих концепций, вы окажетесь в невыгодном положении, потому что не сможете полностью понять результаты исследования.

Улучшите свои навыки критического мышления  

Решение проблем — важная часть работы психолога. Поскольку нет двух одинаковых пациентов, вам нужна способность мыслить на ходу. Вы можете этого не осознавать, но знания математики и психологии могут помочь улучшить ваши навыки критического мышления. Когда вы читаете исследования по психологии, вам необходимо понимать процесс, используемый исследователями для оценки влияния любых важных результатов. Знание статистики — это не просто ряд математических формул — оно соответствует лежащим в основе отношениям между переменными, которые вы обнаруживаете при изучении человеческого поведения.

Сбор и анализ данных  

Работая в области психологии, вполне возможно, что вы будете проводить собственные исследования. Знание математики и статистики поможет вам лучше структурировать свои исследования, улучшить методы сбора данных, а также лучше анализировать и интерпретировать данные. Без этих знаний ваше исследование может — без вашего ведома — содержать недостатки, делающие его менее эффективным. Вы также можете совершить другие ключевые ошибки, например, не собрать данные нужного типа, неправильно проанализировать данные и неверно интерпретировать результаты.