Что узнали. Чему научились. Работа над ошибками. 2 класс
Математика 2 класс.
Тема: Что узнали. Чему научились.
Работа над ошибками.
Цель: формирование способности видеть и анализировать ошибки, допущенные в контрольной работе; закреплять знания, умения и навыки, полученные на предыдущих уроках.
Планируемые результаты: учащиеся научатся находить и исправлять свои ошибки; соотносить свои знания с заданием, которое нужно выполнить; рассуждать и делать выводы; выполнять задания творческого и поискового характера; контролировать и оценивать свою работу и ее результат.
Ход урока
I Организационный момент.
II. Актуализация знаний
1) Работа над ошибками (разбор задач 1 и 2 вариантов).
— Ребята, сегодня у нас будет тема закрепление пройденного материала.
— Какие цели мы можем поставить на урок? (повторить, закрепить изученное).
2).
3). Работа над задачами
• В упаковке 12 штук витаминов. В день можно принимать по 2 штуки. На сколько дней хватит этих витаминов?
• В упаковке 12 штук витаминов. Их надо раздать двум детям. Сколько витаминов получит каждый?
— Чем похожи и чем отличаются данные задачи?
4). Логическая разминка
— Запишите число 25 пятью цифрами 5.
(25= 5 +5 +5+5 + 5.)
— Выразите число 27 тремя девятками.
(27 = 9+9 +9)
III. Работа по теме урока «Что узнали. Чему научились»
Работа по учебнику
1. № 19 (с. 67). (Устное выполнение с комментированием)
2. №8 (с. 63).
— Составьте задачи по данным рисункам.
— Решите задачи самостоятельно: 1 вариант – первую задачу, 2 вариант — вторую задачу.
(Проверка в парах.)
3. № 9 (с. 63). (Устное выполнение.)
IV. Физкультминутка
Так проворны наши руки
Нет им времени для скуки
Руки вверх, вперед, назад –
С ними можно полетать!
Мы на пояс их поставим
И наклоны делать станем
Ими можно помахать,
А прижав, тихонько спать,
Руки вверх поднимем выше
И легко-легко подышим.
V. Продолжение работы по теме урока
Работа по учебнику
1). №48 (с. 70).
— Прочитайте задание 1. Постройте прямоугольник.
— Прочитайте задание 2.
— Можем ли мы сразу выполнить это задание? (Нет.)
— Почему? (Не знаем, чему равен периметр прямоугольника.)
— Найдите периметр прямоугольника рациональным
способом. ((2 + 3) х 2= 10(см).)
— Начертите отрезок.
— Постройте ломаную такой же длины, состоящую из пяти одинаковых звеньев.
2). №40 (с. 69) Самостоятельное выполнение.
Проверка. (Учащиеся по цепочке называют ответы.)
VI. Закрепление ранее изученного материала.
Работа по учебнику
№. 49, 51(с.70). Самостоятельное выполнение. Проверка.
— Оцените свою работу на уроке.
VII. Рефлексия. Подведение итогов урока.
— Какие знания мы закрепляли на уроке?
— Кто правильно вычислил периметр прямоугольника?
— Какие задачи решали на уроке?
— Всё ли вам было понятно?
— Какое задание вам показалось особенно трудным?
VIII. Домашнее задание
Домашнее задание
№ 15 (с. 66), 28 (с. 68) — 1 вариант,
№ 47,48 (с. 70) — 2 вариант.
Памятки по работе над ошибками по математике.
РАБОТА НАД ОШИБКАМИ
1. Решение задачи
Перечитай задачу, проверь краткую запись.
Все ли данные записаны, поставлен ли вопрос.
Поясни, что показывает каждое число, повтори вопрос задачи.
Что нужно знать, чтобы ответить на вопрос задачи?
Объясни, как будешь решать задачу по действиям или выражением.
Запиши решение с пояснением (если решаешь по действиям).
Проверь, написал ли наименование в решении.
Запиши ответ.
Ошибки в вычислении задачи
Перепиши решение задачи, запиши правильный ответ.
2. Решение уравнений
Запиши уравнение, назови компоненты действия.
Как найти неизвестный компонент.
Реши уравнение.
34 + Х =49 49 – х = 34 х — 34 = 15
Х= 49- 34 х = 49 – 34 х = 15+34
Х = 15 х= 15 х= 49
34+15 = 49 49 – 15= 34 49 — 34 = 15
3. Периметр и площадь
Периметр – сумма длин сторон. Измеряется в км, дм, см, мм.
Р= (а+в)*2
Площадь прямоугольника равна произведению длины и ширины. Измеряется в квадратных единицах.
S=а*в
4. Неравенства.
Записать неравенство и поставить знак сравнения,
Если в неравенстве есть действия, то сначала надо сделать вычисления.
5 40
25 : 5 * 46 – 6
25 : 5 46 – 6
5. Формулы для решения задач
Ц = Ст : К Ц – цена
К = Ст : Ц К — количество
Ст = Ц×К Ст – стоимость
S =V × t S – расстояние
V = S : t V – скорость
t = S : V t – время
М общ = М 1 × К М общ – общая масса
М 1 = М общ : К М 1 – масса 1 предмета
К = М общ : М 1 К – количество предметов
Цена | Количество | Стоимость |
5 р. | ? шт. | 15р. |
К= Ст : Ц
15 : 5 = 3 ( тетр.)
Ответ: купили 3 тетради.
Масса 1 | Количество | Общая масса |
? кг | 6 ящ. | 42 кг |
6. Порядок действий.
Действия первой ступени + — выполняются по порядку.
Действия второй ступени × : выполняются по порядку.
В выражениях со скобками первое действие в скобках.
Если
действия 1 и 2 ступени вместе, то сначала выполняются действия второй ступени.
1 2 2 1
54 + 23 – 48= 29 44 + (23 -12) = 55
1 2 2 1
18 : 3 × 2 = 12 34 — 5×3 = 19
Задачи | Дополнительные задания | |
а) №1 S =U · t U = S : t t = S : U ? ? 2 ч. 7ч. __________________________________ 130 км ? км ? б) Составьте модель задачи по чертежу из двух полосок бумаги разного цвета, нанесите числовые данные. Покажите на модели? Какой отрезок пути неизвестен? Покажите на модели. | №1 За два часа автобус прошёл 130 км, а затем с такой же скоростью шёл ещё 7 часов. Какой путь прошёл автобус за всё время движения? | №1 1.Запишите решение задачи выражением. 2.Поставьте другие вопросы к условию этой задачи и ответьте на них. 3.Запишите решение задачи другим способом. |
№2 а) P = (а + в)·2 S = а · в б) Моделирование задачи. Приложите два равных квадрата, так, как показано на чертеже. — покажите длину прямоугольника; — из чего она складывается? — покажите ширину; — чему она равна? | №2 Ирина приложила два равных квадрата с длиной стороны 5см один к другому так, что получился прямоугольник. Вычисли периметр и площадь этого прямоугольника. | №2 Увеличь сторону квадрата на 2 см, сложи прямоугольник, вычисли периметр и площадь прямоугольника. |
Работа над ошибками / math5school.ru
В этом разделе сайта разбираются ошибки, наиболее часто встречающиеся в работах учащихся. Освоив материал ниже перечисленных разделов, можно избежать многих ошибок в будущем.
Для удобства ошибки разбираются по темам:
Тождественные преобразования
Решение уравнений
Решение систем уравнений
Решение неравенств
Упражнения с параметрами
Функции и свойства функций
Начала анализа
Геометрия
Существует мнение, что такие итоговые письменные работы, как ЕГЭ, невозможно выполнить успешно из-за слишком высоких требований. Действительно, предъявляемые требования, несколько выше требований, предъявляемых на обычном школьном уроке. {-1}}=\frac{1}{7} \]
{-1}}=\frac{1}{7} \]
\[ \arccos \frac{\pi }{3}=\frac{1}{2} \]
\[ \arccos \frac{1}{2}=\frac{\pi }{3} \]
Прежде чем перейти к разбору конкретных ошибок, обратите внимание на проблемы, возникающие из-за недостатка общей математической культуры.
Во-первых, многие испытывают затруднения при переводе словесного условия задания на язык математических формул, уравнений или неравенств. Например:
L выражение «доказать, что функция f(x) неотрицательна» записывается f(x) > 0 вместо f(x) > 0;
L выражение «при каких значениях х значение функции f(x) равно 2,5» не ассоциируется с уравнением
f(x) = 2,5;
L выражение «найдите радиус шара, объем которого равен объему куба с ребром а» не записывается соотношением 4/3πr3 = a3, хотя каждая из этих формул учащимся очевидно известна;
L выражение «треугольник, образованный осями координат и прямой, их пересекающей» не вызывает необходимости найти точки пересечения этой прямой с осями координат и т. д.
д.
Во-вторых, некоторые учащиеся путаются в элементарных понятиях, например, не могут четко разделить понятия целого и натурального, положительного и неотрицательного чисел. В результате при выборе из множества решений решения, удовлетворяющего условию (например, при выборе наименьшего целого числа промежутка (a; b)), допускаются ошибки.
В-третьих, часто при отборе корней не учитывается область допустимых значений переменной и т.д.
При подготовке данного раздела сайта использовано учебное пособие «Математика. Репетитор» Будная Е.С., Будная С.Н. (Харьков, «Факт», 2008)
I. Организационный Цели: — Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей. | Проверка готовности к уроку, наличие принадлежностей и черновиков. Дети разделены на группы по уровню знаний, есть группа экспертов, которая помогает остальным. Проверка задания (составить синквейн на основе прошедшего урока) Девиз нашего урока таков: Математику нельзя изучать, наблюдая, как это делает сосед. На прошлом уроке мы с вами писали контрольную работу. Сегодня мы постараемся проанализировать допущенные ошибки и найдем способы заполнить пробелы в знаниях. Для этого выполним работу над ошибками. А нужна ли нам работа над ошибками? Может быть, можно обойтись и без нее. Давайте подумаем и спланируем наш урок, какие основные моменты необходимо выполнить, чтобы успешно справиться с нашей работой? План урока: (слайд 2)
2. Повторить понятия по теме пропорция и отношения. 3. Выполнить различные типовые задания по данной теме. 4. Проанализировать уровень понимания материала. 5. Выполнить работу над ошибками. 6. Провести анализ своей работы на уроке. | Приготовиться к уроку, настроиться на работу Ответы учащихся о том, что работа над ошибками необходима, так как она способствует развитию грамотности, помогает повторить изученный ранее материал. Составляют план урока вместе с учителем. | Личностные самоопределяются, настраиваются на урок Познавательные: ставят перед собой цель: «Что я хочу получить сегодня от урока» Коммуникативные: планируют учебное сотрудничество с учителем и одноклассниками. Регулятивные: организация своей учебной деятельности | II. Актуализация опорных знаний Цели: организовать актуализацию изученных способов действий. | Но прежде укрепим наши знания и вспомним основные понятия по теме пропорция. Слайд 3. Однажды археологи, ведя раскопки, на стене одной из пещер нашли следующую запись: | 10 | 3 | 40 | 12 – Что могла означать эта запись? Может ли это быть пропорцией? Почему? – Запишите эту пропорцию. Прочитайте. – Задайте ученику, работающему у доски три вопроса по теме «Пропорции. Отношения».
– Объясните, какими свойствами пропорции вы пользовались? Слайд 4 – Представьте себе, что найденная археологами надпись стерлась от времени и одно из чисел в пропорции пропало. Например так: | 10 | 3 | | 12 . Можно ли восстановить потерянное число? Решим это уравнение. | настраиваются на урок Фронтальная работа Члены пропорции, верная пропорция – Произведение крайних членов равно произведению средних. Один ученик работает у доски. Остальные в тетрадях). (Ученик, работающий у доски, «прячется» за крыло и выполняет записи там. Дети работают в тетрадях. Трое учеников, быстрее всех верно выполнивших задание, получают жетоны) Пользуясь основным свойством пропорции | (ПУУД). структурирование собственных знаний. (КУУД). организовывать и планировать учебное сотрудничество с учителем и сверстниками. (РУУД). контроль и оценка процесса и результатов деятельности. (ЛУУД). оценивание усвоенного в начальной школе материала. | III. Цель: Закрепить знания по теме пропорция, заполнить пробелы | Слайд 5 Работа по группам. Каждой группе дается задание. Заполните пропуски так, чтобы пропорции оказались верными. (Вспоминаем какая пропорция называется верной) Образец: 10:5= ? :2, 1)? : 3= 6 : 2, 2)18: 3= 24 : ? 3) 3: 1= 9 : ? 4) 6,5: 1,3= ? :0,7 5)21: ? = 63:9 6) ? : 6 = 18 : 9 Слайд 6 Задачи с масштабом. Рис. 1 (приложение) на столе у каждого лист с изображением карты. Необходимо найти расстояние на местности между пунктом А и пунктом В, расположенным на г. Голая. Первый выполнивший задание, в каждой группе получает жетон. Слайд 7 Задачи с составлением пропорции. 1 группа Для варки варенья из черники на 16 кг ягод берут 12 кг сахарного песку. Сколько сахарного песку надо взять на 2 кг ягод? 1,5 кг 2 группа Для приготовления 2 литров компота потребуется 0,5 кг сухофруктов, сколько сухофруктов потребуется для приготовления 5 литров компота? 1,25 кг 3 группа Для приготовления четырех порций салатов потребуется 240 г. огурцов, сколько грамм огурцов потребуется для приготовления 6 порций? 360г 4 группа Из 7,5 кг свежих грибов получается 1,5 нити сушеных грибов. Сколько нитей сушеных грибов взял с собой кок, если он засушил 17,5 кг свежих грибов? 3,5 нитей 5 группа Масса 3 литра нефти составляет 1,8 кг. 6 группа Для приготовления трех порций бифштексов потребуется 450 г. мяса, сколько необходимо взять грамм мяса для приготовления 6 порций? 900 Слайд 8 остановка. Давайте отдохнем и послушаем одну притчу. “Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы. –Кто ты? –спросил верховный жрец? –Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: –Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? –жрецы согнулись от хохота. –Будет хорошо, –насмешливо продолжал жрец, –если ты ошибешься не более, чем на сто локтей. –Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта. –Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство”. Я предлагаю Вам повторить подвиг Фалеса и определить высоту Пирамиды, для этого нам необходимо воспользоваться знаниями составления пропорции: Тень человека ростом 1,5 м растягивается на два шага, а тень от Пирамиды, на которую светит солнце растягивается на сто восемьдесят четыре шага. Какова высота Пирамиды? (Пирамида Хиопса) 138 Тень человека ростом 1,6 м растягивается на три шага, а тень от Пирамиды, на которую светит солнце растягивается на двести пятьдесят пять шагов. Какова высота Пирамиды? (Пирамида Хефрена)136 Тень человека ростом 1,6 м растягивается на три шага, а тень от Пирамиды, на которую светит солнце растягивается на двести семьдесят шагов. Тень человека ростом 1,5 м растягивается на два шага, а тень от Пирамиды, на которую светит солнце растягивается на сто сорок шагов. Какова высота Пирамиды? (Розовая Пирамида Снофру) 105 Тень человека ростом 1,5 м растягивается на два шага, а тень от Пирамиды, на которую светит солнце растягивается на восемьдесят восемь шагов. Какова высота Пирамиды? (Пирамида Микерина) 66 Тень человека ростом 1,6 м растягивается на три шага, а тень от Пирамиды, на которую светит солнце растягивается на двести пятьдесят пять шагов. Какова высота Пирамиды? (Пирамида Хефрена) 136 | Работают в группах. Группы обсуждают решение. Пишут ответ 1 человек выполнивший быстрее всех пишет на доске 2 человека пишут на доске отдых Работают над задачей 3 человека выполняют у доски | ((ПУУД). (РУУД). определяют цель учебной деятельности, осуществляют поиск средства ее достижения(ЛУУД) самоопределение. | IV. работа над ошибками Цель: анализ своей работы, коррекция | Выполнение работы над ошибками в тетрадях для контрольных работ Объяснения правил отступа и записи работы над ошибками. Задание для ребенка с ОВЗ: Задания для ребят, которые выполнили работу на 5. Составить 3 верные пропорции. Придумать три сказочные задачи, для решения с помощью пропорции и решить их. Придумать синквейн для анализа урока. Это стихотворение, которое состоит из пяти строчек по определенным правилам. Правила создания синквейна: строчка – это название темы строчка – это определение темы в двух прилагательных или причастиях строчка – это три глагола, показывающие действие в рамках темы. строчка – фраза из четырех слов, оказывающая отношение автора к теме. строчка – завершение темы, синоним первого слова, выраженный любой частью речи. Пример: Математика Учит, решает, развивает (если требуется помощь, то они выступают в роли консультантов отстающим детям) | Индивидуальная работа Групповая работа | (ПУУД). Поиск и выделение необходимой информации. (КУУД). Умение слушать и вступать в диалог | VII. Рефлексия учебной деятельности на уроке Цели: Инициировать рефлексию детей по поводу психоэмоционального состояния, Д/З Информация о домашнем задании, инструктаж по его выполнению. | Сегодня на уроке мы вспомнили и закрепили основные свойства пропорции, рассмотрели применение этого теоретического материала на практике при выполнении упражнений. Сегодня на уроке вы активно работали, но самые активные получат дополнительную отметку. Подумайте и скажите кто из каждой группы заслужил сегодня «5»? Что больше всего запомнилось на уроке, что не понравилось. Чтение составленных синквейнов. Домашнее задание.стр.128-130 (читать),№659,№655 | Оценивают свою работу и работу одноклассников | (ПУУД). (КУУД). умение с достаточной полнотой и точностью выражать свои мысли. (РУУД). оценивание детьми собственной деятельности, определение позиции ученика (ЛУУД) умение давать верную эмоциональную оценку своей деятельности на уроке. |
Математика. Проверочные и контрольные работы, работа над ошибками. 3 класс. Компетентностный подход! (2020) Борисевич Н.И., «Экоперспектива» ПО НОВОЙ ПРОГРАММЕ !
При покупке на класс предоставляются скидки !!!
ПО НОВОЙ ПРОГРАММЕ!
В пособии представлены варианты проверочных и контрольных работ, а также задания для проведения работы над ошибками. Материал составлен с учетом компетентностного подхода.
Адресуется ученикам, учителям начальных классов и родителям.
Дополнительная информация:
Математика : 3-й кл. : проверочные и контрольные работы, работа над ошибками : для учащихся учреждений общ. сред. образования / Н. И. Борисевич. — 6-е изд. — Минск : Экоперспектива,
сред. образования / Н. И. Борисевич. — 6-е изд. — Минск : Экоперспектива,
2020. — 64 с.
Уважаемый покупатель.
Производитель оставляет за собой право изменять характеристики, комплектацию, описание товара. Мы стараемся своевременно вносить изменения на страницах нашего магазина Белка.By.
Характеристики товара получены из открытых источников, в т.ч. из каталогов производителя и официальных сайтов. 100% точность и полнота описаний не гарантированы.
Если Вы нашли неточности в описании и характеристиках, то отправьте нам на e-mail [email protected] наименование товара и пункт, в котором содержится ошибка. Также вы можете указать в отзыве к этому товару о наличии неточностей в описании.
Данное предложение не является публичной офертой. Выбранный Вами товар может отсутствовать на складе, и/или быть зарезервированным, оплаченным другим покупателем и изменен в цене.
Перед оплатой online или ЕРИП уточняйте у менеджера наличие, цену, комплектацию и параметры товара.
Если выбранный товар был зарезервирован, оплачен другим покупателем, или на складе хранения нет в наличии необходимого количества, то мы постараемся, при условии наличия товара у поставщиков/производителей, организовать поставку товаров белорусских производителей в течение 7-10 дней, российских 7-15 дней. Планируйте свои покупки заранее, учитывая эти сроки, особенно, если они приходятся период повышенного спроса.
В период повышенного спроса срок сборки заказа может составить 1-10 дней.
Доклад»Деятельность учителя математики по предупреждению ошибок»
Деятельность учителя математики по предупреждению ошибок
В ходе обучения математике популярная поговорка «умные люди учатся на чужих ошибках» практически не работает, так как ошибка в большинстве случаев является необходимой и полезной, ведь она позволяет определить пробелы в знаниях школьника и своевременно их устранить. Главное – правильно относится к ошибке и правильно ее использовать.
Любому учителю обидно видеть в работах учеников ошибки, которые вызваны невнимательностью, пропусками переменных, случайными потерями знаков, скобок и так далее.
Для того чтобы снизить вероятность ошибок, необходимо использовать различные методики предупреждения типичных ошибок, что будет в итоге способствовать повышению уровня математической подготовки школьников.
Ошибка – результат неправильного (ошибочного) действия.
В свою очередь, ошибочное действие – это действие, которое не достигло своей цели.
Ошибочные действия различают по нескольким критериям:
- по степени выраженности, то есть определяется величина отклонения от принятой нормы;
- по причинам, которые привели к ошибкам;
-
по степени грубости.
 Важное значение имеет то, на каком этапе обучения совершаются ошибочные действия;
Важное значение имеет то, на каком этапе обучения совершаются ошибочные действия;
- степень повторяемости;
- наличие связи с другими ошибочными действиями, что в итоге перетекает в синдром неуспеваемости.
Под сущностью ошибки принято понимать определенное объективное условие, правило или требование, которое было нарушено или обучающийся его не выполнил.
Причина появления ошибки – это уже субъективные ситуации, процессы либо состояния, которые свойственны интеллектуальной области человека, приведшие к несоблюдению или нарушению правил.
С точки зрения психологического анализа математических ошибок требуется выявить механизм появления конкретной ошибки в рамках конкретной психологической системы усвоения знаний. При анализе ошибки осуществляется ее демонстрация, то есть происходит выявление ее математической сущности, а также указание наиболее вероятных причин ее появления.
Необходимо учитывать, что все ошибки характеризуются содержанием и причиной появления. При этом содержание находится на поверхности явления, а причину следует искать более глубоко.
Ошибки разделяются на два основных вида:
- случайные ошибки – появляются однократно и встречаются только у нескольких человек в классе;
- систематические (устойчивые) ошибки – ошибки, которые возникают постоянно у одного и того же или нескольких обучающихся, или же те ошибки, которые возникают однократно, но у значительного количества обучающихся.
В соответствии с подходами современной дидактики работа над ошибками должна производиться в обязательном порядке. При этом над случайными ошибками проводится индивидуальная работа, а над систематическими – фронтальная.
Работа над ошибками – это организация работы учеников, направленная на анализ и исправление допущенных недочетов.
Основной целью работы над ошибками является разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания.
Правильно организованная работа:
- обеспечивает дифференцированный подход к обучению;
- является профилактикой будущих ошибок;
- позволяет своевременно ликвидировать пробелы в знаниях и навыках детей;
- формирует умение систематизировать и обобщать, закреплять полученные знания.
Грамотный, творческий подход учителя к организации работы над ошибками создает условия для развития адекватного отношения обучающегося к своим ошибкам, умение работать с ними.
Можно говорить о том, что, после проведения работы над ошибками итоговая оценка отражает действительный уровень усвоения знаний и умений обучающихся. Существует практика, когда некоторые учителя практикуют выставление оценок за каждую проведенную работу. При этом часто бывает, что после работы над ошибками, отметка за проверяемую работу повышается (как правило, на один бал).
Существует практика, когда некоторые учителя практикуют выставление оценок за каждую проведенную работу. При этом часто бывает, что после работы над ошибками, отметка за проверяемую работу повышается (как правило, на один бал).
Обычно работа над ошибками проводится в классе, под руководством учителя, но может проводиться и дома, возможно, под контролем родителей.
Если учитель считает возможным дать выполнение работы над ошибками в качестве домашнего задания, он должен убедиться, что все обучающиеся знают и помнят основной алгоритм действий по выполнению работы. Целесообразно, каждому ребенку выдать памятку с порядком выполнения действий. Кроме этого, необходимо предварительно на уроке провести общий анализ допущенных ошибок.
В классе, работу над ошибками проводят, как правило, после контрольных, самостоятельных или творческих работ. Работе над ошибками может быть посвящен как весь урок, так и его часть. Это зависит от характера и количества видов ошибок, от уровня самостоятельности обучающихся и т.п.
Это зависит от характера и количества видов ошибок, от уровня самостоятельности обучающихся и т.п.
При работе на уроке выделяют несколько основных этапов:
- консультация;
- коррекция знаний и умений;
- диагностика результатов;
- оценочная деятельность.
По усмотрению учителя возможны: фронтальная, групповая, индивидуальная работа.
Рассмотрим несколько вариантов проведения работы над ошибками.
В начале урока, после проведения общего анализа проверенной работы, учитель просит поднять руку тех обучающихся, которые допустили ошибки при выполнении задания.
К доске приглашается один из обучающихся, который будет выполнять и комментировать аналогичное задание у доски. Обучающийся определяется либо по его желанию, либо по решению учителя. Остальные ученики выполняют работу у себя в тетрадях. Затем все самостоятельно решают задание проверочной работы.
Остальные ученики выполняют работу у себя в тетрадях. Затем все самостоятельно решают задание проверочной работы.
Таким образом, дети «прорешивая» аналогичное задание, прорабатывают ошибки, допущенные не только ими самими, но и остальными обучающимися. Такой подход целесообразен, когда в данном задании большинство учеников допустили ошибку.
Следующая форма работы используется, когда один или несколько обучающихся допустили ошибки в задании, которое большинство обучающихся выполнили правильно. При данной форме организации урока один обучающийся выполняет работу над своими ошибками у доски, остальные обучающиеся исправляют свои недочеты в тетрадях или выполняют индивидуальные задания.
С одной стороны, этот метод позволяет экономить время, затрачиваемое на данную деятельность, с другой — учитель не может контролировать деятельность других детей. Для исправления возникшей ситуации нужно обеспечить каждому обучающемуся возможность обратиться к учителю за помощью, за консультацией.
Бывают ситуации, когда часть обучающихся выполнила проверочную работу на «отлично», т.е. возникает необходимость организовать деятельность этих обучающихся и одновременно организовать выполнение работы над ошибками остальными школьниками.
В этом случае, есть несколько вариантов организации работы на уроке.
Во-первых, «отличникам» можно предложить выполнение индивидуальных заданий повышенного или углубленного уровней, творческие задания, работу по подготовке, например, информационного сообщения к следующему уроку. С остальными обучающимися проводится работа над ошибками.
Во-вторых, обучающихся, показавших высокий уровень усвоения учебного материала, можно привлечь к консультированию других детей. В этом случае возможна организация групповой и (или) парной работы.
Имеют место случаи, когда педагог, в целях экономии времени, выделяет только типичные ошибки, допущенные обучающимися при выполнении проверочной работы, и на уроке проводит работу только с таким видом ошибок. В этом случае работа организовывается фронтально, анализ и исправление типичных ошибок и недочетов выполняет весь класс вместе. При этом у доски работают обучающиеся по желанию, по очереди или по решению учителя, в зависимости от того, кто какие ошибки допустил.
В этом случае работа организовывается фронтально, анализ и исправление типичных ошибок и недочетов выполняет весь класс вместе. При этом у доски работают обучающиеся по желанию, по очереди или по решению учителя, в зависимости от того, кто какие ошибки допустил.
Для того чтобы школьник сознательно усвоил знания, самим обучающимся должен производиться глубокий анализ содержания каждой допущенной им ошибки, а также поиск причин ее появления. В таком случае совершенная ошибка пойдет обучающемуся только на пользу, ведь она будет своего рода сигналом для педагога о том, что не понимает обучающийся. Однако учитель должен правильно понять ход мыслей обучающегося, который привел его к совершению данной ошибки. Поэтому каждая ошибка должна использоваться для глубокого и более детального понимания правил, теорем или понятий.
В то же время необходимо в каждой ошибке различать ее содержание и причину появления. В содержание ошибки включается то, что объективно является неверным или неадекватно выполнено. Причиной же ошибки является какое-то обстоятельство либо совокупность обстоятельств, которые привели к неправильному выполнению обучающимся каких-то действий.
Причиной же ошибки является какое-то обстоятельство либо совокупность обстоятельств, которые привели к неправильному выполнению обучающимся каких-то действий.
И если содержание ошибки несложно определить по внешним признакам (некорректно выполнено определенное действие, неправильное произношение или написание и т.д.), то причина ошибки внешне себя никак не выдает. Поэтому основной задачей учителя является выявление глубинных причин появления ошибки, в противном случае ему не удастся грамотно выстроить работу по ликвидации данной ошибки и профилактике последующих возможных ошибок.
Алгоритм действий по выполнению работы над ошибками
Алгоритм действий по проведению работы над ошибками определяется учителем самостоятельно, исходя из особенностей класса, общего уровня обученности и т.д.
Например, алгоритм действий обучающегося может выглядеть следующим образом:
1) просмотреть всю работу, обратить внимание на исправления учителя;
2) найти ошибку, выписать задание, в котором она допущена, проанализировать причину ее возникновения:
- ошибка в вычислении – перерешать;
- ошибка в применении формулы (правила, закона) — вспомнить нужную формулу (правило, закон) по данной теме, применить при решении;
- ошибка в построении рисунка – повторить материал в учебнике и выполнить рисунок правильно;
3) решить аналогичное задание.
В практике работы некоторых учителей встречается использование памятки, в которой пронумерованы и записаны основные группы ошибок.
Памятка заранее изготавливается педагогом, тиражируется и по одному экземпляру раздается каждому обучающемуся. Памятки могут быть индивидуальными. Работа с памятками выполняется под контролем педагога.
Если учитель планирует проводить работу над ошибками, с использованием памяток, то при проверке работы на полях тетради, напротив задания, в котором допущена ошибка, ставится номер соответствующего задания в памятке. Это не только облегчает работу обучающихся, но и совершенствует систему обучения. Обучающийся неоднократно обращается к данной памятке, что способствует лучшему запоминанию учебного материала.
В конце работы над ошибками необходимо провести проверку. Существует несколько форм ее организации.
- самопроверка;
- парная работа;
- групповая работа, когда «сильные» обучающиеся выступают в роли консультантов;
- фронтальная работа со всем классом.
Во всех случаях, необходимо обеспечить возможность каждому обучающемуся консультирование и помощь учителя.
В конце работы над ошибками, как и в конце любого урока, необходимо провести рефлексию. Дети анализируют свои ошибки, отмечают, как изменились собственные умения, отмечают моменты, которые остались непонятыми, говорят о том, что вызвало трудности и высказывают свои предложения.
Следует отметить, что проведение работы над ошибками является обязательным и систематическим действием после каждой контрольной и проверочной работы. При этом необходимо обращать внимание и прорабатывать все ошибки, допущенные обучающимися, тщательно проводить отбор задач и примеров для отработки знаний и умений, для закрепления пройденного материала.
Большая часть ошибок, допускаемых обучающимися, не связана с отсутствием или наличием знаний, хотя, конечно, доведение до уровня автоматизма ряда вычислительных операций позволяет существенно снизить вероятность появления ошибок. Однако при этом необходимо, чтобы ученик все равно руководствовался нужными правилами и постоянно сохранял концентрацию внимания.
Знание определенных правил нужно и для того, чтобы обучающийся мог проверить правильность решения и дать его обоснование. В тоже время многие школьники воспринимают алгебру в качестве набора правил, которые абсолютно не связаны между собой, поэтому они заучиваются исключительно для решения какой-то конкретной задачи, а по истечению незначительного промежутка времени просто забываются. В этой связи требуется организовывать процесс обучения правилам с использованием приемов, которые активизируют рефлексивную деятельность школьников по предупреждению и исправлению ошибок, возникающих при формальном усвоении правил.
Если процесс поиска и исправления ошибок сделать максимально поучительным для обучающихся, то анализ ошибок может стать эффективным средством для развития познавательного интереса к математике.
Наиболее распространенными ошибками являются:
- незнание или непонимание правил, формул и определений;
- неправильное применение формул или неумение правильно применять определения и правила;
- совершение вычислительных ошибок;
- невнимательное чтение условия задачи;
- отказ от использования свойств фигур при решении геометрических задач;
- неправильное раскрытие скобок;
- совершение логических ошибок при решении текстовых задач;
- применение формул сокращенного умножения.
К основным причинам совершения ошибок по математике относят:
- пропуски уроков, в результате чего появляются пробелы в знаниях;
- поверхностное изучение нового материала;
- повышенная усталость, вызванная чрезмерной нагрузкой или недостаточным сном, в результате чего понижается скорость мышления и снижается уровень внимания;
- неаккуратный почерк, из-за чего учитель часто не понимает, что написал обучающийся;
- скорость работы. При этом на появление ошибок влияет как высокая скорость работы, из-за которой ученик просто не стремится вникнуть в суть задания, так и медленная. В этом случае замедленная скорость мыслительных операций не позволяет ученику в полной мере контролировать себя, а из-за «зависания» нужная информация просто удаляется из «оперативной памяти»;
- полное либо кратковременное переключение внимания с одной деятельности на другую;
- низкая мотивация, в результате которой теряется внимание, появляются ошибки.
С точки зрения психологии действия учителя при выявлении ошибки, которые проявляются в снижении оценки, являются абсолютно неверными. Ведь это не ведет к ее исправлению, а у ребенка формируется чувство досады и неуверенности в своих силах. В результате обучающиеся продолжают совершать одни и те же ошибки.
Как ни парадоксально звучит следующий тезис, но для того чтобы перестать совершать ошибки, необходимо делать ошибки, находить их и исправлять, ведь «неубитая» ошибка в ходе самостоятельной работы, неизбежно «убивает» обучающегося во время контрольной или на экзамене.
Еще один нюанс, который обязательно следует учитывать учителю, заключается в том, что обучающийся перестает делать ошибки в случаях, когда ответственность за их совершение лежит исключительно на самом школьнике. Поэтому, когда обучающийся на уроке задает, например, такой вопрос: «А можно здесь возвести в квадрат?», – то он старается разделить ответственность за возможную ошибку с учителем. Учитель в таких случаях должен правильно реагировать и говорить, что решение должно приниматься исключительно самим обучающимся. Такой подход позволяет почувствовать школьнику ответственность за свои действия и понять, что только он сам может помочь себе при решении различных задач. Здесь работает тезис о том, что кто не ошибается, тот не учится.
Таким образом, ошибка является полезной, главное – правильно к ней относиться, эффективно и грамотно ее использовать.
Коды исправления ошибок | plus.maths.org
Эта статья основана на выступлении Криса Бадда в продолжающейся работе Gresham Цикл лекций колледжа. Вы можете посмотреть видео выступления ниже, а здесь есть еще одна статья, основанная на нем.
Мы окружены информацией и постоянно получаем и передаем ее другим людям по всему миру. Не зря мы можем назвать 21 век веком информации . Но всякий раз, когда отправляется сообщение, будь то по телефону, через Интернет или через спутники, вращающиеся вокруг Земли, существует опасность появления ошибок.Фоновый шум, технические неисправности и даже космические лучи могут испортить сообщение, и важная информация может быть потеряна. Однако довольно удивительно, что существуют способы кодирования сообщения, которые позволяют автоматически обнаруживать и даже исправлять ошибки. Вот как работают эти коды.
Писец XV века, иллюстратор рукописей, переводчик и писатель Жан Мило за своим столом.
Коды обнаружения ошибок
Необходимость обнаружения ошибок была признана с тех пор, как первые переписчики копировали рукописи вручную.Было важно скопировать их без ошибок, но проверять каждое слово было бы слишком сложной задачей. Вместо этого использовались различные проверки. Например, при копировании Торы буквы, слова и абзацы подсчитывались, а затем сравнивались со средним абзацем, словом и буквой исходного документа. Если они не совпадают, возникла проблема.
Современная цифровая информация кодируется как последовательности нулей и единиц. При передаче двоичной информации простая проверка, которая часто используется, включает так называемую хэш-функцию , которая добавляет к сообщению тег фиксированной длины.Тег позволяет получателю проверить доставленное сообщение, повторно вычислив его и сравнив с сообщением, указанным в сообщении.
Простым примером такого тега является включение контрольной или контрольной цифры в каждый блок данных. Самый простой пример этого метода — сложить цифры, составляющие сообщение, а затем добавить 1, если сумма нечетная, и 0, если она четная. Таким образом, если исходное сообщение — 111, то отправленное сообщение — 1111, а если исходное сообщение — 101, то отправленное сообщение — 1010.В результате каждое отправленное сообщение должно содержать цифры, составляющие четное число. При получении передачи принимающий компьютер суммирует цифры, и, если сумма не четная, он регистрирует ошибку.
Пример использования этой технологии можно найти на штрих-кодах, которые используются почти на всех продаваемых массовых потребительских товарах. В таких потребительских товарах обычно используются коды UPC-A или EAN-13. UPC-A описывает 12-значную последовательность, которая разбита на четыре группы.Первая цифра штрих-кода несет некоторую общую информацию об изделии: она может либо указывать на национальность производителя, либо описывать одну из нескольких других категорий, например номера ISBN (книжный идентификатор). Следующие пять цифр — это идентификация производителя. Следующие пять цифр представляют собой идентификационный номер продукта, присвоенный производителем. Последняя цифра — это контрольная цифра, позволяющая сканеру проверить правильность считывания штрих-кода.
Подобные контрольные цифры используются в числах на вашей кредитной карте, которые обычно представляют собой последовательность десятичных цифр.В этом случае используется алгоритм Люна (подробнее здесь).
Коды исправления ошибок
Предположим, что мы обнаружили ошибку в сообщении, которое мы обманули. Как мы можем продолжить поиск правильной информации, содержащейся в сообщении? Есть разные подходы к этому. Один из них — просто (эффективно) паниковать: выключить всю систему и не продолжать, пока проблема не будет устранена. Печально известный синий экран смерти, изображенный ниже и знакомый многим операторам компьютеров, является примером этого.
Синий экран смерти в Windows 8.
Обоснование этого подхода состоит в том, что в некоторых (действительно, во многих) случаях лучше ничего не делать, чем делать что-то, что, как вы знаете, неправильно. Однако все, что мы можем сделать на этом этапе, — это начать все с нуля, и в процессе мы потеряем всю информацию.
Второй подход, называемый автоматическим запросом на повторение (ARQ), часто используемый в Интернете, заключается в том, что сообщение должно повторяться, если предполагается, что оно содержит ошибку.Мы делаем это постоянно. Например, если вы сканируете товар в супермаркете, а сканер не распознает его, вы просто сканируете его снова.
Однако эта опция недоступна для нас, если мы получаем информацию, скажем, со спутника, мобильного телефона или с компакт-диска. В этом случае, если мы знаем, что при передаче была сделана ошибка, мы должны попытаться исправить ее. Общая идея исправления заключается в добавлении к сообщению дополнительных данных, которые позволяют нам восстановить их даже после того, как была сделана ошибка.Для этого передатчик отправляет исходные данные и присоединяет фиксированное количество контрольных битов, используя код с исправлением ошибок (ECC). Идея состоит в том, чтобы сделать символы из разных символов кода как можно более отличными друг от друга, чтобы даже если один символ в коде был искажен шумом, его все равно можно было отличить от других символов в коде. Коды с исправлением ошибок были изобретены в 1947 году в Bell Labs американским математиком Ричардом Хэммингом.
Иллюстрация спутника США / Европы по изучению топографии поверхности океана (OSTM) / спутника Jason-2 на орбите. Изображение: NASA-JPL / Caltech
Чтобы понять, как работают коды с исправлением ошибок, мы должны определить расстояние Хэмминга между двумя двоичными строками. Предположим, что у нас есть две шестибитовые строки, такие как 1 1 1 0 1 0 и 1 0 1 1 1 1. Тогда расстояние Хэмминга — это количество различающихся цифр. Таким образом, в этом случае расстояние Хэмминга равно 3. Если один бит в символе изменяется, то он имеет расстояние Хэмминга, равное единице от его оригинала.Это изменение может быть связано с действием шума, который повредил сообщение. Если две строки разделены большим расстоянием Хэмминга, скажем 3, то их все равно можно будет различить, даже если один бит изменится из-за шума. Идея простейших кодов с исправлением ошибок состоит в том, чтобы использовать этот факт, добавляя дополнительные цифры к двоичному символу, чтобы символы находились на большом расстоянии Хэмминга друг от друга.
Я проиллюстрирую это на простом примере. Числа от 0 до 7, записанные в двоичном формате:
000 (0) 001 (1) 010 (2) 011 (3) 100 (4) 101 (5) 110 (6) 111 (7)
(Вы можете узнать больше о двоичных числах здесь или просто поверьте мне.)
Многие из этих строк находятся на расстоянии всего одного расстояния Хэмминга. Например, небольшой шум может превратить строку для 2 в строку для 3. Теперь мы добавляем несколько дополнительных цифр четности (мы объясним их математику позже) к этим кодам, чтобы получить код
000000 (0) 001110 (1) 010 011 (2) 011101 (3) 100101 (4) 101011 (5) 110110 (6) 111000 (7)
Смысл этого в том, что каждый из этих кодов находится на расстоянии Хэмминга 3 друг от друга.Предположим, что шум довольно низкий и влияет на изменение одного бита символа. Предположим, мы берем символ 101 011 вместо 5, и он меняется на (скажем) 100 011. Это расстояние Хэмминга, равное одному от исходного символа и расстояние не менее двух от всех остальных. Итак, если мы получаем 100 011, мы ищем ближайший к этому символу в нашем списке. Это должен быть исходный символ, и мы исправляем 100 011 на 101 011, чтобы прочитать символ без ошибок.
Космический полет, Facebook и компакт-диски
Все коды исправления ошибок используют принцип, аналогичный приведенному выше: получить строку, если ее нет в списке. найдите в списке строку, ближайшую к полученной, исправьте строку на эту.Чтобы найти коды для большего количества символов, которые будут работать в присутствии более высоких уровней шума, используется множество математических изощрений. По сути, задача состоит в том, чтобы найти символы, которые бы максимально отличались друг от друга. Наряду с разработкой кода идет разработка эффективного декодера, который используется для быстрого и надежного исправления поврежденных сообщений.
Другим примером кода исправления ошибок является код Рида-Соломона, изобретенный в 1960 году. Первое коммерческое применение в массовых потребительских товарах появилось в 1982 году на компакт-диске, где два кода Рида-Соломона используются на каждой дорожке, чтобы дать даже большая избыточность.Это очень полезно, когда вам нужно восстановить музыку на поцарапанном компакт-диске.
Сегодня коды Рида – Соломона широко используются в цифровых запоминающих устройствах и стандартах цифровой связи (например, в цифровом телевидении), хотя в настоящее время они заменяются кодами проверки на четность с низкой плотностью (LDPC). Кодирование Рида – Соломона очень широко используется в системах хранения данных для исправления пакетных ошибок, связанных с дефектами носителя. Этот код может исправить до 2-х байтовых ошибок на 32-байтовый блок. Одним из важных применений кодирования Рида-Соломона было кодирование цифровых изображений, отправленных обратно космическим зондом «Вояджер», который был запущен в 1977 году и сделал первые спутниковые снимки Юпитера, Сатурна и далеких планет.
Один из основных пользователей исправления ошибок в последнее время находится на Facebook, который, возможно, является крупнейшим хранилищем информации в мире. По оценкам, каждый день на Facebook хранится 300 миллионов фотографий. Эта информация хранится в огромных банках данных по всему миру, в основном на вращающихся дисках. Хотя частота отказов одного диска очень низка, для хранения информации требуется так много дисков, что вероятность того, что один из дисков выйдет из строя в любой момент, высока. Когда это происходит, данные на диске восстанавливаются эффективно и быстро с помощью кода Рида-Соломона, так что Facebook может продолжать работу без перерыва.
Немного математики
В этом последнем разделе мы дадим некоторые математические детали для тех, кому это интересно. (Если вас не интересуют подробности, вы можете перейти к следующей статье.) Разработать коды, которые были бы одновременно эффективными и надежными, совсем непросто, и целая ветвь математики, теория кодирования , была изучена. разработан для этого.
Код Хэмминга (7,4) аналогичен приведенному выше коду Хэмминга, только в этом случае три бита четности добавляются к сообщению с четырьмя информационными битами (а не к сообщению с тремя информационными битами, как указано выше).Если это строка информации (длина которой четыре бита), то передаваемый символ имеет длину семь бит и определяется как где, и, — биты четности. Эти биты четности добавляются так, чтобы группы цифр в коде имели четное количество единиц. На следующей диаграмме показано, что это за группы: каждая из них представлена кружком, а группа битов, состоящая из этого и также лежащих в этом кружке, должна содержать четное количество единиц.
Например, это означает, что если тогда, потому что, и лежат в круге и вместе содержат три единицы, должно быть равно 1, чтобы количество единиц в зеленом круге стало четным.Оба бита четности и должны быть равны 0. Следовательно,
Теперь предположим, что это неправильно передано, так что один бит поврежден, и вместо этого мы получаем сигнал. Посмотрим, сможем ли мы исправить эту ошибку. Группа битов, принадлежащих зеленому кружку (, и), имеет правильную четность (четность), а каждая группа битов, принадлежащих синему и красному кружкам, имеет неправильную четность (нечетность). Так как единственный информационный бит, принадлежащий как красному, так и синему кругу, — это бит, который должен быть оскорбительным.И это правильно.
В более абстрактной обстановке
где — матрица генератора кода 7×4, а все операции вычисляются в модульной 2 арифметике. Поскольку матрица 7×4, умноженная на вектор длины 4, дает вектор длины 7, умножение дает вектор правильной длины, то есть добавляются три бита четности. Это умножение является линейным преобразованием, и код Хэмминга (7,4) является примером линейного кода .Если получена искаженная форма сообщения, то бит, для которого сделана ошибка, обнаруживается с помощью второй и хитро сконструированной матрицы проверки четности 3×7. Эта матрица построена так, что если ошибки нет, то
должен быть нулевым вектором. Если это не нулевой вектор, значит, произошла ошибка. Вектор будет соответствовать одному из столбцов, а расположение этого столбца (первый, второй, третий и т. Д.) Указывает, где в исходной строке была сделана ошибка.Тогда можно легко построить матрицу 4×7 для восстановления исходного символа так, чтобы
Эварист Галуа, нарисованный по памяти его братом в 1848 году, через шестнадцать лет после его смерти.
Код Рида-Соломона более сложен по своей конструкции. В классической реализации кода Рида-Соломона исходное сообщение преобразуется в полином, члены которого являются коэффициентами полинома.Затем переданное сообщение дается путем вычисления полинома в наборе точек. Как и в коде Хэмминга (7,4), код Рида-Соломона является линейным преобразованием исходного сообщения. Декодирование работает путем нахождения наиболее подходящего полинома сообщения. Все умножения полинома выполняются над математическими структурами, называемыми конечными полями . Теория, лежащая в основе построения этих кодов, использует передовые идеи из раздела математики под названием теория Галуа , который был изобретен французским математиком Эваристом Галуа. когда ему было всего 19 лет, и, по крайней мере, за 150 лет до этого он использовался в проигрывателях компакт-дисков.
Об этой статье
Эта статья основана на выступлении Бадда в продолжающемся Gresham Цикл лекций колледжа. Видео выступления находится ниже, а здесь есть еще одна статья, основанная на нем.
Крис Бадд.
Крис Бадд — профессор прикладной математики Университета Бата, вице-президент Института математики и ее приложений, заведующий кафедрой математики Королевского института и почетный член Британской научной ассоциации.Он особенно заинтересован в применении математики в реальном мире и содействии пониманию математики общественностью.
Он является соавтором популярной книги по математике Mathematics Galore! , опубликованный издательством Oxford University Press совместно с К. Сангвином, и представлен в книге 50 Visions of Mathematics ed. Сэм Парк.
Код исправления ошибок — Математическая энциклопедия
код, исправляющий ошибки
Набор сообщений, предназначенных для передачи по каналу связи с шумом, с тем свойством, что «соседство» каждого сообщения (то есть набор наиболее вероятных искаженных версий этого сообщения) не пересекается с окрестностями других сообщений. .Это свойство кода исправления ошибок позволяет исправить ошибки (то есть восстановить переданное сообщение) в тех искаженных сообщениях (полученных на выходе канала), которые принадлежат окрестности сообщения. Элементы кода с исправлением ошибок (кодовые слова) используются при кодировании последовательностей информационных символов, представленных источником информации (см. Информация, источник). Кодирование заключается в представлении информационной последовательности в специальном виде и во введении в нее дополнительной информации (избыточности).Эта избыточность обычно вводится путем добавления к сообщению дополнительных символов тем или иным способом. Например, последовательность символов может быть разбита на блоки фиксированной длины $ k $, и, независимо друг от друга, блоки заменяются разными блоками большей длины $ n $, которые являются элементами так называемого блочного кода с исправлением ошибок. Другие методы [1] известны введением избыточности и связанных с ними кодов исправления ошибок. {n} $ с метрикой $ \ lambda $, а окрестность кодового слова — это шар с центром в кодовом слове.Радиус этого шара определяет корректирующую способность блочного кода. Метрика $ \ lambda $ зависит от характера ошибок, для исправления которых предназначен код. Последующая учетная запись имеет дело только с кодами блоков, которые являются наиболее распространенными.
Для того, чтобы можно было передавать максимальный объем информации по каналу, необходимо для заданной корректирующей способности использовать коды с максимальным количеством элементов (кодовых слов). Построение таких кодов — одна из основных проблем теории кодов с исправлением ошибок.\ prime $. Первая проблема называется проблемой кодирования, вторая — проблемой декодирования. Сложность кодирования и декодирования в значительной степени определяется свойствами используемого кода с исправлением ошибок. В результате это приводит к изучению относительно узкого класса кодов, такого как, например, двоичные линейные коды, рассматриваемые ниже.
Наиболее широко исследуемыми такими кодами являются $ q $ — арные блочные коды в метрике Хэмминга. Это потому, что они нашли множество приложений, а методы их построения связаны с хорошо известными математическими структурами.{n} $ функция $ d (K) = \ min _ {x, y \ in K, x \ neq y} d (x, y) $ называется минимальным расстоянием $ q $ — код $ K $. Код $ K $ это $ t $ — код с исправлением ошибок, если $ d (K) \ geq 2 t + 1 $. При выполнении последнего неравенства каждая окрестность $ U _ {t} (x) $, $ x \ in K $, не пересекается с $ U _ {t} (y) $ для любого другого вектора $ y $ в $ K $.
Значительный прогресс в изучении $ q $ — были введены коды в случае, если $ q $ это степень простого числа.{n} $ называется двоичным кодом.
Для оценки качества конкретных кодов исследуется поведение функции $ A (n, d) $ — максимальное количество векторов кода длины $ n $ с минимальным расстоянием $ d $. Функция $ A (n, d) $ сравнительно хорошо изучен для больших $ d $, $ 2 d \ geq n $, и за небольшие $ d $, $ d = \ textrm {const} $, $ n \ rightarrow \ infty $. {n} $ когда $ d = 2 t + 1 $.{n} $. Такие коды называются совершенными. Известно, что кроме кодов Хэмминга и кодов с такими же параметрами существует только один нетривиальный двоичный совершенный код.
В случае $ n \ rightarrow \ infty $, $ d / n \ rightarrow \ delta $, $ 0 <\ delta <1/2 $, функция
$$ \ overline {\ lim \ limits} \; \ гидроразрыва {1} {п} \ mathop {\ rm log} _ {2} A (n, d) = R (\ дельта) $$
(логарифмическая асимптотика $ A (n, d) $) изучается. Это называется скоростью передачи информации для максимального кода с относительным расстоянием $ \ delta $.Для $ R (\ delta) $ известны существенно разные верхняя и нижняя границы. Нижняя оценка (оценка Варшамова – Гильберта) имеет вид
$$ \ tag {*} R (\ delta) \ geq 1 — H (\ delta), $$
где
$$ H (\ delta) = \ delta \ mathop {\ rm log} _ {2} \ frac {1} \ delta + (1 — \ delta) \ mathop {\ rm log} _ {2} \ \ frac {1} {1 — \ delta} , $$
и гарантирует наличие кодов с указанными выше параметрами. {l} $, $ \ alpha _ {1} \ точки \ alpha _ {n} $ — все возможные двоичные векторы длины $ l $ и $ f $ пробегает множество всех функций алгебры логики, представленных полиномом над $ \ mathop {\ rm GF} (2) $ в $ l $ бинарные переменные и степени не выше $ r $.{l-} r $.
Информационная ставка $ R (K) $ двоичного кода $ K $ длины $ n $ с $ m $ векторов определяется как
$$ R (K) = \ frac {\ mathop {\ rm log} _ {2} m} {n} . $$
Если $ K $
— линейный код размерности $ k $,
тогда $ R (K) = k / n $.
Информационные скорости конструктивных кодов, перечисленных выше, стремятся к нулю при $ n \ rightarrow \ infty $,
$ d / n \ rightarrow \ delta $,
$ \ delta> 0 $.
Конструктивные коды с положительной скоростью передачи информации известны как $ n \ rightarrow \ infty $,
$ d / n \ rightarrow \ delta $,
$ 1/2> \ delta> 0 $,
но меньше, чем информационные скорости кодов, существование которых было установлено оценкой в (*).\ prime \ in U _ {t} (x) $,
$ x \ in K $.
Рассмотренные выше конструктивные коды имеют декодеры небольшой сложности. {l}) $
и двоичный код длины $ n _ {1} $,
размер $ l $
с расстоянием $ d _ {1} $.{l} — r) $,
$ d \ geq r _ {1} $.
Наилучшие результаты дает использование удаленных двоичных кодов для замены отдельных битов RS-кода. Таким образом, коды длины $ n $
можно получить, исправляя фиксированный сегмент $ n $
ошибки с использованием декодера со сложностью порядка $ n \ mathop {\ rm log} n $.
Ансамбль двоичных кодов с проверками на четность низкой плотности определяется ансамблем матриц проверки на четность $ \ {A \} $
состоящий из бинарных матриц определенного типа размерности $ n \ times r $,
которые содержат $ l $
и $ h $
единиц соответственно в каждом столбце и строке, $ 4 Развитие теории кодов с исправлением ошибок стимулировалось работой Шеннона по теории информации, в которой он показал принципиальную возможность передачи по каналу связи с шумом со скоростью, меньшей, чем пропускная способность канала и со сколь угодно малой ошибкой. Изначально теория кодов с исправлением ошибок удовлетворяла требованиям инженеров связи в том, что математические конструкции гарантировали надежную передачу информации при определенных ограничениях на количество и форму ошибок в информации.Впоследствии результаты и методы теории корректирующих кодов нашли применение в других областях. В частности, в математике наилучшие оценки (до 1978 г.) были получены для плотности упаковки сфер в евклидовом пространстве; значительный прогресс был достигнут в оценке сложности типичных дизъюнктивных форм для почти всех булевых функций; построены новые объекты комбинаторики; построены самокорректирующиеся схемы функциональных элементов и др. Линейное пространство, двойственное линейному коду $ K $
есть, конечно, пространство всех векторов $ y $
такое, что скалярное произведение $ (x, y) = 0 $
для всех $ x \ in K $.\ перп $. Лучшая верхняя граница, известная для $ R (d) $
до сих пор (1987) принадлежит Р.Дж. МакЭлис, Э.Р. Родемич, Х. Рамси и Л. Уэлч (ср. [A3]). См. Также Код; Код с исправлением арифметических ошибок; Код с исправлением удалений и вставок; Кодировка, алфавитная; Кодирование и декодирование. Как уже указывалось в основной статье, теория кодирования тесно связана с другими разделами математики, в основном с геометрией чисел (см. Также [a5]) и теорией конечных полей (см.Конечное поле). В 1982 г. М.А.Цфасман, С.Г. Влэдутс и Т.Зинк, используя идеи В.Д. Гоппа и алгебраическая геометрия построили последовательность кодов, превышающих границу Гилберта – Варшамова [a4], тем самым доказав, что $ R (\ delta) = 1 — H (\ delta) $,
ср. (*), не выполняется. Ср. Код Goppa для более подробной информации. «В целом этот учебник хорошо написан и легко читается… всеобъемлющий…» ( IEEE Communications Magazine, апрель 2007 г.) НЕПОДВИЖНЫЙ ИНСТРУМЕНТ ОБУЧЕНИЯ И РУКОВОДСТВО ПО КОДИРОВАНИЮ ИСПРАВЛЕНИЯ ОШИБОК Методы кодирования с исправлением ошибок позволяют обнаруживать и исправлять ошибки, возникающие во время передачи данных в цифровых системах связи.Эти методы почти повсеместно используются в современных системах связи и, таким образом, являются важным компонентом современной информационной экономики. Кодирование с исправлением ошибок: математические методы и алгоритмы предоставляет всестороннее введение как в теоретические, так и практические аспекты кодирования с исправлением ошибок, с презентацией, подходящей для широкого круга аудиторий, включая аспирантов в области электротехники, математики или компьютеров. наука.Педагогика построена таким образом, что математические концепции представляются постепенно, за которыми сразу же следуют приложения к кодированию. Большое количество упражнений расширяет и углубляет понимание учащимися. Уникальной особенностью книги является набор лабораторий программирования, дополненных более чем 250 программами и функциями на соответствующем веб-сайте, который обеспечивает практический опыт и лучшее понимание материала. Эти лаборатории проводят студентов через внедрение и оценку кодов Хэмминга, кодов CRC, кодов BCH и R-S, сверточных кодов, турбокодов и кодов LDPC. Этот текст предлагает как «классическую» теорию кодирования, такую как Хэмминга, BCH, Рида-Соломона, Рида-Мюллера и сверточные коды, так и современные коды и методы декодирования, включая турбокоды, коды LDPC, коды с повторным накоплением. , пространственно-временные коды, факторные графы, декодирование с мягким решением, декодирование по Гурусвами-Судану, диаграммы выхода и итеративное декодирование. Представлены теоретические дополнения по производительности и пределам. Кодирование также входит в его коммуникационный и теоретический контекст информации, а связи с криптосистемами с открытым ключом. Идеально подходит в качестве учебного пособия и профессионального справочника, это подробное руководство будет полезно инженерам-электрикам и компьютерным инженерам, математикам, студентам, исследователям и ученым. НЕПОДВИЖНЫЙ ИНСТРУМЕНТ ОБУЧЕНИЯ И РУКОВОДСТВО ПО КОДИРОВАНИЮ ИСПРАВЛЕНИЯ ОШИБОК Методы кодирования с исправлением ошибок позволяют обнаруживать и исправлять ошибки, возникающие во время передачи данных в цифровых системах связи.Эти методы почти повсеместно используются в современных системах связи и, таким образом, являются важным компонентом современной информационной экономики. Кодирование с исправлением ошибок: математические методы и алгоритмы предоставляет всестороннее введение как в теоретические, так и практические аспекты кодирования с исправлением ошибок, с презентацией, подходящей для широкого круга аудиторий, включая аспирантов в области электротехники, математики или компьютеров. наука.Педагогика построена таким образом, что математические концепции представляются постепенно, за которыми сразу же следуют приложения к кодированию. Большое количество упражнений расширяет и углубляет понимание учащимися. Уникальной особенностью книги является набор лабораторий программирования, дополненных более чем 250 программами и функциями на соответствующем веб-сайте, который обеспечивает практический опыт и лучшее понимание материала. Эти лаборатории проводят студентов через внедрение и оценку кодов Хэмминга, кодов CRC, кодов BCH и R-S, сверточных кодов, турбокодов и кодов LDPC. Этот текст предлагает как «классическую» теорию кодирования ― такую как Хэмминга, BCH, Рида-Соломона, Рида-Мюллера, и сверточные коды ―, так и современные коды и методы декодирования, включая турбокоды, коды LDPC, коды с повторным накоплением , пространственно-временные коды, факторные графы, декодирование с мягким решением, декодирование по Гурусвами-Судану, диаграммы EXIT и итеративное декодирование. Представлены теоретические дополнения по производительности и пределам. Кодирование также входит в его коммуникационный и теоретический контекст информации, а связи с криптосистемами с открытым ключом. Идеально подходит в качестве учебного пособия и профессионального справочника, это подробное руководство будет полезно инженерам-электрикам и компьютерным инженерам, математикам, студентам, исследователям и ученым. ТОДД К. МУН — профессор кафедры электротехники и вычислительной техники в Университете штата Юта и старший член IEEE. Его исследовательские интересы включают применение математических принципов к проблемам, связанным с передачей, извлечением, моделированием, сжатием или анализом сигналов.Он является соавтором широко распространенного учебника по обработке сигналов для выпускников, автором множества статей и презентаций на конференциях, а также детской книги по программированию. Он также широко консультирует по вопросам промышленности. Более эффективная схема кодирования — это код Хэмминга , который аналогичен фонетическому алфавиту из начального раздела. В коде Хэмминга каждая возможная строка сообщения кодируется как определенное двоичное число, причем набор чисел специально выбран так, чтобы все они в некотором смысле существенно различались; Другими словами, каждая пара закодированных сообщений в некоторой степени существенно отличается. Эта мера равна , расстояние Хэмминга . Расстояние Хэмминга между двумя числами — это количество разрядов, в которых они различаются. Например, 1101010 и 1111000 — расстояние Хэмминга 2: 11 0 10 1 0 11 1 10 0 0 Ключевым моментом здесь является то, что если какая-либо пара кодировок находится достаточно далеко друг от друга с точки зрения расстояния Хэмминга, ошибки могут быть обнаружены и исправлены, видя, какое из кодовых слов является наиболее близким к переданному сообщению.Например, рассмотрим кодировку В этой кодировке минимальное расстояние Хэмминга между кодировками равно 2, что означает, что могут быть обнаружены однобитовые ошибки — то есть, если один бит переворачивается во время передачи письма, можно определить, что была сделана ошибка .Однако невозможно определить, каким было исходное сообщение; например, переданное сообщение «010» могло быть однобитовой ошибкой, возникшей в результате отправки «A», «B» или «D». Однако в этой кодировке: минимальное расстояние Хэмминга между кодировками равно 3, что означает, что однобитовые ошибки могут быть исправлены, а двухбитовые ошибки обнаружены. Это код (3,1) из предыдущего раздела. Вообще говоря, кодирование может обнаружить kkk-битовых ошибок, если минимальное расстояние Хэмминга составляет не менее k + 1k + 1k + 1, и исправить kkk-битовых ошибок, если минимальное расстояние Хэмминга составляет не менее 2k + 12k + 12к + 1. Отправьте свой ответ Известно, что зашумленный канал переключает биты с низкой частотой (поэтому можно с уверенностью предположить, что двухбитовых ошибок не будет).Алиса построила следующую частичную кодировку: какое значение должно кодировать Алисе D, чтобы добиться однобитовой коррекции? Хэмминга используют эту идею в сочетании с идеей битов четности и позволяют битам четности перекрываться.n2n — это сумма всех битов (взятых по модулю 2), в позициях которых nnnt младший бит установлен в 1. Например, бит четности в 2 представляет собой сумму битов в позициях 3 = 112,6 = 1102,7 = 1112,10 = 10102,11 = 10112,… 3 = 11_2, 6 = 110_2, 7 = 111_2, 10 = 1010_2, 11 = 1011_2, \ ldots3 = 112, 6 = 1102, 7 = 1112, 10 = 10102 , 11 = 10112,…, поскольку у всех этих позиций второй крайний правый бит установлен на 1. Международный научно-исследовательский журнал техники и технологий (IRJET) e-ISSN: 2395-0056 Том: 07 Выпуск: 05 | Май 2020 www.irjet.net p-ISSN: 2395-0072 © 2020, IRJET | Значение импакт-фактора: 7,529 | Сертифицированный журнал ISO 9001: 2008 | Page 2568 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК Mukunda D S1, Poornachandra prakash3, Manoj kumar P A3, Pavan kalyan V4, Prof.Паван кумар E5 1-5 Кафедра электроники и связи, Технологический институт Саи Видья, Бангалор, Индия ———————— ———————————————- *** — ————————————————— —————— Аннотация Коммуникация — это мощный инструмент, который помогает нам соединять с людьми. В современном мире цифровая связь значительно облегчила нашу жизнь.Но в процессе цифровой связи передаваемые сообщения часто уязвимы для шума. Другими словами, информационный сигнал , отправленный от передатчика, искажается даже до того, как получит обратно в приемник. Следовательно, приемник должен быть способен обнаруживать биты случайных ошибок, добавленные к исходным данным . Эти случайные биты ошибок вызваны помехами окружающей среды и физическими дефектами или даже из-за масштабирования технологии и вариаций параметров и уровней шума. В этой статье описаны математические модели (методы) обнаружения / исправления ошибок, которые могут быть использованы для защиты системы от различных типов ошибок . Эти модели обнаружения / коррекции имеют свои собственные характеристики , уровни сложности и требуют больших усилий для достижения максимальной эффективности в цифровой передаче . В этой статье перечислены многие математические модели обнаружения ошибок и исправления, которые обеспечивают надежную доставку цифровых данных по ненадежным каналам связи. Ключевые слова: переворот битов, память ошибок, обнаружение ошибок и исправление , четность, код Хэмминга. ВВЕДЕНИЕ В большинстве случаев мы предполагаем, что цифровые схемы на более устойчивы к шуму и обрабатывают информацию правильно. Но есть помехи, которые иногда влияют на значение цифрового сигнала . В цифровой системе аналоговые сигналы будут преобразовывать себя в цифровые биты, которые часто называют цифровым потоком. Эти возникающие помехи изменят значение последовательности с логического 0 на 1 или с логической 1 на логический 0. Иногда мы прозаично называем это переворотом битов (Ashenden, 2008, стр. 58). Это изменение положения битов приводит к катастрофическим ошибкам на выходе. Во время передачи, когда входные данные не совпадают с выходными данными, это называется ошибкой. На рисунке ниже показано возникновение ошибки в кодировщике и декодере цифровой системы: Рисунок 1: Ошибка в цифровой системе При цифровой передаче эти ошибки называются ошибками бита.Эти битовые ошибки могут возникать в памяти цифровых схем. Воспоминания являются наиболее важным компонентом для хранения, а также для извлечения любых цифровых данных , которые необходимы в определенное время (Shobha & Kavya, 2015, стр. 1). Типы встроенной памяти включают ROM, SRAM, DRAM, флэш-память и т. Д. На основании ошибки , влияющей на память, существует 2 типа: Мягкие ошибки Жесткие ошибки Мягкие ошибки временны и состоят из перевернуть бит в памяти без постоянного воздействия на емкость памяти для хранения данных. Эти ошибки обычно вызваны нейтронов высокой энергии, генерируемых столкновением космических лучей с атомами в атмосфере. Ошибка мягкая, потому что схема / устройство не повреждается навсегда этим излучением . Частота появления программных ошибок soft error rate зависит от способа изготовления устройства и места, в котором они работают. Ошибки, сохраняющиеся в памяти, называются серьезными ошибками. Если устройство / память подвержены этим типам аппаратных ошибок , оно теряет всю свою способность хранить данные и больше не может использоваться для операций чтения / записи. Операция чтения всегда будет давать значение 0 или 1 независимо от записанного предыдущего битового значения . Эти ошибки вызваны производственными дефектами или электрическими неисправностями после длительного использования. Если сигнал передает данные в двоичной кодировке, любое изменение может изменить значение данных (Shobha & Kavya, 2015, стр. 1). Основываясь на этом изменении данных во время передачи, есть два типа ошибок: Однобитовая ошибка Пакетная ошибка Edit: поскольку я только косвенно ответил на ваш вопрос в заголовке (т.е., горячие темы в кодах кодирования ошибок, связанные с интересной математикой), я думаю, что одна из самых горячих в настоящее время — это коды квантового исправления ошибок. С момента открытия П. Шором того факта, что мы можем исправлять квантовые ошибки, область квантовой информатики резко выросла и совершила квантовый скачок в направлении реализации крупномасштабных квантовых вычислений и надежной квантовой связи. Список разделов математики, используемых в этой области, бесконечен и продолжает расти по мере того, как мы говорим. [\ end Edit] Jyrki уже дал отличный ответ на многие ваши вопросы.Итак, дополним его, обратившись к паре моментов, которые он (она?) Не затронул: 1) Горячей темой в исправлении ошибок является поиск кодов LDPC с очень низким «полом ошибок» для кодов длиной в десятки тысяч битов, это может быть полезно для оптической передачи. Однако мне непонятно, какая здесь математика играет роль? Это зависит от выбранного вами канала (и метода декодирования). В дальнейшем мы рассматриваем только двоичный код (потому что я мало знаю о недвоичном случае!). Самый простой случай — это BEC (канал двоичного стирания), где наборов остановки определяют характеристику BER кода LDPC. Малые наборы остановки подобны кодовым словам с малым весом в традиционном коде; чем больше в вашем коде небольших наборов остановок, тем хуже в целом становится его эффективность исправления ошибок. Остановочные множества можно описать полностью комбинаторно. Остановочный набор матрицы проверки на четность $ H $ — это набор столбцов, в каждой строке которого есть не менее двух $ 1 $ (внутри столбцов).Вы можете перефразировать определение на языке систем множеств, рассматривая $ H $ как матрицу инцидентности; это эквивалентно полной конфигурации . Или вы можете переформулировать это, используя такие термины, как узлы проверки и узлы переменных, как это принято в литературе по коду LDPC. В любом случае, наименьшие стопорные наборы преобладают при достаточно высоком SNR. Таким образом, улучшение BER напрямую соответствует проблеме предотвращения (или, что эквивалентно, проблеме запрещенной конфигурации) в двоичной матрице. Итак, это комбинаторная проблема, изучающая систему множеств, избегая полных конфигураций, которая дает желаемую длину кода, скорость, другие дополнительные свойства, которые вы хотите, такие как конкретный автоморфизм.Так что это почти то же самое, что и старая добрая алгебраическая теория кодирования; устранение кодовых слов с низким весом (или, что эквивалентно, достижение больших минимальных расстояний) теперь заменяется устранением небольших наборов остановки. Фактически, размер наименьшего остановочного набора называется тормозным путем $ H $. Следует отметить, что понятие тормозного пути определено для матрицы проверки на четность. Поскольку один и тот же линейный код имеет различные матрицы проверки на четность, вы не говорите тормозной путь кода.В остальном тормозной путь является более или менее аналогом минимального расстояния, когда речь идет о коде LDPC через BEC. Все намного сложнее для других хорошо изученных каналов, таких как всеми любимый канал AWGN и канал теории кодирования 101, двоичный симметричный канал. Некоторые говорят, что в целом лучший тормозной путь ведет к лучшему BER или, по крайней мере, это неплохой признак. Но так бывает не всегда. Тип субструктуры в $ H $, которая портит ваш алгоритм декодирования при высоком SNR для каналов, отличных от BEC, обычно нелегко описать простой комбинаторикой.Если вам интересно, поиск в IEEE Xplore с такими ключевыми словами, как «наборы треппинга» и «псевдокодовые слова» должен направить вас к нужным статьям. Вы также можете исправить квантовые ошибки, воспользовавшись теорией кодов LDPC. Но я не видел работ, в которых непосредственно изучались бы аналоги наборов остановки, наборов захвата и т. Д. Для квантовых каналов. Основная трудность в квантовой области состоит в том, что не каждый $ H $ определяет квантовый код LDPC; строки должны соответствовать генераторам стабилизатора, который является абелевой подгруппой группы Паули, иначе вам нужно либо определенное количество кубитов в состояниях Белла, совместно используемых отправителем и получателем, либо предположить очень надежный вспомогательный квантовый канал для «принудительного воздействия» ваш $ H $, чтобы определить стабилизатор большей группы.Итак, у вас есть еще кое-что, что нужно учесть, прежде чем вы сможете перевести проблему минимума ошибок LDPC-кодирования для квантовых каналов на язык математики. Или вы можете сказать, что вид математики, играющий роль для этого конкретного подполя, — это те, которые вам нужны для квантовой информации поверх обычной математики для кодов LDPC, таких как комбинаторика, теория информации и вероятность. Поскольку вы упомянули полярные коды в своем третьем вопросе, пространственно связанных кодов LDPC являются одними из самых популярных классов кодов LDPC, которые конкурируют с полярными кодами.Порог шума пространственно-связанного ансамбля при итеративном декодировании совпадает с порогом MAP-декодирования над BEC. Квантовые аналоги пространственно-связанных кодов LDPC и полярных кодов также изучаются / изучаются, хотя и с ограниченным успехом по сравнению с замечательным прогрессом для классического случая. 4) Вероятно, наиболее классическим примером является код Голея (1948) и отдельные простые группы Матье … [Цитата из Википедии о том, как группы Матье являются группами автоморфизмов кодов Голея, расширенных кодов Голея и т. Д.идет сюда] … Это совпадение или за этим что-то стоит? Да. За этим что-то стоит. Например, группа Матье $ M_ {24} $ по определению является группой автоморфизмов расширенного двоичного кода Голея или, что эквивалентно, $ 5 $ -конструкции Штейнера порядка $ 24 $ и размера блока $ 8 $, которая называется . Дизайн Витта в комбинаторной теории проектирования. Вот лекция по этому поводу А. Э. Брауэра. Это одно из тех интересных взаимодействий между конечными простыми группами, схемами и кодами. Я думаю, что этот ответ становится слишком длинным для сообщения на форуме, поэтому в остальном я просто рекомендую вам искать в Интернете с помощью Google или вашей любимой поисковой системы по таким ключевым словам, как коды Голея, рисунки Штайнера, рисунки Витта, простые группы и подобное, аналогичное, похожее. Таким образом, я не буду огорчать своих прежних и нынешних наставников и докторов наук. супервайзер заодно, написав какую-то глупость про то, что я должен знать лучше. 5.Теория и практика кодов В начале истории развития математики кодов с исправлением ошибок было ясно, что такие коды будут иметь большую экономическую ценность, что не всегда верно для идей, разработанных в других частях математики. Исследователи в области математики, как и творческие люди в других областях, хотят вознаграждений и признания за свою работу. Кто-то, кто первым предположил важный математический результат, человек (люди), который первым доказал математический результат, или человек, обнаруживший идеи, которые могут быть применены, — все получают формы признания (см. * Ниже для обсуждения некоторых из эти формы признания). Споры о приоритете, касающиеся того, кто первым разработает важные идеи, возникают в математике, как и в других областях. Одним из самых известных таких споров был спор между Ньютоном и Либницем по поводу того, кто первым разработал исчисление. Другим подобным спором, возникшим в более современные времена, был спор между Ричардом Хэммингом и Марселем Голеем по поводу разработки кодов исправления ошибок. Хотя имя Голея гораздо менее известно, чем имя Шеннона или Хэммингса, он внес очень важный вклад в теорию информации, в том числе привлек внимание к некоторым специальным кодам с очень хорошими свойствами, которые известны как коды Голея .Хотя Голай родился в Швейцарии, он получил докторскую степень. получил степень доктора физики в Соединенных Штатах и большую часть своей карьеры проработал в Америке, работая в Bell Labs и Корпусе связи армии США, прежде чем вернуться в Европу в 1960-х годах. Интересно, что хотя он использовал математику в своей работе, именно его потрясающая интуиция в отношении поведения физических систем помогла Голею внести важный вклад. В частности, он получил более 50 патентов. Голей также внес важный вклад в хроматографию и глобальные навигационные системы, развивая идеи, которые включены в систему Loran C. В идеале нужны коды с большим количеством кодовых слов, которые исправят множество ошибок и для которых длина кодового слова мала. Неудивительно, что эти желания «работают» друг против друга: существует сложный компромисс между количеством ошибок, которые код может исправить, количеством двоичных цифр в кодовом слове и наибольшим количеством кодовых слов, которые может иметь код. . Ниже представлена часть того, что известно о ситуации. Данные приведены для некоторых малых значений e, количества ошибок на кодовое слово, до которых код может исправить.Записи в таблице дают максимальное количество двоичных кодовых слов, которое может иметь данная длина строки и возможность исправления ошибок. Например, не существует двоичного кода, кодовые слова которого имеют длину 5, который исправляет до 1 ошибки и который имеет более 4 кодовых слов. Точно так же не существует двоичного кода с более чем 2 кодовыми словами, где кодовые слова представляют собой строки длиной 7 и которые исправят до 2 ошибок. (*) В науке одной из самых престижных наград была Нобелевская премия.Эти призы, имеющие большую денежную ценность, были профинансированы Альфредом Нобелем около 100 лет назад. Они награждаются в области медицины и в различных науках. Первоначально Нобелевской премии по экономике не было, но в 1969 году была учреждена престижная Нобелевская мемориальная премия по экономике. Эту премию получил математик Джон Нэш, и эта премия была присуждена довольно большому количеству экономистов, чьи работы в высшей степени математичны. Нобелевской премии по математике не создавалось. О причинах этого ходило много «легенд».Хотя кажется, что иногда ученые-математики смотрят «на приз», когда решают, какой объем информации раскрыть о направлении исследований, которым они могут заниматься, до самого недавнего времени с присуждением прибыльных премий Клея и Абеля, самой престижной премии в области математики. была неудачной медалью Филдса. Из-за этого или несмотря на это математики часто быстро публиковали свои работы, даже когда они имели высокий потенциал экономической отдачи. Список литературы
[1] Вт.В. Петерсон, Э.Дж. Велдон, «Коды с исправлением ошибок», M.I.T. (1972) MR0347444 Zbl 0251.94007 [2] E. Berlekamp, «Алгебраическая теория кодирования», McGraw-Hill (1968) MR0238597 Zbl 0988.94521 [3] F.J. MacWill Слоан, «Теория кодов с исправлением ошибок», I-II , Северная Голландия (1977) [4] E.L. Блох, В. Зяблов, «Обобщенные каскадные коды», Москва (1976) MR0607525 [5] В.Д. Колесник, Э. Мирончиков, «Расшифровка циклических кодов», Москва (1968), [6] В. Сидельников, «Экстремальные многочлены, используемые в оценках объема кода» Пробл. Поставить в известность. Коробка передач , 16 : 3 (1980) с. 174–185 Пробл. Передач. Поставить в известность. , 16 : 3 (1980) стр. 17–30 Zbl 0468.94010 [7] V.I. Левенштейн, «Минимальная избыточность кодов, исправляющих ошибки» Пробл.Поставить в известность. Коробка передач , 10 : 2 (1974) с. 110–123 Пробл. Передач. Поставить в известность. , 10 : 2 (1974) стр. 26–42 [8] В.В. Зяблов, М. Пинскер, «Оценка сложности исправления ошибок для кодов Галлагера низкой плотности» Пробл. Поставить в известность. Коробка передач , 11 : 1 (1975) с. 18–28 Пробл. Передач. Поставить в известность. , 11 : 1 (1975) стр. 23–36 Список литературы
[a1] J.H. ван Линт, «Введение в теорию кодирования», Springer (1982) MR1540511 Zbl 0485.94015 [a2] A.Тиетавяйнен, «О существовании совершенных кодов над конечными полями» SIAM J. Appl. Математика. , 24 (1973) стр. 88–96 [a3] R.J. МакЭлис, Э.Р. Родемич, Х. Рамси, Л. Уэлч, «Новые верхние границы скорости кода с помощью неравенств Делсарта – Мак-Вильямса» IEEE Trans. Поставить в известность. Theory , 23 (1977) pp. 157–166 MR439403 [a4] М.А. Цфасман, С.Г. Влэдутс, Т. Зинк, «Модульные кривые, кривые Шимуро и коды Гоппа, лучше, чем оценка Варшанова – Гилберта. « Math.Nachr , 109 (1982) стр. 21–28 [a5] P.M. Грубер, К. Lekkerkerker, «Геометрия чисел», Северная Голландия (1987) (обновленное издание) MR0893813 Zbl 0611.10017 [a6] R. Hill, «Первый курс теории кодирования», Clarendon Press (1986) MR0853914 Zbl 0616.94006 [a7] JH van Lint, G. van der Geer, «Введение в теорию кодирования и алгебраическую геометрию», Birkhäuser (1988) Zbl 0648.94011 Zbl 0639.00048 [a8] V.D. Гоппа, «Геометрия и коды», Kluwer (1988) MR1029027 Zbl 1097.14502 [a9] М.А. Цфасман, С.Г. Влэдутс, «Алгебраические геометрические коды», Kluwer (1989) MR1003354 Zbl 0674.94012
Код исправления ошибок. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Error-correcting_code&oldid=46851 Математические методы и алгоритмы: Мун, Тодд К.: 9780471648000: Amazon.com: Книги
«… Одна из лучших на рынке книг по кодированию ошибок. Я настоятельно рекомендую ее как для академических исследований, так и для практических целей». ( Computing Reviews.com , 16 января 2006 г.) С задней обложки
Об авторе
Коды исправления ошибок | Блестящая вики по математике и науке
Буква Кодировка A 000 B 011 C 101 D 110 Letter Кодировка A 00000 B 00111 C 11001 D ????? (PDF) МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК
ит. Теория информации — Горячие темы в кодировании с исправлением ошибок, связанных с интересной математикой. ?
из AMS
Цифровая революция (Часть III) — Коды коррекции ошибок
n е = 1 е = 2 е = 3 5 4 2 — 6 8 2 — 7 16 2 2 8 20 4 2 9 40 6 2 10 72 12 2 11 144 24 4 12 256 32 4 13 512 64 8 14 1024 128 16 15 2048 256 32


 Технологии: дифференцированная работа, моделирование.
Технологии: дифференцированная работа, моделирование. Тем, кто справился с решением задач, даю дополнительные задания, записанные в третьей колонке. Для учащихся, которые допустили ошибки при решении задач, в первой колонке предлагаю дифференцированную помощь в виде чертежа, моделирования задачи.
Тем, кто справился с решением задач, даю дополнительные задания, записанные в третьей колонке. Для учащихся, которые допустили ошибки при решении задач, в первой колонке предлагаю дифференцированную помощь в виде чертежа, моделирования задачи. №9 по плану.
№9 по плану. Объяснение целей задач урока.
Объяснение целей задач урока.
 Из каких отрезков пути складывается весь путь?
Из каких отрезков пути складывается весь путь?
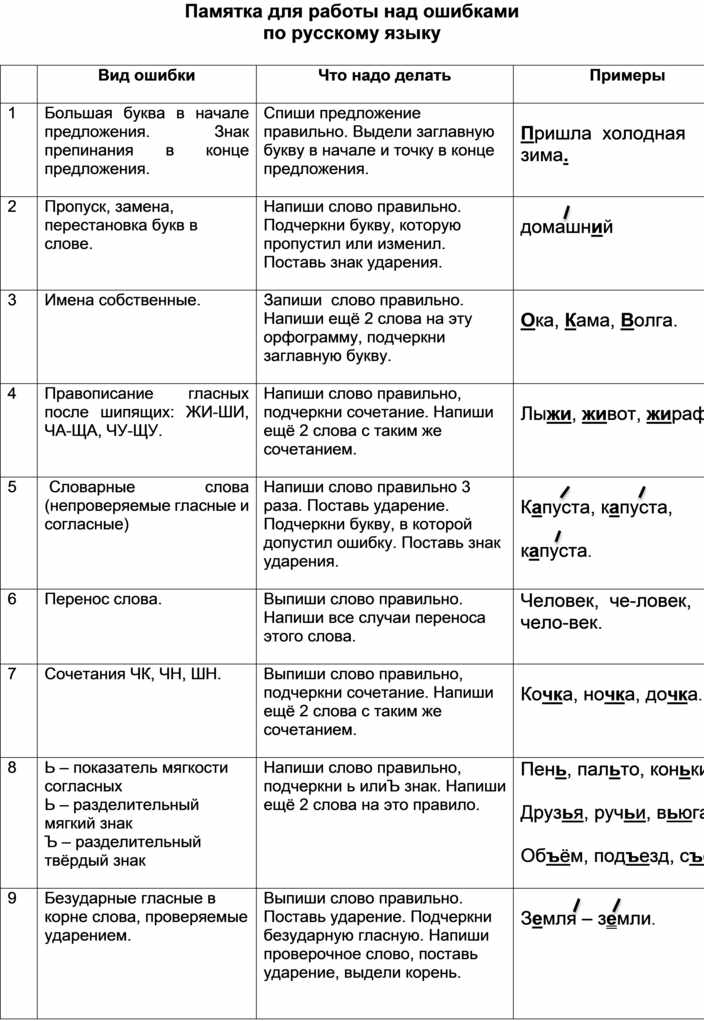 , Казекин (ошибки в вычислении), Суганова Ю., Гудилин А. (неправильно выполнил последнее задание), Заворотнюк М.
, Казекин (ошибки в вычислении), Суганова Ю., Гудилин А. (неправильно выполнил последнее задание), Заворотнюк М.

 ( в вычислении), Казекин Д., Чуканов Р. решают с учителем.
( в вычислении), Казекин Д., Чуканов Р. решают с учителем. Подведение итога работы.
Подведение итога работы.


 Каким способом удобнее всего решить это уравнение?
Каким способом удобнее всего решить это уравнение? Обобщение знаний
Обобщение знаний
 Какова масса 8 литров нефти? 4,8
Какова масса 8 литров нефти? 4,8
 Какова высота Пирамиды? (Гиза)144
Какова высота Пирамиды? (Гиза)144 умение осознанно и произвольно строить речевое высказывание в устной форме (КУУД). умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
умение осознанно и произвольно строить речевое высказывание в устной форме (КУУД). умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
 Структурирование знаний. Анализ объектов.
Структурирование знаний. Анализ объектов. формирование внутреннего плана действий, структурирование полученной информации
формирование внутреннего плана действий, структурирование полученной информации Важное значение имеет то, на каком этапе обучения совершаются ошибочные действия;
Важное значение имеет то, на каком этапе обучения совершаются ошибочные действия;