Работа в термодинамике | ЕГЭ по физике
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$.
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).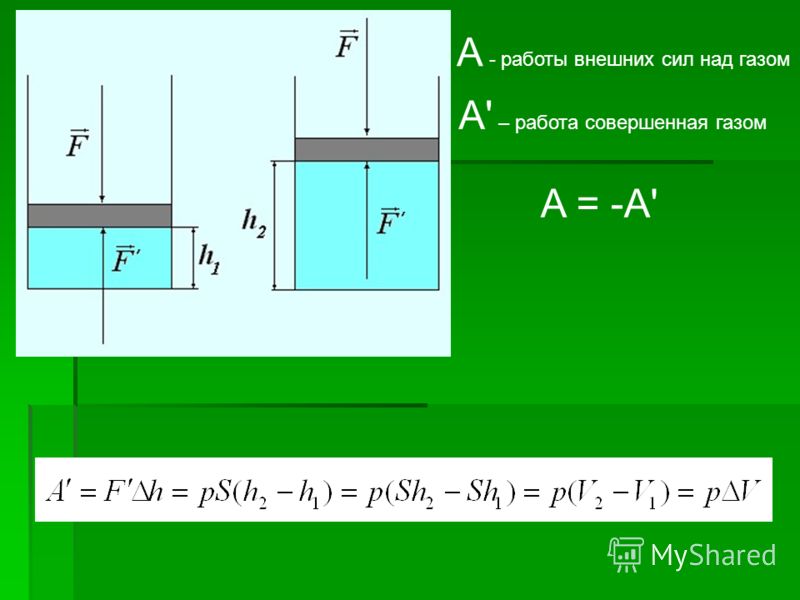
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$).
Если газ отдает тепло окружающей среде, $Q
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т.
к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л.
С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$).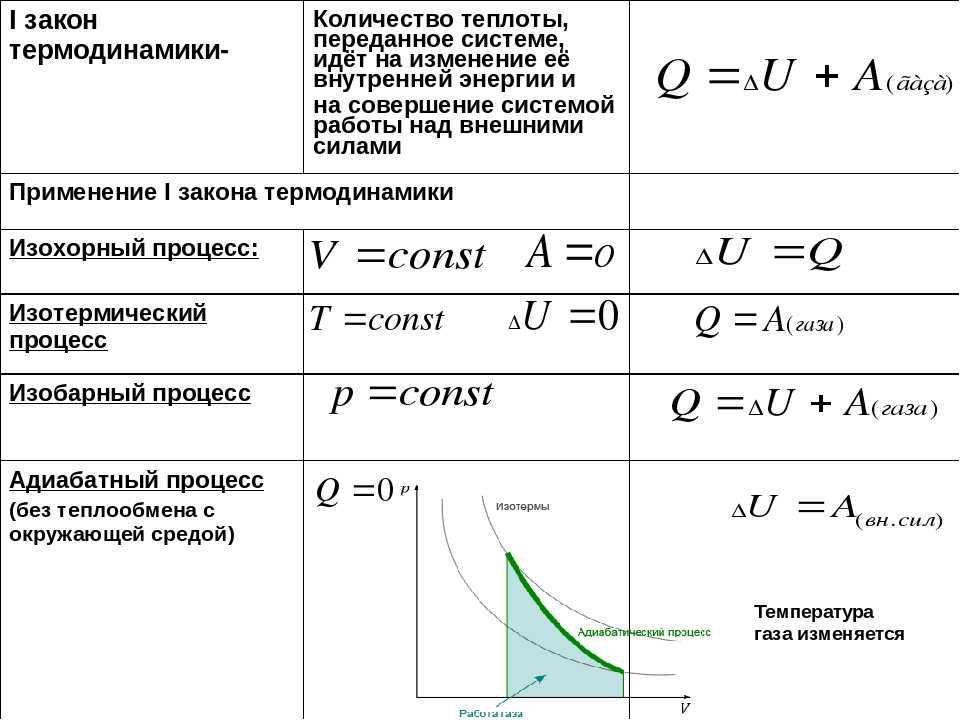
Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
Работа в термодинамике. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Работа в термодинамике.
| Работа в термодинамике. | |
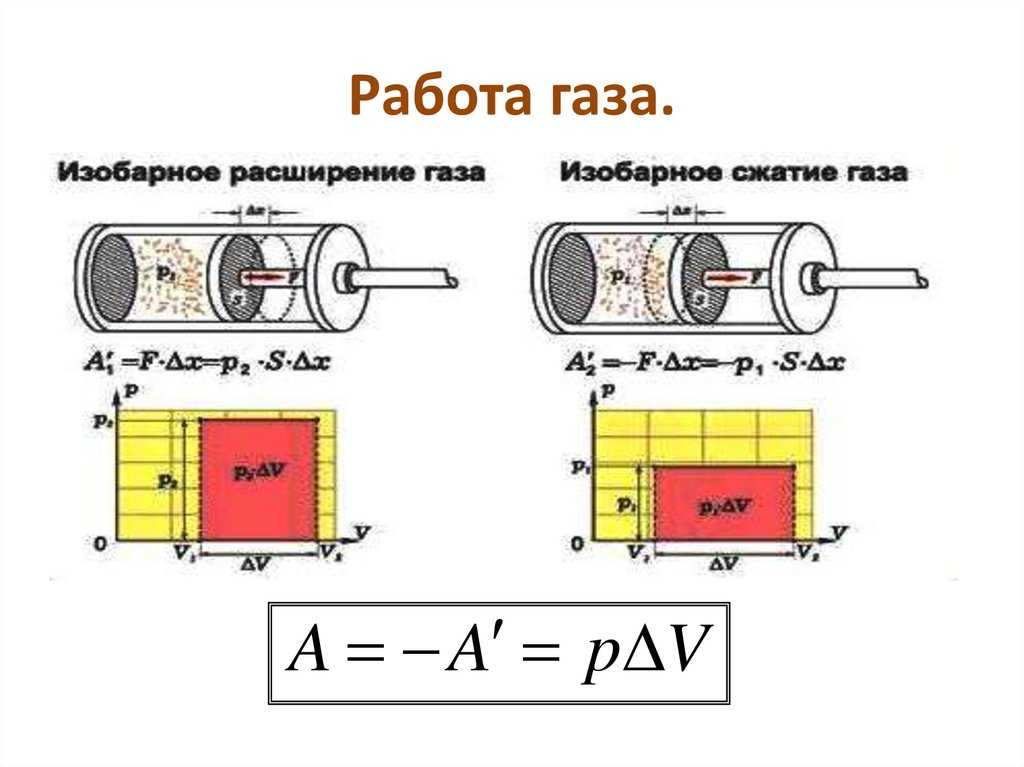
В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела относительно друг друга. При совершении работы меняется объем тела, а его скорость остается раной нулю. Носкорости молекул тела меняются! Поэтому меняется температура тела. Причина в том, что при столкновении с движущимся поршнем (сжатие газа) кинетическая энергия молекул изменяется — поршень отдает часть своей механической энергии. При столкновении с удаляющимся поршнем (расширение) скорости молекул уменьшаются, газ охлаждается. При совершении работы в термодинамике меняется состояние макроскопических тел: их объем и температура. |
|
— сила, действующая на газ со стороны поршня. А — работа внешних сил по сжатию газа. — сила, действующая на поршень со стороны газа. А’ — работа газа по расширению. = — — по 3-ему з-ну Ньютона. Следовательно: А= — А’ = pS, где p— давление, S — площадь поршня. Если газ расширяется: Δh=h2 — h1 — перемещение поршня. V1=Sh1; V2=Sh2. | |
Тогда: A’=F’Δh=pS(h2 — h1)=p(Sh2 — Sh1)=p(V2-V1)=pΔV |
|
При расширении работа газа положительна. При сжатии — отрицательна. Таким образом: A’ = pΔV — работа газа A= — pΔV — работа внешних сил. |
|
Используя уравнение Менделеева-Клапейрона, получим: |
|
Эти выражения справедливы при очень малых (!) изменениях объема или при постоянном давлении (т. |
|
Физический смысл универсальной газовой постоянной. — универсальная газовая постоянная численно равна работе 1 моля идеального газа при изобарном нагревании на 1 К. |
|
Геометрическое истолкование работы. | |
В изобарном процессе площадь под графиком в координатах p,V численно равна работе (вспомните — перемещение на графике скорости!). | |
В общем случае надо процесс разбить на малые части и сосчитать элементарные работы, а затем их сложить (процесс интегрирования): Например, в изотермическом процессе . | |
В изохорном процессе объем не меняется, следовательно, в изохорном процессе работа не совершается! В адиабатном процессе . |
|
е. в изобарном процессе)Теги:
конспект
Термодинамика — раздел физики который имеет дело с энергией и работой системы. Термодинамика занимается только широкомасштабный ответ системы, которую мы можем наблюдать и измерить в опытах. В аэродинамике мы больше всего интересует термодинамика потоки с высокой скоростью, а в двигательные установки которые создают тягу за счет ускоряющий газ. Чтобы понять, как создается тяга, полезно изучать основы термодинамики газов. Состояние газа определяется
значения некоторых измеряемых свойств
как давление,
температура,
и
объем
которую занимает газ. Значения этих переменных и
состояние газа можно изменить. На этом рисунке мы показываем газ
в синей банке в двух разных состояниях. Слева, в штате
1 газ находится под более высоким давлением и занимает меньший объем, чем
в состоянии 2, справа. Мы можем изобразить состояние газа на графике
давления по отношению к объему, который
называется
диаграмма p-V
как показано справа. Ученые определяют работу W как продукт силы F , действующей на расстоянии с : Вт = F * с Для газа работа есть произведение
давление p и громкость V при смене громкости. Вт = р * В Мы можем сделать Быстрые единицы проверяют, чтобы увидеть, что давление сила / площадь умножить на объем площадь * длина дает единицы силы, умноженные на длину, которые являются единицами работы. W = (сила / площадь) * (площадь * длина) = сила * длина В метрической системе единицей работы является джоуль, в английской системе единицей является фут-фунт. Как правило, при изменении состояния громкость и изменение давления. Поэтому правильнее определить работу как интегрированное или суммированное переменное давление, умноженное на изменение объема из состояния 1 в состояние 2. Если мы используем символ S [ ] ds для интеграла, тогда: W = S [p] dV На графике зависимости давления от объема, работа – это площадь под кривой, описывает, как состояние изменяется с состояния 1 на состояние 2. Как упоминалось выше, существует несколько вариантов изменения состояния
газ из одного состояния в другое. Обратите внимание, что не только работа, совершаемая газом, зависит от процесса, но и также тепло, переданное газу. В первом процессе кривая линия от из состояния 1 в состояние 2 теплота газу не передается; процесс был адиабатический . Но во втором процессе прямая линия из состояния 1 в состояние «а», а затем к Состояние 2, тепло передается газу в процессе постоянного давления. Теплота, передаваемая газу, зависит не только от начального и конечные состояния газа, но и процесс, используемый для изменения штат. Деятельность: Экскурсии с гидом
Навигация .
|
Калькулятор комбинированного газового закона
Создано Wojciech Sas, PhD
Рассмотрено Богной Шик и Стивеном Вудингом
Последнее обновление: 06 декабря 2022 г.
Содержание:- Что такое термодинамические процессы? Формула комбинированного газового закона
- Первый закон термодинамики
- Изохорный процесс
- Изобарический процесс
- Изотермический процесс
- Адиабатический процесс
- Расчетный пример
- Цикл Карно
Этот калькулятор комбинированного газового закона является отличным инструментом для решения задач, связанных с 90s1 90s4 90s. Прочтите об изобарических, изохорных, изотермических и адиабатических процессах идеальных газов (газов, которые можно описать уравнением идеального газа) и о том, как идеальные газы могут совершать работу или выделять/поглощать тепло.
Проверьте точные значения для реальных газов, используя наш калькулятор уравнения Ван-дер-Ваальса, и забудьте о термодинамических упражнениях!
Что такое термодинамические процессы? Формула комбинированного газового закона
Мы можем описать идеальный газовый баллон несколькими параметрами: давлением p , объемом V , температурой T и числом частиц n . Их можно соотнести уравнением: p·V = n·R·T , где R обозначает постоянную идеального газа и равен 8,3144598 Дж/(моль·К) .
Во время любого процесса по крайней мере два из этих свойств изменяются , что мы можем скомпилировать в формулу комбинированного газового закона: p·V/T = k , где k — константа.
Из всех трансформаций мы можем выделить несколько, которые охватывают подавляющее большинство примеров из повседневной жизни, или мы можем рассматривать их как хорошие приближения.
В этом калькуляторе комбинированного газового закона мы рассматриваем процессы, в которых количество частиц постоянно . Таким образом, мы можем представить себе газ в закрытом сосуде. Это:
- Изохорный процесс;
- Изобарический процесс;
- Изотермический процесс; и
- Адиабатический процесс.
Первый закон термодинамики
Внутренняя энергия U представляет собой сумму всех видов энергии, присутствующих в системе. Довольно сложно оценить точное значение внутренней энергии. Тем не менее, можно найти изменения тепловой энергии ΔU , которые описываются первым законом термодинамики: ΔU = Q — W , где Q обозначает теплоты, поглощаемой , а Вт равно работе, совершаемой газом .
Изменение внутренней энергии пропорционально изменению температуры ΔT и типу газа по следующему уравнению: ΔU = Cv·n·ΔT , где Cv – молярная теплоемкость при постоянном объеме. Для идеального газа принимает значения:
- 3/2·R для одноатомного газа;
- 5/2·R для двухатомного газа; и
- 3·R для газов с более сложными молекулами.
Эти параметры в реальных газах отличаются от теоретических, но они уже есть в нашем калькуляторе термодинамических процессов.
Общая формула для работы, совершаемой газом, выражается как ∫p(V)dV , если мы рассматриваем давление как функцию объема . Хотя в целом это нетривиально, вы можете проверить, как формула упрощается для процессов, упомянутых ниже.
Изохорический процесс
Во время этого перехода Объем является постоянным параметром , так что начальные свойства P₁ , T₁ изменяются до P₂ , T₂ .
Неизменность объема означает, что газ не совершает никакой работы и теплота, поглощаемая газом, в точности равна изменению внутренней энергии: ΔU = Q = Cv·n·ΔT . Мы можем визуализировать этот процесс для газа, хранящегося в жестком контейнере, который может обмениваться теплом с окружающей средой. Вы можете попробовать наш калькулятор закона Гей-Люссака, так как закон Гей-Люссака соответствует этому термодинамическому процессу.
Изобарический процесс
Мы предполагаем, что давление является постоянным параметром газа во время этого перехода. Поэтому начальные параметры V₁ , T₁ преобразуются в V₂ , T₂ со следующей формой формулы комбинированного газового закона: V₁ / T₁ = V₂ / T₂ .
Поскольку давление неизменно, формула для работы, совершаемой газом, равна Вт = p·ΔV . Теплота, однако, может быть рассчитана как: Q = ΔU + W = Cv·n·ΔT + p·ΔV = Cp·n·ΔT .
Cp известна как молярная теплоемкость при постоянном давлении, а для идеального газа она связана с Cv , так что Cp = Cv + R . Проверьте калькулятор закона Чарльза Омни, так как закон Чарльза связан с изобарическим переходом.
Изотермический процесс
Постоянным параметром в этом переходе является температура , так что начальные свойства p₁ , V₁ изменяются на p₂ , V₂ , и соотношение: p₁·V₁ = p₂·V₂ . В представленном примере видно, что согласно уравнению идеального газа давление является следующей функцией объема: p(V) = n·R·T / V = A / V , где A постоянным на протяжении всего процесса.
Общее выражение для работы, совершаемой газом, можно оценить как W = n·R·T·ln(V₂ / V₁) , где ln обозначает натуральный логарифм заданного числа. Из-за постоянства температуры начальная энергия не меняет , откуда следует равенство: Q = W . Можно сказать, что мы превращаем всю теплоту, поглощаемую газом, в совершаемую им работу, но, с другой стороны, этот переход, как известно, на практике очень медленный. Для более подробного объяснения обратитесь к нашему калькулятору закона Бойля, который описывает термодинамические процессы такого рода.
Адиабатический процесс
При этом переходе изменяются все три параметра, но одновременно газ не обменивается теплом с окружающей средой . Справедлива следующая формула: p₁V₁ γ = p₂·V₂ γ , где γ = Cp / Cv известно как отношение теплоемкости . Работа, совершаемая газом, противоположна его начальному изменению внутренней энергии Вт = -ΔU . Этот процесс описывает переходы, которые происходят быстро , и газ не успевает поглотить или отдать какое-либо тепло.
Расчетный пример
Предположим, что вы хотите найти изменение внутренней энергии , поглощенное тепло и работу, совершенную азотом, хранящимся внутри гибкого контейнера объемом 0,5 м³ при атмосферном давлении и температуре 250 К, который мы нагреваем до 300 К. В этом случае мы рассматриваем изобарический процесс.
Рассчитать конечный объем:
V₂ = V₁·T₂ / T₁
= 0,5 м³ · 300 K / 250 K
= 0,6 м³Определите количество молекул:
n = p·V₁ / (R·T₁)
= 101,325 кПа · 0,5 м³ / (8,314 Дж/(моль·K) · 250 K)
= 24,375 мольНайти теплоемкость Cv азота, которая равна 20,814 Дж/(моль·К) (для идеального двухатомного газа она должна быть равна 20,786 Дж/(моль·К) ).
Оценка изменения внутренней энергии:
ΔU = 20,814 Дж/(моль·К) · 24,375 моль · 50 К
= 25,367 кДжОпределить работу, совершаемую газом:
Вт = 101,325 кПа · 0,1 м³
= 10,133 кДжОцените тепло, поглощаемое азотом:
Q = 25,367 кДж + 10,133 кДж
= 35,500 кДж .