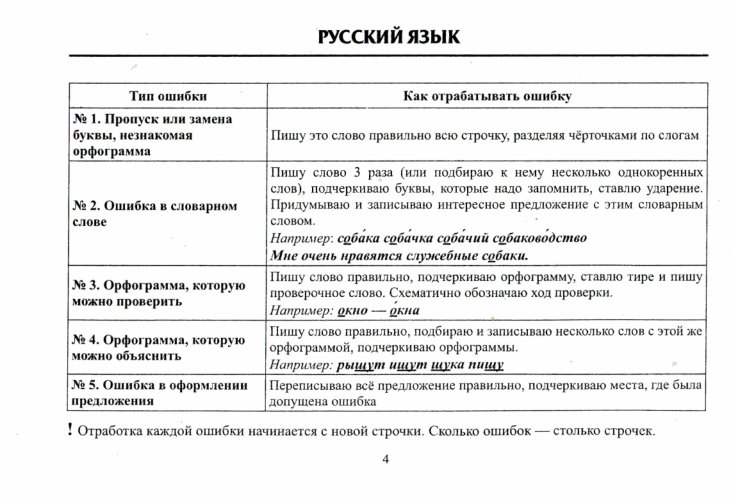
По математике 5 класс работа над ошибками
| Предмет: | Математика |
|---|---|
| Категория материала: | Конспекты |
| Автор: | Тилеубергенкызы Перизат Тилеубергеновна это Вы? |
Число:09.12.2015 г.
Класс: 5 «Б»
Предмет: математика
Тема: Работа над ошибками
Учитель: Перизат Тілеубергеновна
Цели урока:
Образовательные:
-формировать способность видеть и исправлять ошибки;
— дать возможность тем учащимся, которые не справились с решением заданий, решить эти задания, используя помощь учителя.
-формировать навык сравнивать и оценивать свою работу.
Развивающие:
-развивать память, внимание, абстрактно-логическое мышление в процессе устного счёта и решения и сравнения заданий;
-развивать речь;
Воспитательные:
-воспитывать усидчивость, дисциплинированность;
-воспитывать интерес к предмету.
Ход урока
Организационный моментПриветствие с учиникамиПроверить кого нет в классеПроверить чистоту классаПроверить домашнего заданияФронтальный опрос:Что такое НОД и НОК?Какие способы есть, чтобы найти НОД и НОК?В чем разница НОД и НОК?Работа над ошибкамиВ начале урока учащиеся делятся на 3 группы.
По контрольной работе есть учиники которые получили «5», они будут главными в группе. 6 учиники получили «4», они по двум разделились на 3 группы. В классе учащиеся 23, в каждой группе 7 или 8 учащихся.
Кому достанется золотоПо контрольной работе первая и вторая задача было найти НОД и НОК.
На доске будет плакат. На нем будет 3 дороги на большой красивый домик. На дорогах будут задачи на НОК и НОД (легкие). Которые были даны в контрольной работе 1 и 2 задачи. На эти задачи выйдут к доске те которые больше допускали ошибки на 1 и 2 задачи.
В каждой дороге будут по 3 задачи. Какая группа первым закончить решать 3 задачи, если конечно будет без ошибок, им тогда дам 3 золото (монетка шоколад). Потом будем проверять как другая группа решает задачи. Если будут ошибки, исправим и объясним.
1-дорога2-дорога3-дорога
НОД(4,12)=4НОД(5,15)=5НОК(6,18)=18
НОК(6,24)=24НОК(9,18)=18НОД(10,15)=5
НОК(6,12)=12НОД(9,18) =9НОК(7,21)=21
Простые множители.(3 слайд)В контрольной работе 3 и 5 задачи были даны простые множители. В 3 задачи надо найти НОК, а в 5 задачи НОД. В этом задачи только 3 учиника правильно решали, а остальные с ошибками.
В 3 слайде надо найти НОД и НОК которые на 2 части разделены и есть круг внутри есть баллы (10-30).
Когда баллы меньше тогда задачи легче, а если больше тогда труднее. Так как главные группе решали отлично они будут выбирать, а остальные будут решать. Если задачи без ошибки. Тогда им тоже достанется золото, сколько баллов набереть столько золото возьмет.
НОД 10: a=22, b=2 НОК 10: a=2 b=2
НОД 20: c=2, d=2 НОК 20: c=2, d=2
НОД 30: e=2, f=25 НОК 30: e=, f=2
Физкультминутка(4 слайд)Здесь нужен глаз
На редкость зоркий,
Задача очень непроста:
Четыре цифры на разветке
Постав на верные места!
На все решенье – пять минут.
Подсказку – кубики дают!
Итоги урока (5 слайд)
Как вы видите есть сумка, мясорубка и мусорный ящик. На эти рисунки смотря учащися должны сказать, «что им нужно?», «что они хотять в дальнейшим по больше знать?», и « что им не нужно?».
Теперь в конце урока определяется какая группа много получили золото. И этой группе будет отличная оценка, и те которые активно решали задачи им тоже.
Задания на дом №748 cт.169
| Тип материала: | Документ Microsoft Word (docx) |
|---|---|
| Размер: | 219.08 Kb |
| Количество скачиваний: | 89 |
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Математика. 2 класс, Селиванова М.С. . Работа над ошибками , Литера , 9785407008187 2017г. 82,40р.
Селиванова М.С.
Серия: Работа над ошибками
Осталось всего 5 шт.
82,40р.
Только в магазинах
В наличии в 3 магазинах
Ангарск, ПродаЛитЪ Ангарск Центр
Иркутск, ПродаЛитЪ ТЦ Версаль
Улан-Удэ, ПродаЛитЪ EuroZone
Цена в магазине может отличаться
от цены, указанной на сайте.
Поделиться ссылкой в:
Издательство:Литера
ISBN:978-5-407-00818-7
Штрих-код:9785407008187
Страниц:16
Тип обложки:Мягкая
Год:2017
НДС:10%
Код:907336
Описание
Данное учебное пособие может быть использовано как рабочая тетрадь для занятий с вашим ребёнком дома. В нём представлен основной программный материал по математике 2-го класса. Школьник закрепит пройденные темы и успешно отработает необходимые вычислительные навыки.
Также в пособии приведены правила и алгоритмы, служащие подсказкой при выполнении тренировочных упражнений. К заданиям, которые могут вызвать у школьника затруднения, даны ответы.
Смотреть все
115,50р.
-20% после регистрации
Английский язык. 5-11 кл.: Граматика (2017 г.)
Селиванова М.
82,40р.
-20% после регистрации
Математика. 4 класс ФГОС (2017 г.)
Селиванова М.С.
400,00р.
100 задач по математике: Учимся решать все виды простых и составных задач с краткой записью, объяснениями и ответами. 1-4 классы (2022 г.)
Селиванова М.С.
Магазины
373,50р.
Все правила русского языка в картинках: 16 карточек (2019 г.)
Селиванова М.С.
Магазины
108,30р.
Математика.
1 кл.: Все правила с наглядными примерами, контрольными и трени
(2018 г.)Селиванова М.С.
Магазины
103,00р.
Английский язык. 5-11 кл.: Предложение (2018 г.)
Селиванова М.С.
Магазины
83,50р.
Математика. 1 класс ФГОС (2017 г.)
Селиванова М.С.
Магазины
Математика. 3 класс ФГОС (2017 г.)
Селиванова М.С.
Магазины
82,40р.
Математика. 2 класс (2017 г.)
Селиванова М.С.
Магазины
99,10р.
Отновные тригонометрические функции 10-11 классы (2016 г.)
Селиванова М.С.
Магазины
247,30р.
Английский язык. 2-4 кл.: Правила чтения: Учеб. пособие (2015 г.)
Селиванова М.С.
Магазины
247,30р.
Английский язык. 2-4 кл.: Грамматика: Учеб. пособие (2015 г.)
Селиванова М.
С.
Магазины
700,00р.
Английский язык. 5-11 кл.: Грамматика . Все трудности школьной программы (2014 г.)
Селиванова М.С.
Магазины
115,50р.
Правила поведения в школе (2012 г.)
Селиванова М.С.
Магазины
110,60р.
Персонажи любимых книг: Словарик для младших школьников (2010 г.)
Селиванова М.С.
Магазины
Смотреть все
169,00р.
-20% после регистрации
Математика в начальной школе: Самые сложные темы (2018 г.)
Буряк М.В.
82,40р.
-20% после регистрации
Математика. 4 класс ФГОС (2017 г.)
Селиванова М.С.
83,15р.
-20% после регистрации
Русский язык. 4 класс (2017 г.)
Стронская И.М
82,40р.
-20% после регистрации
Русский язык. 3 класс (2017 г.)
Стронская И.
М
169,00р.
Русский язык в начальной школе: Самые сложные темы (2018 г.)
Буряк М.В.
Магазины
83,50р.
Математика. 1 класс ФГОС (2017 г.)
Селиванова М.С.
Магазины
82,40р.
Математика. 3 класс ФГОС (2017 г.)
Селиванова М.С.
Магазины
82,40р.
Математика. 2 класс (2017 г.)
Селиванова М.
С.
Магазины
82,40р.
Русский язык. 2 класс (2017 г.)
Стронская И.М
Магазины
83,15р.
Русский язык. 1 класс (2017 г.)
Стронская И.М
Магазины
195,20р.
Дружим с русским языком. 1 кл.: Раб. тетрадь (2016 г.)
Михайлова С.Ю.
Магазины
90,00р.
Дружим с русским языком. 1 кл.: Раб. тетрадь (2012 г.
)Михайлова С.Ю.
Магазины
90,00р.
Запоминаем слова с непроверяемыми написаниями 2 кл.: Рабочая тетрадь (2012 г.)
Михайлова С.Ю.
Магазины
90,00р.
Дружим с русским языком. 2 кл.: Раб. тетрадь № 2 (2011 г.)
Михайлова с.Ю.
Магазины
100,00р.
Дружим с русским языком. 4 кл.: Раб. тетрадь № 2 (2009 г.)
Михайлова С.Ю.
Магазины
78,50р.
Дружим с русским языком. 2 кл.: Раб. тетрадь № 2 (2009 г.)
Михайлова С.Ю.
Магазины
92,20р.
Пишем без ошибок. 3 кл.: Рабочая тетрадь (2008 г.)
Крючкова Л.С.
Магазины
65,80р.
Дружим с русским языком. 4 кл.: Раб. тетрадь № 1 (2007 г.)
Михайлова С.Ю.
Магазины
65,80р.
Пишем без ошибок. 4 кл.: Рабочая тетрадь: В 2 ч. Ч.2 (2007 г.)
Крючкова Л.
С.
Магазины
65,80р.
Пишем без ошибок. 4 кл.: Рабочая тетрадь: В 2 ч. Ч.1 (2007 г.)
Крючкова Л.С.
Магазины
Смотреть все
242,50р.
Алгебра. 8 кл.: Дидактические материалы (2020 г.)
Жохов В.И., Макарычев Ю.Н.
Магазины
766,00р.
Репетитор по биологии для старшеклассников и поступающих в вузы (2022 г.)
Шустанова Татьяна Анатольевна
Магазины
203,00р.
Математика. 7-11 классы: Карманный справочник (2022 г.)
Лысенко Ф.Ф.
Магазины
131,00р.
Математика. 3 класс: Комплексный тренажер (2022 г.)
Барковская Н.Ф.
Магазины
172,00р.
-20% после регистрации
Математика. 5 класс: Зачетные работы к учебнику Никольского С.М. ФГОС (к новому ФПУ) (2022 г.)
Ахременкова Вера Игоревна
334,00р.
Биология в инфографике (2022 г.
)Мазур О.Ч.
Магазины
122,00р.
Физика. 7-9 кл.: Справочник ФГОС (2018 г.)
Гормцева О.И.
Магазины
419,00р.
-20% после регистрации
Математическая грамотность. Сборник эталонных заданий: Выпуск 1 Часть 1 (2022 г.)
Ковалева Г.С., Рослова Л.О., Краснянская К.А.
100,00р.
3000 примеров по математике. 1 кл.: Считаем и объясняем. Сложение и вычитание (2021 г.)
Узорова Ольга Васильевна
Магазины
555,00р.
-20% после регистрации
Физика. 10 класс: Базовый уровень. Сборник задач (2022 г.)
Заболотский А.А. Комиссаров В.Ф. Петрова М.
94,50р.
Тренировочные примеры по математике. 3 кл.: Счет в пределах 1000 ФГОС (2021 г.)
Кузнецова Марта Ивановна
Магазины
179,50р.
Тренажер по математике. 2 класс ФГОС (2021 г.)
Яценко. И.Ф.
Магазины
153,00р.
География. 5-6 класс: Проверочные работы (2020 г.
)Бондарева М.В. Шидловский И.М.
Магазины
94,50р.
Тренировочные примеры по математике. 1 кл.: Счет от 6 до 10 (ФГОС) (2021 г.)
Кузнецова Марта Ивановна
Магазины
296,50р.
Геометрия. 7-11 кл.: Алгоритмы решения задач (2020 г.)
Виноградова Т.М.
Магазины
322,00р.
-20% после регистрации
Решение задач по химии. 8-11 классы: Решения, методики, советы (2021 г.)
Хомченко И.
Г.
150,00р.
Математика. 4-й класс (2020 г.)
Сазонова В.А.
Магазины
81,50р.
Запоминаем таблицу умножения (2019 г.)
.
Магазины
118,00р.
Таблица умножения за 3 дня (2021 г.)
Узорова Ольга Васильевна
Магазины
86,00р.
3000 примеров по математике. 1 класс. Супертренинг. Цепочки примеров. Три уровня сложности (2020 г.
)Узорова Ольга Васильевна
Магазины
Выделение «хороших» ошибок в студенческой работе
Оценивая контрольные по алгебре в своем классе, я заметил, что концептуальная ошибка продолжает появляться в работах нескольких учеников. Я вытащила свой телефон и сфотографировала различные решения студентов — некоторые с ошибками, некоторые без. На следующий день в классе я показывал выбранные фотографии в качестве руководства, чтобы начать обсуждение различных решений всем классом. (Имена учеников, чьи работы были выставлены, не были раскрыты классу.)
Вот некоторые ответы восьмиклассников, когда мы рассматривали фотографии:
- «О, я вижу, как они использовали уравнение из таблицы значений для определения уклона».
- «Почему умножили 0,5 на 14? Я поступил иначе».
- «Да, я вижу здесь ошибку. Они предположили, что точка пересечения y равна нулю».
- «Мне нравится, как они показали общую разницу в таблице».
Зачем делиться фотографиями студенческих работ? Все приведенные выше комментарии студентов о образце студенческой работы способствовали усвоению концепции. Я мог бы воссоздать решение каждого учащегося на доске; однако учащимся полезно видеть работы друг друга, а не только учителя.
Катрина Шварц пишет в статье KQED 2014 года «Как взгляд на работу учащихся помогает учителям и детям не сбиться с пути»: «Изучение и критика работы учащихся как регулярная часть взаимодействия в классе может быть эффективным способом как для учителей, так и для учеников задуматься над свою работу, создавая при этом культуру сообщества, ориентированную на процесс обучения». Когда образцы работ нескольких учащихся или групп представлены в запланированной последовательности, весь класс может установить связи между математическими понятиями, которые невозможно установить, видя только свою собственную работу.
Ожидание ошибок и уважение к ним
Обсуждение фотографий студенческих работ дает возможность достичь стандарта Common Core «критика рассуждений других», крайне важно, чтобы окружающая среда поддерживала и поощряла всех учащихся.
Учителя могут способствовать формированию такой культуры, признавая «хорошие ошибки». Узнайте больше о том, как создать класс, благоприятный для ошибок, в статье Меган Ласлоки на сайте Edutopia 2021 года «Класс, благоприятный для ошибок».
Что делать, если учащийся не хочет, чтобы его работа была доступна для всех?
Да, даже если личность учащегося не раскрывается, другой одноклассник может узнать его почерк. Вот почему крайне важно создать классовую культуру коллегиального поощрения и уважения. Я бы никогда не стал показывать вопиющие ошибки, которые могли бы поставить ученика в неловкое положение, если бы его личность была известна. Учитель может предварить образец работы ученика словами: «Это была распространенная ошибка; тем не менее, я выбрал этот образец, потому что они явно начали с правильного подхода. Давайте обсудим, чему мы можем научиться на этом примере».
Пока учащиеся работают в группах за партами, сделайте фотографии, которые положат начало осмысленному обсуждению в классе.
Я спрашиваю студента, не хотят ли они обсудить свою работу с классом. Если они не хотят, я спрашиваю, можно ли другому ученику выйти к доске, чтобы интерпретировать и объяснить процесс и шаги. Когда один учащийся объясняет работу другого учащегося, и объяснитель, и решатель практикуют четкую математическую коммуникацию.
Если учащиеся работают у доски в группах (также называемых вертикальными непостоянными поверхностями или VNPS в книге Питера Лильедала Построение классов мышления по математике ), то каждый может увидеть работу группы, если вы пригласите их или прогуляетесь по галерее. Иногда я считаю, что работа группы достойна внимания в будущем, и я делаю фотографию, чтобы ее могли увидеть другие секции (в противном случае работа на доске будет стерта и больше никогда не будет видна).
В статье «Преподавание математики в средней школе » «Изучение ошибок для изменения мышления учащихся» авторы предлагают отображать ошибки, «достойные» обсуждения. Достойные ошибки могут быть вычислительными, концептуальными или процедурными по своей природе.
Достойная ошибка углубит понимание математической цели урока для всех учащихся, а не только для того, кто сделал ошибку.
Desmos Classroom, бесплатный веб-сайт с графическим онлайн-калькулятором, который также включает в себя цифровые задания, имеет функцию, которая позволяет учителям делать снимки ответов учеников во время занятия. Добавляя эти снимки в альбом, учитель может отображать работы учащихся рядом друг с другом, чтобы вызвать дискуссию о мышлении учащихся. В верхней части экрана презентации есть поле, в котором можно задать классу наводящий вопрос о представленной студенческой работе. (Desmos также имеет опцию «анонимизации», позволяющую отображать имена студентов как имена известных математиков.)
Ниже реальный пример фотографии, которую я использовал на уроке алгебры. (Личность учащегося не сообщалась классу.) Это изображение привело к обсуждению нескольких методов сравнения уравнения и таблицы значений. Многие студенты боролись с этой проблемой при оценке по разным причинам.
Моя цель состояла в том, чтобы поделиться примером того, как интерпретировать таблицу значений как уравнение.
Предоставлено Кристал Фроммерт
Сначала я спросил класс, что они заметили в уравнении, написанном над таблицей. «Как они рассчитали наклон и г -перехват? Какое сообщение можно было бы добавить сюда, чтобы четко передать расчет уклона?» В этот момент учащийся может подойти к доске, чтобы аннотировать таблицу общей разницей или формулой наклона.
Боковая арифметика также может привести к интересному обсуждению вычисления десятичных дробей; однако, поскольку это не было в центре внимания урока, я не пошел по этому пути возможного разговора.
Предоставлено Кристал Фроммерт
Во время занятий по математике внимательно следите за примерами работ учащихся, которые помогут лучше понять урок. Эти изображения могут быть взяты как из формирующих, так и из итоговых оценок, таких как домашнее задание, работа в классе, групповая работа, выходные билеты и / или викторины / тесты.
Чтобы определить, какие фотографии лучше всего подходят для обсуждения всем классом, подумайте, какие ошибки заслуживают обсуждения. Во время этих дискуссий я часто заявляю: «Это моя любимая ошибка!» Затем объясните, как ошибка помогает всем в классе лучше понять концепцию.
5 ошибок, которые я совершил при обучении математике
Вы никогда не увидите, чтобы я притворялся идеальным учителем или вел себя так, будто я все понял. Как правило, любой, кто ссылается на эти утверждения, на самом деле не учит! Вы также не увидите, чтобы я утверждал, что есть только один правильный способ преподавания. Я не могу притворяться, что знаю потребности каждого ученика или каждого класса. Преподавание является очень личным, и мы должны постоянно корректировать наше обучение по мере того, как учащиеся, учебная программа и школьная культура меняются. Однако при обучении математике совершаются некоторые распространенные ошибки. Я делал каждую из этих вещей, поэтому я говорю из личного опыта.
Я также видел негативные последствия этих ошибок, а также огромные изменения в успеваемости учеников, когда я вносил необходимые изменения в свои собственные инструкции.
Неправильный словарный запас или формулировка
Использовать неправильный словарный запас или фразы очень просто, и, хотя это может показаться не таким уж большим делом, эти неправильно используемые термины и фразы могут создать множество неправильных представлений у наших учащихся.
Знак равенства означает «Ответ есть».
Многих учащихся учат рассматривать знак равенства как символ, означающий «Ответ есть» или «та-да». Вместо этого знак равенства в математике означает, что то, что находится справа и слева от символа, имеет одинаковое значение.
Вычесть меньшее число из большего
Многим учащимся говорят, что при вычитании сначала нужно писать большее число. Хотя это правило вычитания может работать для младших классов, это не тот случай, когда учащиеся складывают и вычитают положительные и отрицательные целые числа.
Это правило также может создать проблему, когда учащиеся вычитают многозначные числа. Студенты часто чрезмерно обобщают предыдущие знания и вычитают меньшее число из большего, цифра за цифрой.
Умножение увеличивает число, а деление уменьшает его.
Большую часть времени в начальной школе умножение увеличивает число. Однако если учащиеся умножают не только целые числа, это не всегда верно. Точно так же, как умножение не всегда увеличивает число, то же самое можно сказать и о делении. Деление не всегда уменьшает число. Студенты должны развивать чувство числа, которое выходит за рамки целых чисел.
Всегда делить большее число на меньшее
Студентам часто говорят, что они всегда делят большее число на меньшее. Тем не менее, это не всегда так. Когда эта концепция «прилипает», ее потом очень трудно отменить. Один из способов избежать ошибочного представления о том, что сначала ставится большее число, — вместо этого сосредоточиться на частях проблемы равного распределения.
Когда вы умножаете на 10, прибавляйте ноль к числу
Основная часть математики в третьем и четвертом классах учит учащихся, как умножать числа, кратные десяти. Студентам часто говорят, что при умножении числа на десять нужно просто добавить ноль в конце числа. Однако, опять же, это не всегда так, что приводит к одной из распространенных ошибок при обучении математике. Когда учащиеся умножают десятичные числа на десять и степени десяти, они не добавляют ноль в конце числа. Это правило не только приводит учащихся к неправильным представлениям, но также препятствует более глубокому пониманию нашей десятичной системы счисления. Студенты должны знать, что при умножении на 10 или 100 каждая цифра сдвигается влево в таблице разрядов, потому что они добавляют еще один разряд к числу. Вы можете узнать больше о том, как я учу умножать и делить на десять здесь.
В дроби большее число всегда идет внизу
Много раз учащимся говорят всегда писать большее число внизу дроби.
Это правило не только препятствует подлинному пониманию концепции дробей, но и не является точным правилом. Когда ученики пишут неправильные дроби в четвертом классе, числитель больше знаменателя. Студенты, как правило, манипулируют дробями с помощью механических правил и заучивания, а не пытаются понять понятия и процедуры.
Словарные ресурсы по математике
Чтобы помочь в изучении математической лексики, у меня есть готовые к печати Word Walls в версиях для 3-го и 4-го классов.
Процедурное решение проблем
Когда я впервые начал преподавать, я учил решать проблемы . Я преподавал навык, и студенты позже использовали этот навык для решения задач в конце модуля. Проблема с этим подходом заключается в том, что он часто делает ученика пассивным учеником, зависящим от учителя, дающего пошаговые указания, а не независимым мыслителем, который может разработать подход к решению проблемы. Студенты быстро привыкают к тому, что им говорят, как подходить к проблеме, и вряд ли будут пытаться решить новую проблему без четких инструкций.
Теперь я пытаюсь научить решать проблемы с по . Этот подход заключается в том, что учащиеся учатся через реальные контексты, проблемы, ситуации и модели. Студенты должны придать смысл понятиям, чтобы они могли перейти к абстрактным понятиям.
Конечно, важно научить учащихся стратегиям решения проблем . Это методы подхода к задаче, полностью независимые от конкретной темы или предмета. Мне нравится называть или обозначать стратегии, потому что это дает учащимся простой способ рассказать о своих методах, а мне дать предложения. Подробнее о том, как я обучаю стратегиям решения проблем, можно прочитать здесь. Некоторые стратегии включают в себя:
- Нарисуйте картинку, разыграйте ее, используйте модель.
- Найдите образец.
- Угадай и проверь.
- Составьте таблицу или диаграмму.
- Составьте упорядоченный список.
- Напишите уравнение.
Важно не исключать проблему из решения задач, рассказывая учащимся о стратегии, которую они должны выбрать, и о том, как подойти к решению проблемы.
Вместо этого поделитесь проблемой, которая поддается определенной стратегии, и позвольте учащимся решить проблему любым способом, который им нравится. Во время обмена результатами выделяйте работы студентов, которые эффективно и даже неэффективно решают проблему.
Неэффективное использование манипулятивных средств
Раньше я считал, что любой урок, связанный с манипулятивными средствами, был очень концептуальным и увлекательным уроком. К сожалению, это не всегда так. Так заманчиво показать студентам, как именно использовать манипулятивные средства для конкретной концепции. Когда мы делаем это, учащиеся обычно имитируют указания, и может показаться, что они понимают. Однако учащиеся могут бездумно следовать тому, что видят.
Будучи взрослыми, использующими манипуляции, мы «видим» понятия, которые уже понимаем. У детей, у которых нет такого же понимания, некоторые неправильные представления могут развиться при использовании манипулятивных средств. Мы не можем предполагать, что студенты автоматически сделают правильные выводы, взаимодействуя с тем или иным манипулятором.
Мы должны направлять студентов к развитию понимания, в то же время не говоря точно, как использовать процедуры.
Здесь вы можете прочитать о том, как я использую математические манипуляции.
Подробнее об использовании цифровых манипуляторов можно прочитать здесь.
Несбалансированное обучение
Будучи дочерью учителя и 18 лет занимаясь в классе, я своими глазами видела, как маятник в образовательных тенденциях качается туда-сюда. Если вы какое-то время преподавали, вы тоже знаете, что все возвращается — просто с новым именем или новой упаковкой.
В начале своей преподавательской карьеры я легко поддавался влиянию и хотел прыгать в каждую новую подножку. К счастью, меня поддержали учителя-ветераны, которые сказали мне: «Не выплескивай ребенка вместе с водой».
В хорошем обучении редко используется принцип «все или ничего». Вместо этого мы должны использовать сбалансированный подход. Я видел классы, в которых только включали конструктивистское обучение без обучения практике или навыкам.
Кроме того, есть другие классы, в которых только преподают через процедуры без каких-либо концептуальных инструкций. Конечно, есть много других способов иметь несбалансированное обучение.
Вместо этого мы должны сосредоточиться на разработке концептуальных и понимание процедур, развитие навыков и решение проблем. Сбалансированное обучение может включать прямое обучение, исследовательское обучение, совместные группы, независимое обучение, центры, игры и многое другое. Как только концептуальное понимание установлено, целенаправленная практика помогает учащимся развить вычислительную и процедурную беглость. Эта практика укрепляет связь между навыками, концепциями, стратегиями и мышлением.
Переоценка или выставление оценок
Когда я впервые начал преподавать, я чувствовал необходимость получить множество оценок. Я помню, как сидел на курсе повышения квалификации, когда спикер сказал: «Вы оцениваете то, что важно».
С тех пор я отказался от этого подхода.
Да, я смотрю на работы студентов и даю отзывы, но я не часто записываю формальные оценки. Вместо этого у меня есть множество формирующих заметок и оценок, но я больше не пытаюсь ставить ежедневные оценки.
Мы должны быть осторожны, чтобы наши инструкции не наказывали учащихся за то, что они не сразу усвоили понятие. При введении новой концепции или навыка учащимся нужно время, чтобы побороться, исследовать, получить и обработать нашу обратную связь, и это редко может быть выполнено в одном классе.
Я также стараюсь учиться на ошибках и регулярно давать обратную связь.
Когда учащимся предоставляется обратная связь во время решения проблемы, им предоставляется возможность учиться на своих ошибках, а не повторять их. Я часто ставлю точку на пропущенных задачах и предлагаю ученикам найти и исправить свою ошибку. Это заставляет студентов вернуться и посмотреть на свою работу, оценить ее и исправить. Это гораздо более ценно, чем то, что я просто отмечаю это неправильно и возвращаю бумагу студенту.