Презентация к уроку математики «Двузначные числа. Работа над ошибками», 2 класс
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовала
#2 класс #Математика #Учебно-методические материалы #Презентация #Учитель начальных классов #Школьное образование
Урок математики во 2 классе
25 68 51 13 45
Тема урока: Работа над ошибками по теме: «Двузначные числа»
Цель:
Проанализировать типичные ошибки по теме:
«Двузначные числа».
Назови числа, найди ловушку : 3 дес. 7 ед. 9 дес. 2 ед. 4 дес. 4 ед. 8 ед. 1 дес. 5 дес. 0 ед.
Назови числа, найди ловушку: 3 дес. 7 ед. 9 дес. 2 ед. 4 дес. 4 ед. 8 ед. 1 дес. 5 дес. 0 ед.
Придумайте сами своё такое же задание:
Найдите значение выражений 7 + 10 60 – 50 30 + 6 60 + 40 12 + 5 17 – 5 60 + 7 80 – 30
Придумайте сами свои похожие примеры:
Постройте квадрат со стороной 2 см.
Задачи
Назови части задачи
Составь краткую запись к задаче, реши её. В парке гуляло 20 девочек, а мальчиков на 3 больше. Сколько гуляло мальчиков?
Составь краткую запись к задаче, реши её. В парке гуляло 20 девочек, а мальчиков на 3 больше. Сколько гуляло мальчиков?
Проверь: девочек – 20 мальчиков — ?, на 3 > 20 + 3 = 23 (м.) Ответ: 23 мальчика.
Составь краткую запись,
реши задачу.
В магазине было 60 арбузов, продали 40. Сколько арбузов осталось?
Составь краткую запись, реши задачу. В магазине было 60 арбузов, продали 40. Сколько арбузов осталось?
Было – 60 арбузов Продали – 40 арбузов Осталось -? 60 – 40 = 20 Ответ: 20 арбузов.
Составь круговую схему, реши задачу. У тётушки 80 гусей, 30 из них белые, остальные серые. Сколько серых гусей у тётушки?
80 г. — 30 г. ? 80 – 30 = 50 (г.) Ответ: 50 гусей
Мудрый гном — Памятка «Работа над ошибками»
1. Большая буква в начале предложения.
Выпиши предложение правильно. Подчеркни заглавную букву.
Делай так:
Выпал пушистый снег.
2. Знаки препинания в конце предложения.
Выпиши предложение правильно. Подчеркни знак.
Делай так:
Ты любишь отгадывать загадки?
3.
Непроверяемая безударная гласная в корне (словарные слова).
Запиши слово правильно три раза. Запомни, как оно пишется. Обозначь ударение, подчеркни безударную гласную. Запиши два однокоренных слова.
Делай так:
Ягода, ягода, ягода, ягодка, ягодный.
4. Большая буква в именах собственных.
Выпиши слово правильно. Подчеркни заглавную букву. Запиши ещё два слова на эту орфограмму.
Делай так:
Илья, Максим, Пётр.
ЗАПОМНИ!
Имена, отчества и фамилии людей, названия рек, озёр, морей, городов, деревень, клички животных пишутся с большой буквы.
5. Гласные после шипящих.
Выпиши слово правильно. Подчеркни сочетание ЖИ, ШИ, ЧА, ЩА, ЧУ, ЩУ. Придумай и запиши ещё два слова на эту орфограмму.
Делай так:
Малыши, карандаши, шина.
11. Перенос слова.
Раздели слово на слоги для переноса.
Делай так:
Оси-на, ма-ши-на.
12. Ударение.
Выпиши слова. Поставь в них правильно знак ударения.
Делай так:
Алфавит, азбука, портфель.
13. Разделительный твёрдый знак (ъ).
Выпиши слово правильно. Запиши ещё два слова с этой орфограммой. Выдели приставку. Подчеркни гласную.
Делай так:
Съезд, объяснение, объём.
ЗАПОМНИ! Разделительный твёрдый знак (ъ) пишется только после приставок, которые оканчиваются на согласную, перед гласными буквами е, ё, ю, я.
14. Правописание предлога со словом (орфограмма – пробел).
Из предложения, в котором допущена ошибка, выпиши слово вместе с предлогом. Докажи, что предлог со словом пишется отдельно. Обозначь орфограмму — пробел.
Делай так:
К_берегу, к (какому?) берегу, к (крутому) берегу.
ЗАПОМНИ! Предлог — это отдельное слово. Не смешивай приставку с предлогом. У глаголов нет предлогов.
Например: Лодка отплыла от_берега.
15. Правописание приставки со словом.
Выпиши слово. Выдели приставку. Образуй от этого слова однокорен-ные слова с разными приставками.
Делай так:
Заехал, уехал, переехал.
6. Сочетание ЧК, ЧН, НЩ, ЩН.
Выпиши слово правильно. Подчеркни сочетание. Запиши ещё два слова на эту орфограмму.
Делай так:
Дочка, речка, внучка.
ЗАПОМНИ! При переносе одну букву нельзя оставлять на строке и нельзя переносить на новую строку.
7. Мягкий знак (ь), обозначающий мягкость согласных.
Выпиши слово правильно. Подчеркни мягкий знак (ь) и соглас¬ную перед ним. Запиши ещё два слова на эту орфограмму.
Делай так:
Ель, тень, пень.
Коньки, мальчик, пальто.
8. Разделительный мягкий знак (ь).
Выпиши слово правильно, запиши ещё два слова на эту орфограм¬му. Подчеркни разделительный мягкий знак (ь) и гласную букву.
Делай так:
Вьюга, листья, соловьи.
ЗАПОМНИ! Разделительный мягкий знак (ь) пишется после согласных и перед гласными буквами е, ё, ю, я, и.
9. Пропуск, замена, перестановка букв.
Выпиши слово правильно. Подчеркни в нём пропущенную или за-менённую букву. Запиши это слово ещё два раза.
Делай так:
Звонок, звонок, звонок.
10. Слог.
Раздели слово на слоги. Обозначь гласные.
Делай так:
У-чи-тель — 3 слога.
ЗАПОМНИ! Сколько в слове гласных, столько и слогов.
ЗАПОМНИ! Приставка — это часть слова. Она пишется слитно со словом.
16. Проверяемая безударная гласная в корне (а, о, е, и, я).
Выпиши слово. Поставь ударение. Выдели корень. В корне подчеркни безударную гласную. Подбери проверочное слово и запиши рядом.
Делай так:
Волна — волны.
17. Двойные согласные в слове.
Выпиши слово правильно. Раздели слово для переноса. Запиши два однокоренных слова. Подчеркни двойную согласную.
Делай так:
Группа, груп-па, групповой, подгруппа.
18. Парные звонкие и глухие согласные.
Запиши слово правильно. Подчеркни согласную. Подбери проверочное слово и запиши рядом.
Делай так:
Мороз-морозы.
Ягодка-ягода.
ЗАПОМНИ! Согласные на конце и в середине слов пишутся так же, как и перед гласными.
19. Состав слова.
Выпиши слово. Разбери его по составу. Запиши два однокоренных слова.
Делай так:
Поездка, ездить, съездил.
20. Гласные и согласные в приставках.
Выпиши слово правильно. Выдели в нём приставку. Запиши ещё два слова с этой же приставкой. Подчеркни букву, в которой была допущена ошибка.
Делай так:
Полетели, побежали, потянули.
21. Непроизносимые согласные в корне слова.
Выпиши слово правильно. Проверь непроизносимую согласную. Подбери к нему несколько однокоренных слов. Выдели корень. Обозначь орфограмму.
Делай так:
Звёздный — звезда, звёздочка.
Мягкий знак (ь) после шипящих в именах существительных.
Выпиши слово правильно. Определи род. Обозначь орфограмму. Запиши ещё два слова на эту орфограмму.
Делай так:
ж.р. ж.р. ж.р
Ночь, дочь, печь.
ЗАПОМНИ! В именах существительных женского рода в конце слова после шипящих Ж, Ч, Ш, Щ пишется Ь, в именах существительных мужского рода Ь не пишется.
Разбор предложения по членам.
Выпиши предложение. Подчеркни главные члены. Выпиши словосочетания с вопросами.
Делай так:
Утренняя роса покрывала траву.
роса (какая?) утренняя
покрывала (что?) траву
ЗАПОМНИ! Слова в предложении связаны парами по смыслу. Связь слов устанавливается при помощи вопросов от слова к слову.
Звукобуквенный разбор.
Выполни правильно, без ошибок.
Топ-5 распространенных математических ошибок
Перейти к содержимому
Поиск:
Главная » Топ-5 распространенных математических ошибок
Класс
(И как помочь ученикам избежать их)
Все делают ошибки. Это неизбежно. И это, безусловно, верно в отношении математики. Настоящее обучение происходит, когда учителя могут показать ученикам, где они допустили ошибку и как избежать ее в будущем.
Но как бывший учитель математики я также знаю, что также важно создать среду, в которой учащиеся чувствуют себя комфортно, допуская ошибки, и могут обсудить с учителем и другими учениками, где они могли ошибиться.
Публично указывать на ошибки учащегося или выглядеть разочарованным или расстроенным его работой никогда не бывает полезным.
Мы никогда не хотим слышать, как студенты говорят
- «Я просто не могу этого сделать и никогда не смогу».
- «Я ненавижу математику».
- «Если я делаю ошибки, значит, я тупой».
ESGI и ThinkFives опросили сотни учителей, и вот пять самых распространенных ошибок, совершаемых учащимися начальной школы.
Порядок действийПорядок действий сложно понять даже взрослому. Сколько мы видим задач викторин в социальных сетях, в которых людей спрашивают, могут ли они решить простое короткое уравнение (или, может быть, это только я, потому что чем больше я отвечаю на эти вопросы, тем больше их показывает мне Facebook).
Обычно возникают две проблемы с порядком работы.
- Часто учащиеся могут ошибаться в уравнении, потому что путают один математический символ или оператор с другим.
Некоторые символы могут быть похожи друг на друга для начинающих пользователей. Учащийся может спутать символ вычитания с символом деления, то же самое касается сложения и умножения. Учащийся может сказать, что 2 X 4 = 6, потому что он неправильно истолковал «X» как «+». Важно, чтобы учителя просмотрели символы и убедились, что это не концептуальная математическая проблема, а просто неправильное использование символа. - Наиболее распространенная проблема с порядком операций — простое запоминание того, что они из себя представляют. Многие учителя используют песни или стишки, чтобы ученики понимали порядок (PEMDAS). Другой пример — использовать аббревиатуру «Пожалуйста, извините, моя дорогая тетя Салли».
Некоторые символы могут быть похожи друг на друга для начинающих пользователей. Учащийся может спутать символ вычитания с символом деления, то же самое касается сложения и умножения. Учащийся может сказать, что 2 X 4 = 6, потому что он неправильно истолковал «X» как «+». Важно, чтобы учителя просмотрели символы и убедились, что это не концептуальная математическая проблема, а просто неправильное использование символа.- Круглые скобки всегда стоят на первом месте («Пожалуйста»).
- Далее всегда Экспонентов (« Извините»).
- Далее следует умножение , и мы идем слева направо («Мой»).
- Отдел следует и снова слева направо («Дорогой»).
- И, наконец, это Сложение и Вычитание («Тетя Салли»).
Многим учащимся сложно понять дроби. Дети могут воспринимать дробь не как одну величину, а как пару целых чисел. Они могут сравнивать целые числа, что приводит к полному непониманию.
Почему 1/4 + 1/4 = ½?
Первые ошибки могут начаться с непонимания того, что обозначают числитель и знаменатель. Некоторым учителям это помогает наглядно познакомить учащихся с этим понятием. Презентация дробей в увлекательной форме с помощью общих для них предметов, таких как кусочки пиццы, — отличный способ начать.
Что бы вы предпочли: 1 из 6 ломтиков пиццы или 2 ломтика? Если бы я взял оба, у меня было бы 3 из 6 ломтиков (или, если вы похожи на меня, я бы взял 6/6 ломтиков).
Другие учителя используют стену фракций, чтобы показать размеры фракций. Они могут объяснить, что число внизу означает, на сколько частей было разделено целое, а число вверху означает, сколько из этих частей выбрано.
Академия Хана или другие сайты содержат много отличных видео и идей для обучения дробям.
Не проверять свою работуОдним из самых полезных навыков, который учителя могут закрепить, является важность проверки вашей работы. Он не только показывает возможный просчет, но и помогает учащимся избежать ошибок по невнимательности.
Важной частью проверки вашей работы является попытка найти ответ другим способом, если это возможно. Например, добавление трех чисел подряд может быть перепроверено путем добавления их в обратном порядке. Или, если числа умножаются, учащийся может проверить свою работу, используя свой ответ и используя деление, чтобы получить число в вопросе.
Есть также несколько других советов, которые помогут учащимся избежать ошибок по невнимательности.
Помедленнее
Это кажется очевидным, но студенты часто спешат закончить, чтобы перейти к чему-то другому. Поощряйте детей не торопиться и обращать внимание на то, что они делают.
Обведите важную информацию
Будь то рабочий лист или текстовые задачи, обведение важной информации поможет учащимся понять, что делать. Обводя что-то в направлениях, вы поможете им правильно следовать им. И это особенно верно, когда вы вводите текстовые задачи.
Использовать бумагу
Решение задач на бумаге или с использованием миллиметровой бумаги особенно полезно. Простые вопросы можно составить в уме, но решение их на бумаге может привести к вычислительной ошибке.
ПерегруппировкаПерегруппировка — это когда учащиеся объединяются в группы по десять человек при выполнении таких операций, как сложение или вычитание. Обычно это происходит, когда ответ больше 10 или нам нужно вычесть из столбца десятков.
Пример: 15 + 17. Сложение 5 + 7 дает 12, что составляет один десяток и две единицы. Перегруппировка переносит десятку в столбец десятков и оставляет две единицы. Ответ: 32.
Вот несколько советов по обучению перегруппировке.
Шаг 1 :
Для этого можно использовать манипулятор. Предложите учащимся подсчитать единицы и обменять их на десятки. Или, при вычитании, попросите их обменять десять слитков на десять единиц. Это поможет им увидеть и испытать перегруппировку.
Шаг 2 :
Наглядные материалы также помогают вашим учащимся понять, что такое перегруппировка, и помогают детям избежать помощи манипуляторов. Использование рабочего листа или онлайн-визуала, чтобы они могли начать видеть расчеты, особенно полезно для визуалов.
Шаг 3:
После того, как дети сложат и вычтут, используя манипуляции и наглядные пособия, вы можете научить их традиционным шагам выполнения этих операций, используя только карандаш и бумагу. К этому моменту учащиеся усвоят процесс перегруппировки в математике.
Сложение и вычитание целых чисел Возможно, это самая распространенная ошибка в этом списке, но, вероятно, именно поэтому она занимает первое место.
Применение математических функций к более чем 2 числам может вызвать сложности у некоторых учащихся и вызвать разочарование. Когда учащиеся складывают такие числа, как 13, 26 и 7, некоторые из них могут неправильно поставить 7 в разряде десятков, что приведет к неправильному ответу.
Существует множество отличных ресурсов и видео для обучения сложению. Вот по предложенному способу:
- Познакомить с понятием, используя счетные манипуляции.
- Переход к визуальным эффектам.
- Использовать числовую строку.
- Покажите, как учащиеся считают.
- Помогите ученикам найти десятку.
Это также помогает общаться со студентами по номерам. Это отличный способ сломать эту стратегию. Сначала смоделируйте его, а затем попросите учащихся таким же образом рассказать о своем подходе к вопросу.
Какие математические ошибки чаще всего допускают ваши ученики?
Источники
https://www.mindstretcher.com/blog-post/5-common-mistakes-cost-child-many-marks-maths/
https://happynumbers.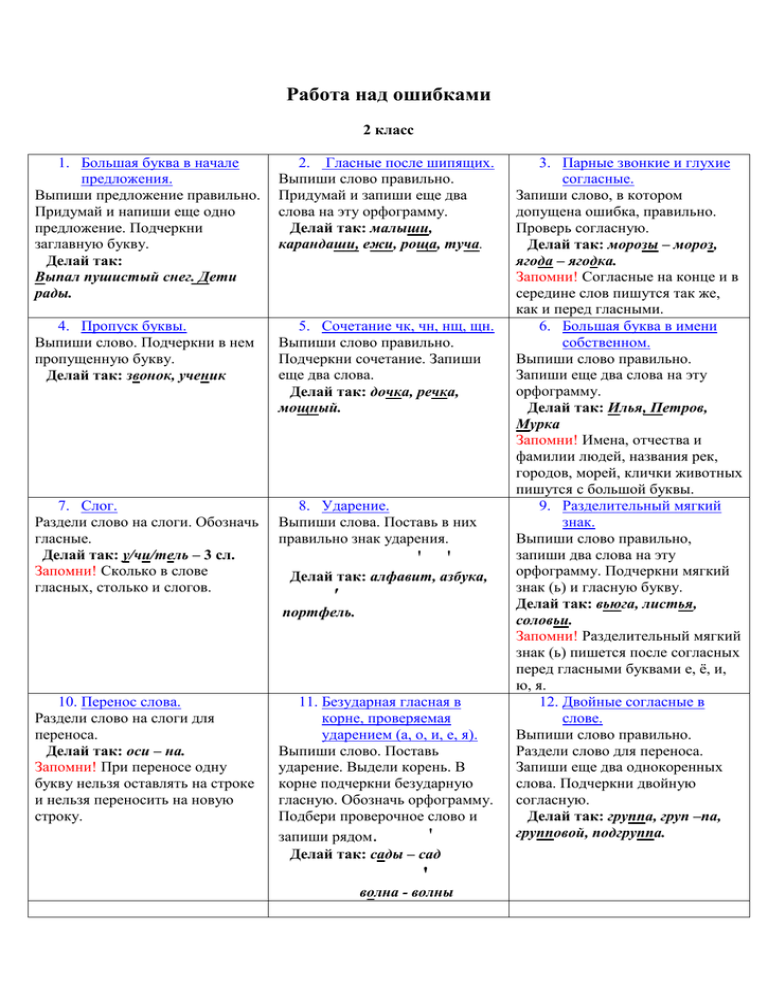
com/blog/what-is -regrouping-in-math/
How to Teach Addition | 7 Simple Steps
Нравится:
Нравится Загрузка…
студенты учитель учитель ресурсы
4 причины, по которым ошибки в математике — это хорошо
Ошибки доказывают, что вы стараетесь! Когда вы преподаете в своем классе, вы можете задаться вопросом… действительно ли ошибки — это хорошо? Разве учащиеся тоже не должны отвечать правильно? Сегодня мы поговорим о том, почему ошибки на уроках математики — это хорошо! Давайте начнем.
Что такое ошибки в математике?
Ошибки в математике могут быть возможностью учиться, развивать любознательность и критическое мышление, а также создавать самозащиту.
Причина № 1. Ошибки в математике — это хорошо:
Ошибки в математике — это возможность для учащихся учиться. На самом деле учащиеся больше всего узнают математику, когда они «делают» математику, а не из ответов. Подумайте на мгновение о прошлой ночи, когда вы пришли к решению проблемы и узнали из этого решения.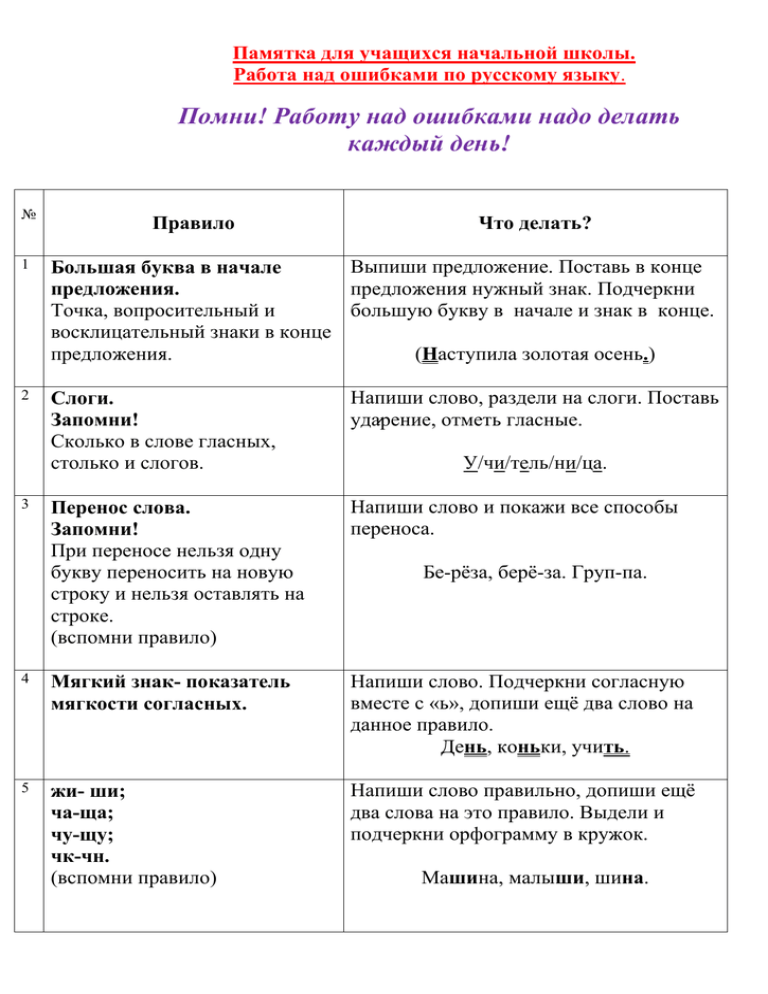
Вы, вероятно, узнали больше из процесса, который вы предприняли, чтобы найти это решение.
Например, если цепь на велосипеде вашего ребенка отвалится, как только вы снова его наденете, вы почувствуете облегчение и радость от того, что поняли это, но на самом деле вы ничему не научились, когда она снова была надета. Вместо этого вы многое узнали (спасибо YouTube) о том, как надевать его обратно и как работают велосипедные цепи. Таким образом, в следующий раз, когда он упадет, вы будете знать, как надеть его обратно. В процессе происходит обучение. То же самое и с математикой!
Когда учащиеся занимаются математикой, они переходят от ошибки к ошибке, по ходу дела обретая смысл. Это то, что мы должны отмечать на уроках математики — процесс, потому что процесс выполнения математических действий — это обучение!
Причина №2 Ошибки в математике — это хорошо:
Ошибки в математике — это возможность развить любопытство и любопытство. Я знаю, вы можете закатить глаза, думая об этом… Верно, Мона, но как насчет моей учебной программы и стандартов, которые я должен преподавать? Я понимаю, и это тоже важно.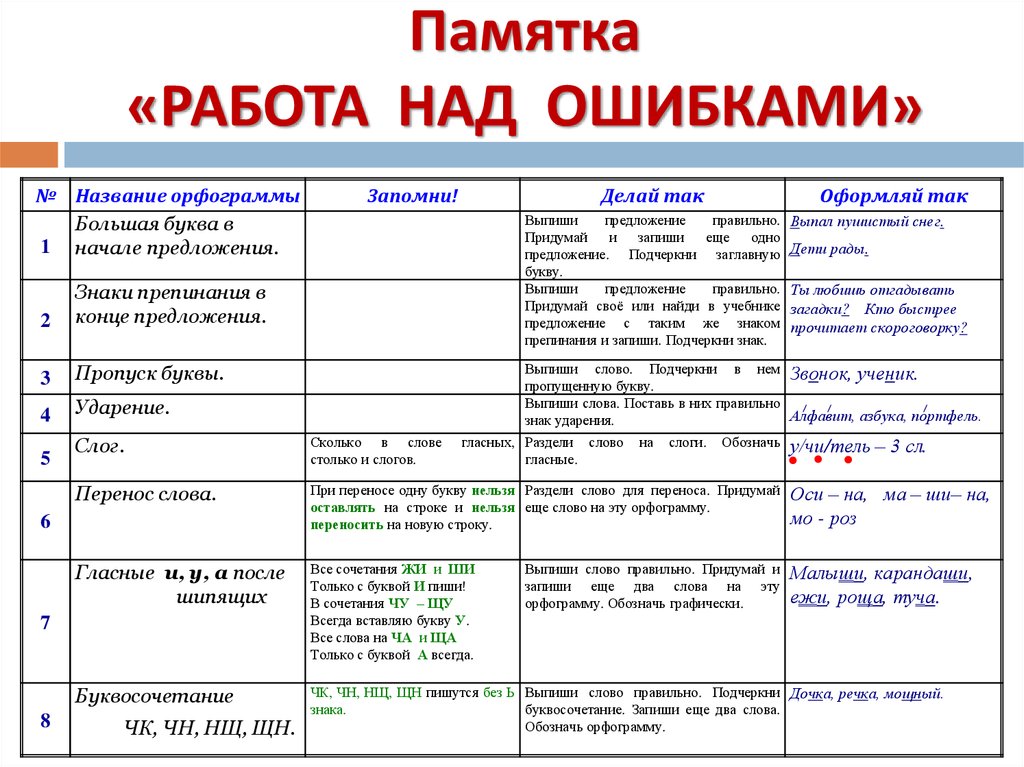
Тем не менее, мы должны научить студентов быть любопытными и интересоваться математикой. Математика — это не только ответы на вопросы, но и их развитие.
Возьмем этот пример, ученики работают над заданием о площади сада (общий вопрос, верно, учителя 3-го класса?). Они вычисляют площадь грядок, но не получают правильного ответа, потому что продолжают пытаться вычислить, сколько земли потребуется для заполнения грядки, поскольку грядки приподняты. Они подталкивают себя к развитию понимания объема, но полностью упускают из виду область. Мы знаем, что когда учащиеся узнают что-то в контексте, они с большей вероятностью запомнят и поймут более глубоко. Несмотря на то, что они не выяснили площадь грядки, ученики подталкивают себя, проявляют любопытство и развивают новое понимание.
Причина №3
Ошибки в математике позволяют учащимся критически относиться к своей работе и работе других. Нет ничего лучше, чем когда ученики сами находят свои ошибки. Мне нравится создавать нормы в нашем математическом классе, где ученики должны проверять работу друг друга и говорить, когда они не согласны или не понимают.
Это часто приводит к тому, что учащиеся указывают, где их сверстники ошиблись в решении. Тогда вместе, как группа, мы сможем обнаружить ошибку и исправить ее!
Причина №4
Ошибки поощряют самозащиту. Вместо того, чтобы учащиеся сидели на своих местах и ждали, пока их спасет учитель, потому что у учителя есть правильные ответы, учащиеся могут решить проблему и защитить себя, когда им нужно повысить уровень своей поддержки. Вот что я имею в виду. Создайте культуру, в которой борьба и неправильные ответы не являются стоп-сигналом. Вместо этого они являются точкой паузы, когда учащиеся возвращаются к проблеме и пересматривают свой путь решения. Ошибки могут быть моментом, когда учащиеся делают паузу, чтобы подумать о других стратегиях, которые они могли бы применить, или рассмотреть проблему с другой точки зрения. Обучая студентов тому, что они могут помочь себе сами, они приобретают навыки, необходимые в жизни для решения проблем с помощью ошибок и трудностей. Затем, когда они исчерпали все свои стратегии, они могут обратиться за помощью с конкретным вопросом или областью путаницы.
Что дальше?
Попробуйте в своем классе. Создайте сообщество в классе со структурами, которые позволят учащимся быть в безопасности от ошибок. Разработайте нормы, позволяющие учащимся использовать ошибки для развития своих математических навыков. Затем вернитесь и дайте нам знать в комментариях, что работает, а что еще остается вопросом!
Взгляните на эту статью от NCTM
Присоединяйтесь к группе учителей математики на Facebook, объединяющей учителей математики со 2-го по 6-й класс!
Участвовать в больших математических дискуссиях об ошибках — отличный способ сделать ошибки важными в математике! Прочтите этот пост в блоге с 5 советами по проведению математических дискуссий, ориентированных на учащихся.
Готовы сделать свой класс сосредоточенным на учениках?
Получите эту бесплатную электронную книгу, которая проведет вас через 5 шагов к созданию класса, в котором мышление ваших учеников находится в центре вашего математического класса.