Математика. 2 класс, Селиванова М.С. . Работа над ошибками , Литера , 9785407008187 2017г. 82,40р.
Селиванова М.С.
Серия: Работа над ошибками
Осталось всего 4 шт.
82,40р.
-20% после регистрации
В наличии в 3 магазинах
Ангарск, ПродаЛитЪ Ангарск Центр
Иркутск, ПродаЛитЪ ТЦ Версаль
Улан-Удэ, ПродаЛитЪ EuroZone
Цена в магазине может отличаться
от цены, указанной на сайте.
Поделиться ссылкой в:
Издательство:Литера
ISBN:978-5-407-00818-7
Штрих-код:9785407008187
Страниц:16
Тип обложки:Мягкая
Год:2017
НДС:10%
Код:907336
Описание
Данное учебное пособие может быть использовано как рабочая тетрадь для занятий с вашим ребёнком дома. В нём представлен основной программный материал по математике 2-го класса.
Школьник закрепит пройденные темы и успешно отработает необходимые вычислительные навыки.Также в пособии приведены правила и алгоритмы, служащие подсказкой при выполнении тренировочных упражнений. К заданиям, которые могут вызвать у школьника затруднения, даны ответы.
Смотреть все
400,00р.-20% после регистрации
100 задач по математике: Учимся решать все виды простых и составных задач с краткой записью, объяснениями и ответами. 1-4 классы (2022 г.)
Селиванова М.С.
373,50р.-20% после регистрации
Все правила русского языка в картинках: 16 карточек (2019 г.)
Селиванова М.С.
108,30р.-20% после регистрации
Математика.
1 кл.: Все правила с наглядными примерами, контрольными и трени
(2018 г.)Селиванова М.С.
83,50р.-20% после регистрации
Математика. 1 класс ФГОС (2017 г.)
Селиванова М.С.
82,40р.-20% после регистрации
Математика. 3 класс ФГОС (2017 г.)
Селиванова М.С.
82,40р.-20% после регистрации
Математика. 2 класс (2017 г.)
-20% после регистрации
Математика.
4 класс ФГОС
(2017 г.)Селиванова М.С.
99,10р.-20% после регистрации
Отновные тригонометрические функции 10-11 классы (2016 г.)
Селиванова М.С.
115,50р.-20% после регистрации
Правила поведения в школе (2012 г.)
Селиванова М.С.
110,60р.-20% после регистрации
Персонажи любимых книг: Словарик для младших школьников (2010 г.)
Селиванова М.С.
103,00р.
Английский язык. 5-11 кл.
: Предложение
(2018 г.)Селиванова М.С.
Магазины
115,50р.
Английский язык. 5-11 кл.: Граматика (2017 г.)
Селиванова М.С.
Магазины
247,30р.
Английский язык. 2-4 кл.: Правила чтения: Учеб. пособие (2015 г.)
Селиванова М.С.
Магазины
247,30р.
Английский язык. 2-4 кл.: Грамматика: Учеб. пособие (2015 г.)
Селиванова М.С.
Магазины
700,00р.
Английский язык. 5-11 кл.: Грамматика . Все трудности школьной программы (2014 г.)
Селиванова М.С.
Магазины
Смотреть все
169,00р.-20% после регистрации
Русский язык в начальной школе: Самые сложные темы (2018 г.)
Буряк М.В.
169,00р.-20% после регистрации
Математика в начальной школе: Самые сложные темы (2018 г.)
Буряк М.В.
83,50р.-20% после регистрации
Математика. 1 класс ФГОС (2017 г.
)Селиванова М.С.
82,40р.-20% после регистрации
Математика. 3 класс ФГОС (2017 г.)
Селиванова М.С.
82,40р.-20% после регистрации
Математика. 2 класс (2017 г.)
Селиванова М.С.
82,40р.-20% после регистрации
Математика. 4 класс ФГОС (2017 г.)
Селиванова М.С.
83,15р.-20% после регистрации
Русский язык. 4 класс (2017 г.)
Стронская И.
М
-20% после регистрации
Русский язык. 3 класс (2017 г.)
Стронская И.М
82,40р.-20% после регистрации
Русский язык. 2 класс (2017 г.)
Стронская И.М
83,15р.-20% после регистрации
Русский язык. 1 класс (2017 г.)
Стронская И.М
49,50р.-20% после регистрации
Запоминаем слова с непроверяемым написанием 4 кл.: Рабочая тетрадь (2007 г.)
Михайлова С.Ю.
72,50р.
-20% после регистрации
Запоминаем слова с непроверяемыми написаниями 3 кл.: Раб. тетрадь (2006 г.)
Михайлова С.Ю.
195,20р.
Дружим с русским языком. 1 кл.: Раб. тетрадь (2016 г.)
Михайлова С.Ю.
Магазины
90,00р.
Дружим с русским языком. 1 кл.: Раб. тетрадь (2012 г.)
Михайлова С.Ю.
Магазины
90,00р.
Запоминаем слова с непроверяемыми написаниями 2 кл.: Рабочая тетрадь (2012 г.)
Михайлова С.
Магазины
90,00р.
Дружим с русским языком. 2 кл.: Раб. тетрадь № 2 (2011 г.)
Михайлова с.Ю.
Магазины
100,00р.
Дружим с русским языком. 4 кл.: Раб. тетрадь № 2 (2009 г.)
Михайлова С.Ю.
Магазины
78,50р.
Дружим с русским языком. 2 кл.: Раб. тетрадь № 2 (2009 г.)
Михайлова С.Ю.
Магазины
Пишем без ошибок.
3 кл.: Рабочая тетрадь
(2008 г.)Крючкова Л.С.
Магазины
65,80р.
Дружим с русским языком. 4 кл.: Раб. тетрадь № 1 (2007 г.)
Михайлова С.Ю.
Магазины
65,80р.
Пишем без ошибок. 4 кл.: Рабочая тетрадь: В 2 ч. Ч.2 (2007 г.)
Крючкова Л.С.
Магазины
65,80р.
Пишем без ошибок. 4 кл.: Рабочая тетрадь: В 2 ч. Ч.1 (2007 г.)
Крючкова Л.С.
Магазины
56,68р.
Запоминаем слова с непроверяемыми написаниями 2 кл.: Рабочая тетрадь (2006 г.)
Михайлова С.Ю.
Магазины
Смотреть все
242,50р.-20% после регистрации
Алгебра. 8 кл.: Дидактические материалы (2020 г.)
Жохов В.И., Макарычев Ю.Н.
766,00р.-20% после регистрации
Репетитор по биологии для старшеклассников и поступающих в вузы (2022 г.)
Шустанова Татьяна Анатольевна
203,00р.-20% после регистрации
Математика. 7-11 классы: Карманный справочник (2022 г.
)Лысенко Ф.Ф.
131,00р.-20% после регистрации
Математика. 3 класс: Комплексный тренажер (2022 г.)
Барковская Наталья Францевна
172,00р.-20% после регистрации
Математика. 5 класс: Зачетные работы к учебнику Никольского С.М. ФГОС (к новому ФПУ) (2022 г.)
Ахременкова Вера Игоревна
334,00р.-20% после регистрации
Биология в инфографике (2022 г.)
Мазур О.Ч.
122,00р.-20% после регистрации
Физика. 7-9 кл.
: Справочник ФГОС
(2018 г.)Гормцева О.И.
419,00р.-20% после регистрации
Математическая грамотность. Сборник эталонных заданий: Выпуск 1 Часть 1 (2022 г.)
Ковалева Г.С., Рослова Л.О., Краснянская К.А.
100,00р.-20% после регистрации
3000 примеров по математике. 1 кл.: Считаем и объясняем. Сложение и вычитание (2021 г.)
Узорова Ольга Васильевна
555,00р.-20% после регистрации
Физика. 10 класс: Базовый уровень. Сборник задач (2022 г.)
Заболотский А.А. Комиссаров В.
Ф. Петрова М.А.
-20% после регистрации
Тренировочные примеры по математике. 3 кл.: Счет в пределах 1000 ФГОС (2021 г.)
Кузнецова Марта Ивановна
179,50р.-20% после регистрации
Тренажер по математике. 2 класс ФГОС (2021 г.)
Яценко. И.Ф.
153,00р.-20% после регистрации
География. 5-6 класс: Проверочные работы (2020 г.)
Бондарева М.В. Шидловский И.М.
94,50р.-20% после регистрации
Тренировочные примеры по математике. 1 кл.: Счет от 6 до 10 (ФГОС) (2021 г.
)Кузнецова Марта Ивановна
216,00р.-20% после регистрации
Математика. 1-4 классы (2023 г.)
Узорова Ольга Васильевна, Нефедова Елена Алексеевна
296,50р.-20% после регистрации
Геометрия. 7-11 кл.: Алгоритмы решения задач (2020 г.)
Виноградова Т.М.
322,00р.-20% после регистрации
Решение задач по химии. 8-11 классы: Решения, методики, советы (2021 г.)
Хомченко И.Г.
150,00р.-20% после регистрации
Математика.
4-й класс
(2020 г.)Сазонова В.А.
81,50р.-20% после регистрации
Запоминаем таблицу умножения (2019 г.)
.
118,00р.-20% после регистрации
Таблица умножения за 3 дня (2021 г.)
Узорова Ольга Васильевна, Нефедова Елена Алексеевна
Математика.Работа над ошибками:3 класс (Ирина Винокурова)
Купить офлайн
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Как проверить ответ? Где прячутся ошибки? Как научиться находить и исправлять свои ошибки? Ответы на эти вопросы вы найдете здесь.
Пособие содержит разные способы решения, типы ошибок, рекомендации, алгоритмы действий по обнаружению ошибок, эффективные приемы самопроверки. Пособие предназначено для самостоятельного использования учениками. Его полезно держать под рукой во время выполнения проверочных и самостоятельных работ. Родителям, учителям, репетиторам помогает запустить и организовать осознанный процесс самопроверки по математике.
.
Описание
Характеристики
Как проверить ответ? Где прячутся ошибки? Как научиться находить и исправлять свои ошибки? Ответы на эти вопросы вы найдете здесь. Пособие содержит разные способы решения, типы ошибок, рекомендации, алгоритмы действий по обнаружению ошибок, эффективные приемы самопроверки. Пособие предназначено для самостоятельного использования учениками. Его полезно держать под рукой во время выполнения проверочных и самостоятельных работ. Родителям, учителям, репетиторам помогает запустить и организовать осознанный процесс самопроверки по математике.
.
Феникс
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили3
Дождитесь, пока отзыв опубликуют.Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Книга «Математика.Работа над ошибками:3 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Ирина Винокурова «Математика.Работа над ошибками:3 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Большинство неправильно понятых математических стандартов во 2-м классе
Когда меня попросили расширить серию статей о наиболее неправильно понятых стандартах до классов K, 1 и 2, я ухватилась за эту возможность. У меня дома четверо сыновей, которые часто говорят, что я никогда не упускаю возможности поговорить о математике и преподавании! Я также заядлый читатель и пользователь предыдущих постов этой серии для 3-8 классов, поэтому я был рад внести свой вклад в это!
В своей роли тренера по математике и путешествуя по стране, работая с преподавателями по единообразному обучению математике, я заметил некоторые общие моменты в обучении в классе K-2, возникающие из-за непонимания математических стандартов.
Преподавание математики в начальных классах совсем не начальное! Это сложная работа, требующая обучения и пристального внимания к обучению, особенно когда учителя углубляются в развитие у учащихся концептуального понимания фундаментальной математики в младших классах. Я надеюсь, что этот пост поможет вам задуматься и научиться поддерживать своих юных математиков!
Стандартный | Общая смещенная инструкция |
| 2.OA.A.1 Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, отнимания, сложения, разъединения и сравнения с неизвестными во всех положения, например, с помощью рисунков и уравнений с символом неизвестного для представления проблемы. | Инструкция направлена на определение ключевых слов для решения проблемы. Инструкция акцентирует внимание на методах получения ответов, а не на математическом мышлении и осмыслении. Преподаватель не рассматривает все 15 типов задач на сложение и вычитание или игнорирует типы задач, которые учащиеся должны освоить к концу второго класса. Мы хотим, чтобы студенты:
*Обычные ситуации сложения и вычитания можно найти здесь . |
| 2.OA.C.4 Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых. | Обучение выходит за рамки стандартов уровня класса и вводит умножение до 3 рд сорт. |
2.NBT.A.4 Сравните два трехзначных числа на основе значений цифр сотен, десятков и единиц, используя символы >, = и < для записи результатов сравнения. | Инструкция сосредоточена на процедуре без понимания позиционного значения. Инструкция делает упор на упорядочивание номеров с использованием процедурных стратегий, а не на сравнение, основанное на более глубоком понимании трехзначных чисел. Инструкция рассматривает это обучение как новый навык, а не намеренно опирается на обучение в первом классе, связывая его со сравнением двузначных чисел. Мы хотим, чтобы студенты:
|
2.NBT.B.7 Сложение и вычитание в пределах 1000 с использованием конкретных моделей или чертежей и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни. | Инструкция фокусируется только на процедурных методах для стандартного алгоритма* без построения концептуального понимания. Обучение сосредоточено на следующих шагах в процедуре и не способствует пониманию учащимися сложения или вычитания одинаковых единиц или составления и разложения единиц десятков и сотен. Мы хотим, чтобы студенты:
*Язык «по стандартному алгоритму» не вводится в стандарты до 4 класса. |
2.MD.B.6 Представлять целые числа в виде длин от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представлять суммы и разности целых чисел в пределах 100 на числовой линейной диаграмме. | Инструкция сосредоточена на процедуре или этапах процесса, а не на понимании того, как сложение и вычитание длины могут быть представлены на числовой прямой. Инструкция сосредоточена на использовании числовой линии в качестве стратегии сложения и вычитания. Мы хотим, чтобы студенты:
|
Я хотел бы более подробно рассмотреть два моих любимых стандарта, оба из которых требуют согласованного обучения для формирования у учащихся концептуального понимания фундаментальных математических идей: 2.NBT.B.7 и 2.MD.B. .6. Давайте копать!
2.NBT.B.7
Сложение и вычитание в пределах 1000 с использованием конкретных моделей или чертежей и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом.
Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
Сколько я себя помню учителем начальных классов и тренером по математике, стандартный алгоритм сложения и вычитания был проблематичным. Учащиеся могут научиться этому как процедуре, без понимания, от благонамеренных учителей или родителей. Меня даже в детстве так учили! Теперь мы знаем, насколько важно для студентов понять «почему» за процедурой. Это лучше готовит их к будущей математике и углубляет их понимание порядкового значения и операций сложения и вычитания, которые позже будут применяться для более успешного понимания дробей, десятичных знаков и работы по алгебре.
Когда я вижу задачу вроде 600 – 432, я знаю, что есть много разных способов помочь учащимся решить это выражение. Студенты, скорее всего, разложат одну из 6 сотен на 10 десятков, а затем разложат десятку на 10 единиц.
После того, как 600 будет написано, нарисовано или представлено с помощью конкретных объектов, таких как блоки с основанием 10 или диски с разрядным числом в виде 5 сотен, 9 десятков и 10 единиц, учащиеся могут вычитать. Можно показать эту работу, используя письменный метод, напоминающий стандартный алгоритм, если установлены явные связи между различными представлениями (моделями или чертежами) и письменным методом. См. пример ниже.
Другим способом решения 600–432 для учащихся может быть использование сложения, сложения из 432, тем самым подчеркивая связь между сложением и вычитанием.
Важным выводом для обучения при работе с 2.NBT.B.7 является то, что нельзя переходить к процедурному обучению до того, как учащиеся поймут смысл системы разрядов при сложении и вычитании в пределах 1000. Дайте учащимся возможность разработать свои собственные методы решения. , помогите им установить связь между представлениями и методами и перейти к эффективности процедуры после того, как будет достигнуто концептуальное понимание.
2.MD.B.6
Представлять целые числа как длины от 0 на диаграмме числовых линий с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представлять суммы целых чисел и различия в пределах 100 на диаграмме числовых линий.
Помню, в начале моей преподавательской карьеры, 20 лет назад (здесь я встречаюсь с самим собой!), и много лет спустя я преподавал числовую линию как стратегию или метод для своих первоклассников складывать и вычесть. Была вовлечена милая лягушка и много говорили о «прыжках» на числовой прямой. Студенты «использовали» эту стратегию и в большинстве случаев приходили к правильному ответу, но понятия не имели, что они делают. Они определенно не связывали числовую прямую с единицами длины и не считали эти единицы. Я мог бы все еще делать это сегодня, если бы не учился у некоторых замечательных Основных Защитников и учителей-лидеров!
В стандартах есть три места, где числовой ряд специально упоминается: здесь во 2 классе, в 3 классе, где дроби рассматриваются как числа, и снова в 6 классе, когда учащиеся изучают рациональные числа.
Числовая линия намеренно не используется до 2-го класса. Также намеренно она вводится с подсчетом «длины». Важно отметить, что заголовок кластера для 2.MD.B.6 относится к «Связать сложение и вычитание с длиной».
Численно-линейные диаграммы могут быть сложными для учащихся, поскольку они используют единицы длины, которые труднее увидеть и сосчитать, чем конкретные объекты или изображения. Диаграммы с числовыми линиями вводятся во 2 классе, когда учащиеся имеют опыт подсчета единиц длины на измерительных инструментах, которые по сути представляют собой специальные диаграммы с числовыми линиями. Важно помочь учащимся «видеть» единицы длины, отсчитываемые между конечными точками, а также числа, обозначающие конечные точки длин от 0,9.0003
Давайте посмотрим на это задание из учебного плана Engage NY:
Вы увидите, что учащиеся используют числовую линию для представления длины в сантиметрах. Они добавляют «больше» к заданному числу, а затем составляют соответствующее уравнение.
Эта задача иллюстрирует сложность и цель 2.MD.B.6 без процедур или выделения ответа.
Я надеюсь, что это помогло вам изучить и поразмышлять над мощными, согласованными инструкциями по математике. Я также надеюсь, что это может дать вам новые идеи для обучения 2 -й класс математики. Я с нетерпением жду вашего ответа и продолжения этой беседы! Пожалуйста, оставьте свои комментарии ниже или вы можете найти меня в Твиттере @mrsmillergrade1. Следите за новостями о моих оценках K и 1!
Об авторе: Энджи Миллер работает специалистом по обучению математике в школьном округе Анакортес в штате Вашингтон. До своей роли помощника учителей она преподавала в начальных классах и специальном образовании в течение 19 лет. Энджи неустанно выступает за справедливость в классе математики за счет улучшения учебной практики, углубления знаний и использования согласованных высококачественных учебных материалов. Благодаря своей работе с Вашингтонской ассоциацией образования, ведущими преподавателями и новыми лидерами она разработала профессиональное изучение математических смен Common Core State Standards для преподавателей по всей стране.
Энджи работает в Институте стандартов UnboundEd по направлению K-2 Math. Энджи является учителем, сертифицированным Национальным советом, и имеет сертификат в области лидерства учителей Вашингтонского университета.
Выделение «хороших» ошибок в работе учащихся
Оценивая контрольные по алгебре в своем классе, я заметил, что концептуальная ошибка продолжает появляться в работах нескольких учеников. Я вытащил свой телефон и сфотографировал различные решения студентов — некоторые с ошибками, некоторые без. На следующий день в классе я показывал выбранные фотографии в качестве руководства, чтобы начать обсуждение различных решений всем классом. (Имена учеников, чьи работы были выставлены, не были раскрыты классу.)
Вот некоторые ответы восьмиклассников, когда мы рассматривали фотографии:
- «О, я вижу, как они использовали уравнение из таблицы значений для определения уклона».
- «Почему умножили 0,5 на 14? Я поступил иначе».
- «Да, я вижу здесь ошибку.
Они предположили, что точка пересечения и равна нулю». - «Мне нравится, как они показали общую разницу в таблице».
Они предположили, что точка пересечения и равна нулю».Зачем делиться фотографиями студенческих работ? Все приведенные выше комментарии студентов о образце студенческой работы способствовали усвоению концепции. Я мог бы воссоздать решение каждого учащегося на доске; однако учащимся полезно видеть работы друг друга, а не только учителя.
Катрина Шварц пишет в статье KQED 2014 года «Как взгляд на работу учащихся помогает учителям и детям не сбиться с пути»: «Изучение и критика работы учащихся как регулярная часть взаимодействия в классе может быть эффективным способом как для учителей, так и для учеников задуматься над свою работу, создавая при этом культуру сообщества, ориентированную на процесс обучения». Когда образцы работ нескольких учащихся или групп представлены в запланированной последовательности, весь класс может установить связи между математическими понятиями, которые невозможно установить, видя только свою собственную работу.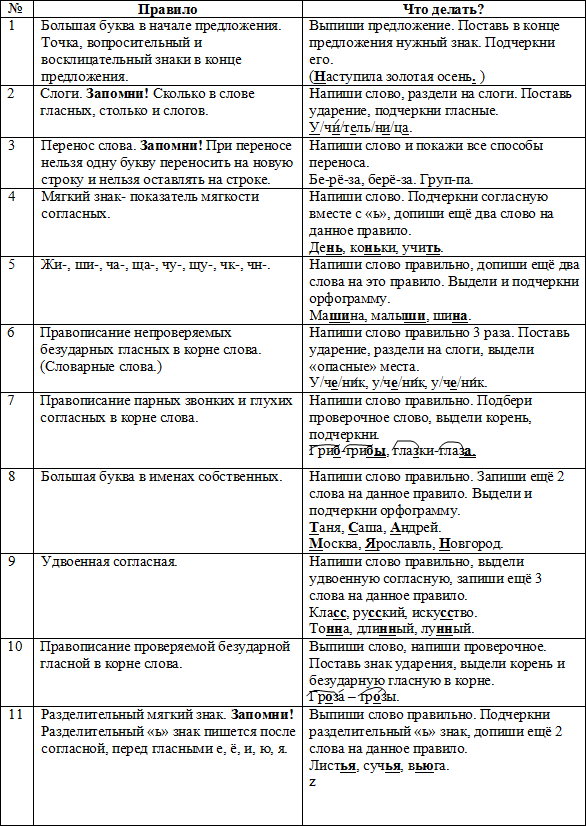
Ожидание и уважение к ошибкам
Обсуждение фотографий студенческих работ дает возможность достичь стандарта Common Core «критика рассуждений других», крайне важно, чтобы окружающая среда поддерживала и поощряла всех учащихся. Учителя могут способствовать формированию такой культуры, признавая «хорошие ошибки». Узнайте больше о том, как создать класс, благоприятный для ошибок, в статье Меган Ласлоки на сайте Edutopia 2021 года «Класс, благоприятный для ошибок».
Что делать, если учащийся не хочет, чтобы его работа была доступна для всех?
Да, даже если личность учащегося не раскрывается, другой одноклассник может узнать его почерк. Вот почему крайне важно создать классовую культуру коллегиального поощрения и уважения. Я никогда не стал бы показывать вопиющие ошибки, которые могли бы поставить студента в неловкое положение, если бы его личность была известна. Учитель может предварить образец работы ученика словами «Это была распространенная ошибка; тем не менее, я выбрал этот образец, потому что они явно начали с правильного подхода.
Давайте обсудим, чему мы можем научиться на этом примере».
Пока учащиеся работают в группах за партами, сделайте фотографии, которые положат начало осмысленному обсуждению в классе. Я спрашиваю студента, не хотят ли они обсудить свою работу с классом. Если они не хотят, я спрашиваю, можно ли другому ученику выйти к доске, чтобы интерпретировать и объяснить процесс и шаги. Когда один учащийся объясняет работу другого учащегося, и объяснитель, и решатель практикуют четкую математическую коммуникацию.
Если учащиеся работают у доски в группах (также называемых вертикальными непостоянными поверхностями или VNPS в книге Питера Лильедала Построение классов мышления по математике ), то каждый может увидеть работу группы, если вы пригласите их или прогуляетесь по галерее. Иногда я считаю, что работа группы достойна внимания в будущем, и я делаю фотографию, чтобы ее могли увидеть другие секции (в противном случае работа на доске будет стерта и больше никогда не будет видна).
В статье «Преподавание математики в средней школе » «Изучение ошибок для изменения мышления учащихся» авторы предлагают отображать ошибки, которые «достойны» обсуждения. Достойные ошибки могут быть вычислительными, концептуальными или процедурными по своей природе. Достойная ошибка углубит понимание математической цели урока для всех учащихся, а не только для того, кто сделал ошибку.
Desmos Classroom, бесплатный веб-сайт с графическим онлайн-калькулятором, который также включает в себя цифровые задания, имеет функцию, которая позволяет учителям делать снимки ответов учеников во время занятия. Добавляя эти снимки в альбом, учитель может отображать работы учащихся рядом друг с другом, чтобы вызвать дискуссию о мышлении учащихся. В верхней части экрана презентации есть поле, в котором можно задать классу наводящий вопрос о представленной студенческой работе. (Desmos также имеет опцию «анонимизации», позволяющую отображать имена студентов как имена известных математиков.
)
Ниже реальный пример фотографии, которую я использовал на уроке алгебры. (Личность учащегося не сообщалась классу.) Это изображение привело к обсуждению нескольких методов сравнения уравнения и таблицы значений. Многие студенты боролись с этой проблемой при оценке по разным причинам. Моя цель состояла в том, чтобы поделиться примером того, как интерпретировать таблицу значений как уравнение.
Предоставлено Кристал Фроммерт
Сначала я спросил класс, что они заметили в уравнении, написанном над таблицей. «Как они рассчитали наклон и г -перехват? Какое сообщение можно было бы добавить сюда, чтобы четко передать расчет уклона?» В этот момент учащийся может подойти к доске, чтобы аннотировать таблицу общей разностью или формулой наклона.
Боковая арифметика также может привести к интересному обсуждению вычисления десятичных дробей; однако, поскольку это не было в центре внимания урока, я не пошел по этому пути возможного разговора.