Самостоятельная работа по теме множества и операции над ними 9 класс – План-конспект урока по алгебре (9 класс) на тему: Множества и операции над ними

План-конспект урока по алгебре (9 класс) на тему: Множества и операции над ними

                                          Множества и операции над ними.

Тип урока: Урок ознакомления с новым материалом.

Цель урока: Показать множества – как фундамент современного математического языка.

Задачи урока:

образовательные: знакомство с понятием множества, подмножества и элементами множеств; способами задания множеств; видами множеств;

развивающие: развитие познавательного интереса учащихся; развитие интеллектуальной сферы личности, развитие умений сравнивать и обобщать.

воспитательные: воспитывать аккуратность и внимательность при решении заданий.

Ход урока

I этап. Формулировка темы, цели, задач урока и мотивация учебной деятельности.

Какие числа вы видите на экране? (натуральные, целые, рациональные, действительные)

Как называют эту схему? (Круги Эйлера)

С какой темой связаны круги Эйлера? (множества чисел).

Как вы думаете, кроме множества чисел есть другие множества?

Что такое множество? (Множество – это определенное количество объектов с похожими свойствами)

БЛИЦ-ОПРОС:

Какие названия применяются для обозначения множеств животных?

Какие названия применяются для обозначения множеств военнослужащих?

Как называется множество цветов, стоящих в вазе?

Какие названия применяют для обозначения множеств кораблей? 

Как называется множество царей (фараонов, императоров и т.д.) данной страны, принадлежащих одному семейству?

Как называется множество картин? 

Как называется множество документов? 

II этап. Ознакомление с новым материалом.

А в математике нет точного определения множества. Но каждый объект, входящий во множество называется его элементом. Откройте учебник на стр.25 и найдите таблицу

Приведите пример собственного множества (множество дней недели; множество планет солнечной системы; множество месяцев; множество знаков зодиака; числовые множества).

Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством  В. Обозначение: А  ⊂ В. Знак  « ⊂ » — знак включения.

На доске А = 3,4,5     В= 1,2,3,4,5,6.

С множествами связаны различные парадоксы, самый простой из парадоксов — это «парадокс брадобрея». Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.

Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление.

Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Бриться или не бриться – вот в чём вопрос!

III этап. Динамическая пауза

1. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4–5 раз.
2. Крепко зажмурить глаза (считать до 3), открыть глаза и посмотреть вдаль (считать до 5). Повторить 4–5 раз.
3. Движения глаз: вверх, вниз, влево, вправо. Повторить 4-5 раз
4. Повороты головой: вверх, вниз, влево, вправо. Повторить 4-5 раз

IV этап. Первичное осмысление и закрепление связей и отношений в объектах изучения.

Откройте задачник на стр.21 пункт 3. Мы выполняем задания, записанные на доске №1, 2, 9

V этап. Самостоятельная работа(Приложение)

VI  этап Домашнее задание

Пункт 3 изучить № 4, 8, 10, 18 (дополнительно)

VII этап. Подведение итогов урока.

Что такое множество?

Кто такой Леонард Эйлер?

Что такое подмножество множества?

На прошлых уроках мы говорили о рациональных неравенствах, сегодня о множествах. Кто догадался какая тема будет следующей?

Список использованных источников и литературы:

Учебники «Алгебра. 9 кл.I и II части» Авторы: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина и др.,— 11-е издание, стер. — М.: «Мнемозина», 2009 г.;

http://mathlog.h21.ru/mnoj.htm;

http://festival.1september.ru;

http://ru.wikipedia.org;

http://mmmf.msu.ru/archive/20092010/Lanin/9.html;

http://www.it-n.ru;

Занимательные математические задачи. Учеб.пособие./Сост.: А. М. Быковских, Г.Я. Куклина. 2-е изд., испр. Новосиб. гос. ун-т. Новосибирск, 2010. 88 с.;

 Математика: Нестандартные задачи./Сост.: А.М.Быковских, канд. физ.-мат. наук, доцент кафедры высшей математики, КрасГУ.-Красноярск, 2006. 27 с.;

 Ященко И.В. Парадоксы теории множеств. (Серия: «Библиотека

«Математическое просвещение»»).  М.: МЦНМО, 2002. — 40 с.: ил.

Самостоятельная работа ученика 9 класса__________________

Вариант 1 №1 Дано множество К= {-10,   3;   -7;   0;   2,6;   3} Составьте его подмножество М, состоящее из неотрицательных чисел: Ответ: М= {                                       } №2. Какое словесное описание у множества?      А= {1,3,5,7,9,11,13, 15…} Ответ: Это множество _____________________ чисел №3.Составьте три слова, буквы которых образуют подмножества множества А={к,а,р,у,с,е,л,ь} Ответ: №4 Дано множество {–6,2;    ;    4}. Перечислите его подмножества, состоящие из двух чисел: А) разного знака Б) положительных В) рациональных Г) среди которых есть иррациональное число Ответ: А) {                          }; {                          } Б) {                          } В) {                          } Г) {                          }; {                          }

Самостоятельная работа ученика 9 класса__________________

Вариант 2 №1 Дано множество L= {-1,3 ; 0 ; 2 ; 3,8 ; 6 ; 11} Составьте его подмножество, состоящее из натуральных чисел. Ответ: D= {                               } №2. Какое словесное описание у множества? А= {2,4,6,8,10,12,14…} Ответ: Это множество _____________________ чисел №3.Составьте три слова, буквы которых образуют подмножества множества А={к,а,р,у,с,е,л,ь} №4 Дано множество {–7,8;    ;    2}. Перечислите его подмножества, состоящие из двух чисел: А) разного знака Б) положительных В) рациональных Г) среди которых есть иррациональное число Ответ: А) {                          }; {                          } Б) {                          } В) {                          } Г) {                          }; {                          }

nsportal.ru

Многовариантная самостоятельная работа по математике. Тема: «Операции над числовым множеством»

Все знают, как дети любят подсматривать, списывать друг у друга контрольные и самостоятельные работы. Причём умудряются это делать даже под носом у учителя. Единственный выход – дать каждому обучающемуся отдельное задание, чтобы списывать было не у кого. Но как же сложно проверять 25 разных вариантов! Я использую многовариантные проверочные работы.

Само задание даётся в общем виде, но к нему выдается отдельный набор данных для каждого ученика. В этих наборах данных все числа соответствуют определенным первоначальным условиям, которых дети не знают. Поэтому все ответы также соответствуют этим условиям.

В данной работе представлены задания для проверки знания обучающимися операций над множествами. Обычно в школьном курсе математики вводятся две операции над числовыми промежутками: объединения и пересечения множеств. Я дополнительно рассматриваю еще разность множеств.

После определения данных операций на уроке решаются несколько тренировочных заданий. Затем, в зависимости от математической подготовки класса, даются проверочные задания для решения в классе или дома.

Здесь представлены два типа заданий. В каждом из них нужно найти результат операций объединения, пересечения, разности над множествами.

В первом задании используются множества, заданные как числовой промежуток. Концы промежутков удовлетворяют условию: a₁ < b < c < a₂. Во втором нужно выполнить операции над множествами, заданными с помощью неравенств.  Числа должны удовлетворять неравенству c₁ < b₁ < b₂ < a < c₂. Подставляя вместо этих переменных числа, удовлетворяющие данному условию, можно подготовить вариант для каждого ученика класса. Проверка осуществляется очень быстро с помощью простой подстановки заданного набора чисел в шаблон ответов.

Работы раздаются на карточках, в которые вписываются ответы.

В данной статье приведены задания в общем виде, числовые данные для 25 вариантов, карточка, которая дается ученику, критерии оценивания работы.

Задания

Критерии оценивания результатов самостоятельной работы.

Каждое задание оценивается отдельно.

1 задание:

Оценка	Правильно решенных заданий	Количество ошибок
«5»	10	0
«4»	9	1
«3»	7-8	2-3

2 задание:

Оценка	Правильно решенных заданий	Количество ошибок
«5»	19-20	0-1
«4»	16-18	2-4
«3»	11-15	5-9

urok.1sept.ru

Урок по математике на тему «Множества и операции над ними» (9 класс0

Открытый урок по математике в 9 классе.

( учитель математики Муниципального общеобразовательного учреждения «Средняя общеобразовательная школа № 3 г. Ершова Саратовской области» Уполовникова О.А.)

Тема урока: « Множества. Операции над множествами».

Цели урока:

Образовательная: ввести понятия множества и подмножества, способы задания множеств, виды множеств и операций над множествами.

Развивающая: развитие логического мышления, познавательного интереса; побуждать учеников к самоанализу своей учебной деятельности.

Воспитательная: воспитание интереса к предмету, умения работать самостоятельно.

Тип урока: изучение нового материала.

Оборудование: компьютер, мультимедийный проектор, презентация (Приложение 1)

Ход урока.

1. Организационный момент. Сообщение темы урока (презентация, слайд 1)

2. Объяснение новой темы.

1) Как вы думаете, что в русском языке означает слово множество? Давайте посмотрим как это слово трактуется в различных словарях (презентация, слайды 2, 3, 4 ).

2) Что же понимается под «множеством» в математике?

В конце 19 века Георг Кантор определил множество как « единое имя для совокупности всех объектов, обладающих данным свойством» (презентация слайд 5).

Понятие множества в современной математике ( презентация слайд 6).

3) Обозначение множеств и его элементов (презентация слайд 7).

4) Способы задания множеств (презентация слайды 8,9).

5) Предварительное закрепление знаний. Выполнить задание № 1 (устно) (слайд 10).

Задайте множество по его словесному описанию. 

1. Целые положительные числа, которые меньше 4.

Выбери правильный вариант ответа:

а) {−4,−3,−2,−1};

б) {1,2,3};

в) {1,2,3,4};

г) {−1,−2,−3,−4,−5}.

2.Множество двузначных чисел, кратных 12.

6) Некоторые виды множеств (слайд 11).

Самостоятельно: запишите по два примера конечных и бесконечных множеств.

Например: конечное – множество двузначных чисел, являющихся квадратами натуральных чисел (16, 25, 36, 49, 64, 81).

7) Понятие подмножества (слайды 12, 13)

Выполнить задание № 2 устно (слайд 14).

Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.

Верно ли, что: а) А    В; б) В С;

в) С   А; г) С  В?

8) Пересечение множеств (слайд 15).

9) Объединение множеств (слайд 16).

10) Разность множеств (слайд 17).

11) Выполнить задание № 3 (слайд 18).

1.Найди объединение, пересечение и разность множеств A и B, если A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}.

2.Даны три множества:

X={x,h,w,d},

Y={w,d,e,f},

Z={w,p,q}.

Найти (X∩Y) U Z .

У доски задание 1 выполняют трое учащихся (слабые), а задание 2 выполняет один более подготовленный ученик.

3. Закрепление изученного материала.

1. № 3.2 (устно).

2. № 3.12 (у доски).

Домашнее задание: № 3.1; № 3.8.

Источники:

1. Учебник «Алгебра 9 класс» под редакцией А.Г.Мордковича.

2. Множества и операции над множествами.

http://www.math5you.ru/theory/main-concept/set

3. http://referatbox.com/12698/ponyatie-mnozhestv-sposoby-zadaniya-mnozhestv/2/

4. http://www.yaklass.ru/p/algebra/9-klass/neravenstva-i-sistemy-neravenstv-9125/mnozhestva-i-operatcii-nad-nimi-12443

5. http://www.grandars.ru/student/vysshaya-matematika/mnozhestvo.html

infourok.ru

Множества и операции над ними. Алгебра, 9 класс: уроки, тесты, задания.

1.	Задание множества по словесному описанию (числа) Сложность: лёгкое	1
2.	Множество натуральных и целых чисел Сложность: лёгкое	2
3.	Подмножества рациональных чисел Сложность: лёгкое	1
4.	Множества и подмножества Сложность: лёгкое	2
5.	Множество в виде числового промежутка (линейное неравенство) Сложность: среднее	5
6.	Принадлежность числа множеству Сложность: среднее	2
7.	Пересечение множеств Сложность: среднее	2
8.	Пересечение и объединение множеств Сложность: среднее	2
9.	Круги Эйлера Сложность: сложное	3
10.	Площадь гаража Сложность: сложное	3
11.	Множество в виде числового промежутка (квадратное неравенство) Сложность: сложное	7

www.yaklass.ru

Презентация к уроку по алгебре (9 класс) на тему: Множества и операции над ними

Слайд 1

Множества и операции над ними

Слайд 2

Множество – это совокупность элементов, отобранных по определенному признаку (признакам). Множество может содержать конечное или бесконечное количество элементов. Определение Пример: { 2 ; 4; 6; 8 } – множество четных однозначных чисел. { — 15; 5 } – множество, состоящее из чисел -15 и 5.

Слайд 3

Числовые множества: N- Z- Q- R- Множество натуральных чисел Множество целых чисел Множество рациональных чисел Множество действительных чисел

Слайд 5

Выполнить задание: Множество А состоит из всех корней уравнения х 3 + х 2 – 6х = 0 а) Решить уравнение б) Записать множество А перечислением его элементов в порядке возрастания в) Записать все возможные способы перечисления. Сколько таких способов?

Слайд 6

Некоторые способы задания множеств

Слайд 7

Задание множества с помощью его характеристического свойства

Слайд 8

Выполнить задание: Записать данное множество в виде промежутка { х | х 2 – 8х + 15 > 0 }

Слайд 9

Выполнить задание: Верно ли, что 1 { х | х 7 – 6х 6 + 3х 3 + 1

Слайд 10

Определение Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А Обозначение: В А знак включения

Слайд 11

Выполнить задание:

Слайд 12

Верно, что

Слайд 13

Верно, что

Слайд 14

Верно, что

Слайд 15

Определение Пересечение множеств А и В – это множество, состоящее из всех элементов, которые принадлежат и множеству А, и множеству В. Обозначение: А В = { х | х ϵ А и х ϵ В }

Слайд 16

Выполнить задание: Найти пересечение множеств А и В, если А = { 11, 22, 33, …, 88, 99 } , В = { 3, 6, 9, … }

Слайд 17

Определение Объединение множеств А и В – это множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств, или множеству А, или множеству В. Обозначение: А В = { х | х ϵ А или х ϵ В }

Слайд 18

Выполнить задание: Найти объединение множеств А и В, если А = { 1, 5, 7, 2, 3 } , В = { 3, 5, 4, 8, 1 }

Слайд 19

В классе № 3.3( а,б ), 3.7, 3.10 Домашнее задание 3.3( в,г ), 3.6, 3.8, 3.11

nsportal.ru

Презентация к уроку по алгебре (9 класс) по теме: Множества и операции над ними. Урок получения новых знаний. Алгебра 9 класс.

Урок разработан учителем математики

МБОУ гимназия № 5 г. Морозовска Ростовской обл.

Касьяновой Натальей Игоревной

---

Урок № 1. Урок ознакомления с новым материалом.

ТЕМА:  Множества и операции над ними.

Цели урока:

1. образовательные: знакомство с понятием  множества, подмножества и элементами множеств; способами задания множеств; видами множеств; знакомство с операциями, выполняемыми над множествами.
2. развивающие: развитие познавательного интереса учащихся; развитие интеллектуальной сферы личности, развитие умений сравнивать и обобщать.
3. воспитательные: воспитывать аккуратность и внимательность при решении заданий.

Ход урока:

I этап. Сообщение темы, цели, задач урока и мотивация учебной деятельности.

I I этап. Ознакомление с новым материалом.

Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).

«Множество есть многое, мыслимое нами как единое» ( Г. Кантор)

Понятие множество связано с таким известным в математике именем как Кантор (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв. В семидесятые годы ХIX века немецкий математик Георг Кантор, исследуя тригонометрические ряды и числовые последовательности, встал перед необходимостью сравнить между собой бесконечные совокупности чисел. Для решения возникших при этом проблем Кантор и выдвинул понятие множества. Это понятие, введенное в достаточно узкой области математики для довольно специальных целей, вскоре стало с успехом применяться в других ее областях. Посвященные ему исследования приобрели самостоятельный интерес и выделились в особый раздел математики – теорию множеств.

Теория множеств появилась на свет 7 декабря 1873 года.

Кантора заинтересовал вопрос, каких чисел больше – натуральных или действительных?

В одном из писем адресованных к своему приятелю Рихарду Дедекинду, Кантор писал, что ему удалось доказать посредством множеств, что действительных чисел больше, чем натуральных. День, которым было датировано это письмо, математики считают днем рождения теории множеств.

Множество — одно из основных понятий современной математики, используемое почти во всех её разделах. К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству. Понятие множества поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.. Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C, … , X, Y, … ,A1,B1, …

Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.

        Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ. Элементы множества обозначаются  строчными (малыми) буквами латинского алфавита. Например: b,c, … , x, y, … , a1, b1, … Если элемент х принадлежит множеству  М, то записывают  х М, если не принадлежит – x M.

Множества можно задать, перечислив все его элементы или указав характеристическое свойство элементов, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.

Примеры множеств:

1. множество дней недели;
2. множество планет солнечной системы;
3. множество месяцев;
4.  множество знаков зодиака;
5. числовые множества.

Приведите свой пример множества.

 С множествами связаны различные парадоксы, самый простой из парадоксов — это «парадокс брадобрея». Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.

Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление.

Однако возник вопрос, брить  ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Бриться или не бриться – вот в чём вопрос!

Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.

Если каждый элемент множества  А является элементом множества В, то множество А называется подмножеством В. Обозначение: А  Ì В.

Знак  « Ì » — знак включения.

Рассмотрим некоторые операции над множествами.

Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно.

Символически пересечение множеств А и В обозначается так: АВ, где символ  — знак пересечения множеств. Используя характеристическое свойство, определение можно записать следующим образом:

Р = А   В= {x xA и xB}.        

Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.

nsportal.ru

Тестирование №1. Теория множеств и операции над ними

II. Тестирование: 41 мин

1. Что такое множество?

А) объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам

В) достоверное знание, соответствие которого объективным явлениям и предметам окружающего мира подтверждено практикой

С) наука о законах и формах правильного мышления

2. Что означает в логике этот знак ?

А) пересечение

В) пустое множество

С) объединение

3. Что означает в логике этот знак ?

А) пересечение

В) пустое множество

С) объединение

4. Что означает в логике этот знак ?

А) пересечение

В) пустое множество

С) объединение

5. Что означает в логике этот знак \ ?

А) разность

В) элемент

С) подмножество

6. Из представленных знаков выберите знак принадлежности:

А)

В)

С)

7. Что называют объединением множеств А и В?

А) новое множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В

В) новое множество, состоящее из тех элементов, которые принадлежат и множеству А, и множеству В

С) новое множество, состоящее из всех элементов А, не входящих в В

8. Что называют пересечением множеств А и В?

А) новое множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В

В) новое множество, состоящее из тех элементов, которые принадлежат и множеству А, и множеству В

С) новое множество, состоящее из всех элементов А, не входящих в В

9. Что называют разностью множеств А и В?

А) новое множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В

В) новое множество, состоящее из тех элементов, которые принадлежат и множеству А, и множеству В

С) новое множество, состоящее из всех элементов А, не входящих в В

10. Для чего в логике нужны круги Эйлера-Венна?

А) для вычислений

В) для оформления решений логических задач

С) для иллюстрации соотношения между множествами

11. Даны множества А= и В=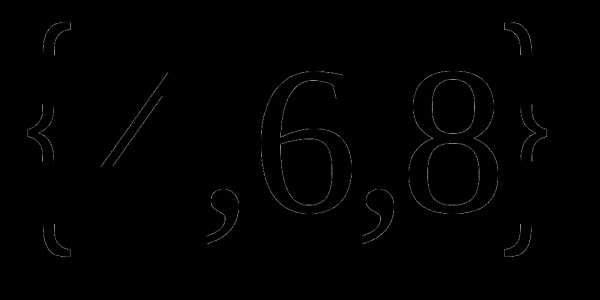, найдите АВ:

А) С=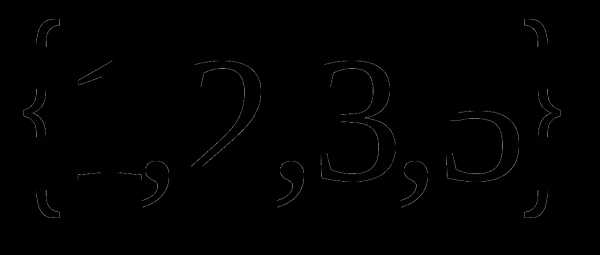

В) С=

С) С=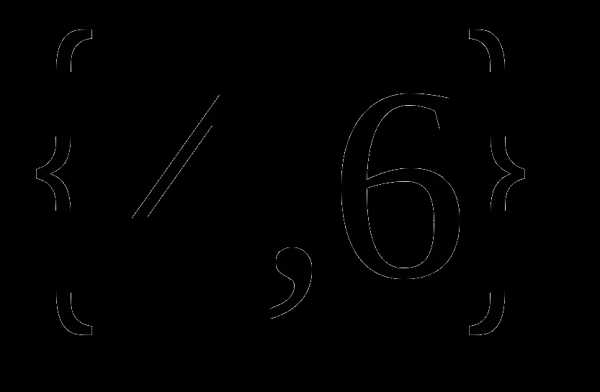

12. Даны множества А= и В=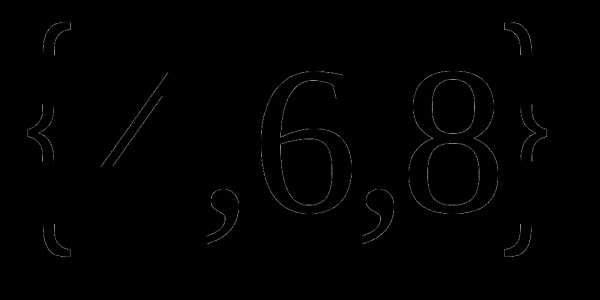, найдите АВ:

А) С=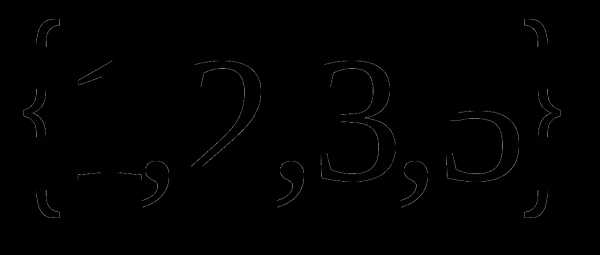

В) С=

С) С=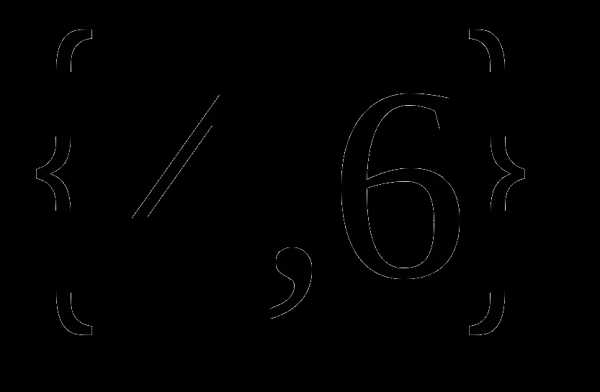

13. Даны множества А= и В=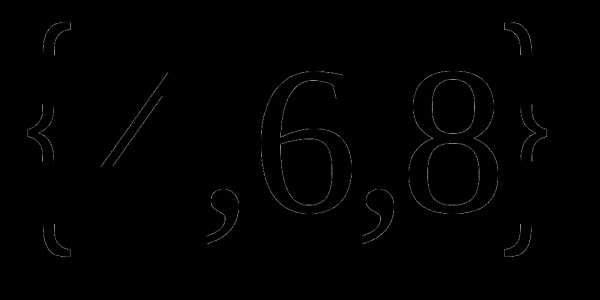, найдите А\В:

А) С=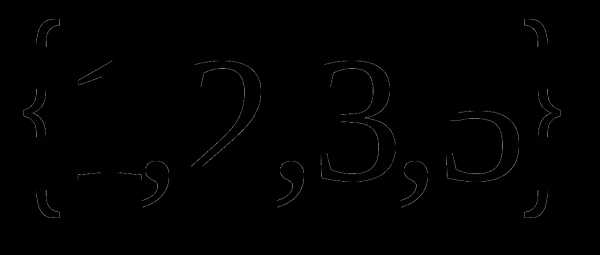

В) С=

С) С=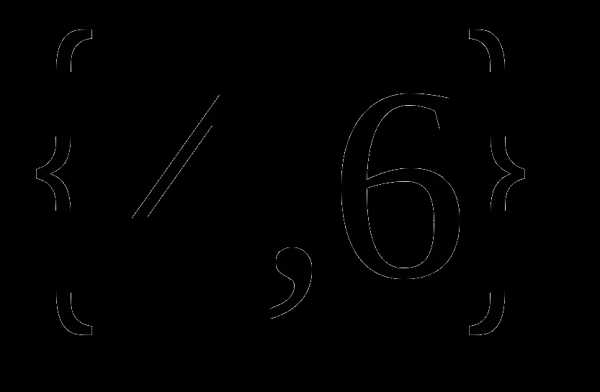

14 Даны множества А= и В=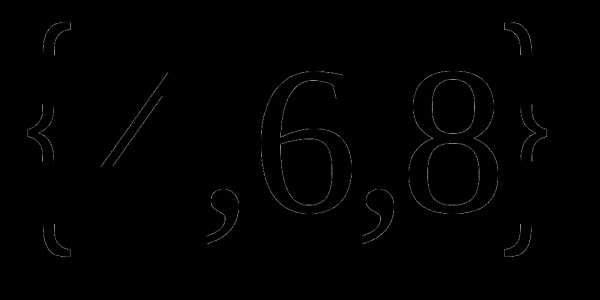, найдите В\А:

А) С=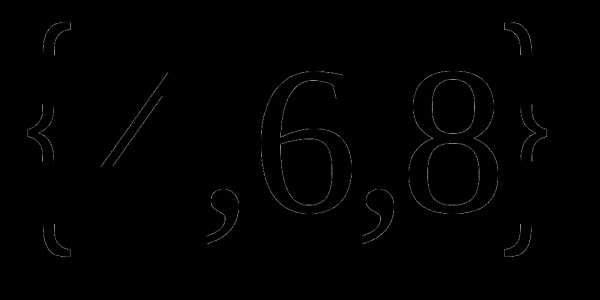

В) С=

С) С=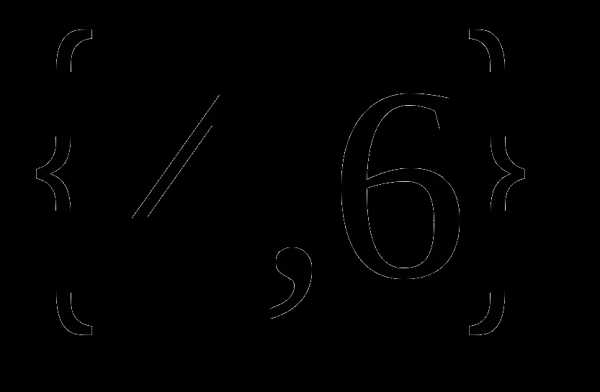

15. Что означает в логике этот знак?

А) элемент

В) подмножество

С) принадлежность

№

infourok.ru