Правило плюс на плюс: Минус на плюс что дает?

Минус на плюс что дает?

Автор Admin На чтение 6 мин Просмотров 2.9к. Опубликовано 20.12.2020

Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.

Запомнить правила умножения или деления положительных и отрицательных чисел очень просто.
Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.

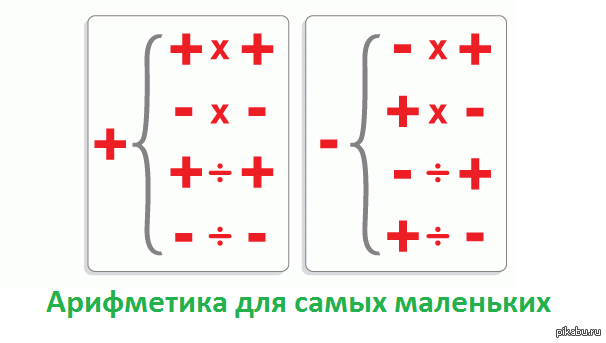
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.

Минус на плюс, плюс на минус.

Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.

Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.

Минус на минус, плюс на плюс.

Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам?

При умножении и делении положительных или отрицательных чисел в результате получается положительное число.

Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?

Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.

Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.

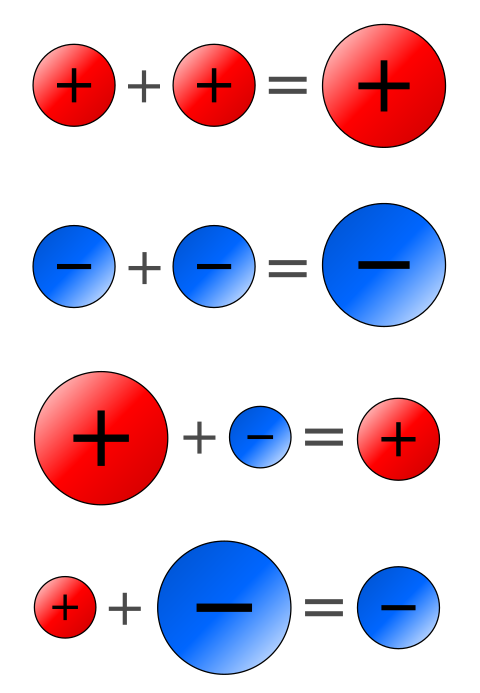
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.

Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.

Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.

Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.

Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?

Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».

Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.

В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:

2а+2а=4а

2а*2а=4а^2

В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?

(-2)+(-2)=-4

(-2)*(-2)=+4

Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.

Почему минус на минус дает плюс?

«Враг моего врага — мой друг».

Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.

Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.

Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.

В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).

Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.

Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.

Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.

Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.

Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).

В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.

Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.

Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:

• сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C
  ) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
• умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
• сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.

Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.

Теперь докажем, что для любых элементов A и B

произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.

Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.

Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу

(–A), поэтому они должны быть равны.

Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).

Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.

А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.

Ответил: Евгений Епифанов

Порядок действий – Элементарная математика

Уменьшение двусмысленности по договоренности

В общем, никто не хочет быть неправильно понятым. В математике так важно, чтобы читатели понимали выражения именно так, как задумал автор, что математика устанавливает соглашения, согласованные правила для интерпретации математических выражений.

Означает ли 10 − 5 − 3, что мы начинаем с 10, вычитаем 5, а затем вычитаем еще 3, оставляя 2? Или это означает, что мы вычитаем 5 − 3 из 10?
Равно ли 2 + 3 × 10 50, потому что 2 + 3 равно 5, а затем мы умножаем на 10, или автор имеет в виду, что мы добавляем 2 к результату 3 × 10?

Чтобы избежать этих и других возможных неясностей, математика установила соглашения (соглашения) о том, как мы интерпретируем математические выражения. Одно из этих соглашений гласит, что когда все операции одинаковы, мы действуем слева направо, поэтому 10 — 5 — 3 = 2, поэтому автору, который хотел бы другую интерпретацию, пришлось бы писать выражение по-другому: 10 — (5). − 2). Когда операции не такие, как в 2 + 3 × 10, некоторым может быть отдано предпочтение перед другими. В частности, умножение выполняется перед сложением независимо от того, какое из чисел появляется первым при чтении слева направо. Например, в 2 + 3 × 10 умножение должно быть выполнено первым, даже несмотря на то, что оно стоит справа от сложения, а выражение означает 2 + 30.
Полные правила порядка операций см. ниже.

Условные обозначения для чтения и записи математических выражений

Основной принцип: «более мощные» операции имеют приоритет над «менее мощными».

Использование числа в качестве показателя степени (например, 58 = 390625) имеет, как правило, «самый сильный» эффект; использование того же числа в качестве множителя (например, 5 × 8 = 40) дает более слабый эффект; сложение имеет, как правило, самый «слабый» эффект (например, 5 + 8 = 13). Хотя эти термины (мощный, слабый) в математике не употребляются, смысл сохраняется в языке «возведение 5 в 8-ю степень». Возведение в степень «мощно», поэтому оно на первом месте! Сложение/вычитание «слабые», поэтому они идут последними. Умножение/деление находится между ними.

Когда важно указать другой порядок , как это иногда бывает, мы используем круглые скобки для упаковки чисел и более слабую операцию, как если бы они представляли одно число.

Например, хотя 2 + 3 × 8 означает то же, что и 2 + 24 (поскольку умножение имеет приоритет и выполняется первым), (2 + 3) × 8 означает 5 × 8, поскольку (2 + 3) пакетное предложение, количество, которое необходимо выяснить перед его использованием. На самом деле (2 + 3) × 8 часто произносится как «два плюс три, количество, умноженное на восемь» (или «количество два плюс три, умноженное на восемь»).

Краткое изложение правил:

• Сначала скобки. Обращение к ним как к «пакетам» часто помогает детям вспомнить их цель и роль.
• Экспоненты рядом.
• Далее умножение и деление. (Ни один из них не имеет приоритета, и когда они идут последовательно, они выполняются слева направо.)
• Сложение и вычитание в последнюю очередь. (Опять же, ни один из них не имеет приоритета, и последовательная строка из них выполняется слева направо.)

Распространенные заблуждения

Многие учащиеся изучают порядок операций, используя PEMDAS (скобки, возведения в степень, умножение, деление…) в качестве вспомогательного средства для запоминания. Это очень часто приводит к ошибочному представлению о том, что умножение предшествует делению, а сложение предшествует вычитанию. Понимание этого принципа, вероятно, является лучшим помощником в запоминании.

Умножить или добавить сначала? Преподавание порядка операций Правила

Назад к Shaped

Математика

Посох в форме

07 мая 2021 г.

9 мин Чтение

Когда учащиеся 3-х классов и старше учатся складывать, вычитать, умножать, делить и работать с основными числовыми выражениями, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Например, вы сначала складываете или умножаете? А умножить или разделить? В этой статье объясняется, что такое порядок операций, и приводятся примеры, которые вы также можете использовать со студентами. Он также содержит два урока, которые помогут вам представить и развить эту концепцию.

Стандартный ключ:

• Выполнять арифметические операции, включая сложение, вычитание, умножение и деление в обычном порядке, независимо от того, есть скобки или нет. (Класс 3)

Порядок операций является примером очень процедурной математики. Легко запутаться, потому что это не столько концепция, которую вы осваиваете, сколько список правил, которые вы должны запомнить. Но не обманывайте себя, думая, что процедурные навыки не могут быть глубокими! В нем могут быть представлены сложные задачи, подходящие для старших школьников и созревшие для обсуждения в классе:

• Изменяется ли правило слева направо, когда умножение подразумевается, а не прописывается? (Например, \(3g\) или \(8(12)\) вместо \(3 \times g\) или \(8 \cdot 12\).)
• Где факториал попадает в порядок операций ?
• Что произойдет, если вы возвели один показатель степени в другой показатель степени, но скобок нет? (Обратите внимание, что этот урок не включает показатели, хотя, если учащиеся готовы, вы можете расширить свой урок, включив их. )

Что важнее в порядке операций?

Со временем математики согласовали набор правил, называемый порядком операций , чтобы определить, какую операцию выполнять первой. Когда выражение включает только четыре основные операции, действуют следующие правила:

1. Умножение и деление слева направо.
2. Сложение и вычитание слева направо.

При упрощении выражения, такого как \(12 \div 4 + 5 \times 3 — 6\), сначала вычислите \(12 \div 4\), так как порядок операций требует сначала вычислить любое умножение и деление (в зависимости от того, что произойдет сначала) слева направо перед оценкой сложения или вычитания. В данном случае это означает, что сначала нужно вычислить \(12 \div 4\), а затем \(5 \times 3\). Как только все умножение и деление завершены, продолжайте складывать или вычитать (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.

\(12 \дел 4 + 5 \умножить на 3 — 6\)
\(3 + 5 \умножить на 3 — 6\)	Потому что \(12 \дел 4 = 3 \)
\(3 + 15 — 6\)	Потому что \(5 \х3 = 15\)
\(18 — 6\)	Потому что \(3 + 15 = 18\)
\(12\)	Потому что \(18 — 6 = 12\)

Рассмотрим в качестве примера другое выражение:

\(6 + 4 \умножить на 7 — 3\)
\(6 + 28 — 3\)	Потому что \(4 \times 7 = 28\), что делается первым, потому что умножение и деление вычисляются первыми.
\(34 — 3\)	Потому что \(6 + 28 = 34\)
\(31\)	Потому что \(34 — 3 = 31\)

Иногда мы могли бы захотеть убедиться, что сложение или вычитание выполняется в первую очередь. Символы группировки , такие как круглые скобки \(( )\), скобок \([ ]\) или скобок \(\{ \}\) позволяют нам определить порядок выполнения конкретных операций.

Порядок операций требует, чтобы операции внутри группирующих символов выполнялись до операций вне их. Например, предположим, что были скобки вокруг выражения 6 + 4:

\ ((6 + 4) \ Times 7 — 3 \)
\ (10 ​​\ Times 7 — 3 \)	Потому что \(6 + 4 = 10\), что делается первым, потому что оно заключено в круглые скобки.
\(70 — 3\)	Потому что \(10 \times 7 = 70\), и скобок больше нет.
\(67\)	Потому что \(70 — 3 = 67\)

Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим в скобки \(7 — 3\)?

\(6 + 4 \times (7 — 3)\)
\(6 + 4 \times 4\)	На этот раз \(7 — 3\) в скобках, поэтому мы делаем это в первую очередь.
\(6 + 16\)	Поскольку \(4 \times 4 = 16\), и когда не осталось скобок, мы продолжаем умножение перед сложением.
\(22\)	Потому что \(6 + 16 = 22\)

Этот набор скобок дает еще один ответ. Итак, когда задействованы круглые скобки, порядок операций следующий:

1. Выполнять операции в круглых скобках или группировать символы.
2. Умножение и деление слева направо.
3. Сложение и вычитание слева направо.

Знакомство с концепцией: порядок операций

Прежде чем ваши учащиеся будут использовать скобки в математике, они должны четко понимать порядок операций без скобок. Начните с повторения правил сложения и умножения в порядке выполнения операций, а затем покажите учащимся, как круглые скобки могут повлиять на этот порядок.

Материалы: Белая доска или способ писать для класса публично

Необходимые навыки и концепции: Учащиеся должны уметь оценивать и обсуждать выражения сложения, вычитания, умножения и деления.

• Спросить : Какую операцию выполнить первой в выражении \(5 \times 7 + 3\) ? Почему?

  Запишите выражение публично. Если студенты не согласны, попросите их объяснить, не говоря им, правы они или нет. При необходимости напомните им, что по порядку операций умножение и деление предшествуют сложению и вычитанию.

• Спросите : Каково значение этого выражения?

  Попросите учащихся оценить выражение. \(5 \times 7 = 35\), поэтому выражение становится \(35 + 3\), что равно \(38\).

• Спросите : Что произойдет, если я поменяю местами символы сложения и умножения? Какое значение я получу?

  Перепишите выражение как \(5 + 7 \times 3\) и выполните вычисление. \(7 \times 3 = 21\), поэтому выражение становится \(5 + 21\), что равно \(26\).

• Спросите : Получили ли мы другие значения при изменении операций?

  Этот результат, вероятно, не удивит ваших учеников. Скорее всего, они знают, что выполнение разных операций над одними и теми же числами даст разные значения. Если позволяет время и учащиеся готовы, предложите им найти выражение, в котором перестановка символов сложения и умножения, как вы сделали, дает одно и то же значение. Если кто-то из учащихся преуспеет, попросите их показать, как они получили выражения. Обратите внимание, что это возможно только тогда, когда среднее число равно 1 (например, \(5 \times 1 + 3\) или \(5 + 1 \times 3\)) или внешние числа равны (например, \(3 \times 7). + 3\) или \(3 + 7 \умножить на 3\)).

• Спросите : Что делать, если я хочу сохранить символы умножения и сложения в одном месте (\(5 \times 7 + 3\)) , но выполнить \(7 + 3\) сначала ? Как вы думаете, как я мог это сделать?

  Кратко обсудите вопрос, затем напишите на доске \(5 \times (7 + 3)\). Обратите внимание на скобки.

• Скажем : Мы называем эти символы скобками. Если в выражении есть скобки, сначала сделайте то, что внутри скобок.
• Спросите : Что находится в скобках в выражении \(5 \times (7 + 3)\) ?

  Убедитесь, что учащиеся правильно понимают, что число \(7 + 3\) находится внутри скобок и что оно должно оцениваться перед вычислением с помощью \(5\).

• Скажем : Теперь давайте закончим вычисление значения. (Значение равно \(5 \times 10\) или \(50\).) Это то же самое значение, которое мы получили раньше?

  Помогите учащимся заметить, что значение не совпадает ни с исходным выражением, ни с выражением с переключенными символами операций.

Сейчас самое время обсудить математическую практику с учетом точности . В математике очень важно, чтобы мы преднамеренно писали математические выражения и делали математические утверждения. Небольшие перепутывания с математическими правилами операций или скобками могут привести к радикальным изменениям! Представьте себе неправильное вычисление выражения, например, при расчете дозировки или стоимости лекарства.

Дайте учащимся еще несколько примеров, показывающих выражение со скобками и без них. Попросите студентов-добровольцев оценить выражения и сравнить их значения. Когда учащиеся приходят к разным значениям, не говорите им, правы они или нет. Вместо этого предложите им найти сходства и различия в своих стратегиях и направьте обсуждение так, чтобы учащиеся увидели, какая стратегия соответствует правилам порядка действий.

Разработка концепции: Порядок действий

Материалы: Электронная доска или способ публичного письма в классе

Предварительные навыки и понятия: Учащиеся должны быть знакомы с порядком действий и чувствовать себя готовыми применять его на практике.

Продолжая знакомить учащихся со скобками, убедитесь, что они не не всегда изменяют значение выражения, хотя часто изменяют.

• Спросите : Какую операцию я выполняю первой в выражении \(3 + 5 \times 8\) и почему?

  Запишите выражение публично. Убедитесь, что учащиеся ясно понимают, что порядок операций требует, чтобы они выполняли умножение перед сложением.

• Спросите : Что произойдет, если я хочу добавить 3 и 5, прежде чем я умножу на 8?

  Позвольте учащимся обсудить идеи о том, как изменить порядок операций. Не говорите ученикам, что они правы, а что нет. Вместо этого поощряйте математический дискурс и сравнивайте разные мнения, чтобы исправить неправильные представления. Обратите внимание, что вариантов ответов может быть много! Например, в задаче может быть явно указано «сначала добавьте 3 и 5», или исторически существовали другие способы группировки, такие как использование горизонтальных черт над выражением. Если они не упоминают скобки, напомните им, что вы делали на первом уроке.

• Скажем : Заключив скобки вокруг \(3 + 5\) , мы говорим, что мы должны сначала сложить 3 и 5, а затем умножить на 8. Сегодня мы собираемся попрактиковаться в нахождении значения выражений с и без скобок и посмотрите, какое значение имеют скобки.
• Напишите следующие три выражения публично, чтобы все учащиеся могли их увидеть.
  • \(3 + 6 \умножить на 2\)
  • \((3 + 6) \умножить на 2\)
  • \(3 + (6 \умножить на 2)\)
• Произнесите : Вычислите все три выражения.

  Дайте учащимся время закончить вычисления. Затем пусть студенты-добровольцы сообщат о том, что они нашли.

• Спросите : Вы получили одинаковое значение для всех трех выражений? Почему или почему нет?

  Учащиеся должны заметить, что выражения 1 и 3 дают одно и то же значение, а выражение 2 отличается. Обсудите, что выражение 2 требует сложения перед умножением, а выражения 1 и 3 требуют умножения перед сложением. Цель состоит в том, чтобы учащиеся увидели, что использование скобок иногда меняет значение выражения, а иногда нет.

• Напишите следующие два выражения публично, чтобы все учащиеся могли их увидеть.
  • \((8 \дел 4) — 2\)
  • \(8 \дел (4 — 2)\)
• Произнесите: Вычислите оба выражения.

  Дайте учащимся время закончить вычисления. Затем пусть студенты-добровольцы сообщат о том, что они нашли.

• Спросите : Значения этих выражений одинаковы? Почему или почему нет?

  Еще раз учащиеся должны увидеть значение использования скобок.

• Скажите: Теперь мы попробуем задание со многими возможными решениями. Ваша цель — найти выражение, в котором можно перемещать скобки без изменения значения. Проблема заключается в том, что скобки должны быть около сложения или вычитания .

  Пройдите пример. Покажите, как в двух приведенных ниже выражениях скобки окружают выражение сложения, и когда они перемещаются, значение выражения остается прежним: 7.

  • \((3 + 4) \умножить на 1\)
  • \(3 + (4 \умножить на 1)\)
• Если это возможно, пусть учащиеся поработают в парах, чтобы создать дополнительные примеры. Учащимся, которые застряли, попросите их заменить 3 и/или 4 в приведенных выше выражениях.
• Спросите : Как вы создавали выражения, которые позволяли вам «двигать» скобки? С какими проблемами вы столкнулись?

  Организуйте обсуждение различных выражений, сделанных учащимися. Предложите учащимся сравнить сходства и различия как в выражениях, которые они сделали, так и в стратегиях, которые они использовали для их выражения.

Подведение итогов и подсказки для оценивания

Важно, чтобы учащиеся могли запомнить правила порядка действий как со скобками, так и без них. Избегайте давать рабочие листы механического обучения. Вместо этого ищите математические задачи, которые естественным образом приводят к выражениям, которые необходимо вычислить, например, подстановка значений в формулу, и попросите учащихся попрактиковаться в порядке выполнения операций в контексте других задач.

***

Хотите повысить уверенность учащихся в математике, помимо практики математических правил порядка операций? Исследуйте HMH Into Math , наше базовое математическое решение K–8.

Математика 3-5 классы 6-8 классы Занятия и уроки

Дополнительная литература

• Фасонный стержень

  20 июня 2023 г.

• Ричард Бланкман
  Фасонный Редактор

  Бренда Ясеволи
  Shaped Ответственный редактор

  15 июня 2023 г.

  No related posts.