Памятка по выполнению работы над ошибками по русскому языку. | Методическая разработка по русскому языку (6 класс) по теме:
Памятка по выполнению
работы над ошибками по русскому языку.
Страшна не сама по себе ошибка, а не проработанная ошибка!
Необходимо проработать, по возможности, все свои ошибки. У кого ошибок очень-очень много, проработайте хотя бы 10 основных ошибок. Самое главное — чтобы ошибки эти больше не повторялись в ваших работах!
В работе над ошибками главное слово – работа.
Итак, цель работы над ошибками — так проработать ошибки, чтобы они не повторялись в дальнейшем. Как проработать?
Работа состоит из трех частей:
- Объяснение допущенных орфографических ошибок.
- Работу над ошибками начинай всегда со списывания по целой строчке слова, в которых ты допустил исправления: буква на букве, грязь, или где ты описался (вместо одной буквы случайно написал другую). Подчёркивай то место, где у тебя исправления.

- Далее идёт работа над ошибками, которые нашел учитель.
Сначала определи, на какую орфограмму твоя ошибка.
Внимание! Место, где была допущена ошибка, необходимо выделять (подчёркивать).
Слово, в котором допущена ошибка Напиши слово верно. | Правило, объясняющее написание | Три примера (чем больше, тем лучше) на это правило |
Не_выучил | НЕ с глаголами пишется отдельно. | Не_знать Не_ был Не_ читают |
объяснил | Разделительный твёрдый знак (ъ) пишется только после приставок, которые оканчиваются на согласную, перед гласными: е, ё, я, ю. | Съезд Объём Подъехать |
у нас | Предлоги с местоимениями пишутся отдельно. | ко мне с тобой к нему |
вьюга | Разделительный мягкий знак (ь) пишется в корне слова после согласных перед гласными буквами: е, ё, ю, я, и. | Деревья Обезьяна Воробьи |
2. Объяснение допущенных пунктуационных ошибок.
1. Указать причину, по которой необходимо поставить знак препинания (например: обособленное определение, однородные члены предложения, сложное предложение, вводное слово…)
2. Выписать предложение, графически объясняя постановку знака препинания, составить схему, подобрать из учебника или из художественной литературы 3 предложения на это правило и записать, объясняя пунктограмму.
ОБРАЗЕЦ:
- Знаки препинания при однородных членах
Сильный ветер сорвал листья с деревьев, разметал их по дороге. О, О
Нужно было продавать мебель, лошадей, дачу. (А. Чехов)
Земля, воздух, месяц, звёзды скованы вместе, склёпаны морозом. (А. Пушкин)
У набережной теснятся пароходы, шхуны, баржи. (А. Серафимович)
- Обособленное определение, выраженное причастным оборотом.
Программа, │написанная в спешке│, выполнила недопустимую операцию.
Матушка,│ знавшая наизусть все его свычаи и обычаи│, всегда старалась засунуть несчастную книгу как можно подалее.(А.С.Пушкин)
Я видел только верхушки лозняка, │теснившегося на этом берегу│. (А.П.Чехов)
С утра до утра шел мелкий дождик, │превращавший глинистые дороги и тропинки в сплошную густую грязь│. (А.И.Куприн)
3. Работа над грамматическими ошибками.
Грамматическая ошибка — это неcоблюдение норм слово- и формообразования, норм синтаксической связи между словами в словосочетании и предложении.
Прочитай предложение, в котором допущена ошибка, выясни смысл каждого слова. Записать без ошибок всё предложение.
Перечень наиболее распространённых грамматических ошибок
№
| Вид ошибки
| Примеры
|
1
| Ошибочное словообразование | Трудолюбимый, надсмехаться |
2
| Ошибочное образование формы существительного | Многие чуда техники, не хватает время |
3
| Ошибочное образование формы прилагательного | Более интереснее, красившее |
4
| Ошибочное образование формы числительного | С пятистами рублями |
5
| Ошибочное образование формы местоимения | Ихнего пафоса, ихи дети |
6
| Ошибочное образование формы глагола | Они ездиют, хочут, пиша о жизни природы |
7
| Нарушения согласования | Я знаком с группой ребят, серьёзно увлекающимися джазом |
8
| Нарушения управления | Нужно сделать свою природу более красивую Повествует читателей |
9
| Нарушение связи между подлежащим и сказуемым | Большинство возражали против такой оценки его творчества |
10
| Нарушение способа выражения сказуемого в отдельных конструкциях | Он написал книгу, которая эпопея |
11
| Ошибки в построении предложения с однородными членами | Страна любила и гордилась поэтом В сочинении я хотел показать значение спорта и почему я его люблю |
12
| Ошибки в построении предложения с деепричастным оборотом | Читая текст, возникает такое чувство… |
13
| Ошибки в построении предложения с причастным оборотом | Узкая дорожка была покрыта проваливающимися снегом под ногами |
14
| Ошибки в построении сложного предложения | Эта книга научила меня ценить и уважать друзей, которую я прочитал ещё в детстве Человеку показалось то, что это… |
15
| Смешение прямой и косвенной речи | Автор сказал, что я не согласен с мнением рецензента |
16
| Нарушение границ предложения | Когда герой опомнился. |
Для более глубокого анализа ошибок напиши отчет
«Почему я сделал ошибки?»
Примерный план
1. Количество ошибок. Правила, на которые были допущены ошибки. Степень трудности диктанта.
2 Причины, послужившие плохому (хорошему ) результату:
А. Не усвоил новый материал.
Б. Забыл пройденное (приведи примеры на забытое правило).
В. Допустил ошибку в словарном слове,
Г. Обстановка в классе во время диктанта.
Д. Твоё собственное самочувствие на уроке и поведение (не мог сосредоточиться, мешал соседу или он тебе, волновался и т.д.).
Оценка собственных знаний, выводы.
План-конспект урока в 6 классе «Работа над ошибками»
Урок русского языка в 6 классе
Тема: Работа над ошибками
Тип урока: урок-игра.
Цели урока:
1. Образовательные:
мобилизовать учащихся на преодоление пробелов в знаниях, которые обнаружились при проверке контрольного сочинения;
убедить детей в том, что работа над ошибками – это один из путей формирования грамотного письма;
повторить орфографические правила: а) правописание безударных гласных в корне слова; б) правописание приставок при-, пре-; в) правописание проверяемых согласных в корне слова; г) правописание имен собственных с большой буквы;
формировать навыки работы над речевыми ошибками;
формировать пунктуационный навык: обосновывать постановку знака или его отсутствие.
2. Развивающие:
— развивать способности самоконтроля;
— продолжить развитие у учащихся умения высказываться на грамматическую тему;
— развивать творческие способности учащихся.
3. Воспитательные:
— воспитание чувства дружбы;
— воспитание трудолюбия, самостоятельности, способности к самоорганизации.
Задачи:
— систематизировать изученное;
— развивать орфографическую грамотность;
— закрепить умение применять при письме правила постановки запятой между однородными членами предложения, в сложном предложении.
Планируемые результаты:
Личностные УУД: формировать умение самооценки степени самостоятельности учащихся в оценивании качества своей учебной работы.
Метапредметные результаты:
Познавательные УУД: высказывать свои предположения, делать выводы в результате совместной работы класса и учителя.
Коммуникативные УУД: уметь оформлять свои мысли в устной и письменной речи, слушать и понимать речь других; участвовать в обсуждении учебной проблемы, учиться работать в парах.
Регулятивные УУД: выбирать действия в соответствии с поставленной задачей и условиями её реализации, адекватно воспринимать оценку учителя.
Предметные результаты УУД: уметь анализировать и исправлять ошибки (речевые, орфографические, пунктуационные).
Оборудование
1. Компьютер
2. Проектор
3. Карточки-задания
Ход урока
1. Орг. момент.
— Здравствуйте, ребята. Садитесь. Начинаем урок русского языка.
Послушайте диалог.
— Опять ты делаешь ошибки?
Когда ты их исправишь, Рыбкин?
— А как без них я обойдусь?
Ведь на ошибках я учусь.
— О чем идет речь в этом диалоге? (Какое слово повторялось в диалоге?)
Часто в жизни мы слышим такие слова: «На ошибках учатся».
Подумайте, что они означают.
Совершая в жизни ошибки, люди стараются их исправить и извлечь из этого урок, чтобы в дальнейшем не совершать этих ошибок.
II. Сообщение темы и целей урока.
— Ребята, сформулируйте, пожалуйста, тему нашего урока.
— Для чего нужна работа над ошибками? Каковы цели сегодняшнего урока?
— Эта работа необходима, так как она способствует развитию грамотности, помогает закрепить изученный ранее материал. Мы повторим орфографические и пунктуационные правила.
1. Сообщение о результатах письменной работы.
На прошлом уроке русского языка мы писали сочинение-рассуждение. В целом класс хорошо справился с этой работой. Мне понравились работы следующих учащихся………………….., ……………….. Посмотрите на экран, вот результаты вашей работы.
Отметки | «5» | «4» | «3» | «2» | Количество учащихся |
Содержание | |||||
Грамотность |
— Сегодня у нас необычный урок. Это урок-игра. А теперь настроимся на продуктивную работу, сосредоточим свое внимание.
Это урок-игра. А теперь настроимся на продуктивную работу, сосредоточим свое внимание.
2. Вопросы-шутки!
— Из какого крана нельзя напиться воды? (из водопроводного, подъемного)
— Из какого ключа не зачерпнешь воды? (из замочного, родникового)
Прокомментируйте увиденные орфограммы в ответах
III. Работа над ошибками.
1. Орфографическая разминка.
1.ПРИ- Пр..ступник, пр..пятствие, пр..косновение, пр..одоление.
2.ПРЕ- Пр..града, пр..рода, пр..чина, пр..мер
2. Самопроверка.
Ответ ученика:
прикосновение (приставка обозначает присоединение)
преграда (близкое к значению приставки пере-)
3. Игра «Найди опасное место».
— Покажите сигнал рукой, если в слове услышите «опасное место».
Ужинать, белье, корова, купался, Витя, мощный, на коне, полет, лужайка, сказки.
(Дети комментируют возможные ошибки)
Игра «Исправь ошибки» (на карточках)
А) Прочитайте стихотворение.
Как вы думаете, почему автора так удивило письмо мальчика?
Пришло письмишко мне,
Гляжу: из лагеря, от мишки.
«Здесь чудный лук, и я лижу, —
Написано в письмишке.
Лук лижет? Что за чудеса?
Наверно, шутит плут…
Читаю дальше: «Здесь лиса,
Красивый длинный прут.
На днях в лесу нашёл я грусть
И очень был доволен»,
Нет-нет, не шутит он! Боюсь,
Мой друг серьёзно болен.
Вернётся – надо подлечить:
Заставить правила учить. (А.Шибаев)
Проверка: Сколько орфограмм нашли в письме? (7)
Б) Найдите в тексте слова, подходящие к этой схеме
-Запишите эти слова. Разберите по составу. Какой частью речи они являются?
(длинный, красивый; прилагательные)
6.Работа по таблице.
— Теперь сделаем работу над ошибками по таблице.
пишу правильно | объясняю | подтверждаю примерами |
Мишки | ||
луг | ||
лежит | ||
лежу | ||
леса | ||
пруд | ||
груздь |
Проверка
пишу правильно | объясняю | подтверждаю примерами |
Мишки | Имя собственное пишу с большой буквы | Витька |
лежит | Безударный гласный в корне слова, проверяемый ударением | лечь |
лежу | ||
леса | лес | |
пруд | Проверяемые согласные в корне слова | пруды |
груздь | грузди | |
луг | луга |
ФИЗКУЛЬТМИНУТКА
7. Найдите и исправьте речевую ошибку. (записать в тетради)
Найдите и исправьте речевую ошибку. (записать в тетради)
Врач прописал больному хорошим лекарством.
Пожарные быстро потушили горящего дома.
Чтобы грамотного человеком стать, надо правила и орфограммы знать.
8. Кто прав?
Петя написал: ПОШЕВЕЛЬНУТСЯ
Саша написал: ПОШЕВЕЛЬНУЦА
Вова написал: ПОШЕВЕЛЬНУТЬСЯ (дети комментируют)
9. Работа над пунктуационными ошибками. (записать предложения, объяснить знаки)
Вынули из сумки хлеб, масло, яйца.
Когда девочки уже закончили обед, недалеко от них запел соловей.
IV. Домашнее задание: сост. орф. практикум «Безударные гласные в корне» (20 слов)
V. Итог урока. Рефлексия.
Итог урока. Рефлексия.
— Ребята, вы сегодня успешно поработали на уроке.
— Какие орфограммы мы повторили сегодня на уроке?
— Какое задание было для вас самым интересным?
— Над какими ошибками работали на уроке? (орфогр., пункт., речевыми)
— С какой целью работали над речевыми ошибками?
Я хочу вам пожелать дальнейших успехов в изучении русского языка и ,чтобы вы не боялись учиться на ошибках.
Карточки с заданиями по анализу математических ошибок для 6-го класса от Линдси Перро Пакет дополнительных занятий по математике
⭐️⭐️⭐️ Этот ОГРОМНЫЙ НАБОР включает в себя полный Дополнительные занятия в 6 классе! Этот комплект включает в себя большинство дополнительных ресурсов в моем магазине, которые соответствуют стандартам математики 6-го класса. ⭐️⭐️⭐️ Включены дополнительные заметки, задания, оценки, сложенные и перевернутые заметки, рабочие листы и т. д.❤️
165
Продукция
400,00 $Цена 400,00 $647,19Первоначальная цена 647,19$Сэкономьте 247,19$
View Bundle
Как выглядит полный год учебной программы и дополнительных мероприятий? Что включено? 165 дней редактируемых учебных материалов (руководство по темпу, заметки, сложенные и перевернутые заметки, рабочие листы, разминки, оценки и распечатки) и более 110 дополнительных занятий. Будущие занятия в 6 классе
Будущие занятия в 6 классе
172
Продукция
450,00 $ Цена 450,00 $ 830,87 $ Исходная цена 830,87 $ Экономия 380,87 $
View Bundle
Отзывы
41
Вопросы и ответы
3
Еще от Линдси ПерроАнализ ошибок часто отсутствует во многих математических классах. Этот ресурс поможет вашим учащимся выявлять и исправлять ошибки, связанные с большинством математических стандартов для 6-го класса.
Об этом ресурсе:
Каждый навык включает от 6 до 20 карточек заданий в двух разных форматах. Традиционные карточки с заданиями в виде карточек и длинные карточки с заданиями по две на странице, где учащиеся могут объяснить и исправить ошибку (ошибки) и показать свою работу.
Включенные навыки: (те, которые связаны, были обновлены)
- Абсолютное значение
- Площадь и периметр
- Сравнить и упорядочить рациональные числа
- Координатные плоскости
- Отображение данных
- Десятичные операции
- Распределительное свойство
- Экспоненты (целое число)
- Дробные операции
- GCF и LCM
- Сети и площадь поверхности
- Одношаговые уравнения
- Положительные и отрицательные числа
- Отношения
- Том
Доступен в следующем комплекте:
- Мегапакет для 6-го класса по математике
Условия лицензирования:
Приобретая этот продукт, вы получаете лицензию на одного преподавателя только для личного использования в собственном классе. Лицензии не подлежат передаче и поэтому не могут передаваться от одного преподавателя к другому. Если учитель, купивший эту лицензию, покидает класс или меняет школу, лицензия и материалы остаются у этого учителя. Никакая часть этого ресурса не может быть передана коллегам или использована всей командой, на уровне класса, в школе или округе без приобретения надлежащего количества лицензий. Если вы являетесь тренером, директором или школьным округом, заинтересованным в передаваемых лицензий , которые будут учитывать ежегодные кадровые изменения, свяжитесь со мной, чтобы узнать стоимость передаваемых лицензий, по адресу [email protected].
Лицензии не подлежат передаче и поэтому не могут передаваться от одного преподавателя к другому. Если учитель, купивший эту лицензию, покидает класс или меняет школу, лицензия и материалы остаются у этого учителя. Никакая часть этого ресурса не может быть передана коллегам или использована всей командой, на уровне класса, в школе или округе без приобретения надлежащего количества лицензий. Если вы являетесь тренером, директором или школьным округом, заинтересованным в передаваемых лицензий , которые будут учитывать ежегодные кадровые изменения, свяжитесь со мной, чтобы узнать стоимость передаваемых лицензий, по адресу [email protected].
Информация об авторских правах:
© Lindsay Perro. Обратите внимание: все материалы, включенные в этот ресурс, принадлежат Lindsay Perro Inc. Покупая, вы получаете лицензию на использование материала, но не являетесь его владельцем. Вы не можете загружать какую-либо часть этого ресурса в Интернет в любом формате, включая школьные/личные веб-сайты или сетевые диски, если только сайт не защищен паролем и к нему могут получить доступ только учащиеся, а не другие учителя или кто-либо еще в Интернете.
✮✮Если вы заинтересованы в получении доступа к эксклюзивному набору бесплатных ресурсов, НАЖМИТЕ ЗДЕСЬ.
Вопросы и ответы
6 класс – математические ошибки
КатегорииСоотношения и отношения пропорциональности
Уважаемые математические ошибки,
Эта студенческая работа [ниже] озадачила нас. Как вы относитесь к тому, что происходит в первой части?
С уважением,
Сбит с толку Бен-Гурионом
***
Для наших читателей, не говорящих на иврите, вот мой перевод задач:
Три брата получил наследство.
А) Старший брат получил 72 600 шекелей, что составляло 33% наследства. Какова была общая сумма наследства?
Б) Второй брат получил 37% наследства. Сколько он получил?
В) Какой процент наследства получил третий брат? Сколько наследства получил третий брат?
***
Дорогой Сбитый с толку,
Увлекательная штука!
Судя по вторым двум задачам, у этого студента есть надежная процедура нахождения заданного процента от исходной суммы.
Но что делать, если исходная сумма неизвестна? Этого требует первая проблема, поскольку полное наследование неизвестно. Один из способов, которым может подойти к этому особо искушенный студент-алгебраист, — это решить следующее уравнение: (33 x ?)/100 = 72 600.
Мне кажется, что этот студент очень старается приблизиться к чему-то подобному этому изощренному подходу. Они смотрят на (20 x 5000)/100 и пытаются понять, как инвертировать процедуру, чтобы найти исходную сумму. Ни одна из попыток не приводит к чему-то точному или работоспособному, но вы можете увидеть попытку найти смысл в инвертировании формулы.
В этой первой попытке — я предполагаю, что это первая попытка — студент пытается поместить наследство брата в нижнюю часть дроби, а проценты двух других братьев — в верхнюю часть дроби. Опять же, здесь нет ничего по-настоящему осмысленного, но вы видите три попытки обращения — 67 вместо 33, умножение на 100 вместо деления на 100 и помещение наследования в конец дроби.
Во второй попытке учащийся пытается масштабировать 72600 на (100 + 33), чтобы раскрыть первоначальное полное наследство. Я рассматриваю это как попытку масштабирования 72600, что в целом неплохая идея, но это все еще является частью более крупной попытки инвертировать процедуру «вперед».
(Мне также кажется возможным, что этот студент пытался решить (33 x ?)/100 = 72600 для «?» и каким-то образом смешал 33 и 100, но тогда я не знал бы, откуда взялось 67. )
Что со всем этим делать? Все, что действительно важно для студента, — это то, что он может узнать дальше, и разработка — это всегда сложная, зависящая от контекста часть изучения студенческой работы. Однако, основываясь только на этом знании, я бы сказал, что они могут быть готовы научиться решать (33 x ?)/100 = 72 600 для «?». Есть и другие менее алгебраические способы сделать это, но мне кажется, что этот студент может быть готов к алгебраическому подходу.
Сначала я подумал, что ученик сделал следующее:
- Сначала учащийся нарисовал шесть кругов, чтобы обозначить «из 6 книг».

- Затем они раздали по одной 66 книг в каждый из 6 кругов. (Если в каждую положить по 11, зачем их считать?)
- Затем учащийся искал способ представить «5 из», которые являются научно-популярными.
- Из этого следует, что остальные книги — художественная литература. Получается шесть шестерок или 36 книг.
Но затем Бриджит и Джули пришли с фантастической, другой интерпретацией. Это похоже на улучшение моего первого наброска.
вы не думаете, что они видели 5 отдельно от 6? Как и в 5 — художественная литература, а 6 — научно-популярная…
— Бриджит Данбар (@BridgetDunbar) 17 июня 2016 г.
Согласен. «На каждые 6 f приходится 5 non=f». При личной встрече я бы спросил: «Как вы думаете, каких больше, не-f или f?»
— Джули Райт (@julierwright) 17 июня 2016 г.
Затем мы приступили к работе, пытаясь придумать некоторые действия для выполнения этой работы. Предположим, что шестиклассники вашего класса решают эту задачу, и у многих из них возникают проблемы, похожие на описанную выше работу. Вы планируете завтрашний урок. С какого занятия вы бы начали урок?
Предположим, что шестиклассники вашего класса решают эту задачу, и у многих из них возникают проблемы, похожие на описанную выше работу. Вы планируете завтрашний урок. С какого занятия вы бы начали урок?
Вот что мы придумали. Какое из этих занятий, по вашему мнению, было бы наиболее полезным? Есть ли какие-то изменения, которые вы бы внесли в любой из них? Есть ли комбинация и последовательность этих действий, которые, по вашему мнению, будут особенно эффективными? (Я попытался упорядочить их ниже. Некоторые подробности о структурах деятельности здесь.) Категории
Отрицательные числа Система счисления
Я знаю, я знаю, о чем ты думаешь. Я даже знаю, что ты собираешься сказать. «Ой! Этих детей просто учат алгоритмам, которым они слепо следуют, не рассуждая. Они даже иногда не могут вспомнить алгоритм! Этот бедный ребенок неправильно помнит алгоритм. Он думает, что должен вычесть меньшее число из большего. Бу, процедурное мышление».
Или, может быть, вы видите это и думаете: «Этот ребенок даже не думает.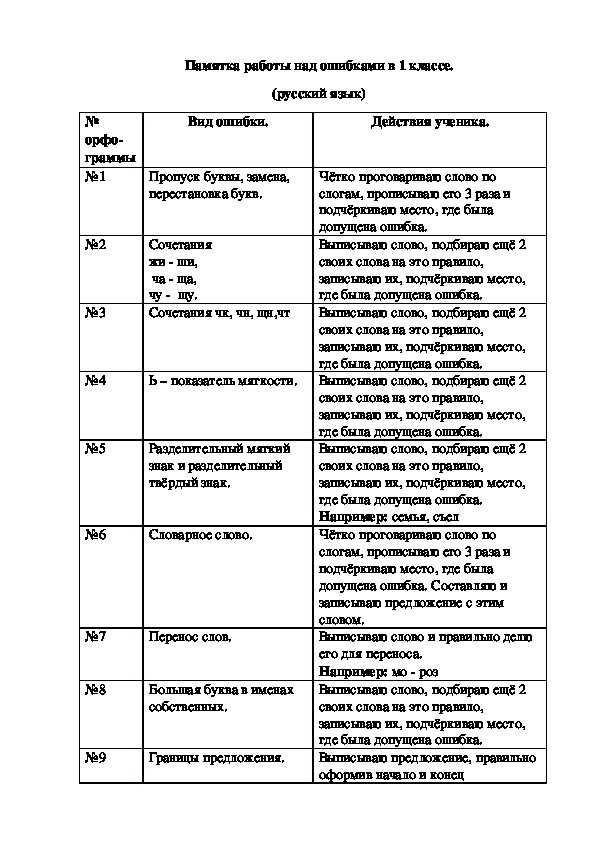
Третий вариант: «Этот ребенок выучил неверное правило. Этот ребенок думает , что вы должны , , вычесть меньшее число из большего.
Каждое из этих объяснений, я думаю, немного ошибочно.
- Первая и третья теории делают прогнозы относительно того, что студент «считает правильным». Что это может означать, как не то, что ученик, когда его спросят, скажет, что он сделал правильно? Но я думаю, что студенты, если им будет предложено поразмышлять над этой работой, быстро найдут ошибку.
- Вторая теория предсказывает, что учащийся при подсказке не мог понять, как правильно вычитать любые двузначные числа. Я готов поставить деньги, чтобы этот ребенок, которому представили 54–32, мог объяснить, как это сделать, с таким же пониманием, как и любой другой ребенок.
Нам нужны некоторые формулировки и различия, чтобы правильно описать, что здесь происходит.
- Малыш не думал медленно, обдуманно, явно.
 Он не находился под влиянием процедуры или концепции.
Он не находился под влиянием процедуры или концепции. - Он просто занимался математикой, не думая о математике, которую он делал. Он плыл по течению, делая то, что, казалось, должно было быть сделано.
Это ставит нас в противоречие со всеми тремя вышеприведенными теориями:
- У ребенка не было явного алгоритма, которому он пытался следовать. Он не находился под его влиянием.
- Ученик не просто оперировал числами вслепую и случайным образом. Он не угадал. Он был 90 157, делая математику, не думая о математике.
- У ребенка не было ошибочного представления о вычитании. Он не находился под влиянием какой-либо конкретной концепции. Он просто делал то, что нужно было делать.
Здесь была ошибка? Или заблуждение? Или ложное убеждение в плохой процедуре? Как именно мы должны описать это?
- Объективно говоря, это ошибка . Слово «ошибка» не относится к мышлению человека, а довольно объективно относится к результату его мышления.
 Объективно говоря, это была ошибка. Малыш сказал что-то не то.
Объективно говоря, это была ошибка. Малыш сказал что-то не то. - Но здесь нет доказательств неправильного представления . Неправильное представление связано с концепциями, а этот ребенок не находился под руководством каких-либо ошибочных концепций. Он понимает, что такое вычитание. Он понимает, что такое стоимость места. Он мог бы рассказать о них.
- Это не ложное убеждение , потому что здесь нет доказательств того, что этот ребенок считает, что то, что он сделал, правильно.
- Это не глупая ошибка , что-то, что происходит случайно и без раздумий.
Вместо этого, может быть, нам следует назвать это умственной предвзятостью или склонностью к подобного рода ошибкам. Эта проблема выявил скрытую предвзятость в склонности этого ребенка вычитать меньшее число из большего числа. Обнаружилось своего рода магнетическое побуждение отнять меньшее число от большего, чем большее от меньшего.
Что нам делать с такими тенденциями? Я думаю, что требуется определенная практика, но я не уверен. Мысли об этом? На чем-нибудь из этого?
Десятичные числа сложны!
«Ребенок должен был понять, что ее ответ должен быть меньше».
Как вы помогаете детям следить за собой таким образом? Следите ли вы таким образом за собой, когда занимаетесь математикой?
(Спасибо, Рут, за представление!)
КатегорииВыражения и уравнения Решение линейных уравнений
На прошлой неделе я опубликовал короткое видео с репетиторства, которое провел с ребенком. Мы решали уравнения, и у него было несколько интересных идей, и было приятно, что эти идеи и его умственная деятельность стали явными.
Вот еще один фрагмент этого видео:
Комментируйте что хотите, но вот несколько подсказок:
- Помогите мне понять его мысли.
 Как он разработал тест на правильность своего решения?
Как он разработал тест на правильность своего решения? - Что это говорит о том, что он думает о 2/0?
Или напишите в комментариях, что вам нравится.
Это вопросы типа «Всегда, иногда, никогда». Типа: «Всегда, иногда или никогда верно, что ромб является параллелограммом».
Как быстрее всего помочь этим ученикам?
(Спасибо за заявку, Тина С!)
КатегорииРаспределительная собственность Система счисления
Вот куча ответов на один и тот же вопрос:
Если это ваш класс (и это Весна!) то как вы ответите?
Загляните в архив и посмотрите другие наши экспонентные ошибки. Что ты заметил?
Спасибо Джули за представление!
Вопрос: Оцените выражение когда , $latex y = -2$ и $latex z = -2$.
Эти сообщения поступили от Джули, которая написала об этом в своем блоге:
Что случилось? Во-первых, я НЕНАВИЖУ PEMDAS И ВСЕХ, КТО ЕЕ ИСПОЛЬЗУЕТ.


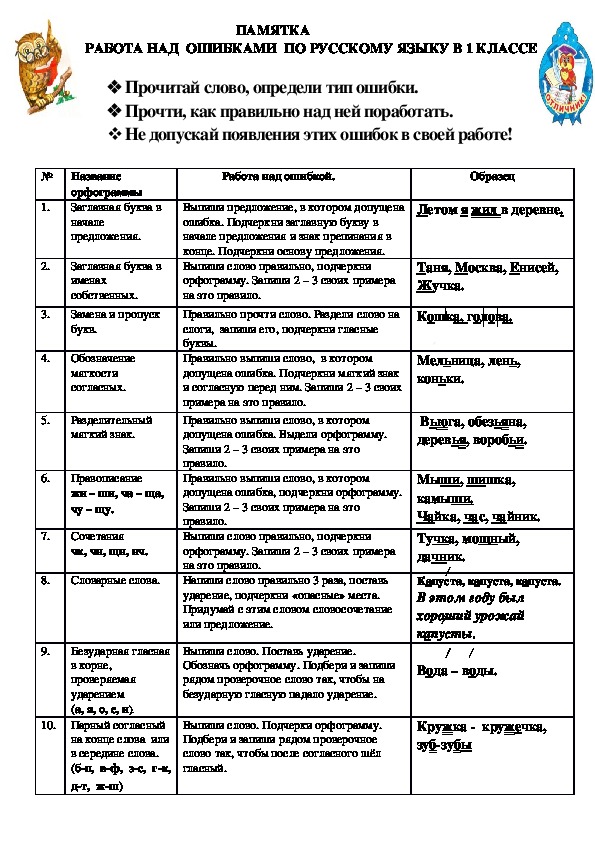 Было уже поздно.
Было уже поздно.
 Он не находился под влиянием процедуры или концепции.
Он не находился под влиянием процедуры или концепции. Объективно говоря, это была ошибка. Малыш сказал что-то не то.
Объективно говоря, это была ошибка. Малыш сказал что-то не то. Как он разработал тест на правильность своего решения?
Как он разработал тест на правильность своего решения?