Ускользающая доброта: что значит быть циклоидом
В психологии, чтобы обозначить совокупность ярко очерченных свойств, присущих определенному типу характера, используется термин под названием «акцентуация». Это только перечень черт, которые указывают на характер человека, не являются болезнью и не выходят за рамки клинической нормы, но они указывают на уязвимость к определенной психологической нагрузке. В данной статье мы более подробно рассмотрим понятие циклоидной акцентуации.
Преимущества и недостатки циклоида
Циклоидный тип личности страдает от резких перепадов настроения и работоспособности, которые не дают ему нормально вести традиционный образ жизни. Такая личность живет все время как на качелях, при этом скачки могут быть совершенно разными – от незначительных перепадов настроения между «в порядке» и «не очень» до полноценных прыжков между радостью и беспросветной грустью. При этом данный человек продолжает нормально взаимодействовать с людьми как отличный деловой партнер, внимательный друг или нежный возлюбленный. Он неконфликтен (кроме моментов глубокого падения), его поведение добродушное и естественное, спокойно воспринимает разные обстоятельства, которые у других вызывают негатив. Темперамент циклоида отличается мягкостью и теплотой, он с юмором и озорной.
Он неконфликтен (кроме моментов глубокого падения), его поведение добродушное и естественное, спокойно воспринимает разные обстоятельства, которые у других вызывают негатив. Темперамент циклоида отличается мягкостью и теплотой, он с юмором и озорной.
Преимущества циклоида в том, что это человек адаптивный и гибкий, часто имеет выраженную эмпатию. Циклоиду легко настроиться на любую волну, поскольку он имеет лабильный эмоциональный диапазон. Он остро ощущает печали и радости жизни. Это позволяет развить творческие навыки и превратить особенности характера в карьеру журналиста, художника. В то же время скачки настроения, в частности во взрослые годы, чувствуются не так остро. Циклоид чаще назовет это градиентом — от небольшой грусти до вселенской тоски или от легкой улыбки до безграничной радости. Таким людям знакомы различные оттенки чувств, удовольствия. Они знают об этом много и могут поделиться знаниями с остальными, давая шанс своему слушателю с другим характером начать радоваться каждому дню.
Что делать циклоиду?
Основная рекомендация для циклоида: помните, что перепады вашего настроения возникают сами по себе и пропадают точно так же. Негативные ощущения просто проходят, и основная задача в том, чтобы перед очередным взлетом не наломать дров, поссорившись с окружающими, уволившись или бросив писать книгу.
Более серьезной опасностью для циклоида является то, что во время неблагоприятных обстоятельств такой характер может трансформироваться в биполярное расстройство, или появится другая психопатия. Отслеживать перепады настроения особенно стоит тем, у кого в семье были случаи психических болезней.
Как себя вести с циклоидом?
Личность с циклоидной акцентуацией прекрасно переносит разнообразные неприятные моменты в межличностных взаимоотношениях, но даже такие люди имеют свою ахиллесову пяту. Они не переносят монотонных занятий на работе или же рутины в отношениях. В погоне за разнообразием и приключениями они порой способны совершать небольшие настоящие безумства, но они будут рады, если их близкий человек захочет принять участие в этой затее.
Если настроение циклоида в негативной фазе, то его самооценку можно легко травмировать, поскольку в это время он зачастую себя недооценивает. Он не верит в себя, у него мало сил, он забрасывает начатое, бросает прошлые цели. Именно поэтому во время фазы падения циклоиду нужно помочь стать последовательным и поддержать его, чтобы он не потерял своих достижений.
Курс Викиум «Эмоциональный интеллект» учит управлять своими эмоциями, что как раз необходимо человеку с подобным типом личности.
циклоидный тип, шизоидный характер: VIKENT.RU
Эрнст Кречмер публикует книгу: Строение тела и характер / Körperbau und Charakter
Главная идея книги: по внешнему виду человека можно многое сказать о его душевной жизни и ряде психических заболеваний. Э. Кречмер предлагал заменить бессистемный рассказ о больном в его медицинской карте системой замеров частей тела, описаниями формы лица и черепа, строения тела, характеристиками волос, кожи и желёз.
«Эта книга переведена на множество языков и выдержала множество изданий. Парадоксально, что, хотя её основная идея не нашла признания, «Строение тела и характер» и сегодня занимает почётное место в библиотеке каждого психиатра. Причина успеха книги заключается в том, что никому — ни до Кречмер а, ни после, — не удалось так точно, тонко и ярко описать особенности основных типов человеческого характера. […]
Итак, человеческие характеры. Циклоидный тип проще, поэтому лучше начать с него. Кречмер пишет, что люди с циклоидным характером общительны и откровенны; они добродушны, понимают шутки и принимают жизнь такой, какая она есть. С ними легко иметь дело, их реакции естественны и понятны. Они чутко улавливают настроение собеседника и ведут себя в соответствии с ним; такое поведение даётся им легко, оно получается само собой, никакого усилия для этого не требуется. В циклоидном характере присутствуют мягкость и теплота, даже в плохом настроении циклоиды остаются общительными и охотно делятся своими тревогами и огорчениями с друзьями, которых у них обычно много.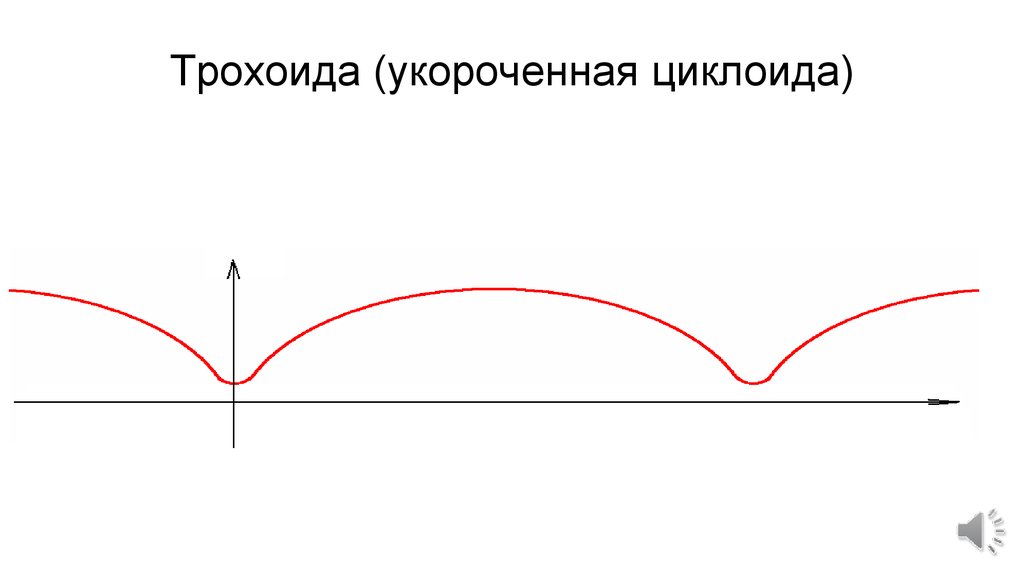 Хорошеё настроение циклоидов характеризуется мягкой весёлостью, богатым юмором, продуктивной энергией.
Хорошеё настроение циклоидов характеризуется мягкой весёлостью, богатым юмором, продуктивной энергией.
Людей, обладающих циклоидным характером, часто называют «солнечной натурой». Некоторым из них свойственны самопроизвольно возникающие периоды некоторого эмоционального спада или подъёма, но, как правило, их настроение тесно связано с событиями, которые происходят вокруг них. Они реагируют на такие события быстро, естественно и адекватно. Кречмер приводит три группы признаков, которые свойственны циклоидному характеру: 1) общительность, добросердечие и душевность; 2) весёлость, остроумие и живость; 3) спокойствие, впечатлительность и мягкость.
Шизоидный характер гораздо сложнеё. Ему свойствен фундаментальный признак — аутизм, о котором стоит поговорить подробнеё. Термин принадлежит Блейлеру, и содержание его гораздо глубже, чем то, которое обычно в него вкладывают (таким упрощением грешат иногда даже профессионалы). Аутизм — это не просто замкнутость; это, по словам Кречмер а, «жизнь в самом себе». По внешнему виду шизоидного человека, по его поведению и манере общаться трудно судить, что он чувствует, каково его настроение, как он относится к тому, что происходит вокруг него. Болеё того: внешние события могут играть для душевного состояния шизоида очень малую роль.
По внешнему виду шизоидного человека, по его поведению и манере общаться трудно судить, что он чувствует, каково его настроение, как он относится к тому, что происходит вокруг него. Болеё того: внешние события могут играть для душевного состояния шизоида очень малую роль.
Гораздо важнеё те спонтанные внутренние процессы, которые в нём происходят. Поэтому для окружающих эмоциональные реакции шизоида могут выглядеть не очень понятными, иногда парадоксальными. Это сильно затрудняет общение с таким человеком, да и сам он не склонен к тому, чтобы окружать себя приятелями. Его общение избирательно, он трудно сходится с новыми людьми, по-настоящему близких друзей у него мало, иногда всего один или два. Если при общении с циклоидом его внутренняя жизнь очевидна, то судить о её содержании у шизоида очень трудно.
Лучше Кречмер а не скажешь, поэтому процитируем его ещё раз. «Мы не можем по фасаду судить, что скрывается за ним, — пишет он. — Многие шизоидные люди подобны римским домам и виллам с их простыми и гладкими фасадами, с окнами, закрытыми от яркого солнца ставнями, но в сумраке их внутренних покоев справляются пиры». «Молодой человек бесцельно проводит годы своей жизни, — продолжает Кречмер . — Он так вял и неуклюж, что хочется растолкать его. Он падает, когда садится на лошадь. Он смущенно, несколько иронически улыбается. Ничего не говорит. В один прекрасный день появляется томик его стихотворений с нежнейшим настроением; каждый толчок, полученный от проходящего неуклюжего мальчишки, перерабатывается во внутреннюю трагедию; ритм строго выдержан и отличается стилем. Таковы шизоидные люди», — заканчивает Кречмер .
«Молодой человек бесцельно проводит годы своей жизни, — продолжает Кречмер . — Он так вял и неуклюж, что хочется растолкать его. Он падает, когда садится на лошадь. Он смущенно, несколько иронически улыбается. Ничего не говорит. В один прекрасный день появляется томик его стихотворений с нежнейшим настроением; каждый толчок, полученный от проходящего неуклюжего мальчишки, перерабатывается во внутреннюю трагедию; ритм строго выдержан и отличается стилем. Таковы шизоидные люди», — заканчивает Кречмер .
Неочевидность внутреннего мира шизоида; отсутствие непосредственности, явной связи его эмоциональных реакций с происходящим вокруг; связанные с этим трудности в общении, — основные особенности этого характерологического типа».
Ротштейн В.Г., Психиатрия. Наука или искусство?, Фрязино, «Век 2», 2004 г., с.39-41.
Марин Мерсенн | Французский математик
- Год рождения:
- 8 сентября 1588 г. Франция
- Умер:
- 1 сентября 1648 г.
 (59 лет)
Париж
Франция
(59 лет)
Париж
Франция
- Известные работы:
- «Истина наук»
- Предметы изучения:
- число Мерсенна Мерсенн премьер основной вибрация маятник
См. весь связанный контент →
Марин Мерсенн (род. 8 сентября 1588 г., недалеко от Уазе, штат Мэн, Франция — умер 1 сентября 1648 г., Париж), французский теолог, естествоиспытатель и математик. Хотя математики лучше всего помнят его поиски формулы для получения простых чисел на основе того, что сейчас известно как «числа Мерсенна», его более широкое значение проистекает из его роли корреспондента, публикующего и распространяющего работы некоторых из его величайших мыслителей. возраст.
Мерсенн получил образование в иезуитском колледже Ла-Флеш вскоре после его основания в 1604 году. Он покинул Ла-Флеш около 1609 года, чтобы изучать теологию в Париже в Сорбонне и Коллеж де Франс. В 1611 году он вступил в строгий римско-католический Орден Минимов, проведя послушничество в Нижоне и Мо. С 1614 по 1618 год он преподавал философию и богословие в Невере. Проживал в Париже, за исключением частых поездок за границу, с 1619 г. до своей смерти в 1648 г.
С 1614 по 1618 год он преподавал философию и богословие в Невере. Проживал в Париже, за исключением частых поездок за границу, с 1619 г. до своей смерти в 1648 г.
Британника Викторина
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Самые ранние публикации Мерсенна, такие как Quaestiones celeberrime in Genesim (1623; «Частые вопросы о Бытии») и La vérité des sciences (1625; «Истина науки»), защищали ортодоксальное богословие, проводя различие между конечной природой , или сущность вещей (познаваемая только Богом) и случайные факты, наблюдаемые человеком. Однако он не соглашался со взглядами скептицистов на то, что мир совершенно непознаваем. Он утверждал, что знание должно свободно развиваться посредством экспериментов и наблюдений, часто упрекая ученых за то, что они не включают точные экспериментальные данные в свои статьи, настаивая при этом на том, что гипотезы в лучшем случае являются вероятными объяснениями.
В 1635 году Мерсенн основал неофициальную частную Академию Парижа (предшественницу Французской академии наук), где многие ведущие математики и естествоиспытатели Франции делились своими исследованиями. Он использовал этот форум для распространения идей Рене Декарта, переехавшего в Нидерланды в 1629 году. «Возражения», добавленные к 9 декартовским0041 Meditationes (1641; «Медитации»). Другие светила, с которыми Мерсенн переписывался, распространял идеи и выступал посредником в спорах, включают Галилео Галилея, Блеза Паскаля, Христиана Гюйгенса и Пьера де Ферма. В 1630-х годах Мерсенн сыграл особенно важную роль в продвижении работ Галилея. Благодаря двум небольшим книгам и обсуждениям работы Галилея в его переписке Мерсенн распространил идеи Галилея за пределы Италии и значительно облегчил принятие механических объяснений против остатков схоластики.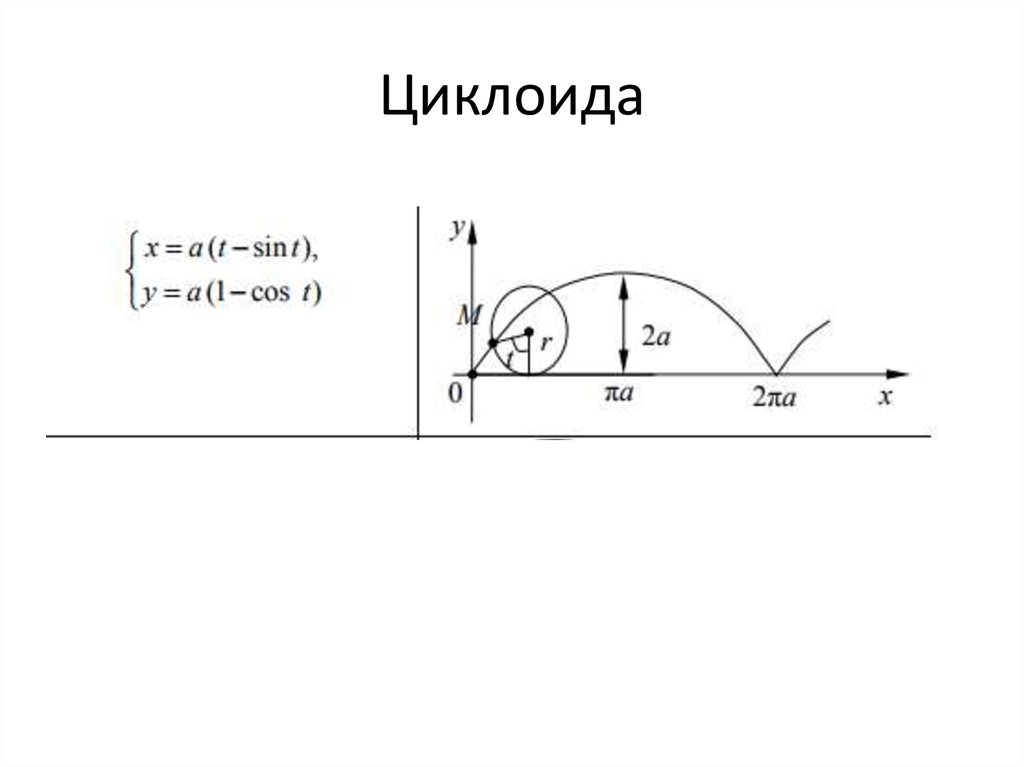
В 1644 году Мерсенн сообщил о некоторых своих исследованиях чисел вида 2 n −1, теперь известных как числа Мерсенна. Он заметил, что если 2 n −1 простое, то n должно быть простым, но обратное не обязательно верно. Хотя ему не удалось найти формулу для простых чисел (не факт, что она вообще существует), числа Мерсенна продолжают интересовать математиков, и его формула по-прежнему полезна при проверке больших чисел, чтобы определить, являются ли они простыми.
Мерсенн совершил несколько длительных поездок в Нидерланды, провинциальную Францию и Италию. Из последней поездки он привез во Францию в 1645 году новости о барометрическом эксперименте Евангелисты Торричелли, который привел к знаменитой работе Паскаля о весе воздуха.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Эта статья была недавно пересмотрена и обновлена Эми Тикканен.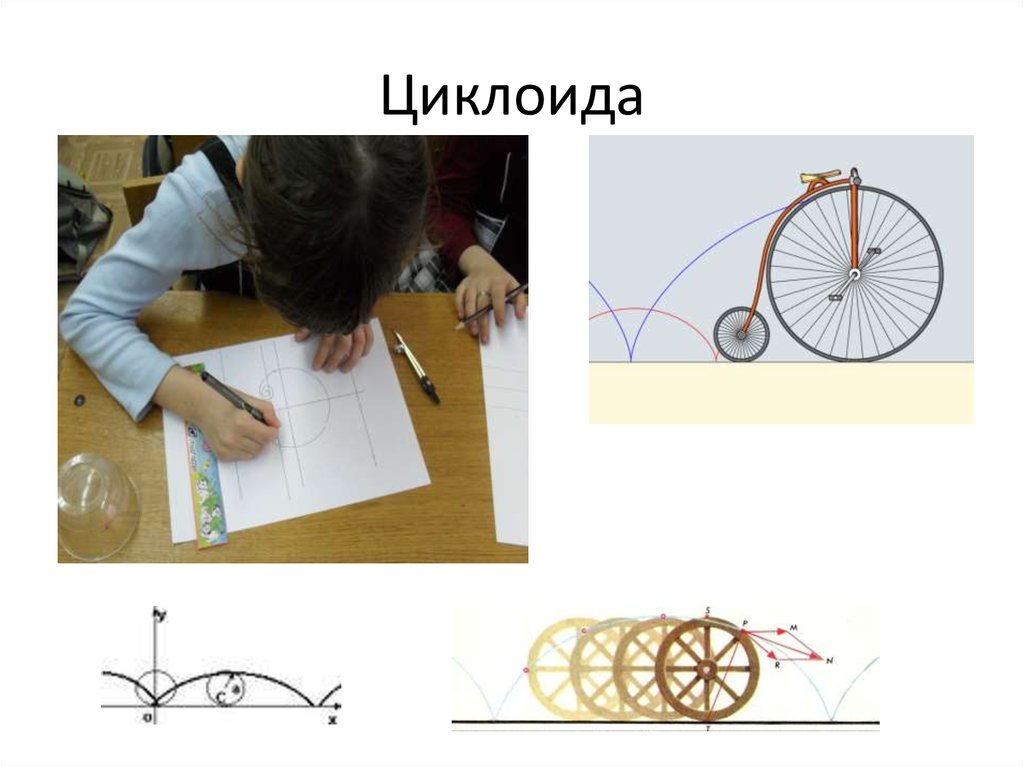
Праздник циклоиды. Недавно я обнаружил новую форму — … | Рай Салливан
Недавно я обнаружил новую форму — циклоиду. Никогда об этом не слышал? Теперь у вас есть шанс учиться вместе со мной и удивляться.
[ПРИМЕЧАНИЕ: этот пост не такой длинный, как кажется. Там много картинок.]
Не так уж часто удается обнаружить новую форму. Я думаю, что большинство из нас полагает, что наши знания о формах уже давно исчерпаны. Мы знаем наши квадраты, круги и треугольники из начальной школы, а позже в старшей школе добавили параболы, эллипсы и синусоиды. Но никто не изучает новую форму в свои 30, верно? Неправильный!
Недавно я обнаружил новую интересную форму: циклоиду. Да, вы правильно прочитали — новая форма. В этом блоге я стремился представить себя (и горстку моих читателей) этой форме. В итоге получилось намного веселее (и зануднее), чем я ожидал. 🧠 🤙
Что такое циклоида?
Согласно Википедии, циклоида определяется как «кривая, описываемая точкой на окружности, когда она катится по прямой без проскальзывания».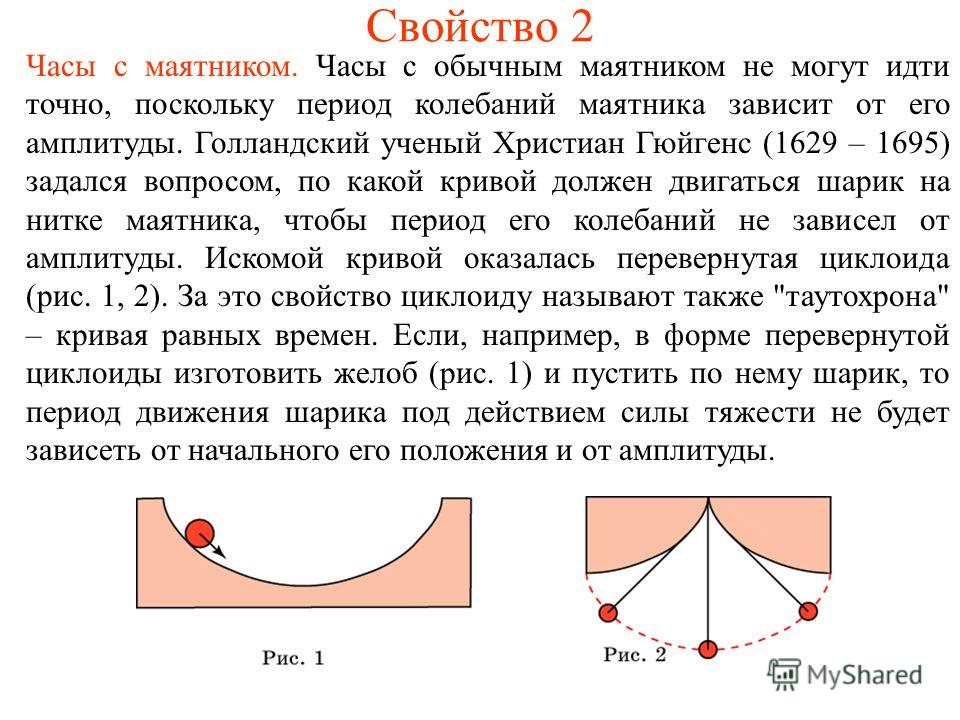 Возможно, это проще представить с помощью следующей анимированной гифки:
Возможно, это проще представить с помощью следующей анимированной гифки:
Циклоида — это красная кривая, описываемая точкой за пределами круга, когда она катится по линии. Вот именно — это циклоида. Просто, верно? Опять неправильно.
История циклоиды
Циклоиду иногда называют «Еленой геометров», потому что за многие годы она вызвала так много споров среди математиков. Один спор вокруг того, кто открыл форму. Самый древний цитируемый кандидат — биограф Пифагора Ямвлих (ок. 245 г. н.э. — ок. 325 г. н.э.). Среди других упоминается множество эрудитов, включая немца Николая Кузанского (1401–1464), француза Шарля де Бовеля (1475–1566), итальянца Галилео Галилея (1564–1642) и француза Марина Мерсенна (1588–1648). Никто точно не знает, кто заслуживает признания.
Ямвлих: греческий философ, икона моды на тоги и (возможно) первооткрыватель циклоиды. Циклоидная известность, по-видимому, не дает вам мраморного бюста. Источник: Википедия.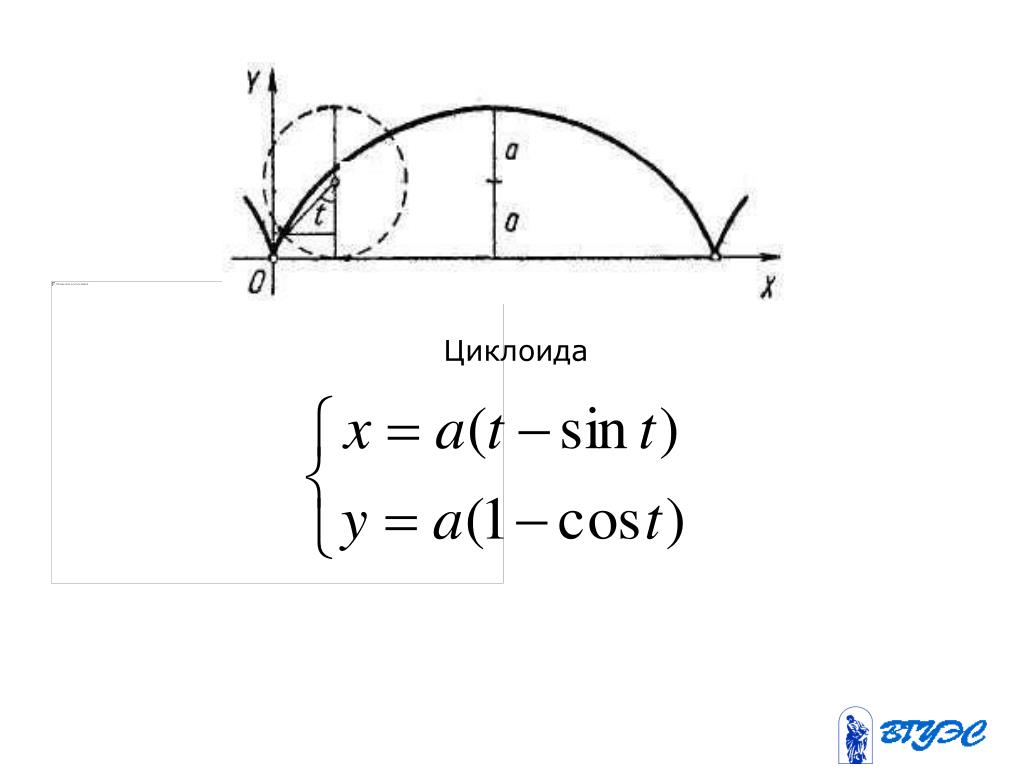
Я предполагаю, что большинство людей, как и я, слышали только о Галилее, который, как оказалось, был первым человеком, серьезно изучившим циклоиды и давшим им свое имя. Он зашел так далеко, что построил модели циклоид из листового металла, пытаясь понять площадь под кривой циклоиды. Вероятно, ему было бы полезно исчисление. Евангелисте Торричелли (1608–1647), изобретшему ртутный барометр, приписывают правильное вычисление площади под одной дугой циклоиды BTW.
Со временем циклоиды привлекли внимание известных математиков, включая Рене Декарта (1596–1650), Пьера де Ферма (1607–1626), Блеза Паскаля (1623–1662), Исаака Ньютона (1642–1726), Готфрида Лейбница. (1646–1716), Гийом де л’Опиталь (1661–1704), Иоганн Бернулли (1667–1748), Леонард Эйлер (1707–1783) и Жозеф Луи Лагранж (1736–1813). Это, безусловно, имена, которые я узнаю.
Видимо, им нравилось создавать конкурсы и задачи, связанные с циклоидами, которые заканчивались драками и обзыванием. Например, Паскаль организовал соревнование по вычислению (1) центра тяжести, (2) площади и (3) объема циклоиды с испанским золотом в качестве приза. Трое судей посчитали, что никто не выиграл, что звучит не очень весело. Кристофер Рен (1632–1723), знаменитый проектировщик собора Святого Павла в Лондоне, представил доказательство для определения длины циклоиды во время конкурса, что на самом деле не входило в число вопросов конкурса, но все же довольно круто. Судьи конкурса утверждали, что он уже решил эту задачу много лет назад, но так и не записал ее. Это привело к публичным дракам. Еще менее весело. (Рен опубликовал свою работу и получил признание FWIW.)
Трое судей посчитали, что никто не выиграл, что звучит не очень весело. Кристофер Рен (1632–1723), знаменитый проектировщик собора Святого Павла в Лондоне, представил доказательство для определения длины циклоиды во время конкурса, что на самом деле не входило в число вопросов конкурса, но все же довольно круто. Судьи конкурса утверждали, что он уже решил эту задачу много лет назад, но так и не записал ее. Это привело к публичным дракам. Еще менее весело. (Рен опубликовал свою работу и получил признание FWIW.)
Еще одна математическая задача была предложена Бернулли в 1696 году и закончилась мелочностью, но об этом мы еще услышим позже.
Знакомство с циклоидами с помощью математики
Теперь, когда мы познакомились с историей циклоидов, вы можете задать себе те же вопросы геометрии, что и наши мертвые друзья-математики Галилей и Рен: какова площадь под циклоидой? Какова длина пути циклоиды? Другими словами, расскажи мне об этой форме, чувак.
У нас (к счастью) есть математика (и YouTube), чтобы помочь нам.
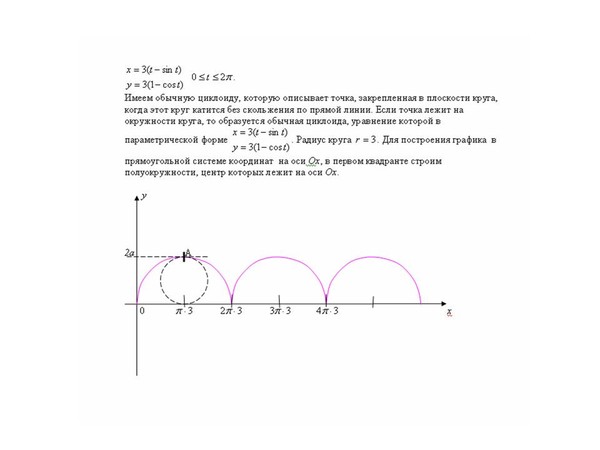
Существуют параметрические уравнения, отображающие путь циклоиды относительно времени (t) по мере того, как круг катится вперед по осям x и y. Я нашел этот вывод YouTube особенно полезным для визуализации его синусоидальной природы. Имеется два уравнения, поскольку положения x и y не зависят друг от друга:
- x(t) = r(t−sin(t))
- y(t) = r(1−cos(t))
Чтобы увидеть эти уравнения в действии, давайте представим, что t = π. В этот момент x(π) = r(π−sin(π)). Поскольку sin(π) = 0, то x(π) = πr. Это половина пути вращения круга, поскольку длина окружности, по которой будет вращаться круг, равна 2πr. Высота будет y(π) = r(1−cos(π)). Поскольку cos(π) = -1, то r(1-(-1))=2 и y(π) = 2r. Это имеет смысл, так как наша точка на окружности будет в самой высокой точке на полпути к рулону, на два полных радиуса выше линии.
Теперь, когда у нас есть уравнения, мы можем использовать вычисления, чтобы найти площадь и длину циклоиды. Да, я поставил перед собой задачу посчитать (не без помощи YouTube и Google). У меня были воспоминания о тригонометрии и исчислении AP с половинными тождествами углов и интегралами. Вот моя работа, со вкусом выполненная маркерами разных цветов:
У меня были воспоминания о тригонометрии и исчислении AP с половинными тождествами углов и интегралами. Вот моя работа, со вкусом выполненная маркерами разных цветов:
Как и в большинстве случаев, связанных с кругами, решения просты. Площадь под циклоидой равна 3πr². Удивительно, но Галилей очень близко подошел к соотношению 3:1 между площадью циклоиды (3πr²) и площадью круга (πr²), используя суперстаромодный метод листового металла, упомянутый ранее. Длина циклоиды всего 8r. Это ответ, который Рен получил ранее. Никаких π или чего-то еще в этом решении.
Честно говоря, это красивые ответы. 😘
Циклоиды в физике
Полезны ли циклоиды помимо их элегантности? Встречаются ли они где-нибудь в природе? Хотя циклоиды не достигают высот некоторых своих геометрических родственников, они все же поражают воображение своим появлением в мире природы.
Вернемся к математическому заданию Бернулли 1696 года. Вот как он поставил свою задачу перед ведущими математиками того времени:
Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам мира.
Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, возможное решение которой принесет славу и останется памятником на века. Следуя примеру Паскаля, Ферма и др., я надеюсь получить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-нибудь сообщит мне решение предложенной задачи, я публично объявлю его достойным похвалы.
Этот человек не боялся говорить о крупной игре — хотя вся фраза «Я публично объявлю его достойным похвалы» кажется менее интересной, чем испанское золото, и более чем сексистской. Затем Бернулли задал свой вопрос:
Если даны две точки А и В на вертикальной плоскости, какую кривую описывает точка, на которую действует только сила тяжести, которая начинается в А и достигает В за кратчайшее время.
Другими словами, если шарик перемещается из более высокой точки в более низкую по кривой (при условии, что точки не находятся непосредственно друг под другом), какой путь должен пройти шарик, чтобы завершить путешествие за кратчайшее время ? Это предполагает, что шарик движется в плоскости без трения с однородным гравитационным полем.
Приз Бернулли в виде «похвалы» еще более забавен, учитывая, что он неправильно нашел правильное решение этой задачи, а затем скопировал правильный вывод у своего брата. Угу.
Бернулли дал шесть месяцев на то, чтобы люди представили решения, но никто этого не сделал. Лейбниц выступал за продление срока представления на полтора года. Именно в этот продолжительный период Исаак Ньютон услышал об этой проблеме. Сообщается, что он нашел вызов в письме Иоганна Бернулли в 16:00. когда он вернулся домой с Королевского монетного двора 29 января, 1697. Он не спал всю ночь и на следующий день анонимно отправил правильное решение. Решение было, по-видимому, настолько хорошим и настолько явно принадлежало Ньютону, что Бернулли определил его как человека, «узнавающего льва по следу его когтя». 🐅
Решение Ньютона за один вечер превзошло две недели, которые понадобились Бернулли для решения задачи. Затем, в манере математического микрофона, Ньютон добавил в свое письмо немного пикантности: «Я не люблю, когда иностранцы ругают меня [пристают] и дразнят меня математическими вещами…» Ньютон никогда не был известен как самый приятный человек.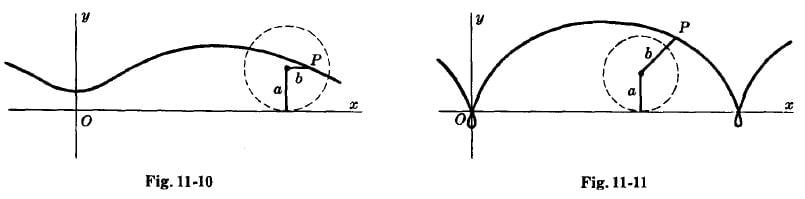 Дикий.
Дикий.
Это самое быстрое решение пути, найденное Ньютоном и Бернулли, называется кривой брахистохроны, что в переводе с греческого означает «кратчайшее время». Как вы могли догадаться по теме этого блога, кривая брахистохроны является частью пути циклоиды. Ниже видео, которое я нашел в Instagram, показывающее эту кривую в действии. Так же я столкнулся с циклоидами:
Кривая брахистохроны в действии. Это всегда самый быстрый путь для объекта, перемещающегося между двумя точками на разной высоте из-за гравитации. Кривая брахистохроны находится посередине на верхнем изображении, а красная кривая — на втором.Это невероятно круто. Всегда интересно видеть силу форм в природе.
Еще одна забавная кривая, которая является частью репертуара циклоиды, — это кривая таутохрона, что в переводе с греческого означает «одно и то же время». Вы можете поместить шарик в любое место на этой кривой, и ему потребуется столько же времени, чтобы скатиться на дно. Он также основан на половине циклоиды. Вот эта кривая в действии:
Он также основан на половине циклоиды. Вот эта кривая в действии:
Есть еще нечто, называемое циклоидальным маятником. Представьте, что вы поместили конец маятника в точку встречи двух перевернутых циклоид. Если вы раскачаете маятник, струна будет изгибаться против циклоид на всем своем пути. Форма конца следов маятника — ЕЩЕ ОДИН ЧЕРТОВЫЙ ЦИКЛОИД. 🤯
Циклоидный маятник между двумя циклоидами, создающий еще одну циклоиду.Есть множество вариаций, которые вы можете сделать с циклоидами с катящимся кругом. Вы можете перекатывать круг вперед, но вместо этого отслеживать точку внутри или снаружи периметра круга, чтобы создать более завитые или плоские кривые. Визуализация каждого представлена на изображении ниже:
Вариации циклоидной кривой из ResearchGate. Вы также можете накатывать круги и фигуры на другие круги и фигуры, чтобы расширить семейство циклоидов, как мы увидим позже.
Наконец, вы можете создать циклоиду в физике прямо сейчас, бросив что-то с любой высоты. Движение объекта к земле будет прямой линией вниз. Поскольку земля (круг) немного вращается на пути вниз, путь, по которому будет двигаться падающий объект, будет очень слегка перевернутой циклоидой (хотя и очень маленькой)!²
Мы, циклоиды в литературе
Циклоиды, должно быть, были в моде, потому что они время от времени появлялись в литературе в предыдущие века. Хотя я не буду документировать все случаи, вот один из классического романа Германа Мелвилла 1851 года «Моби Дик »:
. косвенно поражает тот замечательный факт, что в геометрии все тела, скользящие по циклоиде , например, мой мыльный камень спустится из любой точки в одно и то же время.
Циклоиды в архитектуре
Теперь, когда мы все согласились, что циклоиды невероятно круты, я начал задаваться вопросом, пропускал ли я циклоиды где-либо еще в повседневной жизни.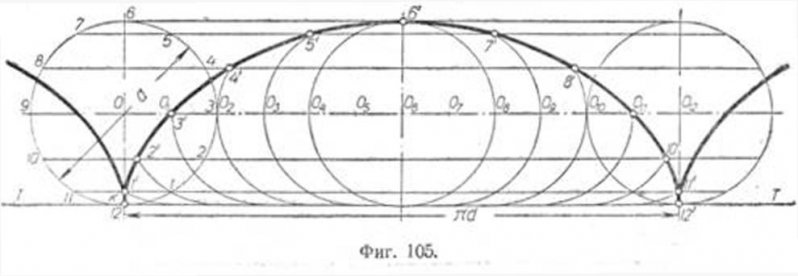
Архитектура полна геометрических форм. Многие из наиболее известных типов арок основаны на кругах (римская арка), эллипсе (полуэллиптическая арка), параболах (параболическая арка) и контактных сетях (цепная арка). Существует множество примеров каждого из них, но я привел несколько наиболее известных из них ниже:
Триумфальная арка в Париже, Франция, представляет собой полукруглую арку, также известную как римская арка. Мост Кью через реку Темзу в Лондоне, Великобритания, представляет собой полуэллиптическую арку. Полуэллиптические арки особенно хороши для создания более широких пролетов арок для таких вещей, как движение лодок и поездов. Мост Биксби-Крик на американском маршруте 1 в Биг-Суре, Калифорния, представляет собой параболическую арку. Фото: Alamy. The Gateway Arch в Сент-Луисе, штат Мичиган, представляет собой цепную арку. Цепные арки являются самыми прочными из всех форм арок, учитывая их равномерное распределение веса. Циклоида очень похожа на арку. Так используются ли циклоидные арки в архитектуре? Согласно моим интернет-исследованиям, они есть, но редко.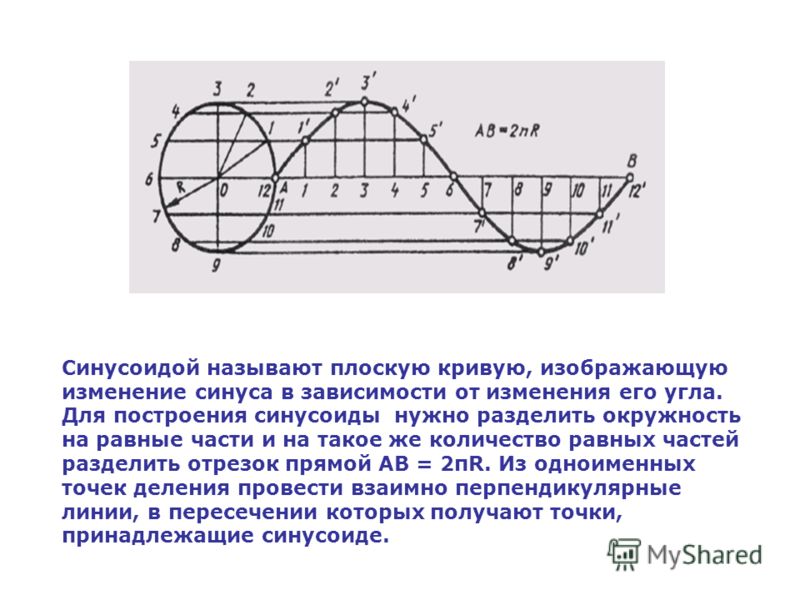 Есть два ярких примера, которые постоянно появляются (в основном из-за их включения в Википедию, посвященную циклоидам).
Есть два ярких примера, которые постоянно появляются (в основном из-за их включения в Википедию, посвященную циклоидам).
Первый — это крыша Художественного музея Кимбелла в Форт-Уэрте, штат Техас. Многочисленные арки этой крыши представляют собой серию циклоидов с небольшим пространством между ними. Это дает успокаивающий вид колеса катящегося. Я копаю это. Отличный выбор для художественного музея.
Циклоидные арки в Художественном музее Кимбелла в Форт-Уэрте, штат Техас.Второй пример циклоидной арки в архитектурном дизайне заставил меня задуматься. На фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, штат Нью-Хэмпшир, есть циклоидные арки. Дартмут — это место, где я учился на бакалавриате, поэтому я буквально видел эту форму каждый день в течение 4 лет. Может поэтому меня так тянет?
Циклоидные арки на фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, Нью-Хэмпшир. Оказывается, в 2016 году наш журнал для выпускников назвал циклоидные арки Хопа одной из 101 причины полюбить Дартмут.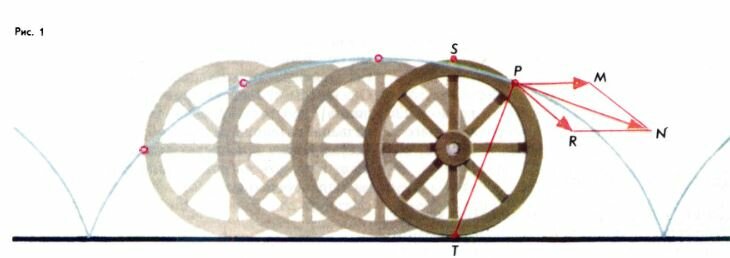 Я не мог удержаться и обратился за дополнительной информацией. Пока ничего существенного в ответ не услышал :
Я не мог удержаться и обратился за дополнительной информацией. Пока ничего существенного в ответ не услышал :
Циклоиды в искусстве и досуге
Вы, наверное, тоже играли с циклоидами в детстве. Игрушка Hasbro Spirograph, которая производится с середины 1960-х годов, основана на модифицированной форме циклоидов, называемых гипоциклоидами. Вместо того, чтобы катить круг по линии, гипоциклоида представляет собой «особую плоскую кривую, образованную следом фиксированной точки на маленьком круге, который катится внутри большего круга».
Игрушка-спирограф. Источник: Википедия.Двумя особыми формами гипоциклоиды являются дельтовидная и астроидная. Вы можете сделать эти формы, ввернув круг внутри другого большого круга с трехкратным и четырехкратным радиусом соответственно:
Дельтовидная (слева) и астроидная (справа) — две особые формы гипоциклоиды. Вероятно, вы уже видели форму астроида. В логотипе футбольной команды Pittsburgh Steelers три астроида разного цвета. Циклоиды продолжают бить меня близко к дому.
Циклоиды продолжают бить меня близко к дому.
Если вы находите эти формы успокаивающими, есть ряд художников, которые создают циклоидные рисунки, подобные показанному ниже, включая в свой дизайн несколько вращающихся кругов разных размеров:
Циклоидная художественная машина, которую я нашел на Pinterest.Циклоидная графика для продажи на Kickstarter.Циклоиды в оптике
Вы также можете катить круги снаружи других кругов и отслеживать их путь, чтобы получить дополнительные производные циклоиды. Одним из частных случаев этой категории является кардиоида. Это форма, созданная путем отслеживания точки на краю круга, катящегося по вне другого круга с таким же радиусом. Путь этой циклоиды имеет ровно один пик, как показано ниже, и напоминает сердце (отсюда и название):
Кардиоида — еще один особый класс циклоид. Кардиоиды постоянно появляются в природе, особенно в каустиках, созданных из двух круглых поверхностей.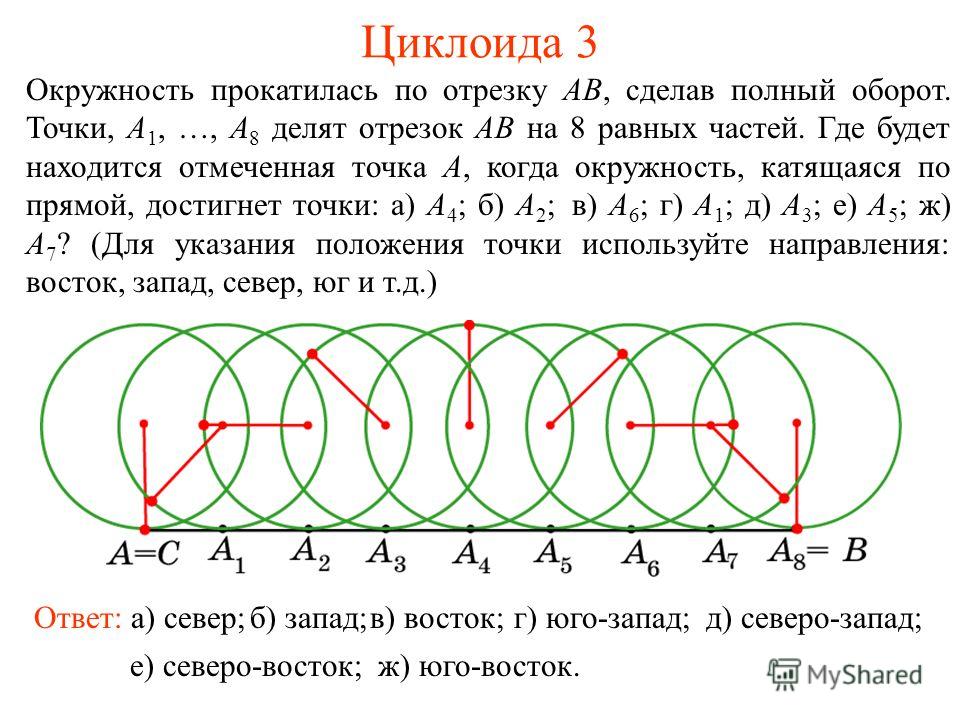 В оптике каустика определяется как «оболочка световых лучей, отраженных или преломленных искривленной поверхностью или объектом, или проекция этой оболочки лучей на другую поверхность. Каустика — это кривая или поверхность, к которой касается каждый световой луч, определяющая границу огибающей лучей как кривую концентрированного света».
В оптике каустика определяется как «оболочка световых лучей, отраженных или преломленных искривленной поверхностью или объектом, или проекция этой оболочки лучей на другую поверхность. Каустика — это кривая или поверхность, к которой касается каждый световой луч, определяющая границу огибающей лучей как кривую концентрированного света».
Мы видим кардиоиды в каустике, созданной множеством круглых объектов, от кофейных чашек до часов.
Кардиоида в каустике кофейной чашки. Кардиоида в каустике часов.Следите за этой формой, когда в следующий раз будете садиться за чашку чая утром! ☕️
Граница центральной области множества Мандельброта (известного фрактальной геометрией и теорией хаоса) также является точной кардиоидой. Я действительно не понимаю, как и почему, но это кардиоида, которая выглядит иначе. Шум. 👍
Центральная область первого периода множества Мандельброта является точной кардиоидой. Циклоидные формы не ограничиваются только кругами. Вы также можете накатывать некруглые формы на другие фигуры и знакомиться с целым рядом новых форм, называемых циклогонами. Например, вот циклогон для качения треугольника и квадрата по прямой:
Например, вот циклогон для качения треугольника и квадрата по прямой:
Циклоиды в космосе
Наблюдение за явлением циклоиды не ограничивается микромасштабом вращающихся колес, часов, чашек и спирографов. Они также видны на планетарном уровне. Поскольку спутник Юпитера Европа (меньший круг) вращается вокруг большой планеты (больший круг), гравитационные силы (линия), действующие на поверхность Луны, имеют циклоидальный характер. Циклоидная форма видна на растрескивающихся ледяных поверхностях Европы на спутниковых снимках. Трещина соответствует орбитальному пути Луны вокруг Юпитера и возникающему в результате гравитационному давлению.
Поверхность спутника Юпитера Европы циклоидальной формы. Источник: Science.org. Образование циклоидальных трещин на Европе.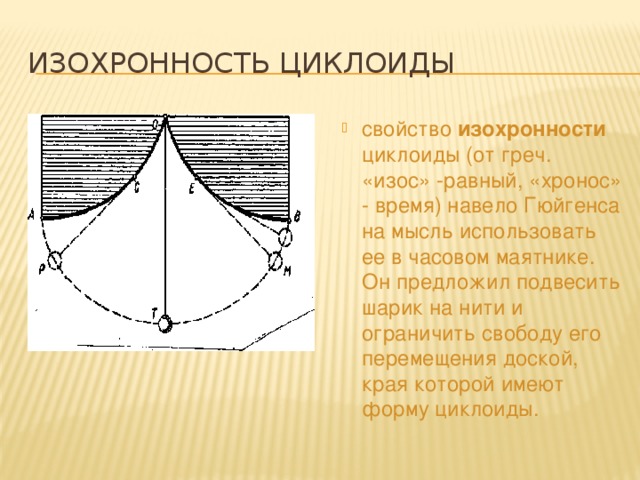
 (59 лет)
Париж
Франция
(59 лет)
Париж
Франция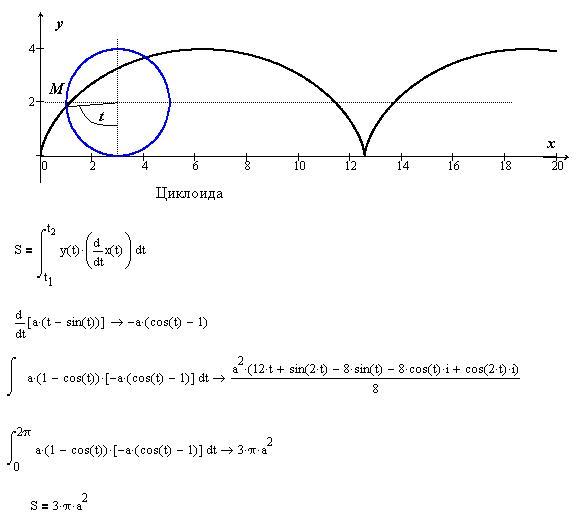 Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, возможное решение которой принесет славу и останется памятником на века. Следуя примеру Паскаля, Ферма и др., я надеюсь получить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-нибудь сообщит мне решение предложенной задачи, я публично объявлю его достойным похвалы.
Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, возможное решение которой принесет славу и останется памятником на века. Следуя примеру Паскаля, Ферма и др., я надеюсь получить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-нибудь сообщит мне решение предложенной задачи, я публично объявлю его достойным похвалы.