Разное

Что такое регрессия в медицине: Регрессия (Regression) | это… Что такое Регрессия (Regression)?

ОпубликованоАвторalexxlab

ищем опухоль при помощи логистической регрессии

У всякого безумия есть своя логика
Уильям Шекспир

Машинное обучение — это подраздел искусственного интеллекта (ИИ) и наук о данных, базирующийся на использовании данных и алгоритмов для имитации процесса наработки опыта человеком с постепенным повышением точности.

С помощью статистических методов алгоритмы обучаются классифицировать данные, строить прогнозы и улучшать процессы сбора и анализа данных. Результаты работы моделей могут влиять на дальнейшее принятие решений, в идеале приводя к оптимальному выбору.

В медицине мы постоянно сталкиваемся с обилием данных: достаточно вспомнить, как выглядит история болезни пациента, особенно не с одной госпитализацией. Также постановка диагноза требует анализа всей имеющейся информации по пациенту, что крайне трудозатратно. Попытки внедрить автоматизацию принятия решений медицинскими специалистами уже происходят, например, в визуализирующих методах диагностики, в обработке гистологических изображений.
Попробуем решить одну из диагностических задач методами искусственного интеллекта.

Собственно набор данных (датасет, dataset), над которым мы будем проводить машинлернинговские операции, размещен в открытом доступе на популярной платформе для соревнований по анализу данных Kaggle.

Это сведения о пациентах со злокачественными и доброкачественными опухолями молочной железы.

Задача: предсказать, какой диагноз имеет пациент. Это задача классификации — отнесения объекта к какой-либо категории.

Для начала разберем, как представить диагноз в виде переменной. Это точно не количественная величина, тогда что?

Как мы уже решили, диагноз — это в какой-то степени категория, к которой мы относим случай. При этом значение точно, без промежуточных вариантов. Можно сравнить с днями недели. Если есть точки на графике, обозначающие события определенного дня, то ни одна из точек не может быть между понедельником и вторником. Если что-то произошло в понедельник, то оно произошло в понедельник, — все просто.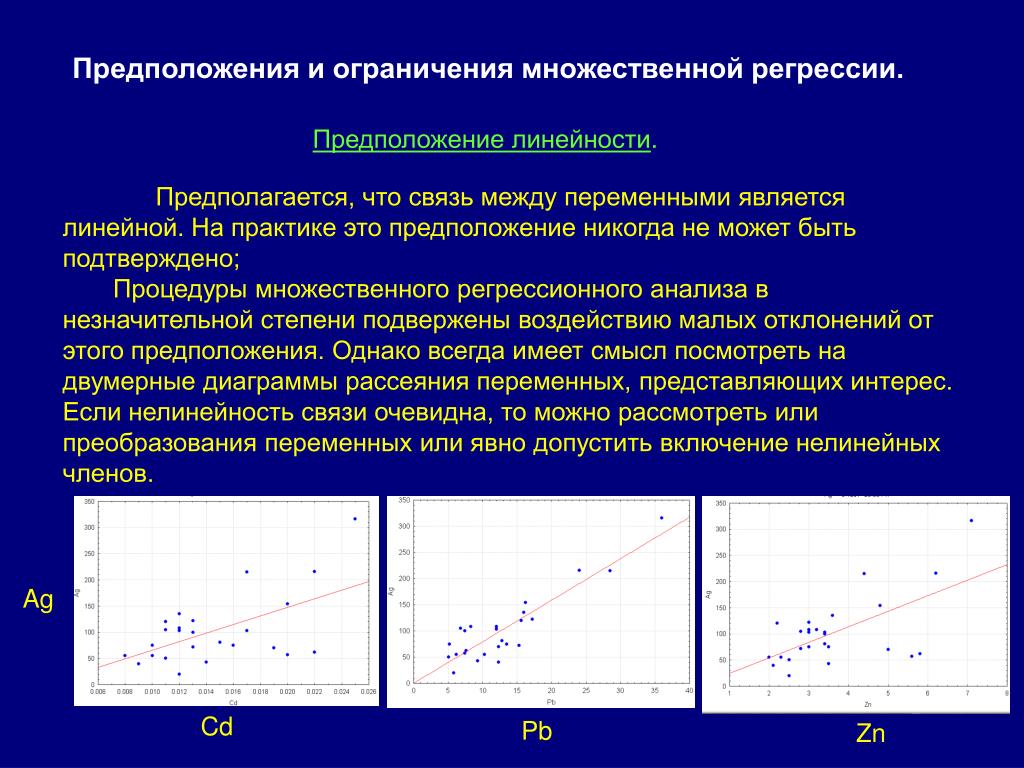 В нашем случае опухоль или доброкачественная, или злокачественная.

В качестве инструмента для работы с категориальными переменными мы будем использовать логистическую регрессию. Эта модель выдает вероятность соответствия той или иной категории.

Немного о самой модели. Логистическая регрессия — один из статистических методов классификации с использованием линейного дискриминанта Фишера. Она входит в топ часто используемых алгоритмов при исследовании данных.

Значением функции является вероятность того, что данное исходное значение принадлежит к определенному классу. Представим, что у нас есть какое-то пространство, в котором в виде точек размещены наши исходные значения. Мы можем поделить это пространство с помощью линейной плоскости на подпространства, в которых будут близкие значения, наиболее вероятно принадлежащие одному классу (типу, категории). Уже упомянутый линейный дискриминант Фишера определяет направления, проекции на которые лучше всего разделят классы. В итоге получаются разделяющие линейные плоскости.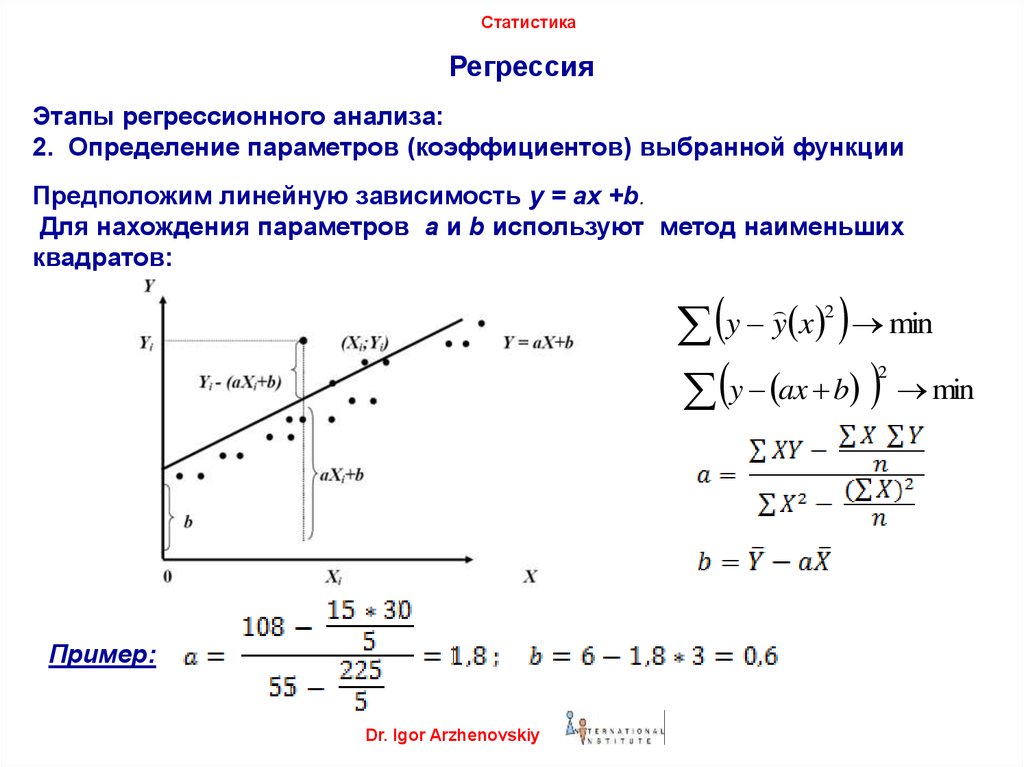
 

Для реализации наших целей будем использовать Google Colab или Jupyter Notebook (не будем погружаться в аспекты его установки, просто воспользуемся версией в браузере, далее выбираем Try Classic Notebook).

Я опишу работу в Google Colab. Блоки кода добавляются с помощью «+Код», запускается код с помощью кнопки со стрелкой слева.

Сначала призовем все необходимые инструменты — готовый код в виде библиотек с уже реализованными за нас функциями, которые мы будем использовать

Загружаем данные по пациентам (скачанные с Kaggle) для работы в ноутбуке. Для этого в поле слева выбираем «Файлы», затем «Загрузить в сессионное хранилище». Последнее означает, что, к сожалению, данные будут храниться лишь во время текущей сессии, то есть после закрытия коллабного ноутбука они исчезнут, как Золушка с бала, и их вновь придется загружать.

С помощью команды .head выведем несколько начальных строк нашей таблички (формат .csv, в котором представлены данные по пациентам, это такой табличный подвид)

Вывод программы («голова» таблички)

Посмотрим, что у нас за данные

Итак, выяснили, какие есть столбцы, сколько в каждом столбце ненулевых значений, а также какого типа данные в каждом из столбцов.  Проверим, есть ли пропуски в значениях.

Нам повезло: нулевых значений ноль. Значит, не нужно как-то заполнять либо наоборот, удалять такие случаи и уменьшать количество пациентов в выборке.

Нам не нужны столбцы «id» и «Unnamed: 32», поскольку они не играют никакой роли в прогнозировании. Удаляем их

Далее нам нужно закодировать значения столбца «диагноз» (который сейчас представлен в виде букв «М» [malignant, злокачественный] и «В» [benign, доброкачественный]) в их числовые представления.

Обозначим входные и выходные данные:

Нашу модель надо сначала обучить, а потом проверить, как она справилась с этой задачей (протестировать). Для этого разобьем данные на тестовые и тренировочные. В качестве инструмента будем использовать модуль train_test_split библиотеки scikit-learn.

Затем необходимо стандартизировать данные. Для «скармливания» модели необходимо, чтобы распределение имело среднее значение 0 и стандартное отклонение 1. Это сделает StandardScaler.

Наконец, призываем непосредственно нашу логистическую регрессию, все из той же библиотеки scikit-learn.

Проверим эффективность нашей логистической регрессии.

Начнем с confusion matrix (матрица ошибок). Матрица представлена в выводе программы в прямоугольных скобках: общие для всей матрицы и внутри отдельные для каждой строки.

Здесь ŷ — это ответ алгоритма на объекте (то, что предсказала модель), y — истинная метка класса на этом объекте (то, как это было указано в нашем изначальном датасете).
Accuracy — это доля правильных ответов алгоритма, получилось (с округлением) 0,977 или 97,7 %.

Формула для расчета accuracy:

где TP — True Positive; TN — True Negative; FP — False Positive; FN — False Negative.

Итак, модель справилась неплохо. Можно ли еще лучше, проверим на других моделях в новых статьях.

Ссылки на ноутбук:

  • https://github.com/KsenyaZ-8/b…

  • https://colab.research.google.com/drive/1h_20UEt-MlNWQLhsaDseqOe8n0L7YPwx?usp=sharing

Логистическая регрессия и ROC-анализ — математический аппарат

Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации.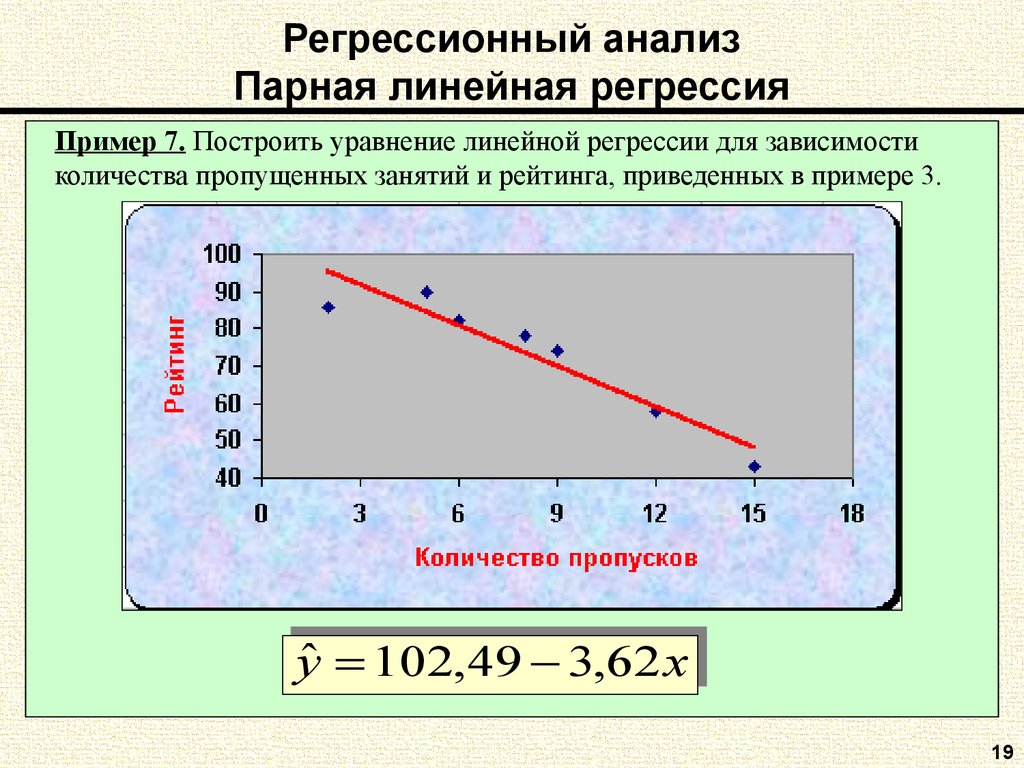 ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.

Введение

Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.

Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.

Логистическая регрессия

Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).

Все регрессионные модели могут быть записаны в виде формулы:

y = F (x_1,\, x_2, \,\dots, \, x_n)

В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:

y = a\,+\,b_1\,x_1\,+\,b_2\,x_2\,+\,\dots\,+\,b_n\,x_n

Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.

Однако здесь возникает проблема: множественная регрессия не «знает», что переменная отклика бинарна по своей природе. {-y}}

где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.

Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):

Рис. 1 — Логистическая кривая

Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:

P’ = \log_e \Bigl(\frac{P}{1-P}\Bigr)

Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии. {-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t

Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).

Рис. 2 — Представление логистической регрессии в виде нейронной сети

Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.

Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.

ROC-анализ

ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.

В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.

В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.

Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.

МодельФактически положительноФактически отрицательно
ПоложительноTPFP
ОтрицательноFNTN

 

  • TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
  • TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
  • FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
  • FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).

Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.

При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:

  • Доля истинно положительных примеров (True Positives Rate): TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
  • Доля ложно положительных примеров (False Positives Rate): FPR = \frac{FP}{TN\,+\,FP}\,\cdot\,100 \,\%

Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.

Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:

S_e = TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%

Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

S_p = \frac{TN}{TN\,+\,FP}\,\cdot\,100 \,\%

Заметим, что FPR=100-Sp

Попытаемся разобраться в этих определениях.

Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:

  • Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
  • Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.

ROC-кривая получается следующим образом:

  • Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.

  • Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.

Канонический алгоритм построения ROC-кривой

Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.

  1. t=min
  2. повторять
  3.      FP=TP=0
  4.      для всех примеров i принадлежит L {
  5.           если f[i]>=t тогда // этот пример находится за порогом
  6.                если i положительный пример тогда
  7.                     { TP=TP+1 }
  8.           иначе // это отрицательный пример
  9.                { FP=FP+1 }
  10.      }
  11.      Se=TP/P*100
  12.      point=FP/N // расчет (100 минус Sp)
  13.      Добавить точку (point, Se) в ROC-кривую
  14.      t=t+d_x
  15.  пока (t>max)

В результате вырисовывается некоторая кривая (рис. 2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.

Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.

При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.

Рис. 4 — Сравнение ROC-кривых

Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).

Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:

AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac{X_{i+1}\,+\,X_i}{2}\Bigr]\,\cdot \,(Y_{i+1}\,-\, Y_i)

Рис. 5 — Площадь под ROC-кривой

С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:

  • показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
  • AUC не содержит никакой информации о чувствительности и специфичности модели.

В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:

Интервал AUCКачество модели
0,9-1,0Отличное
0,8-0,9Очень хорошее
0,7-0,8Хорошее
0,6-0,7Среднее
0,5-0,6Неудовлетворительное

 

Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).

Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:

  1. Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
  2. Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cutt\underline{\,\,\,}off_o = \max_k (Se_k\,+\,Sp_k)
  3. Требование баланса между чувствительностью и специфичностью, т.е. когда Se \approx Sp: Cutt\underline{\,\,\,}off_o = \min_k \,\bigl |Se_k\,-\,Sp_k \bigr |

Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).

Рис. 6 — «Точка баланса» между чувствительностью и специфичностью

Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.

Литература

  1. Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
  2. Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
  3. Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
  4. Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.

 

Другие материалы по теме:

Применение логистической регрессии в медицине и скоринге

Machine learning в Loginom на примере задачи c Kaggle

определение регрессии по Медицинскому словарю

Относящиеся к регрессии: регрессионный анализ, уравнение регрессии, линейная регрессия, корреляция

регрессия

 [ре-грешун]

1. возврат в прежнее или более раннее состояние.

2. стихание симптомов или болезненного процесса.

3. в биологии, тенденция в последующих поколениях к среднему.

4. бессознательный защитный механизм, используемый для разрешения конфликта или фрустрации путем возврата к поведению, которое было эффективным в предыдущие годы. Некоторая степень регрессии часто сопровождает соматическое заболевание. Психически больные могут демонстрировать крайнюю степень регрессии, полностью возвращаясь к инфантильному поведению; это называется атавистическая регрессия. прил., прил. регрессивный.

Энциклопедия и словарь Миллера-Кина по медицине, сестринскому делу и смежным вопросам здравоохранения, седьмое издание. © 2003, Saunders, издательство Elsevier, Inc. Все права защищены.

регрессия

(rē-gresh’n),

1. Затихание симптомов.

2. Рецидив; возвращение симптомов.

3. Любое ретроградное движение или действие.

4. Возврат к более примитивному способу поведения из-за неспособности адекватно функционировать на более взрослом уровне.

5. Бессознательный защитный механизм, с помощью которого происходит возврат к более ранним моделям адаптации.

6. Распределение одной случайной величины при определенных значениях других соответствующих ей переменных (например, формула распределения веса в зависимости от роста и окружности груди). Метод был сформулирован Гальтоном в его исследовании количественной генетики.

[Л. regredior, pp. -gressus, вернуться]

Медицинский словарь Farlex Partner © Farlex 2012

1. Процесс или пример регрессии к менее совершенному или менее развитому состоянию.

2. Психология Возвращение к более ранней или менее зрелой модели чувств или поведения.

3. Медицина Угасание симптомов или процесса болезни.

4. Статистика Метод прогнозирования значения зависимой переменной как функции одной или нескольких независимых переменных при наличии случайной ошибки.

Медицинский словарь American Heritage® Copyright © 2007, 2004, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin. Все права защищены.

регрессия

Любой возврат к исходному состоянию. См. Атавистическая регрессия, Генерализованная аддитивная логистическая регрессия, Гипнотическая возрастная регрессия, Регрессия по методу наименьших квадратов, Линейная регрессия, Регрессия в прошлые жизни, Психорегрессия Medtalk Утихание болезни Sx или возвращение к состоянию здоровья Онкология Отступление СА Психиатрия Частичная, символическая , сознательное или бессознательное желание вернуться-регрессировать в состояние зависимости, как в инфантильном паттерне реагирования или мышления, которое возникает при нормальном сне, игре, физическом заболевании и при различных психических расстройствах.

Краткий словарь современной медицины McGraw-Hill. © 2002 The McGraw-Hill Companies, Inc.

регрессия

(rĕ-gresh’ŭn)

1. Исчезновение симптомов.

2. Рецидив; возвращение симптомов.

3. Любое ретроградное движение или действие.

4. Возврат к более примитивному способу поведения из-за неспособности адекватно функционировать на более взрослом уровне.

5. Склонность потомков исключительных родителей обладать характеристиками, более близкими к характеристикам населения в целом.

6. Бессознательный защитный механизм, с помощью которого происходит возврат к более ранним моделям адаптации.

7. Распределение одной случайной величины при определенных значениях других переменных, относящихся к ней (например, формула распределения веса в зависимости от роста и окружности груди).

[Л. re-gredior, стр. -gressus, вернуться]

Медицинский словарь для медицинских работников и сестринского дела © Farlex 2012

регрессия

1. Психоаналитический термин, означающий возврат к детской или более примитивной форме поведения или мышления, например, от генитальной к оральной стадии.

2. Психологический термин, обозначающий временное возвращение к менее зрелой форме мышления в процессе обучения тому, как справляться с новой сложностью. Когнитивные психологи рассматривают такую ​​регрессию как нормальную часть психического развития.

3. Статистический термин, определяющий отношение двух переменных, при котором изменение одной (независимой переменной) всегда связано с изменением среднего значения другой (зависимой переменной).

Медицинский словарь Коллинза © Robert M. Youngson 2004, 2005

Регрессия

В психологии возврат к более ранним, обычно детским или инфантильным, моделям мышления или поведения.

Упоминается в: Тяжелая утрата, Стокгольмский синдром

Медицинская энциклопедия Гейла. Copyright 2008 The Gale Group, Inc. Все права защищены.

регрессия

(rĕ-gresh’n)

1. Уменьшение симптомов.

2. Рецидив; возвращение симптомов.

3. Любое ретроградное движение или действие.

[Л. re-gredior, pp. -gressus, to go back]

Медицинский словарь для стоматологов © Farlex 2012

Руководство для врачей по интерпретации регрессионного анализа

Введение

исследовать факторы, связанные с заболеваниями и состояниями, или методы лечения для улучшения ухода за пациентами и клинической практики, часто необходима статистическая оценка данных. Регрессионный анализ является важным статистическим методом, который обычно используется для определения взаимосвязи между несколькими факторами и исходами заболевания или для выявления соответствующих прогностических факторов для заболеваний [1].

Данная редакционная статья познакомит читателей с основными принципами и подходом к интерпретации результатов двух типов регрессионного анализа, широко используемых в офтальмологии: линейной и логистической регрессии.

Линейный регрессионный анализ

Линейная регрессия используется для количественной оценки линейной взаимосвязи или связи между непрерывной переменной ответа/результата или зависимой переменной по крайней мере с одной независимой или объясняющей переменной путем подгонки линейного уравнения к наблюдаемым данным [1]. Переменная, для которой решается уравнение, являющееся интересующим результатом или реакцией, называется зависимой переменной [1]. Переменная, которая используется для объяснения значения зависимой переменной, называется предикторной, объяснительной или независимой переменной [1].

В модели линейной регрессии зависимая переменная должна быть непрерывной (например, внутриглазное давление или острота зрения), тогда как независимая переменная может быть непрерывной (например, возраст), бинарной (например, пол), категориальной (например, возрастная макулярная стадия дегенерации или шкала тяжести диабетической ретинопатии), или их комбинация [1].

При исследовании влияния или ассоциации одной независимой переменной на непрерывную зависимую переменную этот тип анализа называется простой линейной регрессией [2].

Однако во многих случаях одной независимой переменной может быть недостаточно для адекватного объяснения зависимой переменной. Часто необходимо контролировать вмешивающиеся факторы, и в этих ситуациях можно выполнить многомерную линейную регрессию, чтобы изучить влияние или связь нескольких независимых переменных на зависимую переменную [1, 2]. При включении множества независимых переменных регрессионная модель оценивает влияние или вклад каждой независимой переменной, сохраняя при этом значения всех других независимых переменных постоянными [3].

При интерпретации результатов линейной регрессии есть несколько ключевых результатов для каждой независимой переменной, включенной в модель:

  1. 1.

    Расчетный коэффициент регрессии — Расчетный коэффициент регрессии указывает направление и силу взаимосвязи или связи между независимыми и зависимыми переменными [4]. В частности, коэффициент регрессии описывает изменение зависимой переменной для каждого изменения независимой переменной на одну единицу, если оно непрерывно [4]. Например, при изучении взаимосвязи между непрерывной прогностической переменной и внутриглазным давлением (зависимая переменная) коэффициент регрессии, равный 2, означает, что на каждую единицу увеличения предиктора приходится две единицы увеличения внутриглазного давления. давление. Если независимая переменная является бинарной или категориальной, то изменение на одну единицу представляет собой переход из одной категории в референтную [4]. Например, при изучении взаимосвязи между бинарной переменной-предиктором, такой как пол, где «женский» установлен в качестве эталонной категории, и внутриглазным давлением (зависимая переменная), коэффициент регрессии, равный 2, означает, что в среднем мужчины у них внутриглазное давление на 2  мм рт. ст. выше, чем у женщин.

  2. 2.

    Доверительный интервал (ДИ) — ДИ, обычно устанавливаемый на уровне 95%, является мерой точности оценки коэффициента независимой переменной [4]. Большой ДИ указывает на низкий уровень точности, тогда как малый ДИ указывает на более высокую точность [5].

  3. 3.

    Значение P — Значение p для коэффициента регрессии указывает, является ли взаимосвязь между независимыми и зависимыми переменными статистически значимой [6].

Логистический регрессионный анализ

Как и линейная регрессия, логистическая регрессия используется для оценки связи между одной или несколькими независимыми переменными и зависимой переменной [7]. Однако отличительной особенностью логистической регрессии является то, что зависимая переменная (результат) должна быть бинарной (или дихотомической), что означает, что переменная может принимать только два разных значения или уровня, например «1 против 0» или «да против нет». [2, 7]. Величина эффекта предикторов на зависимую переменную лучше всего объясняется с помощью отношения шансов (OR) [2]. ОШ используются для сравнения относительных шансов возникновения интересующего исхода с учетом воздействия интересующей переменной [5]. ОШ, равное 1, означает, что шансы события в одной группе такие же, как шансы события в другой группе; разницы нет [8]. ОШ > 1 означает, что одна группа имеет более высокие шансы возникновения события по сравнению с контрольной группой, тогда как ОШ < 1 означает, что одна группа имеет более низкие шансы возникновения события по сравнению с контрольной группой [8]. При интерпретации результатов логистической регрессии ключевые выходные данные включают ОШ, ДИ и p-значение для каждой независимой переменной, включенной в модель.

Клинический пример

Sen et al. исследовали связь между несколькими факторами (независимые переменные) и исходами остроты зрения (зависимая переменная) у пациентов, получающих антиваскулярную терапию эндотелиальным фактором роста по поводу макулярного отека (DMO) с помощью как линейной, так и логистической регрессии [9]. Многофакторная линейная регрессия продемонстрировала, что возраст (оценка –0,33, 95% ДИ – 0,48 до –0,19, p  < 0,001) был значимо связан с остротой зрения с максимальной коррекцией (BCVA) через 100 недель при уровне значимости альфа = 0,05 [9].]. Коэффициент регрессии -0,33 означает, что МКОЗ в 100 недель снижается на 0,33 с каждым дополнительным годом старшего возраста.

Многофакторная логистическая регрессия также продемонстрировала, что возраст и состояние эллипсоидной зоны были статистически значимыми, связанными с достижением буквенной оценки BCVA >70 букв через 100 недель при уровне значимости альфа = 0,05. Пациенты в возрасте ≥75 лет имели меньшие шансы достичь МКОЗ >70 букв в 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,9).6, 95% ДИ от 0,94 до 0,98, p  = 0,001) [9]. Точно так же у пациентов в возрасте от 50 до 74 лет также были меньшие шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами моложе 50 лет, поскольку ОШ меньше 1 (ОШ 0,15, 95). % ДИ от 0,04 до 0,48, p  = 0,001) [9]. Кроме того, у пациентов с неинтактной эллипсоидной зоной были меньшие шансы достичь оценки букв BCVA >70 букв через 100 недель по сравнению с теми, у кого была интактная эллипсоидная зона (ОШ 0,20, 9).5% ДИ от 0,07 до 0,56; p  = 0,002). С другой стороны, пациенты с неоцениваемой/сомнительной эллипсоидной зоной имели повышенные шансы достичь МКОЗ >70 букв через 100 недель по сравнению с пациентами с интактной эллипсоидной зоной, поскольку ОШ больше 1 (ОШ 2,26, 95% ДИ от 1,14 до 4,48; p  = 0,02) [9].

Чем уже ДИ, тем точнее оценка; и чем меньше значение p (относительно альфа = 0,05), тем больше доказательств против нулевой гипотезы об отсутствии эффекта или связи.

Заключение

Проще говоря, линейная и логистическая регрессия являются полезными инструментами для оценки взаимосвязи между предикторными/объяснительными и исходными переменными для непрерывных и дихотомических исходов, соответственно, которые можно применять в клинической практике, например, для понимания риска факторы, связанные с интересующим заболеванием.

Ссылки

  1. Шнайдер А., Хоммель Г., Блеттнер М. Линейная регрессия. Anal Dtsch Ärztebl Int. 2010; 107: 776–82.

    Google ученый

  2. Бендер Р. Введение в использование регрессионных моделей в эпидемиологии. В: Верма М, редактор. Эпидемиология рака. Методы молекулярной биологии. Хумана Пресс; 2009: 179–95.

  3. Шобер П., Веттер ТР. Смешение в наблюдательных исследованиях. Анест Анальг. 2020;130:635.

    Артикул Google ученый

  4. Шобер П., Веттер ТР. Линейная регрессия в медицинских исследованиях. Анест Анальг. 2021; 132: 108–9.

    Артикул Google ученый

  5. Шумилас М. Объяснение соотношения шансов. J Can Acad Детская подростковая психиатрия. 2010;19:227–9.

    Артикул Google ученый

  6. Тизе М.С., Ронна Б., Отт Ю. П. Интерпретация ценностей и соображения. Дж. Торак Дис. 2016;8:E928–31.

    Артикул Google ученый

  7. Шобер П., Веттер ТР. Логистическая регрессия в медицинских исследованиях. Анест Анальг. 2021; 132: 365–6.

    Артикул Google ученый

  8. Zabor EC, Reddy CA, Tendulkar RD, Patil S. Логистическая регрессия в клинических исследованиях. Int J Radiat Oncol Biol Phys. 2022; 112: 271–7.

    Артикул Google ученый

  9. Сен П., Гурудас С., Раму Дж., Патрао Н., Чандра С., Рашид Р. и др. Предикторы остроты зрения после лечения антиваскулярным эндотелиальным фактором роста при макулярном отеке, вторичном по отношению к окклюзии центральной вены сетчатки. Офтальмол Ретин. 2021;5:1115–24.

    Артикул Google ученый

Скачать ссылки

R.E.T.I.N.A. Исследовательская группа

Varun Chaudhary 1,2 , Mohit Bhandari 1,2 , Чарльз С. Викофф 5,6 , Sobha Sivaprasad 8 , Lehana Thabane 2,7 , Peter Kaiser 3 6930693303 693069303 9303 93069303 9306 , . Дэвид Сарраф 10 , Софи Дж. Бакри 11 , Сунир Дж. Гарг 12 , Риши П. Сингх 13,14 , Фрэнк Г. Хольц 15 , Tien Y. Wong 16,17 и Robyn H. Guymer 3,4

Информация об авторе

Авторы и аффилированные лица

  1. 3 Университет Макстера, ONM, Канада,

    Хирургический факультет

    София Бзовски, Мохит Бхандари и Варун Чаудхари

  2. Департамент методов исследования здоровья, фактических данных и воздействия, Университет Макмастера, Гамильтон, Онтарио, Канада

    Марк Р.

    Филлипс, Лехана Табане, Мохит Бхандари и Варун Чаудхари

  3. Центр глазных исследований Австралии, Королевская Викторианская офтальмологическая больница, Восточный Мельбурн, Виктория, Австралия Австралия

    Робин Х. Гаймер

  4. Retina Consultants of Texas (Retina Consultants of America), Хьюстон, Техас, США

    Charles C. Wykoff

  5. Глазной институт Blanton, Хьюстонская методистская больница, США, США

    Charles C. Wykoff

  6. Biostatistics Unit, St. Joseph’s Healthcare Hamilton, Hamilton, ON, Canada

    Lehana Thabane

  7. NIHR Moorfields Biomedical Research Centre, Moorfields Eye Hospital, London, UK

    Sobha Sivaprasad

  8. Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

    Peter Kaiser

  9. Retinal Disorders and Ophthalmic Genetics, Stein Eye Institute, University of California, Los Angeles, CA, USA

    Дэвид Сарраф

  10. Отделение офтальмологии, клиника Мэйо, Рочестер, Миннесота, США

    Софи Дж. Бакри

  11. Служба сетчатки глазной больницы Уиллс, Филадельфия 3 0 Дж. Гар, Пенсильвания

    9003

  12. Центр офтальмологической биоинформатики, Институт глаза Коула, Кливлендская клиника, Кливленд, Огайо, США

    Риши П. Сингх

  13. Кливлендская клиника Медицинский колледж Лернера, Кливленд, Огайо, США

    Rishi P. Singh

  14. Department of Ophthalmology, University of Bonn, Bonn, Germany

    Frank G. Holz

  15. Singapore Eye Research Institute, Singapore, Singapore

    Tien Y. Wong

  16. Singapore Национальный глазной центр, Медицинская школа Duke-NUD, Сингапур, Сингапур

    Tien Y. Wong

Авторы

  1. София Бзовски

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Академия

  2. Mark R. Phillips

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

  3. Робин Х. Гаймер

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

  4. Charles C. Wykoff

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

  5. Lehana Thabane

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

  6. Mohit Bhandari

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

  7. Varun Chaudhary

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

Consortia

от имени R.E.T.I.N.A. study group

  • Varun Chaudhary
  • , Mohit Bhandari
  • , Charles C. Wykoff
  • , Sobha Sivaprasad
  • , Lehana Thabane
  • , Peter Kaiser
  • , David Sarraf
  • , Sophie J. Bakri
  • , Sunir Дж. Гарг
  • , Риши П. Сингх
  • , Фрэнк Г. Хольц
  • , Тьен Ю. Вонг
  • и Робин Х. Гаймер

Вклады

SB отвечал за написание, критический обзор и обратную связь по рукописи. MRP отвечал за концепцию идеи, критический обзор и отзывы о рукописи. RHG отвечала за критический обзор и отзывы о рукописи. CCW отвечала за критический обзор и отзывы о рукописи. LT отвечал за критический обзор и отзывы о рукописи. МБ отвечал за концепцию идеи, критический обзор и отзывы о рукописи. ВК отвечал за концепцию идеи, критический обзор и отзывы о рукописи.

Автор, ответственный за переписку

Переписка с Варун Чаудхари.

Декларации этики

Конкурирующие интересы

SB: Нечего раскрывать. MRP: Нечего раскрывать. RHG: Консультативные советы: Bayer, Novartis, Apellis, Roche, Genentech Inc. — не имеют отношения к данному исследованию. CCW: Консультант: Acuela, Adverum Biotechnologies, Inc, Aerpio, Alimera Sciences, Allegro Ophthalmics, LLC, Allergan, Apellis Pharmaceuticals, Bayer AG, Chengdu Kanghong Pharmaceuticals Group Co, Ltd, Clearside Biomedical, DORC (Голландский центр офтальмологических исследований), EyePoint Pharmaceuticals , Gentech/Roche, GyroscopeTx, IVERIC bio, Kodiak Sciences Inc, Novartis AG, ONL Therapeutics, Oxurion NV, PolyPhotonix, Recens Medical, Regeron Pharmaceuticals, Inc, REGENXBIO Inc, Santen Pharmaceutical Co, Ltd и Takeda Pharmaceutical Company Limited; Научные фонды: Adverum Biotechnologies, Inc, Aerie Pharmaceuticals, Inc, Aerpio, Alimera Sciences, Allergan, Apellis Pharmaceuticals, Chengdu Kanghong Pharmaceutical Group Co, Ltd, Clearside Biomedical, Gemini Therapeutics, Genentech/Roche, Graybug Vision, Inc, GyroscopeTx, Ionis Pharmaceuticals , IVERIC bio, Kodiak Sciences Inc, Neurotech LLC, Novartis AG, Opthea, Outlook Therapeutics, Inc, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Samsung Pharm Co, Ltd, Santen Pharmaceutical Co, Ltd и Xbrane Biopharma AB — несвязанные этому исследованию.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *