что значит быть циклоидом — T&P
Человеческие характеры очень разнообразны, но среди них, тем не менее, можно выделить типичные «рисунки». Для описания некоторых подобных паттернов в психологии существует понятие «акцентуация». Так называют сумму наиболее ярко очерченных свойств характера, которые еще находятся в пределах клинической нормы, но делают человека уязвимым к психологическим нагрузкам определенного типа. Циклоидная акцентуация — один из ее вариантов. T&P рассказывают о том, что отличает циклоида от циклотимика, каковы плюсы и минусы этого типа и что делать, если у вас такой характер.
Акцентуация характера — это не болезнь. Несмотря на то, что некоторые названия вариантов акцентуации: эпилептоид, истероид, шизоид и другие, — образованы от названий психических заболеваний, любой человек с акцентуацией здоров и нормален. У эпилептоида нет эпилепсии, а шизоид не болеет шизофренией (иначе они стали бы эпилептиком и шизофреником). У людей с акцентуацией лишь обострены определенные черты характера. Создатель этого понятия, немецкий психиатр Карл Леонгард, к примеру, писал, что «население Берлина — это на 50% акцентуированные личности и на 50% — стандартный тип людей». Тем не менее, в некоторых неблагоприятных обстоятельствах акцентуация может превратиться в болезнь, «добрав» патологичности.
Создатель этого понятия, немецкий психиатр Карл Леонгард, к примеру, писал, что «население Берлина — это на 50% акцентуированные личности и на 50% — стандартный тип людей». Тем не менее, в некоторых неблагоприятных обстоятельствах акцентуация может превратиться в болезнь, «добрав» патологичности.
Составители Энциклопедического словаря по психологии и педагогике (2013) пишут об этом понятии так: «Акцентуации характера отличаются от психопатий отсутствием одновременного проявления свойственной последним триады признаков: стабильность характера во времени, тотальности его проявлений во всех ситуациях, социальной дезадаптации». Иначе говоря, эпилептоид не всегда стремится маниакально поддерживать порядок, а истероид не в любой ситуации жаждет оказаться в центре всеобщего внимания.
В российской психологии акцентуация характера остается популярным понятием, однако общепринятой классификации на сегодняшний день не существует. Современные версии типологии опираются на работы Карла Леонгарда, монографию советского психиатра Андрея Личко и другие исследования. Работы Личко позволили глубже понять причины появления и этиологию неврозов, поскольку психиатр выдвинул концепцию так называемого «места наименьшего сопротивления», или «слабого звена» в характере.
Работы Личко позволили глубже понять причины появления и этиологию неврозов, поскольку психиатр выдвинул концепцию так называемого «места наименьшего сопротивления», или «слабого звена» в характере.
«Введение понятия “места наименьшего сопротивления” характера, а также описание этих мест применительно к каждому типу — важный вклад в психологическую теорию характера, — пишет в своей монографии российский психолог, специалист в области экспериментальной психологии и нейро-лингвистического программирования, профессор МГУ Юлия Гиппенрейтер. — Он имеет также неоценимое практическое значение. Слабые места каждого характера надо знать, чтобы избегать неправильных шагов, излишних нагрузок и осложнений в семье и на работе, при воспитании детей, организации собственной жизни и т. п.»
Вдоль по радуге в грозу: плюсы и минусы циклоидной акцентуации
Название циклоидной акцентуации характера дала геометрическая кривая — циклоида, или рулетта, как называли ее раньше. Эту кривую рисует катящаяся окружность.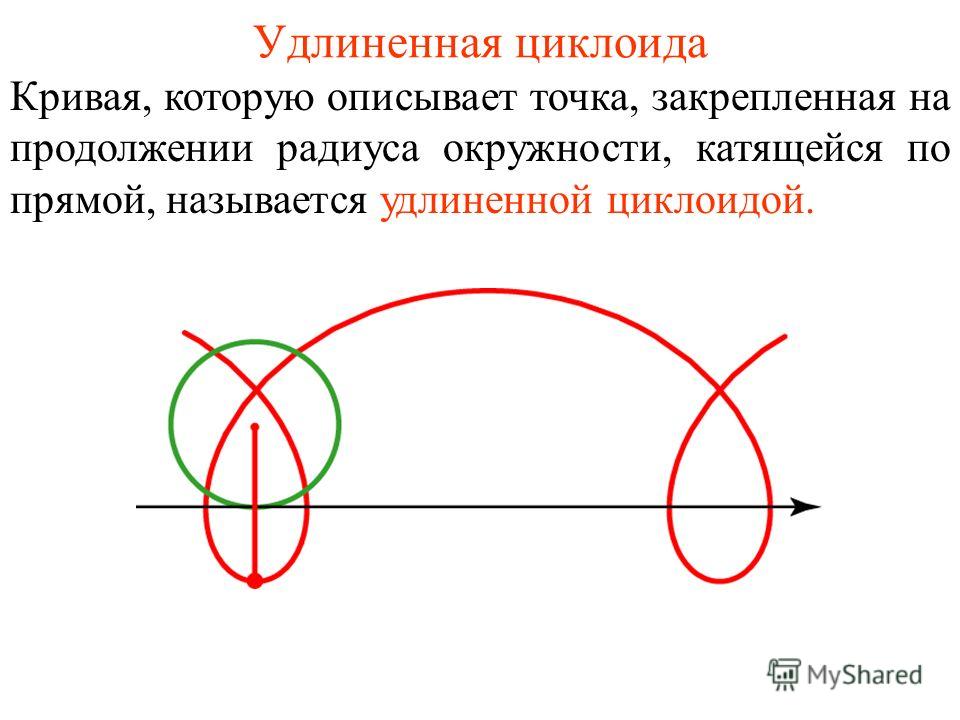 Паскаль писал о ней так: «Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели ее древние… ибо это не что иное, как путь, описываемый в воздухе гвоздем колеса».
Паскаль писал о ней так: «Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели ее древние… ибо это не что иное, как путь, описываемый в воздухе гвоздем колеса».
На плоскости циклоида выглядит как бесконечная последовательность арок, которые упираются своим основанием в горизонталь. Окружность «катится» по этой горизонтали, и точка у нее на боку описывает полукруг, то оказываясь в высшей точке, то падая к подножию. Именно так повышается и падает настроение у человека с циклоидной акцентуацией характера. У циклоида нет циклотимии — психического аффективного расстройства, при котором эмоциональное состояние человека колеблется между депрессией и гипертимией (или даже гипоманией). Циклотимик страдает от резких скачков настроения и работоспособности, которые мешают ему вести привычный образ жизни, — в то время как циклоид просто живет как на качелях, которые постоянно описывают полукруг, поднимая его высоко над землей и вновь опуская к исходной точке.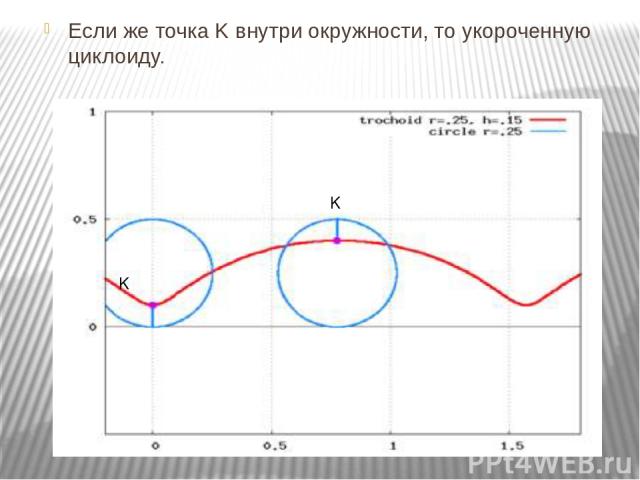
«Диаметр» циклоиды, по которой скользит настроение такого человека, может быть разным: от мягких беспричинных перепадов между «не очень» и «в порядке» до настоящих прыжков от счастья до глубокой тоски и обратно. При этом для окружающих такой человек, как правило, остается отличным деловым партнером, внимательным другом и нежным возлюбленным. Он не склонен к конфликтам (исключая моменты самых глубоких падений), ведет себя естественно и добродушно, спокойно относится ко многим обстоятельствам, которые у других людей вызывают массу негативных чувств. В темпераменте циклоида есть теплота и мягкость, ему присущи юмор и озорство. Он не расстается с этими качествами даже в моменты грусти, хотя становится обходительным одиночкой, не выказывая враждебности к другим.
© Tsto Helsinki
Существенный плюс циклоидной акцентуации характера заключается в том, что она делает человека гибким и адаптивным, способствуя развитию способностей к эмпатии. Циклоид легко настраиватеся на любую волну, поскольку эмоциональные «качели» априори обеспечивают ему широкий психологический диапазон.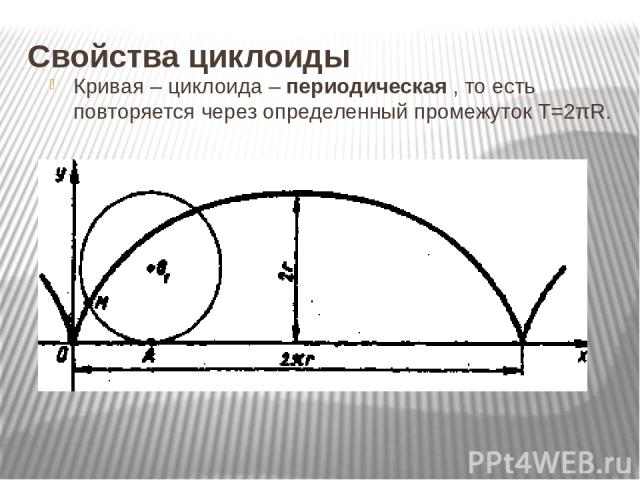 Такой человек остро чувствует радость жизни и ее печаль. Это помогает в развитии творческих навыков и подчас позволяет «превратить» циклоидную акцентуацию в карьеру писателя, художника или журналиста.
Такой человек остро чувствует радость жизни и ее печаль. Это помогает в развитии творческих навыков и подчас позволяет «превратить» циклоидную акцентуацию в карьеру писателя, художника или журналиста.
При этом сами скачки настроения, особенно во взрослом возрасте, не ощущаются ярко. Человек с циклоидной акцентуацией характера скорее назовет это «градиентом» — от светлой грусти до развернутой тоски — и от легкого желания улыбнуться до бодрости, радости и склонности к гедонизму. Разного рода удовольствия, оттенки чувств и нюансы обстоятельств доступны и знакомы таким людям. Они знают о них очень много — и много могут о них рассказать, обеспечив собеседнику, слушателю или читателю с другим складом характера шанс научиться радоваться повседневности.
Эмоциональные градиенты циклоидной акцентуации, с другой стороны, создают специфический ритм жизни: скачет работоспособность, эмоциональность, общительность, самооценка, общий уровень энергии, творческие способности. И в этом случае, конечно, нужно приспособить к акцентуации свой график жизни: например, выбирать проектную работу с ее рывками и паузами, — или свободный график. В последнем случае стоит помнить, что в фазе подъема все обычно получается, складывается и приносит плоды само по себе, — а вот в фазе спада может быть трудно. В нижней точке кривой циклоид становится уязвимым, страдает от недостатка жизненных сил и веры в себя.
В последнем случае стоит помнить, что в фазе подъема все обычно получается, складывается и приносит плоды само по себе, — а вот в фазе спада может быть трудно. В нижней точке кривой циклоид становится уязвимым, страдает от недостатка жизненных сил и веры в себя.
И это пройдет: если вы циклоид
Человеку с циклоидной акцентуацией характера необходимо помнить, что спады его настроения возникают сами по себе — и исчезают так же. Негативное состояние просто «проходит», и главная задача заключается в том, чтобы до начала нового взлета не наделать ошибок, перессорившись с окружающими, бросив институт или недописанную книгу.
Более серьезная опасность для циклоида заключается в том, что в неблагоприятных обстоятельствах такая акцентуация может превратиться в биполярное расстройство, циклотимию или маниакально-депрессивный психоз. Особенно внимательно относиться к своим «перепадам» следует тем, у кого в семье уже были случаи одного из этих психических заболеваний. И все-таки, даже если семейный анамнез налицо, болезни можно избежать, — ведь она развивается как правило не сама по себе, а на фоне длительного и интенсивного стресса.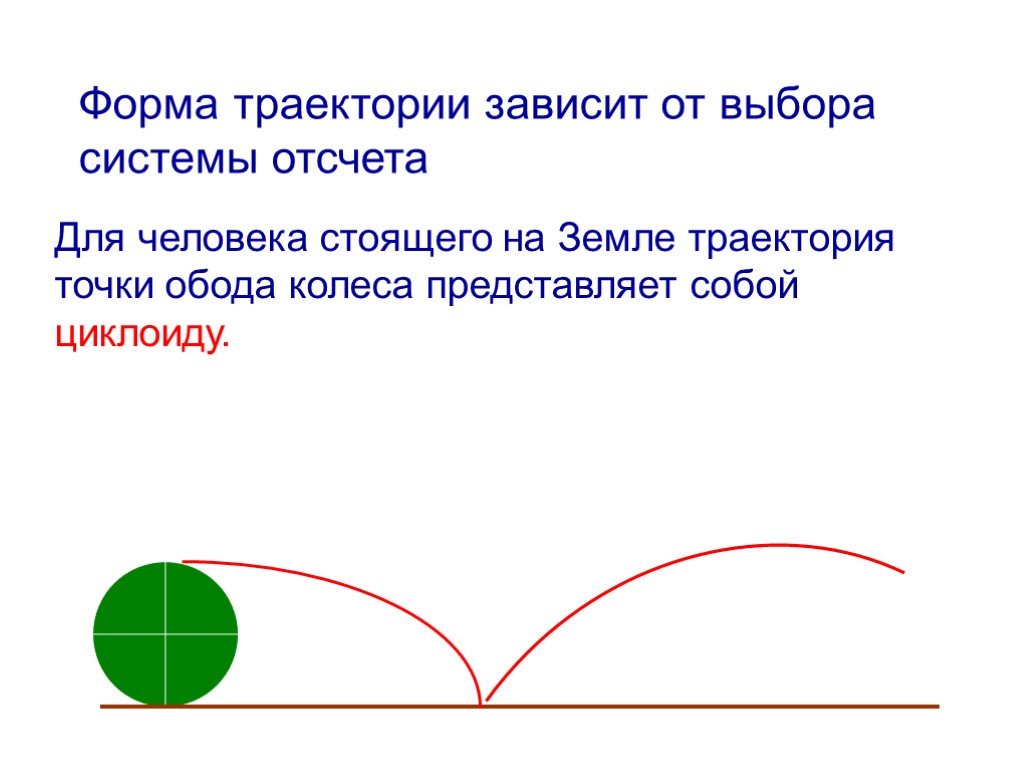 Именно от него циклоиду нужно беречь себя, избегая по-настоящему стрессогенных обстоятельств или смягчая их по мере сил.
Именно от него циклоиду нужно беречь себя, избегая по-настоящему стрессогенных обстоятельств или смягчая их по мере сил.
Гвоздь колеса: если рядом циклоид
Люди с циклоидной акцентуацией характера хорошо переносят многие неприятные моменты межличностных отношений, однако и у них есть «ахиллесова пята». Они не терпят монотонных действий в работе и рутинности в личных отношениях. В погоне за разнообразием и приключениями такие люди подчас могут совершать настоящие маленькие безумства, — но, вероятно, будут рады, если их близкие решат поучаствовать в затее.
В негативной фазе самооценку циклоида легко травмировать, поскольку в эти моменты он склонен себя недооценивать. У него мало сил, нет веры в себя, он бросает начатое, отказывается от прошлых целей. Вот почему в фазе падения человеку с циклоидной акцентуацией важно помочь быть последовательным и поддержать его, чтобы он не потерял достижения и бонусы, заработанные на подъеме.
Описание циклоидного типа личности с примерами ситуаций из жизни
Таких людей называют «человек настроения».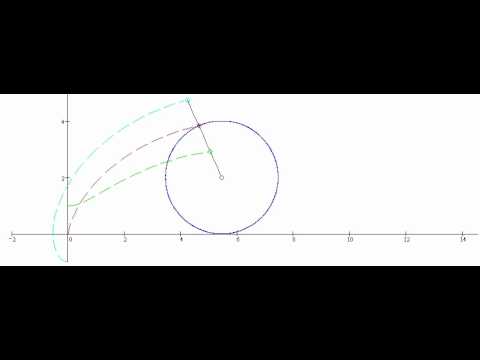 Какое-то время ты видишь его весёлым, лёгким и общительным. И кажется, что он такой всегда. Но вот однажды этот человек приходит на работу «без лица». Угрюмый, раздражительный, замкнутый, не хочет ни с кем говорить. Все сразу кидаются выяснять – что случилось. В ответ он бурчит, что всё нормально, просто его надо оставить в покое. Может даже доходить до конфликтов.
Какое-то время ты видишь его весёлым, лёгким и общительным. И кажется, что он такой всегда. Но вот однажды этот человек приходит на работу «без лица». Угрюмый, раздражительный, замкнутый, не хочет ни с кем говорить. Все сразу кидаются выяснять – что случилось. В ответ он бурчит, что всё нормально, просто его надо оставить в покое. Может даже доходить до конфликтов.
Фото автора Caio: Pexels
Ведь окружающие, особенно близкие, с тревогой воспринимают такие перемены и хотят помочь. А помощи ему действительно не требуется. Через какое-то время, примерно пару недель, он «придёт в себя» и вернётся в привычный образ весельчака. Самое сложное для окружающих – понять природу таких перемен и привыкнуть к этому.
Мало кто выдерживает рядом человека в пониженном настроении. Да и в современном мире стало как-то модно настраиваться на позитив. И с любым твоим негативом будет пытаться бороться каждый желающий. Однако, это раздражает ещё больше.
В этой статье:
Классификация А.Е. ЛичкоОсобенности нервной системыФаза субдепрессииФаза гипертимности
Классификация А.Е. Личко
Циклоидный тип личности описал А.Е. Личко в своей классификации акцентуаций личности. Этот тип акцентуации соответствует дистимическому по Леонгарду. Эти две классификации очень похожи. Но вернёмся к циклоидам.
Новости СМИ2
Личко выделил ведущие черты циклоидного типа:
- Настроение всегда меняется, циклы стабильны. Изменения могут быть спровоцированы внешними событиями, или внутренними процессами. Если даже ничего не предвещало, смена фаз настроения всё равно произойдёт.
- Во время фазы подъёма человек проявляет свои лучшие качества.
- Во время спада настроения происходит сильный упадок, даже до суицидальных мыслей.
Личко описывал эти фазы, называя их фазой гипертимности и фазой субдепрессии. Гипертимная фаза обычно длится дольше, несколько месяцев, иногда несколько лет.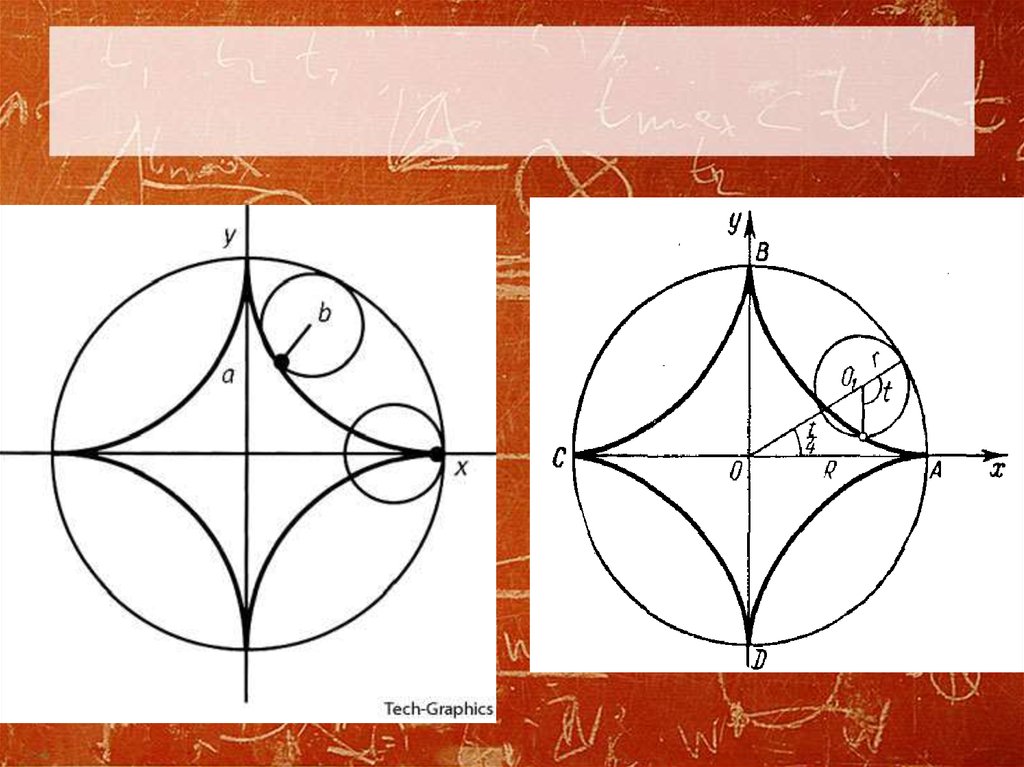 А фаза субдепрессии более короткая – до четырёх недель. Но это средние показатели, всё очень индивидуально.
А фаза субдепрессии более короткая – до четырёх недель. Но это средние показатели, всё очень индивидуально.
Циклоидный тип личности
Во время гипертимной фазы циклоид спокоен или находится в приподнятом настроении, он общителен и открыт, ему нравится работать, заниматься любимыми делами. Во время фазы субдепрессии всё идёт на спад: циклоид закрывается от людей, ему не хочется ничем заниматься, пропадает интерес к жизни. Состояние может ухудшаться до депрессивного. Но затем оно выравнивается само собой.
Циклоида иногда описывают с точки зрения теории Юнга. В фазе подъёма он ведёт себя как «чистый» экстраверт. Он энергичен, отдыхает среди людей, может много общаться и мало спать, много работать, строить отношения. а во время фазы спада он вдруг превращается в интроверта.
Замыкается в себе, устаёт от шума и людей, большие компании и шумная работа для него утомительны, пропадает совсем или меняется хобби, любимые занятия. Вместо тусовок с друзьями он садится вечером с книгой.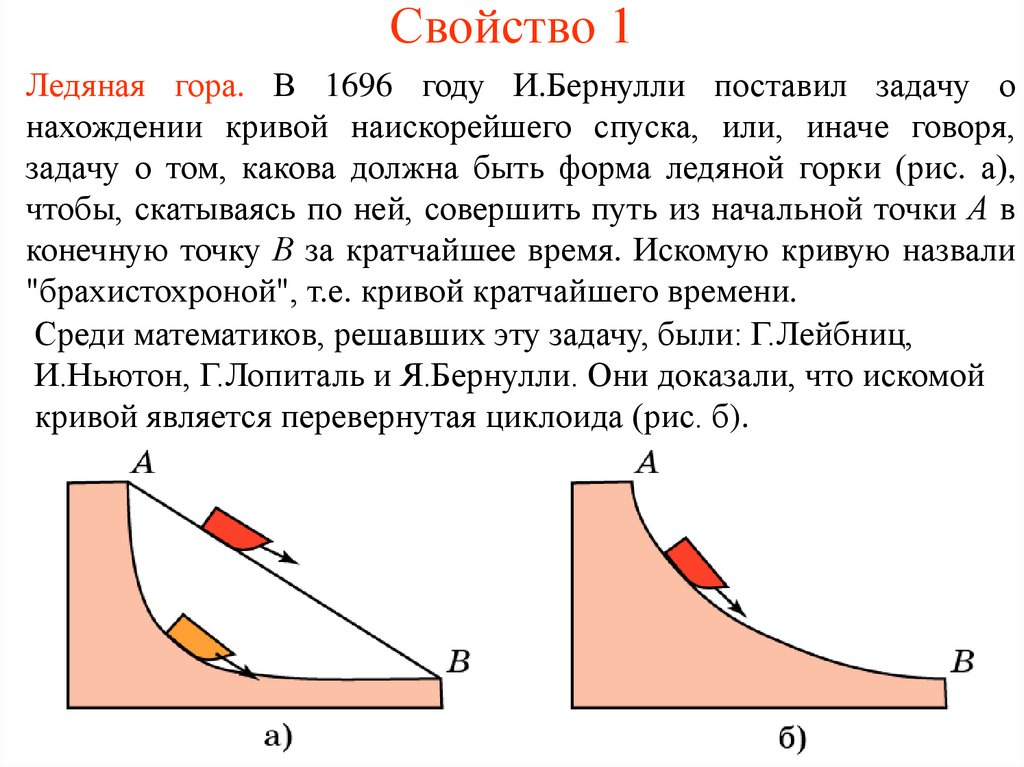 Он погружается в свой внутренний мир, все эмоции и чувства прячутся внутрь. Ему легче быть одному, хотя фон настроения пониженный.
Он погружается в свой внутренний мир, все эмоции и чувства прячутся внутрь. Ему легче быть одному, хотя фон настроения пониженный.
Такие перепады часто затрудняют диагностику, или сам человек не может понять – кто он и какой, что ему подходит.
Именно поэтому, чтобы правильно определить состояние человека, важно наблюдать за его настроением в течение долгого периода. Не торопись подозревать у подруги депрессию, это может быть просто очередной цикл субдепрессии. Помощь здесь не требуется, только время. Особенно, если эта фаза не приобретает тяжёлые формы. И главное, чтобы сам человек понимал, что он так устроен, и это всего лишь очередной цикл. Тогда нет необходимости искать причины апатии, анализировать жизненную ситуацию.
Особенности нервной системы
Основа любой акцентуации – особенности работы центральной нервной системы. Именно она запускает эти циклы. Зная её устройство, можно адаптироваться к своему темпераменту и знать, как поддержать нервную систему в трудные периоды.
Нервная система циклоида, как шарик, который катится. Когда определённая точка шара вверху – у циклоида подъём, а когда она опускается вниз – происходит спад. И так это «шар» катится постоянно, сменяя циклы. Именно поэтому эта акцентуация получила название циклоидная.
GiphyПереходы настроения обычно не резкие, а плавные. Насколько долго длится каждый цикл, и насколько сильно отличаются друг от друга фазы – зависит от индивидуальных особенностей. У кого-то обе фазы не достигают пиковых проявлений, а у кого-то амплитуда колебаний достаточно высокая.
Смена циклов происходит постепенно:
- Сначала нервная система стабильна и устойчива. Человек в тонусе и радостном настроении. Любое напряжение переживается легко, мозг выдерживает его.
- Всё начинает двигаться к спаду. Напряжение в коре головного мозга переживается нервной системой тяжелее, оно копится, энергия падает.
- Напряжение повышается, энергия снижается. Начинается апатия, человек входит а субдепрессивную фазу.

- После жизни в сниженном ритме и энергии, нервная система восстанавливает силы, начинается подъём. Так начинается следующая фаза гипертимности.
Фаза субдепрессии
Как уже говорилось выше, эта фаза длится меньше – до 4х недель. И это хорошо потому, что в ней циклоид проявит свои худшие качества. И в общении с ним будет довольно сложно. Он не хочет общаться, налаживать отношения становится тяжёло. А знакомиться с новыми людьми – вообще пытка.
Фото автора Liza Summer: PexelsЕсли циклоиду нужно принять какое-то решение, то в этой фазе он будет бесконечно колебаться и сомневаться. Всё ему представляется в чёрных и серых красках, будущее видится пессимистичным. Он испытывает безнадёжность и бессмысленность от всего происходящего.
Циклоид становится слабым, растерянным, проваливается в чувство бессилия. В общении с ним кажется, что ему невозможно помочь. На фоне снижения энергии могут даже страдать психические функции – память, например. Всему виной растерянность и заторможенность.
Циклоид в фазе субдепрессии отгораживается от людей, психика защищается от людей отвращением. Окружающие люди раздражают и общение неприятно. И даже к самому себе человек начинает испытывать отвращение и неприязнь.
Если раньше это был заядлый «зожник», то в фазе спада всё его здоровое питание и привычки слетают. Он поддаётся вредным привычкам, алкоголю и сигаретам. Воля слабеет.
Вредные привычки так же могут вылиться в пищевую зависимость и переедание, либо наоборот, в голодание. Проблемы с едой – частый симптом субдепрессивной фазы.
В целом циклоид чувствует себя уставшим, разбитым, не выдерживает даже небольшие нагрузки. Развивается синдром хронической усталости. Нарушается сон. Весь день ему хочется спать и он вялый. А к ночи повышается возбудимость, и из-за бессонницы он не может уснуть.
Фото автора Yan Krukov: PexelsСамооценка в этот период сильно страдает. Человек кажется себе никчёмным и плохим. Его мучает чувство вины за свою апатию, лень и вялость. Но он ничего не может сделать. И от этого ему ещё хуже.
Но он ничего не может сделать. И от этого ему ещё хуже.
Приём антидепрессантов или психотерапия помогают смягчить тяжёлые проявления субдепрессивной фазы.
Фаза гипертимности
Эта та самая белая полоса жизни, которая, к счастью, длится дольше субдепрессивной. В этой фазе циклоид покажет свои лучшие качества: бодрость, энергичность, общительность, открытость, оптимизм, инициативность, повышенная сексуальность и работоспособность, он способен на красивые и запоминающиеся поступки, очень гибкий и адаптивный, всех любит и всем рад, всегда готов помочь и развеселить.
Но и в этой фазе у циклоида есть минусы: он может быстро и непонятно говорить, его самооценка завышена, он открыт до фамильярности и нарушения границ, склонен к эпатажу, не разборчив в контактах. Интересы меняются быстро, он не может усидеть на одном месте. В этой фазе может проявлять легкомыслие и поверхностность.
Циклоиды – яркие, приятные личности. Несмотря на их минусы, с ними многие хотят общаться, дружить и работать. В фазу гипертимности – это прекрасные люди. Но смена их настроения настолько яркая, что даже близким людям может казаться, что в нём живут два разных человека.
В фазу гипертимности – это прекрасные люди. Но смена их настроения настолько яркая, что даже близким людям может казаться, что в нём живут два разных человека.
ЦИКЛОИДНЫЙ — Что такое ЦИКЛОИДНЫЙ?
Слово состоит из 10 букв: первая ц, вторая и, третья к, четвёртая л, пятая о, шестая и, седьмая д, восьмая н, девятая ы, последняя й,
Слово циклоидный английскими буквами(транслитом) — tsikloidnyi
- Буква ц встречается 1 раз. Слова с 1 буквой ц
- Буква и встречается 2 раза. Слова с 2 буквами и
- Буква к встречается 1 раз. Слова с 1 буквой к
- Буква л встречается 1 раз. Слова с 1 буквой л
- Буква о встречается 1 раз. Слова с 1 буквой о
- Буква д встречается 1 раз.
 Слова с 1 буквой д
Слова с 1 буквой д - Буква н встречается 1 раз. Слова с 1 буквой н
- Буква ы встречается 1 раз. Слова с 1 буквой ы
- Буква й встречается 1 раз. Слова с 1 буквой й
Циклоидная чешуя
Циклоидная чешуя, чешуя костистых рыб (лососеобразных, сельдеобразных, карпообразных и др.), характеризующаяся гладким закруглённым задним краем. Каждая из чешуй лежит в глубоком кармане соединительнотканного слоя кожи…
БСЭ. — 1969—1978
ЦИКЛОИДНАЯ ЧЕШУЯ (от греч. kyk- loeides — кругообразный, круглый), разновидность костной чешуи костистых рыб (лососеобразных, сельдеобразных, карпообразных и др.). характеризующаяся гладким закруглённым задним краем (отсюда назв.).
Биологический словарь
Циклоидное зацепление
Циклоидное зацепление, образуется зубчатыми колёсами, профили зубьев которых очерчены по эпициклоиде и гипоциклоиде (см.
БСЭ. — 1969—1978в ст. Линия). Эпициклоида и гипоциклоида являются траекториями точек внешней и внутренней вспомогательных окружностей…
ЦИКЛОИДНОЕ ЗАЦЕПЛЕНИЕ — зубчатое зацепление, в к-ром профили зубьев очерчены по циклоидным кривым — эпициклоидам и гипоциклоидам. Применяется ограниченно (напр., в часовых механизмах, компрессорах).
Большой энциклопедический политехнический словарь
Психоз циклоидный
Психоз циклоидный — (греч. kykloides – кругообразный) – термин K. Leonhard (1954), обозначает фазно протекающие психозы, занимающие промежуточное положение между маниально-депрессивным психозом и шизофренией…
Жмуров В.А. Большой толковый словарь терминов по психиатрии
Психоз циклоидный (греч. kykloides – кругообразный) – термин K.
vocabulary.ruLeonhard (1954), обозначает фазно протекающие психозы, занимающие промежуточное положение между маниально-депрессивным психозом и шизофренией…
Характер циклоидный
Характер циклоидный — отличается тенденцией к смене настроения от приподнятого к подавленному и наоборот. Жмуров В.А. Большой толковый словарь терминов по психиатрии
ХАРАКТЕР ЦИКЛОИДНЫЙ — один из типов акцентуации характера (-> характер: акцентуация). Свойственно чередование фаз хорошего и плохого настроения с различным периодом.
Головин С. Словарь практического психолога
Леонгарда циклоидные психозы
Леонгарда циклоидные психозы — группа атипично (приступообразно) протекающих психозов, по своим клиническим проявлениям занимающим промежуточное между маниакально-депрессивным психозом и шизофренией место (1954).
vocabulary.ru
Леонгарда циклоидные психозы (К. Leonhard) группа психозов с приступообразным течением и глубокими ремиссиями, к которой относятся акинетический и гиперкинетический психозы, а также психоз «страха-счастья»…
Большой медицинский словарь. — 2000
Конституция циклоидная
Конституция циклоидная — пикническое телосложение с такими чертами личности, как неустойчивость настроения, тенденция к спонтанной смене подавленного настроения приподнятым, нередко к сезонным изменениям настроения.
Жмуров В.А. Большой толковый словарь терминов по психиатрии
Конституция циклоидная — пикническое телосложение с такими чертами личности, как неустойчивость настроения, тенденция к спонтанной смене подавленного настроения приподнятым, нередко к сезонным изменениям настроения.
vocabulary.ru
Русский язык
Цикло́идный.
Орфографический словарь. — 2004
Цикл/о́ид/н/ый.
Морфемно-орфографический словарь. — 2002
- Слова из слова «циклоидный»
- Слова на букву «ц»
- Слова, начинающиеся на «ци»
- Слова c буквой «й» на конце
- Слова c «ый» на конце
- Слова, начинающиеся на «цик»
- Слова, начинающиеся на «цикл»
- Слова, оканчивающиеся на «ный»
- Слова, заканчивающиеся на «дный»
- циклодром
- циклоидальный
- циклоида
- циклоидный
- циклометрический
- циклометр
- циклонический
www.
 PracticalStudent.com —
PracticalStudent.com —Что такое циклоида?A Cycloid — это путь или Locus , за которым следует точку на окружности, когда она движется по длинной прямой без скольжение. Построение циклоидыНиже описано, как построить циклоиду для точки P по кругу при вращении по прямой линия без проскальзывания. Сначала нарисуйте круг и линию от его основания к слева или справа. Линия должна быть справа, если круг вращается по часовой стрелке и влево, если круг вращается против часовой стрелки. В этой ситуации мы собираемся найти геометрическое место точка P, которая находится в нижней части окружности, где она касается прямой линии.  Здесь мы использовали заданный квадрат 60°-30°, чтобы получить 12
равные деления. Обозначьте эти секции цифрами от 0 до 12. Здесь мы использовали заданный квадрат 60°-30°, чтобы получить 12
равные деления. Обозначьте эти секции цифрами от 0 до 12.Измерение расстояния между любыми двумя из этих точек с вашей отметкой компаса 12 от этих расстояний вдоль базовая линия, вдоль которой будет вращаться круг. Этикетка эти точки от 0 до 12, как показано. Когда берешь дистанцию между любыми двумя подразделениями круга, который вы должен добавить немного к расстоянию на вашем компасе для учета кривой окружности. Спроецируйте новые точки на линию из центра круг и пометить затем от C1 до C12. Когда круг вращается вдоль линии, точка 1 на окружность переместится в точку 1 на прямой, а значит центр круга теперь будет в точке C1. Следующие строки проекта из равных подразделений
окружность параллельна прямой. С компасом, настроенным на радиус круга, поместите острие компаса на точку C1 и отрежьте линия высоты, исходящая из точки 1 на окружности. затем повторите это для точки C2 и линии высоты 2 и т. д., пока вы достигнете точки C12 и линии 12. Объединив эти новые точки, вы создадите точки точки P для круга, когда он вращается вдоль прямая линия без проскальзывания. Другими словами, вы создали Циклоид . Было бы очень загромождено, если бы вы рисовали каждую круг по пути. И ваш конечный результат Cycloid . Построение касательной и нормали к точка на Cycloid Вы можете построить Tangent и Normal для
любую точку циклоиды с помощью этого метода. Выберите точку. С радиусом круга на отметке компаса на центральная линия вращающегося круга. Теперь нарисуйте круг в этом месте. Проведите вертикальную линию через центр круга. Проведите линию от вершины круга до точки, и вы будет Тангенс . Проведите линию от основания круга до точки и у вас будет Обычный . Как найти центр кривизны точка на циклоиде Вы можете найти Центр кривизны в любой точке на Cycloid с помощью этого метода. Выберите точку. С радиусом круга на отметке компаса на центральная линия вращающегося круга. Теперь нарисуйте круг в этом месте. Проведите вертикальную линию через центр круга. Проведите линию от основания круга до точки
который даст вам Normal . Продолжить эту линию
ниже рисунка. Проведите линию от точки через центр круг до пересечения с другой стороной круга. Нарисуйте линию прямо вниз, пока она не пересечет нормаль. Там, где происходит это пересечение, находится Центр кривизны для точки. Основная циклоида | |
Циклоида и ее свойства Связанные кривые
Циклоида представляет собой кривую, описываемую точкой на окружности, когда она катится по прямой. Циклоида, образованная окружностью радиусом r , катящейся по оси x, представлена параметрическим уравнением:
$\left\{\begin{matrix} x(t)= rt — r\sin(t)\\ y(t)= r-r\cos(t)\\ \end{matrix}\right.$.
Если точка лежит с коэффициентом f , где 0 ≤ f ≤ 1, вдоль радиуса окружности, то уравнение кривой имеет вид:
$\left\{\begin{matrix} x(t)= rt — fr\sin(t)\\ y(t)= r-fr\cos(t)\\ \end{matrix}\right. $.
$.
Взаимодействие Geogebra выше показывает окружность с радиусом 1, катящуюся вдоль оси x . Другие показанные точки — это середина радиуса, четверть и восьмая часть радиуса. Вы можете перетаскивать ползунок угла влево и вправо, чтобы вращать круг и видеть, как точки отслеживают соответствующие кривые. Вы можете увеличивать или уменьшать масштаб и перемещать холст, чтобы увидеть полную кривую. 9{2\pi} = -4r(-1-1) = 8r$
Длина дуги одной арки циклоиды равна 8 r или в 8 раз больше радиуса окружности, которая ее создала.
Интересно, что формула площади имеет множитель π , как площадь круга, но формула длины дуги не имеет множителя π , как длина окружности.
Объем
Объем V твердого тела, образованного вращением дуги циклоиды вокруг x 93$.
Чашка циклоиды
Каков объем циклоиды, вращающейся вокруг своей оси симметрии и имеющей форму чаши? Я придумал следующий объем, используя дисковый метод. 2\cdot R\sin(t)dt$. Это соответствует тому же объему, что и выше. Этот объем казался бы разумным, если бы он был меньше объема цилиндра, созданного радиусом 93$. Объем циклоидной чашки больше половины объема цилиндра, и это кажется разумным.
2\cdot R\sin(t)dt$. Это соответствует тому же объему, что и выше. Этот объем казался бы разумным, если бы он был меньше объема цилиндра, созданного радиусом 93$. Объем циклоидной чашки больше половины объема цилиндра, и это кажется разумным.
Прямоугольный треугольник
Прямой угол спрятан в циклоиде. Угол возникает на пересечении циклоиды и окружности. Диаметр окружности — это гипотенуза.
На изображении выше APC — прямоугольный треугольник. Чтобы доказать это, мы можем доказать, что ортогональная касательная к циклоиде проходит через окружность, где она касается x — ось. Во-первых, давайте найдем наклон касательной к циклоиде в точке t .
(i) $ \ frac {dy} {dx} = \ frac {\ frac {dy} {dt} (r-r \ cos t)} {\ frac {dx} {dt} (rt-r \ sin t) } = $ $\frac{r\sin t}{r — r\cos t} =$ $\frac{r\sin t}{1 — \cos t}$
Наклон ортогоналя был бы отрицательным обратным : $-\frac{dx}{dy} = -\frac{1-\cos t}{\sin t}$. В точке t точка на циклоиде равна $(rt — r\sin t, r — r\cos t)$. Следовательно, уравнение ортогонала:
Следовательно, уравнение ортогонала:
(ii) $y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}[x — (rt — r\sin t)]$
Точка, в которой Окружность, касающаяся оси x , равна rt , потому что t на самом деле является углом, под которым окружность проходит вдоль оси x . Следовательно, мы можем найти значение y , когда x равно rt , подставив x = rt в уравнение ортогонала. (Нет необходимости упрощать уравнение прямой в (ii).)
(iii) $y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}[rt — (rt — r\sin t)]$
(iv) $ y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}(r\sin t)$
(v) $y — (r — r\cos t) = r \cos t — r$
(vi) $y = 0$
Следовательно, для любого t ортогональная ось всегда будет пересекать окружность в точке касания с осью x . А поскольку ортогональный угол по определению является прямым, отрезок PA должен пересечь окружность в точке A, что делает AC диаметром окружности. Если мы позволим y = 0 и решить для x , мы получим x = rt .
Если мы позволим y = 0 и решить для x , мы получим x = rt .
Циклоида и синусоида
Синусоида имеет особое отношение к циклоиде. Если мы построим график переведенной синусоиды $y = r\sin(x — \frac{\pi}{2}) + r$. Это точная синусоида, только масштабированная на r . Форма такая же, как если бы мы изобразили y = sin x . Циклоида и синусоида показаны ниже.
Если мы возьмем точку P на циклоиде и проведем параллель в P, то она пересечет синусоиду в D и E и снова циклоиду в G. Отрезки PD и EG конгруэнтны в силу симметрии и равны r грех т .
Мы можем показать, что DO перпендикулярен оси x . Следовательно, сумма отрезков PD и EG равна длине хорды окружности PK для всех t . Или PK в два раза длиннее PD. Это означает, что площадь, ограниченная циклоидой и синусоидой, равна площади круга. А площадь под синусоиды равна удвоенной площади круга, так как площадь под циклоидой в 3 раза больше окружности. 9{2\pi}$ = $\left [-r\cos(2\pi-\frac{\pi}{2}) + 2\pi r \right ] — \left [-r\cos(0-\ frac{\pi}{2}) + 0 \right ] = $ $2\pi r$
9{2\pi}$ = $\left [-r\cos(2\pi-\frac{\pi}{2}) + 2\pi r \right ] — \left [-r\cos(0-\ frac{\pi}{2}) + 0 \right ] = $ $2\pi r$
циклоида
Кривая образована геометрическим местом точки, прикрепленной к окружности (цикл -> циклоида), которая катится по
прямая 1) . Другими словами:
сочетание линейного (слагаемое t) и кругового движения (слагаемые sin t и cos
т).
В уравнении Уэвелла кривая может быть записана как s = sinφ.
Древний грек уже знал эту кривую.
Значение параметра «а» определяет начальную точку по отношению к окружности:
- (обычный) циклоидный
Начальная точка находится на окружности (a = 1).
Когда начальная точка не находится на окружности, кривая называется трохоидой: - вытянутая циклоида (фр. cyclode
аллонж)
Начальная точка находится вне круга (а > 1). 903:30 - куртатный циклоид (фр. cyclode raccourcie)
Начальная точка находится внутри круга (a < 1).
Если у вас твердая рука, вы можете сделать свою собственную циклоиду на доске, сочетание линейного и кругового движения.
Когда циклоида катится по линии, траектория центра представляет собой эллипс. Для обычной циклоиды получается круг.
(обычная) циклоида
В Голландии мы используем для этой кривой также название «колесная линия» 2) , находясь в трек, за которым следует точка на велосипедное колесо.
Кривая обладает двумя замечательными качествами:
Первое качество состоит в том, что циклоида является брахистохрона 3) , то есть кривая между двумя точками в
вертикальная плоскость, вдоль которой бусине требуется самое короткое время для перемещения 4) . Галилей (который дал название кривой в 169 г.9) заявил в 1638 г. (ложно), что
брахистохрона должна быть дугой окружности. А в июне 1696 года Иоганн Бернулли бросил вызов своему брату Якобу Бернулли — оба были соперниками — решить
проблема. декабрь 1696 г. Иоганн 5) повторил свой
вызов в «Acta eruditorum» с просьбой прислать решения до Пасхи 1697 года. Иоганн и Якоб также Лейбниц , Ньютон и de L’Hpital решено
проблема.
декабрь 1696 г. Иоганн 5) повторил свой
вызов в «Acta eruditorum» с просьбой прислать решения до Пасхи 1697 года. Иоганн и Якоб также Лейбниц , Ньютон и de L’Hpital решено
проблема.
Это одна из первых вариационных задач, подлежащих изучению.
На самом деле, эта кривая является противоположной (зеркально отражающей по оси абсцисс) показанной
изгиб. Без всякой формулы можно понять, что по этой кривой путь быстрее
чем по прямой. Для циклоиды результирующая составляющая силы тяжести равна
больше, а так разгон и скорость, сразу после старта. Также легко
проверить экспериментально, что путь по прямой занимает больше времени.
Эти знания можно использовать во время катания на лыжах: быстрее выбрать спуск, чтобы
вы набираете скорость, чем избегать склонов.
Второе качество состоит в том, что циклоида является таутохроной (иногда называют: изохрона ) 6) . Это означает, что буртик вдоль кривой нуждается в
то же время, чтобы спуститься, независимо от исходной точки. Замечательно! Это был христианин
Гюйгенс , открывший этот факт в 1659 году. В своем трактате «Horologium Oscilatorium»
(1673) он проектирует часы с маятником переменной длины. Маятник движется между
две щеки, обе имеют форму циклоиды. Покачиваясь во внешнюю сторону, маятник
укорачивается. Гюйгенс использовал идею о том, что эвольвента
циклоиды — это та же циклоида (конечно, справедливо и для эволюты).
Это означает, что буртик вдоль кривой нуждается в
то же время, чтобы спуститься, независимо от исходной точки. Замечательно! Это был христианин
Гюйгенс , открывший этот факт в 1659 году. В своем трактате «Horologium Oscilatorium»
(1673) он проектирует часы с маятником переменной длины. Маятник движется между
две щеки, обе имеют форму циклоиды. Покачиваясь во внешнюю сторону, маятник
укорачивается. Гюйгенс использовал идею о том, что эвольвента
циклоиды — это та же циклоида (конечно, справедливо и для эволюты).
Этой конструкцией была компенсирована неравномерность нормального маятника. Для нормального
маятника, то время колебаний лишь в первом приближении не зависит от
отложить в сторону 7) . Гюйгенс был весьма впечатлен, он написал над доказательством: ‘magna nec ingenijs Investigata Priorum’, чтобы быть
переводится как: «это нечто великое, никогда ранее не исследованное гением».
В своих экспериментах Гюйгенс также использовал эвольвенту
круга в его маятниковых часах, чтобы аппроксимировать циклоидный путь.
Однако использование принципа таутохроны при конструировании маятниковых часов
много механических проблем, чтобы сделать его распространенным.
Качество таутохронии можно прочесть и в «Моби Дике», книге Германа Мелвилла, в трактате о котле для китового жира.
Вот некоторые интересные свойства циклоиды:
Куза был первым, кто изучил кривую в наше время, когда пытался
найти площадь круга. Мерсенн (1599) дал первое правильное определение
циклоиды, он попытался найти площадь под кривой, но безуспешно. Он представил
вопрос к Робервалю , решившему его в 1634. Позже Торричелли самостоятельно нашел площадь кривой.
Декарт нашел, как провести касательную к циклоиде, он бросил вызов Роберваль найти решение Робервалю не удалось, но Ферма удалось. Также Вивиани нашел касательную.
В августе 1658 года Паскаль опубликовал задание с двумя призами под именем Амос Деттонвилль . Он задал 9 вопросов о циклоиде, задав площадь и центр тяжести ее сегмента.
Он задал 9 вопросов о циклоиде, задав площадь и центр тяжести ее сегмента.
Говорят, что для Паскаля изучение кривой было хорошим развлечением от сильной зубной боли.
Wallis и Laloure введены, оба не были успешными. Слуза , Ricci , Huygens , Wren и Fermat не участвовали в конкурсе,
но все писали свое решение на Паскале. 10 октября 1658 года Паскаль опубликовал свою собственную
решения вместе с расширением результата Wren .
Газета называлась «Histoire de la Roulette, appel autrement Trochoide ou Cycloide».
Desargues предложил зубья для зубчатых колес в форме циклоиды (около 1635).
Якоб и Иоганн Бернулли показал (1692), что циклоида является катакаустической
круга, где световые лучи исходят от окружности.
Циклоидная арка с лучами, перпендикулярными оси X, приводит к двум циклоидным аркам.
Итак, циклоида была очень популярна среди математиков 17 века.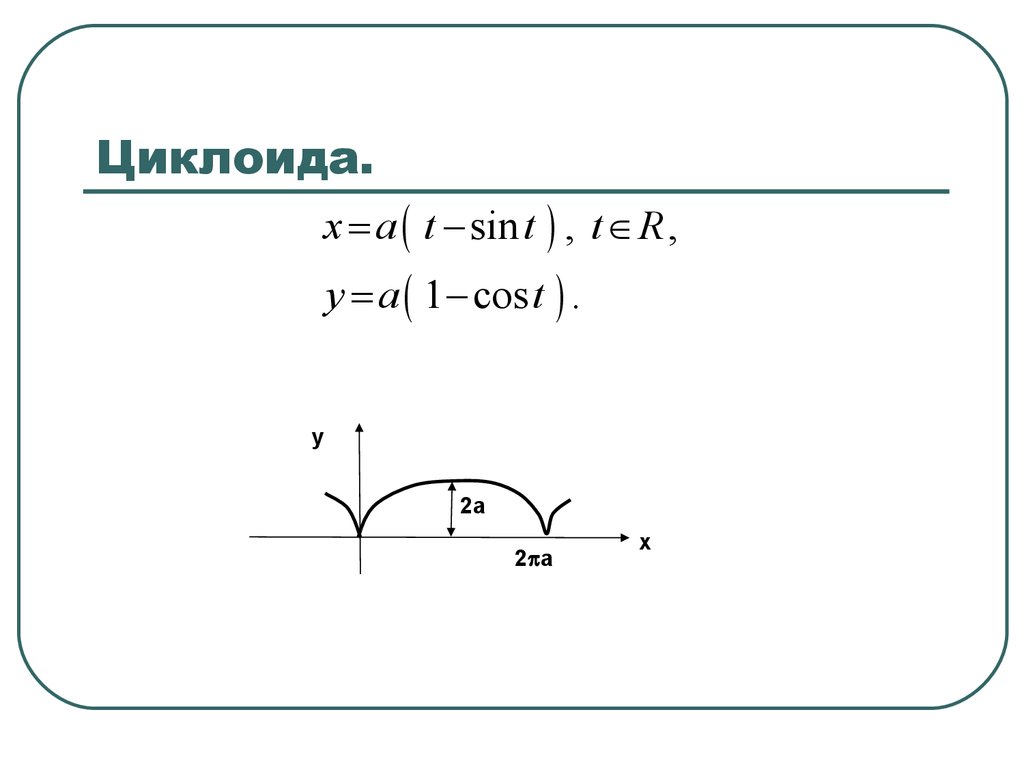 Поэтому позже кривой было присвоено имя ссора кривая , Елена Геометров и яблоко раздора 9) .
Поэтому позже кривой было присвоено имя ссора кривая , Елена Геометров и яблоко раздора 9) .
В Музее фортепиано в Хопкинтоне 10) можно найти пианино, задняя кромка которого имеет форму циклоиды.
Создатель Генри Линдеман назвал инструмент «Циклоидным».
Гранд», в конце 1800-х гг.
Но при взгляде сверху вы видите, что его форма отличается от настоящей циклоиды:
Зубчатые колеса имеют циклоидальную форму, их можно аппроксимировать серией дуг окружности. Также можно использовать числовые таблицы, например, Джордж Одонтограф Гранта , так же называется инструмент для снятия очертания зубьев зубчатых колес.
Кривая представляет собой пойнт-рулетку.
Теперь отслеживаемая точка не лежит на окружности. Когда точка лежит снаружи
круг, кривая называется вытянутой циклоидой (или удлиненная циклоида ).
Когда точка лежит внутри катящегося круга, кривая называется циклоид куртате (или сжатая циклоида ). Последняя кривая следует
клапаном велосипеда. Вот откуда название клапан кривой для циклоиды от.
Последняя кривая следует
клапаном велосипеда. Вот откуда название клапан кривой для циклоиды от.
Первыми исследовали кривую Drer (1525) и Rmer (1674).
С пропеллером Voith-Schneider (VSP),
впервые испытанный в 1927 году, корабль способен точно маневрировать и отходить в сторону.
Пропеллеры вращаются вокруг оси, вертикальной к движению, так что они
Следуйте по пути циклоиды. Положение лопастей определяет направление
судна, и он основан на том же принципе действия плавников рыбы.
Пропеллер называется циклоидальным или трохоидальным пропеллером.
примечания
1) Пусть есть окружность с центром (0,R)
и точку (p, 0) в качестве начальной точки для броска. Тогда координаты г.
циклоида, как функция угла прокатки t
2) На голландском языке: radlijn
3) Брахисто (греч.) или brachus (лат.) = краткий, хронос (Гр.) = время
4) На высоте y шарик приобретает скорость √gy, поэтому
что минимизация времени в пути означает минимизацию интеграла
.

 Слова с 1 буквой д
Слова с 1 буквой д в ст. Линия). Эпициклоида и гипоциклоида являются траекториями точек внешней и внутренней вспомогательных окружностей…
в ст. Линия). Эпициклоида и гипоциклоида являются траекториями точек внешней и внутренней вспомогательных окружностей… Leonhard (1954), обозначает фазно протекающие психозы, занимающие промежуточное положение между маниально-депрессивным психозом и шизофренией…
Leonhard (1954), обозначает фазно протекающие психозы, занимающие промежуточное положение между маниально-депрессивным психозом и шизофренией…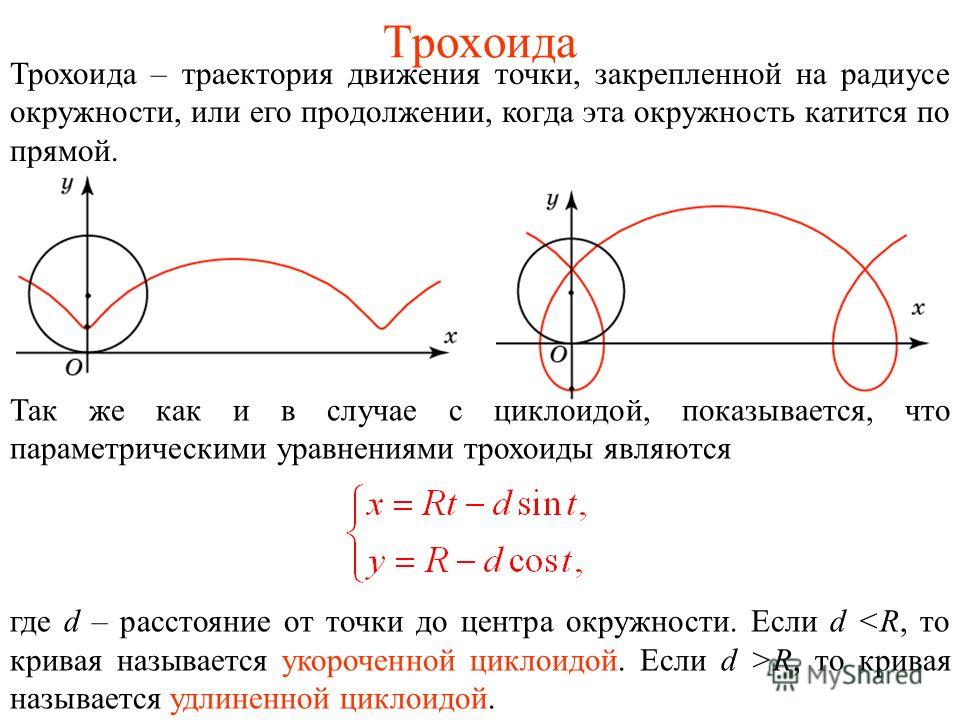

 Эти
линии высоты.
Эти
линии высоты.

