Эдвард лоренц теория хаоса: Теория хаоса

Согласно теории хаоса, даже небольшие изменения в нашем мире приводят к непредсказуемым последствиям в другом месте и в другое время.

Эдвард Лоренц, основоположник теории хаоса, назвал это явление эффектом бабочки.

Человеческое поведение — такая же сложная система. Это означает, что одно, само по себе незначительное, действие приводит нас к сложным и непредсказуемым последствиям.

• Например, лишняя чашка кофе, которую вы выпили с другом в кофейне — не просто лишняя чашка кофе, а событие, которое ведет к другим значительным событиям. Вечером вам трудно уснуть, и вы засиживаетесь допоздна перед монитором -> на следующий день не высыпаетесь и чувствуете себя разбитыми -> из-за этого пропускаете тренировку и допускаете ошибки на работе, что в свою очередь запускает другие последствия.

• Другой пример: вы погружаетесь в работу над важным проектом. Чтобы приступить к работе и сфокусироваться на творчестве нужно время. Неожиданно срабатывает оповещение на телефоне — коллега просит переслать ему файл. Вы отрываетесь от творческой работы и открываете почтовую программу -> там видите еще два письма, требующих незамедлительной реакции. Переходите по ссылке в одном из них и видите комментарий, требующий ответа. Потом проверяете сообщения в мессенджере, потому что уже привыкли проверять его вместе с почтой…

…а вечером обнаруживаете, что времени на важную работу уже не осталось. Это приводит к срыву сроков сдачи или к посредственному качеству  работы. Срыв сроков и посредственная работа в свою очередь станут причиной для последующих событий. И так далее.

Как незначительные события приводят к грандиозным последствиям

Каждое наше действие или решение, так же, как и взмах крыла бабочки, имеет множество значительных и непредсказуемых последствий. Некоторые из них позитивные — они помогают структурировать нашу жизнь и достигать целей, а другие, наоборот, негативные — создают хаос и лишают чувства контроля. Поэтому критически важно осознанно выявлять события, обладающие эффектом бабочки и управлять ими.

Вот еще несколько примеров негативных и позитивных «бабочек»:

Негативные:

• Лишняя чашка кофе.
• Пропуск одной тренировки.
• Неожиданный звонок или сообщение.
• Беспорядок дома или на рабочем месте.
• Неконтролируемая проверка почты или посещение соцсети.

Позитивные:

• Здоровый завтрак.
• Составление плана на день.
• Заряжающий утренний ритуал.
• Подготовка вещей для тренировки с вечера.
• Осознанная 10-минутная фокусировка над сложной задачей.

Хорошая новость в том, что понимание этого принципа позволяет управлять «бабочками»: предупреждать появление негативных и превращать в привычки позитивные.

Так и создается дисциплина — не благодаря силе воли, а благодаря действиям, обладающим эффектом бабочки, превращенным в привычку.

Почему грандиозные планы обречены на провал

Понимание этого принципа дает нам точку приложения рычага.

Вычислив событие, обладающее эффектом бабочки, мы можем направить фокус внимания на него. И тогда все остальное изменится само собой или станет значительно проще.

Когда я осознал ценность фокуса и понял, как бездарно сливаю время на текучку, не стал устраивать революцию в своей жизни, потому что знал, что в долгосрочной перспективе это не сработает.

Вместо этого я ввел одно правило: начинать день не с новостей и проверки почты, а с 50-минутного фокус-блока изучения английского.

Как только я это сделал,  почувствовал себя дисциплинированнее, мои мускулы фокуса стали сильнее, после этого мне было уже легче добавить еще один фокус-блок творческой работы.

Сравните это с традиционным подходом: многие люди хотят сбросить вес или просто стать сильнее.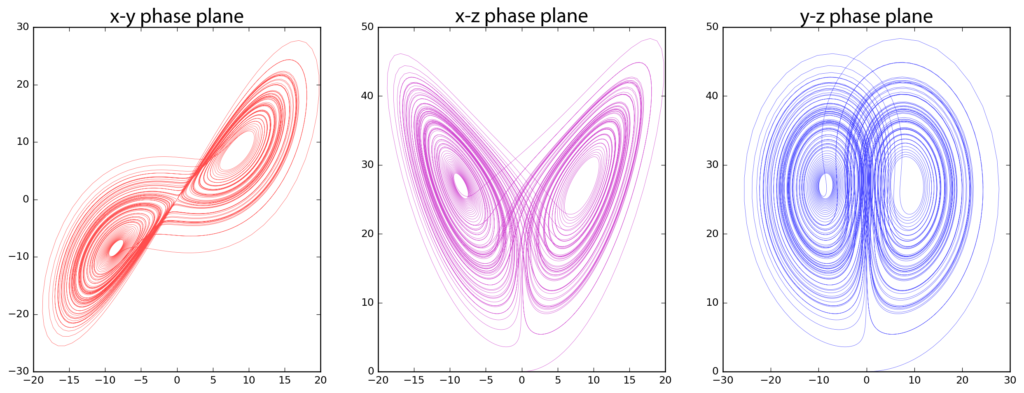 Идея начать с одного маленького действия — ежедневной 5-минутной зарядки или здорового завтрака не вдохновляет их — они презирают такие цели, считая их незначительными.

Вместо этого они «начинают новую жизнь с понедельника»: покупают абонемент в спортзал и спортивную экипировку, нанимают личного тренера, составляют программу тренировки на 6 дней в неделю и садятся на новомодную детокс-диету…

…и все это для того, чтобы через две недели окончательно выгореть и с чувством вины вернуться к привычному комфортному образу жизни.

Подчиняем хаос

Мы не можем постоянно контролировать свои реакции, но можем контролировать события, которые определяют то, что происходит с нами.

Первый шаг к управлению поведением в том, чтобы начать осознанно замечать негативные «бабочки» и заменять их позитивными. Если ваша жизнь структурирована слабо, вы легко найдете в ней десяток таких событий.

Возьмите лист бумаги и разбейте его на три столбца:

1.     В первую колонку выпишите серые зоны — временные блоки, которые проводите вне фокуса: бесцельный интернет-серфинг, непродуктивная поверхностная работа, время с близкими людьми с мыслями о работе.

2.     Во второй колонке выявите триггеры, приводящие в серую зону: привычка начинать день с проверки почты, стопка неоплаченных счетов и входящих бумаг в углу рабочего стола, оттягивающая на себя внимание, отсутствие понятного плана действий.

3.     В третьей колонке выпишите новые события, которыми вы замените привычные триггеры.

Вот пример одной из моих таблиц:

Таблица помогает выявить события, которые приводят нас в серые зоны, и позволяет осознанно управлять ими.

Так, например, одного осознания факта, что я трачу утреннее время на новости и бесцельный серфинг, для меня оказалось не достаточным. Утром я просто не мог заставить себя взяться за серьезную творческую работу: мой мозг как будто еще не проснулся до конца и все внутри меня сопротивлялось этому. По-настоящему продуктивным я становился только ближе к 11 утра.

Тогда я добавил несколько простых действий, которые позволили переломить ситуацию:

• Пятиминутный утренний комплекс упражнений из йоги, который заряжает меня энергией.
• Настроил автоматическую блокировку по расписанию новостных сайтов в программе Focus.
• Первым делом, придя в офис, делаю себе кофе, составляю план на день, привожу рабочий стол к идеальной чистоте: убираю все бумаги и протираю пыль.
• Начинаю день с блока английского, отодвигая все другие дела до его окончания.

Теперь к 12:00 я успеваю выполнить все самые важные дела, а раньше в это время мог только приступать к работе.

Выводы

1.     Человеческое поведение — сложная система. Это означает, что одно, само по себе незначительное, действие приводит нас к сложным и непредсказуемым последствиям.

2.     Люди допускают ошибку, думая о поведении, как о линейном процессе, в котором каждое действие или решение не зависит от предыдущих и не влияет на последующие. Из-за этого теряется связь между причиной и следствием.

3.     Каждое наше действие или решение имеет множество значительных и непредсказуемых последствий. Некоторые из них позитивные — они помогают структурировать нашу жизнь и достигать целей, а другие, наоборот, негативные — создают хаос и лишают чувства контроля.

4.     Понимания этого принципа дает нам точку приложения рычага. Вычислив события, обладающие эффектом бабочки и сфокусировавшись на них, мы делаем все остальное значительно проще.

5.     Первый шаг к управлению жизнью в том, чтобы начать осознанно замечать «негативные бабочки» и заменять их «позитивными».

6.     Мы можем управлять «бабочками»: предупреждать появление «негативных» и превращать в привычки «позитивные». Так создается дисциплина — не благодаря силе воле, а благодаря действиям, обладающим эффектом бабочки, превращенным в привычку.

Саморазвитие #Привычки #Продуктивность 

Основоположник теории хаоса был очень организованным человеком

«Еще мальчиком я любил проделывать разные штуки с цифрами, кроме того, меня завораживали погодные явления», — вспоминал он.

Во время второй мировой войны он служил в качестве метеоролога в ВВС США, а после войны работал на кафедре метеорологии Массачусетского технологического института, которую он возглавил в 1977 году.

После многолетних исследований он пришел к выводу: небольшие изменения, происходящие в атмосфере или аналогичных ей моделях, могут приводить к обширным и неожиданным последствиям. Он назвал это явление «сильной зависимостью от начальных условий».

В 1972 г. профессор опубликовал научную статью «О возможности предсказаний: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?». Эта формулировка иллюстрирует суть возникшей из работ Лоренца теории хаоса, которая сейчас играет важную роль едва ли не во всех областях современной науки — от математики до биологии.

«Эффект бабочки» лег в основу хорошо известных художественных произведений.

Так, в рассказе Рэя Брэдбери «И грянул гром» один из организаторов предвыборной кампании после победы своего кандидата отправляется в путешествие по времени. Фирма, организующая такую поездку, предлагает охоту на динозавров, которым в ближайшее время суждено умереть. Чтобы не нарушить сложную ткань причинно-следственных связей и не изменить будущее, следует двигаться по специальным тропам. Однако герой не смог выполнить этого условия и нечаянно раздавил золотистую бабочку. Возвратившись назад, он видит, что изменились состав атмосферы, правила правописания и итог предвыборной кампании.

В 2004 году был снят фильм «Эффект бабочки», герой которого, мальчик Эван, перенял от своего отца-психопата, странную болезнь — он не помнит некоторых эпизодов своей жизни, в которые происходили довольно странные, а то и ужасные, события.

Поступив в колледж, Эван обнаружил, что, читая свои детские дневники, может возвращаться в прошлое и своими действиями изменять будущее.

Сам же автор теории хаоса, как вспоминает один из его приятелей, был чрезвычайно организованным человеком, пишет Лента.ru.

Лоренц был избран членом Академии наук США в 1975 г. В 1983 г. он вместе с коллегой Генри Стоммелом получил премию Кроуфорда в размере 50 тысяч долларов от Шведской королевской академии наук. Так отмечаются достижения ученых, специальности которых не позволяют претендовать на Нобелевскую премию. В 2004 он был награжден Большой золотой медалью имени М. В. Ломоносова.

Оставив руководство кафедрой в Массачусетском институте, он преподавал в различных вузах Европы и Америки. Лоренц являлся иностранным членом по Отделению океанологии, физики атмосферы и географии (геофизическая гидродинамика) АН СССР (с 1991 — РАН) с 27 декабря 1988 г.

«Показав, что сложные системы со множеством причинно-следственных связей имеют порог предсказуемости, Эд забил последний гвоздь в гроб вселенной Декарта и произвел то, что многие называют третьей научной революцией XX в. после теории относительности и квантовой физики», — сказал Керри Эмануэль, профессор метеорологии в МИТ.

Материал подготовлен интернет-редакцией www.rian.ru на основе информации РИА Новости и открытых источников

Теория хаоса или как увидеть эффект бабочки?

Камила Мамедова

16 сентября 2019, 10:16

Классическая история: Вы отправляетесь в прошлое и убиваете своего дедушку, до того, как он успевает повстречать Вашу бабушку.

Вы все еще так думаете? Тогда, мы идем к Вам!

Мы с американским математиком и метеорологом Эдвардом Лоренцом.

Вот скажите, среди Ваших знакомых есть хотя бы один метеоролог? Наверное, это очень грустный человек, потому что профессия метеоролога, судя по всему, адски скучная.

Настолько скучная, что в 1961 году Лоренц не нашел, чем себя занять, и решил еще раз перепроверить результаты моделирования погодных условий. Взял бумажную распечатку и от руки внес данные в компьютер. 

Как это работает?

Компьютер анализирует начальные условия и выдает нам данные о погоде в следующий четверг, например. Но тут внезапно оказалось, что повторное моделирование дало прямо противоположный результат: в ясный солнечный день внезапно ударит молния и пойдет дождь.

Оказалось, что числа на распечатке, которую использовал Лоренц, выводились с точностью до трех знаков после запятой, т.е. данные были округлены.

Внезапно, число вроде 0,673122 сокращалось до 0,673.

Разница в одну тысячную имела колоссальное значение. Так Лоренц стал одним из пионеров теории хаоса.

В сложной нелинейной динамической системе, коей и является мир социальных связей, в котором мы с Вами живем, малое изменение начальных условий, приводит к огромным изменениям результата!

Лоренц назвал это «эффектом бабочки». Взмах крыльев бабочки в Айове может вызвать целую лавину эффектов, которые приведут к дождливому сезону в Индонезии…

Это также отсылка к рассказу Рэя Бредбери «И грянул гром…», где гибель бабочки в далеком прошлом полностью изменила весь мир настоящего.

Что это значит для нас? А это значит, что любое решение, которое мы принимаем, каждый наш шаг и вздох имеет огромный эффект даже в ближайшем будущем. Когда мы смотрим на событие из прошлого, рассуждаем об истории человечества или просто о своей жизни, мы часто задаемся вопросом «а что, если бы я тогда поступил иначе, что изменилось бы?»

Теория Хаоса дает нам точный ответ на этот вопрос. Изменилось бы ВСЁ.

Некоторые решения в жизни кажутся нам судьбоносными. Это может быть выбор ВУЗа, в который поступить, решение о переезде в другой город или новое полезное знакомство, но, если учесть влияние «эффекта бабочки», то окажется, что в долгосрочной перспективе, даже то, сколько ложек сахара Вы решили положить в утренний чай, внесет несоизмеримый вклад в то, как будет развиваться человечество в дальнейшем.

Но не обольщайтесь, это касается всех и всего. Ваш кот, например, решает судьбу человечества почти в той же степени. При этом, из-за огромного количества переменных, мы никогда не сможем сказать наперед, каким именно будет эффект. Они все накладываются друг на друга, все мелкие события, все переменные, из-за которых предсказать даже ближайшее будущее становиться практически невозможно.

А значит, отправившись в прошлое, лет эдак на шестьдесят, даже просто посмотрев на своего дедушку издалека, каждый Ваш шаг, каждый вздох, каждый контакт с любым предметом в прошлом, внесет несоизмеримо огромный вклад в хаотичную нелинейную динамическую систему под названием «жизнь»

По материалам Научпок

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Новости о науке, технике, вооружении и технологиях.

Подпишитесь и будете получать свежий дайджест лучших статей за неделю!

Email*

Подписаться

Теория хаоса и другие явления, ставшие научными открытиями

Спецпроекты ЛГ / Научная среда / Теории, которые изменили мир

Прощайте, Ньютон и Эйнштейн!

Теория хаоса – это наука о сложных нелинейных динамических системах. Что такое сложные – вроде бы понятно.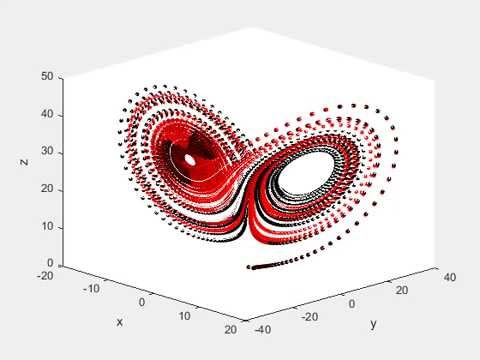 Динамические – это которые непостоянные и неповторяющиеся, то есть непериодические. А нелинейные – вздохните глубже – это рекурсивные системы.

Что такое рекурсия? Вот в фильме «12 друзей Оушена» Джулия Робертс сыграла героиню, которая по фильму в течение некоторого времени играла Джулию Робертс. Это упрощённый пример, потому что для того, чтобы понять рекурсию, надо сначала понять рекурсию (эта фраза рекурсивна!).

Теория хаоса окончательно добила классическую физику Ньютона и релятивистскую физику Эйнштейна, о которых мы рассказали выше. Возможно, Ньютон и Эйнштейн предчувствовали, что с их творениями так поступят, и поэтому большую часть жизни занимались изысканиями неведомой и поныне супертеории, которая упорядочила бы мировую науку раз и навсегда.

Вот как выразил сущность теории хаоса, которую можно назвать теорией нестабильности нобелевский лауреат Илья Пригожин, франко-американский учёный, семья которого в 1917 году эмигрировала из России.

«Если взять устойчивый маятник и раскачать его, то дальнейший ход событий можно предсказать однозначно: груз вернётся к состоянию с минимумом колебаний, т.

Это различие между детерминистическими законами природы и законами, не являющимися таковыми, ведёт нас к более общим проблемам…»

Хаос – это вовсе не синоним беспорядка. Это такое состояние чего-либо, когда от малейшего вздоха или взмаха крылышек какой-нибудь козявки (к козявкам мы ещё вернёмся) меняется, ломается и рушится что-то огромное и величественное и далее пребывает в состоянии сложности, нелинейности и динамичности.

Вплоть до 1960-х годов многие учёные считали, что динамическая система, описываемая простыми уравнениями, должна вести себя относительно просто, хотя уже более столетия было известно, что это верно лишь в некоторых, весьма специальных случаях, таких как Солнечная система. Однако к 1980 году математики и естествоиспытатели обнаружили, что хаос вездесущ.

Пример хаотического поведения из повседневной жизни – движение жидкости в миксере. Это устройство подчиняется простым механическим законам: его нож-смеситель вращается с постоянной скоростью, и взаимодействие жидкости с ножом внутри миксера можно описать простыми детерминистическими уравнениями. Однако возникающее при этом движение жидкости весьма сложно. Её соседние области рассекаются ножом и разделяются, а отдалённые области могут сближаться. Короче говоря, жидкость перемешивается – для этого миксеры и предназначены.

Выражение «теория хаоса» используется преимущественно в популярной литературе. Специалисты же рассматривают эту дисциплину как раздел теории динамических систем.

Фракталы и аттракторы

Все рассказы о теории хаоса довольно хаотичны или по меньшей мере не слишком логичны. Отцом теории хаоса считается американский метеоролог Эдвард Лоренц. «Ещё мальчиком я любил проделывать разные штуки с цифрами, кроме того, меня завораживали погодные явления», – вспоминал Лоренц. Всё это помогло ему сделать важнейшее открытие. Он создал компьютерную модель земной атмосферы, которая показала, что небольшие изменения, происходящие в атмосфере или аналогичных ей моделях, могут приводить к обширным и неожиданным последствиям.

В 1972 году Лоренц опубликовал научную статью, заглавие которой стало нарицательным. Она называлась «О возможности предсказаний: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?». Эта формулировка иллюстрирует суть теории хаоса, которая сейчас играет важную роль едва ли не во многих областях современной науки.

«Показав, что сложные системы со множеством причинно-следственных связей имеют порог предсказуемости, Эд забил последний гвоздь в гроб вселенной Декарта и произвёл то, что многие называют третьей научной революцией XX века после теории относительности и квантовой физики», – сказал о Лоренце Керри Эмануэль, профессор метеорологии из Массачусетского технологического института.

Лоренц открыл и первый «странный аттрактор». Просто аттрактор – это область притяжения фазовых траекторий. То есть место, куда стягиваются «свободные частицы». Аттрактор для простого маятника – нижняя точка его траектории. Покачается и остановится. А странный аттрактор – это такая точка притяжения, из которой система попадает неведомо куда. И ещё потом долго, извините за выражение, «колбасится». Кстати, любая революция – типичный странный аттрактор.

На самом деле у теории хаоса было не меньше дюжины отцов. Одних из них признают за таковых, но отодвигают в тень распиаренного метеоролога с его бабочкой. А других¸ например, нобелевского лауреата Илью Пригожина вообще ранжируют по другой отрасли. Но, впрочем, обо всём по порядку.

Впервые проблемы хаотического движения стал исследовать Анри Пуанкаре, положивший начало ещё и теории катастроф, близкой родственницы теории хаоса. Его дело продолжил Жак Адамар, написавший статью под говорящим названием «Бильярд Адамара». В ней он описал хаотическое блуждание «свободных частиц», воспользовавшись методами русского математика Ляпунова, который также может считаться одним из отцов теории хаоса.

В самом начале теория хаоса была эргодической. Эргодический подход очень наглядно описал ещё один родоначальник и творец теории хаоса великий математик Владимир Арнольд: если вы хотите понять, как высоко вырастет маленькая ёлка, которую вы увидели в лесу, то не обязательно сидеть и ждать двадцать лет. Достаточно посмотреть на соседние взрослые ели. Вот и первые исследователи хаоса, не в силах уследить за суетливыми «свободными частицами», наблюдали поведение в целом всей нелинейной системы.

После Второй мировой войны к изучению хаоса подключились ведущие математики мира, первым среди которых стоит гениальный советский математик академик Андрей Колмогоров, один из величайших учёных прошлого века.

Колмогоров моделировал динамику превращения ламинарного течения жидкости в турбулентное, то есть вихревое. Это было необходимо для аэродинамических экспериментов. Учёный создал математическую модель динамики вихрей, рассматривая их во всё меньшем и меньшем масштабе, до тех пор пока вихри не стали совсем крошечными, когда вязкость жидкости уже на них не влияла. Колмогоров предположил, что вся жидкость состоит из одинаковых маленьких вихревых потоков, то есть однородна. Такая модель дала некоторое продвижение в исследованиях, но в дальнейшем пришлось принять модель Пуанкаре, который, наблюдая течение бурной речки, установил, что вихри не вездесущи, а основная часть потока спокойна. Таким образом, модель однородной жидкости сменилась моделью прерывистости. Следующим шагом была теория советского физика Льва Ландау. Модель Ландау – это нагромождение конкурирующих между собой вихрей. Огромный вклад в науку внесла знаменитая теория КАМ (Колмогорова, Арнольда и Мозера), названная так в честь её создателей Андрея Колмогорова, Владимира Арнольда и Юргена Мозера. Эта теория затрагивала вопросы устойчивости динамических систем, одной из которых, как известно, является Солнечная система.

Тем не менее работа над этой тематикой продвигалась не очень легко, вплоть до появления первых компьютеров.

Именно компьютерное моделирование помогло Лоренцу увидеть тот самый эффект бабочки. А талантливый вундеркинд Бенуа Мандельбро открыл с помощью компьютера совершенно необычные объекты – фракталы. Самый простой фрактал – береговая линия на карте. Сколько ни меняй масштаб карты, линия берега всегда будет изрезанной и витиеватой, то есть фрактальной. Снежинки – тоже фракталы. Если обобщить, то фракталом называется объект, изображения которого постоянны в любых масштабах.

Мандельбро написал книгу «Фрактальная геометрия природы», которая стала классическим описанием теории хаоса. Кто хочет посмотреть живьём на пресловутую рекурсию, может полюбоваться фотографиями фракталов Мандельбро. Фрактально устроены, кстати, кровеносная и бронхиальная системы людей и животных.

Во второй половине XX века теорию хаоса стали применять в самых различных областях – ею пытались объяснить различные процессы и явления: землетрясения, солнечные всплески, колебания в экономических системах, формирование ландшафта, лесные пожары, оползни, эпидемии, биологическую эволюцию и даже возникновение войн.

Илья Пригожин – философ нестабильности

Великий учёный прошлого века Илья Романович Пригожин получил Нобелевскую премию 1977 года по химии за работы по термодинамике необратимых процессов, особенно за теорию диссипативных структур.

Теорию диссипативных систем в России называют синергетикой, в Америке – теорией сложности, но в сущности это всё та же теория хаоса. Просто как во всякой молодой научной дисциплине, мы здесь имеем дело с ещё не сложившейся терминологией.

Заслуга Пригожина ещё и в том, что он проанализировал культурологическое значение новейших научных течений и связал их с эволюцией идеологий и взглядов величайших учёных прошлого:

«Для того чтобы понять идущие в современной науке процессы, необходимо принять во внимание, что наука – культурный феномен, складывающийся в определённом культурном контексте. Иллюстрацией этому может служить, например, дискуссия между Лейбницем и Кларком, представлявшим в их споре взгляды Ньютона. Лейбниц упрекает Ньютона в том, что его представление об универсуме предполагает периодическое вмешательство Бога в устройство мироздания ради улучшения функционирования последнего. Ньютон, по его мнению, недостаточно почитает Бога, поскольку искусность Верховного Творца у него оказывается ниже даже искусности часовщика, способного раз и навсегда сообщить своему механизму движение и заставить его работать без дополнительных переделок.

Лейбницевские представления об универсуме одержали победу над ньютонианскими. Лейбниц апеллировал к всеведению вездесущего Бога, которому вовсе нет никакой нужды специально обращать своё внимание на Землю. И он верил при этом, что наука когда-нибудь достигнет такого же всеведения, – учёный приблизится к знанию, равному божественному. Для божественного же знания нет различия между прошлым и будущим, ибо всё присутствует во всеведущем разуме. Время с этой точки зрения элиминируется неизбежно, и сам факт его исключения становится свидетельством того, что человек приблизился к квазибожественному знанию.

Высказанные Лейбницем утверждения принадлежат к базовому уровню идеологии классической науки, сделавшей именно устойчивый маятник объектом научного интереса, – неустойчивый маятник в контексте этой идеологии предстаёт как неестественное образование, упоминаемое только в качестве любопытного курьёза (а по возможности вообще исключаемое из научного рассмотрения). Но изложенная концепция вечности грешила тем, что в ней не оставалось места для уникальных событий (впрочем, и в ньютоновском подходе не было места для новаций). Материя, согласно этой концепции, представляет собой вечно движущуюся массу, лишённую каких бы то ни было событий и, естественно, истории. История же, таким образом, оказывается вне материи. Так исключение нестабильности, обращение к детерминизму и отрицание времени породили два противоположных способа видения универсума:

– универсум как внешний мир, являющийся в конечном счёте регулируемым автоматом (именно так и представлял его себе Лейбниц), находящимся в бесконечном движении;

– универсум как внутренний мир человека, настолько отличающийся от внешнего, что это позволило Бергсону сказать о нём: «Я полагаю, что творческие импульсы сопровождают каждое мгновение нашей жизни».

Действительно, любые человеческие и социальные взаимодействия, а также вся литературная деятельность являются выражением неопределённости в отношении будущего. Но сегодня, когда физики пытаются конструктивно включить нестабильность в картину универсума, наблюдается сближение внутреннего и внешнего миров, что, возможно, является одним из важнейших культурных событий нашего времени».

Позвольте этой великолепной цитатой знаменитого учёного закончить наш краткий рассказ о величайших научных теориях, изменивших мир и мировоззрение человечества.

Э. Н. Лоренц. Теория Хаоса

СОДЕРЖАНИЕ:

1.Краткая биография………………………………………………………………………3

2.Теория хаоса……………………………………………………………………………..4

  2.1.Основные сведения………………………………………………………………….6

  2.2.Понятие хаоса………………………………………………………………………..6

  2.3.Чувствительность к начальным условиям………………………………………….7

  2.4 Топологическое смешивание……………………………………………………….7

  2.5. Тонкости определения………………………………………………………….…..8

3. Аттракторы………………………………………………………………………………9

4. Странные аттракторы………………………………………………………………….10

5. Простые хаотические системы………………………………………………………..11

• 6. Математическая теория…………………………………………………………….….12
• 7. Хронология……………………………………………………………………………..13
• 8. Применение…………………………………………………………………………….15

9. Список литературы……………………………………………………………….…….17

Краткая биография.

Эдвард Нортон Лоренц (23.05.1917-16.04.2008)- американский математик и метеоролог, один из основоположников Теории Хаоса, автор Эффекта бабочки, Аттрактора Лоренца.

Эдвард  Нортон Лоренц родился в г. Вест-Хартфорд (шт. Коннектикут, США) в 1917 г., учился математике в Гарварде и метеорологии в знаменитом Массачусетском технологическом институте (МИТ), где в 1943 г. получил степень доктора наук. Во время Второй мировой войны служил в качестве метеоролога в ВВС США, после войны в течение долгих лет работал на кафедре метеорологии МИТ, которую и возглавил в 1977 году.

С 1946 года работал в Массачусетском технологическом институте, профессор. Является членом Американской академии гуманитарных и естественных наук, Американского метеорологического общества и Национальной академии наук США. Иностранный член по Отделению океанологии, физики атмосферы и географии(геофизическая гидродинамика) АН СССР (с 1991- РАН) с 27 декабря 1988 г.

В 2004 награжден Большой золотой  медалью имени М.В. Ломоносова

“Еще  мальчиком я любил проделывать  разные штуки с цифрами, кроме  того, меня завораживали погодные явления”, — вспоминал Лоренц. Подобные наклонности  позволили ученому сделать важнейшее  открытие. После многолетних исследований он пришел к выводу: небольшие изменения, происходящие в атмосфере или  аналогичных ей моделях, могут приводить  к обширным и неожиданным последствиям.

В 1972 г. профессор опубликовал научную  статью, заглавие которой стало нарицательным. Она называлась “О возможности предсказаний: может ли взмах крыльев бабочки  в Бразилии вызвать торнадо в  Техасе?”. Эта формулировка отлично  иллюстрирует суть возникшей из работ  Лоренца теории хаоса, которая сейчас играет важную роль едва ли не во всех областях современной науки — от математики до биологии.

В 1975 г. Лоренца избрали членом Академии наук США, его заслуги были отмечены многочисленными наградами. В 1983 г. он и его коллега Генри Стоммел вместе получили Премию Кроуфорда в размере $50 тыс. от Шведской королевской академии наук. Таким образом скандинавы отмечают достижения ученых, специальности которых не позволяют претендовать на Нобелевскую премию.

Эдвард  Лоренц являлся иностранным членом Российской академии наук. Оставив  руководство кафедрой в Массачусетском институте, он преподавал в различных  вузах Европы и Америки. Эдвард также  не оставлял свои научные изыскания, и, по словам семьи, занимался метеорологией  буквально до последних дней жизни.

“Показав, что сложные системы со множеством причинно-следственных связей имеют порог предсказуемости, Эд забил последний гвоздь в гроб вселенной Декарта и произвел то, что многие называют третьей научной революцией XX в. после теории относительности и квантовой физики, — сказал Керри Эмануэль, профессор метеорологии в МИТ. — Он также был безупречным джентльменом, его интеллигентность, честность и скромность показали важный пример будущим поколениям ученых”.

Теория хаоса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос. Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной.

Примерами подобных систем являются атмосфера, турбулентные потоки, биологические популяции, общество как система коммуникаций и его подсистемы: экономические, политические и другие социальные системы. Их изучение, наряду с аналитическим исследованием имеющихся рекуррентных соотношений, обычно сопровождается математическим моделированием, эффект Коновала — распределение частот выпадения положительных результатов, или принятия правильных решений.

Теория хаоса — область  исследований, связывающая математику и физику.

Основные сведенья

Теория хаоса гласит, что  сложные системы чрезвычайно  зависимы от первоначальных условий  и небольшие изменения в окружающей среде ведут к непредсказуемым  последствиям.

Математические системы  с хаотическим поведением являются детерминированными, то есть подчиняются  некоторому строгому закону и, в каком-то смысле, являются упорядоченными. Такое  использование слова «хаос» отличается от его обычного значения.

 Существует также такая  область физики, как теория квантового хаоса, изучающая недетерминированные системы, подчиняющиеся законам квантовой механики.

Пионерами теории считаются  французский физик и философ Анри Пуанкаре (доказал теорему о возвращении), советские математики А. Н. Колмогоров и В. И. Арнольд и немецкий математик Ю. К. Мозер, построившие теорию хаоса, называемую КАМ (теория Колмогорова — Арнольда — Мозера). Теория вводит понятие аттракторов (в том числе, странных аттракторов как притягивающих канторовых структур), устойчивых орбит системы (т. н. КАМ-торов).

Понятие хаоса 

Основная статья: Динамический хаос

Пример чувствительности системы к первоначальным условиям, где x → 4 x (1 — x) и y → x + y, если x y <1 (иначе x + y — 1). Здесь четко видно, что ряды значений x и y через какое-то время заметно отклоняются друг от друга хотя в первоначальных состояниях отличия микроскопические

В бытовом контексте слово  «хаос» означает «быть в состоянии беспорядка». В теории хаоса прилагательное хаотический определено более точно. Хотя общепринятого универсального математического определения хаоса нет, обычно используемое определение говорит, что динамическая система, которая классифицируется как хаотическая, должна иметь следующие свойства:

1. она должна быть чувствительна к начальным условиям
2. она должна иметь свойство топологического смешивания
3. её периодические орбиты должны быть всюду плотными.

Более точные математические условия возникновения хаоса  выглядят так:

1. Система должна иметь нелинейные характеристики, быть глобально устойчивой, но иметь хотя бы одну неустойчивую точку равновесия колебательного типа, при этом размерность системы должна быть не менее 1,5 (т.е. порядок дифференциального уравнения не менее 3-го).

Линейные системы никогда не бывают хаотическими. Для того, чтобы динамическая система была хаотической, она должна быть нелинейной. По теореме Пуанкаре-Бендиксона (Poincaré-Bendixson), непрерывная динамическая система на плоскости не может быть хаотической. Среди непрерывных систем хаотическое поведение имеют только неплоские пространственные системы (обязательно наличие не менее трёхизмерений или неевклидова геометрия). Однако дискретная динамическая система на какой-то стадии может проявить хаотическое поведение даже в одномерном или двумерном пространстве.

Чувствительность  к начальным условиям.

Чувствительность к начальным  условиям в такой системе означает, что все точки, первоначально близко приближенные между собой, в будущем имеют значительно отличающиеся траектории. Таким образом, произвольно небольшое изменение текущей траектории может привести к значительному изменению в её будущем поведении. Доказано, что последние два свойства фактически подразумевают чувствительность к первоначальным условиям (альтернативное, более слабое определение хаоса использует только первые два свойства из вышеупомянутого списка).

Чувствительность к начальным  условиям более известна как «Эффект бабочки». Термин возник в связи со статьёй «Предсказание: Взмах крыльев бабочки в Бразилии вызовет торнадо в штате Техас», которую Эдвард Лоренц в 1972 году вручил американской «Ассоциации для продвижения науки» в Вашингтоне. Взмах крыльев бабочки символизирует мелкие изменения в первоначальном состоянии системы, которые вызывают цепочку событий, ведущих к крупномасштабным изменениям. Если бы бабочка не хлопала крыльями, то траектория системы была бы совсем другой, что в принципе доказывает определённую линейность системы. Но мелкие изменения в первоначальном состоянии системы могут и не вызывать цепочку событий.

Топологическое  смешивание.

Топологическое смешивание в динамике хаоса означает такую схему расширения системы, что одна её область в какой-то стадии расширения накладывается на любую другую область. Математическое понятие «смешивание», как пример хаотической системы, соответствует смешиванию разноцветных красок или жидкости.

Тонкости определения.

Пример топологического  смешивания, где x → 4 x (1 — x) и y → x + y, если x + y <1 (иначе x + y — 1). Здесь синий регион в процессе развития был преобразован сначала в фиолетовый, потом в розовый и красный регионы и в конечном итоге выглядит как облако точек, разбросанных поперек пространства

В популярных работах чувствительность к первоначальным условиям часто  путается с самим хаосом. Грань  очень тонкая, поскольку зависит  от выбора показателей измерения и определения расстояний в конкретной стадии системы. Например, рассмотрим простую динамическую систему, которая неоднократно удваивает первоначальные значения. Такая система имеет чувствительную зависимость от первоначальных условий везде, так как любые две соседние точки в первоначальной стадии впоследствии случайным образом будут на значительном расстоянии друг от друга. Однако её поведение тривиально, поскольку все точки кроме нуля имеют тенденцию к бесконечности, и это не топологическое смешивание. В определении хаоса внимание обычно ограничивается только закрытыми системами, в которых расширение и чувствительность к первоначальным условиям объединяются со смешиванием.

Даже для закрытых систем, чувствительность к первоначальным условиям не идентична с хаосом в  смысле изложенном выше. Например, рассмотрим тор (геометрическая фигура, поверхность вращения окружности вокруг оси лежащей в плоскости этой окружности — имеет форму бублика), заданный парой углов (x, y) со значениями от нуля до 2π. Отображение любой точки (x, y) определяется как (2x, y+a), где значение a/2π является иррациональным. Удвоение первой координаты в отображении указывает на чувствительность к первоначальным условиям. Однако, из-за иррационального изменения во второй координате, нет никаких периодических орбит — следовательно отображение не является хаотическим согласно вышеупомянутому определению.

Аттракторы.

График аттрактора Лоренца  для значений r = 28, σ = 10, b = 8/3

Аттра́ктор (англ. attract — привлекать, притягивать) — множество состояний (точнее — точек фазового пространства) динамической системы, к которому она стремится с течением времени. Наиболее простыми вариантами аттрактора являются притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением) и периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), однако бывают и значительно более сложные примеры. Некоторые динамические системы являются хаотическими всегда, но в большинстве случаев хаотическое поведение наблюдается только в тех случаях, когда параметры динамической системы принадлежат к некоторому специальному подпространству.

Наиболее интересны случаи хаотического поведения, когда большой  набор первоначальных условий приводит к изменению на орбитахаттрактора. Простой способ продемонстрировать хаотический аттрактор — это начать с точки в районе притяжения аттрактора и затем составитьграфик его последующей орбиты. Из-за состояния топологической транзитивности, это похоже на отображения картины полного конечного аттрактора. Например, в системе описывающей маятник — пространство двумерное и состоит из данных о положении и скорости. Можно составить график положений маятника и его скорости. Положение маятника в покое будет точкой, а один период колебаний будет выглядеть на графике как простая замкнутая кривая. График в форме замкнутой кривой называют орбитой. Маятник имеет бесконечное количество таких орбит, формируя по виду совокупность вложенных эллипсов.

Странные аттракторы.

Аттрактор Лоренца как  диаграмма хаотической системы. Эти два графика демонстрируют  чувствительную зависимость от первоначальных условий в пределах занятого аттрактором  региона

Что такое теория хаоса? Кратко — Наука и Техника — Каталог статей

Что такое теория хаоса? Кратко

Теория хаоса представляет собой область математики, изучающей, каким образом малые изменения в исходных условиях способны, применительно к сложным динамическим системам, вести к широкому разбросу результирующих данных. Теория хаоса оказалась применима на практике в самых разных отраслях знания, включая метеорологию, биологию и физику. Хотя системы, типичные для указанных научных дисциплин, являются по сути своей детерминированными и не должны содержать случайных элементов, то хаотичное поведение, которое, со всей очевидностью, проявляют порой эти системы, делает соответствующее прогнозирование весьма затруднительным. Зачинателем теории хаоса был американский математик и метеоролог Эдвард Лоренц (1917-2008). В1961 году Лоренц с помощью компьютера строил модель, предназначенную для прогнозирования погоды. Начал он с ввода данных таких взаимосвязанных переменных, как температура, влажность, атмосферное давление и сила и направление ветра. Впервые запустив программу, он ввел с клавиатуры число .506127 для одной из переменных. Затем, работая с той же программой снова, он ввел сокращенный вариант — .506.И обнаружилось, что прогноз погоды во втором случае существенно отличался от первоначального.

Столь малое значение — .000127, составлявшее разницу между вводимыми данными, обернулось колоссальной разницей в конечном результате.

В1963 году коллеги Лоренца заметили, что если он был прав в своих наблюдениях, то «един взмах крыльев чайки способен навеки изменить картину погоды». В1972 году, озаглавив свою научную статью «Взмах крыльев бабочки в Бразилии вызовет торнадо в штате Техас», Лоренц обозначил проблему. И таким образом теория хаоса получила свое популярное имя: «эффект бабочки». Разумеется, единый взмах крыльев бабочки сам по себе не способен породить торнадо — свою роль играют и многие другие факторы. Однако же если немного видоизменить метафору — одна соломинка способна сломать спину верблюду.

Несмотря на свое название, теория хаоса использует строгий математический аппарат и помогает прояснить скрытый порядок, таящийся в основе, казалось бы, совершенно неупорядоченных систем. Причем охват явлений очень широк: от факторов риска эпилептического припадка до вихревых воздушных потоков, тормозящих движение транспортных средств, и от колебаний численности диких животных в природных популяциях до спадов и подъемов трафика на перегруженных городских улицах.

Булочка с изюмом: теория хаоса в быту

Во времена Лапласа значительная часть ученых придерживалась принципов абсолютного детерминизма – это согласовывалось с имеющимися знаниями о мире и обещало в обозримом будущем объяснить все физические законы. Отчасти успех детерминизма был продиктован огромными успехами ньютоновской механики, позволившей за одно столетие совершить огромный скачок в науке. Основным принципом ньютоновской механики являлось описание всех физических процессов набором дифференциальных уравнений. То есть, зная набор уравнений и некие дополнительные данные, называемые начальными условиями, можно было предсказать параметры системы в любой другой момент времени. Именно по этим принципам и сейчас рассчитываются орбиты планет, спутников и космических аппаратов. Лаплас возвел принципы ньютоновской механики в абсолют: он предположил существование демонов Лапласа. Суть такого демона в простом утверждении: зная начальные условия для всех частиц во Вселенной, он может предсказать параметры этих частиц в любой следующий промежуток времени. Очевидно, что если такой демон существует, то из этого напрямую следует предопределенность любого действия во Вселенной.

В начале XX века теорию детерминизма пошатнуло появление квантовой механики, в особенности открытие принципа неопределенности Гейзенберга – он говорит о том, что невозможно одновременно точно измерить координату и импульс частицы. Но окончательно добил теорию детерминизма именно «эффект бабочки» Лоренца. Когда в 60-х годах он составлял модели для предсказания погоды, все расчеты показывали, что модель действительно хорошо описывает реальные явления в атмосфере, но при этом через некоторое время симуляция начинала все сильнее отличаться от реальности. Однажды Лоренц округлил последний знак одного из начальных условий уравнений и через несколько часов увидел другую картину атмосферы, которая абсолютно не совпадала с реальностью, – малейшая ошибка в начальных условиях привела к совсем другому решению уравнений и к совершенно другому развитию событий. Именно этот эффект в дальнейшем и назовут «эффектом бабочки» – взмах крыльев бабочки в одном конце земного шара может привести к образованию урагана в другом.

Когда Лоренц понял, чем вызвано странное развитие его модели, он сразу догадался, почему его модель в итоге всегда расходилась с реальной атмосферой. Дело в том, что в компьютере было ограничение на размер знаков числа после запятой, – а начальные условия для уравнений нужно было определять с гораздо большей точностью, чем позволял компьютер. Кажется, что это условие можно обойти на современных компьютерах, но здесь вновь появляется принцип неопределенности Гейзенберга: даже если программе можно будет задать параметры с нужной точностью, мы не сможем измерить их с требуемой правильностью. На практике же из-за «эффекта бабочки» невозможен долгосрочный прогноз погоды.

Среди остальных областей науки теория хаоса отличается удивительно красивыми и наглядными результатами – это геометрические фракталы, аттракторы или турбулентность. Аттракторы заслуживают отдельного внимания. Сам по себе аттрактор с физической точки зрения – это всего лишь схема динамики некой системы в интересующих нас координатах. Например, простейший аттрактор может показывать изменение скорости и координаты тела. А в более общем случае может описывать любые параметры – от силы тока в цепи до количества волков в стае. Рецепт построения аттрактора тоже достаточно прост. Нужно взять систему дифференциальных уравнений, описывающих изменение системы во времени, получить решение этой системы и построить график, причем переменная времени из этого решения исключается.

С теорией хаоса наиболее тесно связаны странные аттракторы – аттракторы с фрактальной структурой, описывающие системы с хаотическим поведением. Один из самых известных странных аттракторов открыл тот же Эдвард Лоренц. Интересная особенность аттрактора Лоренца в том, что он охватывает целый ряд физических явлений. Например, с его помощью можно описать конвекцию (перемешивание) воды в плоском слое и работу простейшего лазера.

Пожалуй, самые неожиданные области применения теории хаоса – экология и биология. При помощи методов, используемых при построении аттракторов, ученые смогли визуализировать аттрактор для модели эпидемии кори.

Здесь может возникнуть вопрос – а зачем вообще это нужно? Как было сказано, аттрактор показывает динамику развития системы. Значит, если у нас есть модель системы или ее аттрактор, то мы можем найти на аттракторе наиболее подходящую текущему состоянию точку. И, зная ее, можем определить следующую точку, то есть следующее состояние системы. Говоря более простым языком, мы фактически получаем предсказание будущего!

Конечно, зачастую это предсказание не совсем точное, но даже это уже большой успех. И вполне очевидно, что такие предсказания нужны во всех областях науки. Например, один из ученых, разработавших метод предсказания популяции планктона, – Джордж Сугихара на некоторое время занялся исследованиями в финансовой области, и теперь его разработки применяются в автоматизированной торговле акциями.

Не только математика и биология привели к образованию теории хаоса – множество задач пришло в эту науку и из различных областей физики, от гидродинамики до радиофизики. В 1927 году голландский физик Балтазар ван дер Пол начал исследовать осциллятор (генератор), позже названный его именем, – пример нелинейной системы с автоколебаниями. Автоколебания – это вид колебаний с трением, в котором колебания поддерживаются за счет постоянного подвода энергии. Простейший пример таких колебаний – маятник на часах: колебания в нем должны остановиться за счет действия силы тяжести, но маятник продолжает движение за счет подвода энергии (например, за счет постепенного опускания гири). Нелинейность в генераторе Ван дер Поля возникает из-за того, что затухание колебаний в нем происходит не линейно, а с коэффициентом, в котором есть переменная уравнения.

При исследовании генератора Балтазар ван дер Пол обнаружил, что при периодическом внешнем воздействии наблюдаются области частот с шумами, находящиеся рядом с собственными частотами, что является проявлением хаоса! Также при работе осциллятора возникают предельные циклы – стационарное состояние системы.

Тогда же, в конце 20-х годов, советский физик Александр Андронов установил, что вообще все периодические автоколебания в математическом смысле являются предельными циклами. Благодаря этим открытиям возникла нелинейная теория колебаний – наука, исследующая «сложные» колебания и значительно пересекающаяся с теорией хаоса. И, как во многих других примерах, исследования Ван дер Поля пригодились не только в физике, но и перетекли в биологию – на основе полученных им уравнений создана одна из моделей нейрона (модель ФитцХью–Нагумо).

Фазовый портрет осциллятора Ван дер Поля. Красная линия – предельный цикл

Все эти дисциплины: математика, гидродинамика, радиофизика, биология и многие другие – привели к образованию теории хаоса как отдельной науки. И сейчас она находит все больше применений в различных задачах, порой очень необычных. Например, на основе теории хаоса строится клиодинамика – междисциплинарная наука, которая занимается математическим моделированием исторических процессов. Основная цель этой науки – понять процессы развития человечества: возвышение и падение цивилизаций и государств, динамику населения и распространение религий. Например, один из основателей клиодинамики, Петр Турчин, составил модель, определяющую промежуток времени между двумя последующими кризисами в государстве. В теории такие модели могут предсказать дальнейшее развитие истории! И хотя сейчас перспективы клиодинамики с точки зрения многих ученых весьма сомнительны, кто знает, во что в дальнейшем может перерасти эта наука? Может, в ближайшем будущем мы сможем предсказывать развитие всего человечества на годы или даже на века вперед, как это было у Азимова в «Основании».

В качестве другого примера можно привести моделирование лесных пожаров. Один из подходов к этой задаче состоит в создании клеточной модели леса, где каждому дереву соответствует отдельная клетка, а вероятность пожара зависит от наличия рядом горящих деревьев и некоторых дополнительных факторов – это можно представить как некий морской бой, в котором при попадании могут загораться стоящие рядом корабли.

Теория хаоса стала большой междисциплинарной наукой. Более того, именно в теории хаоса ученые впервые перешли к рассмотрению сложных систем, а не их простейших составляющих, чем зачастую ограничивались раньше. Главным же стимулом для развития этой науки стало появление очень похожих задач в абсолютно разных областях. А фактором, обусловившим развитие теории хаоса, стало широкое распространение компьютеров – без них большая часть расчетов была бы невозможна.

Но, пожалуй, самое важное следствие теории хаоса – расширение междисциплинарных исследований. Много проблем в биологии и экологии было решено с помощью новых математических моделей, и наоборот – некоторые математические модели (например, нейронные сети) были вдохновлены биологическими объектами. И теперь в мире все больше ученых занимаются не математикой или физикой, а чем-то средним между многими областями наук. И зачастую такой подход помогает решить задачи, долгое время считавшиеся сложными, а то и нерешаемыми.

Когда появился эффект бабочки

Зимним днем ​​50 лет назад Эдвард Лоренц, SM ’43, ScD ’48, мягкий профессор метеорологии Массачусетского технологического института, ввел некоторые числа в компьютерную программу, имитирующую погодные условия, и затем ушел. в его офис, чтобы выпить чашку кофе, пока машина работает. Когда он вернулся, он заметил результат, который изменил ход науки.

Компьютерная модель была основана на 12 переменных, представляющих такие вещи, как температура и скорость ветра, значения которых можно было отобразить на графиках в виде линий, восходящих и падающих с течением времени.В этот день Лоренц повторял моделирование, которое он запускал ранее, но он округлил одну переменную с .506127 до .506. К его удивлению, это крошечное изменение радикально изменило всю схему, созданную его программой за два месяца моделирования погоды.

Неожиданный результат привел Лоренца к глубокому пониманию того, как устроена природа: небольшие изменения могут иметь большие последствия. Идея стала известна как «эффект бабочки» после того, как Лоренц предположил, что взмах крыльев бабочки может в конечном итоге вызвать торнадо.А эффект бабочки, также известный как «чувствительная зависимость от начальных условий», имеет важное следствие: прогнозирование будущего может быть почти невозможным.

Подобно результатам флаттера крыла, влияние работы Лоренца сначала было почти незаметно, но могло иметь широкий резонанс. В 1963 году Лоренц обобщил свои открытия в статье «Детерминированный непериодический поток», которую в течение следующего десятилетия ровно трижды цитировали исследователи, не относящиеся к метеорологии. Однако его понимание превратилось в основополагающий принцип теории хаоса, которая быстро распространилась в течение 1970-х и 1980-х годов на такие разнообразные области, как метеорология, геология и биология.«Это стало прекрасным примером, казалось бы, эзотерической части математики, которая нашла экспериментально проверяемое применение в реальном мире», — говорит Дэниел Ротман, профессор геофизики в Массачусетском технологическом институте.

Прочтите новаторскую статью Лоренца 1963 года «Детерминированный непериодический поток» в Журнале атмосферных наук здесь (pdf). Ссылки на статьи Лоренца можно найти здесь.

Как признали многие исследователи к 1980-м годам, работа Лоренца также бросила вызов классическому пониманию природы.Законы, опубликованные Исааком Ньютоном в 1687 году, предложили аккуратно предсказуемую механическую систему — «часовой механизм вселенной». Точно так же французский математик Пьер-Симон Лаплас утверждал в своем томе 1814 года Философское эссе о вероятностях , что если бы мы знали все о Вселенной в ее текущем состоянии, то «ничто не было бы неопределенным, и будущее, как и прошлое, было бы неопределенным. представить [нашим] глазам ».

Непредсказуемость не играет роли во вселенной Ньютона и Лапласа; в детерминированной последовательности, как однажды написал Лоренц, «только одно может случиться дальше.«Все будущие события определяются начальными условиями. Тем не менее, собственные детерминированные уравнения Лоренца продемонстрировали, насколько легко в реальности зародилась мечта о создателях совершенного знания. То, что крошечное изменение в его моделировании имело такое большое значение, в дальнейшем показало, что неточность, присущая любым человеческим измерениям, может быть увеличена до совершенно неверных прогнозов.

«Это было очень шокирующим с философской точки зрения», — говорит Стивен Строгац, профессор прикладной математики в Корнелльском университете и автор книги Nonlinear Dynamics and Chaos .«Детерминизм приравнивался к предсказуемости до Лоренца. После Лоренца мы пришли к выводу, что детерминизм может дать вам краткосрочную предсказуемость, но в долгосрочной перспективе все может быть непредсказуемым. Это то, что мы ассоциируем со словом «хаос».

Погода, война и компьютеры

Эдвард Нортон Лоренц всю жизнь жил в Новой Англии, родился в 1917 году в Западном Хартфорде, штат Коннектикут. Однажды он рассказал, что в детстве «был очарован переменами погоды». Он получил степень бакалавра математики в Дартмуте в 1938 году и степень магистра в Гарварде в 1940 году.Когда Соединенные Штаты вступили во Вторую мировую войну, он присоединился к армейскому авиационному корпусу и восполнил растущие военные потребности, пройдя обучение в качестве синоптика в Массачусетском технологическом институте, где в 1928 году была создана первая в стране учебная программа по метеорологии. После войны он получил докторскую степень. в области метеорологии в Массачусетском технологическом институте и в основном оставался в Институте до своей смерти в 2008 году.

Военная метеорологическая программа, которую завершил Лоренц, была разработана Карлом-Густавом Россби, бывшим профессором Массачусетского технологического института, который был сторонником динамической метеорологии.При таком подходе атмосфера рассматривалась как одна большая система, которую нужно анализировать с помощью уравнений механики жидкости. «С моим математическим образованием я, естественно, нашел, что динамическая метеорология мне нравится», — писал позже Лоренц. Однако до 1950-х годов динамическая метеорология не давала надежных прогнозов. Менее сложная с научной точки зрения альтернатива, называемая синоптическим прогнозированием, которая анализирует погоду путем изучения атмосферных структур, таких как системы высокого и низкого давления, дает лучшие результаты.

Лоренц и другие начали экспериментировать со статистическим прогнозированием, которое основывалось на компьютерах для разработки моделей прогнозирования путем обработки данных наблюдений о таких вещах, как температура, давление и ветер. К концу 1950-х он использовал компьютер для запуска сложных симуляций погодных моделей, которые он использовал для оценки методов статистического прогнозирования. Однако некоторые из его симуляций были слишком регулярными, чтобы быть реалистичными; они давали периодические образцы или точно повторяющиеся последовательности.Как он знал, на самом деле погода работает не так. Когда его моделирование 1961 года отклонилось от ожидаемого пути, он увидел, что даже небольшое изменение, которое он сделал при округлении числа, со временем может существенно изменить ситуацию. Лоренц понял, что именно чувствительность к начальным условиям вызывает непериодическое поведение; чем больше у системы возможностей изменяться, тем меньше вероятность того, что она будет воспроизводить повторяющуюся последовательность. Эта чувствительность затрудняет прогнозирование погоды заранее.

Эту интуицию подтвердил набор уравнений, использующих всего три переменных для представления движения нагретого газа в ящике, который Лоренц использовал в своей знаменательной статье 1963 года.Он отметил, что даже такая радикально упрощенная модель дает «решения, которые никогда в точности не повторяют свою прошлую историю». «Два состояния, различающиеся на незаметную величину, могут в конечном итоге превратиться в два существенно разных состояния… [что означает] приемлемое предсказание мгновенного состояния в далеком будущем может оказаться невозможным».

Лоренц понял, что, если такая простая система была настолько чувствительна к начальным условиям, он открыл нечто фундаментальное. «Работа Эда над теорией хаоса была прекрасным примером очень ясного редукционистского мышления», — говорит Керри Эмануэль 1976 г., доктор философии 78 г., ученый-атмосферник из Массачусетского технологического института, у которого в течение многих лет был офис по соседству с Лоренцем.

Принцип хаоса подчеркивает важность нелинейности, характерной для многих природных систем. Если группа из 100 львов имеет чистый прирост в 10 человек в год, это увеличение численности популяции можно изобразить на графике в виде прямой линии. С другой стороны, группа мышей, которая ежегодно увеличивается вдвое, имеет нелинейный характер роста; на графике численность населения будет увеличиваться. Через десять лет разница между группой, которая началась с 22 мышей, и группой, которая началась с 20 мышей, увеличится до более чем 2000.Учитывая такой тип роста, реальное давление на виды — нормальный уровень смертности, эпидемии, ограниченные ресурсы — часто приводит к хаотическому увеличению и уменьшению размеров их популяций. Хотя не все нелинейные системы хаотичны, все хаотические системы нелинейны, как заметил Лоренц.

Но хаос — это не случайность. Он продемонстрировал это одним из способов, используя уравнения, описывающие движение газа. Когда он изобразил их решения на графике, результат — пара связанных овальных фигур — отдаленно напоминал бабочку.Эта форма, известная как «аттрактор Лоренца», иллюстрирует то, что почти все хаотические явления могут изменяться только в определенных пределах.

К 1965 году Лоренц точно определил то, что он считал основным источником нелинейности погоды: адвекцию, горизонтальное и неравномерное ветровое движение тепла, влаги и других свойств атмосферы. Он также пришел к выводу, что из-за эффекта бабочки невозможно точно предсказать погоду на две недели вперед. Небольшие ошибки, связанные с крупномасштабными погодными характеристиками, такими как неточное определение местоположения шторма, увеличились бы вдвое примерно за три дня.Ошибки при наблюдении мелкомасштабных метеорологических характеристик, таких как неточная запись местоположения отдельных облаков, могут превратиться в ошибки более крупного масштаба в течение дня.

Тем временем несколько ученых начали бороться с открытиями Лоренца. Джозеф Педлоски ’59, SM ’60, доктор философии ’63, ныне заслуженный ученый в Океанографическом институте Вудс-Холла, был новым доцентом Массачусетского технологического института, изучающим нелинейные вихревые движения в океане и атмосфере, когда он увидел выступление Лоренца и понял, что его метеорологические а океанографические модели продемонстрировали хаос.Понимание Лоренца «позволило мне поговорить о хаотическом и апериодическом поведении, и это было очень захватывающе», — говорит он.

Потребовалось больше времени, чтобы теория хаоса распространилась на другие дисциплины; в середине 1970-х биолог Роберт Мэй впервые предположил, что популяции видов колеблются хаотично. Сегодня мы осознаем, что такие разрозненные явления, как сердцебиение и эрозия русла реки, демонстрируют хаотическое поведение. Многие ученые, в том числе Эмануэль, теперь причисляют теорию хаоса к теории относительности и квантовой теории к числу великих научных революций 20-го века.

Танцы с койотами

Легенда в классе, Лоренц год за годом зарабатывал голоса студентов как лучший преподаватель кафедры метеорологии. «В конце концов, награда была прекращена, потому что ее больше никто не выигрывал», — вспоминает Эмануэль. Тем не менее, исследования Лоренца оставались практически незамеченными в течение десяти лет. «Эд был очень застенчивым человеком, который был настолько далек от саморекламы, насколько вы могли представить», — говорит Эмануэль. «Он не часто выступал с научными лекциями».

Коллеги, наконец, убедили Лоренца широко обсудить свои идеи на конференции Американской ассоциации содействия развитию науки в 1972 году.Его статья «Предсказуемость: вызывает ли взмах крыльев бабочки в Бразилии торнадо в Техасе?» представил изображение бабочки, любезно предоставленное метеорологом Филипом Мерилисом, придумавшим название. Раньше Лоренц приводил более прозаический пример, когда чайка вызвала шторм. В 1987 году термин «эффект бабочки» появился в бестселлере Джеймса Глейка « Chaos: Making a New Science », и открытие Лоренца привлекло широкую публику.

Книга Глейка сделала Лоренца научной знаменитостью.Ротман и Строгац, тогда профессора Массачусетского технологического института, начали приглашать его читать ежегодные гостевые лекции для благоговейных студентов. «Каждый год он читал новую лекцию о том, что он сделал за последний год», — говорит Ротман. «Это было потрясающе. В последние пять лет жизни лекции стали улучшаться. Глубже. Ему это очень понравилось ». Но Лоренц отклонял вопросы студентов о своих старых открытиях.

Скромный и тихий даже в окружении знакомых коллег, Лоренц мог более красноречиво рассказывать о своей семье или о природе; он всю жизнь был туристом и лыжником.«Если бы вы поговорили с ним о Белых горах Нью-Гэмпшира, он бы полностью раскрылся», — говорит Эмануэль. Однажды, что невероятно, Эмануэль встретил Лоренца и его жену Джейн на отдыхе в пустыне Южной Калифорнии. Все они отправились в заповедник, где Эмануэль увидел группу койотов, дремлющих под деревом. По прихоти он начал хлопать и кричать, чтобы разбудить койотов, но они не пошевелились.

«Внезапно я услышал очень громкий крик койота, доносящийся прямо за моей спиной, — рассказывает Эмануэль.«Я взлетел примерно на три фута. Потом я обернулся, и это был Эд! Он подкрался ко мне сзади и знал, как разговаривать с койотами. Он сразу их разбудил, и они завели с ним какой-то разговор. Этот громкий звук исходит от того парня, которого обычно трудно слышать.

Поп идет бабочка

Эффект бабочки проник даже в поп-культуру. «Бабочка может взмахнуть крыльями над цветком в Китае и вызвать ураган в Карибском бассейне», — говорит персонаж Роберта Редфорда в фильме 1990 года « Гавана », добавляя, что ученые «могут даже рассчитать шансы».Но они не могут, как ясно дал понять Лоренц в своей книге « The Essence of Chaos » 1990 года. Взаимозависимые причинно-следственные связи природы обычно слишком сложны, чтобы их можно было распутать. Таким образом, мы не можем точно сказать, какая бабочка, если таковая была, могла создать данный шторм. Более того, как заявил Лоренц в своей статье 1972 года: «Если взмах крыльев бабочки может способствовать возникновению торнадо, он также может способствовать предотвращению торнадо». И это было бы невозможно для нас узнать.

Лоренц, таким образом, ответил бы двусмысленно, когда бы его спросили, действительно ли бабочка может вызвать торнадо. «Даже сегодня я не уверен в правильном ответе», — сказал он на лекции 2008 года. Ценность вопроса в том, что он поднимает более важный вопрос: природа очень чувствительна к крошечным изменениям. «Эта идея теперь вошла в повседневное видение многих ученых во всех дисциплинах», — говорит Ротман. «Они понимают, что некоторые вещи хаотичны и что существует экспоненциальное отклонение от начальных условий. Они могут не озвучивать это, но они знают это, потому что это витает в воздухе.Это знак большого достижения «.

Работа Лоренца также привела к улучшениям в прогнозировании погоды, чему он приписал три вещи: более широкий сбор данных, лучшее моделирование и «распознавание хаоса» в погоде, что привело к так называемому ансамблевому прогнозированию. В этом методе синоптики признают, что измерения несовершенны, и поэтому запускают множество симуляций, начиная с немного разных условий; общие черты этих сценариев составляют основу более надежного «консенсусного» прогноза.

Воображая институт Лоренца

Помимо прогнозов, Лоренц «очень интересовался климатом», говорит Эмануэль, и дал понять, что даже если проследить влияние мелких вещей слишком сложно, чтобы позволить кому-либо предсказывать погоду на месяц вперед , эффекты больших вещей, такие как увеличение содержания углекислого газа в атмосфере, нетрудно заметить. «Он не думал, что изменение климата полностью непредсказуемо, и его бы позабавили те, кто говорит, что, поскольку мы не можем предсказать погоду дольше нескольких дней, невозможно предсказать климат», — говорит он.

Сегодня Эмануэль и Ротман работают со сборщиками средств Массачусетского технологического института, чтобы найти поддержку для центра климатических исследований, который они хотели бы назвать Институтом Лоренца. Эмануэль думает, что это поможет компенсировать тот факт, что Лоренц никогда не был титулованным профессором, несмотря на свои многочисленные профессиональные награды. «Он был классическим примером пророка, которого не почитают в его собственной стране, здесь, в Массачусетском технологическом институте», — прямо говорит он.

Предлагаемый Институт Лоренца, по словам Эмануэля, будет сосредоточен на чистых исследованиях, направленных на поиск «основополагающих принципов климата, которые облегчат его понимание.Как писал Лоренц в 2005 году, «часто отмечалось, что часть чистого исследования может привести, иногда намного позже, к практическому применению, которое, скорее всего, не ожидалось ученым, проводящим чистое исследование».

В самом деле, вряд ли можно представить себе прозрение Лоренца в виде одного такого краткого интеллектуального трепета, вызывающего течения, которые все еще влияют на научную атмосферу. Возможно, в какой-нибудь будущий зимний день другой ученый-климатолог из Массачусетского технологического института, устроившийся в Институте Лоренца, вернется после перерыва на кофе и совершит столь же значительный прорыв.

Эдвард Лоренц, отец теории хаоса и эффекта бабочки, умер в возрасте 90 лет | MIT News

Эдвард Лоренц, метеоролог из Массачусетского технологического института, который пытался объяснить, почему так трудно делать хорошие прогнозы погоды и завершился научной революцией под названием теория хаоса, умер 16 апреля от рака в своем доме в Кембридже. Ему было 90.

Профессор Массачусетского технологического института, Лоренц был первым, кто осознал то, что сейчас называется хаотическим поведением в математическом моделировании погодных систем.В начале 1960-х годов Лоренц осознал, что небольшие различия в динамической системе, такой как атмосфера — или модели атмосферы — могут вызвать огромные и часто неожиданные результаты.

Эти наблюдения в конечном итоге привели его к формулировке того, что стало известно как эффект бабочки — термин, возникший из академической статьи, которую он представил в 1972 году и озаглавил: «Предсказуемость: вызывает ли взмах крыльев бабочки в Бразилии торнадо? Техас? »

Ранние открытия Лоренца ознаменовали начало новой области исследований, которая повлияла не только на математику, но и практически на все отрасли науки — биологические, физические и социальные.В метеорологии это привело к выводу, что может быть принципиально невозможно предсказать погоду дольше двух или трех недель с разумной степенью точности.

Некоторые ученые с тех пор утверждают, что 20-й век запомнится тремя научными революциями — теорией относительности, квантовой механикой и хаосом.

«Показав, что определенные детерминированные системы имеют формальные пределы предсказуемости, Эд вбил последний гвоздь в гроб картезианской вселенной и спровоцировал то, что некоторые называют третьей научной революцией 20-го века, вслед за теорией относительности и квантовой физикой. — сказал Керри Эмануэль, профессор атмосферных наук Массачусетского технологического института.«Он также был идеальным джентльменом и своим умом, честностью и смирением установил очень высокие стандарты для своего и последующих поколений».
Â
Лоренц родился в 1917 году в Западном Хартфорде, штат Коннектикут. В 1938 году получил степень бакалавра математики в Дартмутском колледже, степень магистра математики в Гарвардском университете в 1940 году, диплом специалиста по метеорологии в Массачусетском технологическом институте в 1943 году и докторскую степень по метеорологии в Массачусетском технологическом институте. в 1948 году. Во время службы в качестве синоптика в авиакорпусе армии США во время Второй мировой войны он решил получить диплом по метеорологии в Массачусетском технологическом институте.

«Когда я был мальчиком, мне всегда было интересно делать что-то с числами, а также меня восхищали перемены погоды», — написал Лоренц в автобиографическом очерке.

Лоренц был сотрудником кафедры метеорологии Массачусетского технологического института с 1948 по 1955 год, когда он был назначен на факультет доцентом. Он получил звание профессора в 1962 году и был заведующим кафедрой с 1977 по 1981 год. Он стал почетным профессором в 1987 году.

Лоренц, избранный членом Национальной академии наук в 1975 году, получил множество наград, наград и почетных званий. .В 1983 году он и бывший профессор Массачусетского технологического института Генри М. Стоммел были совместно удостоены премии Crafoord Prize в размере 50 000 долларов США от Шведской королевской академии наук — премии, учрежденной для признания областей, не имеющих права на получение Нобелевских премий.

В 1991 году ему была присуждена Киотская премия за фундаментальные науки в области наук о Земле и планетах. Комитет по присуждению Киотской премии процитировал Лоренца за создание «теоретической основы предсказуемости погоды и климата, а также основы компьютерной физики атмосферы и метеорологии».Комитет добавил, что Лоренц «сделал свое самое смелое научное достижение в открытии« детерминированного хаоса », принципа, оказавшего глубокое влияние на широкий круг фундаментальных наук и вызвавшего одно из самых драматических изменений во взглядах человечества на природу со времен сэра Исаака Ньютона. «

Во время отпуска из Массачусетского технологического института он занимал исследовательские или преподавательские должности в обсерватории Лоуэлла во Флагстаффе, штат Аризона; на кафедре метеорологии Калифорнийского университета в Лос-Анджелесе; в Det Norske Meteorologiske Insitutt в Осло, Норвегия; и Национальный центр атмосферных исследований в Боулдере, штат Колорадо.

По словам его семьи, Лоренц, заядлый турист и лыжник, был активен примерно за две недели до своей смерти.

У Лоренца остались трое детей, Нэнси, Эдвард и Шерил, и четверо внуков.

Панихида состоится в 15:00. Воскресенье, 20 апреля, в капелле Сведенборга, 50 Quincy St., Кембридж. Служба новостей MIT обновит это объявление по мере того, как подробности становятся доступными.

Версия этой статьи появилась в MIT Tech Talk 30 апреля 2008 г. (скачать PDF).

теория хаоса | Определение и факты

Теория хаоса , в области механики и математики, изучение очевидно случайного или непредсказуемого поведения в системах, управляемых детерминированными законами. Более точный термин, детерминированный хаос , предполагает парадокс, потому что он связывает два понятия, которые известны и обычно считаются несовместимыми. Первый — это случайность или непредсказуемость, например, в траектории движения молекулы в газе или в выборе при голосовании конкретного человека из популяции.В традиционном анализе случайность считалась более очевидной, чем реальной, происходящей из-за незнания многих действующих причин. Другими словами, обычно считалось, что мир непредсказуем, потому что он сложен. Второе понятие — это понятие детерминированного движения, такого как маятник или планета, которое было принято со времен Исаака Ньютона как пример успеха науки в обеспечении предсказуемости того, что изначально является сложным.

В последние десятилетия, однако, было изучено множество систем, которые ведут себя непредсказуемо, несмотря на кажущуюся простоту и тот факт, что задействованные силы регулируются хорошо понятными физическими законами.Общим элементом этих систем является очень высокая степень чувствительности к начальным условиям и способу их запуска. Например, метеоролог Эдвард Лоренц обнаружил, что простая модель тепловой конвекции обладает внутренней непредсказуемостью — обстоятельство, которое он назвал «эффектом бабочки», предполагая, что простой взмах крыла бабочки может изменить погоду. Более простой пример — автомат для игры в пинбол: движения мяча точно регулируются законами гравитационного качения и упругих столкновений — оба полностью понятны, но конечный результат непредсказуем.

Подробнее по этой теме

Принципы физических наук: Хаос

Многие системы могут быть описаны с помощью небольшого числа параметров и ведут себя очень предсказуемо. Если бы это было не так, …

В классической механике поведение динамической системы можно геометрически описать как движение на «аттракторе». Математика классической механики эффективно распознала три типа аттракторов: одиночные точки (характеризующие установившиеся состояния), замкнутые контуры (периодические циклы) и торы (комбинации нескольких циклов).В 1960-х годах американский математик Стивен Смейл открыл новый класс «странных аттракторов». На странных аттракторах динамика хаотична. Позже было установлено, что странные аттракторы имеют детальную структуру на всех масштабах увеличения; Прямым результатом этого признания стало развитие концепции фрактала (класса сложных геометрических форм, которые обычно проявляют свойство самоподобия), что, в свою очередь, привело к замечательным достижениям в компьютерной графике.

Приложения математики хаоса очень разнообразны, включая изучение турбулентного потока жидкостей, нарушений в сердцебиении, динамики населения, химических реакций, физики плазмы и движения групп и скоплений звезд.

Теория хаоса, эффект бабочки и компьютерный сбой, с которого все началось

Хаотическая система — это система, в которой очень незначительные изменения начальных условий (синий и желтый)… [+] приводят к аналогичному поведению какое-то время, но затем через относительно короткий промежуток времени это поведение расходится.

Как известная песня Боба Дилана: «Вам не нужен метеоролог, чтобы знать, в какую сторону дует ветер». Тем не менее, если у вас достаточно информации о скорости ветра в сочетании с массивом показаний барометров, термометров и т. Д., Вы можете попросить метеоролога, особенно подготовленного метеоролога с доступом к современным компьютерам и программному обеспечению, сделать надежный прогноз.В наши дни мы часто планируем наши мероприятия на свежем воздухе с помощью выпусков новостей, веб-сайтов, приложений и голосовых помощников, которые предоставляют разумные прогнозы на часы или дни вперед. Удивительно, что метеорология может совершить такой подвиг.

С другой стороны, если мы полагаемся на солнечный прогноз при планировании пикника, а вместо этого идет дождь, мы не осуждаем всю область метеорологии и не отвергаем ее как бесполезные догадки. Мы признаем, что это несовершенная наука. Более того, мы признаем, что он может дать нам только вероятности определенного исхода, а не окончательный прогноз того, что должно произойти.По сравнению с тем, что было несколько десятилетий назад, прогнозы намного лучше, но отнюдь не безупречны. И даже с развитием технологий теория детерминированного хаоса показывает, что они никогда не будут идеальными.

Даже с учетом всех достижений, которые мы сделали в прогнозном моделировании, такая сложная система, как … [+] атмосфера Земли, позволяет нам выбрать только множество вероятностных результатов, а не какой-либо конкретный результат с какой-либо уверенностью.

Всем известно, что квантовая теория воплощает в себе случайность или, как знаменитый Эйнштейн выразился, «бросание игральных костей».«Но погода — это крупномасштабный эффект, с которым ньютоновская физика должна уметь справиться. Действительно, это так, и довольно хорошо. Однако теория хаоса указывает на ограниченность предсказаний даже для детерминированной ньютоновской физики.

Второй закон движения Ньютона, результирующая сила, действующая на объект, равна его массе, умноженной на его ускорение, воплощает тип математической взаимосвязи, известной как дифференциальное уравнение. Это уравнение действует как своего рода машина для обработки необработанных данных о начальных условиях для системы частиц — ее точного набора положений и скоростей в любой данный момент, а также сил взаимодействия — и неопределенного определения координат местоположения и скорости в будущее.

В своем трактате 1814 года «Философское эссе о вероятностях» французский математик Пьер Лаплас высказал предположение, что ньютоновская механика провозгласила жесткий детерминизм, который теоретически сделает возможным успешное предсказание всего будущего Вселенной при условии абсолютного знания ее полного состояния в любой момент. данное время. Единственная загвоздка в том, что предсказателю нужно каким-то образом выйти за пределы Вселенной и сразу получить полный снимок всех частиц в ней и их мгновенных траекторий.В философских дискуссиях такое гипотетическое существо было названо Демоном Лапласа. Как писал Лаплас:

«Мы можем рассматривать нынешнее состояние вселенной как следствие ее прошлого и причину ее будущего. Интеллект, который в определенный момент знал бы все силы, приводящие в движение природу, и все положения всех элементов, из которых состоит природа, если бы этот интеллект был также достаточно обширен, чтобы представить эти данные для анализа, он бы объединил в одной формуле движения величайших тел вселенной и мельчайшего атома; для такого интеллекта ничто не было бы неопределенным, и будущее, как и прошлое, предстало бы перед его глазами.”

Представление художника о наблюдаемой Вселенной в логарифмической шкале. Согласно Лапласу, если бы вы знали … [+] сразу все положения и импульсы всех частиц во Вселенной, вы бы смогли определить все в далеком будущем с произвольной точностью.

В том же эссе Лаплас утверждал, что любая необходимость ссылаться на вероятность в природе проистекает из незнания, включая неопределенность в прогнозах погоды.Когда-нибудь, предположил он, прогнозы погоды будут совершенно точными — такими же предсказуемыми, как орбиты планет — и ничего не останется на волю случая. Но даже если бы не квантовые явления, подобные принципу неопределенности Гейзенберга, этого не было бы. Независимо от того, насколько хорошо вы знаете начальные условия, детерминизм не управляет Вселенной.

В начале 1960-х профессор метеорологии Массачусетского технологического института Эдвард Лоренц был убежден, что мэйнфрейм-компьютеры, используемые с большим успехом при планировании испытаний оружия и запуске спутников на орбиту, помогут дать точные прогнозы погоды.Учитывая, что погода определяется набором измеримых факторов, таких как температура, давление и скорость ветра, общепринятое мнение в то время заключалось в том, что надежная модель, полный набор данных и мощное устройство для обработки чисел в принципе могли бы , прогнозируйте погодные условия на будущее. Помня об этой цели, Лоренц построил простую систему уравнений для конвекции воздуха и запрограммировал их в свой компьютер Royal-McBee размером с кабинет, основанный на вакуумной лампе.

Две системы, начиная с идентичной конфигурации, но с незаметно небольшими различиями в… [+] начальные условия (меньше одного атома) какое-то время сохранят одно и то же поведение, но со временем хаос приведет к их расхождению. По прошествии достаточного времени их поведение окажется совершенно не связанным друг с другом.

Он ввел начальный набор данных, включил компьютер и стал ждать распечатки. Поместив вывод рядом с машиной, он решил повторно ввести некоторые данные и запустить программу дольше. Тщательно набрав его, он с удивлением обнаружил, что программа дала совершенно другой прогноз.Наконец, он понял, что компьютерная распечатка округила данные, и то, что он ввел, во второй раз немного отличался от первого. Каким-то образом даже для простой, детерминированной системы уравнений мельчайшее изменение начальных условий привело к совершенно иному поведению.

Как он позже заметит, из-за того, что было названо «эффектом бабочки», чрезвычайная чувствительность к начальным условиям означала, что взмах крыльев бабочки над Амазонкой мог повлиять на погоду в Китае.Это явление, впервые предложенное Лоренцем и другими, нашло широкое применение как детерминированный хаос .

Эффект бабочки, также известный как детерминированный хаос, — это явление, при котором уравнения без … [+] неопределенности будут давать неопределенные результаты, независимо от того, насколько точно выполняются вычисления.

Лоренц не только открыл хаос, но и определил его ключевой механизм. Когда он построил свои данные по нескольким осям, он отметил странное свойство, заключающееся в том, что повторение (построение траектории во времени) любых двух соседних точек приводило к их разделению.Разрыв будет становиться все больше и больше с каждой итерацией, пока математическое «потомство» двух точек не будет настолько разделено, что окажется в совершенно разных областях информационного облака. С другой стороны, точки за пределами облака при повторении быстро приблизятся к нему. Таким образом, динамика уравнений Лоренца служила двум противоречивым целям: отталкиванию траекторий внутри набора данных и притяжению за его пределами. Такая сложная система называется «странным аттрактором», а особая динамика, открытая Лоренцем, называется «аттрактором Лоренца».”

Множественные хаотические пути означают, что в любой момент местоположение и траектория частицы … [+] полностью неопределимы, независимо от того, насколько точно были известны все предыдущие условия.

Вскоре после этого были открыты и другие странные аттракторы, в частности аттрактор Энона, идентифицированный в 1976 году французским математиком Мишелем Эноном. Странные аттракторы обладают своеобразной самоподобной структурой, которую французско-польский математик Бенуа Мандельброт назвал «фракталами».Если вы нанесете на карту странный аттрактор и «взорвете» любую заданную область, эта меньшая область окажется похожей по структуре на все это. Точно так же увеличение любого крошечного участка области показывает образец, аналогичный самой области, и так далее. Математически это подразумевает дробную размерность, отсюда и термин «фрактал».

Набор Мандельброта — это пример фрактала, в котором одна и та же структура и поведение проявляются в … [+] различных масштабах. Такое же поведение проявляется во многих хаотических системах.

Мы в долгу перед Лоренцем за обнаружение ключевого изъяна в лапласовском детерминизме. Даже в классической механике Ньютона, с ее регулярностью часового механизма, некоторые системы настолько чувствительны к начальным условиям, что их практически невозможно предсказать. Если вы не знаете каждую точку данных с идеальной точностью — что практически невозможно с реалистичными измерительными приборами — такие хаотические системы действуют так же беспорядочно, как серия подбрасываний монеты. Таким образом, наряду со случайностью в квантовых системах, эффективная случайность в некоторых классических системах, таких как погода, кажется ключевой особенностью природы.Бог играет в кости разными способами.

В этом месяце в истории физики

Около января 1961 года: Лоренц и эффект бабочки

Еще мальчиком Лоренц был очарован погодой, следя за термометром и записывая максимумы и минимумы возле дома своих родителей в Западном Хартфорде, штат Коннектикут. Он также интересовался математикой, часто решая головоломки с отцом.После окончания Дартмутского колледжа в 1938 году Лоренц планировал заняться математикой, но вмешалась Вторая мировая война: он служил синоптиком в армейском авиационном корпусе. Впоследствии он решил заняться метеорологией, сделав себе раннее имя, публикуя статьи на такие темы, как общая циркуляция атмосферы.

Но его особенно заинтриговали прогнозы погоды, которые, несмотря на помощь научных приборов, все еще оставались в основном интуитивными догадками. С появлением компьютеров Лоренц увидел возможность объединить математику и метеорологию.Он намеревался построить математическую модель погоды, используя набор дифференциальных уравнений, отражающих изменения температуры, давления, скорости ветра и тому подобное. К началу 1960-х Лоренцу удалось создать каркас погодной системы из горстки (12) дифференциальных уравнений. Он вел непрерывную симуляцию на чрезвычайно примитивном компьютере, который каждую минуту выдавал виртуальную погоду на целый день. Система была весьма успешной в получении данных, которые напоминали естественные погодные условия, никогда ничего не происходило одинаково дважды, но явно существовал лежащий в основе порядок.

Однажды зимой 1961 года Лоренц хотел исследовать одну конкретную последовательность более подробно, но он выбрал короткий путь. Вместо того, чтобы начинать весь цикл, он начал с середины, набирая числа прямо из предыдущей распечатки, чтобы дать машине начальные условия. Затем он прошел по холлу за чашкой кофе и, вернувшись через час, обнаружил неожиданный результат. Вместо того, чтобы точно дублировать предыдущий прогон, новая распечатка показала, что виртуальная погода так быстро расходится с предыдущей моделью, что всего за несколько виртуальных «месяцев» все сходство между ними исчезло.

Сначала Лоренц предположил, что в его компьютере Royal McBee вышла из строя электронная лампа, которая была чрезвычайно медленной и грубой по сегодняшним меркам. К его большому удивлению, неисправности не было. Проблема заключалась в набранных им числах. В памяти компьютера хранилось шесть десятичных знаков: 0,506127. Для экономии места на распечатке появилось всего три: .506. Лоренц ввел более короткие округленные числа, предполагая, что разница в одну часть в тысяче несущественна.

Это казалось разумным предположением. Ученых часто учат, что небольшие начальные возмущения приводят к небольшим изменениям в поведении любой данной физической системы, и даже сегодня температура обычно не измеряется в пределах одной части из тысячи. В компьютере Лоренца использовалась чисто детерминированная система уравнений, так что при конкретной отправной точке «погода» каждый раз разворачивалась точно так же, в то время как немного отличающаяся начальная точка заставляла бы погоду разворачиваться немного по-другому.Лоренц полагал, что небольшая числовая вариация похожа на небольшой порыв ветра, который вряд ли существенно повлияет на важные крупномасштабные характеристики погоды. Однако в конкретной системе уравнений Лоренца такие небольшие ошибки оказались катастрофическими. Сегодня это явление известно как чувствительная зависимость от начальных условий. Впоследствии Лоренц назвал свое открытие «эффектом бабочки»: нелинейные уравнения, управляющие погодой, обладают такой невероятной чувствительностью к начальным условиям, что хлопающая крыльями бабочка в Бразилии может вызвать торнадо в Техасе.И он пришел к выводу, что долгосрочное прогнозирование погоды было обречено.

В прошлом такие наблюдаемые в поведении, а именно случайные колебания, происходящие из того, что должно было быть полностью детерминированной системой уравнений, отбрасывались просто как ошибка в расчетах. Лоренц был первым, кто распознал в этом беспорядочном поведении нечто иное, чем ошибку; то, что он увидел, было неоспоримым порядком, рожденным случайностью. Это была не только первая четкая демонстрация чувствительной зависимости от начальных условий, но и Лоренц показал, что это происходит в простой, но физически релевантной модели.

Затем Лоренц создал новую систему с тремя нелинейными дифференциальными уравнениями, сокращенную модель конвекции, известную как «Аттрактор Лоренца». Он предположил, что график, который он создал для моделирования движения, либо достигнет равновесия и остановится, либо создаст петлю, которая в конечном итоге будет реформирована и откатывается, указывая на повторяющийся паттерн. Вместо этого его карта отображала бесконечную сложность, всегда оставаясь в определенных границах, но никогда не повторяясь. Он имел характерную форму двойной спирали, точно напоминающую бабочку с двумя крыльями.

С момента открытия Лоренца компьютерное моделирование преуспело в превращении погодного бизнеса из искусства в науку, но даже после двух-трех дней даже самые лучшие прогнозы в мире остаются спекулятивными, а после недели они бесполезны. Таков парадокс в том, что это хаос.

Дополнительная литература:
Глейк, Джеймс. Хаос: создание новой науки, Viking Penguin, 1987.

Эдвард Н. Лоренц, метеоролог и отец теории хаоса, умер по адресу 90

Эдвард Н.Лоренц, метеоролог, который пытался предсказывать погоду с помощью компьютеров, но вместо этого создал современную теорию хаоса, умер в среду в своем доме в Кембридже, штат Массачусетс. Ему было 90 лет.

Причиной был рак, сказала его дочь Шерил Лоренц. .

Обнаружив «детерминированный хаос», д-р Лоренц установил принцип, который «глубоко повлиял на широкий круг фундаментальных наук и привел к одному из самых драматических изменений во взглядах человечества на природу со времен сэра Исаака Ньютона», — заявил комитет, награждавший ему была присуждена Киотская премия 1991 года в области фундаментальных наук.

Доктор Лоренц наиболее известен своей идеей «эффекта бабочки», идеей о том, что небольшое возмущение, такое как взмах крыльев бабочки, может иметь колоссальные последствия.

Как рассказывается в книге «Хаос» Джеймса Глейка, доктор Лоренц случайно открыл хаос зимой 1961 года. Доктор Лоренц запускал моделирование погоды, используя простую компьютерную модель. Однажды он захотел повторить одну из симуляций в течение более длительного времени, но вместо того, чтобы повторить всю симуляцию, он начал второй прогон в середине, вводя числа из первого прогона для начальных условий.

Компьютерная программа была такой же, поэтому погодные условия во втором заходе должны были точно соответствовать погодным условиям первого. Вместо этого две погодные траектории быстро разошлись по совершенно разным путям.

Сначала он подумал, что компьютер неисправен. Потом он понял, что не вошел в начальные условия точно. Компьютер сохранял числа с точностью до шести десятичных знаков, например 0,506127, а для экономии места при распечатке результатов числа сокращались до трех знаков после запятой, 0.506. При вводе новых условий доктор Лоренц ввел округленные числа, и даже это небольшое расхождение, менее 0,1 процента, полностью изменило конечный результат.

Несмотря на то, что его модель была значительно упрощена, доктор Лоренц понял, что это означает, что точный прогноз погоды — это фантастика.

Для получения идеального прогноза потребуется не только идеальная модель, но и отличное знание ветра, температуры, влажности и других условий во всем мире в определенный момент времени.Даже небольшое несоответствие могло привести к совершенно другой погоде.

Доктор Лоренц опубликовал свои выводы в 1963 году. «Статья, которую он написал в 1963 году, является шедевром ясности изложения того, почему погода непредсказуема», — сказал Дж. Дойн Фармер, профессор Института Санта-Фе в Нью-Мексико.

В следующем году д-р Лоренц опубликовал еще одну статью, в которой описал, как небольшое изменение параметров в модели может привести к совершенно иному поведению, трансформируя регулярные периодические события в, казалось бы, случайный хаотический паттерн.

На собрании Американской ассоциации развития науки в 1972 году он выступил с докладом, озаглавленным, что отражает суть его идей: «Предсказуемость: вызывает ли взмах крыльев бабочки в Бразилии торнадо в Техасе?» ? »

Доктор Лоренц был не первым, кто столкнулся с хаосом. В конце XIX века математик Анри Пуанкаре показал, что гравитационный танец всего трех небесных тел безнадежно сложно вычислить, хотя лежащие в основе уравнения движения казались простыми.Но открытия Пуанкаре были забыты в течение первых трех четвертей 20 века.

Работы доктора Лоренца также не привлекали особого внимания до середины 1970-х годов.

«Когда он, наконец, проник в сообщество, именно это побудило людей действительно обратить на это внимание и привело к огромному развитию», — сказал Эдвард Отт, профессор физики и электротехники в Университете Мэриленда. «Он продемонстрировал хаотическую модель в реальной ситуации».

Родился в 1917 году в Вест-Хартфорде, штат Коннектикут.Эдвард Нортон Лоренц получил степень бакалавра математики в Дартмутском колледже в 1938 году и степень магистра математики в Гарварде в 1940 году. Во время Второй мировой войны он работал прогнозистом погоды, что привело его к поступлению в аспирантуру по метеорологии; он получил степень магистра и доктора метеорологии в Массачусетском технологическом институте в 1943 и 1948 годах.

Доктор Лоренц был сотрудником кафедры метеорологии Массачусетского технологического института с 1948 по 1955 год, когда он стал доцентом.Он получил звание профессора в 1962 году и занимал должность заведующего кафедрой с 1977 по 1981 год. Он стал почетным профессором в 1987 году.

Помимо дочери Шерил из Юджина, штат Орегон, у доктора Лоренц осталась еще одна дочь. , Нэнси Лоренц из Рослиндейла, Массачусетс; сын Эдвард Х. Лоренц из Грасса, Франция; и четверо внуков. Его жена Джейн умерла в 2001 году.

Доктор Лоренц оставался активным почти до конца своей жизни, занимаясь исследованиями и активным отдыхом.

«Он был в походе две с половиной недели назад, — сказала Шерил Лоренц, — и неделю назад он закончил работу с коллегой.”

Когда Лоренц обнаружил эффект бабочки

Погода — один из масштабных примеров хаотических систем; фактически, именно погодные исследования показали, что такое хаос на самом деле; небольшие возмущения в атмосфере могут вызвать огромные изменения климата. Это было обнаружено североамериканским метеорологом-теоретиком Эдвардом Нортоном Лоренцем (1938-2008).

Статья, в которой он представил свои результаты в 1963 году, является одним из величайших достижений физики двадцатого века, хотя в то время мало кто из ученых-неметеорологов заметил это.Это должно было радикально измениться в течение следующих десятилетий. Это изменение отношения во многом связано со знаменитой фразой, которую Лоренц включил в лекцию, которую он прочитал в декабре 1972 года на сессии ежегодного собрания AAAS (Американской ассоциации содействия развитию науки): «бабочка, хлопающая крыльями». в Бразилии может вызвать торнадо в Техасе ». Раньше Лоренц использовал пример с чайкой, вызывающей бурю, но, в конце концов, сделал его более поэтичным с бабочкой, следуя советам коллег.В 1987 году термин «эффект бабочки» получил широкое распространение благодаря бестселлеру Джеймса Глейка «Хаос: создание новой науки» — и открытие Лоренца достигло широкой аудитории.

В своем исследовании погоды он разработал простые математические модели и исследовал их свойства с помощью компьютеров. Но в 1960 году он обнаружил, что произошло нечто странное, когда повторил предыдущие расчеты.Вот как он сам реконструировал события и свою реакцию в книге «Сущность хаоса», которую он написал много лет спустя:

«В какой-то момент я решил повторить некоторые вычисления, чтобы более подробно изучить происходящее. Я остановил компьютер, набрал строку с цифрами, вышедшую из принтера немного ранее, и снова включил его. Я пошел в вестибюль, чтобы выпить чашку кофе, и вернулся через час, в течение которого компьютер моделировал погоду примерно за два месяца.Цифры, выходящие из принтера, не имели ничего общего с предыдущими.

Я сразу подумал, что одна из ламп вышла из строя или что в компьютере произошла другая поломка, что было нередко, но, прежде чем я позвонил техническим специалистам, я решил выяснить, в чем проблема, зная, что это ускорит до ремонта. Вместо внезапного прерывания я обнаружил, что новые значения сначала повторяли предыдущие, но вскоре стали отличаться на одну или несколько единиц в последнем десятичном значении, затем в предыдущем, а затем в предыдущем.Фактически, различия увеличивались в размере более или менее постоянно каждые четыре дня, пока в какой-то момент в течение второго месяца не исчезло какое-либо сходство с исходными цифрами.

Этого было достаточно, чтобы понять, что происходит: числа, которые я ввел в компьютер, были не совсем оригинальными. Это были закругленные версии, которые я сначала отдал в типографию. Первоначальные ошибки, вызванные округлением значений, были причиной: они постоянно росли, пока не контролировали решение.Сегодня мы бы назвали это хаосом ».

То, что Лоренц эмпирически наблюдал с помощью своего компьютера, заключается в том, что существуют системы, которые могут демонстрировать непредсказуемое поведение (что не означает «не подчиняться законам»), в которых небольшие различия в одной переменной оказывают глубокое влияние на систему.