ДЕДУКЦИЯ — это… Что такое ДЕДУКЦИЯ?
ДЕДУКЦИЯ — (от лат. deductio выведение) переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность Д. заключается в том, что от истинных посылок… … Философская энциклопедия
ДЕДУКЦИЯ — (лат. deductio, от deducere выводить). Вывод частных фактов из общих основных положений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ДЕДУКЦИЯ [лат. deductio выведение] лог. способ рассуждения, при котором новое … Словарь иностранных слов русского языка
дедукция — и, ж. déduction f., нем. Deduktion <лат. deductio выведение. 1. дипл. Изложение, изъяснение чего л. Сл. 18. Шведы против сего мира пространную дедукцию писменно Королю подали. ЖПВ 2 493. Министерство потом вручило ему письменную дедукцию своих … Исторический словарь галлицизмов русского языка
Дедукция — Дедукция ♦ Déduction Рассуждать методом дедукции значит выводить из истинных или предположительно истинных суждений (принципов или предпосылок) другие суждения, с необходимостью из них вытекающие. Под дедукцией, пишет Декарт, мы понимаем… … Философский словарь Спонвиля
Под дедукцией, пишет Декарт, мы понимаем… … Философский словарь Спонвиля
дедукция — (от лат. deductio выведение) движение знания от более общего к менее общему, частному, выведение следствия из посылок. Д. тесно связана с индукцией. Логика рассматривает Д. как вид умозаключения. Психология изучает развитие и нарушение… … Большая психологическая энциклопедия
Дедукция — (лат. deductio шығару) бастапқы пайымдаулар (алғышарттар) жиынтығынан қажетті шығарылатын салдарларды алатын рационалды танымның әдісі. Дедукция процесінде пікірлердің тек логикалық қатал, әдепті (корректный) амалдары – логикалық формалары −… … Философиялық терминдердің сөздігі
ДЕДУКЦИЯ — (от латинского deductio выведение), вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или гипотезы,… … Современная энциклопедия
ДЕДУКЦИЯ — (от лат. deductio выведение) вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы,… … Большой Энциклопедический словарь
deductio выведение) вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы,… … Большой Энциклопедический словарь
Дедукция — Дедукция (лат. deductio выведение) метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического… … Википедия
дедукция — выведение, вывод, умозаключение, заключение Словарь русских синонимов. дедукция сущ., кол во синонимов: 3 • вывод (31) • … Словарь синонимов
дедукция — спец. ДЕДУКЦИЯ, вывод, книжн. умозаключение ВЫВОД, заключение, книжн. умозаключение ВЫВОДИТЬ/ВЫВЕСТИ, заключать/заключить, книжн. умозаключать/умозаключить … Словарь-тезаурус синонимов русской речи
Индуктивный и дедуктивный методы познания.
 Теория познания
Теория познанияИндуктивный и дедуктивный методы познания
Индукция — это познание от частного к общему. Например, анализируя частные знания (отдельные факты), исследователь — может прийти к общему знанию, в т.ч. умозаключению, гипотезе. Т.о. из частных знаний — получаются т.н. обобщённые знания. Чем обобщённее (=абстрактнее) знание — тем оно, в целом, полезнее, и могущественнее. Философия, например — совокупность наиболее обобщённых знаний. Наука и технологии, относительно философии — это знания со средней степенью обобщённости.
Именно такие (обобщённые и наиболее обобщённые) знания — дают человеку больше всего могущества (Силы).
Индукция, т.е. познание от частного к общему (обобщённому), по сути, есть основное содержание абстрактного мышления, — т.е. получение обобщённых (=абстрактных) и всё более обобщённых знаний из частных. В целом, именно так возникают и развиваются: искусство, наука и технологии, философия. Абстрактное мышление (индукция) — обуславливает превосходство человека над другими формами жизни на Земле.
Далее: Если индукция — это основное содержание абстрактного мышления, то чем же тогда является противоположный метод (дедукция)? Дедукция — тоже относится к абстрактному мышлению, т.к. она, хоть и не получает обобщённых знаний из частных, но оперирует обобщёнными (= абстрактными) знаниями:
Далее: В обобщённом знании, кстати — всегда содержится частное знание, вернее, много частных знаний, соединённых в одно общее. В этом — сила общих (обобщённых и наиболее обобщённых, = абстрактных) знаний. Например, обобщённое знание, что все деревья покрыты корой — содержит в себе связанные частные знания о каждом из триллионов деревьев, т. е. триллионы частных знаний! (связанных в одно лаконичное и могущественное общее знание о всех их). Узнав, что конкретный объект является деревом, мы получаем, используя дедукцию, знание, что наше конкретное дерево должно быть покрыто корой (т.е. получаем знание от общего к частному). Но ведь мы и так знали о том, что все деревья покрыты корой. По сути, дедукция от общего к частному — это применение уже имеющихся знаний, получение выводов (=новых знаний) на основе уже имеющихся общих знаний…
е. триллионы частных знаний! (связанных в одно лаконичное и могущественное общее знание о всех их). Узнав, что конкретный объект является деревом, мы получаем, используя дедукцию, знание, что наше конкретное дерево должно быть покрыто корой (т.е. получаем знание от общего к частному). Но ведь мы и так знали о том, что все деревья покрыты корой. По сути, дедукция от общего к частному — это применение уже имеющихся знаний, получение выводов (=новых знаний) на основе уже имеющихся общих знаний…
Кстати, дедукцию прославил, в своё время, всем известный, Шерлок Холмс, — имевший «выдающиеся дедуктивные способности».
Одним из проявлений дедукции является также метод познания — экстраполяция. Например, узнав, что открыт новый вид травы, и зная, что все известные виды травы — зелёные, мы можем сделать вывод, что новый вид травы является зелёным. Получаем т.о. — такое новое частное знание: «новый вид травы является зелёным». Т.е. мы этого не проверяли, и не видели, но экстраполировали (применили) имевшееся общее знание — на новый предмет, который в обобщение не входил.
Идём далее: итак, мы рассмотрели, в целом, различные т.н. обычные методы познания. Переходим теперь к специфическим, применимым в случае какой-либо виртуальной реальности окружающего Мира…
На семинаре по философии коснулись индукции и дедукции, преподаватель заявил, что Шерлок Холмс пользуется индукцией. Как так?
Ну да, это известная ошибка автора (если только он не имел в виду чего-то совсем уж нестандартного по значению).
Дедукция — это движение от общего к частному. На классическом примере:
Общее: все люди смертны
Частный случай: Сократ — человек
Дедуктивный вывод: Сократ — смертен
Индукция — это движение от частного к общему.
Частный случай: человек Сократ смертен.
Частный случай: человек Платон смертен.
Индуктивный вывод: Люди смертны
И когда в рассказах речь идёт о дедуктивном методе, на самом деле, он ближе к индукции — Холмс берёт частные случаи (грязь на ботинке, царапины на часах) и строит общую картину. Дедукцией он тоже пользуется, но реже. Но это только на первый взгляд
Если говорить строго, то чуть раньше Конан Дойля жил такой человек как Чарльз Пирс. И он ввёл в употребление термин «абдукция» — это нахождение возможных причин из последствий.
Общее: все люди смертны.
Последствие: Сократ смертен.
Абдуктивный вывод: вероятно, Сократ — человек.
То есть, абдукция не обязательно позволяет прийти к верному заключению (Сократ может быть котом и тоже быть смертным), но позволяет создать логичную теорию в рамках какой-то системы.
И, на самом деле, Шерлок Холмс пользуется именно абдукцией.
На примере, как это происходит. Холмс знает, что Уотсон — врач, и видит у него хорошую осанку. Он предполагает, что он — военный врач.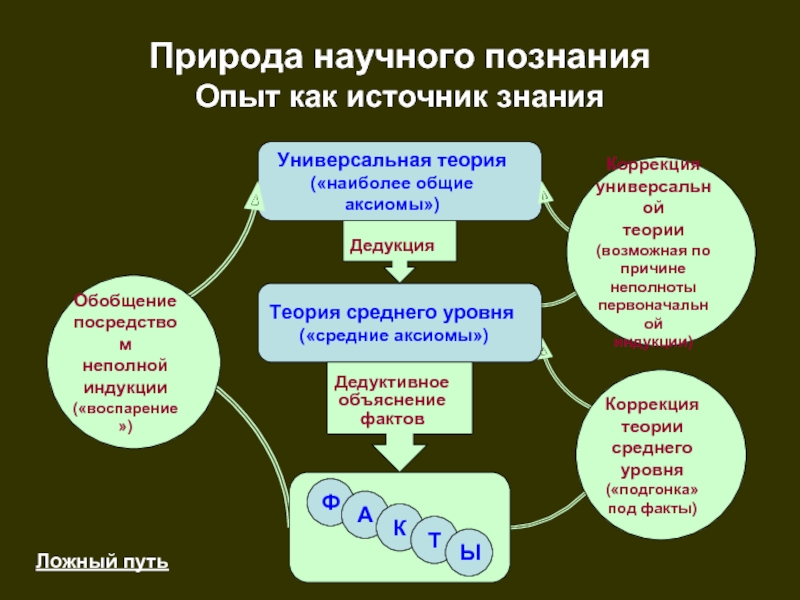 Это индуктивное движение (из двух частных признаков собирается общая картинка), но не строгое — человек мог, например, получить специальность врача после увольнения из армии, или получить хорошую осанку, не будучи военным. То есть, Холмс пользуется абдукцией — строит правдоподобную гипотезу.
Это индуктивное движение (из двух частных признаков собирается общая картинка), но не строгое — человек мог, например, получить специальность врача после увольнения из армии, или получить хорошую осанку, не будучи военным. То есть, Холмс пользуется абдукцией — строит правдоподобную гипотезу.
Потом он говорит, что у вас истощённое лицо, значит, вы болели. Это дедуктивное движение (от общего состояния к частной причине), но тоже не строгое — у человека может быть истощённое лицо из-за того, что он перетрудился или неправильно питался, например. Но именно этот вариант, с болезнью, совпадает с выводами прошлого абдуктивного предположения. И из нескольких абдуктивных выводов Холмс собирает общую картинку: Уотсон — военный врач, воевавший в Афганистане.
Такие дела.
Общенаучные методы познания (анализ и синтез, индукция и дедукция)
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьМетодология – это учение о методах познания и преобразования действительности.
В науке метод часто определяет судьбу исследования, так при различных подходах из одного и того же фактического материала могут быть сделаны противоположные выводы. Познание – это исторический процесс творческой деятельности людей, формирующий их знания, на основе которых возникают цели и мотивы человеческих действий. Научное познание – это зрелая форма познавательной деятельности людей. Оно отвечает на вопросы не только как, но и почему исследованное явление протекает именно таким образом. Научное познание не терпит бездоказательности.
Анализ и синтез. Процесс познания совершается так, что мы сначала наблюдаем общую картину изучаемого предмета, а частности остаются в тени. При таком взгляде на вещи нельзя познать их внутренней структуры и сущности. Для изучения частностей мы должны расчленить изучаемые предметы. Анализ – это мысленно разложение предмета на составляющие его части или стороны. Будучи необходимым приемом мышления, анализ является лишь одним из моментов процесса познания. Невозможно познать суть предмета, только разлагая его на элементы, из которых он состоит. В каждой области знания есть как бы свой предел членения объекта, за которым мы переходим в иной мир свойств и закономерностей. Когда путем анализа частности достаточно изучены, наступает следующая стадия познания – синтез – мысленное объединение в единое целое расчлененных анализом элементов. Анализ фиксирует в основном то специфическое, что отличает части друг от друга.
Анализ и синтез берут свое начало в практической деятельности, которая складывается не только из расчленения предметов, но и из воссоединения частей в единое целое. Постоянно расчленяя в своей практической деятельности различные предметы на их составные части, человек постепенно научился разделять предметы и мысленно.
Индукция и дедукция. Индукция, вид обобщения, связанный с предвосхищением результатов наблюдений и экспериментов на основе данных опыта. Индуктивные обобщения обычно рассматриваются как опытные истины, а потому они всегда незакончены и неполны. Дедукция же это переход от общего к частному.
Как методы исследования индукция – процесс выведения общего положения из ряда частных (менее общих) утверждений, из единичных фактов; дедукция, наоборот, – процесс рассуждения, идущий от общего к частному или менее общему. Обычно различают два основных вида индукции: полную и неполную. Полная индукция – вывод какого-либо общего суждения обо всех предметах некоторого множества на основании рассмотрения каждого элемента этого множества. Понятно, что сфера применения такой индукции ограничена объектами, число которых конечно и практически обозримо.
Полная индукция – вывод какого-либо общего суждения обо всех предметах некоторого множества на основании рассмотрения каждого элемента этого множества. Понятно, что сфера применения такой индукции ограничена объектами, число которых конечно и практически обозримо.
На практике чаще всего применяют формы индукции, которые предполагают вывод обо всех предметах класса на основании познания лишь части предметов данного класса. Такие выводы называются выводами неполной индукции. Они тем ближе к действительности, чем более глубокие, существенные связи раскрываются. Неполная индукция, основанная на экспериментальных исследованиях и включающая в себя теоретическое мышление (в частности, дедукцию), способна давать достоверное заключение. Она носит название научной индукции. Индукция является истинным источником действительного научного прогресса. Великие открытия, скачки научной мысли создаются, в конечном счете, индукцией – рискованным, но важным творческим методом.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Разница между дедуктивным и индуктивным рассуждением
Как отличить эти общие подходы к решению проблем
Дэниел Мисслер в философии
Создано / обновлено: 23 сентября 2020 г.
Практически любой, кто задумывается о том, как решать проблемы формальным образом, сталкивался с концепциями дедуктивного и индуктивного рассуждений. Как дедукция, так и индукция помогают нам ориентироваться в реальных проблемах, таких как, например, кто совершил преступление, наиболее вероятная причина аварии или сколько планет может содержать жизнь в галактике Млечный Путь.
Хотя они оба являются практическими инструментами для решения практических задач, но они подходят к решению проблем по-разному.
Как дедукция, так и индукция представляют собой тип вывода, что означает достижение вывода, основанного на доказательствах и рассуждениях.
Дедукция переходит от идеи к наблюдению, в то время как индукция переходит от наблюдения к идее.
Вывод — это сначала идея, затем наблюдения и заключение. Индукция — это сначала наблюдение, за которым следует идея, которая могла бы объяснить увиденное.
Еще одно большое отличие состоит в том, что выводы дедукции пуленепробиваемы, если вы не допускаете ошибок в процессе. Вывод всегда верен, пока верны посылки. С индукцией вы не получите абсолютной уверенности; качество идеи, модели или теории зависит от качества наблюдений и анализа.
Примеры
Все люди смертны. Гарольд — мужчина. Следовательно, Гарольд смертен.
Вычет
Это третье предложение абсолютно верно, потому что первые два предложения верны.
У меня есть мешок с множеством монет, я вытащил 10 наугад, и все они были пенни, поэтому, вероятно, это мешок, полный пенсов.
Индукция
Это дает некоторую поддержку аргументу, что в сумке только гроши, но это не полная поддержка, как мы видим с дедукцией.
Дальнейшие пояснения
У дедукции есть теории, предсказывающие результат, которые проверяются экспериментами.Индукция делает наблюдения, которые приводят к обобщениям того, как это работает.
Если посылки верны в дедукции, вывод определенно верен. Если предположения верны при индукции, вывод будет только , вероятно, верным — в зависимости от того, насколько убедительны доказательства.
Существует еще один тип рассуждений, называемый «абдуктивное рассуждение», когда вы берете набор наблюдений и просто берете наиболее вероятное объяснение с учетом имеющихся у вас свидетельств.
Дедукцию трудно использовать в повседневной жизни, потому что она требует последовательного набора фактов, которые заведомо истинны.
 Индукция используется постоянно в повседневной жизни, потому что большая часть мира основана на частичных знаниях, вероятностях и полезности теории, а не на ее абсолютной достоверности.
Индукция используется постоянно в повседневной жизни, потому что большая часть мира основана на частичных знаниях, вероятностях и полезности теории, а не на ее абсолютной достоверности.Вычисление более точное и количественное, в то время как индукция более общее и качественное.
Дополнительные примеры
Если A = B и B = C, то A = C.
Вычет
Поскольку все квадраты являются прямоугольниками, и все прямоугольники имеют четыре стороны, поэтому все квадраты имеют четыре стороны.
Вычет
Все кошки обладают острым обонянием. Пушистик — кошка, поэтому у Пушика острое обоняние.
Вычет
Каждый раз, когда вы едите арахис, у вас опухает горло, и вы не можете дышать. Это симптом людей, страдающих аллергией на арахис.Итак, у вас аллергия на арахис.
Индукция
Рэй — футболист.
Все футболисты весят более 170 фунтов. Рэй весит более 170 фунтов.
Вычет
Все автомобили в этом городе едут по правой стороне улицы. Поэтому все автомобили во всех городах едут по правой стороне улицы.
Индукция
Здесь мы видим, что дедукция — это неплохо.Чисто. Но жизнь редко бывает достаточно чистой, чтобы можно было применить ее в совершенстве.
Большинство реальных проблем и вопросов больше относятся к сфере индукции, где у вас могут быть некоторые наблюдения — и эти наблюдения могут привести вас к какому-то обобщению или теории — но вы не обязательно можете сказать наверняка, что вы правы. Речь идет о том, чтобы работать как можно лучше в мире, где знания обычно неполны.
Резюме
- Выведение приведет вас к идеальному выводу, но только в том случае, если все ваши предпосылки верны на 100%.
- Дедукция переходит от теории к эксперименту к проверке, где индукция переходит от наблюдения к обобщению и теории.
- Выведение труднее использовать за пределами лаборатории / науки, потому что часто бывает трудно найти набор полностью согласованных фактов для структурирования аргументации.
- Индукция используется постоянно, потому что это отличный инструмент для решения повседневных проблем, связанных с частичной информацией о нашем мире и выводом полезных выводов, которые могут быть неверными во всех случаях.
- Будьте готовы использовать оба типа рассуждений для решения проблем и знайте, что они часто могут использоваться вместе циклически в паре, например, использовать индукцию, чтобы придумать теорию, а затем использовать дедукцию, чтобы определить, действительно ли она верна.
- Главное, чего следует избегать с этими двумя, — это спорить с силой дедукции (гарантированная истинность) при фактическом использовании индукции (вероятность, основанная на силе доказательств).
Удержание | Encyclopedia.com
gale
просмотра обновлено 11 июня 2018Дедукция — это тип рассуждения, посредством которого человек делает вывод из одной или нескольких данных предпосылок к предложению, которое является их необходимым и логическим следствием (см. Аргументацию; силлогизм).Этот термин появился недавно в истории логики, его французский эквивалент появился только в последнем издании (1835 г.) Dictionnaire de l’Académie française . Аристотель характеризует определенный тип аргумента как ἀπαγωγή, который переводится на латынь как deductio , но лучше переводится на английский как сокращение; аргумент, известный как reductio ad impssibile , относится к этому типу ( Anal. pr. 29b 6; см. также там же, 69a 20). И снова Томас Аквинский использует термин deductio по крайней мере в четырех различных смыслах, ни один из которых не имеет точного современного значения [ см. L.Schütz, Thomas – Lexikon (2-е изд. Падерборн 1895; репр. Штутгарт 1958) 203]. И. Кант также говорит о трансцендентальной дедукции как о части своего трансцендентального метода. см. трансцендентальное (кантиан). Современные логики иногда противопоставляют дедукцию индукции на том основании, что первая заключает от общего к частному, а вторая — от частного к общему; эта характеристика, однако, неточна, поскольку дедукция не обязательно должна приводить к частному, и ее процесс далеко не является логическим обратным индуктивной процедуре (см. индукцию; демонстрация).По поводу конкретных учений по дедукции, см. R. Eisler, Wörterbuch der Philsphischen Begriffe, 3 v. (4-е изд. Берлин 1927–30) 1: 245–247.
См. Также: логический, символический.
[г. houde]
Новая католическая энциклопедия HOUDE, R.
oxford
просмотров обновлено 21 мая 2018de · duc · ation / diˈdəkshən / • п. 1. действие вычитания или вычитания: дивиденды будут выплачены без удержания налога. ∎ сумма, которая является или может быть вычтена из чего-либо, особенно. из налогооблагаемого дохода или налога к уплате: налоговых вычетов. 2. Вывод конкретных случаев со ссылкой на общий закон или принцип: детектив должен раскрыть убийцу путем вывода из фактов. Часто противопоставляется индукции. ∎ вывод, который был сделан.
Оксфордский карманный словарь современного английского
оксфорд
просмотров обновлено 21 мая 2018 г. дедукция, дедукция Использование логических правил для получения набора посылок, из которых должны следовать определенные выводы.Дедукция начинается с теории, переходит к гипотезам, выведенным из теории, а затем проверяет гипотезы с помощью прогнозов и наблюдений. Этот подход к проверке и теории часто называют гипотетико-дедуктивным методом, и, поскольку он делает упор на гипотезах, предсказании и проверке, иногда считается методом par excellence науки. См. Также ИНДУКЦИЯ.Социологический словарь ГОРДОН МАРШАЛЛ
оксфорд
просмотров обновлено 14 мая 2018 г. дедукция Формальный метод логического вывода.Дедукция — это процесс применения одного или нескольких правил вывода к заданному набору фактов (известный как аксиомы , ) и вывода новых фактов. В отличие от других методов вывода, абдукции и индукции, дедукция дает логически обоснованные результаты, то есть не содержит неопределенности.Компьютерный словарь ДЖОН ДЕЙНТИТ
gale
просмотров обновлено 23 мая 2018 г.То, что вычитается; часть отнята; уменьшение выбросов; как в вычетах из валовой прибыли при расчете чистой прибыли для целей налогообложения.
Согласно гражданскому праву , часть или вещь, которую наследник имеет право изъять из наследственной массы до того, как произойдет раздел.
Взнос на благотворительность может быть использован как вычет для уменьшения дохода для целей налога на прибыль, если налогоплательщик выполняет требования, установленные законом.
Энциклопедия американского права Уэста
Дедукция — Энциклопедия Нового Мира
В традиционной аристотелевской логике, дедукция или дедуктивное рассуждение — это умозаключение, в котором посылки, если они верны, призваны гарантировать истинность вывода, а не к абдуктивным и индуктивным рассуждениям, где предпосылки предлагаются как некоторые доказательства для вывода, но не гарантирующие его истинность.
Дедуктивный вывод
Нам действительно нужно сказать, что в дедуктивном выводе посылки «призваны гарантировать заключение», потому что нам нужно создать место для тех умозаключений, которые претендуют на то, чтобы быть дедуктивными, но не могут на самом деле достичь этого статуса, т. Е. они являются неверными дедуктивными выводами — потому что они ложные. Примерами таких ложных или недействительных дедуктивных выводов являются отрицание антецедента (если p, то q. Не p. Следовательно, не q.) И подтверждение консеквента (если p, то q.q верно. Следовательно, p верно.). Эти конкретные недействительные выводы имитируют действительные выводы подтверждения антецедента (то есть Modus Ponens) и отрицания консеквента (то есть Modus Tollens).
Действительный аргумент — это аргумент, структура или форма которого невозможны для того, чтобы посылки были истинными, а вывод — ложным.
Вывод действительного дедуктивного вывода: необходимо по помещениям. В индуктивных и абдуктивных выводах посылки могут быть истинными, в то время как заключение ложным — таким образом, со строгой логической точки зрения, все индуктивные и абдуктивные выводы, строго говоря, недействительны.Пример индуктивного вывода: «Все образцы серебра, которые мы исследовали, плавились при 961,78 ° C, таким образом, все образцы серебра во Вселенной будут плавиться при 961,78 ° C». Пример абдуктивного вывода: «Моя машина не заводилась после ливня. Если дождь вызвал короткое замыкание в моей машине, это могло бы объяснить, почему она не запустилась после ливня. Поэтому ливень вызвал короткое замыкание в моей машине. из-за этого он не запустился «.
Другой способ, которым это иногда описывают, состоит в том, что дедукция — это умозаключение, в котором заключение не имеет большей общности, чем посылки, в противоположность абдуктивному и индуктивному рассуждению, где умозаключение имеет большую общность, чем посылки.Другие теории логики определяют дедуктивное рассуждение как умозаключение, в котором заключение столь же достоверно, как и посылки, в отличие от индуктивного рассуждения, где заключение может иметь меньшую достоверность, чем посылки. Каким бы образом это ни описывалось, вывод дедуктивного вывода обусловлен предпосылками — посылки не могут быть истинными, в то время как вывод ложен. Но в индуктивных и абдуктивных выводах предположения могут быть истинными, но заключение, тем не менее, ложным.
Примеры
Действителен:
- Все люди смертны.
- Сократ — мужчина.
- Следовательно, Сократ смертен.
- Картинка над столом.
- Стол над полом.
- Следовательно, картина находится над полом.
- У всех птиц есть крылья.
- Кардинал — птица.
- Следовательно, у кардинала есть крылья.
Неверно:
- Каждый преступник выступает против правительства.
- Все члены оппозиционной партии выступают против правительства.
- Следовательно, каждый в оппозиционной партии — преступник.
Это недействительно, поскольку посылки не позволяют установить общность между членством в оппозиционной партии и преступностью. Это известная ошибка нераспределенной середины.
Недействительно:
- Если вы совершили мошенничество, вас осудят.
- Вы не совершали мошенничества.
- Следовательно, вы не будете осуждены.
Это неверно, потому что это пример ошибки отрицания антецедента. В этом случае вас могут осудить за другое преступление, которое вы совершили, например, за поджог, даже если вы не совершали мошенничества.
Недействительно:
- Если это Leica, то это камера.
- Это камера.
- Значит, это Leica.
Это неверно, потому что это пример ошибочного утверждения консеквента. В данном случае это камера, но на самом деле это может быть Contax или какая-то другая камера, отличная от Leica.
| Основные формы аргументов исчисления | ||
| Имя | Sequent | Описание |
|---|---|---|
| Modus Ponens | [( p → q ) ∧ p ] ⊢ q | если p, то q; п; поэтому q |
| Modus Tollens | [( p → q ) ∧ ¬ q ] ⊢ p | , если p, то q; не q; поэтому не p |
| Гипотетический силлогизм | [( p → q ) ∧ ( q → r )] ⊢ ( p → r) | если p, то q; если q, то r; следовательно, если p, то r |
| дизъюнктивный силлогизм | [( p ∨ q ) ∧ ¬ p ] ⊢ q | Либо p, либо q; не р; следовательно, q |
| Конструктивная дилемма | [( p → q ) ∧ ( r → s ) ∧ ( p ∨ r )] ⊢ ( q ∨ s ) | Если p, то q; а если r, то s; но либо p, либо r; поэтому либо q, либо s |
| Деструктивная дилемма | [( p → q ) ∧ ( r → s ) ∧ (¬ q ∨ ¬ s )] ⊢ ( p ∨ r ) | Если p, то q; а если r, то s; но либо не q, либо не s; поэтому скорее не p или не r |
| Упрощение | ( p ∧ q ) ⊢ p , q | p и q верны; следовательно p верно |
| Соединение | p , q ⊢ ( p ∧ q ) | p и q истинны по отдельности; следовательно, они верны вместе |
| Дополнение | p ⊢ ( p ∨ q ) | п истинно; поэтому дизъюнкция (p или q) истинна |
| Состав | [( p → q ) ∧ ( p → r )] ⊢ [ p → ( q ∧ r )] | Если p, то q; а если p, то r; следовательно, если p истинно, то q и r истинны |
| Теорема Де Моргана (1) | ( p ∧ q ) ⊢ ( p ∨ q ) | Отрицание (p и q) эквивалентно.к (не p или не q) |
| Теорема Де Моргана (2) | ( p ∨ q ) ⊢ ( p ∧ q ) | Отрицание (p или q) эквивалентно. к (не p и не q) |
| Коммутация (1) | ( p ∨ q ) ⊢ ( q ∨ p ) | (p или q) эквивалентно. к (q или p) |
| Коммутация (2) | ( p ∧ q ) ⊢ ( q ∧ p ) | (p и q) эквивалентно.к (q и p) |
| Ассоциация (1) | [ p ∨ ( q ∨ r )] ⊢ [( p ∨ q ) ∨ r ] | p или (q или r) эквивалентно к (p или q) или r |
| Ассоциация (2) | [ p ∧ ( q ∧ r )] ⊢ [( p ∧ q ) ∧ r ] | p и (q и r) эквивалентны. к (p и q) и r |
| Распределение (1) | [ p ∧ ( q ∨ r )] ⊢ [( p ∧ q ) ∨ ( p ∧ r )] | p и (q или r) эквивалентнок (p и q) или (p и r) |
| Распределение (2) | [ p ∨ ( q ∧ r )] ⊢ [( p ∨ q ) ∧ ( p ∨ r )] | p или (q и r) эквивалентно. к (p или q) и (p или r) |
| Двойное отрицание | p ⊢ p | p эквивалентно отрицанию not p |
| Транспонирование | ( p → q ) ⊢ ( q → p ) | Если p, то q эквивалентно.если не q, то не p |
| Материальное значение | ( p → q ) ⊢ ( p ∨ q ) | Если p, то q эквивалентно. либо не p, либо q |
| Материальная эквивалентность (1) | ( p ↔ q ) ⊢ [( p → q ) ∧ ( q → p )] | (p эквивалентно q) означает, (если p истинно, то q истинно) и (если q истинно, то p истинно) |
| Материальная эквивалентность (2) | ( p ↔ q ) ⊢ [( p ∧ q ) ∨ (¬ q ∧ ¬ p )] | (p эквивалентноto q) означает, либо (p и q истинны), либо (оба p и q ложны) |
| Экспорт | [( p ∧ q ) → r ] ⊢ [ p → ( q → r )] | из (если p и q истинны, то r истинно), мы можем доказать (если q истинно, то r истинно, если p истинно) |
| Импорт | [ p → ( q → r )] ⊢ [( p ∧ q ) → r ] | |
| Тавтология | p ⊢ ( p ∨ p ) | p верно эквивалентно.к p верно или p верно |
Аксиоматизация
Говоря более формально, дедукция — это последовательность утверждений, так что каждое утверждение может быть выведено из предшествующих. Понятно, что это оставляет открытым вопрос о том, как мы доказываем первое предложение (поскольку оно не может следовать ни из чего). Аксиоматическая логика высказываний решает эту проблему, требуя выполнения следующих условий для доказательства:
Доказательство α из ансамбля Σ корректных формул ( wff s) представляет собой конечную последовательность wff s:
- β1 ,…, βi, …, βn
где
- βn = α
и для каждого βi (1 ≤ i ≤ n), или
или
или
- βi — результат Modus Ponens для двух предыдущих wffs, βi-g и βi-h.
Различные версии аксиоматической логики высказываний содержат несколько аксиом, обычно три или более трех, в дополнение к одному или нескольким правилам вывода. Например, аксиоматизация логики высказываний Готтлобом Фреге, которая также является первым примером такой попытки, содержит шесть аксиом высказываний и два правила.Бертран Рассел и Альфред Норт Уайтхед также предложили систему с пятью аксиомами.
Например, версия аксиоматической логики высказываний Яна Лукасевича (1878-1956) имеет набор A аксиом, принятых следующим образом:
- [PL1] p → ( q → p )
- [PL2] ( p → ( q → r )) → (( p → q ) → ( p → r ))
- [PL3] (¬ p → ¬ q ) → ( q → p )
и имеет набор R правил вывода с одним правилом в нем, которое является Modu Понендо Поненс следующим образом:
- [MP] из α и α → β, вывести β.
Правило (а) вывода позволяет нам выводить утверждения, следуя аксиомам или заданным wff s ансамбля Σ.
Естественная дедуктивная логика
В одной из версий естественной дедуктивной логики, представленной E.J. Леммон, что мы должны называть ее системой L, у нас нет никакой аксиомы для начала. У нас есть всего девять примитивных правил, управляющих синтаксисом доказательства.
Девять простых правил системы L:
- Правило предположения (A)
- Modus Ponendo Ponens (MPP)
- Правило двойного отрицания (DN)
- Правило условного доказательства (CP)
- Правило ∧-введения (∧I)
- Правило ∧-исключения (∧E)
- Правило ∨-введения (∨I)
- Правило ∨-исключения (∨E)
- Reductio Ad Absurdum (RAA)
В системе L доказательство имеет определение со следующими условиями:
- имеет конечную последовательность wff s (правильно построенная формула)
- каждая строка оправдана правилом системы L
- последняя строка доказательства — это то, что задумано (В.E.D, quod erat manifestrandum, это латинское выражение, означающее: «что должно было быть доказано»), и эта последняя строка доказательства использует единственную (ые) исходную (ые) посылку (я); или нет предпосылки, если ничего не указано.
Тогда, если посылка не указана, секвенция называется теоремой. Следовательно, определение теоремы в системе L таково:
- теорема — это последовательность, которая может быть доказана в системе L, используя пустой набор предположений.
или другими словами:
- теорема — это секвенция, которая может быть доказана из пустого набора предположений в системе L
Пример доказательства секвенции (в данном случае Modus Tollendo Tollens):
| p → q , ¬ q ¬ p [Modus Tollendo Tollens (MTT)] | |||
| Номер допущения | Номер строки | Формула (wff) | Используемые линии и обоснование |
|---|---|---|---|
| 1 | (1) | ( p → q ) | А |
| 2 | (2) | ¬ q | А |
| 3 | (3) | п | A (для RAA) |
| 1,3 | (4) | q | 1,3, МПП |
| 1,2,3 | (5) | q ∧ ¬ q | 2,4, ∧I |
| 1,2 | (6) | ¬ п | 3,5, RAA |
| Q.E.D | |||
Пример доказательства секвенции (в данном случае теорема):
| ⊢ p ∨ ¬ p | |||
| Номер допущения | Номер строки | Формула (wff) | Используемые линии и обоснование |
|---|---|---|---|
| 1 | (1) | ¬ ( p ¬ p ) | A (для RAA) |
| 2 | (2) | ¬ п | A (для RAA) |
| 2 | (3) | ( п. ¬ п. ) | 2, ∨I |
| 1, 2 | (4) | ( p ∨ ¬ p ) ∧ ¬ ( p ∨ ¬ p ) | 1, 2, ∧I |
| 1 | (5) | ¬¬ п | 2, 4, RAA |
| 1 | (6) | п | 5, DN |
| 1 | (7) | ( п. ¬ п. ) | 6, ∨I |
| 1 | (8) | ( p ∨ ¬ p ) ∧ ¬ ( p ∨ ¬ p ) | 1, 7, ∧I |
| (9) | ¬¬ ( p ¬ p ) | 1, 8, RAA | |
| (10) | ( п. ¬ п. ) | 9, DN | |
| Q.E.D | |||
Каждое правило системы L имеет свои собственные требования к типу входных данных или записей, которые оно может принять, и имеет свой собственный способ обработки и расчета допущений, используемых его входными данными.
См. Также
Список литературы
Все учебники логики — а их сейчас сотни — посвящены дедукции и умозаключениям. Вот несколько репрезентативных:
- Копи, Ирвинг М. и Карл Коэн. Введение в логику .Прентис Холл. (Изданий много; последнее, с 2004 года, — 12-е.)
- Херли, Патрик Дж. Краткое введение в логику . Бельмонт, Калифорния: Обучение Уодсворта / Томпсона. (Изданий много; последняя — 9-я.)
- Jennings, R.E. Continuing Logic , учебник по «Аксиоматической логике» в Университете Саймона Фрейзера, Ванкувер, Канада
- Джонсон, Роберт М. Основы рассуждений: книга логики . Бельмонт, Калифорния: Уодсворт. (Последнее — 4-е издание.)
- Риз, Уильям Л. «Дедукция», в Словарь философии и религии , новое и расширенное издание. Атлантическое нагорье, Нью-Джерси: Humanities Press, 1996.
- Зарефский, Давид. Аргументация: исследование частей I и II эффективного мышления , The Teaching Company, 2002.
Внешние ссылки
Все ссылки получены 7 ноября 2017 г.
Источники общей философии
Кредиты
Энциклопедия Нового Света Писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в Энциклопедию Нового Света :
Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.
(PDF) Соответствующий вывод
39
Карнап Р. (1956): «Методологический характер теоретических концепций», в: Фейгл,
Х. / Скривен, М. (ред., 1956), Миннесотские исследования в Философии науки, т. I, Univ. of
Minnesota Press, Миннеаполис, стр. 38-76.
Клив, Дж. П. (1973/74): «Отчет о введении на основе классической семантики», Анализ 34,
, стр. 118–122.
Фиттинг М. (1983): Методы доказательства для модальной и интуиционистской логики, Рейдель, Дордрехт.
Фридман М. (1974): «Объяснение и научное понимание», Журнал Философии 71, стр.
5-19.
Глаймур, К. (1980): «Гипотетико-дедуктивизм безнадежен», Philosophy of Science 47, стр. 322-
325.
Халлден С. (1951): «О семантической неполноте определенных Lewis Calculi «, Journal of
Symbolic Logic 16, no. 2, 127-129.
Харрисон, Дж. (1972): «Этический натурализм», в: Эдвардс, П. (изд., 1972), Энциклопедия философии
, Vol.3/4, The Macmillan Company & The Free Press, New York, Reprint Edition,
pp.69-71.
Hempel, C.G. (1965), Аспекты в научном объяснении и других эссе, Free Press, New
York — London.
Гессе, М. (1970): «Теории и транзитивность подтверждения», Философия науки 37, стр.
50-63.
Хьюм, Д. (1739/40): Трактат о человеческой природе, (изд. Л. А. Селби-Бигге, Оксфорд 1888, переиздание
1951), Ориг. 1739/40.
Китчер, П.(1976): «Комментарии и критика: объяснение, соединение и объединение», журнал
Философии 73, стр. 207-212.
Китчер П. (1981): «Объяснительное объединение», Философия науки 48, стр. 507-531.
Клини С.С. (1971): Введение в метаматематику, издательство Wolters-Noordhoff Publishing,
Groningen.
Кёрнер, С. (1947): «On Entailment», Proceedings of the Aristotelean Society 21, pp. 143-162.
Кёрнер С. (1959): Концептуальное мышление, Dover Publ., Нью-Йорк.
Кёрнер С. (1979): «О логической достоверности и неформальной адекватности», Философия 54, стр. 377-
379.
Кейперс Т.А. (изд., 1987), Что ближе к истине?, Познаньские исследования в философии
Наука и гуманитарные науки, Том. 10, Rodopi, Amsterdam 1987.
Kutschera, F.v. (1982): Grundlagen der Ethik, W. de Gruyter, Берлин — Нью-Йорк.
Ллойд, Дж. (1984): Основы логического программирования, Springer, Берлин.
Миллер, Д.(1982): «Истина, правдивость, приблизительная истина», Fundamenta Scientiae, том 3,
№ 1, стр. 93-101.
Morscher, E. (1984): «Sein-Sollen-Schlüsse und wie Schlüsse sein sollen», in: Krawietz, W. u.a.
(ред., 1984), Theorie der Normen (Festgabe für Ota Weinberger), Duncker & Humblot,
Berlin.
У. Парри (1933): «Ein Axiomensystem für eine neue Art von Implikation (Analytische
Implikation)», Ergebnisse eines Mathematischen Kolloquiums, vol.4. С. 5-6.
Поппер К. (1948): «Что логика может сделать для философии?», Труды Аристотелевского общества,
Доп. Vol. 22. С. 141-154.
Поппер, К. (1963): предположения и опровержения, Routledge & Kegan, Лондон.
Поппер, К. (1976): Logik der Forschung (6. Auflage), J.C.B. Мор, Тюбинген.
Приор, А. (1954): «Парадоксы производного обязательства», Mind 63, стр. 64-65.
Приор, А. (1960): «Автономия этики», Австралазийский философский журнал 38, стр.199-
206.
Росс, А. (1941): «Императивы и логика», Теория 7, 1941, стр. 53-71; перепечатка в Philosophy of
Science 11, 1944, стр. 30-46.
Радницкий, Г. (1980): «От обоснования теории до сравнения теорий и выбора
вопросов», Revue Internationale de Philosophie 131-132, стр. 179-228.
Rautenberg, W. (1979): Klassische und Nichtklassische Aussagenlogik, Friedr. Vieweg & Sohn,
Браушвейг / Висбаден.
Шурц, Г.(1983a): Wissenschaftliche Erklärung. Ansätze zu einer logisch-pragmatischen
Wissenschaftstheorie, (диссертация), dbv-Verlag für die TU Graz.
Дедуктивный метод — обзор
Дедуктивные базы данных и сообщество баз данных
В середине 1980-х годов сообщество баз данных, вдохновленное разработками дедуктивных баз данных, инициировало проекты по разработке систем-прототипов и алгоритмов реализации. Первые две группы были ECRC в Европе в 1984 году под руководством Николаса; и MCC в США.С. в 1984 г., авторы Цур и Заниоло. За ними последовали Дж. Ульман и его группа в Стэнфорде в 1985 году. ECRC и MCC были одними из первых неуниверситетских организаций, разработавших прототипы.
Группа Николаса разработала систему DDB EKS — V1 [Vieille et al. , 1990], который включал метод оценки сверху вниз, методы дедуктивной оценки запросов ( QSQ / SLD ) [Vieille, 1986], проверку целостности (Soundcheck), проверку согласованности (SATCHMO) [Manthey and Bry, 1988] , и агрегация через рекурсию.Система была завершена в 1990 году. В начале 1990-х Николас и его группа перешли в Groupe Bull. В 1992 году Николя и Вьей возглавили работу по разработке VALIDITY DDB [Friesen et al. , 1996], результат их работы в ECRC. VALIDITY интегрированные объектно-ориентированные функции. ДЕЙСТВИТЕЛЬНОСТЬ продолжала развиваться и продаваться на рынке Калифорнийской корпорацией Next Century Media, Inc.
Цур и Заниоло из MCC разработали систему DDB LDL .Они акцентировали внимание на методах оценки снизу вверх, оценке запросов с использованием полунаивной оценки, магических наборах и подсчете, семантике для стратифицированного отрицания по умолчанию и группировки наборов, наборах ответов и оптимизации порядка соединения. ЛПНП был внедрен в 1988 г. и выпущен в период 1989–1991 гг. [Tsur and Zaniolo, 1986]. Он был одним из первых широко доступных DDB и был распространен среди университетов и компаний-акционеров MCC. Новая система, названная LDL ++, была запущена в 1990 году, которая расширила LDL с помощью мощных немонотонных конструкций, таких как конструкции недетерминированного выбора и XY-стратификация [Zaniolo et al., 1993], которые позже были использованы в Dedalus [Hellerstein, 2010]. Затем проект был продолжен в Калифорнийском университете в Лос-Анджелесе, куда Заниоло переехал в 1991 году.
Проект Ульмана, NAIL! (Это не другая реализация логики!) Разработали раннюю систему NAIL, от которой отказались. В обновленной системе использовался базовый язык под названием Glue. Работаем с ГВОЗДЕМ! проект, первая статья о волшебных наборах [Bancilhon et al. , 1986]. Некоторые другие работы этой группы — одна из первых работ по стратифицированному отрицанию дефолта [Van Gelder, 1986]; первая статья о хорошо обоснованной семантике [Van Gelder et al., 1991]; модульная стратификация [Росс, 1990].
Другие представляющие интерес системы дедуктивных баз данных кратко обсуждаются в обзоре 1995 года по дедуктивным базам данных в [Ramakrishnan and Ullman, 1995]. Опрос фокусируется на методах реализации и содержит таблицу, в которой перечислены 15 проектов, которые привели к внедрению систем. Перечислены следующие системы: Aditi, COL, Concept – Base, CORAL, EKS-VI, Logic – Base, DECLARE, Hy +, X4, LDL / LDL ++, Logres, Glue – Nail, Starburst и XSB, а также следующие функции. каждой системы (ссылки, рекурсия, отрицание по умолчанию, агрегирование, обновления, ограничения, оптимизации, хранилище и интерфейсы).Некоторые системы все еще могут работать. Дополнительную информацию об этих системах см. В [Ramakrishnan and Ullman, 1995]. В настоящее время коммерчески используется только один, XSB.
Эссе для студентов | Служба написания бумаги
Оформить заказ
Крайний срок14 д
- 14 дней
- 10 дней
- 7 дн.
- 5 дней
- 3 дн.
- 48 часов
- 24 ч
- 8 часов
- 3 ч
Получите скидку 10% Продолжать
Новая теория рассуждений Декарта
Стр. Из
НАПЕЧАТАНО ИЗ ОНЛАЙН-СТИПЕНДИИ ОКСФОРДА (Оксфорд.Universitypressscholarship.com). (c) Авторские права Oxford University Press, 2021. Все права защищены. Отдельный пользователь может распечатать одну главу монографии в формате PDF в OSO для личного использования. дата: 06 декабря 2021 г.
- Глава
- (стр.12) 2 Новая теория рассуждений Декарта
- Источник:
- Разум Юма
- Автор (ы):
Дэвид Оуэн (веб-страница автора)
- Издатель:
- Oxford University Press
DOI: 10.1093 / 0199252602.003.0002
Декарт отверг силлогизм и связанный с ним формальный подход к дедуктивным рассуждениям. Одной из главных причин было его забота об истине и способность распознавать новые истины и отличать истину от лжи. Формальная логика не усиливает; заключение дедуктивно действительного аргумента не накладывает никаких ограничений на истины, которые, как мы знаем, еще не наложены предпосылками. Вместо отказа от дедукции в пользу индукции, как Бэкон, Декарт разработал новую, амплиативную теорию дедукции в Правилах .Эта теория вывода была основана на интуиции, предшественнице его более позднего описания ясного и отчетливого восприятия. Один напрямую догадался, что две идеи связаны определенным образом. Один пришел к выводу, что одна идея связана с другой, образуя цепочку идей, причем связь между каждой идеей и ее соседом воспринимается интуицией.
Ключевые слова: Бэкон, дедукция, дедуктивное рассуждение, Декарт, формальная логика, вывод, интуиция, Регулы, силлогизм, истина
Oxford Scholarship Online требует подписки или покупки для доступа к полному тексту книг в рамках службы.Однако публичные пользователи могут свободно искать на сайте и просматривать аннотации и ключевые слова для каждой книги и главы.
Пожалуйста, подпишитесь или войдите для доступа к полному тексту.
Если вы считаете, что у вас должен быть доступ к этому заголовку, обратитесь к своему библиотекарю.
 Индукция используется постоянно в повседневной жизни, потому что большая часть мира основана на частичных знаниях, вероятностях и полезности теории, а не на ее абсолютной достоверности.
Индукция используется постоянно в повседневной жизни, потому что большая часть мира основана на частичных знаниях, вероятностях и полезности теории, а не на ее абсолютной достоверности.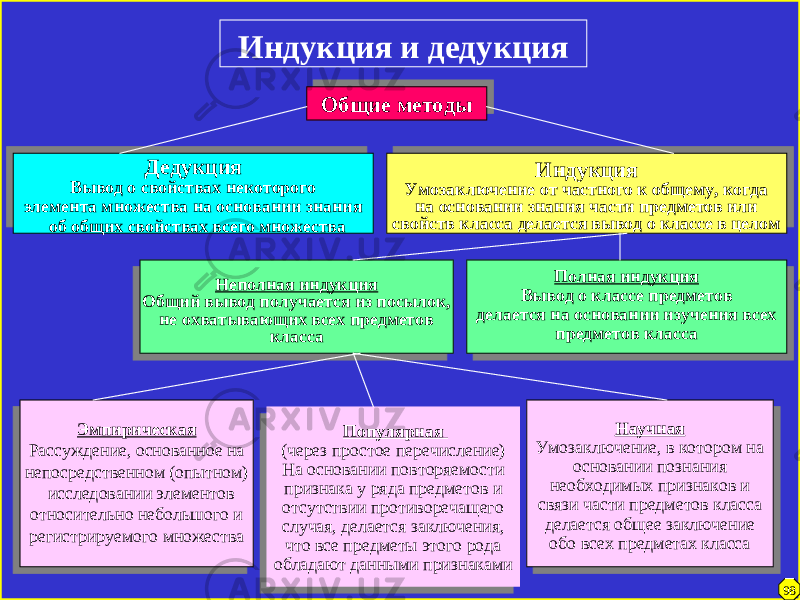 Все футболисты весят более 170 фунтов. Рэй весит более 170 фунтов.
Все футболисты весят более 170 фунтов. Рэй весит более 170 фунтов.