Формальная логика: Формальная логика — Психологос

Формальная логика — Психологос

01 октября 2022 г., 21:28

Формальная логика — наука, изучающая формы мысли (понятия, суждения, умозаключения, доказательства) со стороны их логической структуры, отвлекаясь от конкретного содержания мыслей. Это конструирование и исследование правил преобразования высказываний, сохраняющих их истинностное значение безотносительно к содержанию входящих в эти высказывания понятий.

Формальная логика и мышление

Предмет формальной логики — это не все мышление, а только одна его сторона — логические формы мышления. Формальная логика исследует как бы готовые, имеющиеся, уже возникшие мысли — понятия, суждения и т.д. — и устанавливает определенные соотношения (формулы) между ними. Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития этих мыслей — понятий, суждений, умозаключений.

Формальная логика отвлекается, абстрагируется от непосредственных условий возникновения и развития тех или иных мыслей. Она полностью отвлекается, в частности, и от взаимосвязи мышления с чувственным познанием. Иначе говоря, она вовсе не исследует, в отличие от психологии, как конкретно возникает и обогащается содержание нашего мышления на основе ощущений, восприятий и представлений. В логических формулах, например в силлогизме, соотносятся друг с другом уже как бы застывшие, законченные, полностью четко и до конца сформулированные мысли, т.е. результаты, готовые продукты мышления.

• Мышление

Комментарии (3):

Гость, 08 июня 2012 г., 13:12

Спасибо за статью. Очень четко и грамотно дали определение формальной логике. Хотелось бы, чтобы на этом сайте немного больше шире рассматривали такие темы как силлогизм, алогизм и другие составляющие виды этих тем.

1

ответ

Гость, 07 февраля 2020 г., 10:50

Мне даже интересно, какое мышление бывает не логическим?

1

ответ

Гость, 17 июня 2021 г. , 18:12

У аутистов диалектическая логика.

Материалы по теме:

01 окт. 2022 г.

Логика

Логика — философская наука, изучающая логические формы человеческого мышления и законы, которым подчиняется мышление. Логика изучает не конкретное содержание действительности, а мысли о ней, их структуру, то, что является общим для мыслей данного типа, независимо от их конкретного содержания. Поэтому при изучении логики для того, чтобы понять сущность процесса мышления, специфическое содержание форм и законов, нужно уметь обобщать конкретные рассуждения, уметь оперировать получаемыми формулами и схемами.

4Подробнее

01 янв. 2006 г.

Мышление

Мышление нередко определяют как способность к решению новых, экстренно возникающих задач в ситуациях, где прежние, уже известные решения не срабатывают. Творческое и конструктивное, развитое мышление действительно способно справляться с такими задачами, но это не значит, что если кто-то не нашел творческого решения в новой для него ситуации, у него мышление отсутствовало. В своих простейших формах мышление, как процесс, это всего лишь переработка информации в потоке течения мыслей, образов и ощущений.

7Подробнее

01 окт. 2022 г.

Мысль

Мысль — упакованный смысл, переданный сознанию (всплывший в сознании) в процессе мышления. Мысль (смысл?) — интересная, имеющая значение связь понятий, связь образа цели и элементов ситуации. «Я понял, как это связано!» «Я понял, что можно сделать!»

6Подробнее

01 окт. 2022 г.

Понятие

Понятие — то, что имеет определение, определенный смысл. Это представление, в котором смысл задан (построен) четким, определенным образом. Смысл понятия (образ понятия) имеет границы и правила его использования.

0Подробнее

01 окт. 2022 г.

Суждение

Суждение — высказывание; умственный акт, выражающий отношение говорящего к содержанию высказываемой мысли. Вынося суждение, мы создаем те опоры, которые считаем соответствующими действительности и потому позволяющими двигаться к истине.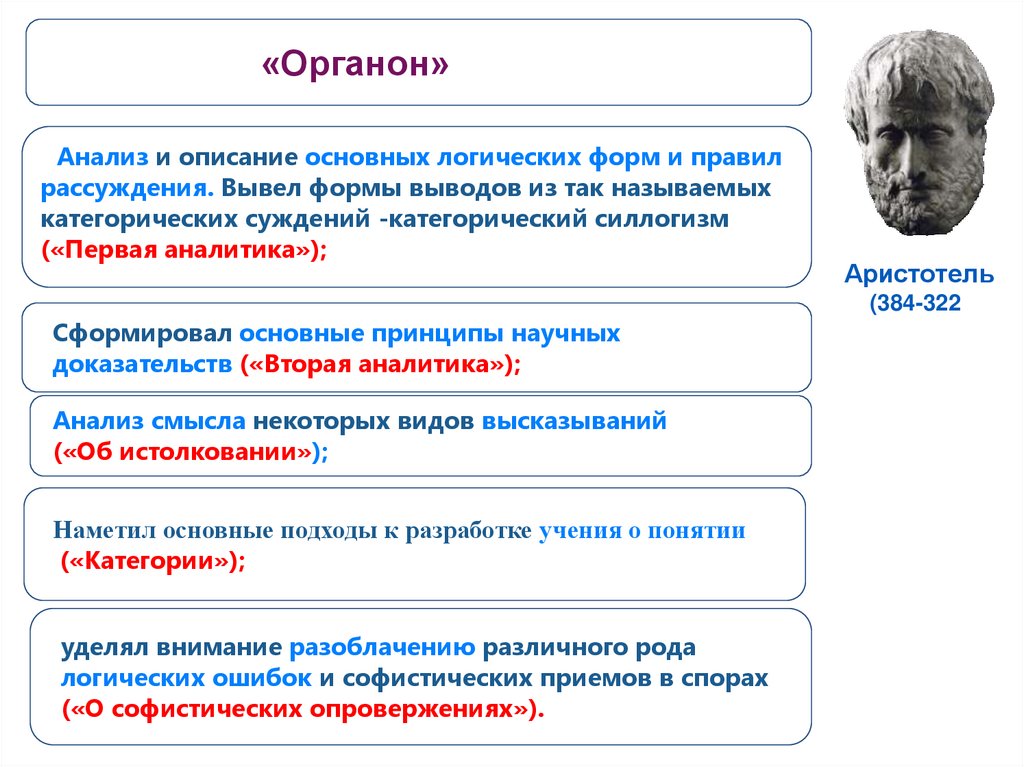 Суждение — это отражение связей между предметами и явлениями действительности или между свойствами и признаками. Например, суждение «Металлы при нагревании расширяются», выражает связь между изменениями температуры и объемом металлов. Устанавливая таким образом различные связи и отношения между понятиями, суждения являются высказываниями чего-то о чем-то.

0Подробнее

01 окт. 2022 г.

Теория познания

0Подробнее

01 окт. 2022 г.

Умозаключение — элементарная частица рассуждения

Умозаключение — мыслительная операция, состоящая в получении нового вывода из нескольких суждений. Люди используют умозаключения, когда нужно в чем-то разобраться: вывести следствие, осуществить доказательство, систематизировать знания, проверить гипотезу… Разумное мышление, в отличие от бессвязного или эмоционально заряженного потока мысли, состоит из рассуждений — сложных умственных конструкций. А рассуждения в свою очередь состоят и умозаключений — элементарных мыслительных операций.

2Подробнее

предикатная, формальная и сентенциальная. Кванторы и возникновение информатики / Хабр

1 | Введение

Логика, как эпистемологический инструмент, — исследующий знание как таковое, — изобретена независимо в трёх отдельных государствах: Греции (Аристотелем), Китае (до правления Цинь Шихуанди) и Индии. В последних двух государствах логика не распространилась настолько, чтобы получить полноценное развитие. В античной же Греции логика сформировалась в своих основах столь определённо, что дополнилась только через 2 тысячелетия…

Значительные изменения в греческую логику, помимо Буля, Моргана и Рассела, внёс Фреге — самая важная фигура основателей формальной семантики. Он разработал логику предикатов и 2 вида кванторов, попытавшись создать «логически совершенный язык» о котором мечтал Лейбниц. Значимой личностью является также Гёдель, который открыл знаменитые две теоремы о неполноте, описывающие невозможность объединения множества доказуемых утверждений со множеством истинных. Он утверждал, что доказательства математики зависят от начальных предположений, а не фундаментальной истины, из которой происходят ответы. Одна из главных идей его работ состоит в том, что ни один набор аксиом, — в том числе математических, — не способен доказать свою непротиворечивость.

На этом этапе некоторые заметят влияние платонизма на австрийского логика. Совершенно верно, ведь Гёдель не раз заявлял о влиянии метафизики Платона на собственную деятельность. Но сам Платон развитию формальной логики способствовал лишь косвенно: в истории он вносит вклад в развитие другого направления — философской логики. Платоном созданы вопросы, на которых основывается вся западная академическая философия вплоть до наших дней. Философия, в том виде, котором она известна, возникла только благодаря учителю Аристотеля.

Платон — учитель Аристотеля

В другие периоды в логику также вносили дополнения: 

• античной школой стоицизма введены термины «модальности», «материальной импликации», «оценки смысла и истины», которые являются задатками логики высказываний;

• также средневековыми схоластами введены несколько понятий;

• Готфридом Лейбницем изменена нотация.

Но главное, что сами логические операции не изменились. «Органон» Аристотеля, как сборник из 6 книг — первоисточник, где подробно описаны главные логические законы. «Органон» (с древнегреческого ὄργανον), означает — инструмент. Аристотель считал, что логика является инструментом к познанию. Он объединяет методом получения информации такие науки:

• Физика — наука о природе;

• Метафизика — наука о природе природы;

• Биология — раздел физики, наука о жизни;

• Психология — раздел физики, наука о душе;

• Кинематика — раздел физики, наука о движении;

• И др.

---

2 | Терминология

У каждой из наук должен быть идентичный фундамент в способе получения гнозисов (знаний), который позволит упорядочить информацию и вывести новые силлогизмы (умозаключения). Только таким образом получится прогресс в познании истины. Без логики наука была бы похожа на коллекционирование фактов, ибо информация бы не поддавалась анализу.

Сам Аристотель находит логике как средству убеждения иное применение: в риторике, спорах, дебатах, выступлениях и т.д., описывая это в труде «Риторика». В западной философии принято давать чёткие определения перед рассуждениями, поэтому определимся с терминами. Логика — наука о правильном мышлении.

• В языковой зависимости возникают трудности трактовки термина «наука», но даже в оригинальном названии труда Фридриха Гегеля «Наука логики» — «Wissenschaft der Logik», употребляется слово «наука» (Wissenschaft). Поэтому придём к консенсусу и будем считать, что научной можно назвать ту дисциплину, в которой возможны открытия, исследование и анализ. Логика в таком случае — наука, ибо внутри неё возможно совершать открытия. Яркий пример — комбинаторика Лейбница.

• Слово «правильный» веет нормативными коннотациями: правильное поведение, правильное выражение лица, и т.д. Перечисленное соответствует некоторым критериям и логика выставляет их (критерии) для правильного мышления.

Бюст Аристотеля

---

3 | Формальная и неформальная логика

Первоначально, деление логики происходит на формальную и неформальную. Формальная логика отличается тем, что, в отличие от неформальной, записывается уравнениями. Неформальная же логика пишется выражениями в форме языка, поэтому она подходит для риторики, а формальная логика для абстрактных наук.

Формальная логика равным образом делится на дедуктивную и индуктивную. Они различаются тем, что в дедуктивном аргументе истинность условий гарантирует истинность умозаключения или вывода. В индукции же, при истинности условий одинаково возможен ложный и истинный вывод.

Законы формальной логики:

1. Закон тождества (А = А): эквивокация или двусмысленность недопустимы. Нельзя подменять одно понятие, другим.

2. Закон непротиворечия (А ∧ ¬А = 0): одно и то же утверждение не может быть истинным и ложным одновременно.

3. Закон исключения третьего или бивалентности (А ∨ ¬А = 1): утверждение может быть либо истинным, либо ложным — третьего не дано.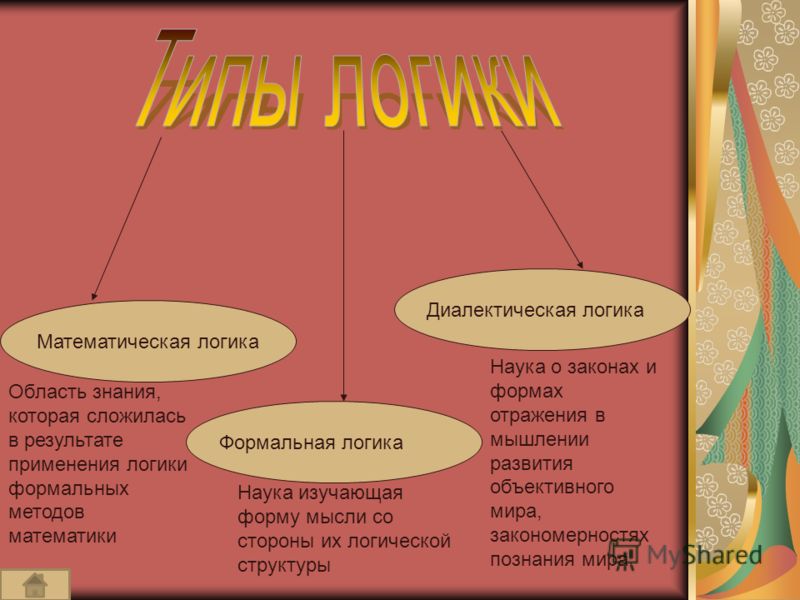

Принципы формальной логики:

1. Принцип достаточного обоснования: достаточными являются такие фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.

---

4 | Сентенциальная логика (алгебра высказываний)

Базовые операции сентенциальной логики — логики высказываний, где заглавная буква означает предложение:

Отрицание (Утверждение ¬A истинно тогда и только тогда, когда A ложно): если имеем утверждение «А» и имеем утверждение «не А», то, когда утверждение «А» будет истинным — утверждение «не А» будет ложным. Также и когда утверждение «А» будет ложным — утверждение «не А» будет истинным.

Конъюнкция (Утверждение A ∧ B истинно, если и A, и B — истинны. Ложно в противном случае): в английском языке — союз «and/&»; в русском — «и». В утверждении «А и В», между «А» с «В» стоит знак конъюнкции — «∧». Утверждение «А и В» является истинным, если «А» с «В» являются истинными одновременно. Если хоть один элемент ложен, то всё утверждение ложно. «А и В» подразумевает, во-первых: истинность «А», во-вторых: истинность «В».

Дизъюнкция (Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны — утверждение ложно): в английском языке — союз «or»; в русском — «или». Существует два типа дизъюнкции — включающая и исключающая (в логике используется включающее «или»). Условия таковы, что утверждение «А или В» будет истинным, когда один или оба элемента истинны, но никогда — когда оба элемента ложны. Это противоречит нашему обыденному мышлению, т.к. когда спрашивают: «Чай или кофе?» мы выбираем один элемент, но в логике подразумевается выбор не только одного, а нескольких возможных.

Импликация (Утверждение A ⇒ B ложно, только когда A истинно, а B ложно): в английском языке — «therefore»; в русском языке — «следовательно». Подразумевает истинность одного элемента при истинности другого. Потому что условия истинности соблюдаются всегда, кроме случая, когда «А» истинно, а «B» ложно. Поэтому утверждение: «А» ложно, следовательно «B» ложно — истинно. Покажется, что когда «А» ложно, а «В» истинно — не соблюдаются условия, но это не так. Если вы скажете, что после дождя промокните — это утверждение будет истинным вне зависимости от того, пошёл дождь или нет.

Эквивалентность (Утверждение A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны): если истинно утверждение «А, следовательно В» и истинно утверждение «В, следовательно А», то истинными являются выражения «А эквивалентно В» и соответственно «В эквивалентно А». Условия истинности соблюдаются в случаях, когда оба элемента истинны или оба ложны.

Значение переменных		Отрицание (для А)	Конъюнкция («И»)	Дизъюнкция («Или»)	Импликация («Следует»)	Эквивалентность («Равносильно»)
A	B	¬A	A ∧ B	A ∨ B	A ⇒ B	A ⇔ B
0	0	0	0	0	1	1
0	1	0	0	1	1	0
1	0	1	0	1	0	0
1	1	1	1	1	1	1

---

5 | Предикатная логика первого порядка

В XX веке, после добавлений в область логики работ Лейбница и Фреге, на основе этой дисциплины создаётся новая — информатика. Программирование сохраняет преемственность с видоизменённой логикой Аристотеля — предикатной логикой, описательная способность которой выше, чем у логики высказываний (сентенциальной).

Прежде чем разобрать этот новый тип логики, поговорим об её отличии от сентенциальной. Главная особенность предикатной логики, что заглавными буквами обозначаются предикаты, а не целые высказывания. Можно сказать, что предикат — это математическая функция, которая «накладывает» множество субъектов на множество утверждений.

Высказывание «Я пошёл в зоопарк» — состоит из субъекта и предиката. В нём субъект — «Я», а предикат — то, что остаётся кроме субъекта («пошёл в зоопарк»). Субъект — тот, кто совершает действие в предложении или имеет выраженное свойство; предикат — всё оставшееся. Таким образом, если в сентенциальной логике высказывание «Я пошёл в зоопарк» выражалось бы одной заглавной буквой, то в логике предикатов использовались бы две буквы (заглавная и подстрочная): «P» — для предиката; «x» — для субъекта. Субъекты обозначаются переменной («x»), потому что в предикатной логике появляются две относительно новые операции: универсальный и экзистенциальный кванторы. Особенность кванторов заключается в том, что ими возможно записать выражение истинное при всех возможных переменных «х» или хотя бы при одном.

Универсальный квантор (квантор всеобщности) обозначается символом — «∀», с указанием переменной под ним. Возьмём утверждение «Все пингвины чёрно-белые». В логике высказываний оно бы выражалось как «X ⇒ P», где «X» — нечто являющееся пингвином, а «P» — нечто являющееся чёрно-белым. В предикатной логике же используются субъекты и предикаты, поэтому нечто являющееся пингвином (субъект), обозначалось бы переменной «х» снизу под предикатом. «»х» — является пингвином, следовательно, является чёрно-белым». Записывается так: P(х) ⇒ B(х), где P(х): х — пингвин; B(х): x — чёрно-белый.

Однако этого недостаточно, ведь непонятно, один субъект «х» чёрно-белый или больше одного, а может вообще все. Поэтому утверждение «»х» — является пингвином, следовательно, является чёрно-белым», берётся в скобки и перед скобками используется символ «∀» с переменной «х» под ним — которые вместе и будут универсальным квантором.

Универсальный квантор переводится как: «Для всех «х» истинно, что …». Теперь утверждение «х — является пингвином, следовательно, является чёрно-белым» с универсальным квантором перед ним, расшифровывается так: «Для всех «х» истинно, что «х» — является пингвином, следовательно, является чёрно-белым». Это означает, что чем бы ни был объект во вселенной, если этот объект пингвин — он является чёрно-белым. Полная запись будет выглядеть так:

Экзистенциальный квантор (квантор существования) обозначается символом — «∃» с указанием переменной под ним. Возьмём утверждение «Некоторые пингвины серые». Как и в прошлый раз, выражение «»x» — является пингвином и «х» — является серым» возносим в скобки и ставим перед ними квантор, в этом случае экзистенциальный с указанной переменной. «»x» — является пингвином и «х» — является серым» записывается так: P(х) ∧ C(х), где P(х): х — пингвин; C(х): x — серый.

Экзистенциальный квантор можно перевести так: «Есть такой «х», для которого будет истинно, что …». Подразумевается, что есть как минимум один «х», для которого выполняются условия выражения. Если вам говорят, что ДНК не существует, достаточно показать одну молекулу дезоксирибонуклеиновой кислоты для опровержения этого утверждения. Также и с кванторами, если существует хотя бы один серый пингвин, то утверждение об отсутствии серых пингвинов будет ложно. Полная запись экзистенциального квантора для выражения «Есть такой «х», для которого будет истинно, что «x» — является пингвином и «х» — является серым», будет выглядеть так:

---

6 | Заключение

Примечательно, что есть возможность перевода одного вида квантора в другой. Возьмём утверждение «Все пингвины не являются серыми». Для универсального квантора текстовая запись будет такая: «Для всех «х», будет истинным утверждение о том, что если «х» — является пингвином, то «х» — не является серым объектом». Но утверждение изменяется и для экзистенциального квантора, используя знак отрицания: «Нет такого «х», для которого бы было истинным утверждение о том, что «x»— является пингвином и «х»— является серым».

В середине XIX века, Готлоб Фреге дополнил логику Аристотеля двумя этими операциями, которые позже сформировались в отдельную дисциплину — предикатную логику. С введением в логику экзистенциального квантора (после универсального) — предикатная логика, в основе своей, завершилась как система…

---

Источники:

1 — Аристотель: «Органон» — «Первая аналитика» и «Вторая аналитика»;

2 — Аристотель: «Риторика»;

3 — Готлоб Фреге: «Исчисление понятий»;

4 — «Monatshefte für Mathematik und Physik» 1931 г.: Курт Гёдель «О принципиально неразрешимых положениях в системе Principia Mathematica и родственных ей системах»;

5 — The Early Mathematical Manuscripts of Leibniz;

6 — Мельников Сергей: «Введение в философию Аристотеля»;

7 — Гильмутдинова Нина: «Логика и теория аргументации»;

8 — youtube. com;

9 — cyberleninka.ru.

Формальная логика Определение и значение

• Основные определения
• Викторина
• Связанное содержимое
• Примеры
• Британский

Показывает уровень оценки в зависимости от сложности слова.

Сохрани это слово!

См. синонимы формальной логики на Thesaurus.com

Показывает уровень обучения в зависимости от сложности слова.

---

сущ.

раздел логики, занимающийся исключительно принципами дедуктивного рассуждения и формой, а не содержанием предложений.

ВИКТОРИНА

ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Происхождение формальной логики

Впервые зафиксировано в 1855–1860 гг.0015

Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2022

Слова, относящиеся к формальной логике

Силлогизм

Как использовать формальную логику в предложении

• Создание формальной логики, теории игр — немалое достижение , статистика и байесовские рассуждения — восхитительные темы, полные очарования и актуальности.

  Сила рационального мышления в мире, который кажется неразумным|Ник Ромео|8 октября 2021 г.|Washington Post

• Основное внимание Пинкера сосредоточено на своего рода сознательном, последовательном рассуждении, которое может отслеживать шаги в геометрическом доказательстве или аргументе в формальной логике.

  Сила рационального мышления в мире, который кажется неразумным|Ник Ромео|8 октября 2021 г.|Washington Post

• Несмотря на то, что Аристотель изобрел формальную логику, он, по-видимому, не заметил в своих рассуждениях определенной степени цикличности.

  Это 10 самых ошибочных научных результатов|Том Зигфрид|10 ноября 2020 г.|Новости науки

• В результате учебные отряды, называемые формальными учебными подразделениями (FTU), укомплектованы менее чем половиной людей, в которых они нуждаются.

  Эксклюзив: флот дронов США в «точке разрыва», говорят ВВС|Дэйв Маджумдар|5 января 2015 г.|DAILY BEAST

• Их логика: морское существо оживет и выпьет оставшийся алкоголь.

  Самые безумные лекарства от похмелья в истории|Джастин Джонс|30 декабря 2014 г.|DAILY BEAST

• Он также надеялся стать капелланом своей местной церкви, и его формальное обучение подходило к концу.

  В тени убитых полицейских|Майкл Дейли|26 декабря 2014 г.|DAILY BEAST

• «Психология БДСМ отсутствует в других формах формальных тренировок и взаимодействий», — добавила Стелла.

  Подземелья и зажимы для гениталий: Внутри легендарного замка БДСМ|Иэн Фриш|20 декабря 2014|DAILY BEAST

• Я помню, что он знаток еды и вина и довольно формален.

  Альфред Хичкок «Угасание в темноте: последние дни великого режиссера»|Дэвид Фриман|13 декабря 2014|DAILY BEAST племянники.

  The Pit Town Coronet, Volume I (of 3)|Charles James Wills

• Различные вопросы, упомянутые губернатором, получают поверхностные и формальные ответы.

  Филиппинские острова, 1493-1898 гг., том XX, 1621-1624 гг. | Разное

• Трессан подошел к нему с сердечной улыбкой на губах, и они поклонились друг другу в официальном приветствии.

  Лето Святого Мартина|Рафаэль Сабатини

• Она сидела в дальнем углу парадной комнаты, осторожно освещенной лампой в тени.

  Веселые приключения Аристида Пужоля|Уильяма Дж. Локка

• Здесь стояли два жестких строгих дивана с прямыми спинками и паучьими ножками.

  The Pit Town Coronet, Том I (из 3) | Чарльз Джеймс Уиллс

Британский словарь определений формальной логики

формальная логика

---

существительное

Также называется: символическая логика изучение систем дедуктивных аргументов, в которых символы используются для представления точно определенных категорий выражений.

формальная система, которую можно интерпретировать как представляющую фрагмент естественного аргумента

Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

LSAT Advanced Formal Logic — подготовка к тесту Каплана

Мы рассмотрели, как работать с простейшим утверждением формальной логики: если X, то Y. Но что происходит, когда наши необходимые или достаточные факторы усложняются? Давайте рассмотрим пару примеров, используя идею овощного салата. Простейшее утверждение и его противоположность могут выглядеть так:
Если в жарком есть морковь, то есть и стручки.
Если в жарком нет стручков гороха, то нет и моркови.
Теперь добавим больше овощей (и более сложную логику):
Если в стир-фрай есть морковь или шпинат, то там есть стручки горошка и перец.
Вот важная мысль: когда вы формируете контрапозитив, вы уже знаете, что необходимые и достаточные факторы меняются местами и отрицаются. Но теперь вы также должны помнить, что «и» становится «или» и наоборот. Таким образом, приведенное выше утверждение становится:
Если в жарком нет стручков гороха или перца, то в нем нет ни моркови, ни шпината.

Подсказка

Может быть очень полезно отдельно отрицать каждый элемент оператора; иначе легко запутаться. Например, если вы отрицаете только первую часть приведенного выше утверждения и говорите кому-то: «Если во фритюре нет стручков гороха или перца…», они могут интерпретировать это как означающее, что ни один из этих овощей не должен быть во фритюре. Но с точки зрения формальной логики технически это означало бы, что вы либо хотите перца, либо не хотите моркови. Однако ни одна из этих идей не является тем, что вы хотите сказать в противопоставлении; предполагаемое значение в том, что я не хочу ни моркови, ни перца.

Расширенные вопросы формальной логики

Ни то, ни другое

Сочетание «ни» и «ни» также может вызвать некоторое недоумение. Самый простой способ справиться с этим — помнить, что «ни X, ни Y» — это то же самое, что «ни X, ни Y». Приведенный выше пример можно перефразировать следующим образом:
Если в жарком нет ни моркови, ни перца, то в нем нет ни стручков гороха, ни шпината.
Итак, если вам нужно отрицать утверждение «ни/ни», то «ни» становится «или», как если бы в утверждении было сказано «и».

Что, если предложение написано не в том порядке, в котором мы ожидаем найти элементы?
Например, как мы интерпретируем предложение, в котором говорится:
В гамбургере есть горчица, если в нем есть лук.
Здесь мы можем взять слово «если» и прочитать следующее за ним утверждение как достаточный элемент. Мы можем преобразовать это предложение в следующее:
Если в гамбургере есть лук, то и горчица.

Только если

Последней проблемой является фраза «только если».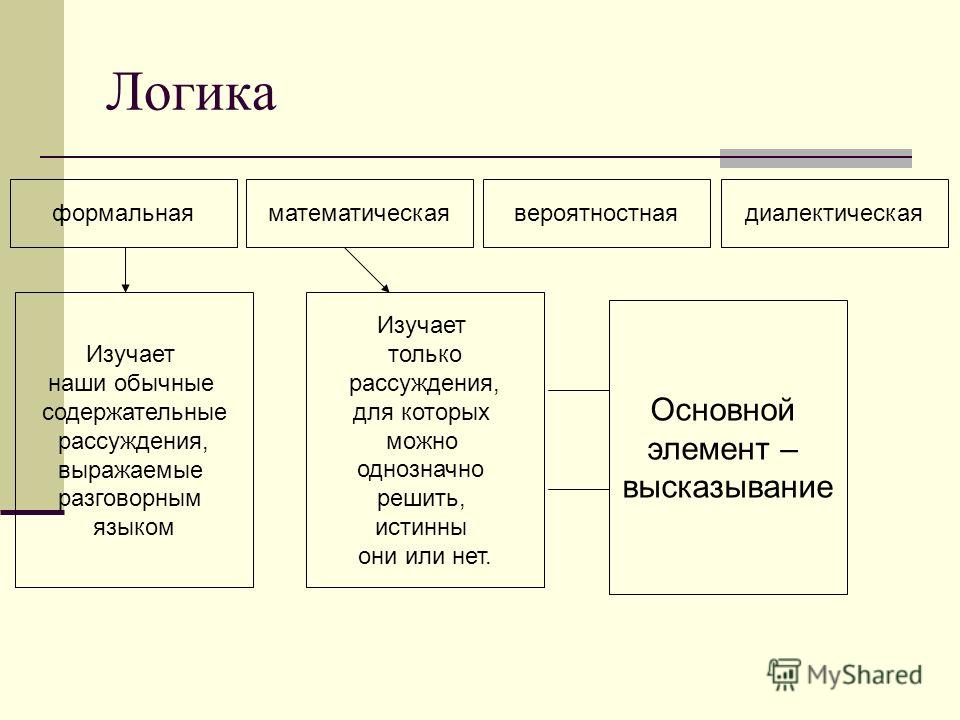 Вернемся к нашему овощному жаркому и посмотрим на следующее предложение:
В жарком стир-фрай есть брокколи, только если в нем есть грибы.
Здесь вы не можете интерпретировать «если» как сигнал о наличии достаточного элемента. Операторы «только если» интерпретируются иначе, чем обычные операторы «если». Утверждение «только если» выше означает то же самое, что и это:

Если в салате есть брокколи, то в нем есть и грибы.

Резюме

 

1. При образовании контрапозитива превращайте «и» в «или» и наоборот.
2. «Ни X, ни Y» означает «Ни X, ни Y».
3. «X, только если Y» означает «Если X, то Y».

Практический вопрос по формальной логике

Крейг не будет изучать органическую химию, если Паула не одолжит ему свои записи, сделанные во время занятий.
Что из следующего согласуется с приведенным выше утверждением? [Выберите все подходящие варианты]
(i) Паула не дает свои записи, а Крейг не занимается органической химией.
(ii) Крейг изучает органическую химию, используя только записи Линды.
(iii) Крейг не занимается органической химией, хотя Паула одалживает ему свои записи.

(iv) Крейг получает B+ по органической химии.
 

 

Пояснение

«Непротиворечивые» утверждения — это утверждения, которые оба могут быть истинными. (i) представляет собой противоположность исходному утверждению, поэтому (i) не только согласуется с исходным утверждением, но и следует из него.
В (iii) Паула предоставила необходимое условие для того, чтобы Крейг взял Орго, то есть она предоставила свои записи, но необходимость — это не то же самое, что достаточность. Таким образом, это вполне согласуется с утверждением, что, даже имея в руках записи Паулы, Крейг решает не брать Орго. (Это очень важная концепция.)
Что касается (iv), оценка Крейга выходит за рамки утверждения, поэтому вполне логично, что он получает B+.