предикатная, формальная и сентенциальная. Кванторы и возникновение информатики / Хабр
1 | Введение
Логика, как эпистемологический инструмент, — исследующий знание как таковое, — изобретена независимо в трёх отдельных государствах: Греции (Аристотелем), Китае (до правления Цинь Шихуанди) и Индии. В последних двух государствах логика не распространилась настолько, чтобы получить полноценное развитие. В античной же Греции логика сформировалась в своих основах столь определённо, что дополнилась только через 2 тысячелетия…
Значительные изменения в греческую логику, помимо Буля, Моргана и Рассела, внёс Фреге — самая важная фигура основателей формальной семантики. Он разработал логику предикатов и 2 вида кванторов, попытавшись создать «логически совершенный язык» о котором мечтал Лейбниц. Значимой личностью является также Гёдель, который открыл знаменитые две теоремы о неполноте, описывающие невозможность объединения множества доказуемых утверждений со множеством истинных.
Он утверждал, что доказательства математики зависят от начальных предположений, а не фундаментальной истины, из которой происходят ответы. Одна из главных идей его работ состоит в том, что ни один набор аксиом, — в том числе математических, — не способен доказать свою непротиворечивость.
На этом этапе некоторые заметят влияние платонизма на австрийского логика. Совершенно верно, ведь Гёдель не раз заявлял о влиянии метафизики Платона на собственную деятельность. Но сам Платон развитию формальной логики способствовал лишь косвенно: в истории он вносит вклад в развитие другого направления — философской логики. Платоном созданы вопросы, на которых основывается вся западная академическая философия вплоть до наших дней. Философия, в том виде, котором она известна, возникла только благодаря учителю Аристотеля.
Платон — учитель АристотеляВ другие периоды в логику также вносили дополнения:
античной школой стоицизма введены термины «модальности», «материальной импликации», «оценки смысла и истины», которые являются задатками логики высказываний;
также средневековыми схоластами введены несколько понятий;
Готфридом Лейбницем изменена нотация.
Но главное, что сами логические операции не изменились. «Органон» Аристотеля, как сборник из 6 книг — первоисточник, где подробно описаны главные логические законы. «Органон» (с древнегреческого ὄργανον), означает — инструмент. Аристотель считал, что логика является инструментом к познанию. Он объединяет методом получения информации такие науки:
Физика — наука о природе;
Метафизика — наука о природе природы;
Биология — раздел физики, наука о жизни;
Психология — раздел физики, наука о душе;
Кинематика — раздел физики, наука о движении;
И др.
2 | Терминология
У каждой из наук должен быть идентичный фундамент в способе получения гнозисов (знаний), который позволит упорядочить информацию и вывести новые силлогизмы (умозаключения). Только таким образом получится прогресс в познании истины. Без логики наука была бы похожа на коллекционирование фактов, ибо информация бы не поддавалась анализу.
Сам Аристотель находит логике как средству убеждения иное применение: в риторике, спорах, дебатах, выступлениях и т.д., описывая это в труде «Риторика». В западной философии принято давать чёткие определения перед рассуждениями, поэтому определимся с терминами. Логика — наука о правильном мышлении.
В языковой зависимости возникают трудности трактовки термина «наука», но даже в оригинальном названии труда Фридриха Гегеля «Наука логики» — «Wissenschaft der Logik», употребляется слово «наука» (Wissenschaft). Поэтому придём к консенсусу и будем считать, что научной можно назвать ту дисциплину, в которой возможны открытия, исследование и анализ. Логика в таком случае — наука, ибо внутри неё возможно совершать открытия. Яркий пример — комбинаторика Лейбница.
Слово «правильный» веет нормативными коннотациями: правильное поведение, правильное выражение лица, и т.д. Перечисленное соответствует некоторым критериям и логика выставляет их (критерии) для правильного мышления.
3 | Формальная и неформальная логика
Первоначально, деление логики происходит на формальную и неформальную. Формальная логика отличается тем, что, в отличие от неформальной, записывается уравнениями. Неформальная же логика пишется выражениями в форме языка, поэтому она подходит для риторики, а формальная логика для абстрактных наук.
Формальная логика равным образом делится на дедуктивную и индуктивную. Они различаются тем, что в дедуктивном аргументе истинность условий гарантирует истинность умозаключения или вывода. В индукции же, при истинности условий одинаково возможен ложный и истинный вывод.
Законы формальной логики:
1. Закон тождества (А = А): эквивокация или двусмысленность недопустимы. Нельзя подменять одно понятие, другим.
2. Закон непротиворечия (А ∧ ¬А = 0): одно и то же утверждение не может быть истинным и ложным одновременно.
3. Закон исключения третьего или бивалентности (А ∨ ¬А = 1): утверждение может быть либо истинным, либо ложным — третьего не дано.
Принципы формальной логики:
1. Принцип достаточного обоснования: достаточными являются такие фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.
4 | Сентенциальная логика (алгебра высказываний)
Базовые операции сентенциальной логики — логики высказываний, где заглавная буква означает предложение:
Отрицание (Утверждение ¬A истинно тогда и только тогда, когда A ложно): если имеем утверждение «А» и имеем утверждение «не А», то, когда утверждение «А» будет истинным — утверждение «не А» будет ложным. Также и когда утверждение «А» будет ложным — утверждение «не А» будет истинным.
Конъюнкция (Утверждение A ∧ B истинно, если и A, и B — истинны. Ложно в противном случае): в английском языке — союз «and/&»; в русском — «и». В утверждении «А и В», между «А» с «В» стоит знак конъюнкции — «∧». Утверждение «А и В» является истинным, если «А» с «В» являются истинными одновременно.
Если хоть один элемент ложен, то всё утверждение ложно. «А и В» подразумевает, во-первых: истинность «А», во-вторых: истинность «В».
Дизъюнкция (Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны — утверждение ложно): в английском языке — союз «or»; в русском — «или». Существует два типа дизъюнкции — включающая и исключающая (в логике используется включающее «или»). Условия таковы, что утверждение «А или В» будет истинным, когда один или оба элемента истинны, но никогда — когда оба элемента ложны. Это противоречит нашему обыденному мышлению, т.к. когда спрашивают: «Чай или кофе?» мы выбираем один элемент, но в логике подразумевается выбор не только одного, а нескольких возможных.
Импликация (Утверждение A ⇒ B ложно, только когда A истинно, а B ложно): в английском языке — «therefore»; в русском языке — «следовательно». Подразумевает истинность одного элемента при истинности другого. Потому что условия истинности соблюдаются всегда, кроме случая, когда «А» истинно, а «B» ложно.
Поэтому утверждение: «А» ложно, следовательно «B» ложно — истинно. Покажется, что когда «А» ложно, а «В» истинно — не соблюдаются условия, но это не так. Если вы скажете, что после дождя промокните — это утверждение будет истинным вне зависимости от того, пошёл дождь или нет.
Эквивалентность (Утверждение A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны): если истинно утверждение «А, следовательно В» и истинно утверждение «В, следовательно А», то истинными являются выражения «А эквивалентно В» и соответственно «В эквивалентно А». Условия истинности соблюдаются в случаях, когда оба элемента истинны или оба ложны.
Значение переменных | Отрицание (для А) | Конъюнкция | Дизъюнкция | Импликация | Эквивалентность | |
A | B | ¬A | A ∧ B | A ∨ B | A ⇒ B | A ⇔ B |
0 | 0 | 0 | 0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 | 1 |
5 | Предикатная логика первого порядка
В XX веке, после добавлений в область логики работ Лейбница и Фреге, на основе этой дисциплины создаётся новая — информатика.
Программирование сохраняет преемственность с видоизменённой логикой Аристотеля — предикатной логикой, описательная способность которой выше, чем у логики высказываний (сентенциальной).
Прежде чем разобрать этот новый тип логики, поговорим об её отличии от сентенциальной. Главная особенность предикатной логики, что заглавными буквами обозначаются предикаты, а не целые высказывания. Можно сказать, что предикат — это математическая функция, которая «накладывает» множество субъектов на множество утверждений.
Высказывание «Я пошёл в зоопарк» — состоит из субъекта и предиката. В нём субъект — «Я», а предикат — то, что остаётся кроме субъекта («пошёл в зоопарк»). Субъект — тот, кто совершает действие в предложении или имеет выраженное свойство; предикат — всё оставшееся. Таким образом, если в сентенциальной логике высказывание «Я пошёл в зоопарк» выражалось бы одной заглавной буквой, то в логике предикатов использовались бы две буквы (заглавная и подстрочная): «P» — для предиката; «x» — для субъекта.
Субъекты обозначаются переменной («x»), потому что в предикатной логике появляются две относительно новые операции: универсальный и экзистенциальный кванторы. Особенность кванторов заключается в том, что ими возможно записать выражение истинное при всех возможных переменных «х» или хотя бы при одном.
Универсальный квантор (квантор всеобщности) обозначается символом — «∀», с указанием переменной под ним. Возьмём утверждение «Все пингвины чёрно-белые». В логике высказываний оно бы выражалось как «X ⇒ P», где «X» — нечто являющееся пингвином, а «P» — нечто являющееся чёрно-белым. В предикатной логике же используются субъекты и предикаты, поэтому нечто являющееся пингвином (субъект), обозначалось бы переменной «х» снизу под предикатом. «»х» — является пингвином, следовательно, является чёрно-белым». Записывается так: P(х) ⇒ B(х), где P(х): х — пингвин; B(х): x — чёрно-белый.
Однако этого недостаточно, ведь непонятно, один субъект «х» чёрно-белый или больше одного, а может вообще все.
Поэтому утверждение «»х» — является пингвином, следовательно, является чёрно-белым», берётся в скобки и перед скобками используется символ «∀» с переменной «х» под ним — которые вместе и будут универсальным квантором.
Универсальный квантор переводится как: «Для всех «х» истинно, что …». Теперь утверждение «х — является пингвином, следовательно, является чёрно-белым» с универсальным квантором перед ним, расшифровывается так: «Для всех «х» истинно, что «х» — является пингвином, следовательно, является чёрно-белым». Это означает, что чем бы ни был объект во вселенной, если этот объект пингвин — он является чёрно-белым. Полная запись будет выглядеть так:
Экзистенциальный квантор (квантор существования) обозначается символом — «∃» с указанием переменной под ним. Возьмём утверждение «Некоторые пингвины серые». Как и в прошлый раз, выражение «»x» — является пингвином и «х» — является серым» возносим в скобки и ставим перед ними квантор, в этом случае экзистенциальный с указанной переменной.
«»x» — является пингвином и «х» — является серым» записывается так: P(х) ∧ C(х), где P(х): х — пингвин; C(х): x — серый.
Экзистенциальный квантор можно перевести так: «Есть такой «х», для которого будет истинно, что …». Подразумевается, что есть как минимум один «х», для которого выполняются условия выражения. Если вам говорят, что ДНК не существует, достаточно показать одну молекулу дезоксирибонуклеиновой кислоты для опровержения этого утверждения. Также и с кванторами, если существует хотя бы один серый пингвин, то утверждение об отсутствии серых пингвинов будет ложно. Полная запись экзистенциального квантора для выражения «Есть такой «х», для которого будет истинно, что «x» — является пингвином и «х» — является серым», будет выглядеть так:
6 | Заключение
Примечательно, что есть возможность перевода одного вида квантора в другой. Возьмём утверждение «Все пингвины не являются серыми». Для универсального квантора текстовая запись будет такая: «Для всех «х», будет истинным утверждение о том, что если «х» — является пингвином, то «х» — не является серым объектом».
Но утверждение изменяется и для экзистенциального квантора, используя знак отрицания: «Нет такого «х», для которого бы было истинным утверждение о том, что «x»— является пингвином и «х»— является серым».
В середине XIX века, Готлоб Фреге дополнил логику Аристотеля двумя этими операциями, которые позже сформировались в отдельную дисциплину — предикатную логику. С введением в логику экзистенциального квантора (после универсального) — предикатная логика, в основе своей, завершилась как система…
Источники:
1 — Аристотель: «Органон» — «Первая аналитика» и «Вторая аналитика»;
2 — Аристотель: «Риторика»;
3 — Готлоб Фреге: «Исчисление понятий»;
4 — «Monatshefte für Mathematik und Physik» 1931 г.: Курт Гёдель «О принципиально неразрешимых положениях в системе Principia Mathematica и родственных ей системах»;
5 — The Early Mathematical Manuscripts of Leibniz;
6 — Мельников Сергей: «Введение в философию Аристотеля»;
7 — Гильмутдинова Нина: «Логика и теория аргументации»;
8 — youtube.
com;
9 — cyberleninka.ru.
Проблема взаимоотношений логики формальной и философской (неформальной и воображаемой Н. А. Васильева)
%PDF-1.3 % 1 0 obj > endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream
Формальная логика | Определение, примеры, символы и факты
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См.
весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины.
Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
(Читайте статью Стивена Пинкера о рациональности в «Британнике»). Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно различных условия: во-первых, вывод должен действительно следовать из посылок, т.
е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, — это, как следует из названия, выводы, достоверность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа.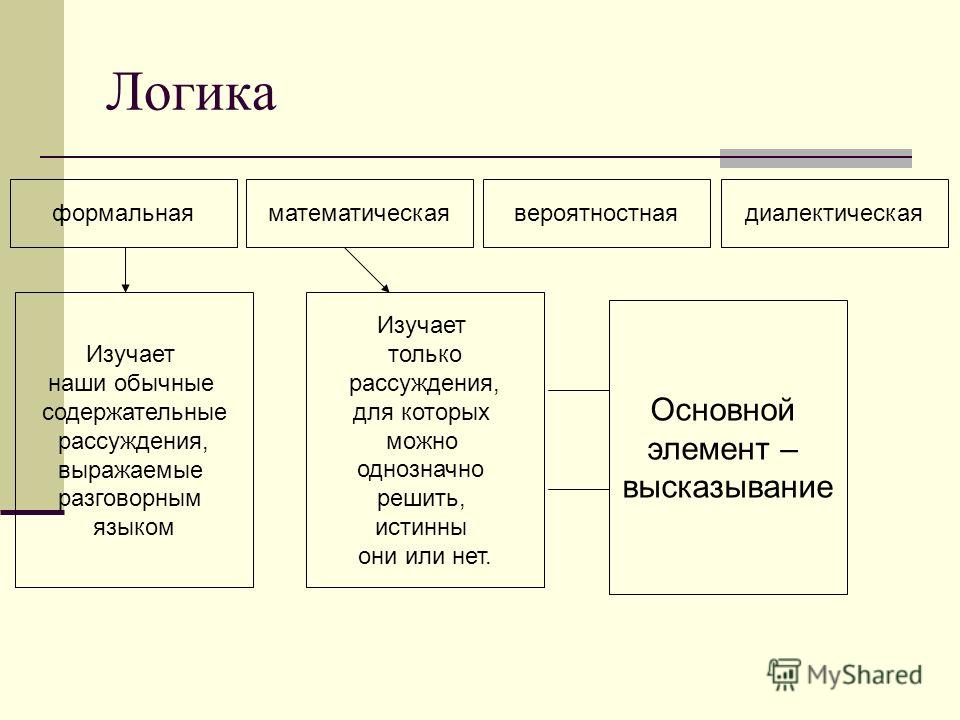
Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое обозначает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые 
не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями.
Простой пример: (6) Ничто одновременно и X , и не-9.0027 х . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется.
Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.
мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.
Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или мысленными построениями?
Формальная логика | Определение, примеры, символы и факты
Альфред Норт Уайтхед
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
См.
весь связанный контент →
формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины.
Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
(Читайте статью Стивена Пинкера о рациональности в «Британнике»). Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно различных условия: во-первых, вывод должен действительно следовать из посылок, т.
е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, — это, как следует из названия, выводы, достоверность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры.
Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа.
Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое обозначает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X .
не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями.
Простой пример: (6) Ничто одновременно и X , и не-9.0027 х . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется.
Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.