Горизонталь и вертикаль фронталь – 3.3. Горизонталь и фронталь плоскости

3.3. Горизонталь и фронталь плоскости

		f0a
	A»
x		2″ 1′
h0a	A’	2′
		1″
		Рис. 3.15

Рассматривая прямые частного положения, мы уже познакомились с прямыми уровня: горизонталью, фронталью и профилью. Теперь рассмотрим горизонталь и фронталь плоскости. Горизонталь плоскости – это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. Следовательно, у всех точек горизонтали координата z постоянна. Поэтому ее фронтальная проекция ( h′′) параллельна оси X (рис. 3.16). Можно сказать, что горизонтальный след плоскости h0α – это тоже горизонталь, только координата z=0. А все горизонтали одной

плоскости параллельны друг другу. Мы знаем, что у параллельных прямых одноименные проекции параллельны. Следовательно, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости (т.е. h′// h0α ).

Обратите внимание, что горизонталь обозначается h, а горизонтальный след – h0 . Говорят,

что горизонтальный след – это нулевая горизонталь.

Фронталь плоскости – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций (рис. 3.17). У фронтали плоскости горизонтальная проекция параллельна оси X, а фронтальная параллельна фронтальному следу, так как у всех точек фронтали координата y постоянна. У фронтального следа y=0, поэтому фронтальный след – это нулевая фронталь.

Напомним, что горизонтали и фронтали плоскости (так же как и любые прямые) предполагаются бесконечными.

Профиль плоскости – это прямая, принадлежащая плоскости и параллельная профильной плоскости проекций.

Для решения рассмотренной ранее задачи построения недостающей проекции точки, принадлежащей плоскости, в ряде случаев удобнее в качестве вспомогательной прямой взять горизонталь или фронталь плоскости.

Исходные данные задачи представлены на рис. 3.18,а. Проведем через фронтальную проекцию горизонтали ( h′′//оси X) (рис. 3.18,б). Горизонталь пересекается с фронтальным следом в точ-

ке 1	′′	– пересечение	f0α и h	′′	). Построив горизонтальную проекцию точки 1, через нее можно
	(1

провести горизонтальную проекцию горизонтали параллельно горизонтальному следу (рис. 3.18,в). С помощью линии проекционной связи строится горизонтальная проекция точки A, лежащая на горизонтали h (рис. 3.18,г). Задача решена.

Возьмем те же самые исходные данные (рис. 3.19,а). Только теперь для построения недостающей проекции точки в качестве вспомогательной прямой используем фронталь плоскости. Через A′′ проведем f ′′ – фронтальную проекцию фронтали (она проходит параллельно фронталь-

ному следу). Там, где она пересечет ось X, будет находиться фронтальная проекция точки 1 (рис. 3.19,б). Поскольку у точки 1 z=0, она принадлежит горизонтальному следу. Продлив h0α , можно построить горизонтальную проекцию точки 1, лежащей на фронтали (рис. 3.19,в), и провести через нее горизонтальную проекцию фронтали ( f ′// X ). На рис. 3.19,г приведено окончательное решение задачи.

studfiles.net

Начертательная геометрия — Википедия

Материал из Википедии — свободной энциклопедии

Запрос «Горизонталь» перенаправляется сюда; о горизонталях на топографических картах см. Изогипса.

Начерта́тельная геоме́трия — инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.

Практически начертательная геометрия ограничивается исследованием объектов трёхмерного евклидова пространства. Исходные данные должны быть представлены в виде двух независимых проекций. В большинстве задач и алгоритмов используются две ортогональные проекции на взаимно перпендикулярные плоскости.

В настоящее время дисциплина не имеет практической ценности в силу развития вычислительной техники и аппарата линейной алгебры, но, вероятно, незаменима как составляющая общего инженерного образования на машиностроительных и строительных специальностях.

Начерта́тельная геоме́трия — наука, изучающая пространственные фигуры при помощи их проецирования (проложения) перпендикулярами на некоторые три плоскости, которые рассматриваются затем совмещёнными одна с другой.

При обыкновенном способе изображения предметов линии, распространяющиеся вдаль от глаза наблюдателя, хотя и изображаются, соответственно с тем, какими они нам представляются, сокращёнными, но это сокращение определяется рисовальщиком обыкновенно на глаз, а фотографией оно хотя в известных случаях и достаточно точно может быть передано, но отношение, в каком потерпели сокращения разные линии изображаемого предмета, остаётся трудно определимым; вдобавок, во многих случаях и фотография ведёт к перспективным ошибкам. Всякий мастер, будет ли то плотник, слесарь, токарь, каменотёс и т. д., может выполнить заказанный предмет согласно желанию заказчика только в том случае, если ему будет дан совершенно такой же предмет на образец, либо его модель, либо конструкторский чертёж, по которому легко и точно определялись бы размеры всех начерченных линий, хотя бы и таких, которые удаляются в глубь картины и потому изображаются сокращёнными. Начертательная геометрия учит изготовлению таких чертежей, в которых предмет изображается почти таким, каким мы его видим, и притом так, что по начерченным линиям можно в точности определить размеры и истинный вид изображаемого предмета.

ru.wikipedia.org

Главные линии плоскости — горизонталь и фронталь — КиберПедия

Горизонталь плоскости.

Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций (рис. 17а,б)).Построение горизонтали начинают с фронтальной проекции, так как она всегда параллельна оси х₁₂. Все горизонтали плоскости параллельны между собой.

а) б)

Рис.17

Фронталь плоскости.

Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (рис. 18а, б). Построение фронтали всегда начинают с горизонтальной проекции, так как она всегда параллельна оси х

12. Все фронтали плоскости параллельны между собой.

а) б)

Рис. 18

Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Проведем в плоскости, заданной двумя пересекающимися прямыми а и в, любую прямую n. Затем через точку К построим прямую m║ n (рис. 19). У параллельных прямых параллельны одноименные проекции.

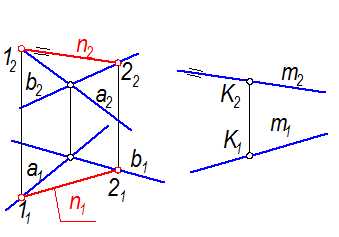
Рис. 19

Теорема о проекциях прямого угла

Помимо позиционных задач, рассмотренных в предыдущих параграфах, в практике приходится решать задачи на определение расстояний, углов и истинных величин плоских фигур. Такие задачи называются метрическими задачами. При их решении необходимо знать условие перпендикулярности прямых и плоскостей. Для этого надо выяснить свойство ортогональной проекции прямого угла.

Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 20).

Рис. 20

На рис. 21 показаны скрещивающиеся прямые, перпендикулярные друг другу.

Рис. 21

Перпендикулярность прямой и плоскости

Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис. 22).

 

Рис. 22

Если прямые а и в будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме о проецировании прямого угла, прямой угол спроецируется в натуральную величину на плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых надо взять горизонталь

h и фронталь f . Тогда прямой угол между перпендикуляром n и h спроецируется в натуральную величину на П₁, а прямой угол между n и f — на П₂.На рис. 23 в точке К, принадлежащей плоскости α(а║b), построен перпендикуляр n к плоскости .

Рис. 23

Применение дополнительного ортогонального проецирования

Для решения задач

Пример. Найти длину отрезка АВ.

Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П₁ и П_2, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П₄ ему параллельную ( П₄║АВ) и П₄^П₁ (рис. 24).

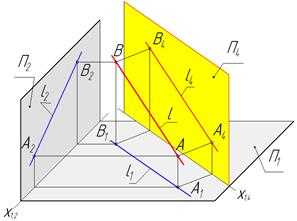
Рис.24

Поэтапное решение задачи на эпюре показано на рис. 25

Рис. 25

Пример 2. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4,перпендикулярной к плоскости α и к плоскости П_1.

Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П₄ является горизонталь h (рис. 26).

 

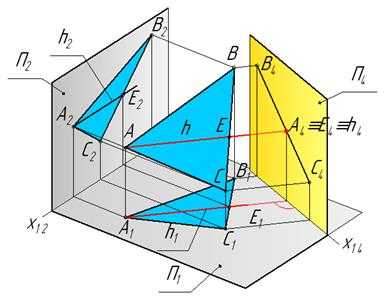
Рис. 26

Исходя из этого, ось х₁₄ проведена перпендикулярно горизонтальной проекции h₁ горизонтали h плоскости ΔАВС (рис. 27).По отношению к плоскости П₄ плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А₄ В₄ С_4.

 

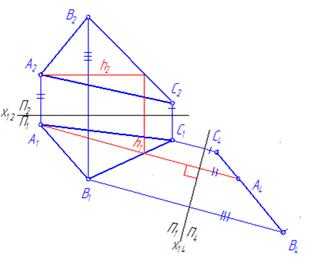
Рис. 27

Пример3. Построить дополнительную ортогональную проекцию прямой общего на плоскость ей перпендикулярную.

Для этого надо сначала построить дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П₄║АВ) и П₄┴П₁.Ось х₁₄ построена параллельно А₁ В₁ . Затем построить дополнительную ортогональную проекцию прямой АВ на плоскость П₅ ей перпендикулярную( П₅┴ АВ) и П₅┴ П₄ (рис. 28).Ось х₄₅ построена перпендикулярно А₄ В₄ ._.На плоскости П₅ прямая будет точкой.

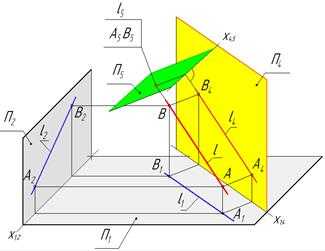
Рис. 28

Рещение задачи на эпюре показано на рис. 29

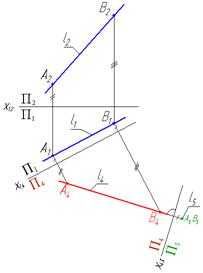
Рис. 29

Пример 4.Определить размеры треугольника АВС.

Чтобы найти величину ΔАВС,являющегося плоскостью общего положения,надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4,перпендикулярной к плоскости α(ΔАВС) и к плоскости П₁ (см.пример2).А затем построить его дополнительную ортогональную проекцию на плоскость П₅ ему параллельную(П_5║ ΔАВС) и П₅┴ П₄ (рис.30а).Решение задачи на эпюре показано на рис.30б.

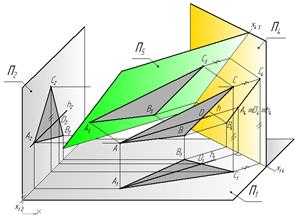
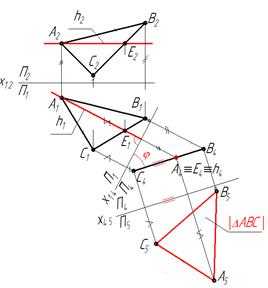
Рис. 30а Рис.30б

 

cyberpedia.su

Фронталь плоскости | Начертательная геометрия

Фронталь плоскости — одна из главных линий плоскости.

Фронталь плоскости

На рисунке показаны: фронталь плоскости α — υ, гризонталь h плоскости α, профильная прямая ω плоскости α, задание линий уровня на эпюре.

Главными линиями плоскости называют: 1. Прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекции; 2. Прямые принадлежащие плоскости и перпендикулярные к какой-либо линии, отмеченной в пункте 1.

Прямые, параллельные плоскости проекции (1), принадлежат плоскости уровня поэтому их называют также прямыми (или линиями) уровня. Линии уровня подразделяют на три вида: а) В случае когда υ⊂α ^ υ║V, то прямая υ представляет собой фронталь плоскости α; б) Если h⊂α ^ h║H, то прямую h называют горизонталь плоскости α; в) В случае когда ω⊂α ^ ω║W, то прямую ω называют профильная прямая плоскости α.

Наименование линии	Горизонтальная проекция	Фронтальная проекция	Профильная проекция
Горизонталь	║αH	║оси x	║оси y
Фронталь	║оси x	║αV	║оси z
Профильная прямая	║оси y	║оси z	║αW

В плоскости можно провести множество фронталей

Фронталь плоскости

по фронталям плоскости можно построить следы плоскости, то есть перейти от какого то способа задания плоскости к заданию следами. И наоборот от задания плоскости следами, по фронталям плоскости можно перейти к другим способам задания той же самой плоскости.

построить фронталь треугольника ABC

Фронталь плоскости

чтобы построить фронталь плоскости выраженной треугольником ABC необходимо: — построить горизонтальную проекцию f` искомой фронтали, причем f` ‖ x, проводим из вершины A треугольника, достигая этим цели наименьшим количеством построений; — в пересечении f` с B`C` противолежащей стороной треугольника отмечаем точку 1`; — находим 1″ в пересечении ее линии проекционной связи со стороной B`C`; — находим f» искомой фронтали, соединив прямой линией точки A» и 1″.

+

ngeo.fxyz.ru

Горизонталь плоскости | Начертательная геометрия

Горизонталь плоскости — одна из главных линий плоскости.

Горизонталь плоскости

На рисунке показаны: горизонталь плоскости α — h, фронталь υ плоскости α, профильная прямая ω плоскости α, задание линий уровня на эпюре.

Главными линиями плоскости называют: 1. Прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекции. 2. Прямые принадлежащие плоскости и перпендикулярные к какой-либо линии, отмеченной в пункте 1.

Прямые, параллельные плоскости проекции (1), принадлежат плоскости уровня, поэтому их называют также, прямыми (или линиями) уровня.

Линии уровня подразделяют на три вида: а) Если h⊂α ^ h║H, то прямая h представляет собой горизонталь плоскости α; б) В случае когда υ⊂α ^ υ║V, то прямую υ называют фронталь плоскости α; в) В случае когда ω⊂α ^ ω║W, то прямую ω называют профильная прямая плоскости α.

Наименование линии	Горизонтальная проекция	Фронтальная проекция	Профильная проекция
Горизонталь	║αH	║оси x	║оси y
Фронталь	║оси x	║αV	║оси z
Профильная прямая	║оси y	║оси z	║αW

В плоскости можно провести множество горизонталей

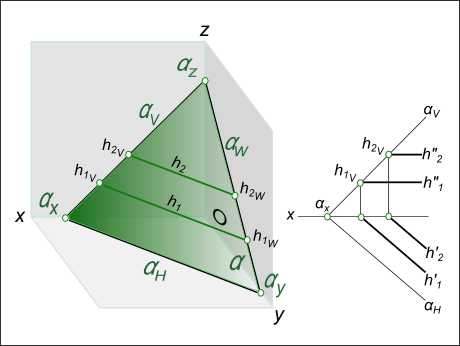
Горизонталь плоскости

и по горизонталям плоскости построить следы плоскости, то есть перейти от какого то способа задания плоскости к заданию следами. И наоборот, от задания плоскости следами, по горизонталям плоскости можно перейти к другим способам задания той же самой плоскости.

построить горизонталь треугольника ABC

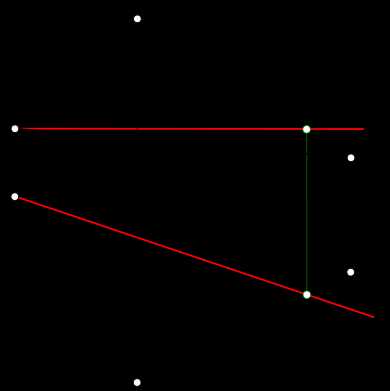
Горизонталь плоскости

чтобы построить горизонталь плоскости выраженной треугольником ABC необходимо: — построить фронтальную проекцию h» искомой горизонтали, причем h» ‖ x, проводим из вершины A треугольника, достигая этим цели наименьшим количеством построений; — в пересечении h» с B»C» противолежащей стороной треугольника отмечаем точку 1″; — находим 1` в пересечении ее линии проекционной связи со стороной B`C`; — находим h` искомой горизонтали, соединив прямой линией точки A` и 1`.

+

ngeo.fxyz.ru

Фронталь Википедия

Запрос «Горизонталь» перенаправляется сюда; о горизонталях на топографических картах см. Изогипса.

Начерта́тельная геоме́трия — инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.

Практически начертательная геометрия ограничивается исследованием объектов трёхмерного евклидова пространства. Исходные данные должны быть представлены в виде двух независимых проекций. В большинстве задач и алгоритмов используются две ортогональные проекции на взаимно перпендикулярные плоскости.

В настоящее время дисциплина не имеет практической ценности в силу развития вычислительной техники и аппарата линейной алгебры, но, вероятно, незаменима как составляющая общего инженерного образования на машиностроительных и строительных специальностях.

Начерта́тельная геоме́трия — наука, изучающая пространственные фигуры при помощи их проецирования (проложения) перпендикулярами на некоторые три плоскости, которые рассматриваются затем совмещёнными одна с другой.

При обыкновенном способе изображения предметов линии, распространяющиеся вдаль от глаза наблюдателя, хотя и изображаются, соответственно с тем, какими они нам представляются, сокращёнными, но это сокращение определяется рисовальщиком обыкновенно на глаз, а фотографией оно хотя в известных случаях и достаточно точно может быть передано, но отношение, в каком потерпели сокращения разные линии изображаемого предмета, остаётся трудно определимым; вдобавок, во многих случаях и фотография ведёт к перспективным ошибкам. Всякий мастер, будет ли то плотник, слесарь, токарь, каменотёс и т. д., может выполнить заказанный предмет согласно желанию заказчика только в том случае, если ему будет дан совершенно такой же предмет на образец, либо его модель, либо конструкторский чертёж, по которому легко и точно определялись бы размеры всех начерченных линий, хотя бы и таких, которые удаляются в глубь картины и потому изображаются сокращёнными. Начертательная геометрия учит изготовлению таких чертежей, в которых предмет изображается почти таким, каким мы его видим, и притом так, что по начерченным линиям можно в точности определить размеры и истинный вид изображаемого предмета.

Терминология[ | ]

• Фронталь — прямая, параллельная фронтальной плоскости проекции в аксонометрическом или ортогональном чертеже, проецируется на фронтальную плоскость в истинную величину.
• Горизонталь — прямая, параллельная горизонтальной плоскости проекции в аксонометрическом или ортогональном чертеже, проецируется на горизонтальную плоскость в натуральную величину.
• Вертикаль — прямая, параллельная вертикальной плоскости проекции в аксонометрическом или ортогональном чертеже, проецируется на вертикальную плоскость в истинную величину^{[источник?]}.

Основные принципы[ | ]

ru-wiki.ru

Начертательная геометрия

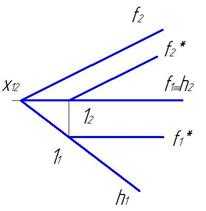
4.1.1. Линии уровня

Прямые линии, параллельные какой-либо плоскости проекций, называются линиями уровня.

Горизонталь h – прямая, параллельная горизонтальной плоскости проекций h∥, П ₁(рис. 12, 13).

Рис. 12. Горизонталь

Рис. 13. Комплексный чертеж горизонтали

Поскольку высоты всех точек горизонтали равны между собой: h₂ ⊥A₂A₂ или h₂∥x₁₂ .

Любой отрезок горизонтали проецируется на П₁ в натуральную величину: [A₁B₁]=[AB] .

Угол наклона h к П₂ также проецируется на П₁ в натуральную величину: ∠α₁=∠α=∠h, П₂.

Фронталь f – прямая, параллельная фронтальной плоскости проекций f∥, П ₂ (рис. 14, 15).

Рис. 14. Фронталь

Рис. 15. Комплексный чертеж фронтали

Поскольку глубина всех точек фронтали одинакова: f₁ ⊥ C₁C₂

Отрезки фронтали и угол наклона к П₁ проецируются на П₁ в натуральную величину: [C₂D₂] =[CD]; ∠β1=∠β=∠f, П₁.

Профильная прямая p – прямая, параллельная профильной плоскости проекций p∥, П ₃ (рис. 16, 17).

Рис. 16. Профильная прямая

Рис. 17. Комплексный чертеж профильной прямой

Поскольку широта всех точек профильной прямой одинакова: p₂ ⊥ E₂E₁ .

Отрезки профильной прямой и углы наклона к П₁ и П₂ проецируются на П₃ в натуральную величину: [E₃F₃] =[EF]; ∠τ₃=∠τ=∠р, П₁∠φ₃=∠φ=∠р, П₂.

cdot-nntu.ru