Горизонталь и вертикаль как выглядит: «Что представляют собой понятия вертикаль и горизонталь?» — Яндекс Кью

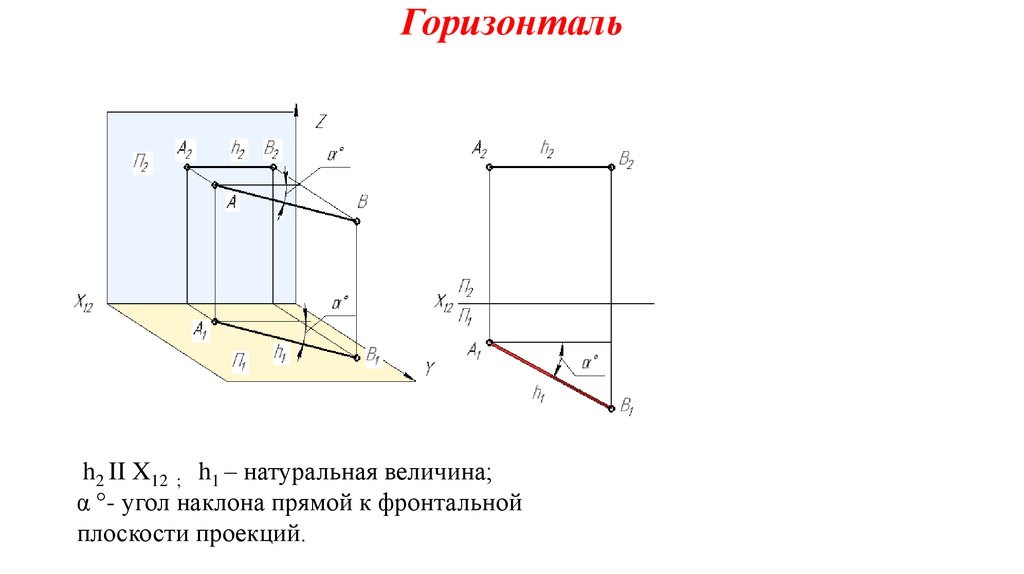
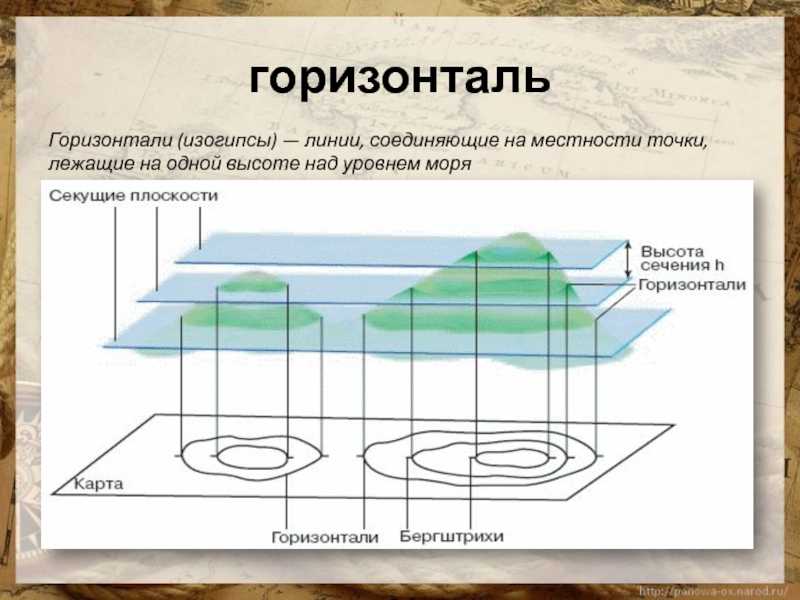
X Горизонталь Y Вертикаль Z Глубина T Время: taxik — LiveJournal

?

Categories:

• Искусство
• Россия
• Cancel

В выходные ходила на необычную выставку «XYZT».
На выставке были представлены разные световые инсталляции, какие-то из них жили своей жизнью, а некоторые были подвластные человеку. Т.е. изменялись от проникновения в них человека.

«Эта выставка – тур по цифровому пространству, с возможностью прикоснуться к алгоритмам и почувствовать материю света. Таким образом каждый зритель может наконец обнаружить и понять, какие они – воображаемые пространства.»
Адриен Мондо и Клер Барден

Выставка-тур состоит из десяти интерактивных инсталляций.

Посещение экспозиции похоже на прогулку сквозь другую, обновленную форму природы на стыке геометрического и органического миров.

Фрагменты реального чувственного опыта, такие как прогулка по траве или прикосновение к песку, перемещаются в абстрактную цифровую среду, состоящую из линий, точек и букв.

Выставка является частью комплексного художественного проекта, вышедшего из исследований сенсорных отношений между человеческим телом и цифровыми объектами в движении. Объекты, созданные художниками, сосредоточены на человеке, но отправная точка и специфика их процессов заключается в рассмотрении вопроса о цифровой разработке адаптивных инструментов.

Для посетителей есть возможность оказаться в пространстве, где остаются только неотъемлемые чувства. Посредством простых манипуляций они могут создавать формы и изменять мир, игрой, похожей на наслаждаться жонглирование без правил, и ощутить любопытство научного исследователя.

Ну или просто сделать много интересных фото и селфи.

Выставка проходит в креативном пространстве на Саввинской набережной, на территории фабрики «Московский шелк»
Москва, Большой саввинский пер. 12 стр. 6 (ст. м. Спортивная) От метро идти минут 15-20.
Выставка в соц.сетях ВК, ФБ, Инста
Спасибо mosblog за интересные анонсы.

Tags: 2016, mosblog, Москва, выставка

Subscribe to Telegram channel taxik

Subscribe

• Пройти по следам ралли «Шёлковый путь» можно на Тверском бульваре в Москве!

  2 декабря на Тверском бульваре в Москве состоялось торжественное открытие фотовыставки » По следам ралли «Шелковый путь», организованный при…

• Выставка 3D картин ВООБРАЖАРИУМ на ВДНХ

  3D Воображариум — это уникальная интерактивная выставка 3D картин, оживающих в объективе фотокамеры. Это самая масштабная выставка в Европе,…

• Выставка «Россия – Моя история. 1945–2016 гг.

  » в ЦВЗ «Манеж»

  Оригинал взят у cultura_v_msc в Выставка «Россия – Моя история. 1945–2016 гг.» в ЦВЗ «Манеж» С 4 по 22 ноября 2016 года в ЦВЗ «Манеж» в…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

• Пройти по следам ралли «Шёлковый путь» можно на Тверском бульваре в Москве!

  2 декабря на Тверском бульваре в Москве состоялось торжественное открытие фотовыставки » По следам ралли «Шелковый путь», организованный при…

• Выставка 3D картин ВООБРАЖАРИУМ на ВДНХ

  3D Воображариум — это уникальная интерактивная выставка 3D картин, оживающих в объективе фотокамеры. Это самая масштабная выставка в Европе,…

• Выставка «Россия – Моя история. 1945–2016 гг.» в ЦВЗ «Манеж»

  Оригинал взят у cultura_v_msc в Выставка «Россия – Моя история. 1945–2016 гг.» в ЦВЗ «Манеж» С 4 по 22 ноября 2016 года в ЦВЗ «Манеж» в…

Вертикально: это как – вверх или вниз и как выглядит вертикальная линия

Казалось бы, что каждому человеку должно быть известно, что обозначают такие термины как «вертикально», «горизонтально». Однако даже взрослые люди зачастую путаются это вверх или нет. В данной статье мы попробуем разобраться, какое положение считается вертикальным, как и где принято использовать это обозначение. Более того, мы поговорим и о том, какое значение отводится обычной вертикальной черте в некоторых школьных науках.

Содержание

Таблица ASCII и вертикаль

Сперва поговорим о том, что же должен представлять человек, когда слышит определение «вертикальная черта». В первую очередь, это обозначение используется именно в ASCII. Вам ничего не говорит данная аббревиатура? И это вполне нормально, поскольку данная шифровка будет знакома исключительно людям, работа которых связана с кодированным текстом.

Это интересно! Считаем правильно: как находить процент от суммы и числа

Для простых обывателей поясним, что ASCII представляет собой достаточно большую таблицу. В ней собраны различные коды. Каждый из этих кодов соответствует печатным и непечатным символам, которые широко используются.

Таблица ASCII

Обратите внимание! Речь идет именно о числовых кодах. Впервые эта таблица была разработана специалистами из Соединенных Штатов Америки в 60-х годах. Практически сразу после разработки она была стандартизирована и после этого начала активно использоваться.

В таблице можно найти и такой символ, как вертикальная линия. Ее код – 0x7C (hex), 124 (dec).

Примечательно, что пользователи операционной системы под названием UNIX, предпочитают именовать данный символ не иначе как «пайп». С английского языка слово «pipeline» можно перевести как конвейер. Но в Советском Союзе понять и принять данную терминологию не смогли. Книги В. Э. Фигурнова, первые издания которых являются советскими, пестрели необычным сравнением вертикальной линии с трубопроводом. Именно поэтому ее и начали именовать как символ трубопровода, заменив тем самым ходовое наименование «pipe».

Это интересно! Как найти и чему будет равна длина окружности

Применение в математике

Наверняка, каждый школьник, который не прогуливал уроки и добросовестно выполнял домашние задания, известно, как выглядит вертикаль. Ведь в математике обозначение используется довольно часто. Причем вариантов применения имеется немало.

Рассмотрим более подробно каждый из них и тем самым немного вспомним школьную программу.

1. |x| знакомое многим обозначение. Значение, которое находится между двумя вертикальными чертами, это абсолютное значение. Тоже никогда не слышали? Тогда напомним о другом термине, которым принято обозначать абсолютное значение. И это – модуль. Следовательно, линия, идущая вниз, обозначает именно модуль.
2. m || n – разделение двумя вертикальными чертами принято считать обозначением параллели. Иными словами, данные прямые (плоскости) всегда будут параллельными, если их разделяет подобный символ.
3. a|b – в такой формуле вертикальная линия представляет собой разделитель. То есть число a делит число b.
4. p(b|a) – более сложная формула. Разделение в виде вертикальной черты говорит о том, что некое событие b возможно только при условии, что произойдет событие a.

Вышеперечисленные формулы и обозначения не являются единственными. bad | sort. Но сразу отметим, что она сложная только на первый взгляд. В действительности программист задал простой алгоритм. С его помощью можно вывести на экран список фруктов, который содержится в файле под названием fruits.txt.

Это интересно! Изучаем символы: как обозначается в математике площадь

Но при этом можно будет увидеть только те фрукты, в названии которых в первых 3-х символах нет «bad». Более того, выведенный список будет сразу отсортирован по алфавиту. Все просто, не так ли? Но какая же формула натолкнула программистов на мысль сравнить вертикаль с трубопроводом?

Та, что приведена выше. На примере этой формулы можно понять, почему же российским программистам пришло в голову сравнить данный символ с трубопроводом. Описанный метод передачи информации направляет поток данных по тому же принципу работы, что и обычный трубопровод. Именно поэтому программисты из Советского Союза посчитали, что термин «pipe», пришедший с Запада, можно заменить на другой «трубопровод». Ведь по вертикали это значит и вниз, и вниз.

Пример программы в информатике с использованием вертикальных линий

Просто о сложном

Практически у каждого человека, который прочитал вышеизложенный текст, гарантированно возникла мысль, что разобраться в том,какая линия вертикальна, сложно. Но в действительности это не так. Итак, сейчас попробуем простым и понятным языком объяснить, что же представляет собой вертикаль.

Это интересно! Урок геометрии: как найти по формуле периметр треугольника

Вертикаль – это направление, которое перпендикулярно горизонтальной плоскости. А теперь вспомним, что такое горизонтальная плоскость. Представьте себе горизонт. Представили? Вот вам и горизонтальная плоскость. Следовательно, плоскость, которая будет располагаться по отношению к горизонту перпендикулярно, должна считаться вертикальной чертой. То есть вертикально, как уже было написано, это вверх и вниз одновременно.

Полезное видео: Рисуем прямые линии (вертикальные и горизонтальные)

Базовая алгебра — графическое построение горизонтальных и вертикальных линий

Предыдущий Следующий

Графики горизонтальных и вертикальных линий

Мы знаем, что линейное уравнение с двумя переменными, такими как знаменитые x и y , можно изобразить в виде прямой линии. (Кстати: это верно только потому, что переменные не имеют показателей степени, но это в другой раз). Есть несколько специальных уравнений, которые также дают прямую линию. Давайте посмотрим на это:

y = 3.

Мы можем изобразить это, составив таблицу точек.

Сначала мы выбираем несколько случайных значений для x , например -2, 0 и 3. Затем мы подставляем эти числа в уравнение вместо x . Но подождите — здесь нет переменной x . Независимо от того, что такое x , y всегда будет 3. Самая простая замена.

x -значение	y -значение	точка ( x , y )
-2	3	(-2, 3)
0	3	(0, 3)
3	3	(3 , 3)

Теперь наносим эти точки на сетку и получаем линию.

Если мы выберем любую точку на линии, как показано на рисунке, y -координата будет 3. Координата x будет меняться, но y всегда будет 3. Вот почему уравнение для этой линии равно y = 3.

Взгляните на эти линии:

Заметили что-нибудь во всех этих горизонтальных линиях? Если вы ответили, что все они y = что-то , то вы правы.

Горизонтальные линии все в форме y = A , где A — любое действительное число.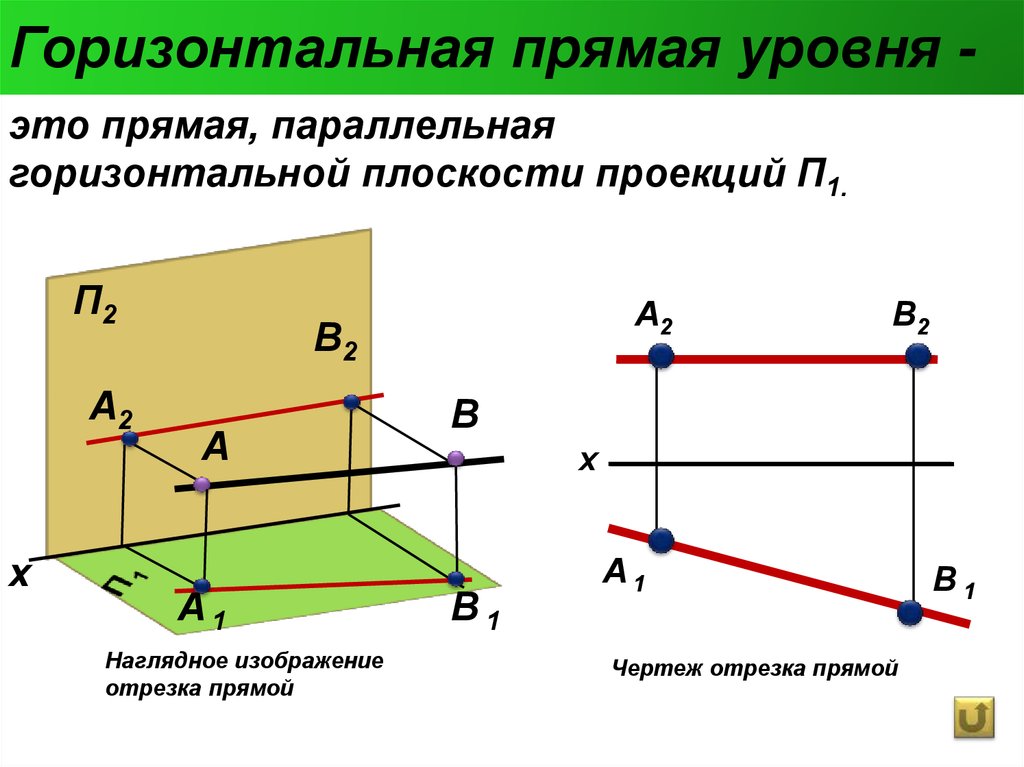

Это потому, что мы изображаем все точки, где y равно некоторому числу.

Теперь взгляните на эти строки:

Все эти чуваки вертикальные и имеют форму x = что-то

. Неудивительно, ведь все точки, лежащие на вертикальной линии, имеют одну и ту же координату x .

Вот несколько точек на линии x = -1:

Видите, как все координаты x равны -1? Так всегда бывает с вертикальными линиями. Вертикальные линии все имеют форму x = B , где B — любое действительное число.

Если мы хотим изобразить линию y = -2, все, что нам нужно сделать, это нанести все точки, которые имеют y -координату -2 и соединить их, как соединить точки.

На самом деле нам не нужно отображать на графике все этих точек. Двух было бы достаточно, но мы хотели бы подчеркнуть свою точку зрения (никаких глупых математических каламбуров).

Предыдущий Следующий

Подробнее об основах алгебры Навигация

Это продукт премиум-класса

Разблокировать эти функции

Устали от рекламы?

Присоединяйтесь сегодня и никогда больше их не увидите.

Начало работы

Графики горизонтальных и вертикальных линий — легко

В вашем браузере отключен JavaScript.

Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

• Математика
• org/ListItem»> Средняя школа
• Линейные уравнения с двумя переменными и их графики
• Графики горизонтальных и вертикальных линий

Рейтинг

Ø 5,0 / 1 оценка

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти к Google

Авторы

Сьюзен Сайфан

Основы по теме

Графики горизонтальных и вертикальных линий

Горизонтальная линия параллельна оси x и перпендикулярна, а также пересекает ось y. Наклон горизонтальной линии всегда равен нулю, так как ее изменение по оси y всегда равно нулю. С другой стороны, вертикальная линия параллельна оси y и перпендикулярна, а также пересекает ось x.

Наклон вертикальной линии не определен, так как ее изменение x всегда равно нулю, что дает наклон с нулем в знаменателе. Посмотрите, как Стефани применяет эти свойства для построения графика движений своего игрового персонажа 8-BitBot при перемещении по вертикали и горизонтали в своей компьютерной игровой программе. Общий основной справочник: CCSS.MATH.CONTENT.8.FA.3

Стенограмма

Графики горизонтальных и вертикальных линий

Стефани очень любит компьютерные игры старой школы. Так что она учится программировать, чтобы сделать свою собственную игру. Чтобы Стефани заставила своего персонажа, 8bitbot, двигаться по правильным путям, ей нужно исследовать графики горизонтальных и вертикальных линий. Начнем с настройки координатной плоскости. Мы нарисуем и пометим ось X, а затем ось Y. Давайте рассмотрим горизонтальную линию, по которой Стефани хочет, чтобы 8bitbot двигался. Изучив несколько точек вдоль этой горизонтальной линии, мы можем написать уравнение, описывающее ее.

Давайте выберем несколько случайно упорядоченных пар: минус 5, минус 2; минус 3, минус 2; ноль, минус 2; и 2, минус 2. Вы замечаете закономерность? Хотя значения x меняются, все значения y одинаковы при отрицательном значении 2. Итак, уравнение этой горизонтальной линии: «у» равно минус двум. Какими еще качествами обладает эта горизонтальная линия? Линия параллельна оси x. Это означает, что он никогда не коснется оси x и, следовательно, не имеет точки пересечения с x. Однако у него есть точка пересечения с нулем, минус 2, и он перпендикулярен оси Y. Кроме того, вы заметили что-нибудь о наклоне этой горизонтальной линии? Наклона вроде нет вообще. Итак, давайте проверим это, взяв две точки с линии и подставив их в формулу наклона. Помните, формула для нахождения наклона: «у» два минус «у» один на «х» два минус «х» один. Мы будем использовать точки минус 5, минус 2 и минус 3, минус 2, чтобы вычислить наклон. Это дает нам ноль, деленный на два. Но ждать! Помните, ноль, деленный на что-либо, равен нулю, поэтому наклон m равен нулю. Стефани понимает горизонтальную линию и вводит в свою программу правило «у» равно минус два. И 8bitbot выключен! Но есть еще одно направление, в котором ему нужно двигаться. Итак, давайте исследуем эту вертикальную линию лестницы. Как и в случае с горизонтальной линией, мы можем выбрать и пометить несколько случайных точек на линии. Видите ли вы закономерность в этих упорядоченных парах? Подобно горизонтальной линии, где значения y не изменились, мы можем видеть, что значения x не меняются, когда линия вертикальна. Следовательно, мы можем написать уравнение, как «х» равно пяти. Какими еще качествами обладает эта вертикальная линия? Эта вертикальная линия параллельна оси y, которая является другой вертикальной линией, поэтому у нее не будет точки пересечения с осью y. Однако он имеет точку пересечения с х в точке пять, ноль и перпендикулярен оси х, которая является горизонтальной линией.
Вертикальная линия также перпендикулярна нашей горизонтальной линии из первого примера. Итак, что это означает для наклона вертикальной линии или вообще всех вертикальных линий? Давайте рассмотрим этот наклон алгебраически, снова используя формулу наклона и любые две точки на линии. Это приводит к тому, что отрицательная единица больше нуля. Вау!!!! Подождите минуту! Мы не можем разделить что-то ни на что. Следовательно, этот наклон не определен. На самом деле все вертикальные линии имеют неопределенный наклон, потому что нет разницы в значениях x. Фу. Это хорошо знать.
Стефани вводит ‘x’ равное 5, чтобы заставить 8bitbot двигаться вертикально. Смотри, он идет! Прежде чем Стефани закончит программировать, давайте повторим. Нашим первым примером была горизонтальная линия с уравнением ‘y’, равным минус двум. Давайте посмотрим еще на несколько горизонтальных линий. Все горизонтальные линии можно записать как ‘y’, равный некоторой константе. В горизонтальных линиях нет термина «x», потому что наклон всегда равен нулю. Наклон любой горизонтальной линии всегда равен нулю, потому что числитель равен нулю, потому что значения y не меняются. Уравнение нашей вертикальной линии было записано как «x» равно 5. Это противоположно по сравнению с горизонтальными линиями, поскольку все вертикальные линии могут быть записаны как «x», равный некоторой константе. Вертикальные линии не имеют члена «y» в уравнении. Независимо от того, какая у вас вертикальная линия, наклон всегда будет неопределенным, потому что в знаменателе ноль.
Это означает, что разницы нет, потому что значения x не изменились. Понимание характеристик горизонтальных и вертикальных линий помогло Стефани написать правильный код для движений 8bitbot. Итак, что сейчас делает 8bitbot? О, бедная Стефани. Должно быть поздно.

Упражнение «Графики горизонтальных и вертикальных линий»

Хотели бы вы применить полученные знания? Вы можете просмотреть и попрактиковаться с заданиями к видео Графики горизонтальных и вертикальных линий .

• Определите характеристики горизонтальных линий.

  Подсказки

  Помните о наклонном дереве. Это поможет вам запомнить наклон различных линий.

  В общем случае линейное уравнение задается формулой $y=mx+b$, где $m$ — наклон, а $b$ — точка пересечения $y$.

  Решение

  Здесь вы видите дерево наклона. Часть дерева, параллельная нижней части дерева, имеет нулевой наклон.

  Любое линейное уравнение типа $y=c$, где $c$ — константа, параллельно основанию дерева и поэтому имеет нулевой наклон. Таким образом, горизонтальная линия, соответствующая $y=3$, параллельна основанию дерева или оси $x$ и, таким образом, имеет нулевой наклон.

  Проверим это, используя формулу наклона для двух заданных точек на прямой, например $(1,3)$ и $(4,3)$. Вы вычитаете $y$-координаты и делите полученную разницу на разницу $x$-координат в соответствующем порядке:

  $m=\frac{y_2-y_1}{x_2-x_1}=\frac{3 -3}{4-1}=\frac03=0$.

  Эта линия имеет некоторые дополнительные свойства:

  • Пересечение $y$ равно $(0,3)$. Строка не имеет $x$-перехвата.
  • Значения $x$ изменяются, а значения $y$ остаются постоянными ($y=3$).
  • Линия перпендикулярна оси $y$.

• Опишите вертикальные линии.

  

  Подсказки

  Помните о формуле наклона: $m=\frac{y_2-y_1}{x_2-x_1}$, и помните, что на ноль делить нельзя!

  Найдите часть дерева склонов, которая представляет собой вертикальную линию.

  Решение

  Здесь вы видите дерево наклона. Линия, параллельная стволу дерева, имеет неопределенный наклон. Любое линейное уравнение типа $x=c$, где $c$ — константа, параллельно стволу дерева и поэтому имеет неопределенный наклон. В частности, горизонтальная линия $x=2$ параллельна стволу и поэтому имеет неопределенный наклон.

  Эта строка имеет некоторые дополнительные свойства:

  • Пересечение $x$ равно $(2,0)$. Строка не имеет $y$-перехвата.
  • Значения $x$ остаются постоянными ($x=2$), а значения $y$ изменяются.
  • Прямая параллельна оси $y$.

  Давайте воспользуемся формулой наклона для двух заданных точек прямой, например, $(2,0)$ и $(2,3)$, чтобы подтвердить, что наклон $x=2$ не определен. Вы вычитаете $y$-координаты и делите полученную разницу на разницу $x$-координат в соответствующем порядке:

  $m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-0}{2-2}=\frac30$.

  Мы не можем делить на ноль, потому что, если бы мы могли, мы могли бы умножить обе части уравнения $m=\frac{3}{0}$ на ноль, чтобы получить $0m=3$, что неверно! Как любое число, умноженное на ноль, равно нулю. Так что наш наклон не определен.

• Определите уравнение, соответствующее линии графика.

  Подсказки

  Уравнение любой горизонтальной линии или линии, параллельной оси $x$, имеет вид $y=c$, где $c$ — константа.

  Уравнение любой вертикальной линии или линии, параллельной оси $y$, имеет вид $x=c$, где $c$ — константа.

  Решение

  Помните:

  • Горизонтальная линия (т. е. параллельная оси $x$) имеет уравнение $y=c$, где $c$ — константа.
  • Вертикальная линия (т.е. параллельная оси $y$) имеет уравнение $x=c$, где $c$ — константа.

  Начнем с горизонтальных линий:

  • красная пересекает ось $y$ в точке $y=2$. Это уже искомое уравнение.
  • Оранжевый пересекает ось $y$ в точке $y=1$.
  • Зеленый пересекает ось $y$ в точке $y=4$.

  Наконец, остаются еще две вертикальные линии:

  • фиолетовая пересекает ось $x$ в точке $x=3$. Это искомое уравнение.
  • синий пересекает ось $x$ в точке $x=1$.

• Определите, является ли линия горизонтальной или вертикальной.

  Подсказки

  В общем случае линейное уравнение задается формулой $y=mx+b$, где $m$ — наклон, а $b$ — точка пересечения $y$.

  При любом наклоне $m\neq 0$ линия не является ни горизонтальной, ни вертикальной.

  Определить точку пересечения $y$ или $x$.

  Горизонтальная (вертикальная) линия не имеет точки пересечения $x$- ($y$-).

  • $y=-2$ — горизонтальная линия.
  • $x=-2$ — вертикальная линия.
  • $y=-2x-2$ — это линия, которая не является ни горизонтальной, ни вертикальной.

  Решение

  Имейте в виду следующее:

  • Уравнение любой горизонтальной линии имеет вид $y=c$, где $c$ — константа.
  • Уравнение любой вертикальной линии имеет вид $x=c$, где $c$ — константа.

  Следующие уравнения соответствуют горизонтальным линиям:

  • $y=0$
  • $у=7$

  Вертикальные линии задаются следующими уравнениями:

  • $x=-2$
  • $х=7$

  Два оставшихся уравнения представляют собой линии, которые не являются ни горизонтальными, ни вертикальными:

  • $y=x+1$
  • $y=7x+7$

• Определите тип линии и соответствующие уравнения.

  

  Подсказки

  Здесь вы видите строку, заданную $y=\frac32x$.

  Вы можете видеть, что линия не является ни горизонтальной, ни вертикальной.

  Горизонтальная линия параллельна оси $x$.

  Вертикальная линия параллельна оси $y$.

  Уравнение любой горизонтальной линии имеет вид $y=c$ с константой $c$.

  Уравнение любой вертикальной линии имеет вид $x=c$ с константой $c$.

  Решение

  На рисунке вы видите три линии:

  • Линия, соответствующая $y=1$, параллельна оси $x$. Эта строка по горизонтали .
  • Прямая, соответствующая $x=4$, параллельна оси $y$. Эта строка по вертикали .
  • Последняя строка в соответствии с $y=-x+2$ проходит ось $y$ в $(0,2)$ и ось $x$ в $(2,0)$. Эта линия не является ни горизонтальной, ни вертикальной.

• Рассчитайте наклон линии по двум точкам и определите тип линии.

  Подсказки

  Используйте формулу наклона для двух заданных точек $(x_1,y_1)$ и $(x_2,y_2)$:

  $m=\frac{y_2-y_1}{x_2-x_1}$.

  Обратите внимание на последовательный порядок вычитания.

  Дерево наклона представляет собой вертикальную линию.

  В общем случае линейное уравнение задается формулой $y=mx+b$, где $m$ — наклон, а $b$ — точка пересечения $y$.

  • Наклон $m=0$ указывает на горизонтальную линию.
  • Наклон $m\neq 0$ указывает на линию, которая не является ни горизонтальной, ни вертикальной.
  • Неопределенный наклон указывает на вертикальную линию.

  Решение

  Чтобы определить, является ли линия, соответствующая заданному набору точек на линии, горизонтальной, вертикальной или ни той, ни другой, мы определяем наклон линии, которую определяет набор точек. Для этого используем формулу наклона:

  $m=\frac{y_2-y_1}{x_2-x_1}$.

  Если знаменатель равен нулю, наклон не определен.

  Для $\mathbf{(3,3)}$ и $\mathbf{(4,3)}$ имеем

  $m=\frac{3-3}{4-3}=\frac01 =0$.

  Таким образом, мы можем заключить, что соответствующая линия горизонтальна.

  Для $\mathbf{(3,3)}$ и $\mathbf{(3,4)}$ имеем

  $m=\frac{4-3}{3-3}=\frac10 $.

  Деление на ноль не определено, поэтому наклон не определен, и соответствующая линия должна быть вертикальной.

  Для $\mathbf{(3,3)}$ и $\mathbf{(4,4)}$ имеем

  $m=\frac{4-3}{4-3}=\frac11=1$.

  На этот раз мы получаем ненулевой наклон. Таким образом, линия не является ни горизонтальной, ни вертикальной.

  С $\mathbf{(0,0)}$ и $\mathbf{(1,3)}$ мы получаем наклон,

  $m=\frac{3-0}{1-0}= \frac31=3$.

  Мы снова получаем ненулевой наклон и, таким образом, линию, которая не является ни горизонтальной, ни вертикальной.

Еще видео по теме Линейные уравнения с двумя переменными и их графики

Пропорциональные отношения

Постоянная скорость изменения

Линейные уравнения с двумя переменными

График линейного уравнения с двумя переменными

Графики горизонтальных и вертикальных линий

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический отдел

• Положения и условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Свяжитесь с нами!

help@sofatutor.