Индукции пример из жизни: Что Это Такое? (Отличие От Индукции, Примеры)

Содержание

Лекция 06. Метод математической индукции

Лекция 6. Метод математической индукции.

Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями, и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).

Индукция (induction – по-латыни наведение) наглядно иллюстрируется известной легендой о том, как Исаак Ньютон сформулировал закон всемирного тяготения после того, как ему на голову упало яблоко.

Ещё пример из физики: в таком явлении, как электромагнитная индукция, электрическое поле создает, «наводит» магнитное поле. «Ньютоново яблоко» – типичный пример ситуации, когда один или несколько частных случаев, то есть наблюдения, «наводят» на общее утверждение, общий вывод делается на основании частных случаев. Индуктивный метод является основным для получения общих закономерностей и в естественных, и в гуманитарных науках. Но он имеет весьма существенный недостаток: на основании частных примеров может быть сделан неверный вывод. Гипотезы, возникающие при частных наблюдениях, не всегда являются правильными. Рассмотрим пример, принадлежащий Эйлеру.

Будем вычислять значение трехчлена при некоторых первых значениях n:

n	1	2	3	4	5	6	7	8
	43	47	53	61	71	83	97	113

Заметим, что получаемые в результате вычислений числа являются простыми.

И непосредственно можно убедиться, что для каждого n от 1 до 39 значение многочлена является простым числом. Однако при n=40 получаем число 1681=41², которое не является простым. Таким образом, гипотеза, которая здесь могла возникнуть, то есть гипотеза о том, что при каждом n число является простым, оказывается неверной.

Лейбниц в 17 веке доказал, что при всяком целом положительном n число делится на 3, число делится на 5 и т.д. На основании этого он предположил, что при всяком нечётном k и любом натуральном n число делится на k, но скоро сам заметил, что не делится на 9.

Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Вопрос о справедливости утверждения в общем случае удается решить посредством применения особого метода рассуждений, называемого

методом математической индукции (полной индукции, совершенной индукции).

6.1. Принцип математической индукции.

♦ В основе метода математической индукции лежит принцип математической индукции, заключающийся в следующем:

1) проверяется справедливость этого утверждения для n=1 (базис индукции),

2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число 1 (предположение индукции), и с учётом этого предположения устанавливается справедливость его для n=k+1.

Доказательство. Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального

n. Тогда существует такое натуральное m, что:

1) утверждение для n=m несправедливо,

2) для всякого n, меньшего m, утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо).

Очевидно, что m>1, т.к. для n=1 утверждение справедливо (условие 1). Следовательно, – натуральное число. Выходит, что для натурального числа утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. ■

Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.

Доказательство, основанное на принципе математической индукции, называется

методом полной математической индукции.

 Пример 6.1. Доказать, что при любом натуральном n число делится на 3.

Решение. Воспользуемся методом полной математической индукции.

1) При n=1 , поэтому a₁ делится на 3 и утверждение справедливо при n=1.

2) Предположим, что утверждение справедливо при n=k, , то есть что число делится на 3, и установим, что при n=k+1 число делится на 3.

В самом деле,

Т.к. каждое слагаемое делится на 3, то их сумма также делится на 3. ■ 

 Пример 6.2. Доказать, что сумма первых

n натуральных нечётных чисел равна квадрату их числа, то есть .

Решение. Воспользуемся методом полной математической индукции.

1) Проверяем справедливость данного утверждения при n=1: 1=1² – это верно.

2) Предположим, что сумма первых k () нечётных чисел равна квадрату числа этих чисел, то есть . Исходя из этого равенства, установим, что сумма первых k+1 нечётных чисел равна , то есть .

Пользуемся нашим предположением и получаем

. ■ 

Метод полной математической индукции применяется для доказательства некоторых неравенств. Докажем неравенство Бернулли.

 Пример 6.3. Доказать, что при и любом натуральном n справедливо неравенство

(неравенство Бернулли).

Решение. 1) При n=1 получаем , что верно.

2) Предполагаем, что при n=k имеет место неравенство (*). Используя это предположение, докажем, что . Отметим, что при это неравенство выполняется и поэтому достаточно рассмотреть случай .

Умножим обе части неравенства (*) на число и получим:

, то есть (1+. ■ 

Доказательство методом неполной математической индукции некоторого утверждения, зависящего от n, где проводится аналогичным образом, но в начале устанавливается справедливость для наименьшего значения n.

В некоторых задачах явно не сформулировано утверждение, которое можно доказать методом математической индукции. В таких случаях надо самим установить закономерность и высказать гипотезу о справедливости этой закономерности, а затем методом математической индукции проверить предполагаемую гипотезу.

 Пример 6.4. Найти сумму .

Решение. Найдём суммы S₁, S₂, S₃. Имеем , , . Высказываем гипотезу, что при любом натуральном n справедлива формула . Для проверки этой гипотезы воспользуемся методом полной математической индукции.

1) При n=1 гипотеза верна, т.к. .

2) Предположим, что гипотеза верна при n=k, , то есть . Используя эту формулу, установим, что гипотеза верна и при n=k+1, то есть

В самом деле,

Итак, исходя из предположения, что гипотеза верна при n=k, , доказано, что она верна и при

n=k+1, и на основании принципа математической индукции делаем вывод, что формула справедлива при любом натуральном n. ■ 

 Пример 6. 5. В математике доказывается, что сумма двух равномерно непрерывных функций является равномерно непрерывной функцией. Опираясь на это утверждение, нужно доказать, что сумма любого числа равномерно непрерывных функций является равномерно непрерывной функцией. Но поскольку мы ещё не ввели понятие «равномерно непрерывная функция», поставим задачу более абстрактно: пусть известно, что сумма двух функций, обладающих некоторым свойством S, сама обладает свойством S. Докажем, что сумма любого числа функций обладает свойством S.

Решение. Базис индукции здесь содержится в самой формулировке задачи. Сделав предположение индукции, рассмотрим функций

f₁, f₂, …, f_n, f_n₊₁, обладающих свойством S. Тогда . В правой части первое слагаемое обладает свойством S по предположению индукции, второе слагаемое обладает свойством S по условию.

Следовательно, их сумма обладает свойством S – для двух слагаемых «работает» базис индукции.

Тем самым утверждение доказано и будем использовать его далее. ■ 

 Пример 6.6. Найти все натуральные n, для которых справедливо неравенство

Решение. Рассмотрим n=1, 2, 3, 4, 5, 6. Имеем: 2¹>1², 2²=2², 2³<3², 2⁴=4², 2⁵>5², 2⁶>6². Таким образом, можно высказать гипотезу: неравенство имеет место для каждого . Для доказательства истинности этой гипотезы воспользуемся принципом неполной математической индукции.

1) Как было установлено выше, данная гипотеза истинна при n=5.

2) Предположим, что она истинна для n=k, , то есть справедливо неравенство . Используя это предположение, докажем, что справедливо неравенство .

Т. к. и при имеет место неравенство

при ,

то получаем, что . Итак, истинность гипотезы при n=k+1 следует из предположения, что она верна при n=k, .

Из пп. 1 и 2 на основании принципа неполной математической индукции следует, что неравенство верно при каждом натуральном . ■ 

 Пример 6.7. Доказать, что для любого натурального числа n справедлива формула дифференцирования .

Решение. При n=1 данная формула имеет вид , или 1=1, то есть она верна. Сделав предположение индукции, будем иметь:

что и требовалось доказать. ■ 

 Пример 6.8. Доказать, что множество, состоящее из n элементов, имеет подмножеств.

Решение. Множество, состоящее из одного элемента а, имеет два подмножества. Это верно, поскольку все его подмножества – пустое множество и само это множество, и 2¹=2.

Предположим, что всякое множество из n элементов имеет подмножеств. Если множество А состоит из n+1 элементов, то фиксируем в нём один элемент – обозначим его d, и разобьём все подмножества на два класса – не содержащие d и содержащие d. Все подмножества из первого класса являются подмножествами множества В, получающегося из А выбрасыванием элемента d.

Множество В состоит из n элементов, и поэтому, по предположению индукции, у него подмножеств, так что в первом классе подмножеств.

Но во втором классе подмножеств столько же: каждое из них получается ровно из одного подмножества первого класса добавлением элемента d. Следовательно, всего у множества А подмножеств.

Тем самым утверждение доказано. Отметим, что оно справедливо и для множества, состоящего из 0 элементов – пустого множества: оно имеет единственное подмножество – самого себя, и 2⁰=1. ■ 

Учебник для студентов юридических вузов и факультетов

2. Полная индукция. Логика: Учебник для студентов юридических вузов и факультетов

ВикиЧтение

Логика: Учебник для студентов юридических вузов и факультетов
Иванов Евгений Акимович

Содержание

2. Полная индукция

Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение).

В простейшем случае это выглядит так. Например, мы ежедневно ведем запись наблюдений за погодой и фиксируем солнечные дни в течение такого отрезка времени, как неделя. Мы можем констатировать, что каждый из дней был солнечным. Это дает возможность сделать общий вывод, что вся неделя в целом была солнечной. На этом примере можно убедиться, что индуктивное умозаключение принимает особую форму, отличную от дедуктивного. В учебных целях ее можно представить так:

Понедельник — солнечный день.

Вторник — солнечный день.

………..

День n — солнечный день.

Понедельник, вторник … день n исчерпывают все дни недели.

Следовательно, неделя была солнечной.

Более сложный случай представляет собой пример индукции, приводившийся в самом начале раздела «Умозаключение», — о том, что «Все планеты Солнечной системы движутся с запада на восток». Этот общий вывод может быть сделан путем непосредственных астрономических наблюдений за каждой планетой в отдельности.

Нетрудно установить, что в обоих случаях умозаключение имеет одинаковую структуру. Она может быть представлена следующей формулой:

S₁ — P

S₂ — P

…. .

S_n — P

S₁, S₂ … S_n … исчерпывают класс S.

Следовательно, все S — Р.

В символической записи это выглядит так:

Каково познавательное значение вывода в форме полной индукции? На первый взгляд кажется, что по сравнению с посылками он не дает никакого нового знания или что его значение ничтожно. К сожалению, такого рода взгляды высказывались и в истории науки. В действительности полная индукция дает новое знание. Если в посылках содержится знание лишь об отдельных элементах какого-либо класса предметов, то в выводе речь идет об этом классе в целом. Следовательно, он познается и оценивается под новым углом зрения: в нем выявляется некая сущность, а соответственно и закономерность. И это естественно: ведь понятия «общее», «сущность», «закономерность» — однопорядковые. Так, выявление того общего, что «Все планеты Солнечной системы движутся с запада на восток», открывает возможности для более глубокого познания причин и сущности планетообразования, закономерностей развития всей Солнечной системы.

Особо ценно, что полная индукция, как и дедукция, способна давать достоверные знания.

Разумеется, заключение в полной индукции может быть истинным и ложным. Оно будет истинным, если, во-первых, все посылки истинны по содержанию и, во-вторых, если между ними и заключением есть отношение логического следования: в данном случае если исчерпаны все элементы исследуемого класса и каждый обладает (или не обладает) тем или иным свойством.

Заключение может оказаться ложным, если хотя бы одно из этих условий не соблюдено. Например, вывод, что «Все бывшие союзные республики СССР объявили о своей независимости», — истинный; а вывод, что «Все бывшие союзные республики СССР вступили в СНГ» — ложный.

Посредством полной индукции могут быть получены важные научные знания более или менее общего характера: «Все планеты Солнечной системы вращаются вокруг своей оси», «На всех планетах происходит смена времен года», «Все планеты светят отраженным светом». Если же установлено, что не все элементы какого-либо класса (или виды рода) обладают данным общим свойством, то обобщение может быть облечено в форму частного суждения. Например: «Некоторые металлы легче воды», «Некоторые металлы — жидкие тела».

Обобщение может принимать форму не только утвердительного, но и отрицательного суждения. Например: «На некоторых планетах нет жизни», «Некоторые планеты не имеют спутников», «Некоторые металлы не являются твердыми телами» и др.

Характерно, что подобные суждения — определенно-частные. Кванторное слово «некоторые» употребляется здесь в смысле «только некоторые» («Только некоторые металлы легче воды»), но не в смысле «некоторые, а может быть и все».

На первый взгляд кажется, что сфера применения полной индукции весьма ограниченна, что она может использоваться лишь там, где число элементов класса нетрудно сосчитать. В действительности полная индукция довольно широко применяется в науках, даже если число исследуемых случаев чрезвычайно велико. Таковы, например, обобщения о динамике численности населения в стране, о соотношении мужчин и женщин в составе населения, об особенностях численности различных возрастных групп и т. д., получаемые на основе сплошных переписей населения. Таковы обобщения ежегодных данных состояния экономики, собираемых государственными статистическими органами. Так, статистическим путем получено обобщение о падении рождаемости в стране за 90-е годы.

При достаточно большом числе статистических данных четко проявляются определенные закономерности. Вспомним в этой связи о «законе больших чисел». Так, рождение мальчика или девочки в отдельной семье — случайность. Но если провести полный статистический анализ родившихся за год в масштабе более или менее крупного региона, то выявится интересная общая закономерность: число мальчиков превышает число девочек на вполне определенную величину. Например: на 100 девочек рождается 106 мальчиков.

Полная индукция применяется и в юридической практике. Юристы нередко пользуются статистикой преступлений, чтобы выявить определенные зависимости, тенденции и выработать соответствующие практические меры. Полную индукцию можно использовать и в раскрытии отдельного преступления.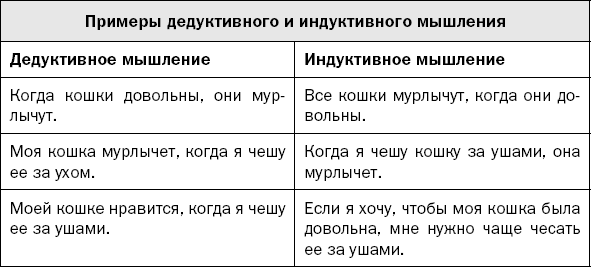 Так, следствие по какому-либо делу может быть завершено, если собран необходимый и достаточный материал обо всех участниках преступления. В противном случае какое-либо дело может быть выделено в отдельное производство.

Однако в целом пределы применения полной индукции обусловлены наличием классов с известным, поддающимся счету числом элементов (так называемых «закрытых классов»). За этими пределами она оказывается неприменимой.

3.13. Что такое индукция?

3.13. Что такое индукция? Вспомним, опосредованные умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Дедуктивные умозаключения, или силлогизмы, разновидности которых мы рассмотрели выше, дают достоверные выводы. Индуктивное умозаключение,

Глава XXVI. Это ли есть «полная радость», обетованная Господом

Глава XXVI. Это ли есть «полная радость», обетованная Господом Боже мой и Господи мой, упование мое и радость сердца моего, скажи душе моей, та ли это радость, о коей Ты речешь нам через Сына Своего: «Простите, и получите, чтобы радость ваша была совершенна» (Ин. 16, 24). Ибо нашел я

Глава V. Индукция

Глава V. Индукция 1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется,

1. Индукция как тип умозаключения

1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги.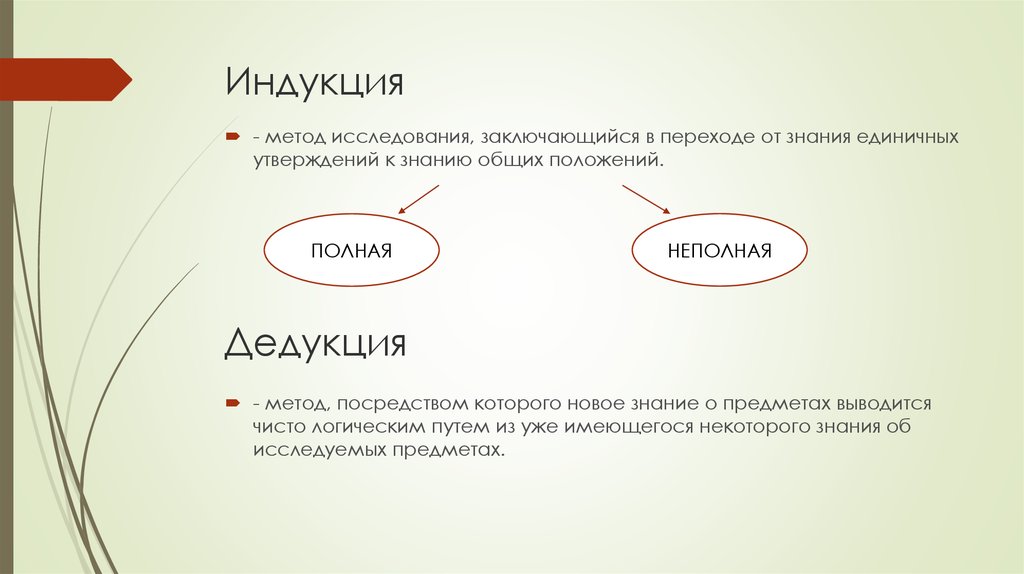 Сначала у него, как кажется, была мысль связать

§ 6. Математическая индукция

§ 6. Математическая индукция «Но не забываете ли вы, что в математике также имеет место индукция?» – может возразить читатель. «Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не

НЕПОЛНАЯ ИНДУКЦИЯ

НЕПОЛНАЯ ИНДУКЦИЯ Индуктивное умозаключение, результатом которого является общий вывод обо всем классе предметов на основании знания лишь некоторых предметов данного класса, принято называть неполной или популярной индукцией. Например, из того, что инертные газы

§ 153. Полная протяженность трансцендентальной проблемы. Членение исследований

§ 153. Полная протяженность трансцендентальной проблемы. Членение исследований Выдержанное в столь общих чертах обсуждение только что постигнутых в качестве возможных и требуемых исследований, какое было возможно для нас до сих пор, конечно же не способно создать

§ 33. Полная конкретность Я как монады и проблема его самоконституции

§ 33. Полная конкретность Я как монады и проблема его самоконституции От Я, как тождественного полюса и субстрата хабитуальных особенностей, мы будем отличать ego, взятое в полной конкретности (это ego мы будем называть «монадой», заимствуя это выражение у Лейбница), принимая

88. Полная потеря памяти

88. Полная потеря памяти Арнольд Конан только что сделал одно неприятное открытие: он вовсе не был Арнольдом Конаном. Или, скорее, он не привык им быть. Все это было довольно странно. Именно так он смог трактовать свою необычную автобиографию. Он родился Аланом Е. Вудом. Вуд,

В. Полная, или развернутая, форма стоимости

В. Полная, или развернутая, форма стоимости z товара А = и товара В, или = v товара С, или = w товара D,или = х товара Е, или = и т. д.(20 аршин холста = 1 сюртуку, или = 10 ф. чаю, или = 40 ф. кофе, или = 1 квартеру пшеницы, или = 2 унциям золота, или = 1/2 тонны железа, или = и

В. ПОЛНАЯ, ИЛИ РАЗВЕРНУТАЯ, ФОРМА СТОИМОСТИ

В. ПОЛНАЯ, ИЛИ РАЗВЕРНУТАЯ, ФОРМА СТОИМОСТИ z товара А = и товара В, или = v товара С, или = w товара D,или = х товара Е, или = и т. д.(20 аршин холста = 1 сюртуку, или = 10 ф. чаю, или = 40 ф. кофе, или = 1 квартеру пшеницы, или = 2 унциям золота, или = 1/2 тонны железа, или = и

ПОЛНАЯ ЧАША

ПОЛНАЯ ЧАША Нан-Ин, японский мастер дзен, живший в эру Мэйдзи (1868–1912), принимал как-то у себя профессора университета, пришедшего порасспросить его о дзен.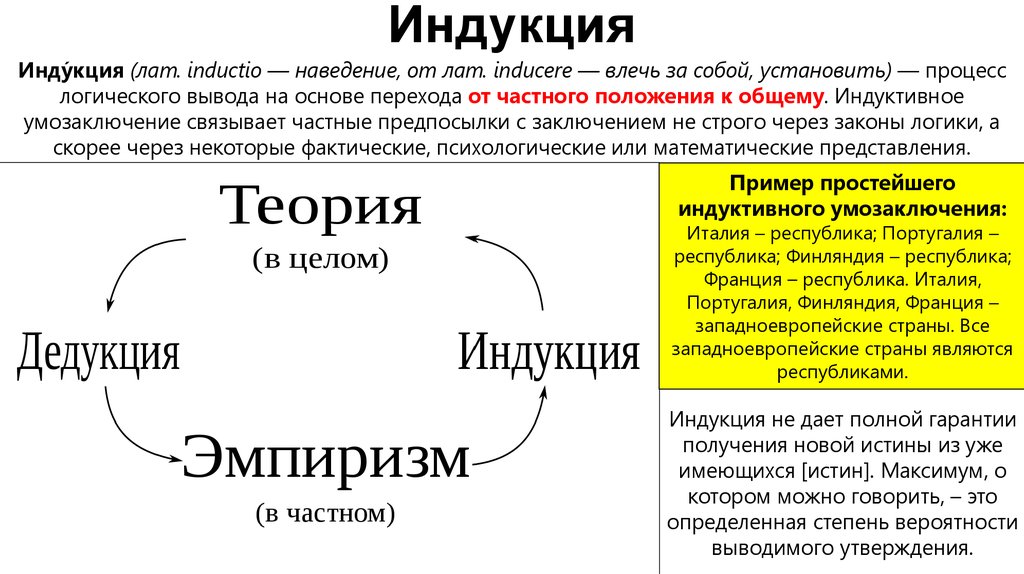 Нан-Ин разливал чай, но, налив гостю полную чашку, он продолжал лить дальше. Профессор смотрел на льющийся через край

Глава 21 Твоя полная свобода — величайший дар Бога

Глава 21 Твоя полная свобода — величайший дар Бога Когда я закончил свою речь на том сатсанге в Токио, с одного из задних рядов поднялся человек и задал мне вопрос, который, как он сказал, не дает ему покоя.«Когда я впервые прочел «Беседы с Богом», они меня очень тронули,

7. Пурна Матсиендрасана — Полная поза Матсиендры

7. Пурна Матсиендрасана — Полная поза Матсиендры Выполнение.Сядьте на землю и положите левую ступню на правое бедро так же, как и в Позе лотоса. Пятка левой ступни находится рядом с пупком. Теперь поднимите правую ступню и поставьте ее с внешней стороны левого колена, как вы

Более полная квантовая теория

Более полная квантовая теория Теория множественных миров Эверетта и ДеВитта – это канва более полной квантовой механики, включающей в себя опыт взаимодействия наблюдателя и наблюдаемого в НОР. Аспект физики, который исходит из того, что взаимоотношение между

Полная и неполная индукция

Полная и неполная индукция Если мы переберём всех футболистов сборной России и выясним, что среди них нет одноногих — это будет полная индукция, она же — «индукция перебором».Если же мы изучим одного футболиста, и придём к выводу, что играть с протезом в сборной —

13.8: Применение электромагнитной индукции

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 4839

OpenStax
OpenStax

Цели обучения

К концу этого раздела вы сможете:

Объяснять, как жесткие диски компьютеров и графические планшеты работают с использованием магнитной индукции
Объясните, как гибридные/электрические транспортные средства и транскраниальная магнитная стимуляция используют магнитную индукцию в своих интересах

Современное общество имеет множество применений закона индукции Фарадея, которые мы рассмотрим в этой и других главах. На этом этапе позвольте упомянуть несколько, которые связаны с записью информации с использованием магнитных полей.

Некоторые компьютерные жесткие диски применяют принцип магнитной индукции. Записанные данные производятся на вращающемся диске с покрытием. Исторически сложилось так, что чтение этих данных работало по принципу индукции. Однако сегодня большая часть входной информации передается в цифровом, а не в аналоговом виде — на вращающемся жестком диске записывается последовательность нулей или единиц. Поэтому большинство устройств считывания с жестких дисков не работают по принципу индукции, а используют технику, известную как гигантское магнитосопротивление 9 .0045 . Гигантское магнитосопротивление — это эффект большого изменения электрического сопротивления, вызванного приложенным магнитным полем к тонким пленкам чередующихся ферромагнитных и немагнитных слоев. Это один из первых крупных успехов нанотехнологий.

Графические планшеты
или планшетные компьютеры , в которых для рисования цифровых изображений используется специально разработанное перо, также применяют принципы индукции. Обсуждаемые здесь планшеты помечены как пассивные планшеты, поскольку существуют и другие конструкции, в которых для письма используется либо перо с батарейным питанием, либо оптические сигналы. Пассивные планшеты отличаются от планшетов и телефонов с сенсорным экраном, которые многие из нас используют регулярно, но все же их можно обнаружить при подписи на кассе. Под экраном, как показано на рисунке \(\PageIndex{1}\), расположены крошечные провода, идущие по всей длине и ширине экрана. Ручка имеет крошечное магнитное поле, исходящее от кончика. Когда наконечник касается экрана, в проводах ощущается изменяющееся магнитное поле, которое преобразуется в ЭДС индукции, которая преобразуется в линию, которую вы только что нарисовали.
Рисунок \(\PageIndex{1}\): Планшет со специальной ручкой для письма — еще одно применение магнитной индукции.
Другим применением индукции является магнитная полоса на обратной стороне вашей личной кредитной карты , которая используется в продуктовом магазине или в банкомате. Это работает по тому же принципу, что и аудио- или видеокассета, в которой головка воспроизведения считывает личную информацию с вашей карты.
Видео
Посмотрите это видео, чтобы увидеть, как фонарики могут использовать магнитную индукцию.

Магнит движется по проводу благодаря вашей механической работе. Индуцированный ток заряжает конденсатор, который хранит заряд, который зажжет лампочку, даже если вы не выполняете эту механическую работу.
Электромобили
и гибридные автомобили также используют преимущества электромагнитной индукции. Одним из ограничивающих факторов, препятствующих широкому распространению 100% электрических транспортных средств, является то, что срок службы батареи не так велик, как время, которое вы можете проехать на полном баке бензина. Чтобы увеличить количество заряда аккумулятора во время движения, двигатель может действовать как генератор всякий раз, когда автомобиль тормозит, используя создаваемую противо-ЭДС. Эта дополнительная ЭДС может быть получена из накопленной энергии в автомобильном аккумуляторе, что продлевает срок службы аккумулятора.
Еще одной современной областью исследований, в которой успешно применяется электромагнитная индукция, является транскраниальная магнитная стимуляция (ТМС) . Множество расстройств, включая депрессию и галлюцинации, можно отнести к нерегулярной локальной электрической активности в головном мозге. При транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозгу. Использование ТМС в качестве диагностического метода хорошо известно.
Видео
Посмотрите это видео на Youtube, чтобы увидеть, как рок-н-ролльные инструменты, такие как электрогитары, используют электромагнитную индукцию для получения сильных ударов.

Эта страница под названием 13. 8: Приложения электромагнитной индукции распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать оглавление
нет
Теги
Электромагнитная индукция
жесткие диски
источник@https://openstax. org/details/books/university-physics-volume-2
из класса на кухню – наука в школе
Автор(ы): Пауло Андре, Ана Рита Бастос и Руте Феррейра
Изучите электромагнитную индукцию и одно из ее хорошо известных применений – индукционную плиту – с помощью этих практических занятий.
Многие современные устройства основаны на электромагнитной индукции. Закон индукции Фарадея, сформулированный в 1831 году, описывает, как переменное магнитное поле индуцирует электродвижущую силу (ЭДС). Применение этого закона включает:
генераторы, производящие большую часть потребляемой в мире электроэнергии
поезда на магнитной подушке
индукционные плиты на кухне
звукосниматели для электрогитары
площадки для беспроводной передачи энергии, используемые для зарядки мобильных устройств.
Преподавание закона индукции Фарадея в средней школе является сложной задачей. Учащиеся в возрасте 16–19 лет должны применять как математические расчеты, так и концептуальное понимание для изучения науки, лежащей в основе электромагнитной индукции, и изучения ее применения в повседневной жизни.
В этом упражнении учащиеся получают непосредственный опыт работы с электромагнитной индукцией. Задания подходят для учащихся, изучающих физику в возрасте 16–19 лет, и в целом они занимают около часа, хотя для подготовки к заданию 2 перед уроком требуется дополнительное время.
Индукционная плита
Luisa Kittner/Pixabay
По окончании занятия учащиеся должны уметь:
понимать с экспериментальной точки зрения закон индукции Фарадея
определить параметры, влияющие на применение закона индукции Фарадея
исследовать взаимосвязь между вариациями магнитного потока и индуцированной электродвижущей силой
сконструировать электрический генератор, используя катушку и индукционную плиту для питания светодиода
Закон индукции Фарадея гласит, что изменение магнитного окружения проволочной катушки индуцирует электродвижущую силу (ЭДС), представленную как ε :
, где N — число витков катушки, а Φ — магнитный поток через катушку.
Если масштаб времени мал, производный член d Φ / d t может быть аппроксимирован до Δ Φ / Δ t . Это приближение особенно полезно, если учащиеся недостаточно знакомы с дифференциальным исчислением.
Магнитный поток зависит от площади катушки A , напряженности магнитного поля B и угла θ , образованный между силовыми линиями магнитного поля и вектором, перпендикулярным (под углом 90°) к плоскости катушки:
Любое изменение напряженности магнитного поля, площади катушки или угла приводит к наведенной ЭДС, которая может быть измеряется гальванометром и используется для демонстрации принципов индукции. Эта установка показана на рисунке 1.
Рисунок 1: Электрическая цепь с гальванометром и квадратной катушкой в магнитном поле с напряженностью B и направлением.
Изображение предоставлено Пауло Андре
Задание 1: свободно падающий магнит
В этом эксперименте, который должны провести учащиеся, магнитный диполь падает через катушку, индуцируя ЭДС, вызывая кратковременное изменение напряженности магнитного поля. Чтобы наблюдать за изменением ЭДС, катушку можно подключить к гальванометру или светодиоду (LED). Преимущество использования светодиода (рисунок 2) состоит в том, что он создает видимый выходной сигнал (вспышку света), когда индуцированная ЭДС превышает пороговое значение (~ 1,5 В).
Рис. 2. Эксперимент со свободно падающим магнитом со светодиодом
Изображение предоставлено Пауло Андре
Материалы
Катушка с N > 10 000 витков
Маленький стержневой магнит
Светодиод
Линейка
Смартфон (для съемки свободного падения)
Процедура
Подсоедините клеммы катушки к контактным площадкам светодиода. Если требуется пайка, этот шаг должен быть сделан учителем заранее.
С помощью линейки поместите магнит на 20 см выше центра катушки (и выровняйте его по центру катушки).
Настройте камеру смартфона на запись события, желательно в замедленном режиме.
Отпустите магнит и наблюдайте за светодиодом (рис. 3).
Поэкспериментируйте с выпуском катушки с разной высоты над катушкой. Какие отличия, если они есть, вы заметили?
Теперь поверните катушку на 180º и повторите эксперимент. Наблюдается ли какое-либо изменение?
Рис. 3: Кадры видео, показывающего свободно падающий магнит. Последний кадр —
, когда магнит находится внутри катушки, а светодиод излучает (красный).
Изображение предоставлено Пауло Андре
Обсуждение
Учителя могут обсудить с учащимися следующие вопросы, чтобы изучить ключевые понятия:
Как интенсивность излучения светодиода зависит от расстояния, на котором высвобождается магнит?
При одинаковом расстоянии падения приводит ли поворот катушки на 180º к различной интенсивности излучения светодиодов?
Учащиеся могут просмотреть свои видеоролики об эксперименте, чтобы найти подтверждение своим ответам, или просмотреть предоставленный видеоролик. В реальной жизни процесс происходит очень быстро, поэтому для уточнения деталей необходимо замедленное видео.
Пояснение
Эксперимент должен показать четкую разницу в интенсивности излучения светодиода по мере увеличения начального расстояния между магнитом и катушкой, что приводит к увеличению скорости магнита и скорости изменения магнитного потока.
Светодиод представляет собой поляризованное устройство, что означает, что он излучает свет только в том случае, если приложенная ЭДС положительна (когда может протекать электрический ток). Является ли ЭДС положительной или отрицательной, зависит от направления движения магнита (какой полюс магнита в данный момент движется через катушку) и в каком направлении катушка подключена к контактным площадкам светодиода.
Мы можем увидеть это более подробно в моделировании, показанном на рисунке 4e. Здесь ЭДС положительна только примерно в течение половины периода времени, в течение которого магнит находится внутри катушки, и что положительная ЭДС имеет более высокое максимальное значение, чем отрицательная ЭДС из-за ускорения магнита при падении через катушку.
Расширение задания 1: математическое моделирование
Хотя мигающий светодиод указывает на индуцированную ЭДС, возникающую в результате изменения магнитного потока, он не дает количественных значений. Мы можем узнать более точно изменяющиеся значения магнитного потока, когда магнит падает через катушку, используя дополнительное уравнение:
, где y — координата магнита, y ₀ — координата центра катушки, B _max — максимальное значение напряженности магнитного поля, а σ — параметр, описывающий спад напряженности магнитного поля.
Здесь мы делаем следующие предположения или приближения:
длина магнита мала по сравнению с катушкой
вектор его магнитного поля совмещен с его продольной осью
Φ (магнитный поток через катушку) максимален, когда геометрические центры катушки и магнита совпадают.
Параметр σ (расстояние для B ~ 37 % от B _max ) можно принять в диапазоне 5–10 мм, полную процедуру экспериментального определения можно найти в Ref. [1].
Для магнита в свободном падении смещение y магнита в момент времени t связано с ускорением свободного падения g уравнением 4:
В таблице 1 приведен пример используемых параметров.
Таблица 1: Примеры значений параметров, использованных для получения результатов на рис. 4.
Параметры Символ Значение Блок
Область катушки А 250 мм ²
Количество витков катушки Н 12000
Максимальная напряженность магнитного поля В _макс. 3 мт
Распад магнитного поля σ 10 мм
Координата центра катушки г ₀ 200 мм
Используя значения в таблице 1, уравнениях 3 и 4 и прилагаемой электронной таблице, мы можем создать математическую модель, которая графически отображает эти изменения, как видно из результатов и графиков на рисунке 4. ^[2] Здесь магнитный поток через катушку и ЭДС индукции показаны как функция положения и времени. Магнит освобождается при y = 0 и t = 0 и падает в положительном направлении оси. Катушка отцентрирована в позиции y ₀ .
Рис. 4: а) Экспериментальная схема. b–e) Смоделированные значения для магнита в свободном падении: магнитный поток как функция положения (b) и времени (d), и ЭДС как функция положения (c) и времени (e)
Изображение предоставлено Пауло Андре
Обсуждение
Используя рисунок 4 и электронную таблицу, учителя могут обсудить с учащимися следующие вопросы:
Как изменяется магнитный поток по мере приближения магнита к центру катушки? (Увеличивается, а после прохождения центра уменьшается – см. рис. 4б.)
На рисунке 4c что происходит с ЭДС, когда магнит проходит через центр катушки? (Происходит смена знака с отрицательного на положительный.)
На рисунке 4e форма кривой ЭДС симметрична до и после прохождения магнита через центр катушки? (Нет, она асимметрична, потому что магнит находится в свободном падении, поэтому его скорость со временем увеличивается, а скорость изменения магнитного потока и ЭДС индукции также увеличивается со временем. )
Мероприятие 2: индукционная плита
Реальное применение закона Фарадея — приготовление пищи с использованием индукционной плиты, когда посуда нагревается за счет электрической индукции, а не за счет теплопроводности пламени или электрической плиты. Индукционные плиты генерируют тепло внутри самой посуды, что делает этот метод приготовления более эффективным. Однако все кастрюли должны быть изготовлены из ферромагнитного металла (обычно из чугуна или нержавеющей стали).
Индукционная плита имеет катушку, питаемую переменным электрическим током, под керамической пластиной. Переменный ток создает колеблющееся магнитное поле, которое индуцирует колеблющийся магнитный поток в основании кастрюли, поставленной на плиту. Это создает электрический ток (называемый вихревым током) в основании кастрюли, нагревая его.
В индукционных варочных панелях напряженность магнитного поля обычно мала (~100 мТл), но колеблется с высокой частотой (27 кГц). Это означает, что скорость изменения напряженности магнитного поля очень высока, что приводит к высоким значениям индуцированной ЭДС и, следовательно, к производимому нагреву.
В этом упражнении учащиеся исследуют индуцированные ЭДС вокруг индукционной плиты, опять же, используя светодиод, подключенный к катушке.
Материалы
Кухонная индукционная плита
Светодиоды (разные цвета излучения)
Медная проволока диаметром 0,2 мм для изготовления катушки
Карандаш
Бумага
Клейкая лента
Указание по технике безопасности
Хотя индукционная плита не нагревается, посуда и вода нагреваются, поэтому учащиеся должны быть предупреждены, чтобы они не легко сбить во время эксперимента. Следует проявлять особую осторожность, если учащиеся должны выполнять этап пайки самостоятельно, и это следует делать только под пристальным наблюдением учителя.
Процедура
Возьмите карандаш, накройте его листом бумаги (это будет внутренняя часть катушки) и намотайте на него 300–400 витков провода.
Наклейте ленту, чтобы закрыть провод и зафиксируйте его на месте; затем уберите карандаш.
Удалите эмаль с медных проводов на каждом конце катушки.
Припаяйте два светодиода к медным проводам встречно-параллельно (параллельно, но с обратной полярностью друг относительно друга). Этот шаг может выполнять учитель, или ученики могут делать это под наблюдением учителя.
Поставьте кастрюлю с водой в центр индукционной плиты.
Поместите змеевик рядом с поддоном.
Включите варочную панель, начиная с минимальной мощности (рис. 5).
Переместите катушку вдоль близлежащих областей варочной панели. Попробуйте выяснить, какие изменения заставляют светодиод становиться ярче или тусклее.
Рис. 5: Катушка возле индукционной плиты с выключенной (слева) и включенной (справа) плитой
Изображение предоставлено Пауло Андре
Обсуждение
Учителя могут обсудить с учениками следующие вопросы, чтобы изучить ключевые понятия.
Как яркость светодиода зависит от расстояния до варочной панели?
Изменится ли яркость светодиода при повороте катушки в том же положении?
Учащиеся должны обнаружить, что магнитное поле в основном сосредоточено в области посуды, а интенсивность поля быстро уменьшается по мере удаления от варочной панели. Вращение катушки приводит к изменению ЭДС согласно уравнению (2) из-за изменения угла между катушкой и силовой линией магнитного поля.
Благодарности
Эта работа была разработана в рамках проекта CICECO-Aveiro Institute of Materials (UIDB/50011/2020 & UIDP/50011/2020), Instituto de Telecomunicações (UIDB/50008/2020-UIDP/50008/2020). ) и WinLED (POCI-01-0145-FEDER-030351), финансируемых из национальных фондов через FCT/MEC и, при необходимости, совместно финансируемых FEDER в рамках Партнерства PT2020 через Европейский фонд регионального развития (ERDF) в рамках операционной конкурентоспособности и Программа интернационализации (POCI).
Ссылки
[1] Enrique A et al. (2015) Измерение магнитного поля небольших магнитов с помощью смартфона: очень экономичная лабораторная практика для вводных курсов физики. European Journal of Physics 36 :1–11. doi: 10.1088/0143-0807/36/6/065002
[2] Амрани Д. (2005) Электродвижущая сила: закон индукции Фарадея получает трактовку свободного падения магнита. Физическое образование 40 :313–314. дои: 10.1088/0031-9120/40/4/F02
Ресурсы
Узнайте больше об индукционных варочных панелях: https://edisontechcenter.org/InductionCooking.html
Узнайте, как использовать закон Фарадея для создания громкоговорителя: Анта А., Гойри Э. (2018 г.) Волны слуха: как построить громкоговоритель. Наука в школе 45 : 38–42.
Узнайте больше об использовании закона Фарадея в сейсмографах: Bazanos P (2012) Сборка сейсмографа из металлолома. Наука в школе 23: 25–32.
Подробное видео, объясняющее закон Фарадея: https://www.youtube.com/watch?v=zRmfNvTzIhk&ab_channel=PhysicsHigh
Посмотрите забавную демонстрацию закона Фарадея: https://www.youtube.com/watch?v=txmKr69jGBk&amp%3Bab_channel=Veritasium&ab_channel=Veritasium
Автор(ы)
Пауло Андре является профессором телекоммуникационной инженерии Высшего технического института Лиссабонского университета, Португалия.
No related posts.