Иррациональный это: ИРРАЦИОНАЛЬНЫЙ | это… Что такое ИРРАЦИОНАЛЬНЫЙ?

Иррациональное | Понятия и категории

ИРРАЦИОНАЛЬНОЕ — не постигаемое разумом, мышлением, невыразимое в логических понятиях. Понятием «иррациональное» Маркс в «Капитале» обозначает превращенный характер преходящих форм, в которых проявляются при определенных социальных условиях глубинные сущностные связи в экономике, культуре и т. п. В иррационализме иррациональное — это особые противоразумные силы, лежащие в основе человеческого духа и даже самого бытия.

Философский словарь. Под ред. И.Т. Фролова. М., 1991, с. 168.

 

Иррациональное. Я пользуюсь этим понятием не в смысле чего-то противоразумного, а как чего-то, лежащего вне разума, чего-то такого, что на разуме не основано. К этому относятся элементарные факты, как, например, что у Земли есть Луна, что хлор есть элемент, что вода при четырех градусах Цельсия достигает своей наибольшей плотности и т.д. Иррациональна также случайность, хотя впоследствии и можно вскрыть ее разумную причинность.

*

Tags: 

Психология

ИРРАЦИОНАЛИЗМ (лат. irrationalis — неразумное) — в узком смысле — философское течение XIX — начала XX вв., отвергающее разум как единственную основу человеческого бытия. В широком смысле И. — характеристика различных философских концепций, авторы которых существенно ограничивают место разума в мире и в человеческой жизни и предлагают в связи с этим изменить основные способы человеческой познавательной деятельности. Он имеет много оттенков. За И. принимают отсутствие строгой логической выстроенности философского дискурса, использование элементов художественной образности, метафор, многозначность текста, отсутствие авторской позиции как выражения «привилегированной» интерпретации. И. часто называют учение о непознаваемости мира. И. тем самым сближается со скептицизмом и агностицизмом. И. — это также декларирование существования иной логики, отличной от традиционного «бинаризма». Этическая форма И. — признание абсурдности, бессмысленности человеческого существования в нечеловеческом, неразумном мире, безнадежность попыток гармонизации отношений между человеком и миром.

И. может быть также связан с признанием существования в самом человеке противоположных сил, не подчиняющихся единой логике…

Tags: 

Философия

ИРРАЦИОНАЛИЗМ — философское учение, так или иначе ограничивающее возможности разума, логики в познании мира, отвергающее безграничные познавательные возможности человеческого интеллекта. Иррационализм утверждает, что рациональное познание должно дополняться познанием внерациональным, т. е. с помощью чувств, художественных образов, интуиции, инстинктов, тайной символики, религиозных догматов и т. д.

Словарь терминов и понятий по обществознанию. Автор-составитель А.М. Лопухов. 7-е изд. переб. и доп. М., 2013, с. 135.

Tags: 

Философия

ИРРАЦИОНАЛИЗМ [лат. irrationalis — бессознательное, неразумное] — философские течения, провозглашающие примат неразумного начала и делающие его основной характеристикой как самого мира, так и его миропонимания.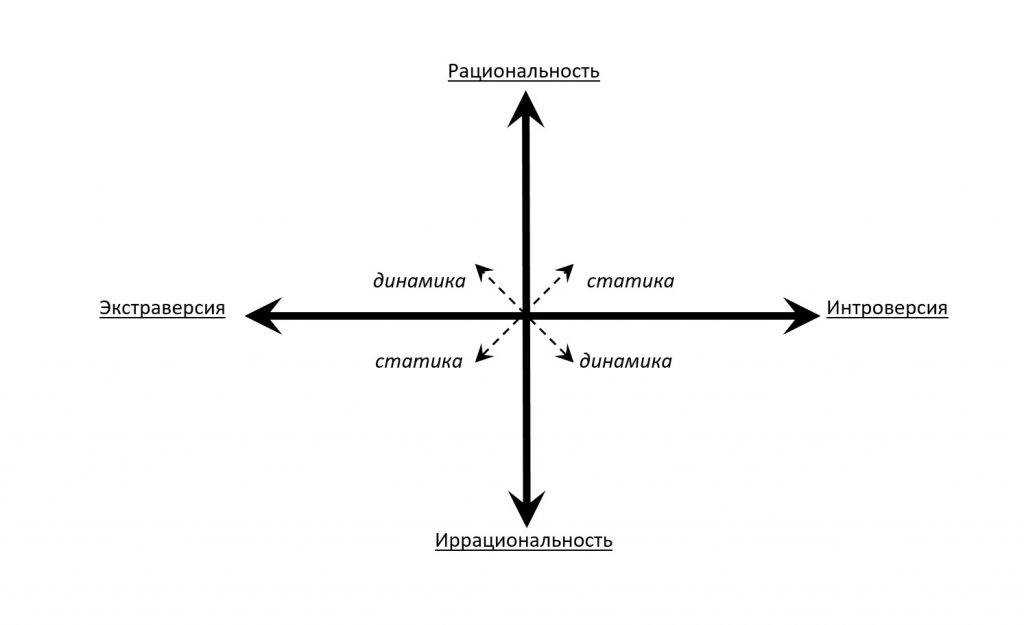 В противоположность философской классике, выдвинувшей на первое место разум и рациональность и поставившей в качестве основной своей цели выявление внутренней логики развития этой рациональности, постклассическая философия знаменует собой отказ от признания разумных оснований действительности и выдвижение на первый план иррационального момента.

Tags: 

Философия

ИРРАЦИОНАЛЬНОЕ (IRRATIONNEL). Не соответствующее научному разуму; то, чего научный разум не может ни познать, ни понять. Если разум всегда прав, как утверждают рационалисты, с которыми я согласен, иррациональное — не более чем иллюзия или переход к крайнему пределу. Мы называем иррациональным (т. е. недоступным теоретическому пониманию) только то, чего не в состоянии практически понять. Следовательно, иррационального не существует. Этого признака достаточно, чтобы отличать иррациональное от неразумного, каковое, напротив, существует в чрезмерном объеме.

Tags: 

Философия

ИРРАЦИОНАЛЬНОЕ (лат. irrationalis — неразумный, бессознательный) — принципиально недоступное рациональному познанию и постижению в рамках логического мышления, лежащее за пределами разума и несоизмеримое с его возможностями, противоположное рациональному. Как философская категория специфична для идеализма и агностицизма, в которых И. понимается как нечто противостоящее разуму, полагающее разум неспособным объять все богатство и разнообразие духовной и материальной действительности; нечто темное, бессознательное, алогичное. И.

Tags: 

Философия

Какие числа называются Иррациональные?

Поможем понять и полюбить математику

Начать учиться

Понятие иррациональности можно встретить в философских учениях, логических концепциях и даже в психологической типологии Карла Юнга. Но нас все-таки интересует математика: что значит иррациональное число и зачем оно нужно.

Определение иррациональных чисел

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры иррациональных чисел:

• π = 3,1415926…
• √2 = 1,41421356…
• e = 2,71828182…
• √8 = 2.828427…
• -√11= -3.31662…

Множество иррациональных чисел договорились обозначать латинской буквой I.

Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Если натуральное число n не является точным квадратом, т. е. n ≠ k², где k ∈ Q, то √n — иррациональное число.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Свойства иррациональных чисел

Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.

Свойства иррациональных чисел:

• результат суммы иррационального числа и рационального равен иррациональному числу;
• результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
• результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
• результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Определение рациональных чисел

А теперь наоборот: рассмотрим противоположное заданной теме определение.

Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.

Рациональные числа —  это те, которые можно представить в виде:

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел

принято обозначать латинской буквой Q.

Примеры рациональных чисел:

• десятичная дробь 1,15 — это 115/100;
• десятичная дробь 0,2 — это 1/5;
• целое число 0 — это 0/1;
• целое число 6 — это 6/1;
• целое число 1 — это 1/1;
• бесконечная периодическая дробь 0,33333. .. — это 1/3;
• смешанное число это 25/10;
• отрицательная десятичная дробь -3,16 — это -316/100.

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами Переместительное свойство сложения: a + b = b + a. Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

128.1K

Какие числа называются целыми

К следующей статье

132.1K

Что такое функция?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Это иррационально?

Здесь мы смотрим, является ли квадратный корень иррациональным. .. или нет!

Рациональные числа

«Рациональное» число может быть записано как «отношение» или дробь.

Пример: 1,5 является рациональным, поскольку его можно записать как отношение 3/2

Пример: 7 рационально, потому что его можно записать как отношение 7/1

Пример 0,317 является рациональным, поскольку его можно записать в виде отношения 317/1000

Но некоторые числа нельзя записать в виде отношения !

Их называют иррациональными (что означает «неразумные» вместо «сумасшедшие!»)

Квадратный корень из 2

Квадратный корень из 2 равен иррациональным . Откуда мне знать? Поясню…

 

Возведение в квадрат рационального числа

Во-первых, давайте посмотрим, что произойдет, если возвести в квадрат рациональное число:

Если рациональное число равно a/b, то при возведении в квадрат оно становится ² /b ² .

Пример:

( 3 4 ) ² = 3 ² 4 ²

0

Обратите внимание, что показатель степени равен 2 , что является четным числом .

Но чтобы сделать это правильно, мы действительно должны разбить числа на их простые множители (любое целое число больше 1 является простым или может быть получено путем умножения простых чисел):

Example:

( 3 4 ) ² = ( 3 2×2 ) ² = 3 ² 2 ⁴

Обратите внимание, что показатели степени по-прежнему являются четными числами. Число 3 имеет показатель степени 2 (3 ² ), а число 2 имеет показатель степени 4 (2 ⁴ ).

В некоторых случаях нам может понадобиться упростить дробь:

Пример: (

16 90 ) ²

Сначала: 16 = 2×2×2×2 = 2 ⁴ , и 90 = 2×3×3×5 = 2×3 ² × 5

5 7 ( 1 6 8 90 ) ² = ( 2 ⁴ 2×3 ² ×5 ) ²

= ( 2 ³ 3 ² ×5 ) ²

= 2 ⁶ 3 ⁴ ×5 ²

Но одно становится очевидным: каждый показатель степени равен 9. 0009 четное число !

Итак, мы видим, что когда мы возводим в квадрат рациональное число, результат состоит из простых чисел, все степени которых равны даже числам.

Когда мы возводим в квадрат рациональное число, каждый простой множитель имеет четный показатель степени .

 

Назад к 2

Теперь давайте посмотрим на число 2: могло ли оно получиться путем возведения в квадрат рационального числа?

В виде дроби 2 равно

2 1

Что равно 2 ¹ 1 ¹ с нечетными показателями !

Но нам нужно четных показателей степени (чтобы его квадратный корень был рациональным)

Мы могли бы записать 1 как 1 ² (чтобы у него был четный показатель степени), и тогда мы имеем:

2 = 2 ¹ 1 ²

Но есть еще нечетный показатель (на 2).

Мы можем упростить все это до 2 ¹ , но это все равно нечетный показатель.

Мы могли бы попробовать что-то вроде 2 = 4 2 = 2 ² 2 ¹ , но мы все еще не можем избавиться от нечетной экспоненты.

О нет, всегда есть нечетных показателей.

 

Таким образом, возведением рационального числа в квадрат можно было бы получить 2 , а не !

Значит, его квадратный корень должен быть иррациональным.

Другими словами: любое значение, которое было возведено в квадрат для получения 2 (т.е. квадратный корень из 2 ), не может быть рациональным числом, поэтому должно быть иррациональным .

Примечание. Еще одно доказательство см. в Доказательстве Евклида о том, что квадратный корень из 2 иррационален.

 

Попробуйте еще несколько номеров

Как насчет квадратного корня из 3?

3 равно 3/1 = 3 ¹

Но число 3 имеет показатель степени 1, поэтому число 3 также нельзя было получить путем возведения в квадрат рационального числа.

Квадратный корень из 3 иррационален

Как насчет квадратного корня из 4?

4 равно 4/1 = 2 ²

Да! Показатель степени — четное число! Таким образом, 4 можно получить, возведя в квадрат рациональное число.

Квадратный корень из 4 равен рациональному

Эту идею также можно распространить на кубические корни и т. д.

Заключение

Чтобы определить, является ли квадратный корень числа иррациональным или нет, проверьте, все ли его простые делители имеют четные степени .

Это также показывает нам, что должно быть иррациональными числами (такими как квадратный корень из двух) … на случай, если мы когда-либо сомневались в этом!

 

Иррациональное определение и значение — Merriam-Webster

1 из 2

нерациональный и-ра-ш(ə-)нəл

ˌi(r)-

: не рационально: например,

а(1)

: отсутствие обычной или нормальной ясности ума или связности

(2)

: не наделенный разумом или пониманием

б

: не регулируется или в соответствии с причиной

иррациональные страхи

с Греческая и латинская просодия

(1)

слога : количество, отличное от требуемого счетчиком

(2)

фута : , содержащий такой слог

д(1)

: — иррациональное число

иррациональный корень уравнения

(2)

: числовое значение, являющееся иррациональным числом

иррациональная длина

иррациональность

i-ˌra-shə-na-lə-tē

ˌi(r)-

существительное

иррационально

и-ра-ш(ə-)нə-лē

ˌi(r)-

наречие

иррациональный

2 из 2

1

: иррациональное существо

2

: иррациональное число

незаконнорожденный

нелогично

непоследовательный

несущественный

неверный

нерациональный

необоснованный

необоснованный

несостоятельный

weak

Просмотреть все синонимы и антонимы в тезаурусе 

Примеры предложений

Прилагательное Он стал иррациональным , когда лихорадка усилилась. У нее было иррациональный боязнь кошек.

Последние примеры в Интернете

Все числа иррациональные . — ПРОВОДНАЯ , 9 февраля 2023 г. Это иррациональное , Путин никогда бы этого не сделал. — CBS News , 4 января 2023 г. Мой жених сказал, что это иррациональное . — Эми Дикинсон, , Кливленд, , 8 декабря 2022 г. Мой жених сказал, что это иррациональное . — Эми Дикинсон, Washington Post , 8 декабря 2022 г. Мой жених сказал, что это иррациональное . — Эми Дикинсон, 9 лет.0057 Чикаго Трибьюн , 8 декабря 2022 г. Некоторые страхи иррациональны , но другие коренятся в реальности. — Бонни Лоу-крамен, Кварц , 14 марта 2023 г. Выбор разных команд для победы в одной и той же игре в разных пулах не является иррациональным . — Виктор Мазер, New York Times , 13 марта 2023 г. Эти страхи могли быть иррационально , учитывая уникальные обстоятельства, способствовавшие краху SVB. — Джефф Стейн, Anchorage Daily News , 13 марта 2023 г.

Но склепаное человечество безнадежно пристрастилось к иррациональное , с достоверно катастрофическими результатами, по всей планете.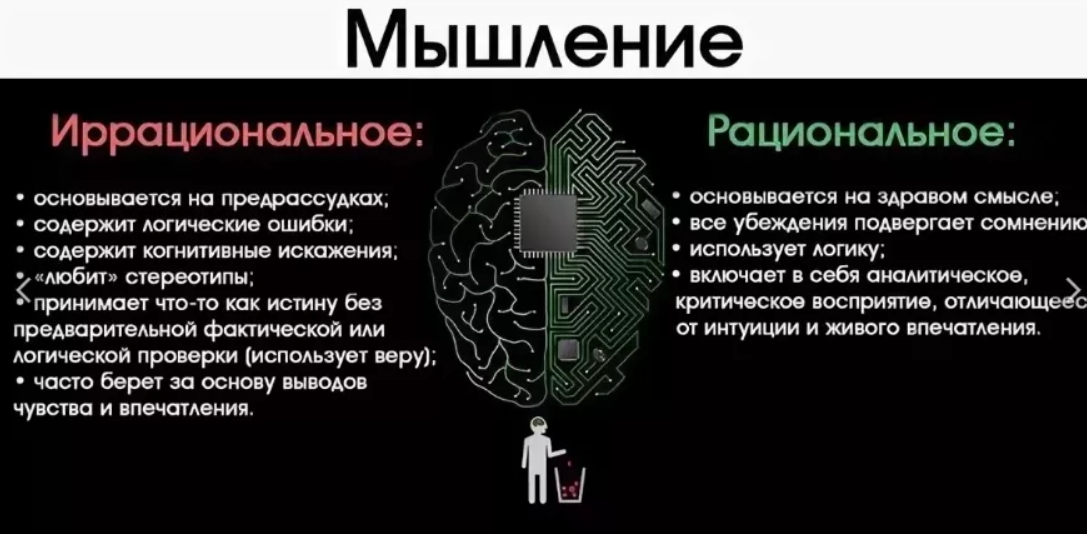 — Элисон Фишберн, Longreads , 17 сентября 2022 г. После приобретения AirTerra и Quiet Logistics в 2021 году AEO, казалось, сделала иррациональных , введя в действие мощности и возможности, которые значительно превышали ее собственный спрос на товары. — Найл Мерфи, Forbes , 17 июня 2022 г. Моральная, социальная и эпистемологическая пустота, в которой оказались немцы после поражения, была заполнена, по крайней мере на время, к иррациональный . — Ричард Дж. Эванс, Новая Республика, , 1 декабря 2021 г. Таким образом, любая попытка объяснить это рано или поздно натолкнется на стену иррационального . — Фил Клей, Harper’s Magazine , 23 ноября 2021 г. Но чувство беспокойства прямо сейчас вовсе не является излишним или иррациональным . — Джессика Дулонг, 9 лет.0057 CNN , 31 августа 2021 г. Попытка умиротворить самых громких в ущерб сообществу только ободряет иррациональных и заставляет замолчать тех, кто хочет вести продуктивную беседу. — Бенджамин Аянян, Star Tribune , 5 мая 2021 г. Вера в возвращение давно умершего ребенка отражает страдание верующего и, конечно же, склонность принять иррациональный . — Дороти Рабиновиц, WSJ , 29 апреля 2021 г. Все мы руководствуемся смесью рационального и иррационального . — Кристофер Беха, Harpers Magazine , 5 января 2021 г. Узнать больше

Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «иррациональный». Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.

История слов

Этимология

Прилагательное

Среднеанглийский, от латинского irrationalis , из in + Rationalis Rational

Первое известное использование

Прилагательное

14-й век, в значении, определенном выше

SUNOUN

1646, в значении, определенном в смысле 1

Time Travelser

1646, в значении, определено в смысле 1

Time.

1646. Первое известное использование иррационального было в 14 веке

Посмотреть другие слова из того же века

Словарные статьи Около

иррациональный

иррациональный

иррациональный

иррационализм

Посмотреть другие записи поблизости

Процитировать эту запись «Иррациональный».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/irrational. По состоянию на 18 апреля 2023 г.

Копировать цитату

Детское определение

иррациональное

прилагательное

нерациональный

(ˈ)ir-ˈ(r)ash-nəl,

-ən-ᵊl

1

: не в состоянии рассуждать

неразумный звери

неразумный от лихорадки

2

: не по причине

иррациональный страх

3

: — иррациональное число.

No related posts.