margin — CSS | MDN
CSS свойство margin определяет внешний отступ на всех четырёх сторонах элемента. Это сокращение, которое устанавливает все отдельные поля одновременно: margin-top, margin-right, margin-bottom и margin-left.
Данное свойство является сокращением для следующих CSS свойств:
margin-topmargin-rightmargin-bottommargin-left
/* Применяется ко всем четырём сторонам */ margin: 1em; margin: -3px; /* по вертикали | по горизонтали */ margin: 5% auto; /* сверху | горизонтально | снизу */ margin: 1em auto 2em; /* сверху | справа | снизу | слева */ margin: 2px 1em 0 auto; /* Глобальные значения */ margin: inherit; margin: initial; margin: unset;
Свойство margin может быть задано с использованием одного, двух, трёх или четырёх значений. Каждое значение имеет тип <length>
<percentage> или является ключевым словом auto. Каждое значение может быть положительным, отрицательным или равным нулю.
Каждое значение может быть положительным, отрицательным или равным нулю.- Когда определено одно значение, такое значение определено для всех четырёх сторон.
- Когда определены два значения, то первое значение определяет внешний отступ для верхней и нижней стороны, а второе значение определяет отступ для левой и правой стороны.
- Когда определены три значение, то первое значение определяет внешний отступ для верхней стороны, второе значение определяет внешний отступ для левой и правой стороны, а третье значение определяет отступ для нижней стороны.
- Когда определены четыре значения, они определяют внешние отступы для верхней стороны, справа, снизу и слева в рассмотренном порядке (по часовой стрелке).
Значения
lengthРазмер отступа как фиксированное значение.

percentageРазмер отступа в процентах относительно ширины родительского блока.
autoБраузер выбирает подходящее значение для использования. Например, в некоторых случаях это значение может быть использовано для центрирования элемента.
| Начальное значение | как и у каждого из подсвойств этого свойства:
|
|---|---|
| Применяется к | все элементы, кроме элементов с табличным типом display, отличным от table-caption, table и inline-table. Это также применяется к ::first-letter и ::first-line. |
| Наследуется | нет |
| Проценты | ссылается на ширину содержащего блока |
| Обработка значения | как и у каждого из подсвойств этого свойства:
|
| Animation type | длина |
margin =
<'margin-top'>{1,4} (en-US)
Простой пример
HTML
<div>Этот элемент отцентрирован.</div> <div>Этот элемент расположен за пределами своего контейнера.</div>
CSS
.center {
margin: auto;
background: lime;
width: 66%;
}
.outside {
margin: 3rem 0 0 -3rem;
background: cyan;
width: 66%;
}
Больше примеров
margin: 5%; /* все стороны: отступ 5% */
margin: 10px; /* все стороны: отступ 10px */
margin: 1.6em 20px; /* верх и низ: отступ 1.6em */
/* право и лево: отступ 20px */
margin: 10px 3% 1em; /* верх: отступ 10px */
/* право и лево: отступ 3% */
/* низ: отступ 1em */
margin: 10px 3px 30px 5px; /* верх: отступ 10px */
/* право: отступ 3px */
/* низ: отступ 30px */
/* лево: отступ 5px */
margin: 2em auto; /* верх и низ: отступ 2em */
/* блок отцентрирован горизонтально */
margin: auto; /* верх и низ: отступ 0 */
/* блок отцентрирован горизонтально */
Горизонтальное выравнивание
Чтобы центрировать что-то горизонтально в современных браузерах, вы можете использовать display: flex; justify-content: center; .
Однако в старых браузерах, таких как IE8-9, которые не поддерживают технологию Flexible Box, они недоступны. Чтобы центрировать элемент внутри своего родителя, используйте margin: 0 auto; .
Схлопывание отступов
Иногда внешние отступы (margins) для верхней и нижней сторон схлопываются в один отступ, который равен наибольшему из двух отступов. Смотри Схлопывание внешних отступов для получения большей информации.
| Specification |
|---|
| CSS Box Model Module Level 3 # margin |
BCD tables only load in the browser
with JavaScript enabled. Enable JavaScript to view data.- Введение в базовую блочную модель CSS
- Схлопывание отступов
margin-top,margin-right,margin-bottomиmargin-left- Логические свойства:
margin-block-start(en-US),margin-block-end(en-US),margin-inline-startиmargin-inline-end. А так же сокращенные варианты:
А так же сокращенные варианты: margin-block(en-US) иmargin-inline(en-US)
Found a content problem with this page?
- Edit the page on GitHub.
- Report the content issue.
- View the source on GitHub.
Want to get more involved? Learn
how to contribute.
This page was last modified on by MDN contributors.
Вращение и отражение объектов в Illustrator
Руководство пользователя Отмена
Поиск
Последнее обновление Nov 15, 2022 09:23:56 AM GMT
- Руководство пользователя Illustrator
- Основы работы с Illustrator
- Введение в Illustrator
- Новые возможности в приложении Illustrator
- Часто задаваемые вопросы
- Системные требования Illustrator
- Illustrator для Apple Silicon
- Рабочая среда
- Основные сведения о рабочей среде
- Ускоренное обучение благодаря панели «Поиск» в Illustrator
- Создание документов
- Панель инструментов
- Комбинации клавиш по умолчанию
- Настройка комбинаций клавиш
- Общие сведения о монтажных областях
- Управление монтажными областями
- Настройка рабочей среды
- Панель свойств
- Установка параметров
- Рабочая среда «Сенсорное управление»
- Поддержка Microsoft Surface Dial в Illustrator
- Отмена изменений и управление историей дизайна
- Повернуть вид
- Линейки, сетки и направляющие
- Специальные возможности в Illustrator
- Безопасный режим
- Просмотр графических объектов
- Работа в Illustrator с использованием Touch Bar
- Файлы и шаблоны
- Инструменты в Illustrator
- Краткий обзор инструментов
- Выбор инструментов
- Выделение
- Частичное выделение
- Групповое выделение
- Волшебная палочка
- Лассо
- Монтажная область
- Выделение
- Инструменты для навигации
- Рука
- Повернуть вид
- Масштаб
- Инструменты рисования
- Градиент
- Сетка
- Создание фигур
- Градиент
- Текстовые инструменты
- Текст
- Текст по контуру
- Текст по вертикали
- Текст
- Инструменты рисования
- Перо
- Добавить опорную точку
- Удалить опорные точки
- Опорная точка
- Кривизна
- Отрезок линии
- Прямоугольник
- Прямоугольник со скругленными углами
- Эллипс
- Многоугольник
- Звезда
- Кисть
- Кисть-клякса
- Карандаш
- Формирователь
- Фрагмент
- Инструменты модификации
- Поворот
- Отражение
- Масштаб
- Искривление
- Ширина
- Свободное трансформирование
- Пипетка
- Смешать
- Ластик
- Ножницы
- Быстрые действия
- Ретротекст
- Светящийся неоновый текст
- Старомодный текст
- Перекрашивание
- Преобразование эскиза в векторный формат
- Введение в Illustrator
- Illustrator на iPad
- Представляем Illustrator на iPad
- Обзор по Illustrator на iPad.

- Ответы на часто задаваемые вопросы по Illustrator на iPad
- Системные требования | Illustrator на iPad
- Что можно и нельзя делать в Illustrator на iPad
- Обзор по Illustrator на iPad.
- Рабочая среда
- Рабочая среда Illustrator на iPad
- Сенсорные ярлыки и жесты
- Комбинации клавиш для Illustrator на iPad
- Управление настройками приложения
- Документы
- Работа с документами в Illustrator на iPad
- Импорт документов Photoshop и Fresco
- Выбор и упорядочение объектов
- Создание повторяющихся объектов
- Объекты с переходами
- Рисование
- Создание и изменение контуров
- Рисование и редактирование фигур
- Текст
- Работа с текстом и шрифтами
- Создание текстовых надписей по контуру
- Добавление собственных шрифтов
- Работа с изображениями
- Векторизация растровых изображений
- Цвет
- Применение цветов и градиентов
- Представляем Illustrator на iPad
- Облачные документы
- Основы работы
- Работа с облачными документами Illustrator
- Общий доступ к облачным документам Illustrator и совместная работа над ними
- Публикация документов для проверки
- Обновление облачного хранилища для Adobe Illustrator
- Облачные документы в Illustrator | Часто задаваемые вопросы
- Устранение неполадок
- Устранение неполадок с созданием или сохранением облачных документов в Illustrator
- Устранение неполадок с облачными документами в Illustrator
- Основы работы
- Добавление и редактирование содержимого
- Рисование
- Основы рисования
- Редактирование контуров
- Рисование графического объекта с точностью на уровне пикселов
- Рисование с помощью инструментов «Перо», «Кривизна» и «Карандаш»
- Рисование простых линий и фигур
- Трассировка изображения
- Упрощение контура
- Определение сеток перспективы
- Инструменты для работы с символами и наборы символов
- Корректировка сегментов контура
- Создание цветка в пять простых шагов
- Рисование перспективы
- Символы
- Рисование контуров, выровненных по пикселам, при создании проектов для Интернета
- 3D-объекты и материалы
- Подробнее о 3D-эффектах в Illustrator
- Создание трехмерной графики
- Проецирование рисунка на трехмерные объекты
- Создание трехмерного текста
- Подробнее о 3D-эффектах в Illustrator
- Цвет
- О цвете
- Выбор цветов
- Использование и создание цветовых образцов
- Коррекция цвета
- Панель «Темы Adobe Color»
- Цветовые группы (гармонии)
- Панель «Темы Color»
- Перекрашивание графического объекта
- Раскрашивание
- О раскрашивании
- Раскрашивание с помощью заливок и обводок
- Группы с быстрой заливкой
- Градиенты
- Кисти
- Прозрачность и режимы наложения
- Применение обводок к объектам
- Создание и редактирование узоров
- Сетки
- Узоры
- Выбор и упорядочение объектов
- Выделение объектов
- Слои
- Группировка и разбор объектов
- Перемещение, выравнивание и распределение объектов
- Размещение объектов
- Блокировка, скрытие и удаление объектов
- Копирование и дублирование объектов
- Поворот и отражение объектов
- Переплетение объектов
- Перерисовка объектов
- Кадрирование изображений
- Трансформирование объектов
- Объединение объектов
- Вырезание, разделение и обрезка объектов
- Марионеточная деформация
- Масштабирование, наклон и искажение объектов
- Объекты с переходами
- Перерисовка с помощью оболочек
- Перерисовка объектов с эффектами
- Создание фигур с помощью инструментов «Мастер фигур» и «Создание фигур»
- Работа с динамическими углами
- Улучшенные процессы перерисовки с поддержкой сенсорного ввода
- Редактирование обтравочных масок
- Динамические фигуры
- Создание фигур с помощью инструмента «Создание фигур»
- Глобальное изменение
- Текст
- Дополнение текстовых и рабочих объектов типами объектов
- Создание маркированного и нумерованного списков
- Управление текстовой областью
- Шрифты и оформление
- Форматирование текста
- Импорт и экспорт текста
- Форматирование абзацев
- Специальные символы
- Создание текста по контуру
- Стили символов и абзацев
- Табуляция
- Текст и шрифты
- Поиск отсутствующих шрифтов (технологический процесс Typekit)
- Обновление текста из Illustrator 10
- Шрифт для арабского языка и иврита
- Шрифты | Часто задаваемые вопросы и советы по устранению проблем
- Создание эффекта 3D-текста
- Творческий подход к оформлению
- Масштабирование и поворот текста
- Интерлиньяж и межбуквенные интервалы
- Расстановка переносов и переходы на новую строку
- Усовершенствования работы с текстом
- Проверка орфографии и языковые словари
- Форматирование азиатских символов
- Компоновщики для азиатской письменности
- Создание текстовых проектов с переходами между объектами
- Создание текстового плаката с помощью трассировки изображения
- Создание специальных эффектов
- Работа с эффектами
- Стили графики
- Создание тени
- Атрибуты оформления
- Создание эскизов и мозаики
- Тени, свечения и растушевка
- Обзор эффектов
- Веб-графика
- Лучшие методы создания веб-графики
- Диаграммы
- SVG
- Создание анимации
- Фрагменты и карты изображений
- Рисование
- Импорт, экспорт и сохранение
- Импорт
- Помещение нескольких файлов в документ
- Управление связанными и встроенными файлами
- Сведения о связях
- Извлечение изображений
- Импорт графического объекта из Photoshop
- Импорт растровых изображений
- Импорт файлов Adobe PDF
- Импорт файлов EPS, DCS и AutoCAD
- Библиотеки Creative Cloud Libraries в Illustrator
- Библиотеки Creative Cloud Libraries в Illustrator
- Диалоговое окно «Сохранить»
- Сохранение иллюстраций
- Экспорт
- Использование графического объекта Illustrator в Photoshop
- Экспорт иллюстрации
- Сбор ресурсов и их массовый экспорт
- Упаковка файлов
- Создание файлов Adobe PDF
- Извлечение CSS | Illustrator CC
- Параметры Adobe PDF
- Информация о файле и метаданные
- Импорт
- Печать
- Подготовка к печати
- Настройка документов для печати
- Изменение размера и ориентации страницы
- Задание меток обреза для обрезки и выравнивания
- Начало работы с большим холстом
- Печать
- Наложение
- Печать с управлением цветами
- Печать PostScript
- Стили печати
- Метки и выпуск за обрез
- Печать и сохранение прозрачных графических объектов
- Треппинг
- Печать цветоделенных форм
- Печать градиентов, сеток и наложения цветов
- Наложение белого
- Подготовка к печати
- Автоматизация задач
- Объединение данных с помощью панели «Переменные»
- Автоматизация с использованием сценариев
- Автоматизация с использованием операций
- Устранение неполадок
- Проблемы с аварийным завершением работы
- Восстановление файлов после сбоя
- Проблемы с файлами
- Поддерживаемые форматы файлов
- Проблемы с драйвером ГП
- Проблемы устройств Wacom
- Проблемы с файлами DLL
- Проблемы с памятью
- Проблемы с файлом настроек
- Проблемы со шрифтами
- Проблемы с принтером
- Как поделиться отчетом о сбое с Adobe
- Повышение производительности Illustrator
Поворот объектов
При повороте объект вращается вокруг указанной фиксированной точки. По умолчанию контрольной точкой является центр объекта. Если выделено несколько объектов, эти объекты будут вращаться вокруг единой контрольной точки, которая по умолчанию является центром выделенного фрагмента или ограничительной рамки. Чтобы повернуть каждый объект вокруг его собственной центральной точки, используйте команду «Трансформировать каждый».
По умолчанию контрольной точкой является центр объекта. Если выделено несколько объектов, эти объекты будут вращаться вокруг единой контрольной точки, которая по умолчанию является центром выделенного фрагмента или ограничительной рамки. Чтобы повернуть каждый объект вокруг его собственной центральной точки, используйте команду «Трансформировать каждый».
Поворот объекта с помощью ограничительной рамки
Выделите один или несколько объектов.
С помощью инструмента «Выделение» переместите указатель за пределы ограничительной рамки рядом с ее маркером, чтобы он принял вид , а затем перетащите его.
Поворот объекта с помощью инструмента «Свободное трансформирование»
Выделите один или несколько объектов.
Выберите инструмент «Свободное трансформирование» .
Поместите курсор снаружи ограничительной рамки, чтобы он принял вид , а затем перетащите его.

Поворот объекта с помощью инструмента «Поворот»
Выделите один или несколько объектов.
Выберите инструмент «Поворот» .
Выполните любое из следующих действий:
Для поворота объекта вокруг его центра перетащите курсор по кругу в окне документа.
Для поворота объекта вокруг другой контрольной точки один раз щелкните в любом месте окна документа, чтобы переместить контрольную точку. Затем переместите курсор в другое место от контрольной точки и перетащите его вращательным движением.
Для поворота копии объекта, а не самого объекта держите нажатой клавишу «Alt» (в Windows) или «Option» (в Mac OS) после начала перетаскивания.
Для более точного управления перетащите курсор дальше от контрольной точки объекта.
Поворот объекта на определенный угол
С помощью команды «Поворот» можно определять точный угол поворота.
Выделите один или несколько объектов.
Выполните одно из действий, описанных ниже.
Для поворота вокруг другой контрольной точки выберите инструмент «Поворот». Затем с нажатой клавишей «Alt» (в Windows) или «Option» (в Mac OS) щелкните в том месте окна документа, где должна быть контрольная точка.
Для поворота вокруг центральной точки выберите команду «Объект» > «Трансформировать» > «Поворот» или дважды щелкните инструмент «Поворот».
Введите угол поворота в текстовом поле «Угол». Для поворота объекта по часовой стрелке введите отрицательное значение, а для поворота против часовой стрелки — положительное.
Если объекты содержат узорную заливку, выберите параметр «Узоры», чтобы повернуть узор. Отмените выделение объектов, если нужно повернуть узор, а не объекты.
Нажмите кнопку «ОК» или «Копировать», чтобы повернуть копию объектов.
Чтобы разместить несколько копий объекта вокруг контрольной точки, переместите контрольную точку из центра объекта в другое место, щелкните «Копировать», а затем последовательно выбирайте команду «Объект» > «Трансформировать» > «Повторить трансформирование».

Поворот объекта с помощью палитры «Трансформирование»
Выделите один или несколько объектов.
Выполните одно из действий, описанных ниже.
Для поворота объекта вокруг его центра, введите значение параметра «Угол» в палитре.
Для поворота объекта вокруг другой контрольной точки щелкните белый квадрат на локаторе контрольной точки в палитре и введите значение параметра «Угол».
Совет. Можно также вызвать палитру «Трансформирование» щелкнув «X», «Y», «Ш» или «В» на панели «Управление».
С помощью палитры «Трансформирование» можно поворачивать символ вокруг точки регистрации. Дополнительные сведения см. в разделе Точка регистрации символа.
Поворот нескольких объектов по отдельности
Выберите объекты, которые нужно повернуть.
Выберите команду «Объект» > «Трансформировать» > «Трансформировать каждый».

Выполните любое из следующих действий в области «Поворот» диалогового окна.
Нажмите кнопку «ОК» или «Копировать», чтобы повернуть копию каждого объекта.
Поворот осей X и Y документа
По умолчанию оси X и Y параллельны горизонтальной и вертикальной сторонам окна документа.
Выберите «Редактирование» > «Установки» > «Основные» (в Windows) или «Illustrator» > «Установки» > «Основные» (в Mac OS).
Укажите угол в текстовом поле «Угол поворота». При положительном значении угла выполняется поворот осей против часовой стрелки, а при отрицательном — по часовой стрелке.
Поворот осей может быть полезен, если изображение состоит из элементов, повернутых на один и тот же угол, например когда логотип и текст повернуты на 20°. Вместо поворота каждого элемента, добавляемого в логотип, можно просто повернуть оси на 20°. Все элементы рисунка будут располагаться вдоль новых осей.
Объект, выровненный по осям по умолчанию (слева) и по осям, повернутым на 20° (справа)
Новые оси не влияют на следующие объекты и действия.
Отражение или зеркальное отображение объектов
Отражение — это зеркальное отображение объекта вдоль заданной невидимой оси. Объекты можно отразить с помощью инструмента «Свободное трансформирование», инструмента «Зеркальное отражение» или команды «Зеркальное отражение». Для указания оси отражения используйте инструмент «Зеркальное отражение».
Чтобы создать зеркальную копию объекта, можно скопировать его одновременно с созданием зеркального отражения.
Отражение объекта с помощью инструмента «Свободное трансформирование»
Выберите объект, который нужно зеркально отразить.
Выберите инструмент «Свободное трансформирование» .
Выполните одно из следующих действий:
Перетащите маркер ограничительной рамки через противоположный край или маркер, пока отражение объекта не достигнет нужного уровня.

Для сохранения пропорций объекта держите нажатой клавишу «Shift» при перетаскивании углового маркера через противоположный маркер.
Отражение объекта с помощью инструмента «Зеркальное отражение»
Выделите объект.
Выберите инструмент «Зеркальное отражение» .
Чтобы нарисовать невидимую ось, относительно которой будет создано зеркальное отражение объекта, щелкните в любом месте окна документа, чтобы задать одну точку оси. Курсор примет форму стрелки.
Наведите курсор на другую точку, чтобы определить невидимую ось, и выполните одно из следующих действий:
Щелкните, чтобы задать одну точку оси (слева), затем щелкните еще раз, чтобы задать вторую точку оси и зеркально отразить объект относительно этой оси (справа).Чтобы зеркально отразить копию объекта, нажмите клавишу «Alt» (в Windows) или «Option» (в Mac OS) и, не отпуская ее, щелкните мышью, чтобы задать вторую точку невидимой оси.

Настройте ось отражения перетаскиванием, а не щелчком мыши. С нажатой клавишей «Shift» перетащите курсор, чтобы зафиксировать угол 45°. Во время перетаскивания курсора невидимая ось отражения поворачивается вокруг точки, заданной в шаге 3, и контур объекта оказывается зеркально отраженным. Когда контур окажется в нужной позиции, отпустите кнопку мыши.
Для более точного управления перетащите курсор дальше от контрольной точки объекта.
Зеркальное отражение путем указания оси
Выберите объект, который нужно зеркально отразить.
Чтобы отразить объект относительно его центральной точки, выберите команду «Объект» > «Трансформировать» > «Зеркальное отражение» или дважды щелкните инструмент «Зеркальное отражение» .
Чтобы отразить объект относительно другой контрольной точки, с нажатой клавишей «Alt» (в Windows) или «Option» (в Mac OS) щелкните в любом месте окна документа.

В диалоговом окне «Зеркальное отражение» выберите ось, относительно которой нужно отразить объект. Можно отразить объект относительно горизонтальной, вертикальной оси или оси, проходящей под углом.
Если объект содержит узоры, которые нужно отразить, выберите параметр «Узоры» (чтобы зеркально отразить только узоры, выключите параметр «Объекты»).
Чтобы оценить результаты эффекта до его применения, установите флажок «Просмотр».
Выполните одно из следующих действий:
Чтобы зеркально отразить объект, нажмите кнопку «ОК».
Чтобы зеркально отразить копию объекта, нажмите кнопку «Скопировать».
Вы можете включить функцию рисования и редактирования в реальном времени, чтобы улучшить живой внешний вид объектов при работе с ними. Чтобы включить эту функцию, выполните следующие действия:
[Windows] Выберите Правка > Установки > Производительность > Рисование и редактирование в реальном времени.
[macOS] Выберите Illustrator > Установки > Производительность > Рисование и редактирование в реальном времени.
Связанные материалы
- Обзор палитры «Трансформирование»
- Перемещение объектов
- Масштабирование объектов
Вход в учетную запись
Войти
Управление учетной записью
Урок Видео: Вертикальные и горизонтальные линии
Стенограмма видео
Вертикальные и горизонтальные линии
В этом видео мы будем учиться как описать и определить горизонтальные и вертикальные линии.
Секундочку! Это не похоже на математику
видео, все о линиях. Это из тех, что сделай сам
видео. Как поставить полку в
минута. Что ж, продолжим просмотр. Возможно, мы чему-то научимся. Для изготовления полки вам понадобится
несколько маленьких кусочков дерева, из которых можно сделать кронштейны, гораздо более длинный кусок дерева для
сама полка, все нужные инструменты для ее установки и красивая ваза с
цветы, чтобы положить на него, как только он будет готов.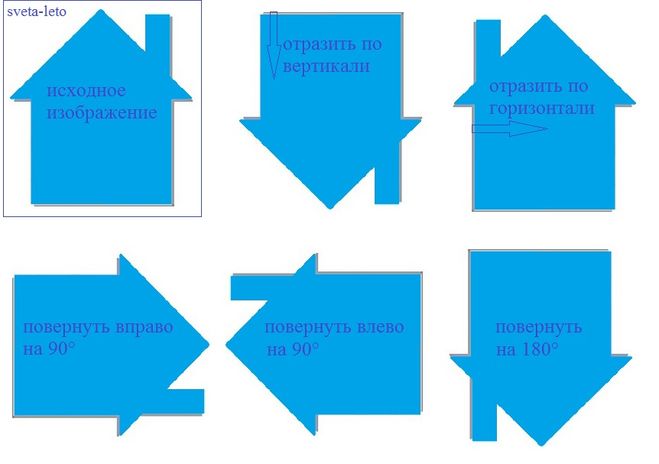
Шаг первый: прикрепите кронштейны к стена, раз, два. Они выглядят правильно, не они? Шаг второй, сбалансируйте полку на кронштейны. Это сработает. Шаг третий, поместите действительно дорогая ваза с цветами прямо на конце нашего — о, у нас есть что-то вроде проблема. Эта полка никуда не годится. Как вы думаете, какую ошибку мы сделал? Ну, чтобы полка могла правильно сбалансировать книги или тарелки или действительно дорогие вазы с цветами, это не может быть наклонен или наклонен каким-либо образом. И если мы посмотрим на эту полку, это слева выше, чем справа. Наверняка есть уклон это. И вот что сделало нашу вазу из цветы опадают.
Мы должны были убедиться, что начали
при том, что те кронштейны, которые мы прикрепили к стене, были идеально на одном уровне друг с другом.
другой. Мы хотим, чтобы линия между ними была
ровно ровно слева направо, не поднимаясь и не опускаясь вообще. И если мы это сделаем, полка будет
быть тем, что мы называем горизонтальным. Нет шансов ни на что
скользить и скользить по этой полке, что ли? Он идеально ровный слева направо
верно; это горизонтально. у нас не очень хорошо получается
Сделай сам, мы?
Мы хотим, чтобы линия между ними была
ровно ровно слева направо, не поднимаясь и не опускаясь вообще. И если мы это сделаем, полка будет
быть тем, что мы называем горизонтальным. Нет шансов ни на что
скользить и скользить по этой полке, что ли? Он идеально ровный слева направо
верно; это горизонтально. у нас не очень хорошо получается
Сделай сам, мы?
Давайте попробуем еще как видео вместо. Привет и добро пожаловать в как поставить забор! Мы собираемся использовать крепкие деревянные столбы для забора, большой молоток, чтобы вбивать их в землю, и катушку. проволока, из которой сделать забор. Хорошо, давайте начнем, должны мы?
Шаг первый: решите, где будет ваш забор
посты пойдут. Шаг второй, начните их стучать,
один два три четыре. Они сделают. И на третьем шаге нам просто нужно
чтобы взять наш моток проволоки и связать его, чтобы сделать хороший прямой забор. Это совсем не так, т.
это? Эти столбы забора ужасны. Мы не можем починить провод к ним. Вы видите ошибку, которую мы
сделал?
Это совсем не так, т.
это? Эти столбы забора ужасны. Мы не можем починить провод к ним. Вы видите ошибку, которую мы
сделал?
Чтобы столбы забора стояли и не упасть, и чтобы мы могли связать проволоку прямо, они не могут быть наклонен или наклонен в сторону каким-либо образом. Когда они были забиты, мы должен был убедиться, что они были идеально прямыми вверх и вниз, идя сверху вниз. дно, не наклоняясь влево или вправо. Они должны были быть тем, что мы называем вертикальный. И если бы мы их исправили вертикально, возможно, проволока, к которой мы привязались, была бы горизонтальной. Похоже, что это видео о горизонтальных и вертикальных линиях все-таки.
Но причина, по которой мы притворялись
было создано своими руками, потому что горизонтальные и вертикальные линии настолько
важно, когда дело доходит до создания вещей. Представим, что вы хотите построить
стена. Возможно, первое, что вы могли бы
ищите хороший, плоский участок земли. Он должен быть идеально ровным от
слева направо. Мы не хотим, чтобы он поднимался или опускался
совсем. Он должен быть горизонтальным. И чтобы на нашей стене не было ни одного
риск падения вообще, мы действительно не хотим, чтобы он был наклонен каким-либо образом. Мы хотим, чтобы он был идеально прямым
вверх и вниз. Он должен быть вертикальным.
Представим, что вы хотите построить
стена. Возможно, первое, что вы могли бы
ищите хороший, плоский участок земли. Он должен быть идеально ровным от
слева направо. Мы не хотим, чтобы он поднимался или опускался
совсем. Он должен быть горизонтальным. И чтобы на нашей стене не было ни одного
риск падения вообще, мы действительно не хотим, чтобы он был наклонен каким-либо образом. Мы хотим, чтобы он был идеально прямым
вверх и вниз. Он должен быть вертикальным.
А вот и кое-что интересное
о нашей вертикальной стене. Посмотрите, что происходит, когда он встречается
горизонтальный грунт. Ты видишь, под каким углом
делает? Это прямой угол, квадрат
угол. Всякий раз, когда вертикальная линия пересекает
горизонтальная линия, они составляют прямой угол. Теперь важно сказать два
вещи здесь. Во-первых, не все прямые углы
из горизонтальных и вертикальных линий. Просто потому, что мы видим прямой угол
не означает, что мы можем посмотреть на образующие его линии и сказать: «О, они горизонтальные».
и вертикально». Но мы можем сказать, что всякий раз, когда
горизонтальная линия встречается с вертикальной линией, она всегда образует прямой угол.
Просто потому, что мы видим прямой угол
не означает, что мы можем посмотреть на образующие его линии и сказать: «О, они горизонтальные».
и вертикально». Но мы можем сказать, что всякий раз, когда
горизонтальная линия встречается с вертикальной линией, она всегда образует прямой угол.
Другое, что важно сказать, что слова «горизонтальный» и «вертикальный» означают не только «прямой». Это прямая линия, но ни по горизонтали, ни по вертикали. Мы даже не можем смотреть прямо линию и назвать ее почти горизонтальной или вертикальной. Это либо есть, либо нет. Мы должны постоянно напоминать себя. Вертикальная линия идеально прямо вверх и вниз. Он идет сверху вниз без наклоняясь влево или вправо. И горизонтальная линия должна быть идеально ровные слева направо без наклона вверх или вниз вообще.
Итак, если мы посмотрим на края
В этом видео мы видим, что оно состоит из двух вертикальных и двух горизонтальных линий. линии. Хотя некоторые строчки в этом
треугольник не является ни горизонтальным, ни вертикальным, мы можем видеть, что его основание
горизонтальный. И эта заглавная буква Т
полностью состоит из горизонтальных и вертикальных линий. Там даже есть строчка
симметрия. И эта линия вертикальна. Есть вертикальные и горизонтальные
линии, куда бы мы ни посмотрели. И, как мы уже видели, один из
лучшее место для начала — это взгляд на здание, потому что без горизонтальных и
вертикальные линии, многие здания просто рухнут.
линии. Хотя некоторые строчки в этом
треугольник не является ни горизонтальным, ни вертикальным, мы можем видеть, что его основание
горизонтальный. И эта заглавная буква Т
полностью состоит из горизонтальных и вертикальных линий. Там даже есть строчка
симметрия. И эта линия вертикальна. Есть вертикальные и горизонтальные
линии, куда бы мы ни посмотрели. И, как мы уже видели, один из
лучшее место для начала — это взгляд на здание, потому что без горизонтальных и
вертикальные линии, многие здания просто рухнут.
Теперь давайте ответим на несколько вопросов где мы должны применить на практике все, что мы только что узнали о горизонтальном и вертикальные линии.
Определить, является ли данная строка горизонтальный, вертикальный или ни тот, ни другой.
В этом вопросе нам дается
линия. Вот. Просто выглядит как обычный прямой
линия. Но нас просят идентифицировать
кое-что об этой линии. Он горизонтальный? Это вертикально? Или это ни один из них? Другими словами, разве это не
горизонтальный или вертикальный? Чтобы правильно ответить на вопрос,
нам нужно действительно понять, что означают слова «горизонтальный» и «вертикальный». Напомним о себе.
Вот. Просто выглядит как обычный прямой
линия. Но нас просят идентифицировать
кое-что об этой линии. Он горизонтальный? Это вертикально? Или это ни один из них? Другими словами, разве это не
горизонтальный или вертикальный? Чтобы правильно ответить на вопрос,
нам нужно действительно понять, что означают слова «горизонтальный» и «вертикальный». Напомним о себе.
Если линия горизонтальна,
идеально ровный слева направо и вообще не наклоняется вверх или вниз. Если бы наша линия была горизонтальной, мы бы
ожидал, что это будет выглядеть так. Теперь, если мы посмотрим на линию, которую мы
учитывая, мы можем видеть, что он наклонен. Если бы это была дорога, и нам пришлось бы
ездить по нему, было бы очень тяжело, совсем по-другому, чем если бы дорожное покрытие
был горизонтальным. Эта линия наклонная или наклонная. Итак, мы знаем, что это не
горизонтальный.
А вертикально? Что мы помним о вертикальном линии? Вертикальная линия идеально прямо вверх и вниз, двигаясь сверху вниз, не наклоняясь ни влево, ни в верно. Если бы наша линия была вертикальной, мы бы ожидайте, что это будет выглядеть так. Но если мы посмотрим на строку, которая нам дано, мы можем видеть, что он вовсе не идет прямо вверх и вниз. Если бы наша линия была стеной дом, он действительно был бы наклонен в сторону. Эта линия не является вертикальной.
Мы использовали наши знания о горизонтальные и вертикальные линии, чтобы посмотреть на эту линию и сказать, что она не горизонтальная или вертикальный; это ни то, ни другое.
Сколько горизонтальных линий в этот многоугольник?
Есть несколько интересных слов в
этот вопрос. Ты помнишь, какое слово
полигон значит? Многоугольник — это просто 2D-форма,
из прямых сторон. Итак, наш вопрос мог быть просто использован
форма слова. И мы знаем имя этого 2D
форму, не так ли? Это прямоугольник. Итак, нас спрашивают, как
сколько горизонтальных линий в этом прямоугольнике?
Итак, наш вопрос мог быть просто использован
форма слова. И мы знаем имя этого 2D
форму, не так ли? Это прямоугольник. Итак, нас спрашивают, как
сколько горизонтальных линий в этом прямоугольнике?
И вы, наверное, видите, сколько линии есть, которые составляют прямоугольник. В прямоугольнике четыре прямых стороны, не так ли? Но наш вопрос не просто спрашивает нам, сколько линий есть. Он спрашивает нас, сколько горизонтальных линии есть. Ты помнишь, какое слово горизонтальный значит?
Чтобы помочь нам вспомнить, мы могли подумать
слова, которое является частью слова горизонтальный. И это слово горизонт. Вы знаете, что горизонт
является? Это линия, которую мы видим в
расстояние, где небо встречается с морем или землей. И хотя вы увидите, что это не так
совершенно прямой, если подойти поближе, то он точно выглядит прямо из
расстояние. Он выглядит идеально ровно слева
вправо без наклона вверх или вниз вообще. И вспоминая слово горизонт
может помочь нам вспомнить, что означает слово «горизонтальный». Как и горизонт, это линия
это совершенно прямо слева направо и не имеет наклона или наклона ни
направление.
Он выглядит идеально ровно слева
вправо без наклона вверх или вниз вообще. И вспоминая слово горизонт
может помочь нам вспомнить, что означает слово «горизонтальный». Как и горизонт, это линия
это совершенно прямо слева направо и не имеет наклона или наклона ни
направление.
Итак, какие линии этого многоугольника
горизонтальный? Ну, эта верхняя линия или сторона
горизонтально, не так ли? А еще есть горизонтальная линия
напротив него снизу. Но если мы посмотрим на две строки
которые составляют стороны нашего прямоугольника, мы видим, что они прямые. И они не наклонные или наклонные
в любом случае. Но вместо того, чтобы бежать слева направо
Правильно, они идут сверху вниз. Это не горизонтальные линии. Это вертикальные линии. И так, мы можем сказать количество
горизонтальных линий, которые есть в этом многоугольнике, две.
Верно или неверно: Горизонтальное и вертикальная линия образует прямой угол.
Этот вопрос состоит из заявление. Нам говорят, что горизонталь и вертикальная линия образует прямой угол. Но это утверждение может быть не правильный. Нам нужно решить. Это правда? Или это ложь?
Теперь нам нужно выработать правильный ответ, есть несколько слов, которые мы должны напомнить себе здесь. Есть слово горизонталь, вертикальный, а также слова под прямым углом. Вы помните, что каждый из эти слова означают? Если что-то горизонтальное, оно работает слева направо без наклона. Это полностью уровень. Вы видите, какой из двух линии на картинке идут слева направо без наклона? Вот этот, пересекающий экран.
Теперь в нашем
картина. Это не работает слева направо
хотя. Потому что это вертикаль
линия. Эта линия проходит вверх и вниз без
наклонный. Это совершенно прямо из
сверху вниз, не уходя ни влево, ни вправо. Итак, мы можем видеть, где наша горизонталь
и вертикальные линии есть.
Эта линия проходит вверх и вниз без
наклонный. Это совершенно прямо из
сверху вниз, не уходя ни влево, ни вправо. Итак, мы можем видеть, где наша горизонталь
и вертикальные линии есть.
И наше утверждение говорит нам, что такие линии образуют прямой угол. Ты помнишь, какой прямой угол является? Прямой угол – это место, где две линии сойтись вместе, чтобы сделать угол 90 градусов или квадратный угол. Вот почему символ права Угол часто представляет собой небольшой квадрат, нарисованный в углу. Так что ты думаешь? Если у нас есть горизонталь и вертикальная линия, составят ли они прямой угол?
Ну, если мы посмотрим на две строки
на нашей картинке они даже не соприкасаются. Они не сформировали право
угол. Но наш вопрос не говорит: «Это
горизонталь и эта вертикаль образуют прямой угол». Он просто говорит нам, что если мы возьмем
горизонтальную линию и возьмем вертикальную линию, они составят прямой угол. Итак, чтобы найти ответ, все, что у нас есть
что делать с нашей горизонтальной линией, так это продолжать ее рисовать. Ну вот. Нам нужно было только добавить немного
более. А теперь наши горизонтали и вертикали
линии соприкасаются.
Итак, чтобы найти ответ, все, что у нас есть
что делать с нашей горизонтальной линией, так это продолжать ее рисовать. Ну вот. Нам нужно было только добавить немного
более. А теперь наши горизонтали и вертикали
линии соприкасаются.
Встречаются ли они на площади
угол? Да, мы видим, что они сделали
один, два прямых угла. И если мы продолжим нашу горизонтальную
линия немного больше, есть больше прямых углов. И этот факт относится к любому
горизонтальные и вертикальные линии. Горизонтальное плюс вертикальное равно
прямой угол. Горизонтальное плюс вертикальное равно
прямой угол. Итак, хотя мы можем исправить
углы множеством других способов — вы видите этот пример вверху? Ни одна из этих строк не
горизонтальные или вертикальные они? Они оба наклонные, но все же
сделать прямой угол. Мы знаем, что утверждение
правильный.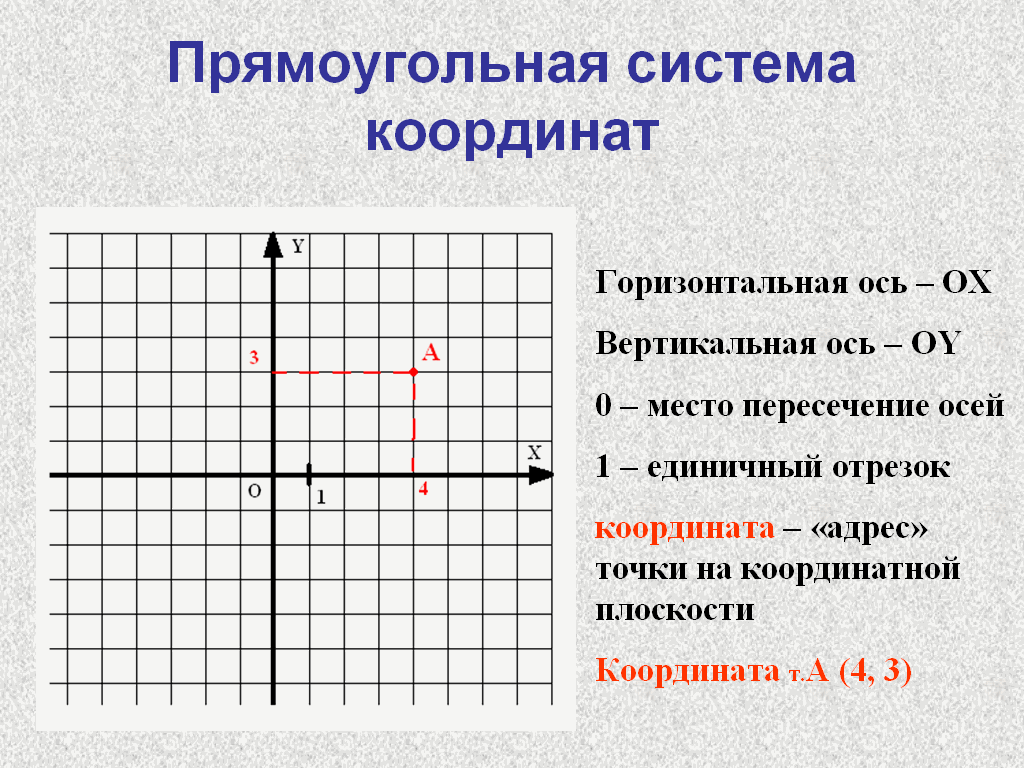
Горизонтальная и вертикальная линии будет образовывать прямой угол. Это предложение верно.
Верно или неверно: данная форма имеет вертикальная линия симметрии.
В этом вопросе нам дается утверждение, и нам нужно решить, верно оно или нет. Под заявлением мы дана картина формы. Это форма, которую заявление говорит о. Теперь вы обратили внимание на слова «линия симметрии» в вопросе? Ты помнишь, какая строчка симметрия есть? Если мы знаем, что форма или объект имеет линию симметрии, мы можем думать о ней как о линии или сгибе, проходящем через середина формы. И если эта форма симметрична, тогда, если бы он был сложен, обе стороны идеально подошли бы друг к другу.
Мы также можем думать о симметрии в
условия рефлексии. Мы знаем, что форма или изображение
имеет симметрию, когда мы можем взять половину формы и увидеть, что она идеально отражает
через линию симметрии и все еще выглядит одинаково. И как мы видим из этих маленьких
изображения, линии симметрии могут идти во всех направлениях. Но наш вопрос говорит только о
один тип линии. Данная фигура имеет вертикальную линию
симметрии.
И как мы видим из этих маленьких
изображения, линии симметрии могут идти во всех направлениях. Но наш вопрос говорит только о
один тип линии. Данная фигура имеет вертикальную линию
симметрии.
Теперь мы знаем, что вертикальная линия это линия, которая идет вверх и вниз. Не наклоняется в стороны все. Это совершенно прямо сверху вниз нижний. Итак, можем ли мы провести линию прямо вверх и вниз сверху вниз где-то на этой фигуре так, чтобы она стала линией симметрия?
Ну, мы знаем, что для строк Чтобы симметрия работала, им нужно пройти через середину объектов. Итак, если мы сможем найти середину эту фигуру, которая здесь, а затем нарисуйте идеально вертикальную линию. Что вы думаете? Это линия симметрии? Если мы сложим эту фигуру поперек пунктирная линия, как вы думаете, будет ли одна сторона идеально складываться поверх другой? Если мы поставим зеркало вдоль пунктирной линия, как вы думаете, мы увидим, что одна сторона является отражением другой? Я думаю, что мы бы, не так ли?
Линия симметрии этой фигуры
не проходит горизонтально из стороны в сторону и никоим образом не наклонена.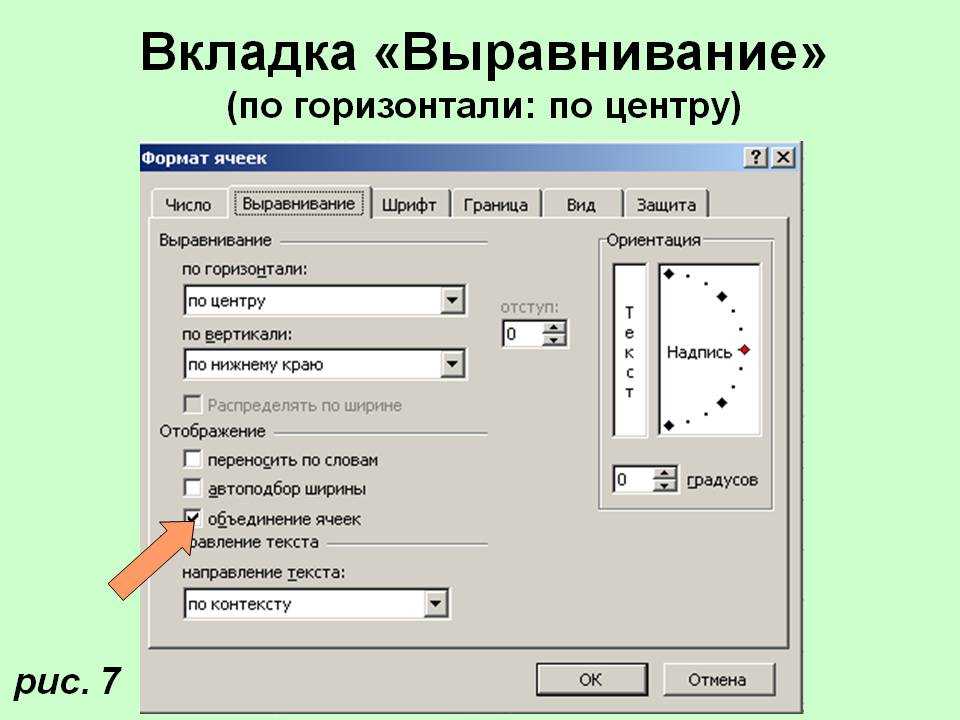 Но мы видим, что форма имеет
вертикальная линия симметрии. Утверждение в вопросе
истинный.
Но мы видим, что форма имеет
вертикальная линия симметрии. Утверждение в вопросе
истинный.
Чему мы научились в этом видео? Мы научились описывать и выделить горизонтальные и вертикальные линии.
Изучаем параллельные линии, перпендикулярные линии, горизонтальные и вертикальные линии
¶Параллельные линии и перпендикулярные линии.
Две невертикальные прямые параллельны тогда и только тогда, когда они имеют одинаковый наклон. Этот факт довольно интуитивен, поскольку две линии, которые не поднимаются и не опускаются с одинаковой скоростью, неизбежно пересекутся (как и две линии, одна из которых поднимается, а другая опускается).
Менее интуитивный, но столь же верный факт заключается в том, что две линии, ни одна из которых не является вертикальной, перпендикулярны тогда и только тогда, когда они имеют противоположные взаимные наклоны. Например, если линия имеет наклон \(-\frac{9}{11}\text{,}\), чем любая линия, перпендикулярная этой линии, имеет наклон \(\frac{11}{9}\)
Пример 7.
 6.1.
6.1.Определите уравнение пересечения наклона линии, которая проходит через точку \((9,-2)\) и параллельна линии с уравнением \(x-3y=14\text{.}\)
Решение
Начнем с определения наклона линии \(x-3y=14\text{.}\) Мы можем сделать это, написав уравнение в форме пересечения наклона, что по существу влечет за собой выделение \(y\text {.}\)
\begin{выравнивание*} х-3у\ампер=14\\ x-3y\вычесть вправо{х}\amp=14\вычесть вправо{х}\\ -3y\amp=-x+14\\ \multiplyleft{-\frac{1}{3}}-3y\amp=\multiplyleft{-\frac{1}{3}}(-x+14)\\ y=\frac{1}{3}x-\frac{14}{3} \end{align*}
Из уравнения \(y=\frac{1}{3}x-\frac{14}{3}\) мы можем определить, что наклон линии \(x-3y= 14 \) равно \(\frac{1}{3}\text{.}\) Поскольку прямая, уравнение которой мы ищем, параллельна \(x-3y=14\text{,}\) и параллельные прямые имеют равные наклон, наклон искомой линии также равен \(\frac{1}{3}\text{.}\)
Линия, которую нам нужно определить, имеет наклон \(\frac{1}{3}\) и проходит через точку \((9,-2)\text{. }\) Используя эту информацию в точечно-наклонной формы линейного уравнения и упрощая результат, уравнение наклона-пересечения для линии определяется следующим образом.
}\) Используя эту информацию в точечно-наклонной формы линейного уравнения и упрощая результат, уравнение наклона-пересечения для линии определяется следующим образом.
\начать{собирать*} у-у_1=м(х-х_1)\\ у-(-2)=\фракция{1}{3}(х-9)\\ у+2=\фракция{1}{3}х-3\\ y+2\subtractright{2}=\frac{1}{3}x-3\subtractright{2}\\ у=\фракция{1}{3}-5 \конец{собрать*}
Пример 7.6.2.
Давайте составим уравнение пересечения наклона линии, проходящей через точку \((-8,16)\), которая перпендикулярна линии, проходящей через точки, показанные на рисунке 7.6.3.
| \(х\) | \(у\) |
| \(-4\) | \(7\) |
| \(10\) | \(-5\) |
Решение
Начнем с определения наклона линии, проходящей через точки, показанные на рисунке 7.6.3. Пусть \((x_1,y_1)\) будет упорядоченной парой \((-4,7)\) и \((x_2,y_2)\) будет упорядоченным \((10,-5)\text{,} \) мы вычисляем наклон следующим образом.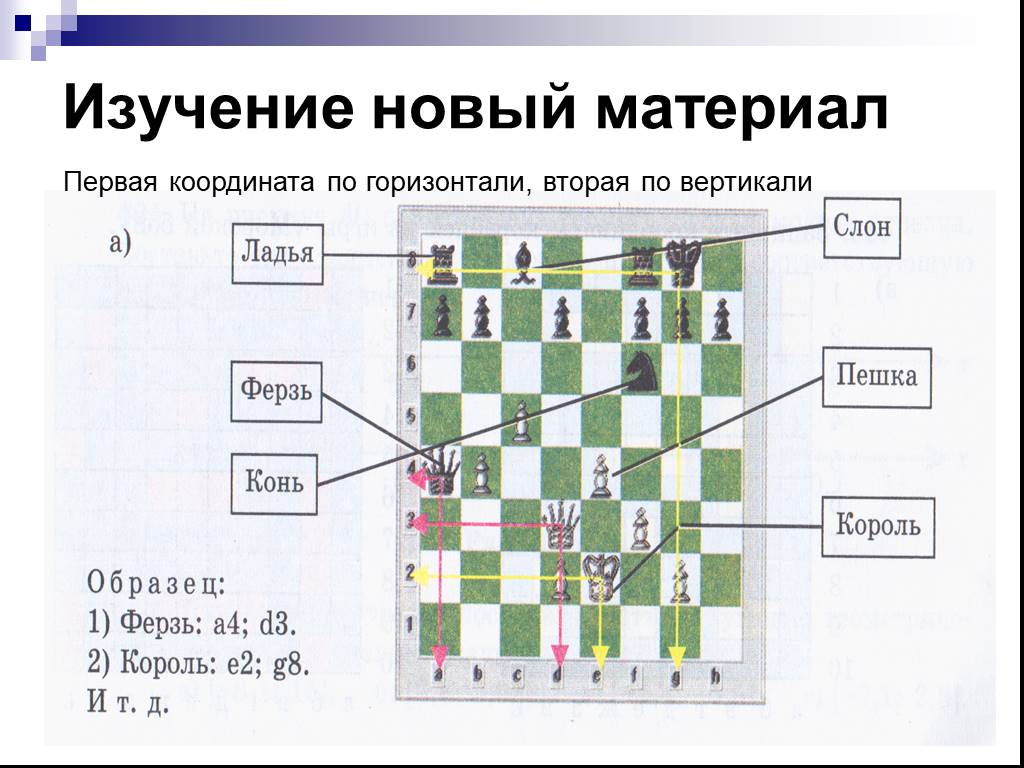
\begin{выравнивание*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-5-7}{10-(-4)}\\ \amp=\frac{-12}{14}\\ \amp=-\frac{6}{7} \end{align*}
Поскольку искомая линия перпендикулярна линии с наклоном \(-\frac{6}{7}\text{,}\), а перпендикулярные линии имеют противоположные обратные наклоны, линия мы ищем имеет наклон \(\frac{7}{6}\text{.}\)
Используя наклон \(\frac{7}{6}\) и упорядоченную пару \((-8 ,16)\text{,}\) определяем уравнение пересечения наклона искомой прямой следующим образом.
\начать{собирать*} у-у_1=м(х-х_1)\\ y-16=\frac{7}{6}(x-(-8))\\ у-16 = \ гидроразрыва {7} {6} (х + 8) \\ y-16=\frac{7}{6}x+\frac{28}{3}\\ y-16 \ addright {16} = \ frac {7} {6} x + \ frac {28} {3} \ addright {\ frac {48} {3}} \\ y=\frac{7}{6}x+\frac{76}{3} \end{gather*}
Горизонтальные линии.
Уравнение горизонтальной линии можно определить так же, как и любую другую невертикальную линию, хотя после этого обобщение может значительно упростить процесс.
Рассмотрим горизонтальную линию, показанную на рисунке 7. 6.4. Пусть \((x_1,y_1)\) будет упорядоченной парой \((-4,-3)\) и \((x_2,y_2)\) будет упорядоченной парой \((2,-3)\text{ .}\) Мы вычисляем наклон ниже.
6.4. Пусть \((x_1,y_1)\) будет упорядоченной парой \((-4,-3)\) и \((x_2,y_2)\) будет упорядоченной парой \((2,-3)\text{ .}\) Мы вычисляем наклон ниже.
\начать{выровнять*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-3-(-3)}{2-(-4)}\\ \amp=\frac{0}{6}\\ \усилитель=0 \конец{выравнивание*}
По наблюдениям, \(y\)-пересечение линии равно \((0,-3)\text{.}\) Это в сочетании с наклоном \(0\) дает нам следующее.
\начать{выровнять*} у\амп=мх+б\\ y\amp=0 \cdot x+(-3)\\ у\ампер=-3 \конец{выравнивание*}
Теперь, когда у нас есть уравнение \(y=-3\text{,}\), подходящим ответом может быть «d’oh!» По наблюдениям, определяющее свойство точек на прямой состоит в том, что все \(y\)-координаты равны \(-3\)
В общем, все горизонтальные линии имеют наклон \(0\text{.}\) Кроме того, горизонтальная линия имеет уравнение формы \(y=k\), где \(k\) — это \(y \)-координата, общая для каждой точки прямой.
Вертикальные линии.
Рассмотрим вертикальную линию, показанную на рисунке 7.![]() 6.5. Когда мы пытаемся вычислить наклон линии, все выходит из-под контроля. Например:
6.5. Когда мы пытаемся вычислить наклон линии, все выходит из-под контроля. Например:
\begin{выравнивание*} м\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{5-(-3)}{2-2}\\ \amp=\frac{8}{0} \end{align*}
Рисунок 7.6.5. Вертикальная линияК последнему выражению мы присоединяем фразу —о-о! Деление на \(0\) никогда не бывает хорошим. Деление на ноль всегда является результатом применения формулы наклона к вертикальной линии, и по этой причине мы говорим, что вертикальная линия не имеет наклона или что наклон не определен.
На рис. 7.6.5 видно, что каждая точка на прямой имеет \(x\)-координату \(2\text{,}\), поэтому уравнение прямой должно быть \(x=2\text {.}\) В общем, вертикальные линии имеют уравнения вида \(x=h\text{,}\), где \(h\) — \(x\)-координата каждой точки на линии
Итак, в отличие от определения уравнений невертикальных, негоризонтальных линий, определение уравнения горизонтальной или вертикальной линии — это просто вопрос записи уравнения.
Например, если вас попросят определить уравнения для горизонтальных и вертикальных линий, проходящих через точку \((-3,7)\text{,}\), соответствующий ответ будет следующим.
Горизонтальная линия имеет уравнение \(y=7\), а вертикальная линия имеет уравнение \(x=-3\text{.}\)
Если в данный момент вы не можете вспомнить, какая форма уравнения является горизонтальной, а какая вертикальной, просто нарисуйте линию и спросите себя: «Какая координата всегда одна и та же, \(x\) или \(y\text{ ?}\)»
Упражнения Упражнения
1.
Укажите уравнения вертикальных и горизонтальных линий, проходящих через точку \((-7,25)\text{.}\)
Решение
Уравнение вертикальной линии \(y=25\), а уравнение горизонтальной линии \(x=-7\)
2.
Каковы наклоны линий, параллельных прямой с уравнением \(-6x+8y=12\text{?}\) Каковы наклоны линий, перпендикулярных этим линиям?
Решение
Начнем с обработки уравнения \(-6x+8y=12\) в форме пересечения наклона.
\begin{выравнивание*} -6x+8y\amp=12\\ -6x+8y\addright{6x}\amp=12\addright{6x}\\ 8у\ампер=6х+12\\ \multipleleft{\frac{1}{8}}(8y) \amp=\multipleleft{\frac{1}{8}}(6x+12)\\ y\amp=\frac{3}{4}x+\frac{3}{2} \end{align*}
Из последнего уравнения видно, что наклон линии \(-6x+8y=12\) равен \(\frac{3}{4}\text{. }\) Итак все линии, параллельные \(-6x+8y=12\), имеют наклоны \(\frac{3}{4}\), а линии, перпендикулярные этим линиям, имеют наклоны \(-\frac{4}{3}\ текст{.}\)
}\) Итак все линии, параллельные \(-6x+8y=12\), имеют наклоны \(\frac{3}{4}\), а линии, перпендикулярные этим линиям, имеют наклоны \(-\frac{4}{3}\ текст{.}\)
3.
Определите уравнения линий, проходящих через точку \((3,5)\) и соответственно параллельных и перпендикулярных линии, изображенной на рисунке 7.6.6. Сформулируйте каждое уравнение в форме пересечения наклона.
Рисунок 7.6.6. Определить уравнение…Решение
Линия, изображенная на рисунке 7.6.6, имеет наклон \(-\frac{1}{2}\), поэтому линии, параллельные этой линии, имеют наклон \(-\frac{1}{2}\ ) и прямые, перпендикулярные ему, имеют наклон \(2\text{.}\)
Используя наклон \(-\frac{1}{2}\) и упорядоченную пару \((3,5)\) в уравнении \(y-y_1=m(x-x_1)\), мы вывести уравнение описанной параллельной прямой следующим образом.
\begin{выравнивание*} y-5\amp=-\frac{1}{2}(x-3)\\ y-5\amp=-\frac{1}{2}x+\frac{3}{2}\\ y-5 \ addright {5} \ amp = — \ frac {1} {2} x + \ frac {3} {2} \ addright {\ frac {10} {2}} \\ y\amp=-\frac{1}{2}x+\frac{13}{2} \end{align*}
Используя наклон \(2\) и упорядоченную пару \((3,5)\) в уравнении \(y-y_1=m(x-x_1)\), мы получаем уравнение описанной перпендикулярной прямой выглядит следующим образом.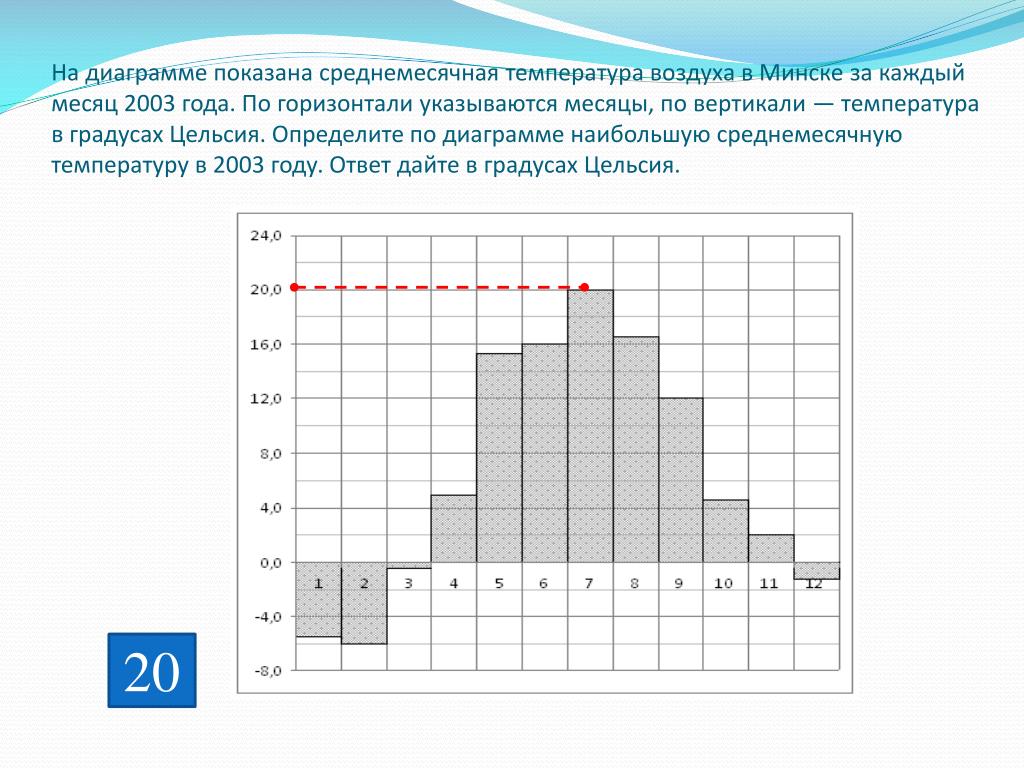
\begin{выравнивание*} у-5\ампер=2(х-3)\\ у-5\ампер=2x-6\\ y-5\addright{5}\amp=2x-6\addright{5}\\ у\ампер=2x-1 \end{align*}
Две новые строки показаны на рисунке 7.6.7 вместе с данной строкой. Они действительно параллельны или перпендикулярны данной прямой.
Рисунок 7.6.7. Визуальная проверка4.
Определите уравнение прямой, проходящей через точку \((9,-2)\) и перпендикулярной прямой с уравнением \(y=14\text{.}\)
Решение
Прямая \(y=14\) горизонтальна, поэтому любая перпендикулярная ей прямая вертикальна. Следовательно, прямая, проходящая через точку \((9,-2)\) и перпендикулярна прямой \(y=14\) имеет уравнение \(x=9\text{.}\)
5.
Определите уравнение прямой, проходящей через точку \((-3,14)\) и перпендикулярной прямой с уравнением \(12x-4y=18\text{.}\) Уравнение состояния в наклоне-пересечении форма.
Решение
Начнем с того, что запишем уравнение \(12x-4y=18\) в форме пересечения наклона.
 </div>
<div>Этот элемент расположен за пределами своего контейнера.</div>
</div>
<div>Этот элемент расположен за пределами своего контейнера.</div>
 А так же сокращенные варианты:
А так же сокращенные варианты: