Конгруэнтность (геометрия) — Congruence (geometry)
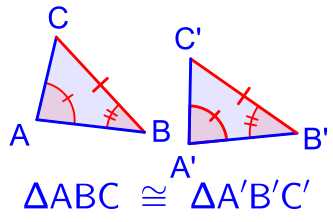
Пример сравнения. Эти два треугольника на левой конгруэнтны, в то время как третья похожа на них. Последний треугольник ни похож ни конгруэнтно ни одному из других. Конгруэнтность позволяет изменение некоторых свойств, таких как местоположение и ориентацию, но оставляет другие неизменными, как расстояние и углы . Неизмененные свойства называются инварианты .В геометрии , две фигуры или объекты конгруэнтны , если они имеют такую же форму и размер, или если один имеет ту же форму и размер , как зеркальное отражение другого.
Более формально, два набора точек называется конгруэнтен тогда и только тогда, когда один может быть преобразован в другую с помощью изометрии , то есть сочетание жестких движений , а именно перевода , в повороте , и отражения . Это означает , что либо объект может быть перемещен и отражение (но не изменяется) таким образом , чтобы точно совпадать с другим объектом. Таким образом , две различные фигуры плоскости на бумажке конгруэнтны , если мы можем вырезать их , а затем сопоставить их полностью. Обращаясь бумагу разрешается.
 Эта диаграмма иллюстрирует геометрический принцип угла угла на стороне треугольник конгруэнции: Учитывая треугольник АВС и треугольник А’В’С «треугольник АВС конгруэнтен с треугольным А’В’СОМ» тогда и только тогда, когда угол ?? САВ конгруэнтно с C’A’B «и ?? угла ABC сравнимая с А’В’СОМ» и BC сравнимая с В’С»
Эта диаграмма иллюстрирует геометрический принцип угла угла на стороне треугольник конгруэнции: Учитывая треугольник АВС и треугольник А’В’С «треугольник АВС конгруэнтен с треугольным А’В’СОМ» тогда и только тогда, когда угол ?? САВ конгруэнтно с C’A’B «и ?? угла ABC сравнимая с А’В’СОМ» и BC сравнимая с ’ѻ элементарной геометрии слово конгруэнтно часто используются следующим образом . Слово равно часто используется вместо конгруэнтных для этих объектов.
- Два отрезков конгруэнтны , если они имеют одинаковую длину.
- Два угла равны , если они имеют одинаковую меру.
- Два круга конгруэнтны , если они имеют одинаковый диаметр.
В этом смысле, две плоские фигуры конгруэнтны означает , что их соответствующие характеристики «конгруэнтны» или «равно» , включая не только их соответствующих сторон и углов, а также их соответствующие диагоналей, периметры и площади.
Соответствующее понятие подобия применяется , если объекты имеют одинаковую форму , но не обязательно имеют одинаковый размер. (Большинство определений считают конгруэнтность быть формой сходства, хотя меньшинство требует, чтобы объекты имеют разные размеры для того , чтобы квалифицировать как аналог.)
Определение конгруэнтности полигонов
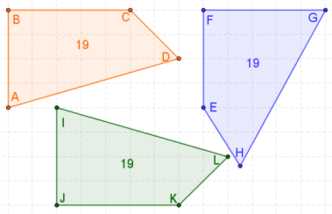 Оранжевые и зеленые четырехугольники конгруэнтны; синий не сравнимые с ними. Все три имеют одинаковый периметр и площадь . (Упорядочение сторон голубого четырехугольника «смешанный» , который приводит в двух внутренних углах и одной из диагоналей , не являющихся конгруэнтен.)
Оранжевые и зеленые четырехугольники конгруэнтны; синий не сравнимые с ними. Все три имеют одинаковый периметр и площадь . (Упорядочение сторон голубого четырехугольника «смешанный» , который приводит в двух внутренних углах и одной из диагоналей , не являющихся конгруэнтен.)Для двух многоугольников быть конгруэнтны, они должны иметь одинаковое число сторон (и , следовательно , одинаковое число-то же самое число-вершин). Два многоугольники с п сторон конгруэнтны тогда и только тогда , когда каждый из них имеет численно идентичные последовательности ( по часовой стрелке , даже если для одного многоугольника и против часовой стрелки для другого) бокового угла бокового угла -… для
Конгруэнтность полигонов могут быть созданы графически следующим образом:
- Во-первых, матч и маркировать соответствующие вершины двух фигур.
- Во- вторых, нарисовать вектор из одной из вершин одной из фигур в соответствующей вершине другой фигуры. Перевести первую цифру этого вектора так , что эти две вершины совпадают.
- В- третьих, повернуть переведенный рисунок о найденной вершины , пока одна пара соответствующих сторон не совпадает.
- В- четвертых, отражает повернутую фигуру об этом согласованной стороне до матча цифры.
Если в любой момент времени шаг не может быть завершен, многоугольники не совпадают.
Конгруэнтность треугольников
Два треугольника равны , если их соответствующие стороны равны по длине, и их соответствующие углы равны в меру.
Если треугольник ABC конгруэнтно треугольника DEF, отношения можно записать математически как:
- △AВС≅△DЕF,{\ Displaystyle \ треугольник \ mathrm {ABC} \ Цун \ треугольник \ mathrm {DEF}.}
Во многих случаях достаточно установить равенство трех соответствующих частей и использовать один из следующих результатов вывести конгруэнтность двух треугольников.
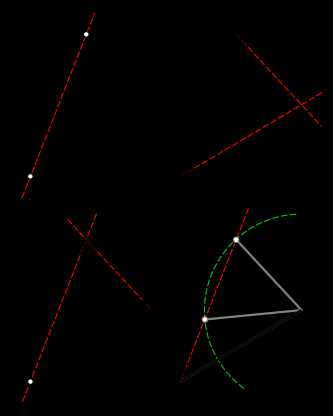 Форма треугольника определяется с точностью до конгруэнции, указав две стороны и угол между ними (SAS), два угла и стороны между ними (ASA) или два углами и соответствующей смежной стороной (ААС). Указание двух сторон и соседний угол (ССА), однако, может дать два различных возможных треугольников.
Форма треугольника определяется с точностью до конгруэнции, указав две стороны и угол между ними (SAS), два угла и стороны между ними (ASA) или два углами и соответствующей смежной стороной (ААС). Указание двух сторон и соседний угол (ССА), однако, может дать два различных возможных треугольников.Определение конгруэнтность
Достаточные доказательства для сравнения между двумя треугольниками в евклидовом пространстве можно показать с помощью следующих сравнений:
- SAS
- SSS (Side-Side-сторона): Если три пары сторон двух треугольников равны по длине, то треугольники равны.
- ASA (Angle-Side-Angle): Если две пары углов двух треугольников равны в измерении, и включённые стороны равны по длине, то треугольники равны.
ASA Постулат был внесен Фалеса (греческого). В большинстве систем аксиом, три критерия — SAS, SSS и ASA — устанавливаются в виде теорем . В школе математика Study Group системы SAS принимается как один (# 15) из 22 постулатов. - ААС (угол-угол-сторона): Если две пары углов двух треугольников равны в измерении, и пару соответствующих не включаются стороны равны по длине, то треугольники равны. ААС эквивалентно условия ASA, тот факт , что если любые два угла приведен, так что это третий угол, так как их сумма должна быть 180 °. АСК и ААС иногда объединяются в одно условие, AAcorrS — любые два угла и соответствующая сторона.
- RHS (правый угол-Гипотенуза-Side), также известный как HL (Гипотенуза-Leg): Если два прямоугольных треугольника имеют гипотенузы равные по длине, и пара коротких сторон равны по длине, то треугольники равны ,
Боковые стороны угла
Условие SSA (Side-Side-Angle), который определяет две стороны и не-прилежащий угол (также известный как АПС или Angle-Side-Side) само по себе не доказать конгруэнтность. Для того чтобы показать конгруэнтность, требуется дополнительная информация, такие как мера соответствующих углов, а в некоторых случаях длинами двух пар соответствующих сторон. Есть несколько возможных случаев:
Если два треугольника удовлетворяет условие SSA и длину стороны , противоположный угол больше или равен длиной смежной стороны (SSA, или длинный боковой короткую сторону угла), то два треугольник равен. Противоположная сторона иногда больше , когда соответствующие углы острые, но
Если два треугольника удовлетворяют условию SSA и соответствующие углы острые и длина стороны, противоположной от угла равна длине смежной стороны, умноженной на синус угла, то два треугольника равны.
Если два треугольника удовлетворяют условию SSA и соответствующие углы острые и длина стороны , противоположной от угла больше , чем длина смежной стороны , умноженной на синус угла (но меньше , чем длина прилегающей стороны), то два треугольника не может быть показано, что конгруэнтны. Это неоднозначный случай , и два различных треугольник может быть образован из данной информации, но дополнительная информация отличающих их может привести к доказательству конгруэнции.
Угол угол угол
В евклидовой геометрии, AAA (Angle-Angle-Angle) (или просто AA, так как в евклидовой геометрии углы треугольника добавить до 180 °) не дает информацию относительно размера двух треугольников и , следовательно , доказывает только сходство и не конгруэнции в евклидовом пространстве.
Однако в сферической геометрии и гиперболической геометрии (где сумма углов треугольника изменяется в зависимости от размера) ААА является достаточным для сравнения на заданную кривизне поверхности.
CPCTC
Этот акроним расшифровывается как соответствующие части конгруэнтных треугольника равны сокращенный вариант определения конгруэнтных треугольников.
Более подробно, это сжатый способ сказать , что если треугольники ABC и DEF конгруэнтны, то есть,
- △AВС≅△DЕF,{\ Displaystyle \ треугольник ABC \ Цун \ треугольник DEF,}
с соответствующими парами углов при вершинах А и D ; В и Е ; и С и Р , а также с соответствующими парами сторон AB и DE ; BC и EF ; и CA и FD , то справедливы следующие утверждения:
- AВ¯≅DЕ¯{\ Displaystyle {\ Overline {AB}} \ Цун {\ Overline {DE}}}
- ВС¯≅ЕF¯{\ Displaystyle {\ Overline {BC}} \ Цун {\ Overline {EF}}}
- AС¯≅DF¯{\ Displaystyle {\ Overline {AC}} \ Цун {\ Overline {DF}}}
- ∠ВAС≅∠ЕDF{\ Displaystyle \ угол BAC \ Цун \ угол EDF}
- ∠AВС≅∠DЕF{\ Displaystyle \ угол ABC \ Цун \ угол DEF}
- ∠ВСA≅∠ЕFD,{\ Displaystyle \ угол BCA \ Цун \ угол EFD.}
Заявление часто используется в качестве оправдания в элементарных доказательств геометрии , когда вывод о конгруэнтности частей двух треугольников , необходимых после конгруэнтность треугольников установлено. Например, если был показаны два треугольника , чтобы быть конгруэнтны по SSS критериев и утверждение , что соответствующие углы конгруэнтны необходимо в качестве доказательства, то CPCTC может быть использован в качестве обоснования данного заявления.
Родственная теорема CPCFC , в котором «треугольники» заменяется «цифрами» , так что теорема применима к любой паре многоугольников или многогранников , которые совпадают.
Определение конгруэнции в аналитической геометрии
В евклидовой системе , конгруэнтность является фундаментальным; это аналог равенства чисел. В аналитической геометрии , конгруэнтность может быть определена интуитивно следующим образом: два отображения фигур на одной декартовой системе координат конгруэнтны тогда и только тогда, когда для любых двух точек в первом отображении, то евклидово расстояние между ними равно евклидова расстояния между соответствующими указывает во втором отображении.
Более формальное определение гласит , что два подмножества и В из евклидова пространства R п называются конгруэнтными , если существует изометрия п : R п → R н (элемент из евклидовой группы Е ( п )) с ф
Равные конические сечения
Два конических сечений конгруэнтны , если их эксцентриситеты и один отчетливый параметр , характеризующий их равны. Их эксцентриситеты устанавливают свои формы, равенство которых является достаточным для установления подобия, а второй параметр затем устанавливает размер. Поскольку две круги , парабола или прямоугольные гиперболы всегда имеют одинаковый эксцентриситет ( в частности , 0 в случае окружностей, 1 в случае параболы, а в случае прямоугольных гиперболы), две окружность, парабола или прямоугольные гиперболы должны иметь только один общее значение параметра, устанавливая их размер, чтобы они были равны. 2{\ Displaystyle {\ SQRT {2}}}
Конгруэнтные многогранники
Для двух многогранников с тем же числом Е ребер, то же числом граней , и тем же числом сторон на соответствующих гранях, существует множество в большинстве E измерений , которые могут устанавливать или не конгруэнтны многогранники. Для кубов , которые имеют 12 ребер, всего 9 измерений необходимы.
Равные треугольники на сфере
Как и с плоскими треугольниками, на сфере два треугольника, разделяющие ту же последовательность угла-боковой угол (ASA) обязательно конгруэнтны (то есть, у них есть три одинаковых сторон и три одинаковых углов). Это можно рассматривать следующий образ: Можно расположить одну из вершин с заданным углом на южном полюсе и запустить сторону с заданной длиной до Нулевого меридиана. Зная как углы с обоих концов отрезка фиксированной длины гарантирует, что две другие стороны исходят с однозначно определенной траектории, и, таким образом, будут встречаться друг с другом в однозначно определенной точке; Таким образом, ASA является действительным.
Теоремы конгруэнтно боковой угол на стороне (SAS) и боковые стороны на стороне (SSS) также держат на сфере; кроме того, если две сферические треугольники имеют одинаковый угол угол угол (ААА) последовательность, они конгруэнтны (в отличие от плоских треугольников).
Плоскость-треугольник конгруэнцтеорема угол угол на стороне (ААС) не выполняется для сферических треугольников. Как и в плоской геометрии, бок о бок угол (SSA) не означает конгруэнтность.
нотация
Символ обычно используется для сравнения является равным символ с тильдой над ним, ≅ , соответствующий Unicode символ « приблизительно равное» (U + 2245). В Великобритании, три-бар , знак равенства ≡ (U + 2261) иногда используется.
Смотрите также
Рекомендации
внешняя ссылка
ru.qwertyu.wiki
Конгруэнтные фигуры | Математика
Конгруэнтные фигуры.
Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно: Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. ИЗБРАННЫЕ ВОПРОСЫ ТЕОРИИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ ПЛОСКОСТИ И ЕЕ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ. З. А. Скопец, Л. И. Кузнецова
(стр. 227-246)
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
§ 4. Конгруэнтные фигуры. А. М. Абрамов НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ.
П е р в о е о п р е д е л е н и е . Фигура Фх конгруэнтна фигуре
Ф, если существует сохраняющее расстояния отображение
фигуры Ф на Фх.
Так как перемещения сохраняют расстояния, часто употребляется
такой метод доказательства конгруэнтности фигур Ф и Фх:
находится перемещение, при котором образом фигуры Ф является
Фх.
В т о р о е о п р е д е л е н и е . Если существует перемещение,
отображающее фигуру Ф на Фх, то говорят, что фигура Фх конгруэнтна
Ф.
Замечание, сделанное перед этим определением, показывает,
что если фигура Фх конгруэнтна фигуре Ф в смысле второго определения,
то Фх конгруэнтна Фив смысле первого определения.
257 Конгруэнтные фигуры.
Для доказательства эквивалентности этих двух определений
остается показать, что если существует сохраняющее расстояния
отображение G, область определения которого — фигура Ф, а
множество значений — Фх, то существует и перемещение F (изометрическое
отображение всей плоскости, а не ее подмножества Ф),
при котором образ фигуры Ф — фигура Фх.
Т е о р е м а 4.1. Для любого сохраняющего расстояния отображения
G произвольной фигуры Ф в плоскость существует перемещение
F, являющееся продолжением G на всю плоскость (для любой
точки X фигуры Ф имеем: F (X) — G (X)).
Д о к а з а т е л ь с т в о . Если Ф состоит из одной или двух
точек, то утверждение теоремы — очевидное следствие A.IV.1.
Рассмотрим другие возможности.
Первый случай: Ф — подмножество прямой.
Пусть А и В — различные точки Ф. Обозначим через Лх и Вг
образы точек А а В при отображении G. Так как G сохраняет расстояния,
|Лх5х1 = |Л5|. Вследствие А.IV.1. существует перемещение
F, переводящее А в Аъ В в Вх.
Отображения G и F сохраняют расстояния. Значит, G (Ф),
F (Ф) — подмножества прямой Л^. Возьмем отличную от Л и Б
точку Xфигуры Ф. НапрямойЛхбх имеется ровно одна точка Х1г
для которой |ЛХ| = |ЛхХх|, |fiX| =|SxXx|. Поэтому и F, и G
переводят X в X’, т. е. F — продолжение G на всю плоскость.
Второй случай: Ф содержит точки А, В, С, не принадлежащие
одной прямой.
Так как G сохраняет расстояния, точки Ах — G (Л), Вх — G (В),
Сх = G (С) также не принадлежат одной прямой, причем | Лх-SxN
= | АВ\, |ВхСх1 = |ВС|, |ЛхСх1 =|ЛС|. Как показано при доказательстве
теоремы 2.1 существует перемещение F, которое, как и
С, переводит Л в Аг, В в Въ С в Сх. Если Ф не содержит других
точек, кроме Л, б и С, теорема доказана. Пусть X — произвольная
точка Ф, отличная от Л, Б, С.
В этом случае мы докажем, что F (X) = G (X), показав, что существует
не более одной точки плоскости, удаленной от Л’ на расстояние
| ЛХ|, от В’ — на |fiX| и от С’— на |СХ|.
В самом деле, имеется не более двух точек Y1 и Y» плоскости,
для каждой из которых расстояние от Ах равно |ЛХ|, а от Вх —
|£Х| (теорема 1.З.), причем эти точки симметричны относительно
прямой АВ. Но \C’Y’\^ | C’Y»\: если эти расстояния равны, а
Y* ф Y», то С’ — точка меди-
атрисы к отрезку Y’Y», т. е.
С’ € (ЛхВх). Это противоречит
предположению С £ (АВ).
Надо добавить, что хотя приведенные
определения и эквивалентны,
числа, показывающие,
сколько имеется отображений,
устанавливающих конгруэнт
Конгруэнтные фигуры.
258 Конгруэнтные фигуры.
ность фигуры Ф фигуре Фх в смысле первого и второго определений,
могут оказаться различными. Так, с сохранением расстояний
отрезок на отрезок равной длины отображается двумя способами,
а перемещений, переводящих первый отрезок во второй, существует
четыре.
Так как перемещения плоскости образуют группу, сразу получаем:
У.4.1. Отношение конгруэнтности на множестве фигур является
отношением эквивалентности.
Отношение конгруэнтности фигур обозначается знаком е^.
Т е о р е м а 4.2. Для любого луча р’ в заданной полуплоскости
а’ с границей р существует единственный луч q’, имеющий общее
начало с р’, такой, что угол p’q’ конгруэнтен данному углу h’k’.
Д о к а з а т е л ь с т в о . Если в полуплоскости а’ существует
такой луч q’, что Z. p’q’ ^ A.h’k’, то перемещение, отображающее
угол h’k’ на угол p’q’, переводит Ох в О (рис. 8), а луч h’ ,(или k’)
отображается на луч р’\ при этом полуплоскость ah, содержащая k’
(соответственно полуплоскость а*, содержащая Н’), отображается
на а’р. как уже говорилось выше, при перемещениях крайние (граничные)
точки множества отображаются на крайние (граничные)
точки его образа. Таких перемещений в силу A.IV.2 имеется два.
Обозначим их через Ft и F%. Тогда
FAh’)=p’\ f!«)=«;,
F2 (kr) = p’, F2 (a’) = a’.
Fi (k1) и F
g (p’) — искомые лучи. Теорема существования доказана.
Для доказательства единственности остается показать, что
Fy (k’) = F2 (h’). Обозначим через q’ луч Ft (k’). Возьмем на лучах
р’ и q’ точки А и В: \ОА \ = \0В\.
Симметрия относительно медиатрисы ОМ отрезка АВ переводит
р’ в q’, q’ в р’у а полуплоскость а’р, содержащую^ q\ — в полуплоскость
a’q, содержащую р’.
Рассмотрим перемещение Som ° Ft. Имеем:
Som о Fi (&’) = S0M (qr) = p’.
s om o F ,K) = sM(«;) = a;.
Итак, образы флага 0$a’k при перемещениях F2 и Som ° FL
совпадают. В силу единственности перемещения, отображающего
один из данных флагов на другой, Som ° Fx = F2. Так как F2 (h’) =
= (So.m 0 Fj) (h’) = Som (p ) = q’, теорема доказана.
Т е о р е м а 4.3. Если треугольники АуВ^Су и А2В.,С2 таковы,
что BiAjCi ^ Z. В2А2С2, \AiBi\ = \А2В2\, \AiCi\== 1Л2С2!, то
АА2В2С2 ^ ААхВхСх.
Д о к а з а т е л ь с т в о . Так как Z-B^Cx ^ Z.B.2A2C2, существует
перемещение F, отображающее Ах на А2, луч АгВх на луч
259 Конгруэнтные фигуры.
А2Въ а луч Afix на луч Л2С2. Воспользовавшись условиями
\AxBx| = | Л2В2|, \AxCx| = 1Л2С21 и единственностью точки луча,
удаленной от его начала на данное расстояние, получаем, что
Аналогично доказываются другие признаки конгруэнтности
треугольников: по трем сторонам, по стороне и двум прилежащим
к ней углам.
О п р е д е л е н и е . Угол, конгруэнтный своему смежному, называется
прямым углом.
Для выпуклого угла имеются два угла, смежные с ним (рис. 9).
Поэтому вначале необходимо доказать корректность этого определения:
если Z.lg^Z.2, то Z . l ^ Z . 3 (рис. 9).
Угол 2 при симметрии Sa отображается на конгруэнтный ему
угол. Но луч ОА при симметрии Sa отображается на себя и по условию
Z. 1 Z. 2. Так как по теореме 4.2 от луча О А можно отложить
в данной полуплоскости лишь один угол, конгруэнтный данному,
$а _____
то [ОБ) ==> [ОС). Следовательно, и прямая р при симметрии Sa
отображается на’себя.
Из теоремы 3.4 вытекает, что Sp (а) — а. Поэтому угол 1 при
симметрии Sp отображается на угол 3, т. е. Z. 1 Ш АЗ.
Если две прямые пересекаются, то, как известно, они задают
четыре выпуклых угла. Из доказанной корректности определения
прямого угла следует, что если один из этих четырех углов прямой,
то и все четыре угла прямые.
О п р е д е л е н и е . Дее прямые, образующие при пересечении
прямые углы, называются взаимно перпендикулярными.
Т е о р е м а 4.4. Для любой точки О плоскости и любой прямой
р существует одна и только одна прямая, проходящая через О
и перпендикулярная р.
Д о к а з а т е л ь с т в о . Рассмотрим два случая.
Первый случай’. О $ р.
а) С у щ е с т в о в а н и е . Пусть О* = Sp (О) и М — точка
пересечения прямых 00′ и р (рис. 10, а). При еимметрии Sp лучи
МО и МО’ отображаются друг на друга, луч MN — на себя. Поэтому
углы OMN и O’MN — смежные и конгруэнтные углы. Это
означает, что прямые 00′ и р перпендикулярны.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О
260 Конгруэнтные фигуры.
проходят два перпендикуляра к прямой
р (рис. 11,6). Тогда, как это следует из
теоремы 4.2, прямые О А и О В при симметрии
Sp отображаются на себя. Так как эти
прямые пересекаются в точке О, отсюда получаем,
что эти прямые имеют вторую общую
точку O’— Sp (О). Но через две точки
проходит единственная прямая, поэтому
(ОА) = (ОВ). Это противоречит сделанному
допущению.
Конгруэнтные фигуры 2
Второй случай1. О £ р.
а) С у щ е с т в о в а н и е . Возьмем
произвольную точку A tp. Как мы только
что показали, существует прямая AM (М £
<: р), проходящая через А и перпендикулярная
р (рис. 11, а). Вследствие A.IV.1 существует
перемещение, отображающее точки
М и О друг на друга. При этом перемещении
прямая р отображается на себя,
а прямая AM — на такую прямую ОА’, что
Z. 1 ^ Z. Г, Z.2^ Z.2′. Так как Z. l^Z.2,
в силу транзитивности отношения конгруэнтности
фигур Z. Г Z. 2′, т. е. (ОА’) J. р.
б) Е д и н с т в е н н о с т ь . Допустим, что через точку О € р
проходят два перпендикуляра р и р’ к прямой а (рис. 11, б). Тогда
луч ОР’ содержится в одном из углов АОР и РОВ. Пусть для определенности
[OP’) а Z-РОВ. При симметрии с осью ОР угол РОВ
отображается на угол РОА (эти углы прямые), луч ОР’ — на некоторый
луч ОР», содержащийся в угле РОА и отличный от луча
ОР. При этом Z-P»OA /-Р’ОВ. Это противоречит теореме 4.2:
от луча ОА в полуплоскости с границей ОА отложены два угла
(Z-P’OA и Z.POA), конгруэнтные углу Р’ОВ.
С доказательством этой теоремы нетрудно сделать вывод, что
медиатриса любого отрезка является серединным перпендикуляром
этого отрезка.
О п р е д е л е н и е . Луч ОМ угла АО В называется биссектрисой
этого угла, если углы АОМ и ВОМ, являющиеся подмножествами
данного угла, конгруэнтны.
Т е о р е м а . 4 . 5 . Для любого угла плоскости, отличного от развернутого,
существует биссектриса этого угла и притом только
одна.
Д о к а з а т е л ь с т в о . 1. Существование. Если прямая АВ —
граница развернутого угла, то любой луч с началом О € (А В),
перпендикулярный к прямой АВ и содержащийся в данном развернутом
угле (рис. 12, а), является его биссектрисой. Отметим, что
неединственность биссектрисы развернутого угла вытекает из того
обстоятельства, что в отличие от других углов вершина (край->;
няя точка) развернутого угла не единственна.
261 Конгруэнтные фигуры.
Если угол АО В — выпуклый (рис. 12, б), его биссектриса —
луч с началом О, содержащий середину М отрезка CD (С (: [ОА),
D (; [ОВ), |ОС|= |OD|). Действительно, \ОМ\ — ось симметрии
угла АОВ, а точка М — внутренняя точка этого угла, так как
Z-AOB — выпуклая фигура.
Луч ON, противоположный лучу ОМ, — биссектриса невыпуклого
угла АОВ.
2. Единственность. Если ОК и ОМ — различные биссектрисы
угла АОВ (рис. 13), то симметрии Sok и Som отображают угол на
себя. Кроме того, Е (/L.AOB) = Z.AOB. Но существует не более
двух перемещений, отображающих один из данных конгруэнтных
углов на другой (см. доказательство теоремы 4.2.) Противоречие.
Допустив, что существует более одной биссектрисы у невыпуклого
угла, приходим к противоречию с только что доказанной единственностью
биссектрисы выпуклого угла.
262 Конгруэнтные фигуры.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Школьная математика. Математика в школе.
matematika.advandcash.biz
Доказательство Вертикальные углы конгруэнтны — манекены 2019
Когда две линии пересекаются, чтобы сделать X, углы на противоположных сторонах X называются вертикальными углами. Эти углы равны, и вот официальная теорема, которая говорит вам об этом.
Вертикальные углы конгруэнтны: Если два угла — вертикальные углы, то они конгруэнтны (см. Выше рисунок).
Вертикальные углы — одна из наиболее часто используемых вещей в доказательствах и других типах проблем геометрии, и они являются одной из самых простых вещей, которые можно обнаружить на диаграмме. Не пренебрегайте их проверкой!
Вот проблема алгебраической геометрии, которая иллюстрирует это простое понятие: Определите меру шести углов на следующем рисунке.
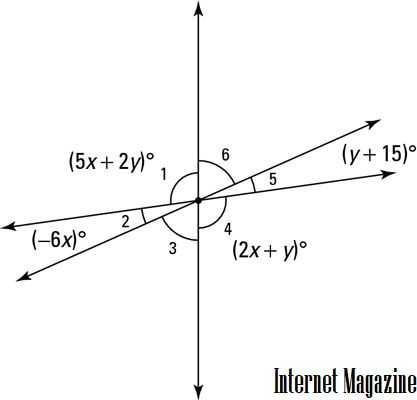
Вертикальные углы конгруэнтны, поэтому
и, следовательно, вы можете установить их значения равными друг другу:
Теперь у вас есть система из двух уравнений и двух неизвестных. Для решения системы сначала разрешите каждое уравнение для y :
y = -3 x
y = -6 x — 15
Далее, поскольку оба уравнения решены для y , вы можете установить два выражения x равными друг другу и решить для x :
, подключите -5 для x в первом упрощенном уравнении: y = -3
= 15 Теперь подключите -5 и 15 в угловые выражения, чтобы получить четыре из шести углов:
Чтобы получить угол 3 , обратите внимание, что углы 1, 2 и 3 образуют прямую линию, поэтому они должны суммироваться до 180 °: Наконец, угол 3 и угол 6 совпадают с вертикальными углами, поэтому угол 6 должен быть равен 145 °. Вы заметили, что углы на рисунке абсурдно не в масштабе? Не забывайте, что вы не можете ничего принять относительно относительных размеров углов или сегментов диаграммы.
ru.no-dummy.com
Конгруэнтный треугольник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Конгруэнтный треугольник
Cтраница 1
Конгруэнтные треугольники являются, конечно, частным случаем, однако совсем по другим причинам; это особые подмЬожестна множества треугольников. Треугольная пирамида есть частный случай пирамиды, но не то же, что тетраэдр; иначе правильная треугольная пирамида была бы правильным тетраэдром, что, разумеется, неверно. Пожалуй, треугольная пирамида есть пара, состоящая из тетраэдра и одной из его вершин. Впрочем, я думаю, что в традиционной геометрии не пускаются в такие тонкости, ее язык, освященный двухтысячелет-ними традициями, кажется просто незыблемым. [1]
Его профильной проекцией является конгруэнтный треугольник. [2]
Разбиваем многоугольник на элементарные треугольники и строим в стороне конгруэнтный треугольник ЛВС, к стороне Л С пристраиваем треугольник ACD, к стороне AD пристраиваем треугольник ADE, и наконец, к стороне АЕ пристраиваем треугольник АЕМ. В результате получим две конгруэнтные фигуры. [3]
CD, а это и значит, что все грани тетраэдра есть попарно конгруэнтные треугольники. [4]
Чтобы доказать утверждения I, II, III и IV, соединим центр окружности с вершинами многоугольника, проведем перпендикуляры от центра к сторонам и выберем конгруэнтные треугольники. [5]
В одной из своих работ, касающихся аксиом евклидовой плоскости, Н. Ф. Четверухин [2] показал, что система аксиом Молерупа ( в которой последний совершенно не пользуется конгруэнтностью углов) может быть получена из группы аксиом конгруэнтности ( Гильберта) при помощи подходяще выбранного определения конгруэнтности углов; если же конгруэнтными углами назвать соответственные — углы двух конгруэнтных треугольников, то, не нарушая системы Гильберта, можно в ней сделать некоторые сокращения. [6]
Понятие конгруэнтности достаточно наглядно: два треугольника конгруэнтны, если они одинаковой формы и одного размера. Однако дети часто находят трудными те рассуждения с конгруэнтными треугольниками, которые применяются для доказательства теорем. [7]
Правда, для этого окажется недостаточным ни параллельный сдвиг, совмещающий конгруэнтные треугольники, ни преобразование подобия, растягивающее или сжимающее геометрические фигуры, ни даже проектирование, переводящее окружность в эллипс. Наложить любые две буквы ( 1) друг на друга нам удастся лишь в том случае, если мы их непрерывно деформируем. [8]
На плоскости V и W основание пирамиды проецируется в отрезки прямых, расположенные на осях ОХ и OY, а боковые, грани — в разные по величине треугольники. Боковые грани, наклоненные к плоскостям V и W под одинаковыми углами, проецируются на них в конгруэнтные треугольники. [9]
Теперь ясно, что ответ на поставленный вопрос положителен: если многоугольники равновелики, то их равносоставленность может быть установлена при помощи движений, сохраняющих ориентацию. В самом деле, по теореме Бойяи — Гервина можно разбить два равновеликих многоугольника на соответственно конгруэнтные части, а потому — на соответственно конгруэнтные треугольники. Но два конгруэнтных треугольника либо получаются друг пз друга движением, сохраняющим ориентацию, либо же ( как на рис. 40) могут быть разбиты каждый на три части, получающиеся друг из друга движениями, сохраняющими ориентацию. [10]
Если ребенок знает, что такое ромб или параллелограмм, то он может визуально определить свойства этих фигур. Многие из этих свойств ученики перечислят в свободной беседе: в параллелограмме противоположные стороны равны и параллельны, противоположные углы равны, а соседние углы дополняют друг друга до развернутого; диагонали, пересекаясь, делятся пополам; параллелограмм имеет центр симметрии, его можно разложить на конгруэнтные треугольники, равными параллелограммами можно замостить плоскость — вот целая куча визуальных свойств, которые могут быть упорядочены. Я уже разъяснял, как здесь начинается дедуктивное построение; эти свойства не вводятся, а развертываются из локальных начал. Свойства параллелограмма должны быть дедуктивно связаны друг с другом; некоторые должны считаться исходными, из которых выводятся остальные. Так появляются определения; и тогда можно понять, почему квадрат является в то же время и ромбом, а ромб — параллелограммом. Так ребенок учится определениям и узнает, что определение — нечто большее, чем просто описание, что это — средство дедуктивного упорядочения свойств некоторой вещи. [11]
Существуют еще два способа покрытия плоскости правильными многоугольниками. В одном из них используются правильные конгруэнтные треугольники, причем в каждой вершине сходятся по шесть треугольников, а в другом используются конгруэнтные квадраты, причем в каждой вершине сходятся по четыре квадрата. Из этих трех способов покрытия плоскости покрытие с помощью шестиугольников является наилучшим для упаковки вписанных единичных кругов внутри таких многоугольников. Мы вычислим эффективность такой упаковки, которую обозначим через Е, а также эффективность упаковки единичных кругов в квадраты, которую обозначим через Es, а эффективность упаковки третьего типа оставим в виде упражнения. Рассмотрим задачу упаковки равных кругов радиуса г 1 / 2 на плоскости таким образом, что каждый круг касается шести других кругов, как показано на фиг. Каждый такой круг можно рассматривать как круг, вписанный в правильный шестиугольник с тем же центром; эти шестиугольники заполняют плоскость. [12]
Не думайте, что геометрия на поверхности шара целиком и полностью отличается от евклидовой. Большинство евклидовых теорем, которые не зависят от идеи параллельных прямых, остаются верными для сферической геометрии. Для нее сохраняются, например, и теория конгруэнтных треугольников, и свойство равенства углов при основании равнобедрещого. [13]
Следовательно, А АВС Ш А ОаОьО и, конечно, конгруэнтные треугольники имеют одинаковые радиусы описанных вокруг них окружностей. Так как отрезок АР перпендикулярен отрезку OjOc, который параллелен отрезку ВС, то высотами треугольника АВС являются прямые АР, ВР и СР. Поэтому точка Р совпадает с точкой Н ( [ И ], стр. [14]
Ни одна из перечисленных проблем не подходит для такого построения. Возможно, что допускается вычисление с помощью линейной алгебры пересечения сферы с плоскостью или двух сфер, однако для того, чтобы открыть, что эти пересечения являются окружностями, нужно знать, что такое реальная сфера в реальном пространстве. Разумеется, можно с помощью алгебраического доказательства убедиться, что радиус окружности равен длине стороны вписанного в нее правильного шестиугольника, однако такое доказательство может понравиться лишь тому, кто стремится затемнить все существенное. Линейная алгебра не только совершенно непригодна для того, чтобы открыть возможность замощения плоскости конгруэнтными треугольниками; с ее помощью это утверждение почти невозможно доказать. Можно было бы проиллюстрировать почти на всех разобранных выше примерах, насколько бессильны в них методы линейной алгебры. [15]
Страницы: 1 2
www.ngpedia.ru
Конгруэнтные регулярные лица подразумевают конгруэнтные двугранные углы?
I have seen definitions of regular polyhedra where it is assumed only that the faces are congruent and regular (equilateral). I have seen also definitions where two conditions are assumed:
- Congruent regular faces.
- Congruent Dihedral angles.
I belive that the condition (1) above implies the condition (2) above.
Is this right?
Update:
The following link: A congruence problem for polyhedra
Has the following :
Theorem 1.2 (Cauchy, 1839). Two convex polyhedra with corresponding congruent and similarly situated faces have equal corresponding dihedral angles.
I believe this is the line of search that I would go for.
Final Update: At this point the answers with counter-examples are good. I wanted to point out to the book in this link Polyhedra
A set of counter-examples is given in Figure 2.18. But most important is the following theorem:
Theorem: Let $P$ be a convex polyhedron whose faces are congruent regular polygons. Then the following statements about $P$ are equivalent:
- The vertices of $P$ all lie on a sphere.
- All the dihedral angles of $P$ are equal.
- All the vertex figures are regular polygons.
- All the solid angles are congruent.
- All the vertices are surrounded by the same number of faces.
Again, thanks to all who helped.
Я видел определения правильных многогранников, где предполагается, что грани конгруэнтные и регулярные (равносторонние). Я также видел определения, в которых предполагаются два условия:
- Конгруэнтные обычные лица.
- Конгруэнтные двугранные углы.
Я считаю, что условие (1) выше означает условие (2) выше.
Это право?
Update:
Следующая ссылка: A congruence problem for polyhedra
Имеет следующие:
теоремы 1.2 (Коши, 1839). Два выпуклых многогранника с соответствующим конгруэнтным и аналогично расположенными гранями имеют одинаковые двугранные углы.
Я считаю, что это линия поиска, в которую я бы пошел.
Окончательное обновление: На этом этапе ответы на встречные примеры хороши. Я хотел, чтобы указал на книгу в этой ссылке Polyhedra
На рисунке 2.18 приведен набор встречных примеров. Но наиболее важным является следующая теорема:
Теорема Пусть $P$ выпуклый многогранник, грани которого являются конгруэнтными правильные многоугольники. Тогда следующие утверждения о $P$ эквивалентны:
- Вершины $P$ все лежат на сфере.
- Все двугранные углы $P$ равны.
- Все фигуры вершин являются правильными многоугольниками.
- Все твердые углы конгруэнтны.
- Все вершины окружены одинаковым числом лиц.
Опять же, спасибо всем, кто помогал.
geometry platonic-solids81
math.stackovernet.com
Большая Энциклопедия Нефти и Газа, статья, страница 1
Конгруэнтность
Cтраница 1
Конгруэнтность нельзя раскрывать механически, так как индексы, соединенные знаком, не всегда подразделяются одинаково, поскольку отражают разные понятия. Часто при раскрытии знака конгруэнтности меняется содержание понятий и, соответственно, терминология, например 553.31 Железорудные месторождения, а образованный с помощью индекс 622.341 означает Добыча железных руд. [1]
Конгруэнтность mod S минимальная среди всех тех, для которых элементы 5 сравнимы друг с другом. Поэтому из условий теоремы следует, что К — смежный ласс mod К. Но последнее очевидно, так как из а Ъ ( 9) следует аТ ЪТ ( 0), и поскольку К — смежный класс для 9, то каждое из условий аТ К, ЪТ К влечет за собой другое. [2]
Конгруэнтность целей в данном случае означает, что целевые установки владельцев компании и ее управленческого персонала, ответственного за инвестиционную политику, главным образом в плане ее исполнения, могут не совпадать в полном объеме, однако эти различия не носят сколько-нибудь критического характера с позиции владельцев. [3]
Конгруэнтность целей ( задач) является одним из ключевых терминов в научной литературе по системам управления и контроля деятельности. [4]
Конгруэнтность фигур обладает рядом важных свойств. [5]
Конгруэнтность фигур обладает следующими свойствами. [6]
Отношение конгруэнтность связывает некоторые неосновные объекты, называемые отрезками и углами. Эти объекты мы определим ниже. Таким образом, на самом деле имеется два отношения конгруэнтности: одно — связывающее отрезки, а другое — углы. [7]
Понятие конгруэнтности достаточно наглядно: два треугольника конгруэнтны, если они одинаковой формы и одного размера. Однако дети часто находят трудными те рассуждения с конгруэнтными треугольниками, которые применяются для доказательства теорем. [8]
Понятия конгруэнтности и равенства не всегда совпадают. Конгруэнтные отрезки всегда равны. [9]
Знак конгруэнтности ( подразделяется как) позволяет переносить из одного раздела в другой последние цифры индекса, сходные по содержанию. [10]
Знак конгруэнтности может связывать не только близко расположенные индексы. [11]
Аксиомы конгруэнтности целесообразно взять в редакции Мура1), который для случая линейной конгруэнтности в основном берет аксиомы Гильберта, но не пользуется понятием конгруэнтности углов. [12]
Назовем некоторую конгруэнтность правильной, ебли она однозначно определяется любым своим смежным классом. Наконец, будем говорить, что алгебраическая система А правильная, если все конгруэнтности на ней правильны. Соединяя теоремы 6 и 5, легко сформулировать необходимые и достаточные условдя правильности системы. Однако эти условия слишком громоздки и желательно вместо них иметь хотя бы только необходимые или только достаточные, но более конкретные условия. Грубо, это можно сделать, например, следующим образом. [13]
Аксиома о конгруэнтности всех двойных точек добавляется здесь в целях формальной пол нош. [14]
Исходя из конгруэнтности характеристик, чертят одну такую кривую на прозрачной бумаге и перемещают ее параллельно самой себе таким образом, чтобы высшая ее точка А двигалась на параболе ОАМ. А дают соответственные числа оборотов, причем масштаб абсцисс определяется по отрезку а, которому соответствует число оборотов исходного положения кривой дросселирования. Полученная кривая DD2D4 имеет горизонтальную касательную, точка касания которой дает наименьшее допустимое число оборотов. [15]
Страницы: 1 2 3 4
www.ngpedia.ru