Математические методы в психологии — Образовательная платформа «Юрайт». Для вузов и ссузов.
- Скопировать в буфер библиографическое описание
Высоков, И. Е. Математические методы в психологии : учебник и практикум для академического бакалавриата / И. Е. Высоков. — Москва : Издательство Юрайт, 2017. — 386 с. — (Высшее образование). — ISBN 978-5-534-02728-0. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/401835 (дата обращения: 07.10.2022).
- Добавить в избранное
Учебник и практикум для академического бакалавриата
- Посмотреть кому понравилось
- Поделиться
- Описание
- Программа курса
- Видео: 10
- Тесты: 10
- Нет в мобильном приложении
- Аннотация
- Программа курса
- Медиаматериалы 10
- Тесты 10
Данное издание является примером выработки профессионального психологического подхода к использованию математических методов в практической деятельности.
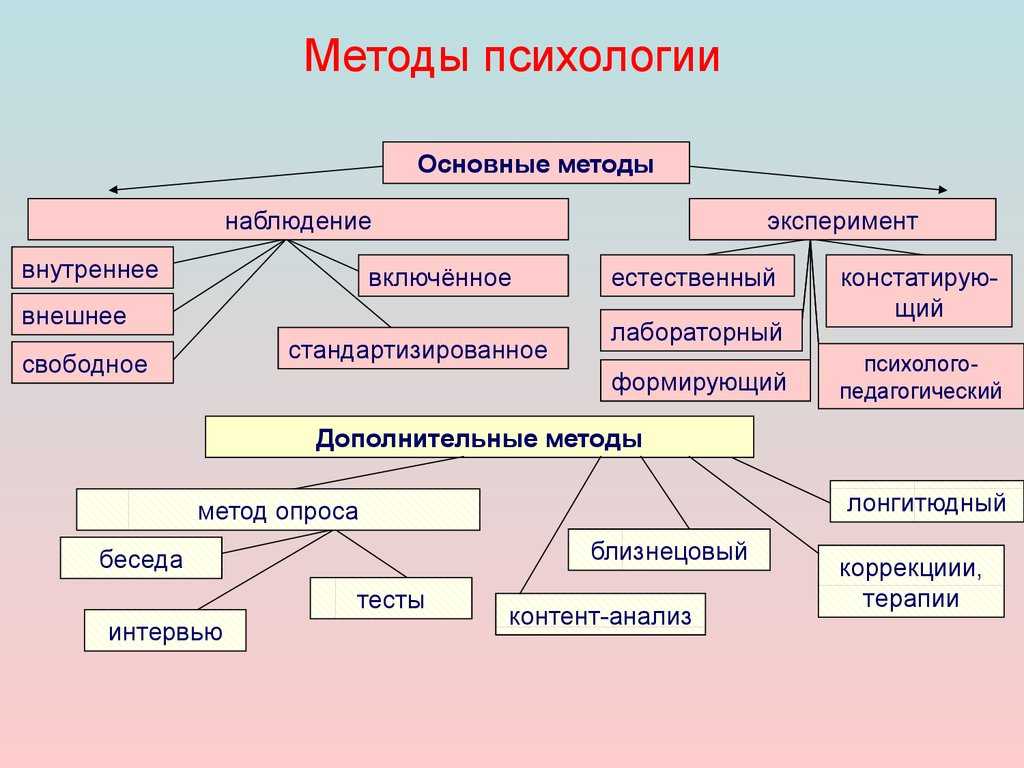
что это и основные виды
Содержание
- Суть и задачи
- Этапы развития и формирования
- Основные виды
- Стратегии обработки данных при работе с гипотезами
- Преимущества и недостатки
- Принципы применения в исследованиях
Психология — гуманитарная дисциплина. Поэтому у студентов начальных курсов возникает много вопросов, когда им приходится изучать высшую математику. Многие не знают, что такое математические методы в психологии — обязательный инструмент для анализа или усложненный прием, который можно заменить. Ответ можно получить только на практике, изучив особенности работы методики.
Поэтому у студентов начальных курсов возникает много вопросов, когда им приходится изучать высшую математику. Многие не знают, что такое математические методы в психологии — обязательный инструмент для анализа или усложненный прием, который можно заменить. Ответ можно получить только на практике, изучив особенности работы методики.
Суть и задачи
Математическая психология применяется для оценки полученных результатов и моделирования абстрактных ситуаций, требующих проверки. Аналитическое исследование не используется для изучения конкретного явления. Оно рассматривает психическую деятельность совокупно.
Объект исследований — естественная структура, имеющая психические свойства, модель, теоретическую базу. Предмет — создание и применение алгоритма для моделирования подобной структуры.
Математические методы нужны для обработки данных, собранных путем наблюдения или эксперимента. С их помощью решают задачи:
- на установление сходства или различия;
- на группировку, классификацию информации;
- на оценку, анализ источников данных;
- на составление прогноза на основе полученной информации.

Сущность матметодов — описание психологических явлений с помощью количественных показателей. Применение алгоритмов при подсчете результатов снижает риск появления ошибки. Информацию можно собирать, обрабатывать и классифицировать одновременно.
Этапы развития и формирования
Сейчас математика занимает отдельное место в психологии. Ее выделение в самостоятельную дисциплину шло постепенно. В этом процессе есть отдельные этапы, подробно рассмотренные в книге Первитской А. М. «Математические методы в психологии»:
- Первый — конец 19 – начало 20 века. Результаты эксперимента впервые обрабатываются заданным алгоритмом. Сформировались первые законы и дисциплины.
- Второй — 40–50 г. Появилась первая модель психических процессов, разработанная с использованием матанализа. Проведение практических испытаний.
- Третий — с 60 годов по настоящее время. Официальное признание самостоятельности отрасли. Включение в список обязательных для изучения дисциплин.

- Четвертый — время наступления неизвестно. Этот этап будет переходом математической психологии в теоретическую.
Математическую психологию часто воспринимают как совокупность матметодов, но на самом деле они — только часть дисциплины, как эксперимент — часть исследования.
Основные виды
Шкала измерений — удобный способ обработки данных. В первую очередь используют количественную шкалу. С ее помощью данные ранжируют — распределяют по показателям. Данные размещаются в порядке убывания или возрастания. Каждому значению добавляют ранг, определяющий минимальный и максимальный показатель. Сравнение рангов необходимо для распределения данных по группам.
Корреляционный анализ — установление связи между явлениями. Корреляцию оценивают по силе, направлению. Показатели могут возрастать и убывать, из-за чего меняется тип зависимости данных. Он бывает линейным (показатели равноудалены), но чаще выражен в форме кривой.
Факторный анализ — прогнозирование результатов. Изначально данные расцениваются как равные показатели, для получения результатов их табулируют (заносят в таблицу) или используют графическое построение.
Изначально данные расцениваются как равные показатели, для получения результатов их табулируют (заносят в таблицу) или используют графическое построение.
Стратегии обработки данных при работе с гипотезами
Гипотеза — предположение, требующее проверки. Чтобы использование методов математической обработки в психологии давало достоверный результат, исследователи должны соблюдать правила выбора, проверки гипотезы:
- Статистические гипотезы бывают нулевыми и альтернативными. Они несовместимы и взаимоисключающие.
- Проверять гипотезу нужно с помощью статистических критериев — правил, по которым принимают истинную и отклоняют ложную гипотезу.
- Критерии бывают параметрическими (данные распределены по шкале) и непараметрическими (распределение данных не учитывается).
- Порядок проверки критериев включает выбор критерия, определение зависимости или независимости выборки, количество выборок.
- Гипотезу оценивают по числовым характеристикам. Точечно, выбрав одно число на оси, или интервально, используя измерение отрезка данных на оси.

Выбор способа проверки гипотезы зависит от поставленной задачи.
Преимущества и недостатки
С помощью алгоритмов можно оперировать большим объемом данных и получать достоверные результаты. Недостатки:
- Результаты моделирования необходимо подтверждать экспериментом в реальных условиях.
- Моделирование не дает заглянуть дальше исследуемой области данных.
- При выборе эксперимента повышается риск «подгонки» реальных данных под моделируемый процесс.
Принципы применения в исследованиях
Принципы применения математических методов — положения, которые используют в психологии. Они определяют применение и стратегии дальнейшего развития науки. К ним относятся:
- Принцип детерминизма. Требует объяснения изучаемых феноменов через общепринятые факты (под общепринятыми понимаются факты, официально признанные учеными и опубликованные в соответствующей литературе).
- Деятельность, личность и сознание едины. Личность — носитель сознания, а сознание неотделимо от личности.
 Деятельность — форма взаимодействия личности с миром, определяемая причинно-следственной связью.
Деятельность — форма взаимодействия личности с миром, определяемая причинно-следственной связью. - Личностный и системный подход. Требует рассматривать объекты как отдельные, присущие одному человеку и группе.
- Обусловленность рефлекторной и социальной составляющей. Объективный мир влияет на психику, поэтому психические явления — отражение окружающей действительности.
- Принцип совокупности. Требует исследования явления как единого целого.
- Принцип развития. Явления необходимо рассматривать во время развития, с учетом причин появления и возможных вариантов объединения.
- Принцип иерархии. Предполагается рассматривать психологические явления как лестницу, с подчинением низших ступеней высшим.
- Единство теории, эксперимента и практики. Теория проверяется практическим экспериментом, необходимым для поиска решения.
Чтобы получать достоверные результаты, психолог должен соблюдать все принципы.
Несмотря на все недостатки, матметоды все же остаются подходящим инструментом проверки гипотез, снижающими вероятность погрешности.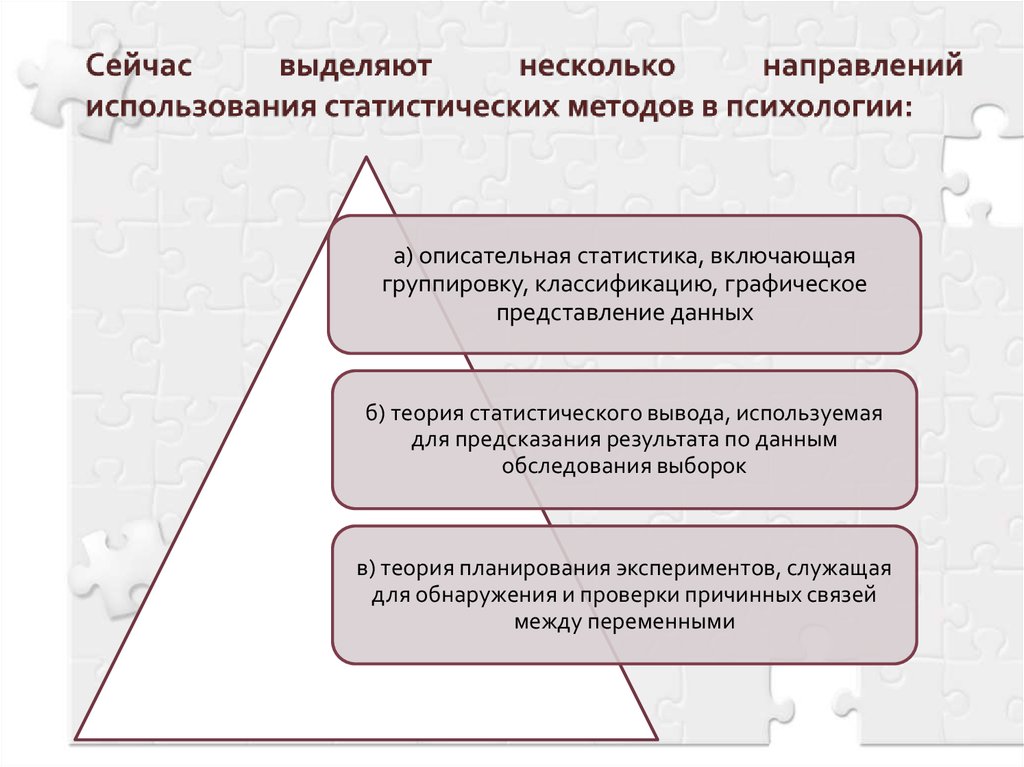 Точность результатов в большей степени зависит от навыков исследователя, чем от выбранного способа оценки.
Точность результатов в большей степени зависит от навыков исследователя, чем от выбранного способа оценки.
Рейтинг автора
Написано статей
Об авторе
Организатор конкурса:Профессиональное Церемония награжденияпобедителей конкурса: Ежегодный Обсуждениепроектов конкурса Профессиональное КонкурсИстории успеха Конкурс эссе Подписка на новости | Национальный
по итогам 2005 года | |
Автор:
Наследов А. Актуальность. Использование математических методов — непременное условие проведения большинства психологических исследований в наши дни. Данная книга помогает специалистам, не имеющим основательной математической подготовки, представить результаты своей работы в виде, максимально отвечающем требованиям современной психологической науки.
Социальная, научная и практическая значимость. «Исследование в любой области, в том числе и в психологии, предполагает получение результатов — обычно в виде чисел. Однако просто собрать данные недостаточно. Даже объективно и корректно собранные данные ничего не говорят. Исследователю необходимо умение организовать их, обработать и проинтерпретировать, что невозможно без применения математических методов. Конечно, можно сослаться на наличие современных компьютерных программ, применение которых сейчас становится нормой для исследователя. Значение для развития психологии. «…Психология в любых ее приложениях — и практических, и теоретических, может развиваться только на основе количественных исследований, связывающих теорию и практику с фактами».
Цели. «Жанр книги по первоначальному замыслу — учебное пособие для студентов факультета психологии. Но в процессе работы над книгой источником идей являлась не только практика преподавания, но и опыт участия в многочисленных исследованиях в роли руководителя или консультанта. В итоге появились основания надеяться, что книга станет не только учебником для студентов, но будет полезна для широкого круга исследователей — как справочник и практическое руководство по анализу и интерпретации данных. Справочному назначению книги способствует предметный указатель и англо-русский терминологический словарь, а практическое руководство воплощено в пошаговых инструкциях по применению каждого из методов. Назначение книги — формирование умений самостоятельно анализировать и, главное, интерпретировать эмпирические данные — результаты исследований». Аудитория, на которую рассчитан проект. Книга полезна для самых разных групп читателей: для начинающих психологов, для студентов-выпускников психологических и педагогических специальностей, для психологов-исследователей, для преподавателей психологии, читающих соответствующие курсы или руководящих дипломными и диссертационными проектами.
Основное содержание работы (или ее этапы). «Структура книги соответствует стремлению представить множество математических методов в виде упорядоченной, логически и иерархически взаимосвязанной системы. Во вступлении дано общее описание этой системы и ее частей (модели измерения, описания и статистического вывода). Основной материал книги изложен в трех частях. В первой части даны элементарные основы применения математических методов. Ее назначение — подготовка читателя к восприятию основного материала книги. Этому способствуют задачи и упражнения в конце глав. Вторая часть включает в себя детальное описание основных методов статистического вывода.
Результаты, выводы. С конца XIX века «возможность применения математических методов в психологии перестает вызывать сомнения. Но вопрос о необходимости их применения до сих пор вызывает дискуссии. Между тем, проблема может быть решена признанием того, что психология — это и наука и искусство. НАСЛЕДОВ АНДРЕЙ ДМИТРИЕВИЧ — СПбГУ, ф-т психологии, доцент кафедры педагогики и педагогической психологии, канд. психол. наук «Психологические особенности технически-опосредованного педагогического общения» Все проекты конкурса | ||
Общество математической психологии | Прошедшие встречи
| июль 2022 года | Личный MathPsych/ICCM 2022 | Торонто, Канада | |
июль 2022 г. | Виртуальный MathPsych/ICCM 2022 | Только виртуальный | |
| ноябрь 2021 г. | MathPsych на виртуальной психономике 2021 | Только виртуальный | |
| июль 2021 г. | Виртуальный MathPsych/ICCM 2021 | Только виртуальный | |
| Февраль 2021 | Австралазийская конференция по математической психологии, 2021 г. | Ньюкасл, Новый Южный Уэльс | |
| ноябрь 2020 г. | MathPsych на виртуальной психономике 2020 | Только виртуальный | |
| июль 2020 | Виртуальный MathPsych/ICCM 2020 | Только виртуальный |
Ноябрь 2019 г. | Сопутствующая встреча | Монреаль, Квебек, Канада | |
| Июль 2019 г. | Ежегодное собрание | Монреаль, Квебек, Канада | |
| Ноябрь 2018 г. | Сателлитная встреча | Новый Орлеан, Лос-Анджелес | |
| Июль 2018 г. | Ежегодное собрание | Мэдисон, Висконсин | |
| Ноябрь 2017 г. | Сателлитная встреча | Ванкувер, Британская Колумбия, Канада | |
| июль 2017 г. | Ежегодное собрание | Ковентри, Соединенное Королевство | |
| Ноябрь 2016 г. | Сателлитная встреча | Бостон, Массачусетс | |
| Август 2016 г. | Ежегодное собрание | Нью-Брансуик, Нью-Джерси | |
Июль 2015 г. | Годовое собрание | Ньюпорт-Бич, Калифорния | |
| Июль 2014 г. | Ежегодное собрание | Квебек, Квебек, Канада | |
| Август 2013 г. | Ежегодное собрание | Потсдам, Германия | |
| Июль 2012 г. | Ежегодное собрание | Колумбус, Огайо | |
| Июль 2011 г. | Ежегодное собрание | Бостон, Массачусетс | |
| Август 2010 г. | Ежегодное собрание | Портленд, штат Орегон | |
| Август 2009 г. | Ежегодное собрание | Амстердам, Нидерланды | |
| Июль 2008 г. | Ежегодное собрание | Вашингтон, округ Колумбия | |
Июль 2007 г. | Ежегодное собрание | Ирвин, Калифорния | |
| Июль 2006 г. | Ежегодное собрание | Ванкувер, Британская Колумбия, Канада | |
| август 2005 г. | Ежегодное собрание | Мемфис, Теннесси | |
| Июль 2004 г. | Ежегодное собрание | Анн-Арбор, Мичиган | |
| Июль 2003 г. | Ежегодное собрание | Огден, Юта | |
| Июль 2002 г. | Ежегодное собрание | Оксфорд, Огайо | |
| Июль 2001 г. | Ежегодное собрание | Провиденс, Род-Айленд | |
| Август 2000 г. | Ежегодное собрание | Кингстон, Онтарио, Канада | |
Июль 1999 г.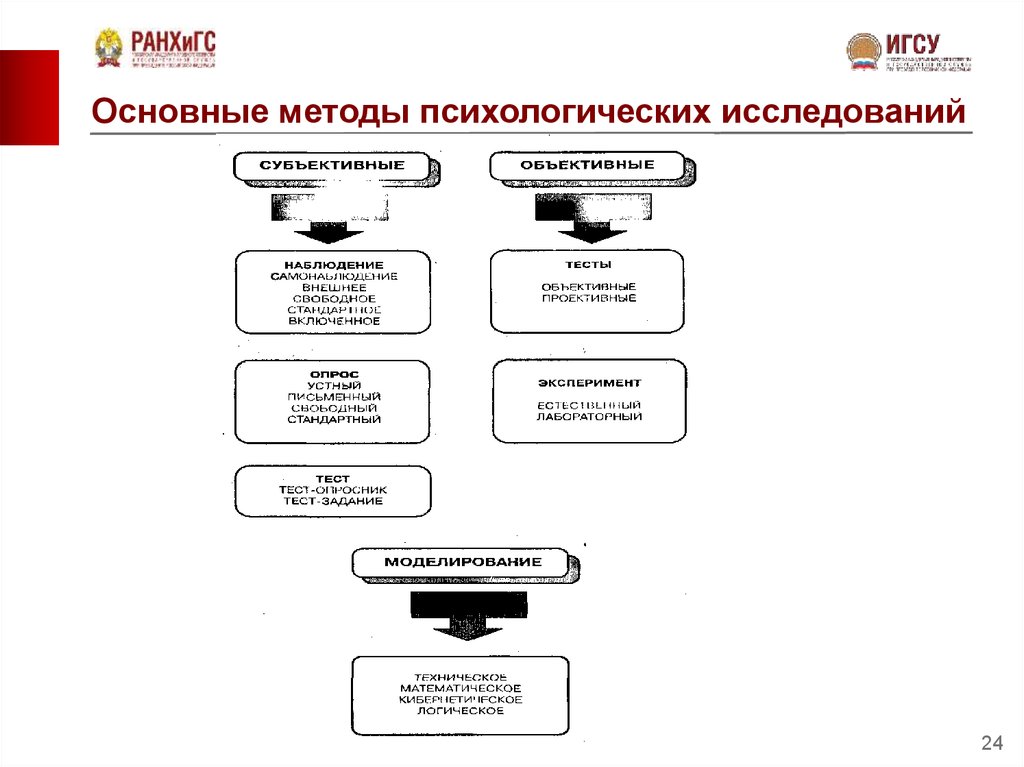 | Ежегодное собрание | Санта-Крус, Калифорния | |
| Август 1998 г. | Ежегодное собрание | Нэшвилл, Теннесси |
Наш архив неполный. Если у вас есть какой-либо из недостающих документов или информации, пожалуйста, свяжитесь с нами по ссылке ниже!
Общество математической психологии | Похожие собрания
Journal of Mathematical Psychology публикует исследовательские статьи, монографии и обзоры,
заметки и комментарии, рецензии на книги по всем разделам математической и теоретической психологии.
Приветствуются эмпирические исследования, имеющие прямое отношение к теоретическим вопросам психологии.
Статьи по фундаментальным измерениям и математическим моделям, например, основанным на коннекционизме,
другие нейронные сети или концепции обработки информации по-прежнему представляют особый интерес для
журнал. Также приветствуются теоретические работы и эмпирические исследования, касающиеся моделей в таких областях.
как поведение животных, искусственный интеллект и компьютерное моделирование психологических процессов,
теория принятия решений, человеческий фактор и взаимодействие человека с компьютером, обучение и память, мотивационные
динамика, решение проблем, психолингвистика, психофизика, психометрия (если работа касается
объяснение психологических понятий или моделей процессов), а также ощущение и восприятие.
Также приветствуются теоретические работы и эмпирические исследования, касающиеся моделей в таких областях.
как поведение животных, искусственный интеллект и компьютерное моделирование психологических процессов,
теория принятия решений, человеческий фактор и взаимодействие человека с компьютером, обучение и память, мотивационные
динамика, решение проблем, психолингвистика, психофизика, психометрия (если работа касается
объяснение психологических понятий или моделей процессов), а также ощущение и восприятие.
Онлайн-подача в Journal of Mathematical Psychology : портал подачи (www.ees.elsevier.com/jmp)
Руководство по написанию учебных статей в Journal of Математическая психология : Учебное пособие.
Редакторы
Главный редактор
| Проф. Адель Дидерих | Университет Джейкобса |
Младшие редакторы
Проф. Клинтин Дэвис-Стобер Клинтин Дэвис-Стобер | Университет Миссури |
| Д-р Этибар Н. Джафаров | Университет Пердью |
| Эндрю Хиткот | Университет Тасмании |
| Юрген Хеллер | Университет Тюбингена |
| Мишель Регенветтер | Университет Иллинойса в Урбана-Шампейн |
Робин Д. Томас Томас | Университет Майами |
| Фрэнсис Терлинкс | Университет Левена, Бельгия |
Редактор учебников
| Проф. Джо Хоупт | Техасский университет в Сан-Антонио |
Редакторы-консультанты
| Росио Алькала-Кинтана | Мадридский университет Комплутенсе |
| Грег Эшби | Калифорнийский университет в Санта-Барбаре |
Проф. Рафал Богач Рафал Богач | Оксфордский университет, Соединенное Королевство |
| Доктор Скотт Браун | Университет Ньюкасла |
| Дэвид Будеску | Фордхэмский университет |
| Доктор Ричард Чечил | Университет Тафтса |
| Сюзанна Дитлевсен | Копенгагенский университет, Дания |
| Ральф Энгберт | Потсдамский университет, Германия |
| Мигель Гарсия-Перес | Мадридский университет Комплутенсе, Испания |
| Клаудия Гонсалес-Валлехо | Университет Огайо |
Дэниел В. Хек Хек | Марбургский университет |
| Чан-Бин (CB) Хуан | Китайская академия наук, Пекин, Китай |
| Мэтт Джонс | Университет Колорадо в Боулдере |
| Наталья Карелайя | INSEAD, Фонтенбло, Франция |
| Константинос Кацикопулос | Университет Саутгемптона, Соединенное Королевство |
Проф. Ян Крайбич Ян Крайбич | Университет штата Огайо |
| Дэниел Р. Литтл | Мельбурнский университет |
| Тим Плескац | Канзасский университет |
| Лука Стефанутти | Университет Падуи, Падуя, Италия |
| Рейнхард Сосать | Оснабрюкский университет, Германия |
| Дженнифер Трублад | Университет Индианы в Блумингтоне |
| Мариус Ашер | Тель-Авивский университет, Израиль |
Проф. Цзюнь Чжан Цзюнь Чжан | университет Мичигана |
Редакционно-консультационный совет
| Доктор Джером Буземейер | Университет Индианы |
| Ганс Колониус | Ольденбургский университет |
| Эй Джей Марли | Университет Виктории |
Проф. Джей И. Мён Джей И. Мён | Университет штата Огайо |
| Роджер Рэтклифф | Университет штата Огайо |
| Ричард Швейкерт | Университет Пердью |
Ричард М.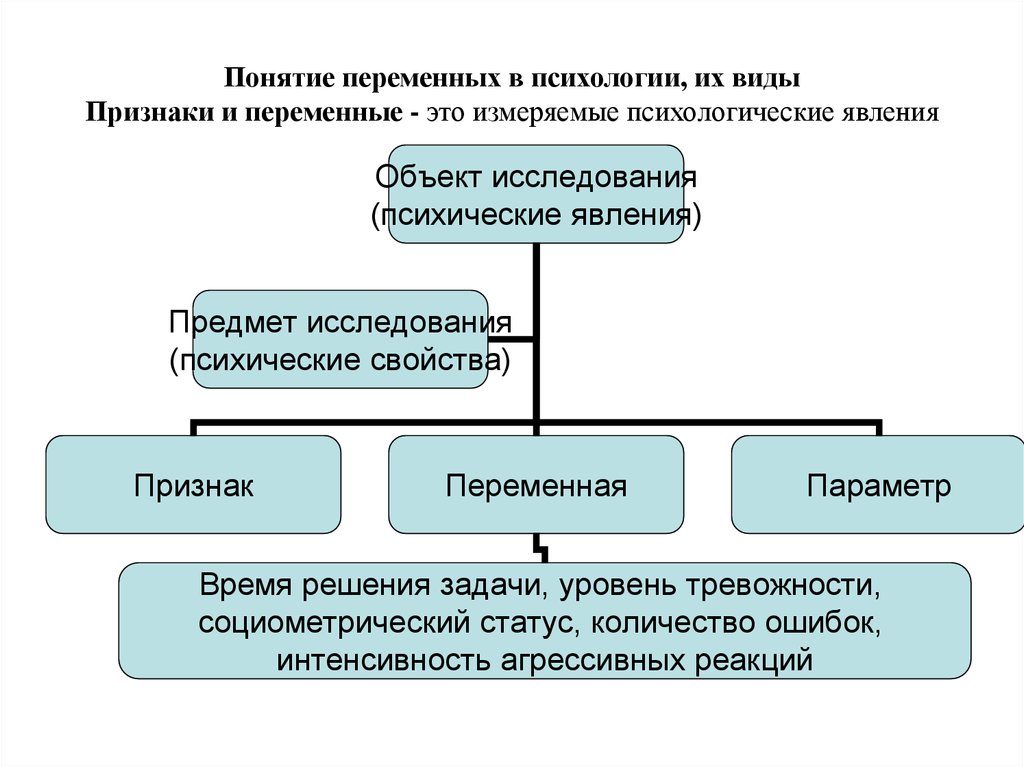 Шиффрин Шиффрин | Университет Индианы |
| Филип Смит | Мельбурнский университет |
| Джеймс Т. Таунсенд | Университет Индианы |
| Томас Валлстен | Университет Мэриленда в Колледж-Парке |
Past editors of Journal of Mathematical Psychology
| 2015 — 2018 | Philip Smith | |||||||||||||||||||||||||||||||
| 2010 — 2014 | Prof. Jay I. Myung Jay I. Myung | |||||||||||||||||||||||||||||||
| 2005 — 2009 | Dr. Jerome Busemeyer | |||||||||||||||||||||||||||||||
| 2001 — 2004 | Ричард Швейкерт | |||||||||||||||||||||||||||||||
| 1995 — 2000 | Hans Colonius | |||||||||||||||||||||||||||||||
| 1990 — 1994 | Thomas Wallsten | |||||||||||||||||||||||||||||||
| 1985 — 1989 | Джеймс Т. Таунсенд | |||||||||||||||||||||||||||||||
| 1980 — 1984 | A. A. J. Marley | |||||||||||||||||||||||||||||||
| 1976 — 1979 | William H. Batchelder | |||||||||||||||||||||||||||||||
| 1975 — 1975 | . Duncan Luce | |||||||||||||||||||||||||||||||
| 1971 — 1974 | J. E. Keith Smith | |||||||||||||||||||||||||||||||
| 1964 — 1970 | Ричард С. Аткинсон |
Общество по математической психологии | Награды
Общество математической психологии вручает ежегодную награду
за исключительные опубликованные исследования в области математики
психологии начинающим следователем. Ранее известный как «Новый
Премия исследователя», она была переименована в честь Уильяма К. Эстеса в 2009 году.
признавая его вклад в наше Общество и область
математическая психология вообще.
Ранее известный как «Новый
Премия исследователя», она была переименована в честь Уильяма К. Эстеса в 2009 году.
признавая его вклад в наше Общество и область
математическая психология вообще.
Право на участие, номинация и отбор
Премия Уильяма К. Эстеса за раннюю карьеру присуждается за исключительные
опубликовал исследование в области математической психологии
ранний исследователь карьеры. «Начинающий исследователь» предназначен для
включают лиц, которые либо являются студентами, либо не старше восьми лет
лет после докторской степени. в срок номинации. Публикации от
будет рассматриваться не более чем за восемь лет до крайнего срока выдвижения кандидатур. Награда вручается за тело
работ в области математической психологии. Единоличный автор
публикациям придается наибольшее значение, но комитет может рассмотреть
кандидаты, которые были первыми авторами более чем одной публикации. назначенное лицо не обязательно должно быть членом Общества. Самовыдвижения
не будет рассматриваться.
назначенное лицо не обязательно должно быть членом Общества. Самовыдвижения
не будет рассматриваться.
Победитель будет выбран специальной комиссией, назначенной Исполнительный комитет; отборочную комиссию обычно возглавляет Президент общества. Победитель будет объявлен на Ежегодном Заседание Общества математической психологии. Получатель получит Не облагаемая налогом премия в размере 250 долларов плюс до 1000 долларов на дорожные расходы. приглашен выступить с докладом на одном из будущих собраний Общества.
Номинации должны быть отправлены по электронной почте не позднее 15 апреля каждого года. Номинации должны включать:
- краткое изложение значимости исследования на одной странице
- текущий CV
- рекомендательное письмо от номинатора
- письмо от номинанта, в котором говорится, что он согласен быть рассмотренным для получения награды
Пожалуйста, отправьте все материалы Лесли Блаха по адресу info@mathpsych. org с темой: Номинация на премию «Ранняя карьера» <имя кандидата> .
org с темой: Номинация на премию «Ранняя карьера» <имя кандидата> .
Прошлые лауреаты премии Уильяма К. Эстеса за раннюю карьеру
| 2022 | Адам Ост | |
| 2021 | Дэниел В. Хек Хек | |
| 2020 | Гай Хокинс | |
| 2019 | Джо Остервейл | |
| 2019 | Дора Мацке | |
| 2018 | Дэвид Келлен | |
| 2017 | Дженнифер Трублад | |
| 2016 | Джо Хоупт | |
| 2015 | Крис Донкин | |
| 2015 | Брэндон Тернер | |
| 2014 | Иоахим Вандекеркхове | |
| 2013 | Вольф Ванпэмел | |
| 2012 | Клинтин Дэвис-Стобер | |
| 2011 | Чарльз Кемп | |
| 2010 | Янне Куяла | |
2009 г. | Томас Л. Гриффитс | |
| 2008 г. | Скотт Браун | |
| 2007 г. | Даниэль Наварро | |
2006 г. | Эрик-Ян Вагенмакерс | |
| 2005 г. | Джош Тененбаум | |
| 2004 г. | Марк Ховард | |
2003 г. | Майкл Ли | |
| 2002 г. | Джордж Карабатсос | |
| 2001 г. | Дэвид Хубер | |
1999 г. | Мишель Регенветтер | |
| 1998 г. | Робин Д. Томас | |
1997 г. | Адель Дидерих | |
| 1996 г. | Джерри Балакришнан | |
| 1995 г. | Джей И. Мён | |
1994 г. | Зигмунт Пизло | |
| 1993 | Майкл Д’Змура | |
| 1991 г. | Питер Ваккер | |
1990 г. | Рами Цвик | |
| 1989 г. | Теодор Альпер | |
| 1988 | Майкл Радд | |
1987 г. | Роберт М. Нософски |
Общество математической психологии вручает ежегодную награду самым выдающимся статья опубликована в Journal of Mathematical Psychology за предыдущие три года. премия названа в честь Р. Дункана Люса в знак признания его основоположной роли в области математической психологии, и в нашем Обществе и в журнале. Премия R. Duncan Luce Outstanding Paper Award спонсируется Elsevier Inc.
Право на участие, номинация и отбор
Учитываются публикации, датированные любым из трех предшествующих календарных лет. Номинации должны включать точное название, авторов и дату публикации в Журнал математической психологии . Назначенные авторы не обязательно должны быть членами
Общество. Самовыдвижения рассматриваться не будут.
Номинации должны включать точное название, авторов и дату публикации в Журнал математической психологии . Назначенные авторы не обязательно должны быть членами
Общество. Самовыдвижения рассматриваться не будут.
Победитель будет выбран специальной комиссией, назначенной Исполнительным комитетом. и по согласованию с редактором Journal of Mathematical Psychology . Победитель будет объявлен на ежегодном собрании Общества математической психологии.
Номинации должны быть отправлены по электронной почте не позднее 15 апреля каждого года. Пожалуйста, отправьте все материалы Лесли Блаха через [email protected] с темой: Номинация на премию Luce Outstanding Paper Award <имя номинанта> .
Прошлые лауреаты премии R. Duncan Luce Outstanding Paper Award
| 2022 | Константин Мейер-Грант и Кристоф Клауэр | |
| 2021 | Питер Квам | |
| 2020 | Ченг-Та Ян, Шулан Се, Ченг Джу Се, Марио Фифик, Йен-Тин Ю и Чун-Хао Ван | |
| 2019 | Майкл Калиш, Джон Данн, Олег Бурдаков и Олег Сысоев | |
| 2018 | Дэниел Р. Литтл, Ами Эйдельс, Марио Фифик и Тони Ван Литтл, Ами Эйдельс, Марио Фифик и Тони Ван | |
| 2017 | Аннелис Бартлема, Рууд Ветцельс, Майкл Ли и Вольф Ванпэмел | |
| 2016 | Дени Кузино, Ги Л. Лакруа, Жилен Жигер и Себастьен Эли Лакруа, Жилен Жигер и Себастьен Эли | |
| 2015 | Джо Хоупт и Джеймс Т. Таунсенд | |
| 2014 | Брэндон Тернер и Пер Седерберг | |
| 2013 | Джеффри Роудер, Ричард Д. Мори, Пол Л. Спекман и Джордан М. Провинс Мори, Пол Л. Спекман и Джордан М. Провинс | |
| 2012 | Кристоф Клауэр и Дэвид Келлен | |
| 2011 | Клинтин Дэвис-Стобер | |
| 2010 | Дидерик Аэртс | |
2009 г. | Джефф Айверсон | |
| 2008 г. | Р. Дункан Люс и Рагнар Стейнгримссон | |
| 2007 г. | Робин Д. Томас Томас | |
| 2006 г. | Джером Бусемейер и Адель Дидерих | |
| 2005 г. | Майкл Левин | |
2004 г. | Эхтибар Н. Джафаров | |
| 2003 г. | Луи Наренс | |
| 2002 г. | Филип Смит | |
2001 г. | Джон Миямото | |
| 2000 г. | Ричард Чечил |
Общество математической психологии вручает ежегодную награду самым выдающимся
статья, опубликованная в Computational Brain & Behavior за предыдущие три года.
Премия Computational Brain & Behavior Outstanding Paper Award спонсируется Springer.
Право на участие, номинация и отбор
Учитываются публикации, датированные любым из трех предшествующих календарных лет. Номинации должны включать точное название, авторов и дату публикации в Вычислительный мозг и поведение . Назначенные авторы не обязательно должны быть членами Общества. Самовыдвижения рассматриваться не будут.
Победитель будет выбран специальной комиссией, назначенной Исполнительным комитетом и в консультации с редактором Computational Brain & Behavior . Победитель будет Объявлено на ежегодном собрании Общества математической психологии.
Номинации должны быть отправлены по электронной почте не позднее 15 апреля каждого года.
Пожалуйста, отправьте все материалы Лесли Блаха по адресу [email protected] с темой: Номинация на премию Computational Brain & Behavior Outstanding Paper Award <имя номинанта> .
Победители прошлых наград Computational Brain & Behavior Outstanding Paper Award
| 2022 | Крейг А. Сандерс и Роберт М. Нософски | |
| 2021 | Даниэль Наварро | |
| 2020 | Адам Н. Хорнсби, Томас Эванс, Питер С. Рифер, Рози Прайор и Брэдли С. Лав Хорнсби, Томас Эванс, Питер С. Рифер, Рози Прайор и Брэдли С. Лав | |
| 2019 | Ансельм Рот, Бренден Лейк и Тодд Гурекис |
Общество математической психологии вручает ежегодную награду за пожизненный вклад
члена Общества. Победители объявляются на ежегодном собрании
Общество и принять участие в «Разговоре со старшим научным сотрудником» в следующем ежегодном
встреча.
Победители объявляются на ежегодном собрании
Общество и принять участие в «Разговоре со старшим научным сотрудником» в следующем ежегодном
встреча.
Вклад может быть в любой из следующих областей:
- Вклад в математическое моделирование психологических явлений
- Наставничество студентов, преподавателей и других лиц с особым акцентом на развитие области математической психологии
- Служба, продвигающая область математической психологии
Право на участие, номинация и отбор
Получатели должны быть членами Общества математической психологии.
Номинации должны быть отправлены по электронной почте не позднее 15 апреля каждого года.
Назначения должны быть сделаны активным членом Общества математической психологии. Номинация
должны быть представлены в электронном виде Секретарю до установленного срока. Номинации должны включать:
Номинации должны включать:
- Текущее резюме кандидата
- Два номинационных письма объемом не более двух страниц каждое. Одно из писем должно прийти от номинант и один от другого члена Общества
- Письмо от номинанта, в котором говорится, что он согласен быть рассмотренным для получения награды и планирует принять участие в следующем году. Ежегодная встреча для беседы со старшим научным сотрудником
- Имя (имена) предполагаемого интервьюера для беседы со старшим научным сотрудником на ежегодном собрании
Самовыдвижения не допускаются. Каждый год отборочная комиссия будет продолжать рассматривать ранее представленных номинаций. Комитет предлагает обновить существующие номинации, а также новые номинации.
Номинации должны быть отправлены по электронной почте не позднее 15 апреля каждого года. Пожалуйста, отправьте все материалы Лесли Блаха по адресу [email protected] с темой: Премия старшего научного сотрудника Общества математической психологии <имя кандидата> .
Пожалуйста, отправьте все материалы Лесли Блаха по адресу [email protected] с темой: Премия старшего научного сотрудника Общества математической психологии <имя кандидата> .
Прошлые лауреаты премии старшего научного сотрудника Общества математической психологии
| 2022 | Джером Буземейер | |
| 2021 | Эй Джей Марли | |
| 2020 | Джеймс Т. |


 Деятельность — форма взаимодействия личности с миром, определяемая причинно-следственной связью.
Деятельность — форма взаимодействия личности с миром, определяемая причинно-следственной связью. Д. «Математические методы психологического исследования. Анализ и интерпретация данных». СПб.: Речь, 2006. 2-е изд., испр. и доп.
Д. «Математические методы психологического исследования. Анализ и интерпретация данных». СПб.: Речь, 2006. 2-е изд., испр. и доп.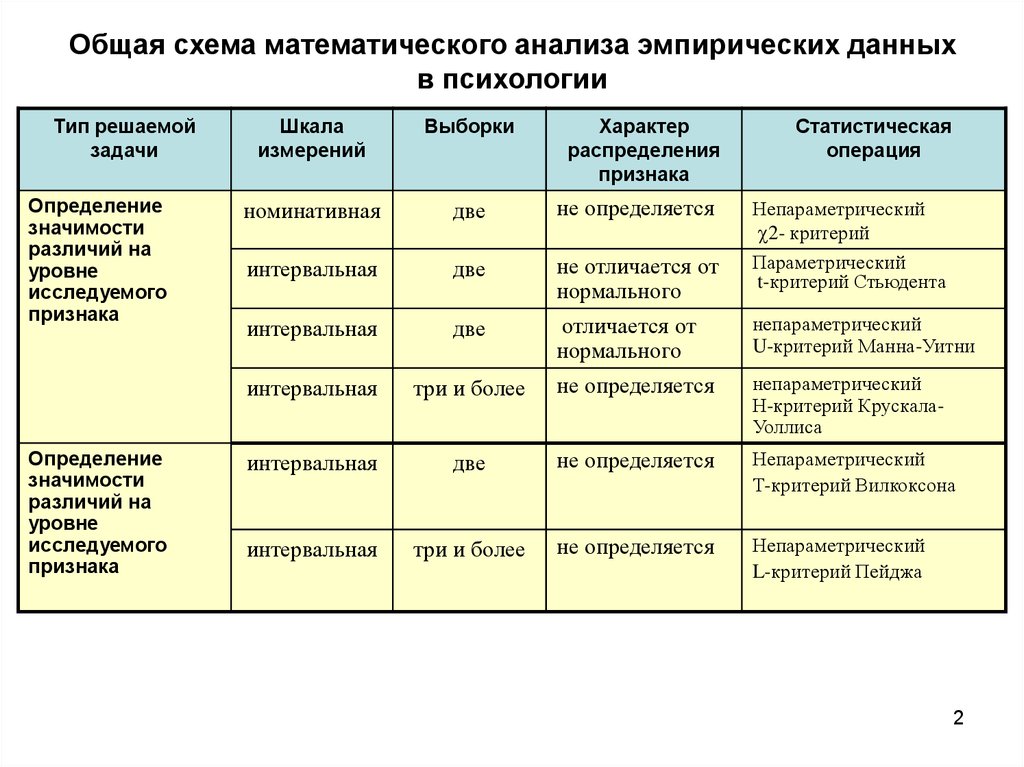 Но любая программа обработки данных переводит один набор чисел в другой набор чисел. При этом предлагается богатый набор способов такого преобразования, замечательным образом расширяющий возможности анализа данных. И для использования этих возможностей психолог должен уметь: а) организовать исследование так, чтобы его результаты были доступны обработке в соответствии с проблемами исследования; б) правильно выбрать метод обработки; в) содержательно интерпретировать результаты обработки. Эти умения не заменят ни компьютерная программа, ни «живой» математик — ее создатель. Таким образом, применение математики как общенаучного метода, наряду с экспериментом, неизбежно приобретает в психологии свои особенности, связанные со спецификой предмета. Неотъемлемой частью подготовки полноценного специалиста-психолога является изучение не только экспериментальной психологии, но и математических методов психологического исследования». Книга рекомендована Ученым советом факультета психологии СПбГУ к использованию в качестве учебного пособия.
Но любая программа обработки данных переводит один набор чисел в другой набор чисел. При этом предлагается богатый набор способов такого преобразования, замечательным образом расширяющий возможности анализа данных. И для использования этих возможностей психолог должен уметь: а) организовать исследование так, чтобы его результаты были доступны обработке в соответствии с проблемами исследования; б) правильно выбрать метод обработки; в) содержательно интерпретировать результаты обработки. Эти умения не заменят ни компьютерная программа, ни «живой» математик — ее создатель. Таким образом, применение математики как общенаучного метода, наряду с экспериментом, неизбежно приобретает в психологии свои особенности, связанные со спецификой предмета. Неотъемлемой частью подготовки полноценного специалиста-психолога является изучение не только экспериментальной психологии, но и математических методов психологического исследования». Книга рекомендована Ученым советом факультета психологии СПбГУ к использованию в качестве учебного пособия.

 Их изложение предваряется классификацией, которая позволяет выбрать метод в зависимости от исследовательской ситуации — от исходных данных и задач исследования. При изложении каждого метода особое внимание уделяется границам его применения, возможным альтернативам, технике вычислений («вручную» и на компьютере), особенностям интерпретации результатов. Третья часть содержит описание самых распространенных многомерных методов. Применение этих методов возможно только с использованием специальных компьютерных программ. Поэтому их математические основы и порядок вычислений даются лишь в самых общих чертах, а основное внимание уделяется назначению, содержательной интерпретации результатов и, конечно, компьютерной обработке».
Их изложение предваряется классификацией, которая позволяет выбрать метод в зависимости от исследовательской ситуации — от исходных данных и задач исследования. При изложении каждого метода особое внимание уделяется границам его применения, возможным альтернативам, технике вычислений («вручную» и на компьютере), особенностям интерпретации результатов. Третья часть содержит описание самых распространенных многомерных методов. Применение этих методов возможно только с использованием специальных компьютерных программ. Поэтому их математические основы и порядок вычислений даются лишь в самых общих чертах, а основное внимание уделяется назначению, содержательной интерпретации результатов и, конечно, компьютерной обработке». Действительно, искусству практического консультирования или терапии вряд ли необходимо математическое обеспечение. Другое дело область познания, в том числе — того, что лежит в основе различных практических приемов. И здесь уже недостаточно обыденного понимания на уровне здравого смысла, необходим особый инструмент — научный метод, опирающийся на «количественные определения»». «…Необходимо помнить, что качество любого исследования определяется прежде всего соответствием исходных данных той реальности, которая является предметом изучения. Если исследователь понимает, какое отношение имеют его данные к действительности (что они отражают), если он уверен в соответствии данных тому, что изучается, и способен это обосновать, то … Ответы на остальные вопросы исследования читатели найдут в этой книге».
Действительно, искусству практического консультирования или терапии вряд ли необходимо математическое обеспечение. Другое дело область познания, в том числе — того, что лежит в основе различных практических приемов. И здесь уже недостаточно обыденного понимания на уровне здравого смысла, необходим особый инструмент — научный метод, опирающийся на «количественные определения»». «…Необходимо помнить, что качество любого исследования определяется прежде всего соответствием исходных данных той реальности, которая является предметом изучения. Если исследователь понимает, какое отношение имеют его данные к действительности (что они отражают), если он уверен в соответствии данных тому, что изучается, и способен это обосновать, то … Ответы на остальные вопросы исследования читатели найдут в этой книге».