Тест Люшера как метод оценки психоэмоционального состояния студенток с разным уровнем здоровья
- English
- Русский
Тест Люшера как метод оценки психоэмоционального состояния студенток с разным уровнем здоровья
ˑ:
УДК/UDC 796.01:159.9 Поступила в редакцию 19.12.2016 г.
Доктор педагогических наук, профессор А.А. Горелов1, 3
Кандидат педагогических наук, доцент Е.Н. Копейкина2
Доктор педагогических наук профессор О.Г. Румба3
Доктор педагогических наук, профессор В.П. Сущенко1
1Санкт-Петербургский государственный политехнический университет, Санкт-Петербург
2Белгородский государственный национальный исследовательский университет, Белгород
3Военный институт физической культуры, Санкт-Петербург
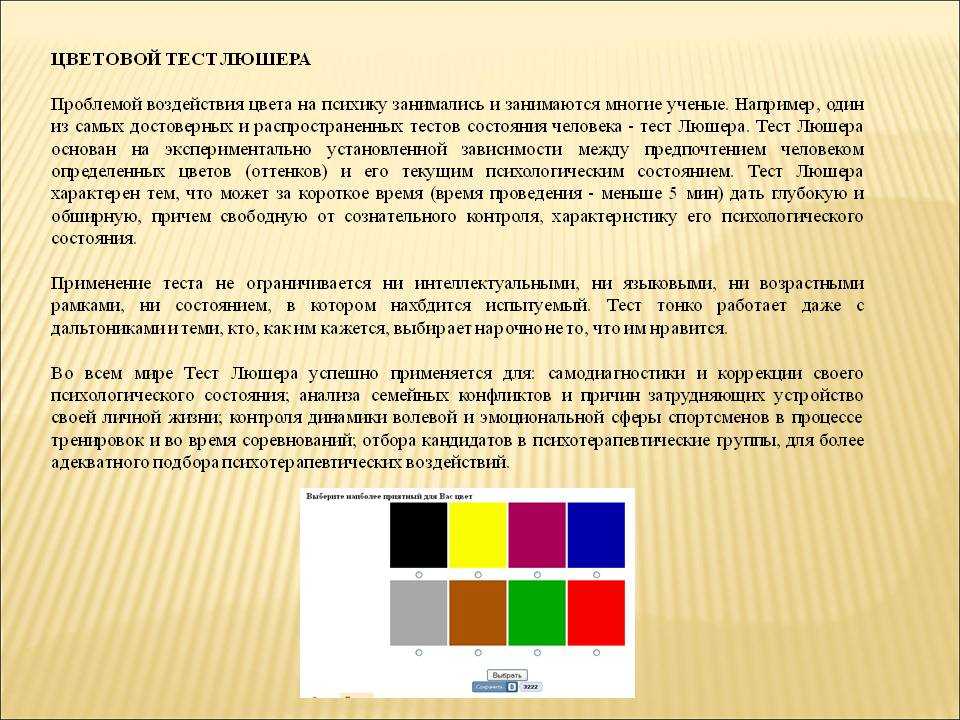
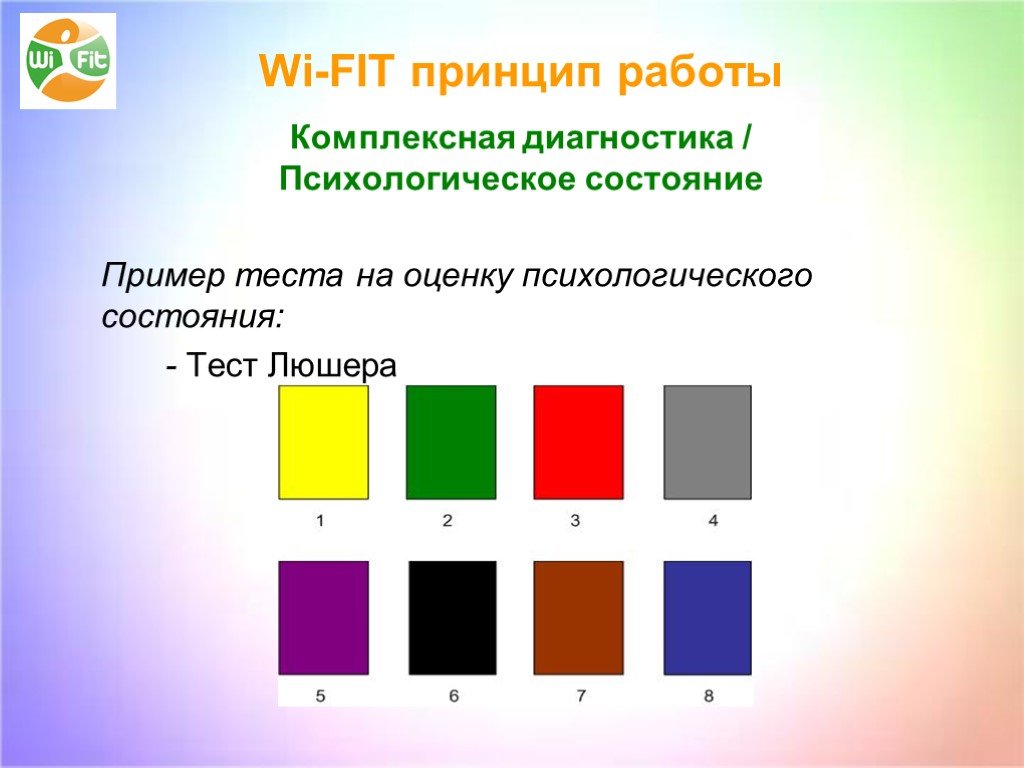
Цветовой тест Макса Люшера, относящийся к проективным методикам, используется в практике психологических, педагогических и медико-биологических исследований в качестве индикатора оценки направленности человека на определённую деятельность, а также раскрывает наиболее устойчивые черты его личности.
При этом хорошо известно, что воздействие цвета может вызывать как физиологический, так и психологический эффект.
В статье приводятся данные анализа психоэмоционального состояния студенток основной и специальной медицинской групп, а также отдельно выделенной группы студенток с нарушениями дыхательной системы с помощью цветового теста Макса Люшера (ЦТЛ).
Результаты показали, что большинству девушек основной медицинской группы (ОМГ) свойственна устремлённость в будущее.
Они желают найти своё место в жизни, стать самодостаточными и добиться успеха в обществе.
Однако они не совсем удовлетворены достигнутыми на пути к цели результатами, что вызывает у них чувство беспокойства и некоторую раздражительность.
Для большинства девушек специальной медицинской группы (СМГ) характерны эмоциональная направленность на себя и как следствие особая чувствительность и ранимость.
Как и девушки ОМГ, они стремятся найти своё место в жизни, стать самодостаточными и добиться успеха в обществе.

Большинство девушек группы с нарушениями дыхательной системы (ГрДС), подобно девушкам СМГ, отличаются повышенным вниманием к себе и в связи с этим особой чувствительностью и ранимостью.
Как и девушки других групп, они стремятся найти своё место в жизни, стать самодостаточными и добиться успеха в обществе.
Ключевые слова: цветовой тест Люшера, студентки различных медицинских групп, психоэмоциональное состояние, стрессоустойчивость, активность, коммуникативные способности.
Литература
- Собчик Л.Н. Метод цветовых выборов – модификация восьмицветового теста Люшера: практическое руководство / Л.Н. Собчик. – СПб.: Речь, 2007. – 128 с.
Цветовой тест М. Люшера | Psylist.net
 Обоснование необходимости именно 8 цветов не дается. Хотя логически можно допустить, что с увеличением их числа будет прогрессивно нарастать субъективная сложность выборов испытуемого и, следовательно, увеличиваться длительность обследования и ненадежность каждого отдельного выбора.
Обоснование необходимости именно 8 цветов не дается. Хотя логически можно допустить, что с увеличением их числа будет прогрессивно нарастать субъективная сложность выборов испытуемого и, следовательно, увеличиваться длительность обследования и ненадежность каждого отдельного выбора.В руководстве к цветовой методике не указаны стандартные характеристики цветовых тонов стимульного материала, хотя М. Люшер упоминает, что отобрал их из тысяч разных оттенков. Ознакомление с вариантами стимульного материала, изданными в ФРГ, Анлии и Швейцарии, показывает, что:
Имеются расхождения в размере и форме карточек.- Разнятся способы предъявления карточек (отдельные карточки либо цветовые квадраты, напечатанные на одной из страниц руководства к методике).
- Не совпадают полиграфические характеристики карточек (глянцевитость-матовость, глубина печати, наличие-отсутствие защитного слоя).
- По 1-2 карточкам незначительно расходятся оттенки цветов.
Практический опыт показал, что незначительные отклонения оттенков цвета в тестовом наборе от эталона не изменяют статистически значимо усредненных результатов группового обследования. Однако точно определить границы допустимых колебаний оттенков в настоящее время не представляется возможным. И поэтому для получения сопоставимых результатов следует пользоваться стандартным цветовым набором.
Однако точно определить границы допустимых колебаний оттенков в настоящее время не представляется возможным. И поэтому для получения сопоставимых результатов следует пользоваться стандартным цветовым набором.
Иногда задается вопрос о возможности использования вместо цветовых карточек, карточек с названиями цветов. Систематически, насколько нам известно, этот вопрос не исследовался. Поскольку существенная замена оттенка того или иного цвета из стандартного набора статистически значимо изменяет групповые предпочтения, сопоставимость этих двух процедур тестирования кажется весьма проблематичной. Тем более, что групповые стереотипы представлений об «истинном» красном, «истинном» синем и т.д. цветах не совпадают с оттенками цветов М. Люшера.
В специально поставленном исследовании нами установлено, что, выполняя задачу на свободную сортировку цветов на четыре группы (самые приятные, приятные, безразличные и неприятные), испытуемые чаще всего идут путем, рекомендуемым М. Люшером: сначала выбирают наиболее приятные, потом приятные, потом безразличные, и последними остаются неприятные цвета.
Переделка инструкции после выбора испытуемым первых пяти цветов (– теперь выбирать наиболее неприятный цвет –), как показывает опыт, нецелесообразна: подавляющее большинство испытуемых никаких затруднений в выборах не испытывает. В свою очередь, изменение инструкции тормозит работу испытуемого (удлиняет обследование) и способствует ошибкам в записи выборов экспериментатором.
Повышение информативности второго выбора проверялось специально. Выборке здоровых испытуемых предлагалось заполнить анкету САН с инструкцией «Как я себя чувствую в последнее время» и последовательно без перерывов разложить цветовые карточки 10 раз. В корреляционном анализе соотносились характеристики цветовых предпочтений, усредненные по первым двум раскладкам, первым трем и т.д. до 10 включительно, а также шкальные и частные оценки анкеты САН. Если под «информативностью» понимать количество статистически значимых коэффициентов корреляции между показателями анкеты САН и соответствующим усредненным набором предпочтений, то можно утверждать, что информативность Цветовых предпочтений существенно растет от 1 к 8 предъявлениям, а затем резко падает.
Предъявление испытуемому набора из 8 карточек имеет как положительные, так и отрицательные стороны. А именно:
- Процедура обследования группы тормозится тем, что один экспериментатор может работать только с одним испытуемым.
- Испытуемый невольно запоминает свою раскладку цветов, и невозможно гарантировать, что при дальнейших обследованиях эта память не будет влиять на его цветовые предпочтения.
- Легко запоминается и психофизиологическое содержание предпочтения каждого из восьми цветов. Поэтому, если такая информация каким-либо путем стала доступной испытуемому, он начинает невольно выбирать уже не из цветов, а из содержания этих цветов.
Для устранения указанных недостатков нами предложен и апробирован вариант «Попарное сравнение». В этой модификации испытуемому последовательно предъявляются 28 карточек, на каждой из которых по два цветовых квадрата. Эта серия карточек дает возможность сравнить попарно каждый цвет из стандартного набора с каждым. При такой процедуре без затруднений можно обследовать одновременно 6 испытуемых; в подавляющем большинстве своем не запоминаются не только порядок выборов, но даже не фиксируются количество и состав цветовых стимулов; у испытуемого не остается времени для выборов по психофизиологическому содержанию (если он знает характеристики цветов). Специально проведенные исследования показали, что обследования по обоим вариантам предъявления стимульного материала приводят к статистически существенно не различающимся среднегрупповым оценкам цветовых предпочтений.
В этой модификации испытуемому последовательно предъявляются 28 карточек, на каждой из которых по два цветовых квадрата. Эта серия карточек дает возможность сравнить попарно каждый цвет из стандартного набора с каждым. При такой процедуре без затруднений можно обследовать одновременно 6 испытуемых; в подавляющем большинстве своем не запоминаются не только порядок выборов, но даже не фиксируются количество и состав цветовых стимулов; у испытуемого не остается времени для выборов по психофизиологическому содержанию (если он знает характеристики цветов). Специально проведенные исследования показали, что обследования по обоим вариантам предъявления стимульного материала приводят к статистически существенно не различающимся среднегрупповым оценкам цветовых предпочтений.
Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД
Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД
Скачать PDF
Скачать PDF
- Обычная статья — Теоретическая физика
- Открытый доступ
- Опубликовано:
- The HAL QCD collaboration,
- Takumi Iritani 1 ,
- Sinya Aoki 2,3 ,
- Takumi Doi 1,4 ,
- Tetsuo Hatsuda 1,4 ,
- Yoichi Ikeda 5 ,
- Takashi Inoue 6 ,
- Noriyoshi Ishii 5 ,
- Hidekatsu Nemura 5 &
- …
- Kenji Sasaki 2
Журнал физики высоких энергий том 2019 , Номер статьи: 7 (2019) Процитировать эту статью
344 доступа
18 цитирований
1 Альтметрика
Сведения о показателях
Аннотация
Существует два метода изучения двухбарионных систем в решеточной КХД: прямой метод, который извлекает собственные энергии из плато временной корреляционной функции, и метод HAL КХД, который извлекает наблюдаемые из нелокального потенциала, связанного с пространственно-временным корреляционная функция. Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал на м π = 0,51 ГэВ в (2+1)-ароматной решетке КХД с использованием пристеночных и размытых кварковых источников с пространственными протяженностями, La = 3,5 , 4,8. фм. Показано, что «псевдоплато» на ранних временных срезах ( t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализовано только на т > 5 ∼ 15 фм, что соответствует обратной величине наименьшей энергии возбуждения.
Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал на м π = 0,51 ГэВ в (2+1)-ароматной решетке КХД с использованием пристеночных и размытых кварковых источников с пространственными протяженностями, La = 3,5 , 4,8. фм. Показано, что «псевдоплато» на ранних временных срезах ( t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализовано только на т > 5 ∼ 15 фм, что соответствует обратной величине наименьшей энергии возбуждения. Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов теперь решен, по крайней мере, для рассматриваемой здесь конкретной системы: они количественно согласуются друг с другом только в том случае, если возбужденное загрязнение правильно удалены в бывшем.
Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов теперь решен, по крайней мере, для рассматриваемой здесь конкретной системы: они количественно согласуются друг с другом только в том случае, если возбужденное загрязнение правильно удалены в бывшем.
Скачайте, чтобы прочитать полный текст статьи
Ссылки
Сотрудничество HAL QCD, T. Iritani et al.
 , Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ].
, Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ].Коллаборация HAL КХД, Т. Иритани и др., Связаны ли два нуклона в КХД на решетке для масс тяжелых кварков? Проверка непротиворечивости с помощью формулы конечного объема Люшера , Физ. Ред. D 96 (2017) 034521 [arXiv:1703.07210] [ВДОХНОВЕНИЕ].
Т. Ямадзаки, К.-и. Ishikawa, Y. Kuramashi and A. Ukawa, Исследование зависимости энергии связи легких ядер от массы кварка в решетке аромата 2+1 КХД , Phys. Ред. D 92 (2015) 014501 [arXiv:1502.04182] [ВДОХНОВЕНИЕ].
ОБЪЯВЛЕНИЕ Google ученый
NPLQCD коллаборация, М.Л. Wagman et al., Барион-барионные взаимодействия и спин-ароматная симметрия из квантовой хромодинамики решетки , Phys.
 Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ].
Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ].Коллаборация CalLat, E. Berkowitz et al., Двухнуклонное рассеяние высших парциальных волн на решеточной КХД , Phys. лат. B 765 (2017) 285 [arXiv:1508.00886] [ВДОХНОВЕНИЕ].
М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 1. Стабильные состояния частиц , Общ. Мат. физ. 104 (1986) 177 [ВДОХНОВЕНИЕ].
М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 2. Состояния рассеяния , Общ. Мат. физ. 105 (1986) 153 [ВДОХНОВЕНИЕ].
М. Люшер, Два состояния частиц на торе и их связь с матрицей рассеяния , Nucl.
 физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].
физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Н. Исии, С. Аоки и Т. Хацуда, Ядерная сила из КХД решетки , Физ. Преподобный Летт. 99 (2007) 022001 [nucl-th/0611096] [INSPIRE].
С. Аоки, Т. Хацуда и Н. Исии, Теоретические основы ядерных сил в КХД и их приложения к центральным и тензорным силам в КХД-моделировании закаленных решеток , Prog. Теор. физ. 123 (2010) 89 [arXiv:0909.5585] [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый
HAL Сотрудничество КХД, Н. Ишии и др., Адрон-адронные взаимодействия из волновой функции Намбу-Бете-Солпитера в мнимом времени на решетке , Phys.
 лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].
лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].Коллаборация HAL КХД, С. Аоки и др., Решетчатый подход КХД к ядерной физике , PTEP 2012 (2012) 01A105 [arXiv:1206.5088] [ВДОХНОВЕНИЕ].
С. Аоки, КХД на решетке и ядерная физика , в Современные перспективы КХД на решетке: квантовая теория поля и высокопроизводительные вычисления. Proceedings, International School, 93rd Session , Les Houches, France, 3–28 августа 2009 г., стр. 591–628 (2010) [arXiv:1008.4427] [INSPIRE].
Коллаборация NPLQCD, S.R. Beane et al., Легкие ядра и гиперядра из квантовой хромодинамики в пределе SU(3) Flavor Symmetry , Физ. Ред. D 87 (2013) 034506 [arXiv:1206.5219] [ВДОХНОВЕНИЕ].
Сотрудничество HAL QCD, T.
 Inoue et al., Потенциалы двух барионов и H-дибарионы из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ].
Inoue et al., Потенциалы двух барионов и H-дибарионы из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ].А. Фрэнсис, Дж. Р. Грин, П.М. Junnarkar, C. Miao, T.D. Rae and H. Wittig, Решеточная КХД, исследование дибариона H с использованием гексакваркового и двухбарионного интерполяторов , arXiv:1805.03966 [ВДОХНОВЕНИЕ].
T. Iritani для коллаборации с HAL КХД, Барионные взаимодействия в решеточной КХД: прямой метод против потенциального метода HAL КХД , PoS(LATTICE2016)107 (2016) [arXiv:1610.09779] [INSPIRE].
С. Аоки, Т. Дои и Т. Иритани, Проверка работоспособности связанных состояний NN в КХД решетки с формулой конечного объема Люшера — Раскрытие симптомов ложных плато — , EPJ Web Conf. 175 (2018) 05006 [arXiv:1707.
 08800] [ВДОХНОВЕНИЕ].
08800] [ВДОХНОВЕНИЕ].Артикул Google ученый
Т. Иритани для коллаборации с HAL КХД, Двухбарионные системы из метода HAL КХД и миража во временной корреляции прямого метода , EPJ Web Conf. 175 (2018) 05008 [arXiv:1710.06147] [ВДОХНОВЕНИЕ].
Сотрудничество HAL QCD, T. Iritani et al., Систематика потенциала HAL КХД при низких энергиях в решеточной КХД , Phys. Ред. D 99 (2019) 014514 [arXiv:1805.02365] [ВДОХНОВЕНИЕ].
Г. Паризи, Стратегия вычисления спектра адронных масс , Phys. Представитель 103 (1984) 203 [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ Google ученый
Г.П. Lepage, The Analysis of Algorithms for Lattice Field Theory , in From Actions to Answers: Proceedings of the TASI 1989 , T.
 Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ].
Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ].https://en.wikipedia.org/wiki/Sanity_check.
К. Мурано, Н. Исии, С. Аоки и Т. Хацуда, Нуклон-нуклонный потенциал и его нелокальность в решетке КХД , Прогр. Теор. физ. 125 (2011) 1225 [arXiv:1103.0619] [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый
К. Нисидзима, Формулировка полевых теорий составных частиц , Phys. Ред. 111 (1958) 995 [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый
W. Zimmermann, О проблеме связанного состояния в квантовой теории поля , Nuovo Cim.
 10 (1958) 597 [ВДОХНОВЕНИЕ].
10 (1958) 597 [ВДОХНОВЕНИЕ].Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый
Р. Хааг, Квантовые теории поля с составными частицами и асимптотическими условиями , Phys. Ред. 112 (1958) 669 [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый
Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, Ядра гелия, дейтрон и динейтрон в решетке аромата 2+1 КХД , Физ. Ред. D 86 (2012) 074514 [arXiv:1207.4277] [ВДОХНОВЕНИЕ].
ОБЪЯВЛЕНИЕ Google ученый
Т. Дои и М.Г. Эндрес, Единый алгоритм сжатия для мультибарионных корреляторов на решетке , Вычисл.
 физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].
физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Коллаборация NPLQCD, K. Orginos et al., Две нуклонные системы на m π ∼ 450 МэВ из КХД на решетке , Физ. Ред. D 92 (2015) 114512 [arXiv:1508.07583] [ВДОХНОВЕНИЕ].
Коллаборация NPLQCD, S.R. Beane et al., Комментарий к статье «Связаны ли два нуклона в решеточной КХД для масс тяжелых кварков? — Проверка работоспособности с помощью формулы конечного объема Люшера — , arXiv:1705.09239 [INSPIRE].
М. Люшер и У. Вольф, Как рассчитать матрицу упругого рассеяния в двумерных квантовых теориях поля с помощью численного моделирования , Нукл. физ. B 339 (1990) 222 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Р.А. Брицено, Дж.Дж. Дудек и Р.Д. Янг, Процессы рассеяния и резонансы в КХД на решетке , Rev. Mod. физ. 90 (2018) 025001 [arXiv:1706.06223] [ВДОХНОВЕНИЕ].
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Сотрудничество HAL QCD, S. Gongyo et al., Самый странный дибарион из решетки QCD , Phys. Преподобный Летт. 120 (2018) 212001 [arXiv:1709.00654] [ВДОХНОВЕНИЕ].
HAL КХД коллаборация, Т. Иритани и др., N Ω дибарион из решеточной КХД вблизи физической точки , arXiv:1810.03416 [INSPIRE].
Сотрудничество HAL QCD, T. Inoue et al., Strange Nuclear Physics из КХД на решетке , in 13th International Conference on Hypernuclear and Strange Particle Physics (HYP 2018) , Портсмут, Вирджиния, США, 24–29 июня 2018 г.
 [arXiv:1809.08932] [INSPIRE].
[arXiv:1809.08932] [INSPIRE].T. Amagasa et al., Совместное использование данных решетчатой КХД в широко распространенной файловой системе , J. Phys. конф. сер. 664 (2015) 042058 [ВДОХНОВЕНИЕ].
Артикул Google ученый
http://www.lqcd.org/ildg.
http://www.jldg.org.
Columbia Physics System (CPS), http://usqcd-software.github.io/CPS.html.
Bridge++, http://bridge.kek.jp/Lattice-code/.
М. Шрек и Х. Фогт, Фиксация кулоновской, ландауской и максимально абелевой калибровки в решеточной КХД с мульти-GPU , Вычисл. физ. коммун. 184 (2013) 1907 [arXiv:1212.
 5221] [ВДОХНОВЕНИЕ].
5221] [ВДОХНОВЕНИЕ].Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый
T. Boku et al., Многоблочный/многоядерный предобуславливатель SSOR для кваркового решателя QCD для компьютера K , PoS(LATTICE2012)188 (2012) [arXiv:1210.7398] [INSPIRE].
М. Терай и др., Настройка производительности решетчатого кода КХД на узле компьютера K (на японском языке), IPJ Trans. Доп. вычисл. Сист. 6 (2013) 43.
Скачать ссылки
Открытый доступЭта статья распространяется в соответствии с лицензией Creative Commons Attribution License (CC-BY 4.0), которая разрешает любое использование, распространение и воспроизведение на любом носителе при условии указания автора(ов) и источника.
Информация об авторе
Авторы и организации
RIKEN Nishina Center, Wako, 351-0198, Japan
Takumi Iritani, Takumi Doi & Tetsuo Hatsuda
Центр гравитационной физики, Институт теоретической физики им.
 Киото, 606-8502, Япония
Киото, 606-8502, ЯпонияСинья Аоки и Кенджи Сасаки
Центр вычислительных наук Университета Цукуба, Цукуба, 305-8577, Япония
Синья Аоки
Междисциплинарная программа теоретических и математических наук RIKEN (iTHEMS), Вако, 351-0198, Япония
Такуми Дои и Тецуо Хацуда
Исследовательский центр ядерной физики (RCNP), Осакский университет, Осака, 567-0047, Япония
Ёити Икэда, Нориёси Исии и Хидэкацу Немура
Университет Нихон, Колледж наук о биоресурсах, Канагава, 252-0880, Япония
Такаси Иноуэ
908343 905 Автор0003- Такуми Иритани
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Sinya Aoki
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Takumi Doi
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Тецуо Хацуда
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yoichi Ikeda
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Takashi Inoue
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Noriyoshi Ishii
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Hidekatsu Nemura
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Kenji Sasaki
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Иритани, Такуми ;
- Аоки, Синя ;
- Дои, Такуми ;
- Хацуда, Тецуо ;
- Икеда, Ёити ;
- Иноуэ, Такаши ;
- Исии, Нориёси ;
- Немура, Хидэкацу ;
- Сасаки, Кендзи
- Публикация:
Журнал физики высоких энергий
- Дата публикации:
- март 2019
- DOI:
- 10.

Консорциумы
Сотрудничество HAL QCD
Автор, ответственный за переписку
Такуми Иритани.
Дополнительная информация
ArXiv ePrint: 1812.08539
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате. , при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и укажите, были ли внесены изменения.
Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на эту статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя.
Чтобы просмотреть копию этой лицензии, посетите https://creativecommons. org/licenses/by/4.0/.
org/licenses/by/4.0/.
Перепечатка и разрешения
Об этой статье
Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД
Согласованность метода конечных объемов Люшера и метода HAL КХД для двухбарионных систем в решеточной КХД
Аннотация
Существует два метода изучения двухбарионных систем в решеточной КХД: прямой метод, который извлекает собственные энергии из плато временной корреляционной функции, и метод HAL КХД, который извлекает наблюдаемые из нелокального потенциала, связанного с пространственно-временной корреляционной функцией. . Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал при m π = 0,51 ГэВ в КХД на решетке (2+1)-аромата с использованием пристеночных и размытых кварковых источников с пространственными протяженностями, La = 3,6, 4,3, 5,8 фм. Показано, что «псевдоплато» на ранних временных срезах (t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализуется только при t > 5 ∼ 15 фм, что соответствует обратной наименьшей энергии возбуждения.
. Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал при m π = 0,51 ГэВ в КХД на решетке (2+1)-аромата с использованием пристеночных и размытых кварковых источников с пространственными протяженностями, La = 3,6, 4,3, 5,8 фм. Показано, что «псевдоплато» на ранних временных срезах (t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализуется только при t > 5 ∼ 15 фм, что соответствует обратной наименьшей энергии возбуждения. Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов теперь решен, по крайней мере, для рассматриваемой здесь конкретной системы: они количественно согласуются друг с другом только в том случае, если возбужденное загрязнение правильно удалены в бывшем.
Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов теперь решен, по крайней мере, для рассматриваемой здесь конкретной системы: они количественно согласуются друг с другом только в том случае, если возбужденное загрязнение правильно удалены в бывшем.
 , Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ].
, Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ]. Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ].
Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ]. физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].
физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ]. лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].
лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].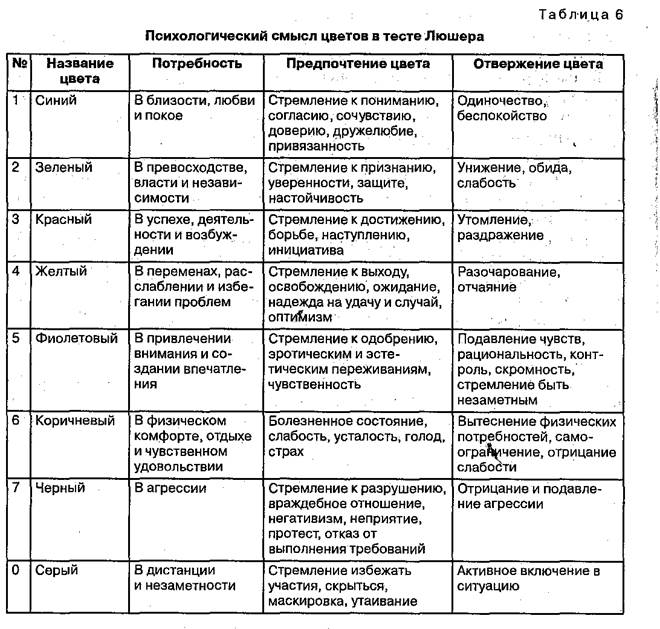 Inoue et al., Потенциалы двух барионов и H-дибарионы из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ].
Inoue et al., Потенциалы двух барионов и H-дибарионы из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ]. 08800] [ВДОХНОВЕНИЕ].
08800] [ВДОХНОВЕНИЕ]. Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ].
Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ]. 10 (1958) 597 [ВДОХНОВЕНИЕ].
10 (1958) 597 [ВДОХНОВЕНИЕ]. физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].
физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].
 [arXiv:1809.08932] [INSPIRE].
[arXiv:1809.08932] [INSPIRE]. 5221] [ВДОХНОВЕНИЕ].
5221] [ВДОХНОВЕНИЕ]. Киото, 606-8502, Япония
Киото, 606-8502, Япония