Современная методика обучения математике и методическая подготовка учителя Текст научной статьи по специальности «Науки об образовании»
УДК 377
СОВРЕМЕННАЯ МЕТОДИКА ОБУЧЕНИЯ МАТЕМАТИКЕ И МЕТОДИЧЕСКАЯ ПОДГОТОВКА УЧИТЕЛЯ
Н.Л.Стефанова
Российский государственный педагогический университет имени А.И.Герцена, Санкт-Петербург,
NLStephanova@mail. ru
Рассматриваются процессы, происходящие в теории и методике обучения математике. Анализируются их социальные и методологические причины. Выявляется влияние этих процессов на преобразование системы методической подготовки учителя математики и определяются направления ее развития.
Ключевые слова: теория и методика обучения математике, преобразования системы профессионального образования, будущие учителя математики, методическая подготовка
In the article the processes in the scientific field «theory and methods of mathematical education» are considered. Their social and methodological reasons are analyzed. The influence of these processes on the system of professional education of intending mathematics teachers and directions of its development are revealed and determined.
The influence of these processes on the system of professional education of intending mathematics teachers and directions of its development are revealed and determined.
Keywords: theory and methods of mathematical education, transformation of the system of professional education, intending mathematics teachers, methods of teaching and learning mathematics
Сегодня в ходе общественных обсуждений часто можно услышать мнение о малой эффективности российской науки в целом. Особенно много претензий к педагогической науке и, в частности, к такому ее разделу, как методика обучения различным предметам. Не обращаясь к рассмотрению проблем педагогической науки в целом, считаю возможным высказать свое мнение относительно состояния и перспектив развития методики обучения математики, которая является сферой моих научных интересов. Тем более, что состояние этой науки оказывает непосредственное влияние на качество подготовки учителя математики — ключевой фигуры в системе общего среднего математического образования. Не буду отрицать, что в настоящее время качество этого образования вызывает в обществе существенные нарекания.
Не буду отрицать, что в настоящее время качество этого образования вызывает в обществе существенные нарекания.
Основная претензия, высказываемая в адрес методики обучения математики (впрочем, как и другим предметам), состоит в том, что при достаточно большом количестве проводимых исследований уровень математической подготовки школьников остается весьма низким. Это правда. Зайдя на сайт ВАК РФ можно обнаружить, что за 2010 г. было утверждено 55 диссертаций по специальности 13.00.02 — теория
и методика обучения, из них 15 — по методике математики. При этом результаты ГИА и ЕГЭ по математике, а также результаты международного тестирования PISA по проверке математической грамотности, которые показывают российские школьники, — более чем скромные. Виновата ли в этом только методическая наука? И можно ли говорить о прямой связи между выполненными методическими исследованиями и качеством общего среднего математического образования?
Вузовская методическая наука (это мне известно наверняка, ничего не могу утверждать относительно академической науки, но могу только предполагать, что и там ситуация не лучше) финансируется крайне слабо, точнее, финансируется общая профессиональная деятельность, куда входит и научная составляющая деятельности преподавателей. Грантов по методике практически нет. Это означает, что государство не заинтересовано в выполнении такого рода исследований. Но есть и другая сторона. Выполненные исследования (например, при подготовке кандидатских и докторских диссертаций) не находят реального применения в школьном образовательном процессе, так как у нас в стране отсутствует промежуточная структура, которая занималась бы внедрением
Грантов по методике практически нет. Это означает, что государство не заинтересовано в выполнении такого рода исследований. Но есть и другая сторона. Выполненные исследования (например, при подготовке кандидатских и докторских диссертаций) не находят реального применения в школьном образовательном процессе, так как у нас в стране отсутствует промежуточная структура, которая занималась бы внедрением
в практику и распространением полученных научных результатов.
Методика — наука прикладная. Ее эффективность зависит в том числе и от состояния сферы ее приложения, в нашем случае — системы общего среднего математического образования. Система эта переживает нелегкие времена. С одной стороны, результаты итоговой государственной аттестации по математике весьма низкие. При этом демографическая ситуация такова, что и с такими результатами все желающие выпускники школы поступают в высшие учебные заведения, в том числе, кстати, и в педагогические, где готовят учителей. Исчезает главная составляющая, обеспечивающая качество образования, — мотивация учащихся. В этом случае какие бы новшества ни предлагала методическая наука для внесения в процесс обучения учащихся, требуемого результат получить все равно не удастся. На это можно возразить: вот пусть методическая наука и занимается проблемами повышения мотивации учащихся в процессе обучения математике. Она этими проблемами занимается, наряду с многими другими, но социальные приоритеты оказывают значительно более сильное влияние на формирование мотивации учащихся по сравнению с теми приемами и средствами, которыми может оперировать методика обучения математике. Ведь сегодня в массовом сознании все больше укрепляется мысль о том, что не так уж важно получить качественное профессиональное образование, которое может быть построено только на хорошей школьной базе, лишь бы получить любое высшее образование (а то и просто диплом). Ведь успех в жизни зависит от того, сможешь ли ты устроиться на престижную (т.е. хорошо оплачиваемую) работу, при этом совсем не обязательно по специальности. Одним из проявлений этой позиции является узаконенная возможность подавать документы (и результаты ЕГЭ) на несколько существенно различающихся программ в разные вузы.
В этом случае какие бы новшества ни предлагала методическая наука для внесения в процесс обучения учащихся, требуемого результат получить все равно не удастся. На это можно возразить: вот пусть методическая наука и занимается проблемами повышения мотивации учащихся в процессе обучения математике. Она этими проблемами занимается, наряду с многими другими, но социальные приоритеты оказывают значительно более сильное влияние на формирование мотивации учащихся по сравнению с теми приемами и средствами, которыми может оперировать методика обучения математике. Ведь сегодня в массовом сознании все больше укрепляется мысль о том, что не так уж важно получить качественное профессиональное образование, которое может быть построено только на хорошей школьной базе, лишь бы получить любое высшее образование (а то и просто диплом). Ведь успех в жизни зависит от того, сможешь ли ты устроиться на престижную (т.е. хорошо оплачиваемую) работу, при этом совсем не обязательно по специальности. Одним из проявлений этой позиции является узаконенная возможность подавать документы (и результаты ЕГЭ) на несколько существенно различающихся программ в разные вузы. И подают выпускники школ документы туда, где их примут, а не туда, где они действительно хотели бы учиться. Все это негативно влияет на формирование мотивации учеников.
И подают выпускники школ документы туда, где их примут, а не туда, где они действительно хотели бы учиться. Все это негативно влияет на формирование мотивации учеников.
Другая сторона проблемы связана с внедрением результатов методической науки в практику обучения учащихся. Осуществляет это учитель. Учителя (в общей своей массе) не могут быть заинтересованы во внедрении научных обществ в свою практическую деятельность, так как главным показателем их деятельности становятся результаты написания ЕГЭ (или ГИА) их учениками. В отсутствие необходимой мотивации у учащихся на овладение математическими знаниями учитель вынужден заниматься подготовкой учащихся к итоговой аттестации, рассматривать это в качестве своей основной задачи как в старшей школе (особенно в 11-м классе), так и в 9-м классе основной школы.
На этом считаю необходимым завершить разговор о причинах неэффективности методической
науки (методике обучения математике), связанных с внедрением ее результатов в систему общего среднего образования. Перейду к более продуктивному обсуждению особенностей и перспектив развития этой науки. Чтобы их понять следует окинуть ретроспективным взглядом этапы ее становления и развития.
Перейду к более продуктивному обсуждению особенностей и перспектив развития этой науки. Чтобы их понять следует окинуть ретроспективным взглядом этапы ее становления и развития.
В 20-е годы ХХ в. методика обучения (в том числе и математике) в России оформилась как отдельная область педагогической науки, выделившись из дидактики. На протяжении многих лет она в основном занималась проблемами построения математического содержания общего среднего образования и созданием методического обеспечения, облегчающего процессы усвоения учащимися предложенного содержания и преподавания математики учителем. Конечно, исследовались и другие проблемы, например методики реализации принципа политехнизма в процессе обучения математике. При этом абсолютное большинство методических исследований были ориентированы на математику как цель усвоения учащимися.
Сегодня акценты в методике обучения математике перенесены на рассмотрение математического содержания не как цели изучения, а как средства решения образовательных и развивающих задач. Развитие пространственного воображения, критического мышления, оценочной деятельности, формирование способов и приемов деятельности, которые можно использовать для разрешения проблемных ситуаций и решения практических задач, — вот далеко не полный перечень проблем, которыми занимается современная методика математики. Это в том числе связано с реализацией требований общества к образованию вообще и общему среднему математическому образованию, в частности. Эти требования вытекают из необходимости реализовать компетентностный подход в системе образований, внедрить новые государственные стандарты, где особый акцент делается на формирование мировоззренческой составляющей образования, достижение метапредметных образовательных результатов и формирование универсальных учебных умений.
Развитие пространственного воображения, критического мышления, оценочной деятельности, формирование способов и приемов деятельности, которые можно использовать для разрешения проблемных ситуаций и решения практических задач, — вот далеко не полный перечень проблем, которыми занимается современная методика математики. Это в том числе связано с реализацией требований общества к образованию вообще и общему среднему математическому образованию, в частности. Эти требования вытекают из необходимости реализовать компетентностный подход в системе образований, внедрить новые государственные стандарты, где особый акцент делается на формирование мировоззренческой составляющей образования, достижение метапредметных образовательных результатов и формирование универсальных учебных умений.
Уровень и характер развития методической науки в первую очередь влияет на качество методической подготовки учителя как важнейшей части его профессиональной подготовки. Можно предположить, что «неэффективная» методическая наука должна проявляться и в низком качестве методической подготовки будущих учителей. Однако здесь мы наблюдаем другую картину. Например, можно привести результаты международного исследования по оценке качества подготовки будущих учителей математики (TEDS-M — Teacher Education And Development Study), которое было проведено в 2008 г. в 14 странах [1] (см. табл.). Исследования такие проводятся постоянно под эгидой Международной Ассоциации оценки достижений в области образования (IEA).
Однако здесь мы наблюдаем другую картину. Например, можно привести результаты международного исследования по оценке качества подготовки будущих учителей математики (TEDS-M — Teacher Education And Development Study), которое было проведено в 2008 г. в 14 странах [1] (см. табл.). Исследования такие проводятся постоянно под эгидой Международной Ассоциации оценки достижений в области образования (IEA).
Рейтинг стран по результатам международного исследования TEDS-M
Страна Средний балл по международной шкале
Тайвань 649
Россия 566
Сингапур 533
Швейцария 549
Германия 540
Польша 524
США 502
Таиланд 476
Оман 474
Малайзия 472
Филиппины 450
Грузия 443
Ботсвана 425
Чили 394
В таблице приведен рейтинг стран по количеству набранных участниками исследования (студентами выпускных курсов педагогических вузов) баллов по результатам выполнения ими заданий по методике обучения математике. В этом рейтинге Россия занимает второе место, опережая такие европейские страны, как Швейцария, Германия, Польша.
Причины таких хороших показателей российских будущих учителей математики кроются не только в том, что в нашей стране методическая подготовка является обязательной составляющей профессиональной образования будущего учителя, но и в том, что она носит системный характер.
В США, где с опытом профессиональной подготовки учителей математики я знакомилась на протяжении нескольких лет, нет научно обоснованной системы методической подготовки. Тем более там подготовка учителя математики к преподавательской деятельности не является неотъемлемой частью системы профессионального образования, включающей еще и предметную, и психолого-педагогическую подготовку будущего учителя. И, как можно видеть, там результаты проведенного мониторинга весьма скромные.
Призывы сделать профессиональную подготовку, прежде всего методическую, некоторым довеском к фундаментальному предметному образованию (университетского типа) могут привести к существенному снижению уровня профессиональной компетентности учителя математики. Для такой массовой профессии, как учитель, в нашей многомиллионной стране это может иметь весьма негативные последствия как для системы общего среднего образования, так и для развития общества в целом.
Для такой массовой профессии, как учитель, в нашей многомиллионной стране это может иметь весьма негативные последствия как для системы общего среднего образования, так и для развития общества в целом.
Нельзя сказать, что специалисты полностью удовлетворены существующей системой методиче-
ской подготовки, и она не должна меняться. Как раз наоборот. Выделим основные направления возможных изменений рассматриваемой системы.
Несомненно, методическая подготовка должна изменить свои содержательно-структурные характеристики. Она должна строиться как ступенчатая с выделением двух ступеней — подготовка учителя математики основной школы и старшей школы. Это обусловлено, во-первых, существенными различиями в методике обучения математике в основной и старшей школе (разные цели, задачи, уровень развития учебно-познавательной деятельности учащихся и т.д.). Эти различия существовали всегда, и указанные ступени давно выделены (достаточно вспомнить учебники по методике преподавания математики под редакцией С. Е.Ляпина [2]). Во-вторых, выделение этих двух ступеней в методической подготовке поддерживает и новый федеральный государственный образовательный стандарт по направлению «Педагогическое образование», в соответствие с которым в бакалавриате идет подготовка учителя математики для основной школы, а в магистратуре — для старшей школы.
Е.Ляпина [2]). Во-вторых, выделение этих двух ступеней в методической подготовке поддерживает и новый федеральный государственный образовательный стандарт по направлению «Педагогическое образование», в соответствие с которым в бакалавриате идет подготовка учителя математики для основной школы, а в магистратуре — для старшей школы.
С другой стороны, в рассматриваемой системе явно должна быть выделена содержательноуровневая структура. На первом уровне целесообразно изучать методику обучения математике как цели изучения на базовом уровне, на втором — то же самое, но рассматривать математику на профильном уровне и, наконец, на третьем — рассматривать методику обучения математике как средство формирования универсальных учебных умений и достижения метапредметных результатов. Кстати, этот уровень мы выделили как высший, так как он является наиболее сложным и пока еще недостаточно осмысленным и разработанным.
Должно измениться и содержание методической подготовки, причем как с точки зрения предметного содержания, так и с точки зрений технологий обучения. Необходимо для обязательного рассмотрения включить вопросы методики обучения стохастике, элементам логики, решению ситуационных (компетентностных) задач, а значит и математическому моделированию. В технологической составляющей содержания должны стать приоритетными развивающие технологии обучения математике, в частности развития самостоятельности и исследовательского потенциала учащихся. Особое место необходимо отвести рассмотрению специфики использования современных информационных технологий при обучении математике вплоть до дистанционного обучения. И, наконец, современные технологии оценки достижений учащихся в процессе обучения математике тоже должны найти место в содержании методической подготовки учителя математики.
Необходимо для обязательного рассмотрения включить вопросы методики обучения стохастике, элементам логики, решению ситуационных (компетентностных) задач, а значит и математическому моделированию. В технологической составляющей содержания должны стать приоритетными развивающие технологии обучения математике, в частности развития самостоятельности и исследовательского потенциала учащихся. Особое место необходимо отвести рассмотрению специфики использования современных информационных технологий при обучении математике вплоть до дистанционного обучения. И, наконец, современные технологии оценки достижений учащихся в процессе обучения математике тоже должны найти место в содержании методической подготовки учителя математики.
Третье направление изменения системы методической подготовки связано с проблемами ее реализации. Традиционно подготовка будущего учителя осуществляется по классической схеме: сначала сообщаются знания в стенах вуза, а затем студенты на практике пытаются применить эти
знания. При этом сообщаемые знания можно условно назвать «фундаментальными» (возможно, не совсем правомерно из-за ярко выраженного прикладного характера методической науки), так как они отражают наиболее существенные стороны осуществления процесса обучения математике, независимо от конкретного учебника математики или конкретной методики.
При этом сообщаемые знания можно условно назвать «фундаментальными» (возможно, не совсем правомерно из-за ярко выраженного прикладного характера методической науки), так как они отражают наиболее существенные стороны осуществления процесса обучения математике, независимо от конкретного учебника математики или конкретной методики.
Сегодня понятно, что такой путь организации профессиональной подготовки учителя недостаточно эффективен. Наиболее продуктивным является технология обучения, когда в процессе обучения анализируются и выделяются существенные особенности построения реального процесса обучения математике, которые затем обобщаются и включаются в систему профессиональных знаний. При этом может быть реализована и обратная связь, но она не должна быть ни единственной, ни даже приоритетной. Такой опыт реализации профессиональной подготовки учителя есть не только в нашей стране, но и за рубежом. Существенную помощь в реализации этой схемы осуществления методической подготовки могут оказать мультимедийные технологии, которые позволяют даже в вузовской аудитории наблюдать и анализировать реальный процесс обучения учащихся.
Таким образом, можно констатировать, что сегодня как методика обучения математике, так и система методической подготовки будущего учителя математике, созданные в России, являются несомненным достижением нашей системы образова-
ния, которое высоко оценивается международным образовательным сообществом. Отвечая на актуальные и перспективные требования общества к уровню и качеству математического образования учащихся, они совершенствуются и развиваются. Направления этого развития связаны с новыми представлениями о роли математики в современном обществе и об ее влиянии на личностное становление человека.
1. Отчет о научно-исследовательской работе по теме «Качество педагогического образования в России (по результатам международного исследовния по изучению педагогического образования и оценке качества подготовки будущих учителей математики TEDS)» (заключительный). РАО. Институт содержания и методов обучения. Руководитель Г.С.Ковалева — http://teds.educ.msu.edu
2. Методика преподавания математики. Ч.І и II. Пособие для учителей и студентов педагогических институтов / Под общей ред. С.Е.Ляпина. Л.: Учпедгиз, 1955, 1956.
Ч.І и II. Пособие для учителей и студентов педагогических институтов / Под общей ред. С.Е.Ляпина. Л.: Учпедгиз, 1955, 1956.
Bibliography (Transliterated)
1. Otchet o nauchno-issledovatel’skoj rabote po teme «Kachestvo pedagogicheskogo obrazovanija v Rossii (po re-zul’tatam mezhdunarodnogo issledovnija po izucheniju peda-gogicheskogo obrazovanija i ocenke kachestva podgotovki budushhikh uchitelej matematiki TEDS)» (zakljuchitel’nyj). RAO. Institut soderzhanija i metodov obuchenija. Ruko-voditel’ G.S.Kovaleva — http://teds.educ.msu.edu
2. Metodika prepodavanija matematiki. Ch.I i II. Posobie dlja uchitelej i studentov pedagogicheskikh institutov / Pod obshhej red. S.E.Ljapina. L.: Uchpedgiz, 1955, 1956.
404 Cтраница не найдена
Размер: A A A
Цвет: C C C
Изображения
Вкл. Выкл.
Выкл.
Обычная версия сайта
Сведения об образовательной организации
Вход для администратора сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
 .. в эфире «Международная панорама!» … .. в эфире «Международная панорама!» … | ||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||
|
Основная литература
| |||
| Учебники для 2-ых классов по новым фгос О реализации национальной образовательной инициативы «наша новая школа» в 2012 году | Учебники для 5, 7 классов Организация обучения учащихся на занятии: фронтальная, групповая (две команды разновозрастного состава), парная работа | ||
| Учебники для общеобразовательных учреждений. Мировая художественная… Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа №1 имени и. Д. Бувальцева | Учебники издательства «Мнемозина» по литературе, вошедшие в Федеральный… Умк по литературе для 5-6 классов под ред. Г. И. Беленького. Авторы: М. А. Снежневская, О. М. Хренова, Э. Э. Кац | ||
| Давид Вениаминович Ривман Криминальная виктимология Серия «Учебники… Р49 Криминальная виктимология — спб.  : Питер, 2002. — 304 с. — (Серия «Учебники для вузов») : Питер, 2002. — 304 с. — (Серия «Учебники для вузов») | Рабочая учебная программа Галиаскарова Ирина Рэмовна (учитель начальных… Учебник: «Литературное чтение» для 2-ого класса. В 2-х ч. / Л. Ф. Климановой и др. «Просвещение» ОАО «Московские учебники», 2011… | ||
| Рабочая программа учителя начальных классов 1 класс г. Пермь 2011… Комплект включает учебники для начальной школы по основным предметам, соответствующим базисному учебному плану | Рабочая учебная программа Хохловой Людмилы Павловны (учитель начальных… Учебник: «Литературное чтение» для 2-ого класса. В 2-х ч. / Л. Ф. Климановой и др. «Просвещение» ОАО «Московские учебники», 2011… | ||
| Старшая школа Ступень Класс Учебный предмет, курс, дисциплина Программа… Рабочая программа по русскому языку для 10-11 классов, составленная на основе примерной программы к фкгс полного общего образования… | Пояснительная записка к тематическому планированию по физической. .. ..В. И. Лях, А. А. Зданевич. – М.: Просвещение, 2005 и является частью Федерального учебного плана для образовательных учреждений Российской… |
Снегурова Виктория Игоревна — Диссертации
Научная тема: «МЕТОДИЧЕСКАЯ СИСТЕМА ДИСТАНЦИОННОГО ОБУЧЕНИЯ МАТЕМАТИКЕ УЧАЩИХСЯ ОБЩЕОБРАЗОВАТЕЛЬНЫХ ШКОЛ»
Основные научные положения, сформулированные автором на основании проведенных исследований:
I. Монографии:
1.Современная методическая система математического образования: коллективная монография / Н.Л. Стефанова, Н.С. Подходова, В.В. Орлов и др.; Под ред. Н.Л. Стефановой, Н.С. Подходовой, В.И. Снегуровой. – СПб.: Изд-во РГПУ им. А.И. Герцена, 2009. – 413 с. 26 п.л./3,8 п.л.
2.Снегурова В.И. Теоретические основы построения методической системы дистанционного обучения математике в средней школе. Монография. СПб.: Изд-во РГПУ им. А.И.Герцена, 2010 (июнь). 12,9 п.л.
II. Научные статьи в журналах из перечня ВАК:
Научные статьи в журналах из перечня ВАК:
3.Снегурова В.И. Особенности методики проектирования методической системы дистанционного обучения математике // Известия Российского государственного университета А.И.Герцена, Научный журнал. № 10 (52). Психолого-педагогические науки (психология, педагогика, теория и методика обучения) – СПб.: Изд-во РГПУ им. А.И.Герцена, 2008. С. 124 — 136 0,78 п.л.
4.Снегурова В.И. Модели дистанционного обучения в системе среднего образования // Вестник Российского университет дружбы народов. Серия: Информатизация образования, № 2, 2009. – Москва: Изд-во РУДН, 2009. С. 95 – 106, 0,85 п.л.
5.Снегурова В.И. Дистанционный ресурс по алгебре и началам анализа как средство обучения // Вестник Российского университета дружбы народов. Серия: Информатизация образования, № 3, 2009. – Москва: Изд-во РУДН, 2009. С. 106 – 120, 0, 71 п.л.
6.Снегурова В.И. Об основаниях классификации моделей дистанционного обучения математике // Вестник Поморского университета. Серия Гуманитарные и социальные науки, № 4, 2009. – Архангельск: Изд-во ПГУ. С. 171-176, 0,4 п.л.
Серия Гуманитарные и социальные науки, № 4, 2009. – Архангельск: Изд-во ПГУ. С. 171-176, 0,4 п.л.
7.Снегурова В.И. Проблемы и ограничения дистанционного обучения математике // Вестник Новгородского государственного университета им. Ярослава Мудрого, № 53, 2009. – Великий Новгород: Изд-во НовГУ, 2009. С. 57-60, 0,4 п.л.
8.Снегурова В.И. Использование ЭОР нового поколения для организации дистанционного обучения математике // Открытое и дистанционное образование, № 4(36), 2009. – Томск: Изд-во ТГУ, 2009. С. 38-43, 0,6 п.л.
9.Снегурова В.И. Проектирование системы методического сопровождения сетевого учителя как подсистемы методической системы дистанционного обучения математике // Научно-теоретический журнал Научные проблемы гуманитарных исследований. Выпуск 10 (1), 2009. – Пятигорск: Изд-во Института региональных проблем Российской государственности на Сев. Кавказе, 2009. С. 68-75, 0,6 п.л
10.Снегурова В.И. Дистанционное обучение математике учащихся общеобразовательной школы // Письма в Эмиссия. Оффлайн (The Emissia. Offline Letters): электронный научный журнал. — Август 2010, ART 1442. — CПб., 2010 г. — URL: http://www.emissia.org/offline/2010/1442.htm. 0,4 п.л.
Оффлайн (The Emissia. Offline Letters): электронный научный журнал. — Август 2010, ART 1442. — CПб., 2010 г. — URL: http://www.emissia.org/offline/2010/1442.htm. 0,4 п.л.
11. Снегурова В.И. Учет специфики математического содержания при организации дистанционного обучения математике учащихся общеобразовательных школ // Письма в Эмиссия. Оффлайн (The Emissia. Offline Letters): электронный научный журнал. — Сентябрь 2010, ART 1455. — CПб., 2010 г. — URL: http://www.emissia.org/offline/2010/1455.htm. 0,4 п.л.
12. Снегурова В.И. Общая схема реализации дистанционного обучения математике учащихся общеобразовательных школ // Письма в Эмиссия. Оффлайн (The Emissia. Offline Letters): электронный научный журнал. — Октябрь 2010, ART 1460 — CПб., 2010 г. — URL: http://www.emissia.org/offline/2010/1460.htm. 0,4 п.л.
III. Книги, пособия, программы и рекомендации:
13.Г.А.Бордовский, И.Б.Готская, Снегурова В.И. и др. Организация дистанционной поддержки профильного обучения по учебным дисциплинам естественно-научного направления. (Проект программы повышения квалификации для учителей школ) // Программы повышения квалификации для заместителей директоров и учителей школ по организации дистанционной поддержки профильного обучения. – СПб.: ООО «АкадемПринт», 2004. – 34 с., 2 п.л./0,2 п.л.
(Проект программы повышения квалификации для учителей школ) // Программы повышения квалификации для заместителей директоров и учителей школ по организации дистанционной поддержки профильного обучения. – СПб.: ООО «АкадемПринт», 2004. – 34 с., 2 п.л./0,2 п.л.
14.Бордовский Г.А., Готская И.Б., Снегурова В.И. и др. Дистанционная поддержка обучения математике. (Методические рекомендации по организации дистанционной поддержки учебных дисциплин по направлениям профильного обучения) // Комплект методических рекомендаций для заместителей директоров и учителей школ по организации дистанционной поддержки профильного обучения. – СПб.: ООО «АкадемПринт», 2004. – 200 с., 12,5 п.л. / 0,7 п.л.
15.Методика и технология обучения математике. Лабораторный практикум: учеб. пособие для студентов матем. факультетов пед. университетов. М.: Дрофа, 2007. – 320 с., 20 п.л. / 1 п.л.
16.Бордовский Г.А., Готская И.Б., Ильина С.П., Снегурова В.И. Использование электронных образовательных ресурсов нового поколения в учебном процессе: Научно-методические материалы. СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. – 31 с., 2 п.л./ 0,95 п.л.
СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. – 31 с., 2 п.л./ 0,95 п.л.
17.Стефанова Н.Л., Подходова Н.С., Снегурова В.И. и др. Методика и технология обучения математике: курс лекций. М.: Дрофа, 2008. – 415 с., 25,9 п.л. / 2 п.л.
18.Снегурова В.И. Методические материалы для сетевых педагогов по учебному предмету Математика. Образование Медиа, СПб, 2008. – 177 с., 11 п.л.
19.И.В Головина, В.И. Снегурова, Е.Э.Шитик. Методические материалы для сетевых педагогов по учебному предмету Химия. Образование Медиа, СПб, 2008. – 101 с., 6,3 п.л. / 2,1 п.л.
20.Бордовский Г.А., Готская И.Б., Снегурова В.И. и др. Подготовка и поддержка педагогов-кураторов, участвующих в Интернет-обучении школьников: Методические материалы. Образование Медиа, СПб, 2008. – 84 с., 5,3 п.л. / 1,6 п.л.
21.Бордовский Г.А., Готская И.Б., Снегурова В.И. и др. Подготовка и поддержка сетевых педагогов, ведущих Интернет-обучение школьников: Методические материалы. Образование Медиа, СПб, 2008. – 72 с. , 4,5 п.л. / 1,6 п.л.
, 4,5 п.л. / 1,6 п.л.
IV. Научные статьи, материалы научных конференций, докладов:
22.Кочуренко Н.В. Снегурова В.И. Подготовка студентов на занятиях по решению задач к осуществлению индивидуализации обучения // Актуальные проблемы подготовки будущего учителя математики. Межвузовский сборник научных трудов. Выпуск 3./Под редакцией Ю.А.Дробышева и И.В.Дробышевой. – Калуга: Изд-во КГПУ им. К.Э.Циолковского, 2001. 0,25 /0,13 п.л.
23.Снегурова В.И. О показателях сложности задач в школьном курсе математики // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на Всероссийскую научную конференцию «54-е Герценовсие чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2001. 0,25 п.л.
24.Снегурова В.И. Об использовании термина «технология» в обучении // Методика и предметные технологии в ВУЗе и школе: Материалы проблемного семинара. — СПб.: Изд-во РГПУ им. А.И.Герцена, 2001. 0,15 п.л.
25.Снегурова В.И., Ярмолюк В.Е. Комплекс электронной поддержки как средство повышения уровня профессиональной подготовки учителя математики // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на между¬народную научную конфе¬ренцию «56-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И. Герцена, 2003. 0,25 п.л. / 0,12 п.л.
– СПб.: Изд-во РГПУ им. А.И. Герцена, 2003. 0,25 п.л. / 0,12 п.л.
26. Снегурова В.И. Проблемы подготовки учителя математики в современных условиях // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «58-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2005. 0,38 п.л.
27. Снегурова В.И., Ярмолюк В.Е. Модель рейтинговой оценки знаний студентов // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «59-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2006. 0,63 п.л. / 0,36 п.л.
28. Снегурова В.И. Особенности содержания курса математики в профильной школе // Инновационный вуз в пространстве образовательного округа. Четвертые-пятые Герценовские чтения в г. Волхове. Материалы научно-практической конференции. – СПб. 2006. 0,63 п.л.
29. Снегурова В.И. Особенности деятельности учителя в системе дистанционного обучения на этапе формулирования целей // Наука и высшая школа – профильному обучению (материалы Всероссийской научно-практический конференции17-18 октября 2006 г. ): В 2 ч. Часть 2. — СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. 0,6 п.л.
): В 2 ч. Часть 2. — СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. 0,6 п.л.
30. Снегурова В.И. Специфика формирования проектных умений учащихся в условиях дистанционного обучения математике // Метаметодика как перспективное направление развития предметных методик (материалы Четвертой Всероссийской научно-практической конференции 7-8 декабря 2006 года). – СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. 0,63 п.л.
31.Снегурова В.И. Общие положения конструирования методики освоения содержания курса «Элементарная математика и практикум по решению задач» в условиях рейтинговой оценки знаний студентов // Метаметодика как перспективное направление развития предметных методик (материалы Четвертой Всероссийской научно-практической конференции 7-8 декабря 2006 года). – СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. 0,63 п.л.
32.Снегурова В.И. Телекоммуникационные проекты в системе дистанционного обучения математике // Профильное обучение: проблемы элективных курсов (к 210-летию со дня рождения РГПУ им. А.И.Герцена): материали Всероссийской научно-практической конференции 22 марта 2007 года. – СПб., 2007. 0,44 п.л.
А.И.Герцена): материали Всероссийской научно-практической конференции 22 марта 2007 года. – СПб., 2007. 0,44 п.л.
33.Снегурова В.И., Чибичян М.С. О построении системы диагностики в процессе дистанционного обучения математике // Инновационный вуз в пространстве образовательного округа. Шестые Герценовские чтения в г. Волхове. Материалы научно-практической конференции. – СПб. 2007. 0,75 п.л. / 0,4 п.л.
34.Снегурова В.И. Об определении понятия «дистанционное обучение» // Университетский округ в региональной образовательной системе: опыт, проблемы, перспективы: Материалы Первой Всероссийской научно-практической конференции университетских округов России 7-8 февраля 2007. – СПб, 2007. 0,63 п.л.
35.Снегурова В.И. О структуре дистанционного ресурса по математике // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «60-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. 0,65 п.л.
36. Снегурова В.И. Об основаниях вариативности при конструировании дистанционного курса по математике // Актуальные вопросы преподавания математики и информатики: Сборник научных трудов Второй Всероссийской научно-практической конференции, 16 апреля 2007 г. – Биробиджан: Изд-во ДВГСГА, 2007. 0,45 п.л.
Снегурова В.И. Об основаниях вариативности при конструировании дистанционного курса по математике // Актуальные вопросы преподавания математики и информатики: Сборник научных трудов Второй Всероссийской научно-практической конференции, 16 апреля 2007 г. – Биробиджан: Изд-во ДВГСГА, 2007. 0,45 п.л.
37.Снегурова В.И. Обеспечение психологической комфортности учащихся в процессе дистанционного обучения // Материалы IV Всероссийского съезда РПО 18-21 сентября 2007. В 3 т. Том III. Изд-во «Круг». 0, 1 п.л.
38.Снегурова В.И. Использование электронных образовательных ресурсов нового поколения в учебном процессе // Подросток в современном мире: Материалы VI научно-практической конференции. – СПб: УО-ОСПб и ЛО, 2008. 0,37 п.л.
39.Снегурова В.И. О взаимодействии сетевого учителя и учащихся в процессе дистанционного обучения математике // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «61-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2008. 0,5 п.л.
– СПб.: Изд-во РГПУ им. А.И.Герцена, 2008. 0,5 п.л.
40.Снегурова В.И. Основные направления использования электронных образовательных ресурсов нового поколения в учебном процессе // “Time content management” в системе педагогических технологий: Сборник статей и методических материалов. – СПб.: «Европейский дом», 2008. 0,63 п.л.
41.Снегурова В.И. Основные направления использования дистанционных образовательных технологий в практике педагога-предметника // “Time content management” в системе педагогических технологий: Сборник статей и методических материалов. – СПб.: «Европейский дом», 2008. 1 п.л.
42.Снегурова В.И. О создании системы методического сопровождения сетевого учителя // Актуальные вопросы преподавания математики и информатики: Сборник научных трудов Третьей Всероссийской научно-практической конференции, 16 апреля 2008 г. – Биробиджан: Изд-во ДВГСГА, 2008. 0,45 п.л.
43.Снегурова В.И. Формы взаимодействия учащихся и сетевого учителя в процессе дистанционного обучения математике // Метаметодика как перспективное направление развития предметных методик обучения: сборник научных статей. Выпуск 5. – СПб.: САГА, 2008. 0,63 п.л.
Выпуск 5. – СПб.: САГА, 2008. 0,63 п.л.
44.Снегурова В.И. О содержании системы методического сопровождения сетевого учителя математики // Альманах современной науки и образования. – Тамбов: «Грамота», 2008. – №12(19): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,6 п.л.
45. Снегурова В.И. О методах и формах в системе методического сопровождения сетевого учителя // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «62-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2009. 0,38 п.л.
46. Снегурова В.И. Дистанционные образовательные технологии в системе повышения квалификации учителей математики // Актуальные вопросы преподавания математики и информатики: Сборник научных трудов Четвертой международной научно-практической конференции, Биробиджан, 16 апреля 2009 г. Часть 2. – Биробиджан: Изд-во ДВГСГА, 2009. 0,38 п.л.
47. Снегурова В.И.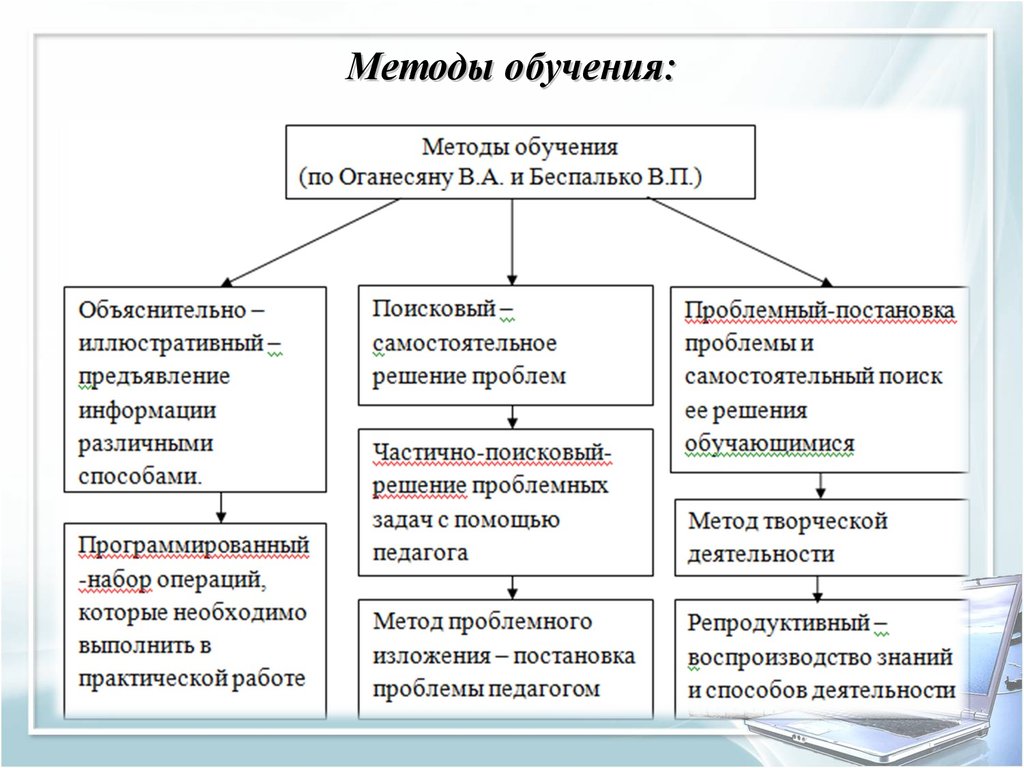 Принципы конструирования системы методического сопровождения сетевого учителя // Альманах современной науки и образования. Тамбов: Грамота, 2009. № 6 (25): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,36 п.л.
Принципы конструирования системы методического сопровождения сетевого учителя // Альманах современной науки и образования. Тамбов: Грамота, 2009. № 6 (25): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,36 п.л.
48. Снегурова В.И. Направления организации самостоятельной деятельности учащихся в процессе обучения // Самостоятельная деятельность учащихся: через традиции к инновациям: Сборник научно-методических статей и методических материалов. СПб, Издательство «Европейский Дом», 2009. 0,5 п.л.
49. Снегурова В.И. Управление деятельностью учащихся в процессе дистанционного обучения математике // Самостоятельная деятельность учащихся: через традиции к инновациям: Сборник научно-методических статей и методических материалов. СПб, Издательство «Европейский Дом», 2009. 0,6 п.л.
50. Снегурова В.И. Основные направления организации самостоятельной работы по математике // Самостоятельная деятельность учащихся: через традиции к инновациям: Сборник научно-методических статей и методических материалов. СПб, Издательство «Европейский Дом», 2009. 0,5 п.л.
СПб, Издательство «Европейский Дом», 2009. 0,5 п.л.
51. Снегурова В.И. Электронные образовательные ресурсы нового поколения как основа построения индивидуального образовательного маршрута учащегося в условиях дистанционного обучения // Наука и высшая школа – профильному обучению: сборник научных статей по итогам Второй Всероссийской научно-практической конференции 23-24 октября 2008 года. Выпуск 2. – СПб.: Сударыня, 2009. 0,38 п.л.
52.Снегурова В.И. Отбор и структурирование теоретического содержания и задач в системе дистанционного обучения математике // Письма в Эмиссия. Оффлайн (The Emissia.Offline Letters): электронный научный журнал. – Июнь 2009, ART 1334. – CПб., 2009г. – URL: http://www.emissia.org/offline/2009/1334.htm, 0,43 п.л.
53.Снегурова В.И. Цели в системе дистанционного обучения математике // Альманах современной науки и образования. Тамбов: Изд-во «Грамота», 2009. № 12 (29): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,42 п.л.
0,42 п.л.
54.Снегурова В.И. Основные направления совершенствования системы самостоятельной работы студентов в условиях реализации ФГОС 3-го поколения // Педагогическое образование в переходный период: результаты исследований 2009 года: Сборник статей по материалам внутрвузовской научной конференции, 3 марта 2010 года. – СПб.: Изд-во «Лемма», 2010 (апрель). 0,44 п.л.
55. Снегурова В.И. Средства обучения как компонент методической системы дистанционного обучения математике // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на международную научную конференцию «63-е Герценовские чтения». – СПб.: Изд-во РГПУ им. А.И.Герцена, 2010 (апрель). 0,31 п.л.
56. Снегурова В.И. Принципы дистанционного обучения математике в средней школе // Инновационные технологии обучения физико-математическим дисциплинам: м-лы II Международной науч.-практ. Интернет-конф., г. Мозырь, 11-14 мая 2010 г. – Мозырь: УО МГПУ им. И.П.Шамякина, 2010 (май). 0,4 п.л.
57. Снегурова В.И. Структурирование средств и методов обучения в процессе дистанционного обучения математике // Альманах современной науки и образования. Тамбов: Изд-во «Грамота», 2010 (июль). № 7 (38): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,42 п.л.
Снегурова В.И. Структурирование средств и методов обучения в процессе дистанционного обучения математике // Альманах современной науки и образования. Тамбов: Изд-во «Грамота», 2010 (июль). № 7 (38): Математика, физика, строительство, архитектура, технические науки и методика их преподавания. 0,42 п.л.
Использование исторического материала на уроках математики в 5-6 классах. | Статья по математике (5, 6 класс) на тему:
ИСПОЛЬЗОВАНИЕ ИСТОРИЧЕСКОГО МАТЕРИАЛА НА УРОКАХ
МАТЕМАТИКИ В 5-6 КЛАССАХ
Киселева Надежда Александровна
«Кто хочет изучить настоящее, не зная прошлого, тот никогда его не поймёт».
Г. Лейбниц
Первое впечатление, которое может сложиться о математике, — что она связана с вычислениями. Это и так, и не совсем так. Кроме вычислений, в ней существуют интересные, особенные, порой занятные вещи даже в привычной для всех школьной математике.
Отличительной чертой математики по праву считают её обобщенность. Самыми главными чертами являются логичность и строгость рассуждений. Ещё одно свойство математики – обаяние её истории. Изучая историю математики, порой убеждаешься в значимости тех обыденных понятий, которыми пользуешься, не задумываясь.
Ещё одно свойство математики – обаяние её истории. Изучая историю математики, порой убеждаешься в значимости тех обыденных понятий, которыми пользуешься, не задумываясь.
Некоторые из основных задач учителя математики – раскрыть её красоту и величие, пробудить интерес обучающихся к этой прекрасной науке. В помощь учителю можно найти ряд пособий, не утративших своей ценности и актуальности, несмотря на давний год выпуска. Так, трёхтомная «История математики в школе» замечательного математика и педагога Герша Исааковича Глейзера была первоначально издана на молдавском языке (1960, 1963, 1966), подготовленный автором русский вариант был опубликован посмертно (1981—1983) и переведён на языки СССР и других стран.
Хоть фундаментальные основы обучения математике остались с тех времен прежними, но все же содержание курса претерпело некоторые изменения. Например, внедрение стохастической линии и элементов логики в учебный курс. С течением времени менялись тенденции в применяемых методах и формах, появились современные технологии. Да и нынешние ученики уже не те, что прежде. Поэтому способы изучения исторического материала на уроках математики нуждаются в пересмотре в соответствие с актуальными условиями процесса обучения.
Да и нынешние ученики уже не те, что прежде. Поэтому способы изучения исторического материала на уроках математики нуждаются в пересмотре в соответствие с актуальными условиями процесса обучения.
Особо остро в мотивации нуждаются ученики 5-6 классов. К 6 классу только начинает зарождаться новый вид учебного мотива – мотив самообразования, но психофизиологические особенности возраста затрудняют этот процесс. У учителя есть все возможности для преодоления данной трудности при помощи использования исторического материала.
Значение исторических знаний в процессе обучения
Знание истории — важный фактор формирования мировоззрения. Исторические знания в процессе обучения направлены на создание представлений об исторической действительности, научной картины, направления человеческого общества.
Математика и история — две неразрывные области знания. Сведения из истории математики, исторические задачи сближают эти два школьных предмета. История обогащает математику гуманитарным и эстетическим содержанием, развивает образное мышление учеников. Математика, развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять.
Математика, развивающая логическое и системное мышление, в свою очередь занимает достойное место в истории, помогая лучше ее понять.
Изучив федеральный государственный образовательный стандарт основного общего образования, мы видим, что использование исторического материала на уроках математки позволяет удовлетворить целый ряд требований стандарта:
- формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
- формирование осознанного, уважительного и доброжелательного отношения к культуре, к истории, религии, традициям, ценностям народов России и народов мира;
- умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение определять понятия, создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
- умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
- умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе;
- овладение базовыми историческими знаниями, а также представлениями о закономерностях развития человеческого общества с древности до наших дней в социальной, экономической, политической, научной и культурной сферах;
- формирование умений применения исторических знаний для осмысления сущности современных общественных явлений, жизни в современном мире;
- развитие умений искать, анализировать, сопоставлять и оценивать содержащуюся в различных источниках информацию о событиях и явлениях прошлого и настоящего, способностей определять и аргументировать своё отношение к ней;
- осознание значения математики и информатики в повседневной жизни человека;
- формирование представлений о социальных, культурных и исторических факторах становления математической науки;
- формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления;
- развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений.
 [17]
[17]
Возрастные особенности обучающихся в 5-6 классах
Наши идеи мы реализуем применительно к 5-6 классам, так как использование материала позволяет компенсировать трудности, возникающие при обучении математике в связи с возрастными особенностями.
В подростковом возрасте происходит изменение характера познавательной деятельности. Подросток становится способным к более сложному аналитико-синтетическому восприятию предметов и явлений. У него формируется способность самостоятельно мыслить, рассуждать, сравнивать, делать относительно глубокие выводы и обобщения. Развивается способность к абстрактному мышлению. Для подросткового возраста характерно интенсивное развитие произвольной памяти, возрастание умения логически обрабатывать материал для запоминания. Внимание становится более организованным, всё больше выступает его преднамеренный характер.
Характерная особенность подросткового возраста – половое созревание организма. У девочек оно начинается практически с одиннадцати лет, у мальчиков несколько позже. Половое созревание вносит серьёзные изменения в жизнь ребёнка, нарушает внутреннее равновесие, вносит новые переживания, влияет на взаимоотношения мальчиков и девочек.
Половое созревание вносит серьёзные изменения в жизнь ребёнка, нарушает внутреннее равновесие, вносит новые переживания, влияет на взаимоотношения мальчиков и девочек.
В связи с этим стоит обратить внимание на такую психологическую особенность данного возраста, как избирательность внимания. Это значит, что дети откликаются на необычные, захватывающие уроки и классные дела, а быстрая переключаемость внимания не даёт возможности сосредоточиться долго на одном и том же деле. Однако если создаются труднопреодолимые и нестандартные ситуации, ребята занимаются работой с удовольствием и длительное время. [18]
.
СОДЕРЖАНИЕ ИСТОРИЧЕСКОГО МАТЕРИАЛА
В КУРСЕ МАТЕМАТИКИ В 5-6 КЛАССАХ
Продуктивность использования исторического материала напрямую зависит от его содержания и объема. Они должны соответствовать целям и задачам урока, а также возрасту учащихся. Таким образом, необходимо провести отбор материала вследствие анализа имеющихся источников: литературы, интернет-ресурсов.
Содержание исторического материала
Чтобы у обучающихся не возникло представление, что математика – наука безымянная, необходимо знакомить их с именами людей, творивших науку, богатыми в эмоциональном отношении эпизодами их жизни. Слава великих ученых, история их жизни являются сильным воспитательным средством. Знакомство с биографиями крупных ученых, с методами их работы дает исключительно много для формирования характера учащихся, их идеалов.
Подавляющее большинство школьников не имеют ни малейшего представления о развитии математики. Проследив за историческим развитием математических открытий, ученики лучше понимают и убеждаются в том, что точка зрения на одно и то же понятие становится со временем удобнее и проще.
При введении нового математического термина не лишним будет познакомиться с историей его происхождения. После небольшой исторической справки дети с большей активностью принимают участие в изучении нового объекта.
Большую роль в развитии школьников играют познавательные задания исторического характера. Задания данного вида имеют определенные методологические и педагогические цели: установление взаимосвязи между историей страны и края, раскрытие причинно-следственных связей, закономерностей исторического процесса, углубление, расширение, конкретизация, повторение и закрепление заданий по предмету. Кроме того эти задания являются средством активизации познавательной деятельности.
Задания данного вида имеют определенные методологические и педагогические цели: установление взаимосвязи между историей страны и края, раскрытие причинно-следственных связей, закономерностей исторического процесса, углубление, расширение, конкретизация, повторение и закрепление заданий по предмету. Кроме того эти задания являются средством активизации познавательной деятельности.
2
Анализ учебников по математике для 5-6 классов
Виленкин Н.Я. Математика. 5 класс
В обращении к читателю авторы сообщают: «Вы продолжаете изучать одну из самых древних и важных наук – математику. Многими математическими знаниями люди пользовались еще в глубокой древности – тысячи лет назад. Они были необходимы древним купцам и строителям, воинам и землемерам, жрецам и путешественникам… В учебнике вы найдете много интересных и полезных для себя сведений не только из области математики, но и из истории…»[2]
Для обозначения рассказов об истории возникновения и развития математики есть специальный условный знак —
Таблица 1.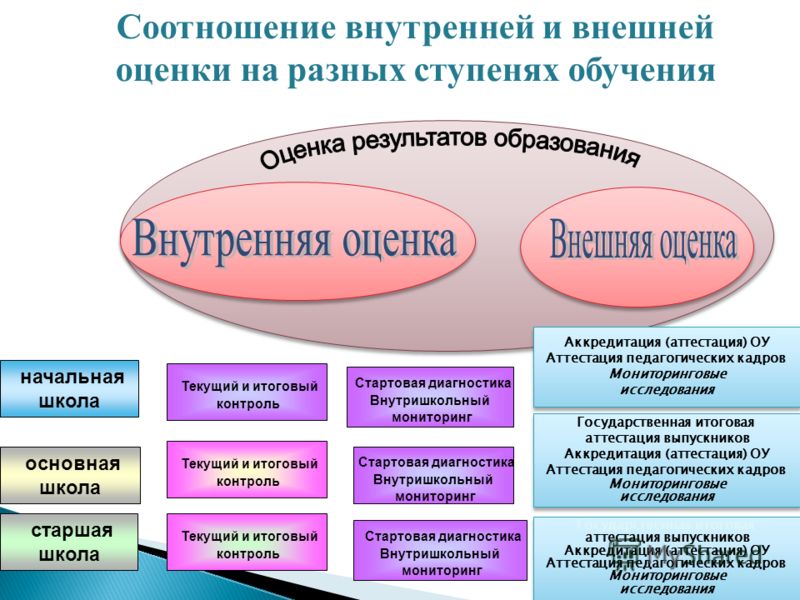
Тема | Биография математи ков | История развития науки | История происхождения терминов | Исторические задачи |
Глава 1. Натуральные числа. §1. Натуральные числа и шкалы. | ||||
3. Плоскость. Прямая. Луч. | + | |||
5. Меньше или больше. | + | |||
§2.Сложение и вычитание натуральных чисел. | ||||
6. Сложение натуральных чисел и его свойства. | + | |||
10. Уравнение. | + | + | ||
16. Степень числа. Квадрат и куб числа. | + | + | ||
§4. Площади и объемы. | ||||
19. Единицы измерения площадей. | + | |||
21. Объемы. Объем прямоугольного параллелепипеда. | + | + | ||
Глава 2. §5. Обыкновенные дроби. | ||||
28. Смешанные числа. | + | |||
29. Сложение и вычитание смешанных чисел. | + | + | + | |
§6. Десятичные дроби. Сложение и вычитание десятичных дробей. | ||||
33. Приближенные значения чисел. Округление чисел. | + | |||
§7. Умножение и деление десятичным дробей. | ||||
38. Среднее арифметическое. | + | + | ||
§8. | ||||
40. Проценты. | + | |||
42. Измерение углов. Транспортир. | + | |||
43. Круговые диаграммы. | + | + | ||
Виленкин Н.Я. Математика. 6 класс
Таблица 2.
Тема | Биография математи ков | История развития науки | История происхождения терминов | Исторические задачи |
Глава 1. §1. Делимость чисел. | ||||
7. Наименьшее общее кратное. | + | |||
§2. Сложение и вычитение дробей с разными знаменателями. | ||||
11. Сравнение, сложение и вычитание дробей с разными знаменателями | + | |||
12. Сложение и вычитание смешанных чисел. | + | |||
§3. Умножение и деление обыкновенных дробей. | ||||
19. Дробные выражения. | + | |||
§4. | ||||
25. Шар | + | |||
Глава 2. Рациональные числа. §5. Положительные и отрицательные числа. | ||||
27. Противоположные числа. | + | + | ||
30. Изменение величин. | + | |||
§6. Сложение и вычитание положительных и отрицательных чисел. | ||||
34. Вычитание. | + | |||
§7. | ||||
38. Свойства действий с рациональными числами. | + | |||
§8. Решение уравнений. | ||||
42. Решение уравнений. | + | |||
§9. Координаты на плоскости. | ||||
47. Графики. | + | |||
Козлова С.А. Математика. 5 класс
Практически весь исторический материал помещен отдельным блоком под названием «Исторические страницы».
Таблица 3.
Тема | Биография математи ков | История развития науки | История происхождения терминов | Исторические задачи |
Раздел 1. Числа. Глава 1. Натуральные числа и нуль. | ||||
1.3. Натуральные числа и нуль. Запись, чтение чисел. | + | + | ||
1.6. Округление натуральных чисел. | + | |||
Глава 2. Действия с натуральными числами. | ||||
2. | + | |||
Исторические страницы. | + | |||
Любителям математики. | + | |||
Раздел 2. Делимость. Глава 3. Делимость натуральных чисел. | ||||
3.7. Единицы измерения времени. | + | |||
Исторические страницы. | + | |||
Раздел 3. | ||||
Исторические страницы. | + | |||
Любителям математики. | + | |||
Раздел 4. Геометрические фигуры. | ||||
Исторические страницы. | + | |||
Любителям математики. | + | |||
Проекты. | + | |||
Козлова С. А. Математика. 6класс
А. Математика. 6класс
Таблица 4.
Тема | Биография математи ков | История развития науки | История происхождения терминов | Исторические задачи |
Раздел 1. Десятичные дроби. | ||||
Исторические страницы. | + | |||
Раздел 2. Пропорции и проценты. Глава 4. Пропорции. | ||||
4.4. Прямая и обратная пропорциональные зависимости. | + | |||
4. | + | |||
Исторические страницы. | + | |||
Раздел 3. Положительные и отрицательные числа. | ||||
Исторические страницы. | + | |||
Раздел 4. Понятие о действительных числах. | ||||
Исторические страницы. | + | |||
Проекты. | + | |||
Конечно, в учебниках мы встречаем и исторические страницы. Читая их, узнаём о появлении и развитии математических понятий, возникновении и совершенствовании методов решения задач. И, тем не менее, творчески работающему учителю тесно в рамках того исторического содержания, которое приводится в учебнике.
Читая их, узнаём о появлении и развитии математических понятий, возникновении и совершенствовании методов решения задач. И, тем не менее, творчески работающему учителю тесно в рамках того исторического содержания, которое приводится в учебнике.
Анализ дополнительной литературы
Потрясающим источником дополнительного материала для учителя служит пособие Г.И.Глейзера «История математики». В книге в виде коротких статей содержится материал из истории математики, доступный ученикам 4-6 классов. В пособии дан набор задач по арифметике, алгебре и геометрии известных математиков прошлых лет. Книга иллюстрирована.
Очень схоже по содержанию пособие Малыгина К.А. «Элементы историзма в преподавании математики в средней школе».
Также можно воспользоваться следующими источниками:
- Мир математики: в 40 т. Т. 3: Энрике Грасиан. Простые числа. Долгая дорога к бесконечности.
- Мир математки: в 40 т. Т. 15: Бизенц Торра. От абака к цифровой революции. Алгоритмы вычисления.

- Мир математики: в 40т. Т.21: Ламберто Гарсия дель Сид. Замечательные числа. Ноль, 666 и другие бестии.
- Мир математки: в 40 т. Т. 31: Хоакин Наварро. Тайная жизнь чисел. Любопытные разделы математики.
- Мир математики: в 45 т. Т. 37: Хоакин Наварро. Женщины-математики. От Гипатии до Эмми Нётер.
- Мир математики: в 45 т. Т. 38: Иоланда Гевара, Карлес Пюиг. Измерение мира. Календари, меры длины и математика.
Но в данном случае необходимо отобрать материал самостоятельно, так как эта серия книг рассчитана на взрослого читателя.
Полностью написана для школьников и содержит адаптированный для них материал работа Калининой М.И. и др. «Открываю математику: учебное пособие для 4 кл. нач.».
Обзор интернет-источников
Среди интернет-ресурсов нам показались наиболее приемлемыми для работы следующие:
http://www.math.ru/
http://math5school.ru/
http://club.umnitsa.ru/forum/matematiki-mnogo-ne-byvaet-ssylki-na-interesnye-matematicheskie-resursy
http://kartinkinaden. ru/nauka/879-interesnye-fakty-iz-istorii-matematiki.html
ru/nauka/879-interesnye-fakty-iz-istorii-matematiki.html
Именно там можно почерпнуть большую часть биографических сведений.
СПИСОК ЛИТЕРАТУРЫ
- Глейзер Г.И. История математики в школе:IV-VI кл. Пособие для учителей / Г.И. Глейзер. – М.: Просвещение, 1981. – 239 с.
- Виленкин Н.Я. Математика. 5 класс: учеб. для учащихся общеобразоват. организаций / Н.Я. Виленкин, В.И.Жохов, А.С. Чесноков, С.И. Швацбурд. – 34-е изд., стер. – М.: Мнемозина, 2015. – 280 с.
- Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. организаций / Н.Я. Виленкин, В.И.Жохов, А.С. Чесноков, С.И. Швацбурд. – 34-е изд., стер. – М.: Мнемозина, 2015. – 288 с.
- Калинина М.И. Открываю математику: учебное пособие для 4 кл. нач. шк./М.И. Калинина, Г.В. Бельтюкова, О.А. Ивашова, З.Г Алексеева, Т.В. Бокалова, О.А. Граничина , О.О. Еремеева, Н.Г. Каменкова, Е.Е. Останина, С.В. Сурикова. – М.: Просвещение, 2005. – 224 с.
- Козлова С.А. Математика. 5 класс.
 Учебник в 2 ч. / С.А. Козлова, А.Г. Рубин. — 2-е изд. — М.: Баласс, 2015. — Ч.1 — 208с., Ч.2 — 208с.
Учебник в 2 ч. / С.А. Козлова, А.Г. Рубин. — 2-е изд. — М.: Баласс, 2015. — Ч.1 — 208с., Ч.2 — 208с. - Козлова С.А. Математика. 6 класс. Учебник в 2 ч. / С.А. Козлова, А.Г. Рубин. — 2-е изд. — М.: Баласс, 2013. — Ч.1 — 208с., Ч.2 — 208с.
- Лазарев, В.С. Проектная деятельность в школе: учеб. пособие для учащихся 7-11 кл. / В.С. Лазарев. – Сургут, РИО СурГПУ, 2014. – 135 с.
- Малыгин К.А. Элементы историзма в преподавании математики в средней школе. Пособие для учителя.
- Мир математики: в 40 т. Т. 3: Энрике Грасиан. Простые числа. Долгая дорога к бесконечности. / Пер. с англ. – М.: Де Агостини, 2014. – 144 с.
- Мир математки: в 40 т. Т. 15: Бизенц Торра. От абака к цифровой революции. Алгоритмы вычисления. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с.
- Мир математики: в 40т. Т.21: Ламберто Гарсия дель Сид. Замечательные числа. Ноль, 666 и другие бестии. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с.
- Мир математки: в 40 т. Т. 31: Хоакин Наварро.
 Тайная жизнь чисел. Любопытные разделы математики. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с.
Тайная жизнь чисел. Любопытные разделы математики. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с. - Мир математики: в 45 т. Т. 37: Хоакин Наварро. Женщины-математики. От Гипатии до Эмми Нётер. / Пер. с исп. – М.: Де Агостини, 2014. – 144 с.
- Мир математики: в 45 т. Т. 38: Иоланда Гевара, Карлес Пюиг. Измерение мира. Календари, меры длины и математика. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с.
- Сауткина С. И. Проблемно- диалогическое обучение в образовательной модели «Школа 2100» — 30.08.2016 URL: https://kopilkaurokov.ru/nachalniyeKlassi/prochee/probliemno-dialoghichieskoie-obuchieniie-v-obrazovatiel-noi-modieli-shkola-2100
- Стефанова Л.Н. Методика и технология обучения математике. Курс лекций: пособие для ВУЗов / под научн.ред. Л.Н Стефановой, Н.С.Подходовой. — М.: Дрофа, 2005. – 416 с.
- Федеральный Государственный Образовательный Стандарт Основного Общего Образования URL: http://минобрнауки.рф /документы/938.
- Шаповаленко И.В. Возрастная психология (Психология развития и возрастная психология).
 / И.В. Шаповаленко — М.: Гардарики, 2005. — 349 с.
/ И.В. Шаповаленко — М.: Гардарики, 2005. — 349 с. - Яковлева Н.Ф. Проектная деятельность в образовательном учреждении: учеб. пособие / Н.Ф. Яковлева – 2-е изд., стер. – М.: ФЛИНТА, 2014. – 144 с.
Стратегическое использование технологий в преподавании и изучении математики
Скачать PDF
Позиция Национального совета учителей математики
Вопрос: Какова роль технологий в преподавании и изучении математики?
Должность NCTM
Крайне важно, чтобы преподаватели и учащиеся имели регулярный доступ к технологиям, которые поддерживают и совершенствуют математическое осмысление, рассуждения, решение проблем и общение. Эффективные учителя оптимизируют потенциал технологий, чтобы развивать понимание учащихся, стимулировать их интерес и повышать уровень владения математикой. Когда учителя используют технологии стратегически, они могут обеспечить более широкий доступ к математике для всех учащихся.
Технологические средства включают в себя инструменты, которые являются как конкретными, так и нейтральными по отношению к содержанию. В математическом образовании к предметно-ориентированным технологиям относятся системы компьютерной алгебры; среды динамической геометрии; интерактивные апплеты; портативные вычислительные устройства, устройства для сбора и анализа данных; и компьютерные приложения. Эти технологии помогают учащимся изучать и определять математические понятия и отношения. Нейтральные к содержанию технологии включают в себя инструменты для общения и совместной работы, а также цифровые средства массовой информации на основе Интернета, и эти технологии расширяют доступ учащихся к информации, идеям и взаимодействиям, которые могут поддерживать и улучшать осмысление, что имеет центральное значение для процесса владения знаниями. Результаты ряда исследований показали, что стратегическое использование технологических инструментов может способствовать как изучению математических процедур и навыков, так и развитию передовых математических навыков, таких как решение задач, рассуждение и обоснование (например, Гаданидис и Гейгер). , 2010 г.; Кастберг и Литам, 2005 г.; Нельсон, Кристофер и Мимс, 2009 г.; Пирс и Стейси, 2010 г .; Рошель и др., 2009, 2010; Су и Мойер, 2007).
, 2010 г.; Кастберг и Литам, 2005 г.; Нельсон, Кристофер и Мимс, 2009 г.; Пирс и Стейси, 2010 г .; Рошель и др., 2009, 2010; Су и Мойер, 2007).
В сбалансированной программе по математике стратегическое использование технологий усиливает преподавание и изучение математики (Dick & Hollebrands, 2011). Простого доступа к технологиям недостаточно. Учитель и учебная программа играют решающую роль в использовании технологических инструментов (King-Sears, 2009; Roschelle, et al., 2010; Suh, 2010). Преподаватели и разработчики учебных программ должны принимать решения со знанием дела и уметь определять, когда и как технологии могут надлежащим образом и эффективно повысить эффективность обучения учащихся (ISTE, 2008). Все школы и программы по математике должны предоставлять учащимся и учителям доступ к учебным технологиям, включая классное оборудование, портативные и лабораторные устройства с математическим программным обеспечением и приложениями, а также веб-ресурсы, а также надлежащее обучение для обеспечения их эффективного использования.
Программы обучения и повышения квалификации учителей должны постоянно обновлять знания практикующих специалистов о технологиях и их применении для поддержки обучения. Эта работа с практиками должна включать в себя разработку уроков математики, которые используют преимущества высокотехнологичной среды и интеграцию цифровых инструментов в повседневное обучение, прививая понимание силы технологий и их потенциального влияния на понимание и использование математики учащимися. Нельсон, Кристофер и Мимс, 2009 г.; Пирс и Стейси, 2010). В дополнение к обогащению опыта учащихся как изучающих математику, использование этих инструментов максимизирует возможности, предоставляемые учащимися растущими знаниями и комфортом с технологическими средствами коммуникации и поиска информации (Gadanidis & Geiger, 2010; Project Tomorrow, 2011). .
Ссылки
- Дик, Т. П., и Холлебрандс, К. Ф. (2011). Основное внимание в математике средней школы: технология поддержки рассуждений и осмысления.
 Рестон, Вирджиния: NCTM.
Рестон, Вирджиния: NCTM. - Гаданидис, Г., и Гейгер, В. (2010). Социальный взгляд на технологии улучшил математическое обучение — от сотрудничества до производительности. ЗДМ, 42 (1), 91–104.
- Международное общество технологий в образовании. (2008). Национальные стандарты образовательных технологий для учителей . Извлекаются из http://www.iste.org/standards/nets-for-teachers.aspx
- Кастберг, С., и Литам, К. (2005). Исследование графических калькуляторов на уровне средней школы: значение для подготовки учителей математики. Современные проблемы технологий и педагогического образования , 5 (1), 25–37.
- Кинг-Сирс, М. (2009). Универсальный дизайн для обучения: Технология и педагогика . Ежеквартальный выпуск по неспособности к обучению, 32 (4), 199–201.
- Нельсон, Дж., Кристофер, А., и Мимс, К. (2009). TPACK и Интернет 2.0: трансформация преподавания и обучения. Tech Trends, 53 (5), 80–85.

- Пирс, Р., и Стейси, К. (2010). Отображение педагогических возможностей, предоставляемых программным обеспечением для анализа математики. Международный журнал компьютеров для математического обучения. 15 (1), 1–20.
- Проект завтра (2011). Новые 3 элемента образования: включено, вовлечено, наделено полномочиями. Как современные студенты используют новейшие технологии для обучения . Получено с http://www.tomorrow.org/speakup/pdfs/SU10_3EofEducation(Students).pdf
- Рошель, Дж., Рафанан, К., Бханот, Р., Эстрелла, Г., Пенуэль, В.Р., Нуссбаум, М., Кларо, С. (2009). Объяснение группы строительных лесов и обратная связь с портативными технологиями: влияние на изучение математики учащимися. Исследования и разработки в области образовательных технологий , 58 , 399–419.
- Рошель Дж., Шехтман Н., Татар Д., Хегедус С., Хопкинс Б., Эмпсон С., Кнудсен Дж. и Галлахер Л. (2010). Интеграция технологий, учебного плана и профессионального развития для продвижения математики в средней школе: три крупномасштабных исследования.
 Американский журнал исследований в области образования, 47 (4), 833–878.
Американский журнал исследований в области образования, 47 (4), 833–878. - Suh J., & Moyer, PS (2007). Развитие репрезентативной беглости учащихся с использованием балансов виртуальной и физической алгебры. Journal of Computers in Mathematics and Science Teaching, 26 (2), 155–173.
- Suh, JM (2010). Технические знания для разных учащихся [Выпуск, посвященный технологиям]. Преподавание математики в средней школе, 15 (8), 440–447.
(октябрь 2011 г.)
Заявления о позиции NCTM определяют конкретную проблему, вопрос или потребность и описывают их отношение к математическому образованию. Каждое заявление определяет позицию Совета или отвечает на главный вопрос. Совет директоров NCTM утверждает заявления о позиции.
Каковы преимущества обучения математике с использованием технологий?
Это гостевая запись в блоге от Кристин Шаральди , консультанта по образованию и тренера по обучению со специализацией в области образовательных технологий, Mind-Brain-Education, Universal Design for Learning (UDL) и 21st Century Skills/Global. Образование.
Образование.
Продолжайте читать, чтобы узнать о преимуществах использования технологий на уроках математики.
Технология предоставляет динамичные возможности для обучения в классах по математике и естественным наукам. Мы можем улучшить процесс обучения и оживить концепции с помощью привлекательных и интерактивных средств массовой информации. Мы также можем предложить дополнительную поддержку для удовлетворения потребностей всех учащихся и создания индивидуального учебного процесса. Вот несколько важных способов, которыми учащиеся могут воспользоваться, когда мы включаем технологии в наши уроки математики и STEM.
Преподавание математики с использованием технологий — используйте мультимедиа
Мультимедиа делает обучение живым! Мы можем использовать видео, анимацию, интересные фильмы и другие средства массовой информации в процессе обучения, чтобы помочь нашим учащимся развивать навыки и понимание. И это может помочь мотивировать и воодушевить наших студентов в их обучении!
Г-н ДеМайо, учитель третьего класса в Юнион-Бич, штат Нью-Джерси, создает специальные фильмы, чтобы помочь своим ученикам понять темы урока, такие как таблица умножения и заимствования при вычитании . Он ведет канал на YouTube с «образовательными» уроками и музыкальными видео, в которых участвуют школьные учителя и повторяющиеся любимые персонажи, такие как марионетки Стивен и Энди.
Он ведет канал на YouTube с «образовательными» уроками и музыкальными видео, в которых участвуют школьные учителя и повторяющиеся любимые персонажи, такие как марионетки Стивен и Энди.
Фильмы так приятно смотреть, что дети смотрят их снова и снова и просят еще на разные темы! По сравнению с предыдущими учебными годами г-н ДеМайо обнаружил, что этот мультимедийный подход к смешанному обучению привел к лучшему запоминанию и лучшему пониманию учащимися концепций даже на уроках математики и STEM.
Мы не все будем снимать фильмы, как мистер ДеМайо, но он является хорошим примером того, что у всех нас есть возможность находить и создавать отличный контент, которым мы можем поделиться со своими учениками с помощью цифровых инструментов, платформ и приложений.
Интерактивные визуализации и исследования
Визуализация математики (или предметов STEM) выходит за рамки вовлечения учащихся; Исследования мозга показывают, что он является неотъемлемой частью изучения математики . Нейробиологи из Стэнфордского университета изучают, как мозг мыслит математически, и данные показывают, что зрительные пути задействованы даже при вычислении символьных чисел. По словам Джо Боулер и команды Стэнфордской высшей школы образования youcubed , визуальное представление всех математических понятий и включающее визуальные действия на всех уровнях обучения, может очень помочь учащимся.
Технология предоставляет учащимся дополнительные возможности видеть и взаимодействовать с математическими понятиями. Студенты могут исследовать и делать открытия с помощью игр, симуляций и цифровых инструментов.
Прекрасная платформа для учителей и учащихся — графический онлайн-калькулятор Desmos . Классные занятия Desmos стр. — отличная отправная точка для того, чтобы вовлечь учащихся в игру и проверку математических идей, а также в совместное использование и совместную работу.
Классные занятия Desmos стр. — отличная отправная точка для того, чтобы вовлечь учащихся в игру и проверку математических идей, а также в совместное использование и совместную работу.
Новое дополнение к STEM-предложению Texthelp, EquatIO mathspace , создает цифровую доску, на которой учащиеся и учителя могут комбинировать математические уравнения и формулы с графиками Desmos, геометрическими формами, манипуляциями и рисунками от руки, чтобы стимулировать визуальное решение задач.
Индивидуальные уроки математики с использованием технологий
Расширенный доступ к технологиям для математики позволяет сделать процесс обучения более индивидуальным. Поскольку нет двух абсолютно одинаковых учащихся, технологии могут предоставить отдельным учащимся контент и поддержку, которые особенно полезны для их индивидуальных потребностей. Дети могут просматривать уроки, учебные пособия, скринкасты и другие обучающие материалы на своих устройствах и в своем собственном темпе. Таким образом, если один учащийся все еще не понимает тему, а другой готов к дополнительным испытаниям, технология может позволить каждому сделать соответствующий следующий шаг.
Таким образом, если один учащийся все еще не понимает тему, а другой готов к дополнительным испытаниям, технология может позволить каждому сделать соответствующий следующий шаг.
Прекрасным примером того, как технологии помогают учащимся, является феномен Академии Хана . Сал Хан не собирался создавать некоммерческую образовательную организацию, когда начал размещать записи своих уроков математики на YouTube (как он восхитительно объясняет в своем выступлении на TED Talk). Он всего лишь пытался помочь обучать своих кузенов издалека и не видел причин устанавливать видео в приватный режим. Из отзывов своих двоюродных братьев, а затем и других людей со всего мира, которые нашли его видео, он понял, насколько ценен этот носитель и насколько важна возможность выбирать, перематывать и контролировать уроки.
В результате его работы появилась платформа Академии Хана, предоставляющая учащимся индивидуальный подход к обучению различными способами. Например, пользователи могут проходить тесты, чтобы узнать, какие концепции они усвоили и с чем им нужно попрактиковаться. Или учащиеся, которые лучше учатся с помощью письменного текста, могут получить доступ к стенограммам, которые сопровождают обучающие видео. Предоставление возможности направлять и контролировать пути обучения — веская причина для включения технологий в наши собственные занятия по математике.
Или учащиеся, которые лучше учатся с помощью письменного текста, могут получить доступ к стенограммам, которые сопровождают обучающие видео. Предоставление возможности направлять и контролировать пути обучения — веская причина для включения технологий в наши собственные занятия по математике.
Свяжите математические концепции с реальным миром
Учителя могут использовать технологии, чтобы помочь учащимся увидеть, как концепции, которые они изучают на уроках математики или STEM, могут применяться в повседневной жизни. Вместо того, чтобы давать своим ученикам лист решения задач, преподаватель Дженни Магьера записала короткое видео в молочном отделе супермаркета, поставив реальную задачу: решить, какая сделка будет лучшей. Она предложила своим ученикам выяснить, какую марку и размер сыра купить, исходя из цен и рекламных акций, которые можно увидеть на полках. Запись видео сценариев за пределами класса, таких как этот, можно легко сделать с помощью смартфона, а затем опубликовать на YouTube или на веб-сайте класса.
Запись видео сценариев за пределами класса, таких как этот, можно легко сделать с помощью смартфона, а затем опубликовать на YouTube или на веб-сайте класса.
Интеграция технологий в математический класс позволяет учащимся общаться с людьми за пределами класса, чтобы расширить их понимание и взгляды на то, что они изучают. Учителя могут организовывать интерактивные видеозвонки в режиме реального времени с экспертами по широкому кругу учебных тем, используя такие сайты, как Skype in the Classroom и Nepris . Один учитель на Nepris разместил запрос к отраслевым экспертам, чтобы они рассказали, как они используют математические концепции в своей повседневной работе, и в результате ученики смогли виртуально встретиться с дизайнером игровой площадки, который продемонстрировал, как он использует измерения, умножение и многое другое в своем решении. изготовление и планирование.
изготовление и планирование.
Технологии дают нам возможность расширить и обогатить наши уроки математики с помощью технологий. Каким образом технологии помогли вашим ученикам в изучении математики или STEM? Пожалуйста, поделитесь своими комментариями!
Издательство Inderscience Publishers – связь научных кругов, бизнеса и промышленности посредством исследований
- Рассекречивание лучших вещей в жизни
Исследовательская статья в International Journal of Pluralism and Economics Education использует структурированный подход к сравнению денежных теорий. В нем команда предлагает таксономию, классификацию для сравнения денежных теорий на основе их основной денежной функции. Работа актуальна после финансового кризиса 2007/2008 гг., поскольку денежные системы сталкиваются с повышенным вниманием, и это правильно.
В работе исследуются четыре направления мысли: «сохранение стоимости», «средство обмена», «средство платежа» и «расчетная единица», и они применяются к историческим примерам.
 в их бумаге. Сохранение стоимости относится к функции денег как средства сохранения стоимости покупательной способности с течением времени. Средство обмена относится к функции денег как общепризнанного посредника при обмене товаров и услуг. Платежные средства подчеркивают активную роль денег как средства погашения долгов и выполнения обязательств. Расчетная единица относится к функции денег как эталона измерения или единицы стоимости, в которой выражаются цены, заработная плата и другие экономические ценности.
в их бумаге. Сохранение стоимости относится к функции денег как средства сохранения стоимости покупательной способности с течением времени. Средство обмена относится к функции денег как общепризнанного посредника при обмене товаров и услуг. Платежные средства подчеркивают активную роль денег как средства погашения долгов и выполнения обязательств. Расчетная единица относится к функции денег как эталона измерения или единицы стоимости, в которой выражаются цены, заработная плата и другие экономические ценности.Возможно, очевидно, что ни одна таксономия не может охватить все денежные теории, Ян Грейтенс из Duale Hochschule Baden-Württemberg в Штутгарте, Германия, объясняет классификацию, основанную на этих четырех направлениях мысли.
«Согласно концепции «сохранения стоимости», сохранение покупательной способности является наиболее значимой функцией», — пишет он. «Мысль о« средстве обмена »поддерживает стабильную денежную стоимость в обращении товаров и услуг». Затем Грейтенс добавляет, что «мышление о« платежных средствах »подчеркивает активную роль денег и возможное влияние общества на деньги и экономику».
 Наконец, он объясняет, что «напротив, подход к« расчетной единице »сводит деньги к пассивной роли, эластично приспосабливаясь к потребностям реальной экономики».
Наконец, он объясняет, что «напротив, подход к« расчетной единице »сводит деньги к пассивной роли, эластично приспосабливаясь к потребностям реальной экономики».Грейтенс отмечает, что для лучшего понимания денежных систем мы не можем рассматривать такую таксономию как хронологическое представление изменений, эволюции. Прогресса нет, утверждает он. Вместо этого все направления мысли, изложенные в его исследовании, продолжаются и в современном мире денег.
Greitens, J. (2022) «Структурированный подход к сравнению монетарных теорий», Int. J. Плюрализм и экономическое образование, Vol. 13, № 3, стр. 262–276.
DOI: 10.1504/IJPEE.2022.10051865 - Немного похоже на мост в мутной воде
Исследователи, пишущие в International Journal of Critical Infrastructures , обсуждают возможные инженерные решения для строительства подводного туннеля как части будущей транспортной инфраструктуры.
Подводный, но плавучий туннель может стать ответом на создание связующей инфраструктуры между местами, разделенными водоемами.
 Такой подход исключает необходимость рытья туннеля под дном водоема, будь то река, озеро или море. Тем не менее, инженерные требования огромны, и любая такая конструкция должна быть устойчива к току и коррозии, а также к чрезвычайным происшествиям, таким как цунами.
Такой подход исключает необходимость рытья туннеля под дном водоема, будь то река, озеро или море. Тем не менее, инженерные требования огромны, и любая такая конструкция должна быть устойчива к току и коррозии, а также к чрезвычайным происшествиям, таким как цунами.Сахил Рана и М. Абдул Акбар из Департамента гражданского строительства Национального технологического института доктора Б. Р. Амбедкара в Джаландхаре, Пенджаб, Индия, отмечают, что в прошлом предлагались подводные плавучие туннели. Современное автоматизированное проектирование и программное обеспечение могут моделировать напряжения и деформации, которые строительные конструкции могут испытывать в реальном мире в различных условиях. Это означает, что теперь должно быть возможно определить, осуществимы ли данный дизайн и расположение.
Команда провела всесторонний обзор различных инженерных анализов, проведенных до сих пор для предполагаемых подводных плавучих туннелей. Обзор охватывает работу из этой междисциплинарной области инженеров-транспортников, инженеров-геотехников, морских инженеров, инженеров-строителей, инженеров-механиков и других.
 Исследователи также рассмотрели различные политические выводы относительно этой новой транспортной технологии. Их вывод состоит в том, что такие туннели в конечном итоге произведут революцию в области связи и транспорта. Такие туннели могли бы оказать серьезное влияние, например, на объединение островных кластеров или соединение регионов, где пролетный мост был бы неуместен или невозможен.
Исследователи также рассмотрели различные политические выводы относительно этой новой транспортной технологии. Их вывод состоит в том, что такие туннели в конечном итоге произведут революцию в области связи и транспорта. Такие туннели могли бы оказать серьезное влияние, например, на объединение островных кластеров или соединение регионов, где пролетный мост был бы неуместен или невозможен.Они отмечают, что еще не существует стандартных способов наблюдения за подводными плавучими туннелями, и предстоит проделать большую работу с точки зрения креплений и тросов, а также понимания реакции таких туннелей при использовании в водоеме. Команда добавляет, что воздействие таких потенциально огромных сооружений на водную жизнь, особенно на крупные организмы, также необходимо учитывать при запуске этих туннелей.
Рана, С. и Акбар, Массачусетс (2023) «Обзор исследовательских разработок по подводному плавучему туннелю», Int. J. Критические инфраструктуры, Vol. 19, № 1, стр.
 58–78.
58–78.
DOI: 10.1504/IJCIS.2023.10038938 - Виртуальные визиты: врач проверит вас прямо сейчас запланированы, и какие из них можно легко провести онлайн, а не в кабинете врача. Работа в International Journal of Industrial and Systems Engineering предполагает, что виртуальные встречи могут быть жизнеспособной альтернативой личным консультациям во многих случаях. Это особенно актуально, когда требуется последующая консультация, которая не требует физического осмотра, образцов, анализов или сканирования.
Сяо Ю и Армаган Байрам из отдела разработки промышленных и производственных систем Мичиганского университета в Дирборне, Дирборн, штат Мичиган, США, объясняют, как виртуальные визиты к врачу могут стать экономически эффективной альтернативой обычному посещению и как пациенты могут получить необходимую помощь удаленно. Это дает преимущества как медицинскому работнику, так и пациенту с точки зрения затрачиваемого времени и усилий, а также снижает риск приобретенных инфекций.

Команда отмечает, что планирование виртуальных встреч в рамках напряженного графика личных встреч и обеспечение того, чтобы медицинские работники и пациенты действительно получали пользу от онлайн-опыта, затруднено. Команда разработала открытую миграционную сеть для имитации потока пациентов через клинику. Затем они использовали это для математического моделирования оптимальной частоты последующих визитов, интервалов повторных посещений, другими словами, как для виртуальных, так и для офисных встреч. Имея в руках такую модель, команда предполагает, что менеджеры в сфере оказания медицинских услуг должны иметь возможность более систематически принимать решения в отношении того, как часто пациенты в долгосрочных, хронических медицинских ситуациях должны видеться во плоти. , так сказать, или виртуально.
Приблизительно половина населения США живет с хроническими заболеваниями, и аналогичные цифры наблюдаются в других странах развитого мира. Таким образом, эффективное лечение заболеваний может улучшить качество жизни миллионов людей, а также позволить им свести к минимуму симптомы или, по крайней мере, лучше справляться со своим состоянием.
 Виртуальные приемы могут быть интегрированы в такое управление, сокращая количество поездок к врачу, которые необходимо совершить пациенту, тем самым избавляя их от неудобств, беспокойства и затрат. Виртуальные приемы также могут снизить риск инцидента или несчастного случая или даже риск заражения пациента неприятной инфекцией от третьего лица по пути в кабинет врача и обратно, что остается важным моментом в продолжающемся COVID-19.пандемия.
Виртуальные приемы могут быть интегрированы в такое управление, сокращая количество поездок к врачу, которые необходимо совершить пациенту, тем самым избавляя их от неудобств, беспокойства и затрат. Виртуальные приемы также могут снизить риск инцидента или несчастного случая или даже риск заражения пациента неприятной инфекцией от третьего лица по пути в кабинет врача и обратно, что остается важным моментом в продолжающемся COVID-19.пандемия.Yu, X. и Bayram, A. (2023) «Оптимизация интервалов повторных посещений пациентов для виртуальных и офисных приемов при лечении хронических заболеваний», Int. J. Промышленная и системная инженерия, Vol. 43, № 3, стр. 363–383.
DOI: 10.1504/IJISE.2021.10040234 - Подводная акустическая беспроводная связь
Акустическая связь через воду хорошо известна у многих видов морских существ, китов, дельфинов и других китообразных, и, возможно, это самые известные примеры. Но ракообразные и рыбы слишком часто общаются через воду с помощью звука.
 Люди использовали сонар, звуковую навигацию и дальномер еще со времен Леонардо да Винчи, который впервые описал технику акустического прослушивания в 149 году.0. Современные активные сонарные методы, конечно же, намного сложнее, чем его пассивная техника.
Люди использовали сонар, звуковую навигацию и дальномер еще со времен Леонардо да Винчи, который впервые описал технику акустического прослушивания в 149 году.0. Современные активные сонарные методы, конечно же, намного сложнее, чем его пассивная техника.Теперь в исследовании International Journal of Intelligent Internet of Things Computing обсуждается система акустической связи, похожая на отправку электронной почты под водой. Доктор Актарул Хасан и Шен Вей из Школы информатики Чжэцзянского научно-технического университета, Ханчжоу, Китай, и их коллега Юбо Пэн из Центра продвижения электронной коммерции провинции Чжэцзян демонстрируют доказательство концепции устройства акустической связи на базе Arduino. контроллеры.
В их системе пьезоэлектрический преобразователь действует как динамик для воспроизведения низкочастотного сигнала. На приемном конце «канала» тот же тип пьезоэлектрического преобразователя используется в качестве микрофона для обнаружения входящего сигнала.
 Команда показала, что в диапазоне от 1 до 3 килогерц (кГц) они могут передавать и получать информацию со скоростью 200 бит в секунду акустически через воду и могут отправлять необходимую информацию с веб-страницы, преобразованную в азбуку Морзе. , через воду, которую затем можно было бы расшифровать, а информацию использовать для отображения страницы на компьютере на принимающей стороне. Система построена на интернет-протоколе TCP/IP. Рабочее расстояние между передатчиком и приемником может составлять до 25 метров с текущей настройкой. Команда добавляет, что улучшения в технологии могут значительно увеличить радиус действия их системы, что сделает ее гораздо более полезной.
Команда показала, что в диапазоне от 1 до 3 килогерц (кГц) они могут передавать и получать информацию со скоростью 200 бит в секунду акустически через воду и могут отправлять необходимую информацию с веб-страницы, преобразованную в азбуку Морзе. , через воду, которую затем можно было бы расшифровать, а информацию использовать для отображения страницы на компьютере на принимающей стороне. Система построена на интернет-протоколе TCP/IP. Рабочее расстояние между передатчиком и приемником может составлять до 25 метров с текущей настройкой. Команда добавляет, что улучшения в технологии могут значительно увеличить радиус действия их системы, что сделает ее гораздо более полезной.Команда предполагает, что их система с батарейным питанием может работать с небольшой лодки. Они отмечают, что базовая демонстрация передачи веб-страницы предполагает, что теперь должна быть возможна простая «беспроводная» телеметрия и дистанционное управление подводными устройствами.
Хасан, М.
 А., Пэн, Ю. и Вей, С. (2022) «Подводная беспроводная связь с использованием TCP/IP», Int. J. Intelligent Internet of Things Computing, Vol. 1, № 4, с. 273–286.
А., Пэн, Ю. и Вей, С. (2022) «Подводная беспроводная связь с использованием TCP/IP», Int. J. Intelligent Internet of Things Computing, Vol. 1, № 4, с. 273–286.
DOI: 10.1504/IJIITC.2023.10048055 - Обратите внимание!
В статье для журнала International Journal of System of Systems Engineering группа из Индии обсуждает использование интеллектуальной утилиты под названием GreenNotes. Исследователи объясняют, что этот инструмент можно использовать для отслеживания регулярных целей в 21 веке для умных городов и людей.
Рохит Растоги, Каран Будхвани и Харш Миттал из отдела CSE инженерного колледжа ABES в Газиабаде отмечают, что GreenNotes — это небольшая часть программного обеспечения, которое запускается как плагин или расширение в веб-браузере и перехватывает в облако. Облачная доступность может улучшить переносимость приложения, а также открыть возможность его использования в качестве инструмента для совместной работы. По словам команды, GreenNotes позволяет пользователям быстро делать заметки, а также выполнять преобразование голоса в текст, таким образом, действуя как современная версия диктофона.
 Расширение также имеет встроенный инструмент напоминания. Команда отмечает, что она использует модель freemium, в которой базовые функции доступны бесплатно, но премиум-функции можно приобрести в браузере Chrome.
Расширение также имеет встроенный инструмент напоминания. Команда отмечает, что она использует модель freemium, в которой базовые функции доступны бесплатно, но премиум-функции можно приобрести в браузере Chrome.Команда рассмотрела другие связанные расширения для браузера, чтобы выявить их плюсы и минусы и сравнить их с расширениями GreenNotes. Одним из преимуществ является мягкое удаление, поэтому я отмечаю, что его можно обратимо отправить в корзину, а не удалить навсегда в первую очередь. Расширение также предлагает опцию WYSIWYG, которая используется не всеми конкурирующими расширениями. Он имеет функцию редактирования уценки, которой, опять же, нет в других доступных расширениях. Функция преобразования голоса в текст уникальна среди рассмотренных расширений. Мобильная версия расширения для настольного браузера находится в разработке.
Rastogi, R., Budhwani, K. и Mittal, H. (2023) «GreenNotes: интеллектуальный служебный инструмент для отслеживания регулярных целей в 21 веке для умных городов и людей», Int.
 J. Система системной инженерии, Vol. 13, № 1, стр. 1–29.
J. Система системной инженерии, Vol. 13, № 1, стр. 1–29.
DOI: 10.1504/IJSSE.2023.10053192 - Выбор органических продуктов
Исследование, опубликованное в Международном журнале зеленой экономики , посвящено исследованию многих факторов, влияющих на отношение потребителей и покупательские привычки, когда речь идет об органических пищевых продуктах. Мохд Фархан из Школы бизнеса Миттал в Пенджабе, Индия, предполагает, что продолжающийся COVID-19Пандемия привела к тому, что многие потребители стали лучше осознавать, как качество пищи, которую они едят, влияет на их здоровье. Это привело к повышению осведомленности об органических пищевых продуктах.
Фархан провел опрос 600 человек в Индии и Непале, чтобы выяснить, как за последнее время изменились пищевые привычки и модели потребления. Он проанализировал данные, используя интеллектуальные частичные наименьшие квадраты и тесты Манна-Уитни.
Анализы показали, что безопасность, информированность и доверие положительно повлияли на склонность человека к потреблению органических продуктов в отличие от других пищевых продуктов.
 Фархан также показал, что предполагаемая польза для здоровья, а также гедонистические и социальные ценности положительно влияют на отношение потребителей к органическим продуктам питания. Это неизбежно привело к тому, что потребители с большей вероятностью стали покупать органические продукты питания. Результаты подчеркивают важность осведомленности и просвещения в отношении органических продуктов питания. Вполне вероятно, что в ближайшие несколько лет спрос продолжит расти, и производители и продавцы должны знать об этом, чтобы извлечь выгоду из повышения осведомленности своих потенциальных клиентов и найти способы удовлетворить растущий спрос.
Фархан также показал, что предполагаемая польза для здоровья, а также гедонистические и социальные ценности положительно влияют на отношение потребителей к органическим продуктам питания. Это неизбежно привело к тому, что потребители с большей вероятностью стали покупать органические продукты питания. Результаты подчеркивают важность осведомленности и просвещения в отношении органических продуктов питания. Вполне вероятно, что в ближайшие несколько лет спрос продолжит расти, и производители и продавцы должны знать об этом, чтобы извлечь выгоду из повышения осведомленности своих потенциальных клиентов и найти способы удовлетворить растущий спрос.Пандемия COVID-19 выдвинула на первый план проблемы со здоровьем во всем мире, и многие люди ищут более здоровые продукты питания, чтобы справиться с рисками, связанными с болезнью. Конечно, можно возразить, что преимущества органических продуктов питания по сравнению с неорганическими могут быть не такими значительными, как это часто утверждается.
 Тем не менее, повышение осведомленности о еде и здоровье, а также просвещение всегда будут полезны, и те люди, которые выбирают органические продукты, могут также внести другие изменения в свои привычки питания и образ жизни во имя улучшения своего здоровья, что принесет дополнительные, более ощутимые преимущества.
Тем не менее, повышение осведомленности о еде и здоровье, а также просвещение всегда будут полезны, и те люди, которые выбирают органические продукты, могут также внести другие изменения в свои привычки питания и образ жизни во имя улучшения своего здоровья, что принесет дополнительные, более ощутимые преимущества.Производители и продавцы органических продуктов питания должны честно демонстрировать преимущества своей продукции и показывать, что обычно более высокая цена компенсируется сопутствующим улучшением здоровья и экологических факторов.
Фархан, М. (2022) «Потребление органических продуктов питания на развивающихся рынках после COVID-19: модель ценностно-отношение-поведение», Int. J. Зеленая экономика, Vol. 16, № 3, стр. 294–311.
DOI: 10.1504/IJGE.2022.10053419 - В поисках мошенников
Появляется все больше свидетельств того, что большая часть материалов в Интернете полностью фальшивая. Это, пожалуй, известно. Действительно, есть столь же убедительные доказательства того, что огромное количество людей в Интернете тоже являются фейками.
 Большая часть вовлеченности и виральности контента в социальных сетях и других местах — это не что иное, как автоматизированная деятельность ботов и фермы кликов. Многое из этого делается как часть продвижения дезинформации в политических целях, и многое делается для того, чтобы обмануть рекламодателей, заставив их представить, что их платную рекламу видят реальные люди.
Большая часть вовлеченности и виральности контента в социальных сетях и других местах — это не что иное, как автоматизированная деятельность ботов и фермы кликов. Многое из этого делается как часть продвижения дезинформации в политических целях, и многое делается для того, чтобы обмануть рекламодателей, заставив их представить, что их платную рекламу видят реальные люди.Однако в, возможно, более приземленном мире реальных пользователей при поиске информации о продуктах и услугах, в которых они заинтересованы, необходимо уметь обнаруживать поддельные отзывы. В обзоре International Journal of Intelligent Engineering Informatics были рассмотрены подходы к обнаружению вводящих в заблуждение отзывов. Один недавний анализ показывает, что две трети оценок или отзывов клиентов о продуктах, продаваемых на крупных сайтах электронной коммерции, являются поддельными. Эти поддельные обзоры не только искажают среднее мнение о данном продукте, часто повышая низкое количество «звезд» для некачественного продукта, чтобы сделать его более продаваемым пятизвездочным товаром, но также незаконно повышают общий профиль продавца.

Радждавиндер Сингх Бопараи и Рекха Бхатия с факультета компьютерных наук и инженерии Пенджабского университета в Патиале, Пенджаб, Индия, обсуждают современное состояние исследований по этой проблеме. Они также изучают различные инструменты искусственного интеллекта, искусственного интеллекта и машинного обучения, предназначенные для пометки ненастоящих отзывов на коммерческих веб-сайтах. Команда выявляет пробелы в исследовательской литературе, а также ограничения существующих инструментов и указывает, как эти пробелы можно заполнить.
В обзорах, вводящих в заблуждение, может быть множество источников и авторов, что затрудняет определение конкретного стиля письма как подделки. Значительный пробел в текущих исследованиях и инструментах, который может быть заполнен будущими исследованиями, приведет к разработке более репрезентативной модели, которая будет универсальной, функциональной и портативной и сможет быстро и точно помечать как фальшивые вводящие в заблуждение отзывы, основанные на реальных событиях.
 данные. Учитывая недавнее публичное появление так называемых языковых моделей и инструментов, вполне вероятно, что мы будем видеть все больше и больше поддельных отзывов в Интернете. Однако те самые инструменты, которые генерируют такой вводящий в заблуждение контент, также могут использоваться для обнаружения его присутствия. Мы неизбежно увидим игру в кошки-мышки между сайтами электронной коммерции и мошенниками, а в центре внимания окажутся потребители, которые ищут достойный продукт по хорошей цене.
данные. Учитывая недавнее публичное появление так называемых языковых моделей и инструментов, вполне вероятно, что мы будем видеть все больше и больше поддельных отзывов в Интернете. Однако те самые инструменты, которые генерируют такой вводящий в заблуждение контент, также могут использоваться для обнаружения его присутствия. Мы неизбежно увидим игру в кошки-мышки между сайтами электронной коммерции и мошенниками, а в центре внимания окажутся потребители, которые ищут достойный продукт по хорошей цене.Бопараи, Р.С. и Бхатия, Р. (2022) «Стратегии обнаружения вводящих в заблуждение веб-обзоров: опрос», Int. J. Интеллектуальная инженерная информатика, Vol. 10, № 5, стр. 411–433.
. DOI: 10.1504/IJIEI.2022.10053698. аудио стеганография.Стеганография использовалась тысячи лет для сокрытия информации. Сообщение, написанное так называемыми «невидимыми чернилами», является примитивным примером стеганографии. В компьютерный век информация была скрыта в текстовых, графических и звуковых файлах, не оставляя никаких видимых или заметных изменений.
 Стеганография предполагает сокрытие информации, а также существование этой информации, чтобы ее мог найти только предполагаемый получатель.
Стеганография предполагает сокрытие информации, а также существование этой информации, чтобы ее мог найти только предполагаемый получатель.Аудиостеганография обычно считается экономичным средством шифрования данных в сети, поскольку она имеет низкий уровень шумовых искажений и, как правило, может быть встроена незаметно. Р. Рамьядеви и В. Пурнима из отдела компьютерных наук Института науки и технологии SRM в Тамил Наду, Индия, оценили максимальное количество символов, цифр, букв и других символов, которые можно добавить в аудиофайл. файл без изменения его структуры. Но что еще более важно, они рассмотрели предел слышимых искажений и нарушений скорости передачи данных, когда файл воспроизводится как обычный звуковой файл на медиаплеере. Если есть очевидное искажение, то тот факт, что файл использовался для аудио стеганографии, может быть более очевидным для третьей стороны. Формат wav, официально известный как формат звуковых файлов формы волны, был разработан в 1991 от IBM и Microsoft и широко используется на персональных компьютерах и других устройствах.

Исследование группы показывает, что точность можно повысить при низких уровнях внедрения и обеспечить оптимальное пиковое отношение сигнал/шум при запутывании информации, если первый, второй и третий младшие значащие биты (LSB) аудиофайла используются в стеганографическая обработка. Команда сравнила 8-битный и 16-битный звук с импульсно-кодовой модуляцией (ИКМ) и использовала среднеквадратичную ошибку (MSE), среднюю абсолютную ошибку (MAE), отношение сигнал-шум (SNR) и кросс-корреляционный анализ. идентифицировать скрытые текстовые данные в данном аудиопотоке. Команда пишет, что 16-битный стереофонический WAV-файл может содержать чуть более 30000 символов с пробелами, при этом присутствие этой добавленной информации не может быть обнаружено третьей стороной, не подозревающей о ее присутствии в файле. 8-битный монофонический wav-файл может содержать более 8000 символов с пробелами.
При использовании первых трех младших разрядов точность составляла 98 процентов, а частота ложных срабатываний составляла менее 5 процентов.
 Конечно, надежность скрытого сообщения в аудиофайле зависит от длины скрытого текстового сообщения, сообщает команда. Дополнительная дополнительная информация будет более очевидна для третьей стороны, проверяющей файлы на наличие такого рода запутывания сообщений в коллекции звуковых файлов.
Конечно, надежность скрытого сообщения в аудиофайле зависит от длины скрытого текстового сообщения, сообщает команда. Дополнительная дополнительная информация будет более очевидна для третьей стороны, проверяющей файлы на наличие такого рода запутывания сообщений в коллекции звуковых файлов.Рамьядеви Р. и Пурнима В. (2022) «Использование звуковой стеганографии для организации и анализа текста в файлах WAV», Int. J. Интеллектуальная инженерная информатика, Vol. 10, № 5, с.397–410.
DOI: 10.1504/IJIEI.2022.10053658 - Волатильность климатических инвестиций в Индии во время COVID-19
Как пандемия COVID-19 повлияла на инвестиции в инициативы по изменению климата в развивающихся странах? Новое исследование в International Journal of Green Economics посвящено влиянию болезни на такие инвестиции в Индии.
Пейюш Бангур из Женского института исследований в области управления, ориентированного на развитие (WISDOM) в Раджастане, использовала модель GARCH (1,1) для изучения индийского индекса CARBONEX и обнаружила, что, как и следовало ожидать, в этих инвестициях наблюдается повышенная волатильность.
 области во время пандемии. Действительно, согласно анализу Бангура, дисперсия увеличилась почти на 150%. Выводы имеют важные последствия для окупаемости инвестиций, а также для реагирования на изменение климата, показывая, что доверие к климатическим инвестициям упало в разгар пандемии. Эта работа может помочь определить будущие инвестиционные меры, когда мы столкнемся с новой пандемией.
области во время пандемии. Действительно, согласно анализу Бангура, дисперсия увеличилась почти на 150%. Выводы имеют важные последствия для окупаемости инвестиций, а также для реагирования на изменение климата, показывая, что доверие к климатическим инвестициям упало в разгар пандемии. Эта работа может помочь определить будущие инвестиционные меры, когда мы столкнемся с новой пандемией.Антропогенные выбросы углерода вызывают изменение климата. Последствия в ближайшие годы, вероятно, будут разрушительными, особенно для тех, кто уже живет в экстремальных условиях. К сожалению, общая социальная модель во всем мире предполагает экономический рост, и это имеет свою цену с точки зрения используемых ресурсов и производимого загрязнения. Если мы хотим решить проблемы, с которыми мы сталкиваемся, нам необходимо использовать парадигму экономического роста, чтобы помочь нам сократить выбросы, снизить нашу зависимость от неустойчивых ресурсов и решить проблему изменения климата.
Торговля выбросами углерода, инвестиции в устойчивые технологии и возобновляемые источники энергии находятся в авангарде этого процесса.
 S&P BSE CARBONEX of India был первым тематическим индексом, основанным на углероде, и был запущен в ноябре 2012 года при поэтапной поддержке Верховного комиссара Великобритании в Индии. Этот индекс отражает инвестиции в «зеленую» экономику. Бангур предполагает, что «результаты исследования могут быть полезны инвесторам, менеджерам компаний, регулирующим органам, ученым и государственным чиновникам». Он добавляет, что «зеленые» инвестиции вернутся в постпандемическом мире. «Последствия волатильности могут послужить ориентиром для запуска первоначальных политических действий в случае последующих случаев аналогичного характера», — говорит он.
S&P BSE CARBONEX of India был первым тематическим индексом, основанным на углероде, и был запущен в ноябре 2012 года при поэтапной поддержке Верховного комиссара Великобритании в Индии. Этот индекс отражает инвестиции в «зеленую» экономику. Бангур предполагает, что «результаты исследования могут быть полезны инвесторам, менеджерам компаний, регулирующим органам, ученым и государственным чиновникам». Он добавляет, что «зеленые» инвестиции вернутся в постпандемическом мире. «Последствия волатильности могут послужить ориентиром для запуска первоначальных политических действий в случае последующих случаев аналогичного характера», — говорит он.Бангур, П. (2022 г.) «Инвестиции в изменение климата и COVID-19: данные о волатильности доходности», Int. J. Зеленая экономика, Vol. 16, № 3, стр. 235–245.
DOI: 10.1504/IJGE.2022.10053454 - Предприятия, поощряющие лояльность покупателей
Лояльность покупателей может быть ключевым компонентом постоянного успеха в бизнесе, особенно на рынке с большим количеством конкурентов и ограниченным числом потенциальных клиентов.
 Бизнес должен быть вовлечен в текущие исследования, чтобы знать, что помогает удерживать клиентов на постоянно меняющихся рынках. В частности, ключевым может быть определение того, какие стимулы могут работать для повышения лояльности клиентов.
Бизнес должен быть вовлечен в текущие исследования, чтобы знать, что помогает удерживать клиентов на постоянно меняющихся рынках. В частности, ключевым может быть определение того, какие стимулы могут работать для повышения лояльности клиентов.Система карт лояльности, пожалуй, самая известная программа поощрения, которая вознаграждает лояльность и предположительно увеличивает количество повторных сделок. Основная концепция заключается в том, что клиенты подписываются на программу и получают вознаграждение, когда они совершают повторные покупки или взаимодействуют с бизнесом другими способами, например, приглашая друзей, оставляя отзывы или следя за бизнесом в социальных сетях. Обычно они зарабатывают баллы на своей карте за различные действия, и их можно обменять на скидки в магазине, бесплатные подарки или даже ваучеры или купоны, которые можно использовать в соответствующих торговых точках, таких как рестораны, кинотеатры или даже туристические компании и тематические парки.
 . Конкретные вознаграждения и стимулы, которые компания предлагает своим постоянным клиентам, сильно различаются в зависимости от типа бизнеса и предпочтений целевой аудитории. Некоторые компании используют физические карты, которые сканируются в момент покупки, другие предлагают своим клиентам загрузить приложение для мобильного телефона.
. Конкретные вознаграждения и стимулы, которые компания предлагает своим постоянным клиентам, сильно различаются в зависимости от типа бизнеса и предпочтений целевой аудитории. Некоторые компании используют физические карты, которые сканируются в момент покупки, другие предлагают своим клиентам загрузить приложение для мобильного телефона.Конечно, у бизнеса есть преимущество не только в сохранении клиентов, но и в получении дополнительной информации об их покупательских привычках и других действиях, связанных с использованием карты лояльности. Отслеживание активности дает компаниям бесценную информацию о поведении клиентов, чтобы они могли более эффективно работать с маркетинговыми кампаниями.
В исследовании, опубликованном в International Journal of Business Innovation and Research , были рассмотрены различные факторы, побудившие клиентов совершать покупки в двух торговых точках India Ondoor и Reliance Fresh, а также выяснить, играют ли карты лояльности роль в удержании клиентов.
 Ньягарама Омбога Томас и Сапна Сингх из Департамента менеджмента Университета SRK в Бхопале и Мохит Гангвар из Университета Бхабха также в Бхопале использовали описательный дизайн исследования для сбора данных с помощью вопросника.
Ньягарама Омбога Томас и Сапна Сингх из Департамента менеджмента Университета SRK в Бхопале и Мохит Гангвар из Университета Бхабха также в Бхопале использовали описательный дизайн исследования для сбора данных с помощью вопросника.Анализ данных, проведенный исследователями, показал, что существует множество факторов, влияющих на покупательский выбор покупателей, в том числе доступность продукта, разнообразие торговых марок, атмосфера в данной торговой точке, политика возврата, цена, обслуживание, рекламные акции и расположение магазина. Но программы корпоративных карт лояльности оказали сильное влияние на тех клиентов, которые были зарегистрированы в программе.
Томас, Н.О., Сингх, С. и Гангвар, М. (2023) «Удержание клиентов с помощью программы карт лояльности», Int. J. Бизнес-инновации и исследования, Vol. 30, № 2, стр. 200–217.
doi: 10.1504/ijbir.2021.10038500
. Интегрированный подход к разработке технологического педагогического содержания знаний — CITE Journal
Технологии по математике. , 2000) заявил: «Технология имеет важное значение в преподавании и изучении математики; это влияет на то, чему учат, и способствует обучению учащихся» (стр. 24). Будут ли технологии улучшать или препятствовать обучению учащихся, зависит от решений учителей при использовании технологических инструментов, решений, которые часто основаны на знаниях, полученных в ходе программы подготовки учителей. В рекомендациях Ассоциации преподавателей математики (AMTE, 2006) говорится, что программы подготовки учителей должны «предоставлять возможности [учителям] приобретать знания и опыт, необходимые для внедрения технологий в контекст преподавания и изучения математики» (стр. 1). . Типы знаний и навыков, которые нужны будущим учителям для поддержки использования учащимися технологий, дополнительно описаны в Международном обществе технологий в образовании 9.0031 Национальные стандарты образовательных технологий для учителей , которые были первоначально выпущены в 2000 г. и обновлены в 2008 г.
, 2000) заявил: «Технология имеет важное значение в преподавании и изучении математики; это влияет на то, чему учат, и способствует обучению учащихся» (стр. 24). Будут ли технологии улучшать или препятствовать обучению учащихся, зависит от решений учителей при использовании технологических инструментов, решений, которые часто основаны на знаниях, полученных в ходе программы подготовки учителей. В рекомендациях Ассоциации преподавателей математики (AMTE, 2006) говорится, что программы подготовки учителей должны «предоставлять возможности [учителям] приобретать знания и опыт, необходимые для внедрения технологий в контекст преподавания и изучения математики» (стр. 1). . Типы знаний и навыков, которые нужны будущим учителям для поддержки использования учащимися технологий, дополнительно описаны в Международном обществе технологий в образовании 9.0031 Национальные стандарты образовательных технологий для учителей , которые были первоначально выпущены в 2000 г. и обновлены в 2008 г. Существуют настоятельные рекомендации по использованию технологий для обучения учащихся, изучающих математику, и для подготовки учителей, которые будут преподавать математику.
Существуют настоятельные рекомендации по использованию технологий для обучения учащихся, изучающих математику, и для подготовки учителей, которые будут преподавать математику.
Цель этой статьи — поделиться и обсудить некоторые примеры из материалов, разработанных в рамках проекта «Подготовка к преподаванию математики с помощью технологий» (PTMT), созданного для подготовки учителей к использованию технологий для обучения математике способами, подходящими для учащихся, живущих в мире, который включает в себя быстро меняющиеся цифровые технологии (см. http://www.ncsu.edu/project/ptmt/mods.htm). На данный момент в рамках проекта разработаны материалы, посвященные только содержательным областям статистики и вероятности, и примеры будут сосредоточены на этих контекстах. Мы представляем наши руководящие принципы и примеры из материалов, а также обсуждение результатов полевых испытаний и последствий.
Руководящие принципы
На педагогическое образование и исследования учителей большое влияние оказала идея Шульмана (1986) о педагогическом содержании учителей (PCK). Например, Саймон (1995) использовал PCK для описания важных компонентов цикла обучения математике, который включает в себя знания учителем математики, математические действия и представления, изучение учащимися определенного содержания и их гипотезы о текущих знаниях учащихся, а также их личные теории. о математике, обучении и преподавании. Совсем недавно несколько авторов описали технологии, педагогику и знание содержания (TPACK) как тип знаний учителей, необходимых учителям для понимания того, как эффективно использовать технологии для преподавания конкретного предмета (Koehler & Mishra, 2005; Mishra & Koehler, 2008 г.; Niess, 2005 г., 2006 г.; Комитет AACTE по инновациям и технологиям, 2008 г.). Келер и Мишра (2005; Mishra & Koehler, 2008) утверждали, что TPACK представляет собой интеграцию знаний учителей о содержании, педагогике и технологиях (рис. 1).
Например, Саймон (1995) использовал PCK для описания важных компонентов цикла обучения математике, который включает в себя знания учителем математики, математические действия и представления, изучение учащимися определенного содержания и их гипотезы о текущих знаниях учащихся, а также их личные теории. о математике, обучении и преподавании. Совсем недавно несколько авторов описали технологии, педагогику и знание содержания (TPACK) как тип знаний учителей, необходимых учителям для понимания того, как эффективно использовать технологии для преподавания конкретного предмета (Koehler & Mishra, 2005; Mishra & Koehler, 2008 г.; Niess, 2005 г., 2006 г.; Комитет AACTE по инновациям и технологиям, 2008 г.). Келер и Мишра (2005; Mishra & Koehler, 2008) утверждали, что TPACK представляет собой интеграцию знаний учителей о содержании, педагогике и технологиях (рис. 1).
Рисунок 1. Компоненты технологического педагогического содержания знаний.
Сосредоточив внимание на пересечении трех компонентов технологии, содержания и педагогики, Нисс (2005) описал четыре различных аспекта, составляющих TPACK учителей:
- Общая концепция того, что значит преподавать предметная интегрирующая технология в процесс обучения;
- Знание учебных стратегий и представлений для преподавания конкретных тем с использованием технологий;
- Знание понимания, мышления и обучения учащихся с помощью технологий; и
- Знание учебной программы и учебных материалов, объединяющих технологии с обучением.

Эти четыре аспекта TPACK существенно расширяют описанные Саймоном (1995) компоненты знаний учителей в цикле обучения математике за счет включения акцента на технологию.
Программы подготовки учителей все больше внимания уделяют использованию технологий для обучения математике в школе (например, Powers & Blubaugh, 2005). В 2003 году Керсент, Хортон, Стол и Гарофало сообщили, что 21% учителей математики, ответивших на их опрос, преподавали курс, посвященный технологиям. Несколько лет спустя Leatham (2006) сообщил, что 29% педагогов-преподавателей математики прошли в своих учебных заведениях курсы, посвященные преподаванию математики с использованием технологий.
Такое внимание к необходимости курса по использованию технологий в обучении математике обнадеживает, но может быть недостаточно распространено в программах подготовки учителей. Результаты комплексного национального исследования показывают, что участие учителей в отдельных курсах по технологиям (часто лишенных содержания) не сильно коррелирует с их способностями интегрировать технологии в обучение (Moursund & Bielefeldt, 19). 99). Появляются данные, свидетельствующие о том, что модель, объединяющая технологии, педагогику и содержание, более эффективна для подготовки учителей к использованию технологий в своих классах (Комитет AACTE по инновациям и технологиям, 2008 г.; Niess, 2005 г.; Suharwoto, 2006 г.).
99). Появляются данные, свидетельствующие о том, что модель, объединяющая технологии, педагогику и содержание, более эффективна для подготовки учителей к использованию технологий в своих классах (Комитет AACTE по инновациям и технологиям, 2008 г.; Niess, 2005 г.; Suharwoto, 2006 г.).
Учитывая меняющийся характер технологий, важно, чтобы учителя разработали модель преподавания и обучения, выходящую за рамки специфики технологического инструмента, чтобы они могли принимать обоснованные решения о надлежащем использовании технологий в математике (Conference Board of Математические науки, 2001). Следуя модели компонентов TPACK (Koehler & Mishra, 2005; Niess, 2005) и при поддержке рекомендаций по надлежащему использованию технологий в обучении учителей математики (AMTE, 2006; Garofalo, Drier, Harper, Timmenman, & Shockey, 2000; Suharwoto, 2006), такая модель объединила бы математику, технологии и педагогику с упором на мышление учащихся.
Ключевой особенностью нашего подхода к подготовке учителей к обучению математике с использованием технологий является комплексная разработка TPACK для учителей. Учителя должны понимать, что критически важные решения, которые они принимают, основаны на их понимании каждой области (технологии, педагогики и содержания) и зависят от их убеждений и концепций. Мы предполагаем, что, интегрально развивая понимание учителями математики, педагогики и технологий с упором на мышление учащихся, мы поможем учителям сформировать более полную картину того, что необходимо при обучении математике с помощью технологий, и, в свою очередь, подготовиться к тому, чтобы информированные решения о надлежащем использовании технологий.
Учителя должны понимать, что критически важные решения, которые они принимают, основаны на их понимании каждой области (технологии, педагогики и содержания) и зависят от их убеждений и концепций. Мы предполагаем, что, интегрально развивая понимание учителями математики, педагогики и технологий с упором на мышление учащихся, мы поможем учителям сформировать более полную картину того, что необходимо при обучении математике с помощью технологий, и, в свою очередь, подготовиться к тому, чтобы информированные решения о надлежащем использовании технологий.
Преимущества использования технологии и интегрированного подхода
Создание на основе работы Пи (1987), Бен-Цви (2000) предоставили полезную информацию об использовании технологий как способов расширения или реорганизации статистической или математической работы. По словам Пи, технологические инструменты обычно используются двумя разными способами, которые подчеркиваются в наших учебных материалах для учителей. Технологии могут усилить способности учащихся решать проблемы или реорганизовать то, как учащиеся думают о проблемах и их решениях. Идея 9.0031 усилитель заключается в том, что инструмент ускоряет процесс, который мог бы быть выполнен без его использования. Например, технологические инструменты можно использовать для быстрого создания больших списков псевдослучайных чисел (см. Видео 1), а также для создания графических представлений или эффективного вычисления линий регрессии методом наименьших квадратов (Видео 2).
Технологии могут усилить способности учащихся решать проблемы или реорганизовать то, как учащиеся думают о проблемах и их решениях. Идея 9.0031 усилитель заключается в том, что инструмент ускоряет процесс, который мог бы быть выполнен без его использования. Например, технологические инструменты можно использовать для быстрого создания больших списков псевдослучайных чисел (см. Видео 1), а также для создания графических представлений или эффективного вычисления линий регрессии методом наименьших квадратов (Видео 2).
Технологические инструменты также можно рассматривать как реорганизатор . Благодаря динамическим функциям перетаскивания, связыванию нескольких представлений и наложению показателей на графики технологические инструменты могут использоваться таким образом, чтобы расширить возможности учителей без технологий, чтобы помочь учащимся реорганизовать и изменить свои статистические концепции. Например, наложение статистических показателей, таких как среднее значение, на графическое представление (см. Видео 2) может помочь изменить то, как учителя и учащиеся концептуализируют эти показатели по отношению к двумерному распределению, особенно потому, что статистические показатели обновляются по мере изменения данных пользователем. перетаскивание точек на графике. Эта визуализация невозможна без технологии и может дать учащимся возможность реорганизовать свои представления о двумерных распределениях.
Видео 2) может помочь изменить то, как учителя и учащиеся концептуализируют эти показатели по отношению к двумерному распределению, особенно потому, что статистические показатели обновляются по мере изменения данных пользователем. перетаскивание точек на графике. Эта визуализация невозможна без технологии и может дать учащимся возможность реорганизовать свои представления о двумерных распределениях.
Эти видеопримеры полезны для иллюстрации того, как технологии могут использоваться для ускорения математического процесса и потенциально могут изменить то, как учащиеся и учителя думают о математических идеях. Однако сама технология не изменит понимания учителей. Скорее, поставленная задача, заданные вопросы и возможности поразмышлять и обсудить, какие технологии генерируются и как эти результаты соотносятся с математическими идеями и педагогическими проблемами, — вот что приводит к лучшему пониманию.
Чтобы проиллюстрировать комплексный подход, используемый в наших материалах PTMT для разработки TPACK будущих учителей, приводятся два отрывка (см. приложения A и B). В Приложении A (pdf) представлено подробное описание того, как технологические инструменты генерируют псевдослучайные числа, а также рассматриваются как математические, так и педагогические вопросы, связанные с проведением моделирования с использованием технологий. В Приложении B (pdf) множественные представления используются для обучения (или закрепления) будущих учителей пониманию регрессии наименьших квадратов. Алгебраические представления намеренно используются в дополнение к представлениям, созданным технологически, чтобы способствовать более глубокому пониманию регрессии. Оба отрывка помогают проиллюстрировать интегрированный подход к развитию знаний учителей об учебных стратегиях и представлениях для преподавания важных тем вероятностей и анализа данных — второй компонент TPACK Нисса (2005).
приложения A и B). В Приложении A (pdf) представлено подробное описание того, как технологические инструменты генерируют псевдослучайные числа, а также рассматриваются как математические, так и педагогические вопросы, связанные с проведением моделирования с использованием технологий. В Приложении B (pdf) множественные представления используются для обучения (или закрепления) будущих учителей пониманию регрессии наименьших квадратов. Алгебраические представления намеренно используются в дополнение к представлениям, созданным технологически, чтобы способствовать более глубокому пониманию регрессии. Оба отрывка помогают проиллюстрировать интегрированный подход к развитию знаний учителей об учебных стратегиях и представлениях для преподавания важных тем вероятностей и анализа данных — второй компонент TPACK Нисса (2005).
Еще одним важным компонентом TPACK являются знания учителей об обучении учащихся с помощью технологий (третий компонент Нисса). Результаты исследования понимания учащимися статистических идей используются для того, чтобы сделать выводы, поднять проблемы и задать вопросы учителям по всем материалам (например, см. утверждения, выделенные синим шрифтом в приложениях A и B). После того, как учителя приступили к изучению статистического вопроса с помощью технологического инструмента, часто задаются педагогические вопросы, направленные на развитие их понимания того, как технологии и различные представления могут поддерживать статистическое мышление учащихся. Хотя будущим учителям может быть трудно ответить на эти вопросы, присутствие таких вопросов в тексте создает возможности для педагогических возмущений, которые могут побудить их к размышлению и критическому мышлению при разработке TPACK.
утверждения, выделенные синим шрифтом в приложениях A и B). После того, как учителя приступили к изучению статистического вопроса с помощью технологического инструмента, часто задаются педагогические вопросы, направленные на развитие их понимания того, как технологии и различные представления могут поддерживать статистическое мышление учащихся. Хотя будущим учителям может быть трудно ответить на эти вопросы, присутствие таких вопросов в тексте создает возможности для педагогических возмущений, которые могут побудить их к размышлению и критическому мышлению при разработке TPACK.
Эффективная стратегия, используемая в учебном блоке, предложенная исследованием, заключается в том, что учащиеся решают математическую задачу и просят их поразмышлять над своим мышлением и рассмотреть свою работу с точки зрения ученика (Simon & Tzur, 2004). Однако потенциальным учителям часто не хватает опыта работы со студентами, использующими технологии. Таким образом, они не могут представить себе, как учащийся может решить математическую задачу с помощью инструмента способами, которые могут отличаться от их собственного пути решения, и предвидеть трудности, с которыми учащиеся могут столкнуться. Чтобы предоставить возможность для тщательного анализа и размышлений о работе студентов с технологиями, в наши материалы PTMT включен видеокейс.
Чтобы предоставить возможность для тщательного анализа и размышлений о работе студентов с технологиями, в наши материалы PTMT включен видеокейс.
Дизайн видеокейса основывался на предложениях и следствиях работы Ламперта и Болла (1998), Тауэрса (1998) и Бауэрса, Кенехана, Сейла и Доерра (2000). Тауэрс (1998) и Лэмперт и Болл (1998) обсудили проблемы, с которыми сталкиваются будущие учителя, переключая свое внимание на события в классе, чтобы внимательно изучить работу и мышление учащихся. Они больше привыкли сосредотачиваться внутри себя на изучении практики учителя — той роли, к которой они готовятся. Они также предположили, что при использовании видео- и мультимедийных записей классной практики необходимо принимать целенаправленные решения, чтобы облегчить это переключение внимания на учащихся. Таким образом, видео ориентировано на студентов, а не на преподавателя, представлены письменные работы студентов и поставлены вопросы, ориентирующие будущих преподавателей на работу студентов.
При проектировании нашего видеокейса было принято решение показывать только преподавателя при вводе урока и постановке конкретных вопросов, а в остальном ориентироваться в основном на работу учащихся. Поскольку учащиеся в видео работают с компьютером, а цель состоит в том, чтобы разработать TPACK для будущих учителей, мы использовали формат «картинка в картинке», который объединяет видео работы учащихся с помощью TinkerPlots с видео взаимодействия двух учащихся. (Конольд и Миллер, 2004). Кроме того, больший из двух кадров — это видео работы компьютера. Этот формат был создан специально для того, чтобы будущие учителя могли сосредоточиться на конкретных действиях учащихся в программной среде при решении задачи анализа данных.
При разработке материалов для своих видеокейсов Lampert and Ball (1998) и Bowers et al. (2000) специально включили и выступили за то, чтобы будущие учителя выполняли математические задачи, используемые в видеороликах. Бауэрс и др. (2000) также рекомендовали будущим учителям выполнить математическую задачу перед просмотром видео. В видеокейсе будущие учителя используют TinkerPlots для анализа одного и того же набора данных и ответов на точные вопросы, которые были заданы ученикам. Будущие учителя выполняют это задание перед просмотром видео, размышляют о своем математическом мышлении и использовании программного обеспечения, а затем делают прогнозы о том, как учащиеся средней школы могут подойти к той же задаче. Этот процесс размышлений и предвосхищения работы учащихся может создать возможности для удивления и возможного возмущения, когда будущие учителя наблюдают, как учащиеся выполняют работу, которая не соответствует их ожиданиям.
В видеокейсе будущие учителя используют TinkerPlots для анализа одного и того же набора данных и ответов на точные вопросы, которые были заданы ученикам. Будущие учителя выполняют это задание перед просмотром видео, размышляют о своем математическом мышлении и использовании программного обеспечения, а затем делают прогнозы о том, как учащиеся средней школы могут подойти к той же задаче. Этот процесс размышлений и предвосхищения работы учащихся может создать возможности для удивления и возможного возмущения, когда будущие учителя наблюдают, как учащиеся выполняют работу, которая не соответствует их ожиданиям.
Все видео (18 минут) синхронизировано с расшифровкой. В начале видео показано, как учитель использует следующую цитату, чтобы заинтересовать учащихся набором данных (видео 3): «Государственные школы обычно больше и дешевле (особенно если вы живете в штате), чем частные школы. Частные школы, как правило, более избирательны и предлагают более индивидуальный подход» (Источник: http://apps. collegeboard.com/search/adv_typeofschool.jsp).
collegeboard.com/search/adv_typeofschool.jsp).
Затем видео переходит к той части урока, где учитель задает конкретный вопрос о том, лучше ли процент выпускников в частных школах, чем в государственных (Видео 4). Она возвращается к вступительной цитате и сосредотачивает внимание учащихся на задаче. Оставшаяся часть видео показывает, как Кэти и Джордон работают с TinkerPlots для анализа данных, часть которых показана на видео 5. Видеокейс также включает отсканированные копии рабочих листов с ответами учащихся.
Видеокейс позволяет выявить несколько вопросов для будущих учителей. Первоначально занимаясь математической задачей, многие будущие учителя сравнивают государственные и частные колледжи с параллельными ящичковыми диаграммами, на которых они накладывают средние значения для каждого из них. В их суждениях часто учитываются как меры центра, так и разброса. Студенты создают точечный график показателей выпускников и перекрашивают случаи в зависимости от того, являются ли они публичными или частными. Таким образом, они используют цвет как инструмент для рассмотрения второй переменной в наборе данных.
Таким образом, они используют цвет как инструмент для рассмотрения второй переменной в наборе данных.
Когда они просматривают и размышляют над работой студентов в видео, потенциальные преподаватели обращают внимание на то, как студенты часто сосредотачиваются на отдельных точках данных, выбирают случаи на графике и просматривают соответствующие значения для третьей переменной (студент-преподаватель). соотношение) в карточках данных. Видеокейс позволяет будущим учителям понять, что, хотя работа учащихся не выглядит такой формальной, как их собственная, ученики координируют три переменные в своем ответе на вопрос о двух переменных.
Будущие учителя также могут учитывать фокусирующие эффекты контекста и вопросов, заданных учащимся. Первоначальная цитата, использованная для начала урока, явно относится к большему индивидуальному вниманию в частных колледжах. Этих студентов, кажется, привлекает показатель соотношения студентов и преподавателей как показатель индивидуального внимания в колледже. Это было отмечено будущими учителями при анализе студенческих работ. В частности, в ответ на задание «Опишите, как внимание студентов к признаку «соотношение студентов и преподавателей» повлияло на их анализ», один из будущих учителей в классе (Георгий) ответил следующим образом:
Это было отмечено будущими учителями при анализе студенческих работ. В частности, в ответ на задание «Опишите, как внимание студентов к признаку «соотношение студентов и преподавателей» повлияло на их анализ», один из будущих учителей в классе (Георгий) ответил следующим образом:
Студенты были озадачены тем фактом, что колледжи с высоким соотношением студентов и преподавателей могут иметь более высокий процент выпускников, чем колледжи с более низким соотношением. Они ошибочно предполагали, что более низкое соотношение количества студентов и преподавателей автоматически означает, что в школе будет более высокий процент выпускников.
Джордж наблюдал, как студенты нажимали на отдельные значки данных в распределении и пытались разобраться в нескольких точках данных в середине распределения, которые не соответствовали первоначальной тенденции, которую они обнаружили. Таким образом, он делал вывод о том, о чем они могли думать, основываясь на работе, которую он наблюдал за их работой с технологией.
Другой студент, Джей, раскритиковал задание, сказав: «Я бы сказал, что это был уместный вопрос, на который относительно легко ответить, но единственным ограничением является то, что они не очень хорошо разбираются в колледже». Джей оценивал задачу, основываясь на координации своей работы, своего мышления и своих наблюдений за работой студентов, и делал вывод, что студенты могут не иметь полного понимания некоторых переменных в наборе данных. Видеокейс сыграл решающую роль в нашей разработке всего модуля для разработки TPACK будущих учителей. Анализируя работу студентов, будущие учителя занимались рассуждениями, которые находятся на стыке технологии, педагогики и содержания.
Оценка и последствия
Научный подход к разработке модуля (Battista & Clements, 2000) был реализован посредством использования циклического процесса, который включал (а) объяснение видения, философии и целей учебного процесса. материалы, (b) создание инструментов для оценки того, были ли достигнуты учебные цели, (c) сбор данных контрольной группы, (d) разработка уроков, (e) сбор данных при тестировании материалов с учащимися, и (f) пересмотр материалов на основе по анализам данных.
Поскольку цель материала заключалась в разработке TPACK для учителей, был разработан предварительный инструмент для оценки понимания учителями каждой из этих областей. Вопросы в разделе содержания были выбраны из Гарфилда (2003) и других из базы данных ARTIST (https://app.gen.umn.edu/artist). Из-за небольшого размера выборки тест Уилкоксона на сумму знаковых рангов был использован для сравнения различий в выигрышах от пре-теста к пост-тесту с уровнем альфа 0,10.
Материалы прошли четыре итерации полевых испытаний в классе с предварительными учителями, анализ данных полевых испытаний и последующие исправления. Модуль был реализован в 400-уровневом курсе «Преподавание математики с использованием технологий» в нашем университете. Этот курс предназначен для будущих учителей среднего и среднего звена и нескольких начинающих аспирантов с небольшим опытом использования технологий. Типичные размеры классов были 13-20. Осенью 2005 г. во время 5-недельного курса по анализу данных и вероятности преподаватель (не один из авторов) использовал уже существующую учебную программу курса в качестве контрольной группы. В каждом из последующих семестров (весна 2006 г., осень 2006 г., весна 2007 г., осень 2007 г.) курс читал тот же преподаватель, что и осенью 2005 г., и для 5-недельного блока по анализу данных и вероятности использовались новые материалы. Кроме того, весной 2007 года модуль был внедрен в раздел курса, который вел другой преподаватель. В первые три семестра реализации у студентов собирали письменные работы и сдавали пре- и посттесты. В течение первых двух семестров внедрения в 2006 г. занятия в классе записывались на видео и были опрошены несколько студентов.
В каждом из последующих семестров (весна 2006 г., осень 2006 г., весна 2007 г., осень 2007 г.) курс читал тот же преподаватель, что и осенью 2005 г., и для 5-недельного блока по анализу данных и вероятности использовались новые материалы. Кроме того, весной 2007 года модуль был внедрен в раздел курса, который вел другой преподаватель. В первые три семестра реализации у студентов собирали письменные работы и сдавали пре- и посттесты. В течение первых двух семестров внедрения в 2006 г. занятия в классе записывались на видео и были опрошены несколько студентов.
Анализ данных первого пилотного тестирования материалов (Экспериментальный I) показал, что, хотя учителя улучшили свое понимание статистических и вероятностных концепций и использования ими технологических инструментов, их педагогические знания не улучшились. Успехи в эксперименте I ( n = 18) были значительно выше ( p = 0,10), чем в контрольной группе ( n = 15), особенно в вопросах, связанных со знанием содержания ( p = 0,007). и технологии ( р = 0,058). Обзор учебных материалов показал, что упор на педагогику не был сильно представлен, поэтому материалы были пересмотрены, чтобы сделать упор на педагогику.
и технологии ( р = 0,058). Обзор учебных материалов показал, что упор на педагогику не был сильно представлен, поэтому материалы были пересмотрены, чтобы сделать упор на педагогику.
Переработанные материалы предоставили учителям гораздо больше возможностей для рассмотрения и обсуждения педагогических вопросов. Такие возможности включали в себя более подробное описание педагогики в основном тексте, включая типичные трудности учащихся с понятиями или технологическими инструментами. Другие возможности включали более целенаправленные педагогические вопросы, которые требовали от учителей тщательного рассмотрения педагогического выбора, который они могли бы сделать при использовании технологического инструмента со студентами на конкретном уроке. Например, см. текст, выделенный синим цветом, в приложениях A (раздел 2) и B (раздел 5).
В следующем семестре, когда были протестированы пересмотренные материалы, прогресс в педагогических знаниях студентов был очевиден. Например, рассмотрим три педагогических вопроса в Приложении C. Снимок оценок по нескольким тестовым заданиям (Таблица 1) иллюстрирует возросшие успехи в знании педагогического содержания и TPACK. Учителя осенью 2006 г. (Экспериментальный II) были в большей степени способны выбрать подходящий набор данных для создания урока, посвященного изучению среднего и медианы (вопрос 20), и могли обосновать свой выбор более сложным обоснованием, которое включало внимание к форме распределения, включая эффекты. выбросов, асимметрии или повторных измерений (вопрос 21). Кроме того, они были немного более способны правильно интерпретировать понимание учащимися корреляции на основе работы учащихся с графическим калькулятором и их утверждений (вопрос 22).
Снимок оценок по нескольким тестовым заданиям (Таблица 1) иллюстрирует возросшие успехи в знании педагогического содержания и TPACK. Учителя осенью 2006 г. (Экспериментальный II) были в большей степени способны выбрать подходящий набор данных для создания урока, посвященного изучению среднего и медианы (вопрос 20), и могли обосновать свой выбор более сложным обоснованием, которое включало внимание к форме распределения, включая эффекты. выбросов, асимметрии или повторных измерений (вопрос 21). Кроме того, они были немного более способны правильно интерпретировать понимание учащимися корреляции на основе работы учащихся с графическим калькулятором и их утверждений (вопрос 22).
Table 1
Scores on Select Pedagogy Questions Across Semesters
|
| Fall 2005 | Весна 2006 | Fall 2006 | |||
Q# |
| Pre | Post | Pre | . | Pre | Post |
20 | % correct | 33% | 39% | 44% | 33% | 50% | 67% |
21 | . | 1.29 | 0.72 | 1. | 1.13 | 2.33 | |
22 | % correct | 56% | 61% | 56% | 61% | 50% | 73% |
. понимание учителем технологии, педагогики и содержания. Вопросы, которые мы создали, оценивали знания будущих учителей в области статистики и концепций вероятности (CK), использование технологий для конкретных математических задач (TC), а также педагогические решения, которые будущие учителя могут принимать при обучении вероятностным и статистическим концепциям с использованием технологий и без них (PCK, TPCK). ). Эти оценки, особенно последний тип, были длинными и предназначались для бумаги и карандаша, поэтому они не давали глубокого представления о том, что преподаватели развили или развивали. Таким образом, сравнения, которые можно было провести между контрольной и экспериментальной группами, были ограничены используемыми мерами.
). Эти оценки, особенно последний тип, были длинными и предназначались для бумаги и карандаша, поэтому они не давали глубокого представления о том, что преподаватели развили или развивали. Таким образом, сравнения, которые можно было провести между контрольной и экспериментальной группами, были ограничены используемыми мерами.
Подробная информация о количественном и качественном анализе эффективности этих материалов приведена в другом месте. Холлебрандс, Уилсон и Ли (2007, 2008) провели обширный анализ работы будущих учителей над видеокейсом и того, как будущие учителя интерпретируют работу учащихся с технологиями и начинают размышлять о том, как мышление учащихся может влиять на их работу с видеоматериалами. задача или технологический инструмент. Полученные данные показывают, что материалы видеокейса предоставляют возможности, и мы видели доказательства того, что будущие учителя строят модели мышления учащихся таким образом, чтобы способствовать реструктуризации их TPACK. Ли, Холлебрандс и Уилсон (2007) сообщили об успехах и трудностях, с которыми сталкиваются будущие учителя при переносе своей работы по повторной выборке с моделированием вероятности в модуле на создание задачи моделирования вероятности для учащихся. Хотя будущие учителя обычно создают соответствующие модели вероятностей с помощью технологических инструментов, они не всегда предлагают учащимся на своих уроках повторять выборку, использовать большие размеры выборки или использовать различные представления для анализа данных.
Хотя будущие учителя обычно создают соответствующие модели вероятностей с помощью технологических инструментов, они не всегда предлагают учащимся на своих уроках повторять выборку, использовать большие размеры выборки или использовать различные представления для анализа данных.
Ли и Ли (2008) провели количественный и качественный анализ того, как модуль успешно привлекает будущих учителей в координационный центр и распространяется в контекстах вероятностей и статистики. Их анализ выявил сильные стороны текста модуля и упущенные в тексте возможности для привлечения внимания будущих учителей к этой важной концепции анализа данных. Результаты послужили основанием для пересмотра модуля и конкретных вопросов, которые необходимо поднять в процессе профессионального развития преподавателей для обучения внедрению модуля.
Заключение
Поскольку технологии становятся повсеместной частью повседневного опыта, учителям математики, многие из которых являются «цифровыми иммигрантами», важно опираться на опыт «цифровых аборигенов» учащихся (Пренски, 2002, с. 1). Для этого учителя должны знать, как извлечь выгоду из возможностей технологий для создания уроков, которые помогут учащимся лучше понять математику. Учебная модель, которая вовлекает будущих учителей в решение задач по математике с использованием технологических инструментов и побуждает их размышлять над этим опытом с точки зрения учителя, обеспечивает целостный опыт обучения, аналогичный тому, с которым они столкнутся в классе. Разрабатывая TPACK для будущих учителей математики, они не только готовятся к работе в классах сегодня, но и получают знания и навыки для навигации в классах завтрашнего дня. Тем не менее, существует явная необходимость в лонгитюдных исследованиях для наблюдения за влиянием акцента на TPACK в учебных материалах для учителей на практику учителей со своими учениками.
1). Для этого учителя должны знать, как извлечь выгоду из возможностей технологий для создания уроков, которые помогут учащимся лучше понять математику. Учебная модель, которая вовлекает будущих учителей в решение задач по математике с использованием технологических инструментов и побуждает их размышлять над этим опытом с точки зрения учителя, обеспечивает целостный опыт обучения, аналогичный тому, с которым они столкнутся в классе. Разрабатывая TPACK для будущих учителей математики, они не только готовятся к работе в классах сегодня, но и получают знания и навыки для навигации в классах завтрашнего дня. Тем не менее, существует явная необходимость в лонгитюдных исследованиях для наблюдения за влиянием акцента на TPACK в учебных материалах для учителей на практику учителей со своими учениками.
Ссылки
Комитет AACTE по инновациям и технологиям. (2008). Справочник по технологическим педагогическим знаниям (TPCK) для педагогов. Нью-Йорк: Рутледж.
Нью-Йорк: Рутледж.
Ассоциация педагогов-преподавателей математики. (2006). Подготовка учителей к использованию технологий для улучшения изучения математики: позиция Ассоциации преподавателей математики . Получено с http://www.amte.net/Approved%20AMTE%20Technology%20Position%20Paper.pdf
Баттиста, М., и Клементс, Д. (2000) Разработка учебных программ по математике как научная деятельность. В A. Kelly & R. Lesh (Eds.), Справочник по дизайну исследований в области математики и естественных наук (стр. 737-760). Махва, Нью-Джерси: Lawrence Erlbaum Associates, Publishers.
Бен-Цви, Д. (2000). К пониманию роли технологических инструментов в статистическом обучении. Математическое мышление и обучение 2 (1 и 2) , 127-155.
Бауэрс, Дж., Кенехан, Г., Сейл, Дж., и Дорр, Х.М. (2000, февраль). Проектирование мультимедийных тематических исследований для учителей preservice: Педагогические вопросы и технологические дизайнерские решения. В Труды Общества информационных технологий и педагогического образования, Сан-Диего, Калифорния. (Служба размножения документов ERIC № ED 444-556)
В Труды Общества информационных технологий и педагогического образования, Сан-Диего, Калифорния. (Служба размножения документов ERIC № ED 444-556)
Конференционный совет математических наук. (2001). Математическое образование учителей . Провиденс, Род-Айленд: Американское математическое общество.
Гарфилд, Дж. Б. (2003). Оценка статистических рассуждений. Статистический журнал исследований в области образования 2(1), 22–38. Получено с http://www.stat.auckland.ac.nz/~iase/serj/SERJ2(1).pdf
Гарофало, Дж., Драйер, Х.С., Харпер, С., Тиммерман, М.А., и Шоки, Т. (2000). Содействие надлежащему использованию технологий в подготовке учителей математики. Современные проблемы технологий и педагогического образования, [онлайн-сериал] 1 (1), получено с https://citejournal.org/vol1/iss1/currentissues/mathematics/article1.htm
Hollebrands, K. F., Wilson, PH и Ли, HS (2007 г. , октябрь). Будущие учителя используют видеокейс для проверки работы учащихся при решении математических задач с использованием техники. Материалы двадцать девятого ежегодного собрания Североамериканского отделения психологии математического образования , Лейк-Тахо, Юта. Получено с http://www.allacademic.com//meta/p_mla_apa_research_citation/1/8/8/5/6/pages188561/p188561-1.php
, октябрь). Будущие учителя используют видеокейс для проверки работы учащихся при решении математических задач с использованием техники. Материалы двадцать девятого ежегодного собрания Североамериканского отделения психологии математического образования , Лейк-Тахо, Юта. Получено с http://www.allacademic.com//meta/p_mla_apa_research_citation/1/8/8/5/6/pages188561/p188561-1.php
Холлебрандс, К. Ф., Уилсон, П. Х., и Ли, Х. С. (2008 г.). ). Понимание процессов будущих учителей математики для понимания работы учащихся с технологиями . Рукопись представлена для публикации.
Международное общество технологий в образовании. (2008). Национальные стандарты образовательных технологий для учителей. Получено с http://www.iste.org/Content/NavigationMenu/NETS/ForTeachers/NETS_for_Teachers.htm
Керсент Г., Хортон Б., Стол Х. и Гарофало Дж. (2003). Технологические убеждения и практика факультета математического образования. Журнал технологий и педагогического образования, 11 (4), 567-595.
Журнал технологий и педагогического образования, 11 (4), 567-595.
Келер, М.Дж., и Мишра, П. (2005). Что происходит, когда учителя разрабатывают образовательные технологии? Развитие технологического педагогического содержания знаний. Journal of Educational Computing Research, 32(2), 131-152.
Конольд, К., и Миллер, К. (2004). Исследование динамических данных TinkerPlots™ (версия 1.0).
Эмеривилл, Калифорния: Key Curriculum Press.
Ламперт, М., и Болл, Д.Л. (1998). Преподавание, математика и мультимедиа: исследования реальной практики. Нью-Йорк: Издательство педагогического колледжа.
Литам, К. (2006 г., январь). C , характеризующий подготовку будущих учителей математики средней школы к преподаванию математики с помощью технологий. Статья представлена в Ассоциации преподавателей математики, Тампа, Флорида. Слайды взяты с http://www.mathed.byu.edu/%7Ekleatham/ResearchProjects/AMTEpresentation2006. htm
htm
Lee, H.S., Hollebrands, K.F., & Wilson, P.H. (2007). Проектирование и использование вероятностных симуляций учителями математики на подготовительных курсах. Слайды доступны по адресу http://www.ncsu.edu/project/ptmt/PTMT_NCTM2007Symposium.pdf URL НЕ РАБОТАЕТ
Ли, Х. С., и Ли, Дж. Т. (2008 г., февраль и март). Использование интервалов для координации понимания центра и распространения: предварительный отчет. В Материалы конференции по исследованиям в области математического образования для студентов , Сан-Диего, Калифорния. Получено с http://cresmet.asu.edu/crume2008/Proceedings/Lee&Lee%20LONG.pdf
Mishra, P., & Koehler, M. (2008, март). Внедрение технологического педагогического содержания знаний. Документ, представленный на ежегодном собрании Американской ассоциации исследований в области образования, Нью-Йорк.
Морсунд Д. и Билефельдт Т. (1999). Будут ли новые учителя готовы преподавать в эпоху цифровых технологий? Национальный обзор информационных технологий в педагогическом образовании . Санта-Моника, Калифорния: Milken Exchange по образовательным технологиям и Международное общество технологий в образовании.
Санта-Моника, Калифорния: Milken Exchange по образовательным технологиям и Международное общество технологий в образовании.
Национальный совет учителей математики. (2000). Принципы и стандарты школьной математики . Рестон, Вирджиния: Автор.
Нисс, М.Л. (2005). Подготовка учителей к обучению естественным наукам и математике с использованием технологий: разработка технологии педагогического содержания знаний. Преподавание и педагогическое образование, 21, 509-523.
Нисс, М.Л. (2006). Гостевая редакционная статья: Подготовка учителей к преподаванию математики с помощью технологий. Современные проблемы технологий и педагогического образования [Сериал онлайн], 6 (2). Получено с https://citejournal.org/vol6/iss2/mathematics/article1.cfm
Pea, RD (1987). Когнитивные технологии для математического образования. В A. Schoenfeld (Ed.), Когнитивные науки и математическое образование (стр. 89-122). Хиллсдейл, Нью-Джерси: Эрлбаум.
89-122). Хиллсдейл, Нью-Джерси: Эрлбаум.
Пауэрс, Р., и Блабо, В. (2005). Технология в математическом образовании: подготовка учителей к будущему. Современные проблемы технологий и педагогического образования [Сериал онлайн], 5 (3). Получено с https://citejournal.org/vol5/iss3/mathematics/article1.cfm
Пренски, М. (2002, сентябрь/октябрь). Цифровые аборигены, цифровые иммигранты, Часть I. На горизонте , 9(5) 1, 3-6.
Шульман, Л. (1986). Те, кто понимает: Рост знаний в обучении. Исследователь в области образования, 15 (2), 4-14.
Саймон, Массачусетс (1995). Реконструкция математической педагогики с конструктивистской точки зрения. Журнал исследований в области математического образования, 26 (2), 114-145.
Саймон, М.А., и Цур, Р. (2004). Объяснение роли математических задач в концептуальном обучении: разработка гипотетической траектории обучения. Математическое мышление и обучение 6 (2), 91-104.
Математическое мышление и обучение 6 (2), 91-104.
Сухарвото, Г. (2006 г.). Учителя средней математики для повышения квалификации педагогических знаний в области технологии в предметной, интегрированной с технологиями программе подготовки учителей . Неопубликованная докторская диссертация, Университет штата Орегон.
Тауэрс, Дж. (1998). Близкие встречи сложного типа: использование видеокассет в обучении учителей . Документ представлен на ежегодном собрании Американской ассоциации исследований в области образования , , Сан-Диего, Калифорния. (Служба воспроизведения документов ERIC № ED 420 625).
Примечание автора
Проект «Подготовка к преподаванию математики с помощью технологий» поддерживается Национальным научным фондом в рамках гранта № DUE 04-42319.присужден Университету штата Северная Каролина. Любые мнения, выводы и выводы или рекомендации, выраженные в настоящем документе, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Более подробную информацию о проекте и материалы можно найти на http://www.ncsu.edu/project/ptmt.
Более подробную информацию о проекте и материалы можно найти на http://www.ncsu.edu/project/ptmt.
Холлилин Ли
Университет штата Северная Каролина
[email защищен]
Карен Холлебрандс
Университет штата Северная Каролина
[email защищен]
Appendix A
Simulating Randomness in Technology Tools
(download pdf)
Appendix B – The Least Squares Regression Line
(download pdf)
Appendix C
Образцы тестовых заданий и правильных ответов
20) Вы планируете урок, чтобы помочь учащимся решить, когда среднее значение или медиана являются более подходящей мерой центральной тенденции. Какой из следующих наборов данных будет наиболее подходящим для вас? [ принимаются два правильных ответа, a или b ]
a.
б.
в.
д.
21) Объясните свой выбор ответа на вопрос №20.
Рубрика оценки
| 3 | Они выбирают вариант a , и их объяснение подчеркивает важность выбросов или асимметрии данных на эти факторы (асимметрию или асимметрию данных) среднее и срединное. ИЛИ Они выбирают вариант b , и их объяснение подчеркивает важность повторного измерения (в 4 и 10) и его влияние на среднее значение и медиану. |
| 2 | Они выбирают вариант a или b , и у них есть неполное объяснение, которое обсуждает форму или центры, но не связывает их (форму и центры). Их объяснение также подчеркивает различия между средним значением и медианой |
| 1 | Учитывает только тот факт, что среднее значение и медиана различаются при выборе a и b . Не обращает внимания на распределения или влияние этого распределения на эти показатели. Не обращает внимания на распределения или влияние этого распределения на эти показатели. |
| 0 | Неполный, недостаточный, неправильный (например, выбирает c или d и обосновывает использование набора данных, поскольку среднее значение и медиана аналогичны) |
| x | y |
73 | 68 |
77 | 79 |
84 | 74 |
82 | 76 |
81 | 72 |
79 | 77 |
76 | 74 |
78 | 69 |
125 | 117 |
80 | 79 |
. :
:
Когда группы делятся своей работой над этой задачей, эта группа показывает результат выше и утверждает, что «поскольку коэффициент корреляции ( r ) имеет значение, близкое к 1, данные являются линейными, и вы можете использовать уравнение y = 0,91 x + 2,88, чтобы найти y по любому x .
Какое утверждение лучше всего отражает наиболее вероятную интерпретацию понимания учащимися корреляции как индикатора линейной зависимости?
- Уравнение, полученное на основе линейной регрессии, следует интерпретировать независимо от значения коэффициента корреляции.
- О линейной зависимости можно судить по значениям корреляции выше 0,8.
- Коэффициент корреляции, близкий к 1 ( r = 0,96), позволяет использовать уравнение линейной регрессии в качестве правила функции для получения любого значения y для данного x .

- Коэффициент корреляции, близкий к 1 ( r = 0,96) предполагает, что между двумя переменными может существовать сильная положительная линейная зависимость, но необходимо учитывать другие индикаторы, такие как диаграмма рассеяния и остатки.
4929 всего просмотров, 2 просмотров сегодня
Преподавание математики с помощью технологий: 8 виртуальных ресурсов Национальный совет учителей математики (NCTM) добавил, что для вовлечения учащихся необходимы технологические инструменты.
Какие технологии можно использовать на уроках математики? В следующем разделе предлагается несколько идей, которые могут помочь при обучении детей математике.
8 Виртуальные ресурсы, которые помогают преподавать математику
Вот несколько эффективных инструментов для обучения математике с помощью технологий.
1. VmathLive
VmathLive – это онлайн-соревнования по математике для учащихся классов K–8. Это платный продукт.
Это платный продукт.
Предложение состоит из четырех основных компонентов:
- Область «Интеллектуальная информационная панель учителя», которая отслеживает успеваемость учащихся, включая показатели активности, прогресс класса в достижении целей и этапов, а также предупреждения для учащихся, испытывающих затруднения.
- Компонент «Обучение», позволяющий учащимся продвигаться в своем собственном темпе, отвечая на вопросы из 334 математических тем.
- Компонент «Мастер», который задает студентам вопросы о том, что они узнали.
- Компонент «Играть» с соревнованиями в реальном времени от учащихся из США.
VmathLive стоит 10 долларов США за учащегося или 200 долларов США за класс (до 25 учащихся), согласно странице продукта компании на момент публикации.
Demo
2. Desmos
Desmos предлагает бесплатный графический онлайн-калькулятор, а также цифровые задания для 6–12 классов.
Основное предложение — это калькулятор, который соответствует функциональным возможностям многих калькуляторов TI стоимостью более 100 долларов. Это популярный вариант для тех, кто хочет эффективно обучать математике с помощью технологий. Другое предложение от Desmos, цифровой центр деятельности, представляет собой несколько интерактивных уроков, которые учащиеся могут проводить на своем планшете или устройстве. Существует раздел, который позволяет учителям создавать уроки и делиться ими с другими учителями.
Это популярный вариант для тех, кто хочет эффективно обучать математике с помощью технологий. Другое предложение от Desmos, цифровой центр деятельности, представляет собой несколько интерактивных уроков, которые учащиеся могут проводить на своем планшете или устройстве. Существует раздел, который позволяет учителям создавать уроки и делиться ими с другими учителями.
Brighterly — это цифровая платформа для обучения детей математике. Brighter по-другому подходит к онлайн-репетиторству — помогает детям понять, как работает математика, показывает ее практическое применение и пробуждает у детей интерес к этому предмету. Это платный продукт.
С его помощью вы можете облегчить учебу:
- Применяя подходы к обучению, не допускающие ошибок.
- Использование интерактивных занятий по математике для вовлечения учащихся.
- Подружитесь со своим ребенком, чтобы способствовать обучению без стресса.
- Объяснение того, как математические понятия работают в реальной жизни.

- Обучение математическим процедурам, чтобы дети могли применять их к контекстуальным математическим задачам.
В Brighterly родители могут регистрировать учеников на ее индивидуальный курс математики. Тысячи детей по всему миру используют его ярче.
4. EquatIO
EquatIO – это инструмент для создания математических уравнений, формул, графиков Desmos и многого другого на компьютерах или устройствах Chromebook.
Продукт предназначен для оцифровки математики с помощью простых методов ввода. Учителя могут печатать, писать от руки или диктовать выражения, чтобы добавить результат в документ, и имеется большая библиотека, полная готовых выражений. Другими словами, это своего рода умный помощник, который может заменить ручку и бумагу, а также предлагает возможности прогнозирования. Продукт работает с программным обеспечением для обучения грамоте Read&Write (платное), которое помогает сочетать доступность и обучение математике с технологиями.
EquatIO бесплатен для учителей. Платные лицензии доступны для других типов пользователей и групп.
5. Ура!
Кахут! интерактивная игра, в которой учащимся в одном классе предлагаются вопросы с несколькими вариантами ответов. Этот инструмент обучения предлагает бесплатные и платные планы.
Учителя могут искать готовые вопросы и ответы по различным предметам или создавать свои собственные (платно). Вопросы проецируются на экран в классе, и учащиеся выбирают ответ на своих устройствах. Студенты, набравшие наибольшее количество баллов, отображаются перед следующим вопросом, создавая веселую атмосферу соперничества.
Кахут! имеет базовый бесплатный план, а также два платных плана (1 или 3 доллара за учителя в месяц), которые предлагают более продвинутые функции.
6. Онлайн-игры
Обучение детей математике с помощью онлайн-игр является популярным методом вовлечения. Вот два бесплатных веб-сайта, на которых представлен широкий выбор интерактивных игр для учащихся 1–6 классов:
- Arcademics.
 com — отмеченный наградами образовательный веб-сайт, предлагающий бесплатные многопользовательские игры, аркадные математические игры и многое другое. Игры соответствуют математическим стандартам Common Core и охватывают такие темы, как фигуры, математические функции, целые числа, дроби и алгебра.
com — отмеченный наградами образовательный веб-сайт, предлагающий бесплатные многопользовательские игры, аркадные математические игры и многое другое. Игры соответствуют математическим стандартам Common Core и охватывают такие темы, как фигуры, математические функции, целые числа, дроби и алгебра. - Math Playground предлагает несколько математических и логических игр, а также аркадные игры и математические видеоролики. Для небольшого количества игр требуется платная подписка.
7. SMART Board Занятия/игры
Классы, оснащенные досками SMART, могут воспользоваться бесплатными занятиями и играми, доступными в Интернете.
Такие сайты, как SMART Exchange и iSmartboard.com, помогают учителям находить тысячи увлекательных уроков, и они организованы по классам. Многие задания и игры представлены учителями, которые уже используют их для обучения детей математике в классе.
8. Sumdog
Sumdog — это адаптивный обучающий инструмент для обучения математике с помощью технологий учащихся классов K-8. Платные планы подписки открывают доступ к премиальным инструментам для учителей.
Платные планы подписки открывают доступ к премиальным инструментам для учителей.
Sumdog предлагает обучение на основе игр, которое мотивирует и вовлекает учащихся. На компьютерах и планшетах учащиеся отвечают на вопросы в своем собственном темпе, а действия соответствуют их уровню навыков. Положительное подкрепление вознаграждает учащихся за достижения в игре, а учителя получают данные об оценке, чтобы направлять уроки и изучать индивидуальные потребности учащихся. Исследования эффективности и тематические исследования показали улучшение успеваемости учащихся с помощью продукта.
Ценовые предложения доступны на сайте Sumdog.
9. Видео на YouTube
YouTube — отличный источник интерактивных видеороликов, которые помогают учащимся изучать математические концепции и применять полученные знания на практике. Вот некоторые из наиболее примечательных каналов YouTube для обучения математике:
- Академия Хана предлагает множество бесплатных видеороликов, посвященных базовым и продвинутым понятиям.

- Математика предлагает короткие видеоролики по темам для начальной и средней школы с упором на такие предметы, как геометрия и дроби.
- Numberphile предлагает красочные видеоролики на такие темы, как число Пи, простые числа и такие игры, как Yahtzee.
Учителя также могут создавать свои собственные видеоролики на YouTube, чтобы получить уникальный взгляд на преподавание математики с помощью технологий. Примеры варьируются от более сложного и дурацкого шоу до более простого и сфокусированного клипа в реальном мире.
Это видео об округлении было создано мистером ДеМайо, учителем третьего класса из Юнион-Бич, штат Нью-Джерси. Здесь он и его друзья Стив и Энди смотрят на эту тему с причудливой и забавной точки зрения.
Это видео о ценах на продукты было создано Дженни Магиера, бывшей учительницей, которая в настоящее время работает директором по программам в образовательной организации. Здесь она просит студентов вычислить, какой из трех вариантов покупки острого сыра чеддер является лучшим с точки зрения математики.
Здесь она просит студентов вычислить, какой из трех вариантов покупки острого сыра чеддер является лучшим с точки зрения математики.
Вовлечение учащихся в математику
Согласно NCTM, учителя должны обладать знаниями в области применения технологий, помогающих преподавать математику. Эффективное использование некоторых из вышеупомянутых ресурсов требует стратегического подхода.
Вы можете усилить эту способность, получив онлайн-магистр математического образования, которое включает факультативный курс по технологиям на уроках математики. В этой программе на получение степени вы углубите свое понимание математических концепций и их использования во всем спектре K-12. Вы разработаете содержание математики и педагогику, необходимые для привития глубокого интереса к математике у следующего поколения учащихся.
Продвиньтесь по карьерной лестнице, получив диплом онлайн-университета Аврора. Учитесь у преподавателей-практиков, которые помогают работающим специалистам достигать своих целей. Узнайте, что значит учиться в гибкой и удобной учебной среде, получая при этом личное внимание и поддержку, которых вы ожидаете от небольшого колледжа.
Узнайте, что значит учиться в гибкой и удобной учебной среде, получая при этом личное внимание и поддержку, которых вы ожидаете от небольшого колледжа.
Использование технологий в обучении учителей начальных классов математики: социокультурная перспектива
На этой странице
РезюмеВведениеОбщие сведенияСсылкиАвторское правоСтатьи по теме
Центральным принципом реформы математического образования является неотъемлемая роль технологий на всех уровнях обучения. Нынешние технологические изменения в сочетании с изменениями в содержании математики и методах обучения требуют, чтобы учителя элементарной математики могли разрабатывать уроки с интенсивным использованием технологий для изучения и открытия этих концепций с помощью соответствующих компьютерных приложений. На практике, однако, большинство компьютерных приложений, предназначенных для обучения математике, состоят из программного обеспечения, разработанного для конкретной образовательной цели: решения в сценарии банки. Кроме того, экономические ограничения часто стоят на пути включения такого специального программного обеспечения в учебную среду. В этой статье мы обсудим альтернативу этому традиционному подходу, который смещает учебный фокус с конкретных компьютерных приложений на более сложное использование программного обеспечения общего назначения. В частности, использование электронных таблиц в образовательных целях будет разработано в качестве образца для этого подхода.
Кроме того, экономические ограничения часто стоят на пути включения такого специального программного обеспечения в учебную среду. В этой статье мы обсудим альтернативу этому традиционному подходу, который смещает учебный фокус с конкретных компьютерных приложений на более сложное использование программного обеспечения общего назначения. В частности, использование электронных таблиц в образовательных целях будет разработано в качестве образца для этого подхода.
1. Введение
В недавнем прошлом, когда мы говорили о компьютерных приложениях как педагогических инструментах на уроках математики, мы имели в виду программное обеспечение, разработанное для определенной образовательной цели. Тем не менее, экономические ограничения часто стоят на пути включения специального программного обеспечения в учебную среду и, таким образом, бросают вызов компьютерной педагогике математики и текущим программам обучения учителей. Возможный способ решения этой проблемы состоит в том, чтобы сместить акцент с использования конкретных компьютерных приложений в качестве средств обучения и обучения на модернизацию общего программного обеспечения в образовательной среде. Обучение с использованием готовых компонентов, так сказать. Например, электронные таблицы широко доступны в школах, колледжах и университетах. Тем не менее, электронная таблица, чтобы стать средой обучения математике, требует от преподавателя ряда различных навыков, которые являются элементами индивидуальной подписной педагогики [1, 2].
Обучение с использованием готовых компонентов, так сказать. Например, электронные таблицы широко доступны в школах, колледжах и университетах. Тем не менее, электронная таблица, чтобы стать средой обучения математике, требует от преподавателя ряда различных навыков, которые являются элементами индивидуальной подписной педагогики [1, 2].
Каким образом можно внедрить электронные таблицы в качестве инструментов мышления на уроках математики? Что требуется от учителей математики, чтобы превратиться в технологически мыслящих познающих и отражающих агентов [3], способных продвигать компьютеризированную педагогику подписи [4], чтобы стать областью дисциплинированных исследований и, в частности, уметь включать электронные таблицы в учебный процесс? практика преподавания математики? В данной статье мы попытаемся рассмотреть эти вопросы с социокультурной точки зрения.
Одним из основных предположений текущей реформы математического образования является то, что область педагогического образования поддается дисциплинированному исследованию. Это означает, что то, как учителя изучают математику, влияет на то, как они будут ее преподавать. Надлежащее использование компьютеров в обучении математике может включать сопоставление самостоятельных действий учащегося и действий с помощью. Компьютерные технологии позволяют обеим перспективам обучения быть опосредованными с помощью различных семиотических средств. В частности, электронная таблица имеет большой потенциал для использования в качестве генератора новых смыслов [4–6]. Педагогика с использованием электронных таблиц может улучшить преподавание математических понятий в форме вспомогательного исполнения и облегчить обсуждение значения математики в дискурсе в классе.
Это означает, что то, как учителя изучают математику, влияет на то, как они будут ее преподавать. Надлежащее использование компьютеров в обучении математике может включать сопоставление самостоятельных действий учащегося и действий с помощью. Компьютерные технологии позволяют обеим перспективам обучения быть опосредованными с помощью различных семиотических средств. В частности, электронная таблица имеет большой потенциал для использования в качестве генератора новых смыслов [4–6]. Педагогика с использованием электронных таблиц может улучшить преподавание математических понятий в форме вспомогательного исполнения и облегчить обсуждение значения математики в дискурсе в классе.
Однако в такой интеллектуальной среде роль учителя становится чрезвычайно сложной, поскольку он или она должны быть способны пережить двусмысленность в смыслообразующей среде. Это говорит о том, что педагогика с использованием электронных таблиц сильно зависит от компетентности учителей завтрашнего дня. Такая компетенция может быть развита путем соответствующей реструктуризации программ обучения учителей с упором на электронные таблицы как на инструменты познания.
2. Исходная информация
Традиционное преподавание математики делает упор на использование процедур, запоминание алгоритмов, выполнение именно того, что учитель хочет от учащихся, и поиск «одного правильного ответа». Математика в том виде, в каком ее чаще всего преподносили учащимся в начальных школах, не была предметом обсуждения, дебатов или творческого мышления, и при этом учащиеся не поощрялись к поиску более чем одного способа решения задачи или к поиску альтернативных способов решения задачи. Операция. Ограниченный вычислительный опыт может быть результатом этой традиции, но не более того. Такая операциональная педагогика не может связать математическую деятельность учащихся с доступными математическими методами [7]. В результате учащиеся, подсказанные учителем, следуют алгоритмам, необходимым для «решения задачи», но не понимают и не могут понять, почему и как эти алгоритмы отвечают на поставленный вопрос. Однако, по словам Пуанкаре, выдающегося французского математика и физика конца XIX в. С 19 по 20 век, проявляя заметный интерес к математическому образованию, учащиеся «хотят знать не только, все ли силлогизмы доказательства правильны, но и почему они связываются друг с другом именно в таком порядке, а не в другом» (цит. по [8, стр. 104] ). Учитывая это, неудивительно, что учащиеся прониклись жесткими ментальными представлениями о математике и ее значениях. Это прискорбно, потому что репрезентативная гибкость оказывается инструментом мышления, ценным во многих областях, включая математику. Гибкое применение как общих, так и содержательных правил и стратегий исследователи из разных областей связывают с показателем более высокого уровня мышления и проявлением профессионального мастерства. В частности, одним из ключей к успешному преподаванию и обучению математике является структурная гибкость в выборе и использовании мысленных представлений математических понятий. Чтобы преодолеть такую педагогическую неэффективность, современный американский образовательный документ Common Core State Standards [9] предложил шесть учебных смен, одна из которых называется «двойной интенсивностью».
С 19 по 20 век, проявляя заметный интерес к математическому образованию, учащиеся «хотят знать не только, все ли силлогизмы доказательства правильны, но и почему они связываются друг с другом именно в таком порядке, а не в другом» (цит. по [8, стр. 104] ). Учитывая это, неудивительно, что учащиеся прониклись жесткими ментальными представлениями о математике и ее значениях. Это прискорбно, потому что репрезентативная гибкость оказывается инструментом мышления, ценным во многих областях, включая математику. Гибкое применение как общих, так и содержательных правил и стратегий исследователи из разных областей связывают с показателем более высокого уровня мышления и проявлением профессионального мастерства. В частности, одним из ключей к успешному преподаванию и обучению математике является структурная гибкость в выборе и использовании мысленных представлений математических понятий. Чтобы преодолеть такую педагогическую неэффективность, современный американский образовательный документ Common Core State Standards [9] предложил шесть учебных смен, одна из которых называется «двойной интенсивностью». Последние два слова означают, что обучение математике должно быть ориентировано на обучение как вычислительным процедурам, так и математическим понятиям, которые делают возможными вычисления [10]. Основной стратегией, лежащей в основе сдвига двойной интенсивности, является использование визуальных представлений математических процедур и понятий. Теоретически эта стратегия вытекает из «предположения [Выготского] о том, что психическая деятельность опосредована знаковыми системами, производными от культуры» [11, с. 227].
Последние два слова означают, что обучение математике должно быть ориентировано на обучение как вычислительным процедурам, так и математическим понятиям, которые делают возможными вычисления [10]. Основной стратегией, лежащей в основе сдвига двойной интенсивности, является использование визуальных представлений математических процедур и понятий. Теоретически эта стратегия вытекает из «предположения [Выготского] о том, что психическая деятельность опосредована знаковыми системами, производными от культуры» [11, с. 227].
В этот момент возникает дилемма. Хотя мы много знаем о внутренних представлениях, используемых математиками, мы гораздо меньше знаем о том, как они пришли к этим представлениям [8]. Другими словами, хотя мы довольно много знаем о том, что значит быть математиком, мы все еще мало знаем о том, как стать математиком. Если кто-то хочет видеть класс как математическое сообщество, занятое предположениями, дебатами, открытиями, доказательствами и решением проблем [9, 10, 12], важно понять, как можно создать такой класс.
Обнаружение того, что профессиональные математики, например, в школьном возрасте хорошо справлялись с вычислительными тестами, не означает, что мы должны пытаться реализовать математическую программу, подчеркивающую только основные факты. Скорее, мы должны внимательно изучить, как компетентные математики достигли этого конечного состояния и какую систему поддержки они использовали. Конструктивистский подход к обучению широко предлагался как способ объяснить, как люди получают новую информацию. С этой точки зрения учащиеся создают свои собственные внутренние представления о внешнем мире. Эта точка зрения была широко принята математическим сообществом, но, как многие указывали, конструктивизм — понятие, толкуемое свободно [13].
Возможно, одна из наиболее существенных проблем с ответвлениями конструктивизма, которые слишком тесно связаны с репрезентативной перспективой, заключается в том, что это приводит к нескольким проблемам. Во-первых, это парадокс обучения: если обучение запускается внутренними репрезентациями, то как можно построить внутренние ментальные репрезентации объектов, которые более сложны, чем те, которые уже существуют в уме? Во-вторых, поскольку цель обучения репрезентативным позициям состоит в том, чтобы обеспечить явное и прозрачное представление математических понятий, когда обучение терпит неудачу, единственным выходом учителя является предоставление все более и более явных и прозрачных представлений. Это неизбежно ведет к собственной форме редукционизма, который может лишить математические понятия и отношения их смысла.
Это неизбежно ведет к собственной форме редукционизма, который может лишить математические понятия и отношения их смысла.
Трудности, с которыми репрезентативные позиции сталкиваются при предложении адекватного описания обучения, показывают, что описания того, как человек учится, могут быть гораздо более сложными, чем описания существующих ментальных репрезентаций. Представляется, что репрезентативные взгляды на обучение могут, с другой формулировкой, привести к тем же проблемам с математическим образованием, которые обсуждались выше. У нас все еще остаются некоторые фундаментальные вопросы, касающиеся того, как дети учатся и как мы можем описать это обучение.
Мы критикуем репрезентативные позиции не для того, чтобы дистанцироваться от конструктивизма, а для того, чтобы прояснить направления, предлагающие больший или меньший потенциал для конструктивистских педагогов. Как указывалось выше, конструктивизм — это широкий зонт, под которым разбили свои шатры многие теоретические положения, и некоторые из этих положений приводят к противоречиям между взглядами на знание и активным учеником.
Наша позиция аналогична позиции Cobb et al. [14], в которых они описывают обучение математике как индивидуальную, так и как коллективную деятельность, выходящую за рамки репрезентативного представления. В том же ключе Шенфельд [15] подошел к вопросу о смешении индивидуального и коллективного, предполагая, что люди могут изучать математические идеи, становясь учениками в культурно принятой математической практике, и что занимающиеся математикой считают себя практиками математического осмысления. . Далее Шенфельд утверждает, что студенту не нужно знать все основы (например, формулы), прежде чем он или она начнет думать как математик. Наоборот, учащемуся следует дать возможность решать настоящие проблемы, а не выполнять рутинные упражнения, в которых территория уже обозначена заученной формулой. В «реальных проблемах», в отличие от рутинных проблем, стратегии, методы и процедуры, которые следует использовать для решения проблемы, с самого начала не ясны. Столкнувшись с реальной проблемой, нужно активно работать над частями проблемы, чтобы прийти к разумному решению.
3. Математическое обучение как социокультурный феномен
Предыдущие исследования авторов [6, 16–19] показывают, что в случае с математикой сосредоточенность на действии позволяет сформировать естественный мост между нынешними конструктивистами в математическом образовании и социокультурных исследователей. Поскольку социокультурные исследователи находились под влиянием Теории Деятельности , как объясняют выготские ученые [20], вероятно, было неизбежно, что преподаватели математики и социокультурные исследователи начнут устанавливать связи (например, [6, 21–25]). Большинство социокультурных исследователей избегают теорий обучения, в которых используется метафора, отделяющая разум от того, что нужно изучать. Наоборот, речь идет об объединении внешнего мира с внутренним миром разума, по крайней мере, в двух смыслах: разум социально распределен и связан с понятием опосредования (например, [11, 26, 27]). В этих подходах к обучению картезианское различие между разумом и окружающей средой [28] заменяется эйнштейновским взглядом на постоянные согласованные отношения [29]. –31].
–31].
С социокультурной точки зрения изучение математики является результатом активного участия в культурно принятой математической практике и является результатом активного взаимодействия между учащимся и его или ее культурой. Из этого можно сделать вывод, что если кто-то хочет, чтобы учащиеся думали как математики, то необходимо создать класс, который носит характеристику активного математического сообщества с участием [32]. В идеале это должно включать как аффективные, так и когнитивные элементы. Как сообщают Рот и Ли [33], даже хорошее самочувствие или ощущение угрозы в связи с деятельностью или социальным составом учебной среды может повлиять на способность учащегося эффективно учиться и вносить свой вклад. В таком идеальном классе учащимся предоставляется возможность решать реальные проблемы с помощью культурных инструментов, таких как манипуляции, геоборды, традиционные и нетрадиционные символы и представления, а также универсальное и специализированное программное обеспечение для моделирования математики в различных форматах: диаграмма , числовые, геометрические, графические, символьные и так далее. Успешное участие в этом сообществе разовьет навыки, связанные с навыками экспертов в математическом сообществе [34].
Успешное участие в этом сообществе разовьет навыки, связанные с навыками экспертов в математическом сообществе [34].
Знаменитый список эвристик Полиа [35], или, другими словами, стратегий решения задач, предложил общее направление для творческого решения задач в математике. Как физические, так и электронные манипуляции предоставляют новые средства для эвристики и позволяют учащимся решать проблемы посредством действий, основанных на пробах и ошибках. Однако могут потребоваться некоторые усилия, чтобы поощрить использование этого базового типа обучения, изобретенного разумом на уроках элементарной математики. У студентов нет опыта обучения на ошибках. Стремясь придумать неправильный ответ, они не верят, что его можно усвоить и превратить в мыслительный механизм. Вне классной комнаты многие нематематические действия несут в себе компонент проб и ошибок. Как выразился Бейтсон [36]: «единица, демонстрирующая характеристики проб и ошибок, будет правомерно называться ментальной системой» (стр. 465).
465).
Конкретный подход к построению обучающей среды, принятый в этой статье, рассматривает индивидуальное психическое функционирование как неотъемлемо расположенное в социальном контексте и опосредованное культурными инструментами и знаками, такими как компьютеры и семиотические устройства программного обеспечения. Идеи, представленные в этой статье, были включены в несколько курсов компьютерного обучения математике для учителей начальной школы и без отрыва от работы, предложенных авторами. Эти идеи повлияли на отношение учителей к технологиям и заставили их расширить их использование на другие темы, не «охваченные» в курсах, и, в конечном итоге, включить идеи, полученные на курсах, в свое собственное обучение.
4. Опосредованное математическое действие
Социокультурный подход к разуму рассматривает людей как вступающих в контакт с учебной средой посредством действия, в котором они участвуют [27]. В свою очередь действие использует различные средства и знаки, называемые опосредованными средствами. Основное утверждение этого подхода состоит в том, что опосредующие средства формируют человеческую деятельность многими существенными способами. Таким образом, термин опосредованное действие отражает фундаментальную связь между действием и опосредованными средствами, которые оно использует. Любое умственное действие, направленное на решение математической задачи и опосредованное соответствующими орудиями и знаками, может быть названо опосредованное математическое действие. Именно это действие является основным компонентом сред, описанных ниже.
Основное утверждение этого подхода состоит в том, что опосредующие средства формируют человеческую деятельность многими существенными способами. Таким образом, термин опосредованное действие отражает фундаментальную связь между действием и опосредованными средствами, которые оно использует. Любое умственное действие, направленное на решение математической задачи и опосредованное соответствующими орудиями и знаками, может быть названо опосредованное математическое действие. Именно это действие является основным компонентом сред, описанных ниже.
Еще один базовый принцип, связанный с этим подходом, состоит в том, что человеческое умственное функционирование, особенно математическое действие, возникает в ходе общения и, таким образом, по своей сути является социальным. В определенной социокультурной среде, в современном классе начальной математики, опосредованное математическое действие может быть основано на использовании технических средств, таких как физические и электронные манипуляции, различных семиотических устройств, включая математические символы, компьютерные диаграммы и графики, системы обозначений. программного обеспечения, а также пиктограммы и графические изображения. Цель обучающего дискурса в такой обстановке состоит в том, чтобы использовать опосредующие средства в качестве генераторов значения, которое, в свою очередь, формирует математическое действие. С социокультурной точки зрения «всякое истинное понимание диалогично по своей природе» (Волошинов, цит. по [27, с. 54]), и это утверждение тесно связывает смысл с диалогической направленностью дискурса. Что касается введения компьютера в дискурс, то первостепенное значение имеет создание среды, способной вовлечь учащегося в целенаправленную диалогическую встречу с компьютером. Дидактический акцент такой среды состоит в том, чтобы предотвратить нежелательные последствия авторитарного дискурса и обеспечить возможность так называемого внутренне убеждающего дискурса, пробуждающего новый смысл для учащегося [27]. Участие в культурных мероприятиях, обеспечиваемых компьютерной средой, позволяет учащемуся усвоить среду как инструмент мышления, а затем перейти к структурной реорганизации сознания, которая позволяет мыслить без таких инструментов.
программного обеспечения, а также пиктограммы и графические изображения. Цель обучающего дискурса в такой обстановке состоит в том, чтобы использовать опосредующие средства в качестве генераторов значения, которое, в свою очередь, формирует математическое действие. С социокультурной точки зрения «всякое истинное понимание диалогично по своей природе» (Волошинов, цит. по [27, с. 54]), и это утверждение тесно связывает смысл с диалогической направленностью дискурса. Что касается введения компьютера в дискурс, то первостепенное значение имеет создание среды, способной вовлечь учащегося в целенаправленную диалогическую встречу с компьютером. Дидактический акцент такой среды состоит в том, чтобы предотвратить нежелательные последствия авторитарного дискурса и обеспечить возможность так называемого внутренне убеждающего дискурса, пробуждающего новый смысл для учащегося [27]. Участие в культурных мероприятиях, обеспечиваемых компьютерной средой, позволяет учащемуся усвоить среду как инструмент мышления, а затем перейти к структурной реорганизации сознания, которая позволяет мыслить без таких инструментов. Именно эта культурная среда обеспечивает «развитие умения пользоваться социокультурно выработанными инструментами, опосредующими интеллектуальную деятельность» [37, с. 35].
Именно эта культурная среда обеспечивает «развитие умения пользоваться социокультурно выработанными инструментами, опосредующими интеллектуальную деятельность» [37, с. 35].
5. Неправильный ответ как средство мышления
В контексте теории семиотического (то есть знакового) опосредования слово текст относится к любой значимой вербальной и невербальной семиотической структуре. Текст может быть как простым, как красный сигнал светофора, так и сложным, как многотомная Британская энциклопедия. В учебном дискурсе примерами текста являются задача и реакция (ответ) учащегося на нее. Компьютеризированный дискурс в классе дает возможность интерактивной обратной связи с ответом учащегося и в этом смысле позволяет расширять текст. Таким образом, три компонента среды обучения — задача, ответ, обратная связь и, возможно, уточненный ответ — представляют собой динамическую структуру текста дискурса в классе.
Лотман [38] ввел две функции, которые текст может выполнять одновременно: однозначную и диалогическую. Однозначная функция текста состоит в том, чтобы предоставлять постоянную информацию, которая не может быть оспорена и не может быть открыта для просмотра. Любой вопрос (текст) со статичной смысловой структурой не подлежит обсуждению ни при каких обстоятельствах и ищет то, что принято называть «единственно правильным ответом». Диалогическая функция текста заключается в обеспечении гибкости в интерпретации, обеспечении возможности согласования и появления новых значений и поощрении его согласования в когнитивно разнообразной учебной среде.
Однозначная функция текста состоит в том, чтобы предоставлять постоянную информацию, которая не может быть оспорена и не может быть открыта для просмотра. Любой вопрос (текст) со статичной смысловой структурой не подлежит обсуждению ни при каких обстоятельствах и ищет то, что принято называть «единственно правильным ответом». Диалогическая функция текста заключается в обеспечении гибкости в интерпретации, обеспечении возможности согласования и появления новых значений и поощрении его согласования в когнитивно разнообразной учебной среде.
Что касается последовательности Инициация-Ответ-Оценка интерпсихического функционирования [39], однозначная функция обратной связи как текста обеспечивает постоянную информацию и имеет дело с пассивной оценкой ответа как такового. С другой стороны, диалогическая функция оценивания (обратной связи) как текста акцентирует внимание на возможности вызова диалога обучаемого с окружающей средой в случае неправильного ответа. Акцент на диалогическом дискурсе вытекает из традиции Выготского, рассматривающей «социальное измерение сознания (как являющееся) первичным во времени и фактически (и) индивидуальное измерение сознания (как являющееся) производным и вторичным» [40, с. 30]. Появляется все больше свидетельств того, что изучение математики учащимися более эффективно в социальной среде класса посредством беседы, вспомогательных действий, поиска альтернативных решений и сотрудничества. Следовательно, при проектировании вычислительной среды обучения в традициях Выготского крайне важно обыграть ее функциональный дуализм.
30]. Появляется все больше свидетельств того, что изучение математики учащимися более эффективно в социальной среде класса посредством беседы, вспомогательных действий, поиска альтернативных решений и сотрудничества. Следовательно, при проектировании вычислительной среды обучения в традициях Выготского крайне важно обыграть ее функциональный дуализм.
Другими словами, однозначная функция интерактивной среды, в рамках которой было инициировано задание, заключается в обеспечении инертной связи между ответом учащегося (ввод) и компьютерной оценкой (вывод). Точно так же его диалогическая функция состоит в том, чтобы генерировать новое значение, чтобы формировать деятельность учащегося. В частности, диалогическая функция среды опосредованного действия состоит в том, чтобы вызывать последующую активную познавательную деятельность в случае возникновения рассогласования между входом и выходом информационной цепи. Таким образом, функциональный дуализм среды, присваивающей неправильный ответ как мыслительному устройству, позволяет выйти за рамки трансляционной модели общения с однонаправленной и монологической структурой его информационного контура. Вместо того, чтобы предлагать просто пассивную оценку ответа учащегося, эта среда дает возможность учиться на неправильном ответе (гипотезе), внося свой вклад в дискурс с помощью самостоятельно созданной проблемы. Таким образом, речь оказывается внутренне убедительной; то есть его динамическая структура позволяет «интеранимировать» [27] студенческим задором разрешить противоречие, возникающее в информационном контуре, посредством последующей целенаправленной деятельности, опосредованной компьютером.
Вместо того, чтобы предлагать просто пассивную оценку ответа учащегося, эта среда дает возможность учиться на неправильном ответе (гипотезе), внося свой вклад в дискурс с помощью самостоятельно созданной проблемы. Таким образом, речь оказывается внутренне убедительной; то есть его динамическая структура позволяет «интеранимировать» [27] студенческим задором разрешить противоречие, возникающее в информационном контуре, посредством последующей целенаправленной деятельности, опосредованной компьютером.
С этой точки зрения, когда компьютер указывает на несоответствие между графическим вводом и числовым выводом, учащийся может расценивать такой результат не как отрицательную оценку, а как промежуточную внешнюю поддержку целенаправленной деятельности. Таким образом, присваивая неправильный ответ как средство мышления, учащийся может в конечном итоге понять смысл того, что не так с этим ответом.
6. Иллюстрация 1: Задачи с множественным выбором на прямоугольных сетках
Conference Board of the Mathematical Sciences [41], зонтичная организация, объединяющая 16 профессиональных обществ в США, рекомендовала будущим учителям начальных классов предоставить возможность использовать технологические инструменты «исследовать и углублять свое понимание математики, даже если эти инструменты не те, которые они в конечном итоге будут использовать с детьми» (стр. 34). В частности, установление стандартов обучения математике на начальном уровне в США, Common Core State Standards [9].] рекомендуют учащимся изучать десятичные дроби, «используя конкретные модели или рисунки и стратегии, основанные на позиционном значении» (стр. 35). Одной из таких моделей, с помощью которых могут быть введены операции с десятичными знаками, является прямоугольная сетка. Используя эту модель, можно обсудить три эквивалентных представления рациональных чисел, одним из которых является процент. В более сложной ситуации, подходящей для подготовки кандидатов в учителя начальных классов, понятие процента можно изучать на прямоугольных сетках с числом ячеек, отличным от 100. Van den Heuvel-Panhuizen et al. [42] утверждали, что «понимание учащимися процентов имеет свои нечисловые, контекстуальные корни» (стр. 25). Это говорит о том, что когнитивное взаимодействие между иконическими и числовыми обозначениями может привести к признанию формально-дробного характера понятия процента.
34). В частности, установление стандартов обучения математике на начальном уровне в США, Common Core State Standards [9].] рекомендуют учащимся изучать десятичные дроби, «используя конкретные модели или рисунки и стратегии, основанные на позиционном значении» (стр. 35). Одной из таких моделей, с помощью которых могут быть введены операции с десятичными знаками, является прямоугольная сетка. Используя эту модель, можно обсудить три эквивалентных представления рациональных чисел, одним из которых является процент. В более сложной ситуации, подходящей для подготовки кандидатов в учителя начальных классов, понятие процента можно изучать на прямоугольных сетках с числом ячеек, отличным от 100. Van den Heuvel-Panhuizen et al. [42] утверждали, что «понимание учащимися процентов имеет свои нечисловые, контекстуальные корни» (стр. 25). Это говорит о том, что когнитивное взаимодействие между иконическими и числовыми обозначениями может привести к признанию формально-дробного характера понятия процента.
Рассмотрим, например, 10 цветных ячеек в сетке из 50 ячеек. Какой процент сетки окрашен? В отличие от сетки из 100 ячеек, подсчет цветных ячеек в прямоугольной сетке не сразу дает процентное число. Возможное решение такой задачи заключается в подсчете количества окрашенных клеток с последующей нормировкой этого числа на всю сетку. Иными словами, деятельность на прямоугольной сетке, опосредованная нечисловым представлением проблемной ситуации, может привести к пониманию числовой структуры понятия процента как «отношения между двумя числами или величинами (выраженными) посредством отношения» [43, с. 150] и, тем самым, может поддерживать сознательное признание его дробно-арифметической природы.
Как описано в другом месте [44], в отношении 10 цветных ячеек в сетке из 50 ячеек учащемуся может быть предоставлен множественный выбор ответов из набора четырех процентных чисел с включением правильного ответа: 20%, 24 %, 30% и 40%. Как видно из рисунка 1, студент выбрал 24% в качестве ответа, что неверно. В результате компьютер выдал сообщение, в котором учащемуся предлагалось построить эти 24% на соседней сетке из 50 ячеек (рис. 1). Работа в соседней сетке происходит так же, как и в случае с сеткой из 100 ячеек, описанной ранее. Интерактивная обратная связь отображает процент сетки, окрашенной учащимся в соседней сетке. После того, как учащийся успешно построил графическое изображение своего неправильного ответа, в текстовом поле отобразится сообщение, предлагающее учащемуся вернуться к левой сетке и исправить исходное предположение. Наконец, когда учащийся вводит правильный ответ в поле для ответов, сообщение в текстовом поле под соседней сеткой исчезает, и компьютер дает указание учащемуся перейти к следующей задаче, отображая соответствующее сообщение в левом текстовом поле.
В результате компьютер выдал сообщение, в котором учащемуся предлагалось построить эти 24% на соседней сетке из 50 ячеек (рис. 1). Работа в соседней сетке происходит так же, как и в случае с сеткой из 100 ячеек, описанной ранее. Интерактивная обратная связь отображает процент сетки, окрашенной учащимся в соседней сетке. После того, как учащийся успешно построил графическое изображение своего неправильного ответа, в текстовом поле отобразится сообщение, предлагающее учащемуся вернуться к левой сетке и исправить исходное предположение. Наконец, когда учащийся вводит правильный ответ в поле для ответов, сообщение в текстовом поле под соседней сеткой исчезает, и компьютер дает указание учащемуся перейти к следующей задаче, отображая соответствующее сообщение в левом текстовом поле.
Обратите внимание, что работа с прямоугольными сетками аналогична тому, что несколько авторов в разных дисциплинах назвали методом «гипотеза-эксперимент-инструкция» (ГЭИ) [45–48]. В частности, этот метод применялся на уроках математики и естественных наук во многих японских начальных и неполных средних школах. Действительно, среда с прямоугольной сеткой ставит перед учащимися вопрос о процентной форме цветной части прямоугольной сетки и дает набор альтернативных ответов. Затем обеспечивает компьютерную обратную связь относительно правильности ответов учащихся и действий, направленных на размышление-обоснование-обсуждение ответов через действие. Наконец, среда побуждает учащихся еще раз выбрать альтернативу из заданного набора ответов. Как и в методе вуза, педагогика превращения неправильного ответа в генератор нового смысла дает студентам возможность использовать взаимодействие между действиями и компьютерной обратной связью в качестве мыслительного устройства. Именно такого интерментального функционирования учебной среды пока не хватает во многих классах, как отмечают Верч и Тома [49].] выразился, «в последнее время так часто упоминается как желание обучения» (стр. 173).
Действительно, среда с прямоугольной сеткой ставит перед учащимися вопрос о процентной форме цветной части прямоугольной сетки и дает набор альтернативных ответов. Затем обеспечивает компьютерную обратную связь относительно правильности ответов учащихся и действий, направленных на размышление-обоснование-обсуждение ответов через действие. Наконец, среда побуждает учащихся еще раз выбрать альтернативу из заданного набора ответов. Как и в методе вуза, педагогика превращения неправильного ответа в генератор нового смысла дает студентам возможность использовать взаимодействие между действиями и компьютерной обратной связью в качестве мыслительного устройства. Именно такого интерментального функционирования учебной среды пока не хватает во многих классах, как отмечают Верч и Тома [49].] выразился, «в последнее время так часто упоминается как желание обучения» (стр. 173).
7. Иллюстрация 2: Улучшение решения задач в контексте с помощью визуальных инструментов
Присутствие компьютера в классе начальной математики ставит перед преподавателями математики вопрос о новых областях математической деятельности для учащихся, согласованных с помощью компьютера. По словам Носса и Хойлса [50], понимание значения манипулятивных и вычислительных математических средств является «задачей создания новых математических сценариев, основанных на том, что может дать компьютер» (стр. 7). Один из таких сценариев проистекает из распространенного заблуждения о процентах от данного количества как об операции над этим количеством. В частности, многие студенты считают, что увеличение количества на заданный процент является обратимой операцией в том смысле, что уменьшение нового количества на тот же процент приводит к исходному количеству. Это, конечно, неправда.
По словам Носса и Хойлса [50], понимание значения манипулятивных и вычислительных математических средств является «задачей создания новых математических сценариев, основанных на том, что может дать компьютер» (стр. 7). Один из таких сценариев проистекает из распространенного заблуждения о процентах от данного количества как об операции над этим количеством. В частности, многие студенты считают, что увеличение количества на заданный процент является обратимой операцией в том смысле, что уменьшение нового количества на тот же процент приводит к исходному количеству. Это, конечно, неправда.
Например, если цена книги в 40 долларов была увеличена на 50%, а затем новая цена, 60 долларов, была уменьшена на те же 50%, сокращение не привело бы к цене в 30 долларов, хотя многие могут подумать, что это так. Другими словами, распространено заблуждение, что операция «увеличение-уменьшение» числа на один и тот же процент должна приводить к одному и тому же числу. Могут ли компьютерные манипуляции помочь ученику преодолеть это заблуждение? И если да, то как должна быть устроена такая среда, чтобы обеспечить эффективное опосредование такого рода процентных проблем культурными инструментами?
Имея это в виду, была разработана среда, в которой набор таких задач может быть решен путем активного использования кнопок цвета/стирания в качестве когнитивных инструментов. Намерение состояло в том, чтобы вовлечь учащихся в действия по увеличению-уменьшению цвета на сетке из 100 ячеек, а затем дать им набор эквивалентных текстовых задач в символьной (числовой) форме. Было обнаружено, что, хотя учащиеся успешно понимали концепцию процентов на сетке из 100 ячеек, они часто не могли связать деятельность, связанную с действием, с символической формулировкой соответствующей словесной задачи, когда задача была отделена от ее действия. связанный партнер в учебной среде. Опять же, именно через математическое действие, опосредованное электронными манипуляциями как культурным инструментом, студенты должны были сконструировать значение процента как необратимой операции.
Намерение состояло в том, чтобы вовлечь учащихся в действия по увеличению-уменьшению цвета на сетке из 100 ячеек, а затем дать им набор эквивалентных текстовых задач в символьной (числовой) форме. Было обнаружено, что, хотя учащиеся успешно понимали концепцию процентов на сетке из 100 ячеек, они часто не могли связать деятельность, связанную с действием, с символической формулировкой соответствующей словесной задачи, когда задача была отделена от ее действия. связанный партнер в учебной среде. Опять же, именно через математическое действие, опосредованное электронными манипуляциями как культурным инструментом, студенты должны были сконструировать значение процента как необратимой операции.
Однако, когда словесные задачи на проценты и связанные с ними связанные действия были представлены в виде объектно-символической единицы, учащиеся — группа из 6-ти классов — могли связать свои действия на 100-клеточных сетках с непосредственным символизмом словесных задач эффективно. Рисунок 2 иллюстрирует этот момент. Эта улучшенная среда позволила учащимся лучше понять необратимость процентной операции и мыслить с помощью инструментов, предоставляемых электронными сетками. В терминах Выготского именно включение знаков (прямоугольных сеток) в математическое действие коренным образом изменило действие и позволило интернализировать мышление, необходимое для понимания процента как операции на символическом уровне. Эта улучшенная среда предоставила учащимся инструменты для размышлений, которые позволили им лучше понять процент как необратимую операцию.
Эта улучшенная среда позволила учащимся лучше понять необратимость процентной операции и мыслить с помощью инструментов, предоставляемых электронными сетками. В терминах Выготского именно включение знаков (прямоугольных сеток) в математическое действие коренным образом изменило действие и позволило интернализировать мышление, необходимое для понимания процента как операции на символическом уровне. Эта улучшенная среда предоставила учащимся инструменты для размышлений, которые позволили им лучше понять процент как необратимую операцию.
Как упоминалось на вступительных страницах, одно из основных предположений текущей реформы математического образования заключается в том, что область педагогического образования поддается дисциплинированному исследованию. Это подразумевает признание того, что то, как учителя изучают математику, влияет на то, как они будут ее преподавать; то, чего, как заметил Куни [3], простодушно не хватало реформаторскому движению недавнего прошлого. В настоящее время стало общепризнанным, что исследователи в этой области «оценивают размытие содержания и педагогики… потому что… то, что мы изучаем, заключено в том, как мы это узнали… (и) думаем об учителе как о пытливом уме, а не как об объекте исследования». пытливый ум» [3, с. 627]. Что касается технологического компонента научных исследований и разработок в области подготовки учителей математики, такое смещение акцентов усилий по реформе подчеркивает важность анализа того, как взгляды учителей на математику и ее педагогику меняются, развиваются и совершенствуются на протяжении их профессионального развития. Другой важный вопрос, который здесь возникает, заключается в том, как использование технологий влияет на системы убеждений учителей относительно связи между математическим действием и опосредованными средствами, формирующими это действие.
пытливый ум» [3, с. 627]. Что касается технологического компонента научных исследований и разработок в области подготовки учителей математики, такое смещение акцентов усилий по реформе подчеркивает важность анализа того, как взгляды учителей на математику и ее педагогику меняются, развиваются и совершенствуются на протяжении их профессионального развития. Другой важный вопрос, который здесь возникает, заключается в том, как использование технологий влияет на системы убеждений учителей относительно связи между математическим действием и опосредованными средствами, формирующими это действие.
Следует отметить, что в контексте курса подготовки учителей математики (сайт, используемый авторами для проверки вышеизложенных педагогических идей) вся информация, касающаяся разнообразия записи электронной таблицы, а также математические/педагогические демонстрации могут быть представлены учителю. кандидатов не как конечный продукт, а в режиме реального времени, что позволяет им активно участвовать в дискурсе о синтаксисе, содержании и педагогике среды. То есть будущие учителя могут получить опыт преподавания с помощью технологий не через авторитетный дискурс с по существу монологическими предположениями, которые его подчеркивают, а скорее через многоголосый эгалитарный разговор о зарождении, развитии и реализации идей.
То есть будущие учителя могут получить опыт преподавания с помощью технологий не через авторитетный дискурс с по существу монологическими предположениями, которые его подчеркивают, а скорее через многоголосый эгалитарный разговор о зарождении, развитии и реализации идей.
Одним из основных преимуществ, которые технологии привносят в классную комнату, является появление открытой интеллектуальной среды, позволяющей исследовать множество идей. В такой обстановке технологии можно рассматривать как культурные инструменты, которые не только реорганизуют когнитивные процессы, но и трансформируют социальные практики в классе [23]. Роль учителя становится чрезвычайно сложной, поскольку он или он одновременно заменяется компьютером в качестве внешнего авторитета для проверки истины и должен быть адаптивным и рефлексивным партнером в продвижении, способным выжить в неопределенности в порождающей смысл динамической среде. Таким образом, отношение учителей к такой структурированной дидактической среде может дать дополнительное представление о концептуализации новых моделей взаимодействия между содержанием и педагогикой при разработке современных программ подготовки учителей математики.
Например, один кандидат в учителя, размышляя над процентной активностью, описанной выше, выразила свое мнение: « открытая педагогика является важным компонентом в классе математики. Много раз ребенок улавливает вещи, которых никто никогда не замечал, потому что он не так привязан к взгляду на мир через ограничения, которые иногда ограничивают взгляды более образованного человека. Всегда приятно смотреть на мир глазами ребенка! Наша образовательная система часто является изучением того, чему человечество научилось в прошлом, и мы, учителя, следуя традиции, делаем все возможное, чтобы систематизировать и представить эту совокупность знаний следующему поколению. Однако математика является динамичной дисциплиной и должна быть представлена учащимся как таковая. Мы не должны ограничивать их молодые умы. » Это согласуется с мнением другого кандидата в учителя о моделях взаимодействия, сформированных эгалитарным дискурсом в классе: « учащиеся могут заинтересоваться и захотеть изучить направление или ответвление задания, о котором учитель, возможно, раньше не думал. Студенты могут унаследовать энтузиазм не только от учителя, но и от других учеников. Эта (открытая) среда определенно способствует творчеству. ”
Студенты могут унаследовать энтузиазм не только от учителя, но и от других учеников. Эта (открытая) среда определенно способствует творчеству. ”
Конкретный пример такого творчества был обнаружен в совместной работе двух учителей начальной школы, которые продемонстрировали, как можно использовать прямоугольные сетки для преподавания рутинных тем по арифметике. Карикатура, показанная на рисунке 3, показывает арифметическую задачу с «человеческим смыслом», которая, в частности, иллюстрирует тот факт, что истоки опосредованной деятельности можно найти в социальных формах человеческого существования, сформированных культурным фоном. Этот пример демонстрирует способность кандидатов в учителя быть рефлексивными и адаптивными, способными понять, как их ученики «узнают и верят в то, что они делают» [3, с. 628]. Более того, их собственные взгляды на преподавание и обучение гарантируют их способность использовать семантическую многоголосость технологического дискурса в будущих педагогических установках и решениях.
Паттерны «привилегирования» [27], обнаруженные в ответах кандидатов в учителя на вопрос, что повлияло на их выбор темы для заключительного проекта, дают еще более глубокое понимание их системы убеждений, на которую повлияло личное знакомство с силой электронных таблиц. на основе технологии. Например, один кандидат в учителя признал потенциал электронных таблиц для реорганизации использования учебных материалов: «Я хотел использовать Excel таким образом, чтобы предоставить учащимся больше, чем задачи из учебника». Этот комментарий указывает на высокую оценку использования электронных таблиц для помощи учащимся в установлении математических связей: «использование электронной таблицы для обсуждения площади и периметра — очень мощный инструмент, поскольку он дает учащимся возможность подумать и получить интуитивное представление о факторинге».
В заключение отметим, что в этой статье не рассматриваются детали программирования электронных таблиц, связанные с созданием обсуждаемых сред. Однако осознание того, что можно создать с помощью электронной таблицы, имеет гораздо большее значение, чем задействованные конкретные синтаксические структуры. Семиотическая неоднородность и синтаксическая универсальность электронной таблицы сильно отличают ее от готовой программы. Действительно, на усмотрение технически грамотного учителя могут быть выбраны различные формы семиотического опосредования. Наконец, возможность изменить вербальное посредничество по требованию конкретного класса позволяет учителю, используя общедоступные технические средства, решать вопросы, касающиеся социального и культурного разнообразия, и задействовать индивидуальные различия, существующие в постоянно разнородном сообществе учащихся.
Однако осознание того, что можно создать с помощью электронной таблицы, имеет гораздо большее значение, чем задействованные конкретные синтаксические структуры. Семиотическая неоднородность и синтаксическая универсальность электронной таблицы сильно отличают ее от готовой программы. Действительно, на усмотрение технически грамотного учителя могут быть выбраны различные формы семиотического опосредования. Наконец, возможность изменить вербальное посредничество по требованию конкретного класса позволяет учителю, используя общедоступные технические средства, решать вопросы, касающиеся социального и культурного разнообразия, и задействовать индивидуальные различия, существующие в постоянно разнородном сообществе учащихся.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Список литературы
R. A. R. Guring, N.L. Chick и A. A. Ciccone, Eds., Изучение фирменных педагог. Дедал , том.
 134, нет. 3, стр. 52–59, 2005.
134, нет. 3, стр. 52–59, 2005.Посмотреть по адресу:
Сайт издателя | Google Scholar
Т. Дж. Куни, «Исследования и педагогическое образование: в поисках точек соприкосновения», Journal for Research in Mathematics Education , vol. 25, нет. 6, pp. 608–636, 1994.
Посмотреть по адресу:
Google Scholar
С. Абрамович, Дж. Истон и В. О. Хейс, «Параллельные структуры компьютерной педагогики подписи: случай интегрированных электронных таблиц », Компьютеры в школах , том. 29, нет. 1–2, стр. 174–190, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Абрамович и Э. Чо, «О математических задачах, поставленных начальными учителями: случай электронных таблиц», Spreadsheets in Education , vol.
 3, нет. 1, pp. 1–19, 2008.
3, нет. 1, pp. 1–19, 2008.Посмотреть по адресу:
Google Scholar
С. Абрамович, «Когнитивная неоднородность в компьютерно-опосредованном математическом действии как средство развития концепции», Journal of Computers in Mathematics and Science Teaching , vol. 22, нет. 1, pp. 19–41, 2003.
Посмотреть по адресу:
Google Scholar
H. Freudenthal, Математика как образовательная задача , Reidel, Dordrecht, The Netherlands, 1974
J
. Адамар,
Разум математика: психология изобретений в области математики , Princeton University Press, Принстон, штат Нью-Джерси, США, 1996.Общие базовые государственные стандарты, карьера», 2010 г., http://www.corestandards.org/.
Посмотреть по адресу:
Google Scholar
Национальный совет учителей математики, Принципы и стандарты школьной математики , Автор, Рестон, Вирджиния, США, 2000.
Посмотреть по адресу:
Сайт издателя | Академия Google
Национальный совет учителей математики, Профессиональные стандарты преподавания математики , Автор, Рестон, Вирджиния, США, 1991.
П. Кобб, «Где разум? Конструктивистские и социокультурные взгляды на математическое развитие», Educational Researcher , vol. 23, нет. 7, pp. 13–20, 1994.
Посмотреть по адресу:
Google Scholar
П. Кобб, Б. Яворски и Н. Пресмег, «Эмергентные и социокультурные взгляды на математическую деятельность», в Теории математического обучения , Л. П. Стеффе, П. Нешер, П. Кобб, Г. А. Голдин и Б. Грир, ред. , стр. 3–20, Lawrence Erlbaum Associates, Mahwah, NJ, USA, 1996.
, стр. 3–20, Lawrence Erlbaum Associates, Mahwah, NJ, USA, 1996.
View по адресу:
Google Scholar
A. H. Schoenfeld, «Обучение математическому мышлению: решение проблем, метапознание и осмысление в математике», в Handbook of Research on Mathematics Teaching and Learning , D. A. Grouws, Ed., стр. 334–370, Макмиллан, Нью-Йорк, США, 1992.
Посмотреть по адресу:
Google Scholar
С. Абрамович, «Счет и рассуждение с использованием манипулятивных материалов: точка зрения Северной Америки», в Интерфейсы предметов, преподаваемых в начальных школах, и возможные модели их интеграции , Н. Петрович, изд., стр. 9–20, Университет Нови-Сад, Факультет образования, Сомбор, Сербия, 2012. на объектах: метафора обучения математике с помощью технологий», в Использование информационных технологий в математике , Д. Тук и Н. Хендерсон, ред., стр. 143–171, Haworth Press, Бингемтон, штат Нью-Йорк, США, 2001. Коннелл и С. Абрамович, «Новые инструменты для новых мыслей: влияние изменения «Инструментов для мышления» на курс методов элементарной математики», в Трудах Международной конференции по информационным технологиям и педагогическому образованию , стр. 1052–1057, 19.99.
Тук и Н. Хендерсон, ред., стр. 143–171, Haworth Press, Бингемтон, штат Нью-Йорк, США, 2001. Коннелл и С. Абрамович, «Новые инструменты для новых мыслей: влияние изменения «Инструментов для мышления» на курс методов элементарной математики», в Трудах Международной конференции по информационным технологиям и педагогическому образованию , стр. 1052–1057, 19.99.
Посмотреть по адресу:
Google Scholar
М. Л. Коннелл и М. Буниев, «Общие рекомендации SSDMA и конструктивизма по технологиям в математическом образовании», The Researcher , vol. 12, нет. 1, pp. 21–27, 1997.
Посмотреть по адресу:
Google Scholar
J. V. Wertsch, The Concept of Activity in Soviet Psychology , ME Sharpe, Armonk, NY
, USA, 1981.
П. Кобб, «Культурные инструменты и изучение математики: пример», стр. Журнал исследований в области математического образования , том. 26, нет. 4, pp. 362–385, 1995.
Журнал исследований в области математического образования , том. 26, нет. 4, pp. 362–385, 1995.
Посмотреть по адресу:
Google Scholar
П. Кобб, М. Стефан, К. Макклейн и К. Гравемейер, «Участие в математических практиках в классе», в A Journey in Mathematics Education Research , E. Yackel, K. Gravemeijer, and A. Sfard, Eds., стр. 117–163, Springer, Дордрехт, Нидерланды, 2011.
Посмотреть по адресу:
Google Scholar
М. Гус, «Социокультурный анализ развития педагогической идентичности будущих и начинающих учителей как пользователей технологий», Journal of Mathematics Teacher Education , vol. 8, нет. 1, стр. 35–59, 2005 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar. ’98) , S.Berenson, K. Dawkins, M.Blanton et al., Eds., vol. 1, стр. 227–233, 1998.
Dawkins, M.Blanton et al., Eds., vol. 1, стр. 227–233, 1998.
Посмотреть по адресу:
Google Scholar
Дж. Мошкович, «Ситуативный и социокультурный взгляд на двуязычных учащихся-математиков», Mathematical Thinking and Learning , vol. 4, нет. 2–3, стр. 189–212, 2002.
Посмотреть по адресу:
Google Scholar
Н. Мерсер, «Нео-Выготскианская теория и обучение в классе», в Язык, грамотность и обучение в образовательной практике: Читатель , B. Stierer and J. Maybin, Eds., pp. 92–110, The Open University, Bristol, Pa, USA, 1994. Разум: социокультурный подход к опосредованному действию , Harvard University Press, Cambridge, Mass, USA, 1991.
Н. Хомский, Картезианская лингвистика: глава в истории рационалистической мысли , Harper and Row, New Йорк, штат Нью-Йорк, США, 1966 г.
У. Беван, «Современная психология: путешествие внутрь луковицы», American Psychologist , vol. 46, нет. 5, pp. 475–483, 1991.
Посмотреть по адресу:
Google Scholar
П. Кобб, Э. Якель и Т. Вуд, «Конструктивистская альтернатива репрезентативному взгляду на разум в математическом образовании, Journal for Research in Mathematics Education , vol. 23, нет. 1, стр. 2–33, 1992.
Посмотреть по адресу:
Google Scholar
Л. М. Розенблатт, «Письмо и чтение: теория транзакций», Tech. Rep. 13, Университет Карнеги-Меллона, Центр изучения письма, Питтсбург, Пенсильвания, США, 1988.
Посмотреть по адресу:
Google Scholar
А. Куоко, Э. П. Гольденберг и Дж. Марк, «Современный вопросы учебной программы: организация учебной программы на основе математических привычек», Учитель математики , том. 103, нет. 9, стр. 682–688, 2010.
103, нет. 9, стр. 682–688, 2010.
Посмотреть по адресу:
Google Scholar
W.-M. Рот и Ю.-Дж. Ли, «Забытое наследие Выготского»: теория культурно-исторической деятельности, Review of Educational Research , vol. 77, нет. 2, стр. 186–232, 2007 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Л. Коннелл, Д. М. Пек, У. Бакстон и Д. Килберн, «Настоящее сотрудничество: анализ программы концептуальных изменений в элементарной математике», в Ежегоднике педагогического образования: Партнерство в сфере образования II , S. Odell and M.O. ‘Hair, Eds., стр. 255–274, Harcourt Brace and Javonovich, New York, NY, USA, 1994. How to Solve It , Princeton University Press, Princeton, NJ, USA, 1945.
G. Bateson, Steps to the Ecology of Mind: A Revolutionary Approach to Man’s Understanding of Himself , Ballantine, New York, Нью-Йорк, США, 1972.
Б. Рогофф, Обучение мышлению: когнитивное развитие в социальном контексте , издательство Оксфордского университета, Оксфорд, Великобритания, 1990.
Ю. Лотман, «Текст в тексте», Советская психология , том. 24, нет. 3, pp. 32–51, 1988.
Посмотреть по адресу:
Google Scholar
H. Mehan, Learning Lessons , Harvard University Press, Cambridge, Mass, USA, 1979. 9.0002 Lygotsky
3
, «Сознание как проблема психологии поведения», Journal of Russian and East European Psychology , том. 17, нет. 4, стр. 3–35, 1979.
Посмотреть по адресу:
Google Scholar
Conference Board of the Mathematical Sciences, The Mathematical Education of Teachers II , The Mathematical Association of America, Washington, DC, USA , 2012.
М. Ван ден Хойвель-Панхуизен, Дж. А. Миддлтон и Л. Стрифленд, «Задачи, созданные учащимися: простые и сложные задачи в процентах», For the Learning of Mathematics , vol. 15, нет. 3, стр. 21–27, 1995.
Ван ден Хойвель-Панхуизен, Дж. А. Миддлтон и Л. Стрифленд, «Задачи, созданные учащимися: простые и сложные задачи в процентах», For the Learning of Mathematics , vol. 15, нет. 3, стр. 21–27, 1995.
Посмотреть по адресу:
Google Scholar
Депаэпе Ф., Де Корте Э., Оп’т Эйнде П. и Вершаффель Л. Проценты преподавания в начальной школе: сравнительное исследование четырех стран, ” в Мощные среды для содействия глубокому концептуальному и стратегическому обучению , Л. Вершаффель, Э. Де Корте, Г. Канселар и М. Вальке, ред., стр. 147–171, Leuven University Press, Левен, Бельгия, 2005 г.
Посмотреть по адресу:
Google Scholar
С. Абрамович, «Математические концепции как новые инструменты в вычислительных приложениях», Journal of Computers in Mathematics and Science Teaching , vol. 19, нет. 1, стр. 21–46, 2000.
1, стр. 21–46, 2000.
Посмотреть по адресу:
Google Scholar
Г. Хатано, «Социальные и мотивационные основы математического понимания», Новые направления развития детей и подростков, , вып. 41, стр. 55–70, 2006.
Посмотреть по адресу:
Google Scholar
Г. Хатано и К. Инагаки, «Когда предполагается концептуальное изменение? Когнитивно-социокультурный взгляд», в Intentional Conceptual Change , G. M. Sinatra and P.R. Pintrich, Eds., стр. 407–427, Lawrence Erlbaum Associates, Mahwah, NJ, USA, 2003.
Просмотр по адресу:
Google Scholar
Дж. В. Кнапп, «Преподавание поэзии через ВУЗ (гипотеза-эксперимент-инструкция)», Journal of Adolescent and Adult Literacy , vol. 45, нет. 8, стр. 718–729. , 2002.
, 2002.
Посмотреть по адресу:
Google Scholar
Ю. Кобаяши, «Концептуальное приобретение и изменение посредством социального взаимодействия», Human Development , vol. 37, нет. 4, стр. 233–241, 1994.
Посмотреть по адресу:
Google Scholar
Дж. В. Верч и К. Тома, «Дискурс и обучение в классе: социокультурный подход», в Конструктивизм в образовании , Л. П. Стеффе и Дж. Гейл, ред., стр. 159–174, Lawrence Erlbaum Associates, Hillsdale, NJ, USA, 19.95.
Просмотр по адресу:
Google Scholar
R. Noss and C. Hoyles, Windows на математическом значении , Kluwer Academic Publishers, Dordrecht, The Netherlands, 1996.
12712712712712712712712712712712 712712712712712712712 712712712712 712712712712712712711 2014 Сергей Абрамович и Майкл Л.

 — 112 c.
— 112 c. , испр. и доп. Учебное пособие для СПО / Виктор Алексеевич Далингер. — М.: Юрайт, 2016. — 111 c.
, испр. и доп. Учебное пособие для СПО / Виктор Алексеевич Далингер. — М.: Юрайт, 2016. — 111 c. И. Целищева. — М.: Владос, 2018. — 192 c.
И. Целищева. — М.: Владос, 2018. — 192 c.
 : Вентана-Граф, 2018. — 264 c.
: Вентана-Граф, 2018. — 264 c. И.Методика обучения математике в начальной школе. 2 класс
И.Методика обучения математике в начальной школе. 2 класс Курс лекций. Учебное пособие для студентов вузов. Гриф УМО МО РФ
Курс лекций. Учебное пособие для студентов вузов. Гриф УМО МО РФ А.Методика обучения математике в начальной школе. Учебное пособие для академического бакалавриата
А.Методика обучения математике в начальной школе. Учебное пособие для академического бакалавриата В.Методика обучения доказательству с использованием средств естественного вывода при изучении курса математики основной школы
В.Методика обучения доказательству с использованием средств естественного вывода при изучении курса математики основной школы С.Методика обучения математике в 2 частях. Часть 1. Учебник для академического бакалавриата
С.Методика обучения математике в 2 частях. Часть 1. Учебник для академического бакалавриата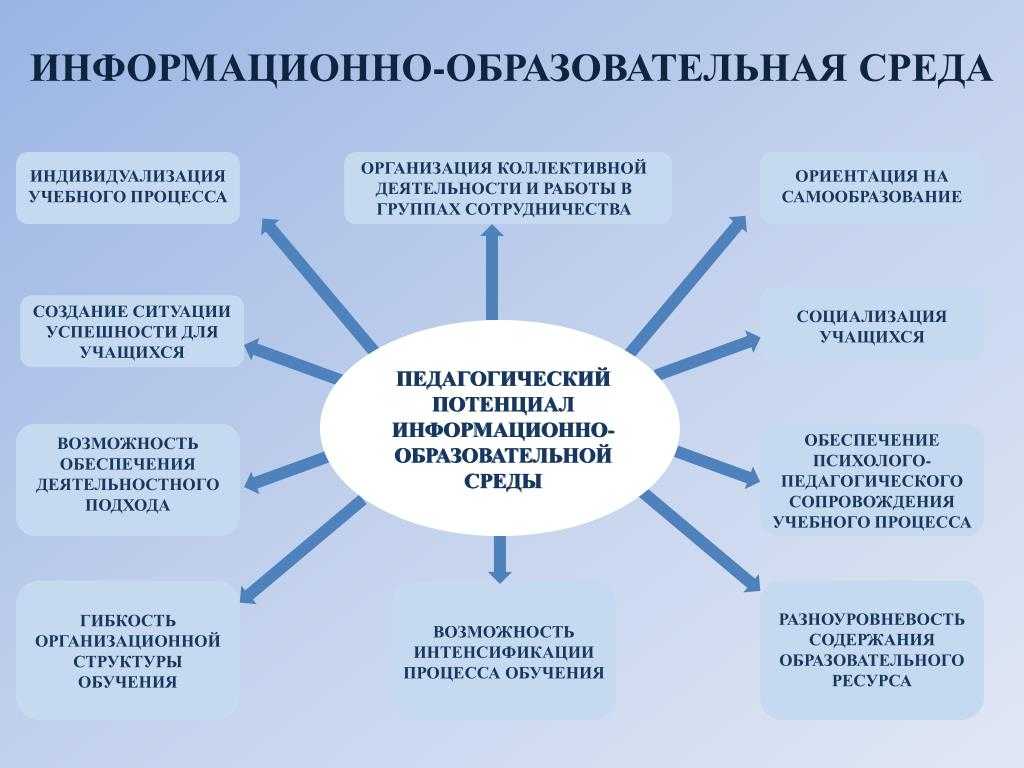 Н.Математика. Методика обучения. 1 класс. ФГОС
Н.Математика. Методика обучения. 1 класс. ФГОС А., Перевощикова Е.Н., Кузнецова Л.И., Григорьева Т.П. Теория и технология обучения математике в средней школе:Учеб. Пособие для студентов математических специальностей педагогических вузов/Под ред. Т.А.Ивановой. Н.Новгород: НГПУ, 2009.
А., Перевощикова Е.Н., Кузнецова Л.И., Григорьева Т.П. Теория и технология обучения математике в средней школе:Учеб. Пособие для студентов математических специальностей педагогических вузов/Под ред. Т.А.Ивановой. Н.Новгород: НГПУ, 2009.
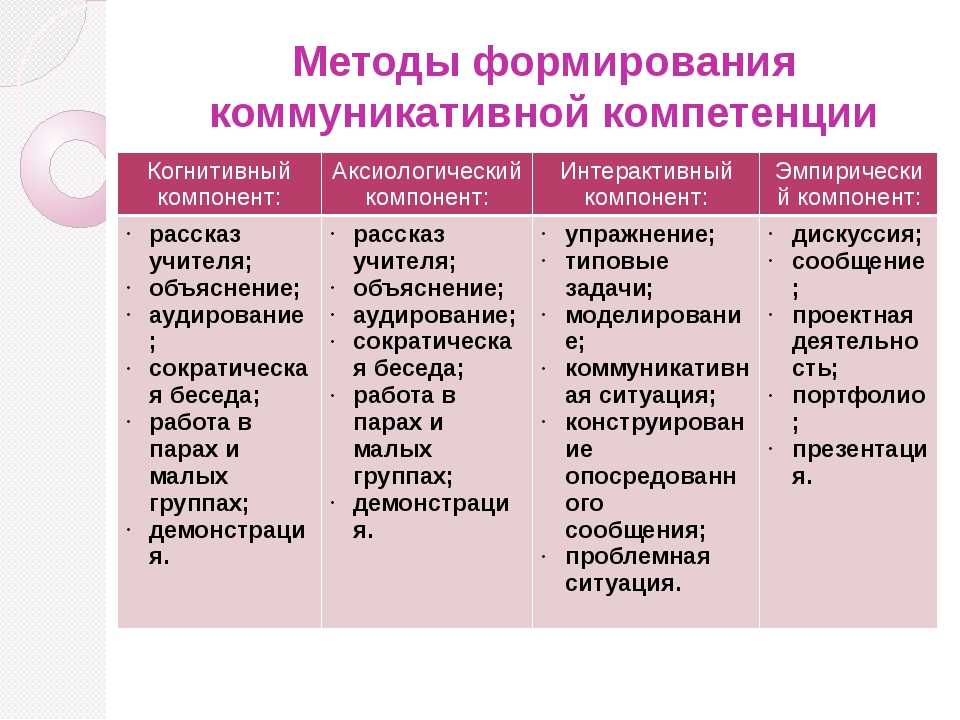 Дополнительная литература
Дополнительная литература Для учителя. – М.: Просвещение, 1990.
Для учителя. – М.: Просвещение, 1990. С. Личностно ориентированное обучение в современной школе. – М., 1996.
С. Личностно ориентированное обучение в современной школе. – М., 1996.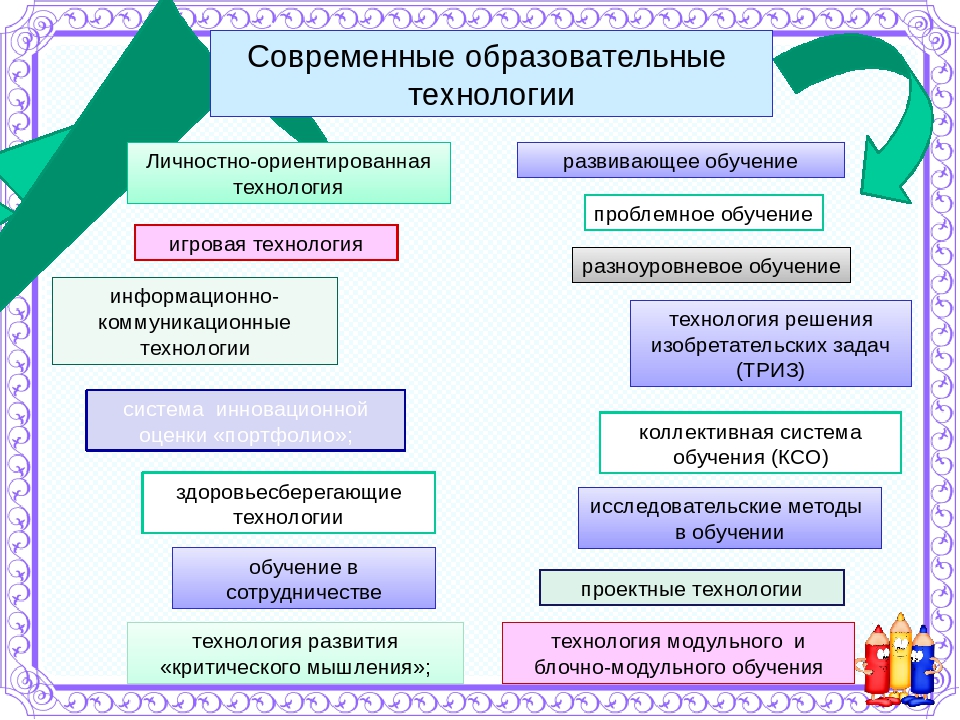 [17]
[17]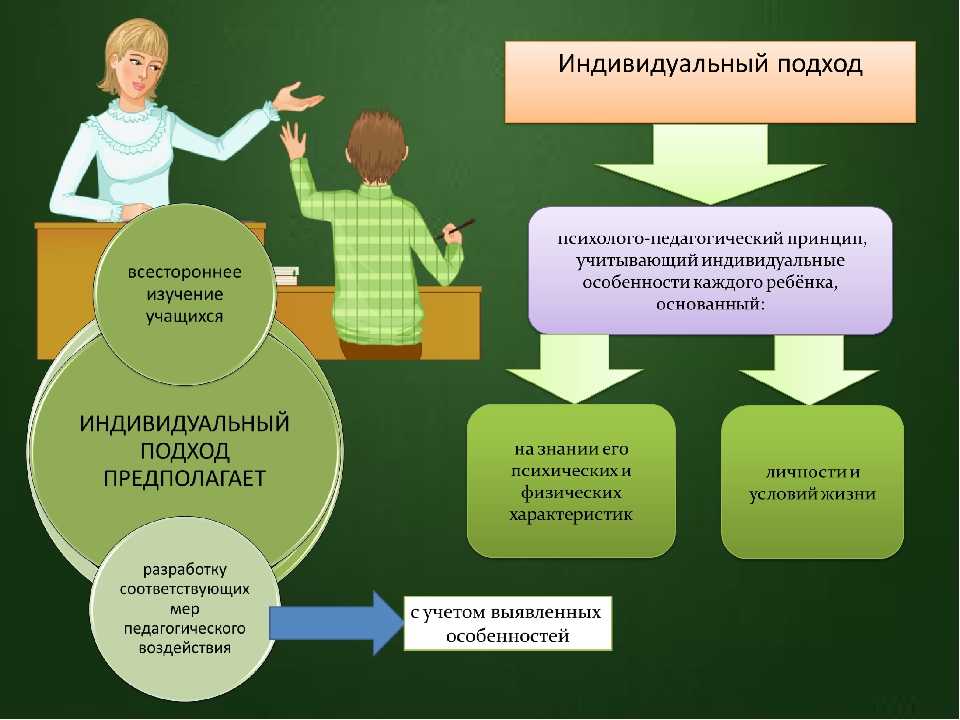
 Дробные числа.
Дробные числа. Инструменты для вычислений и измерений.
Инструменты для вычислений и измерений. Обыкновенные дроби.
Обыкновенные дроби.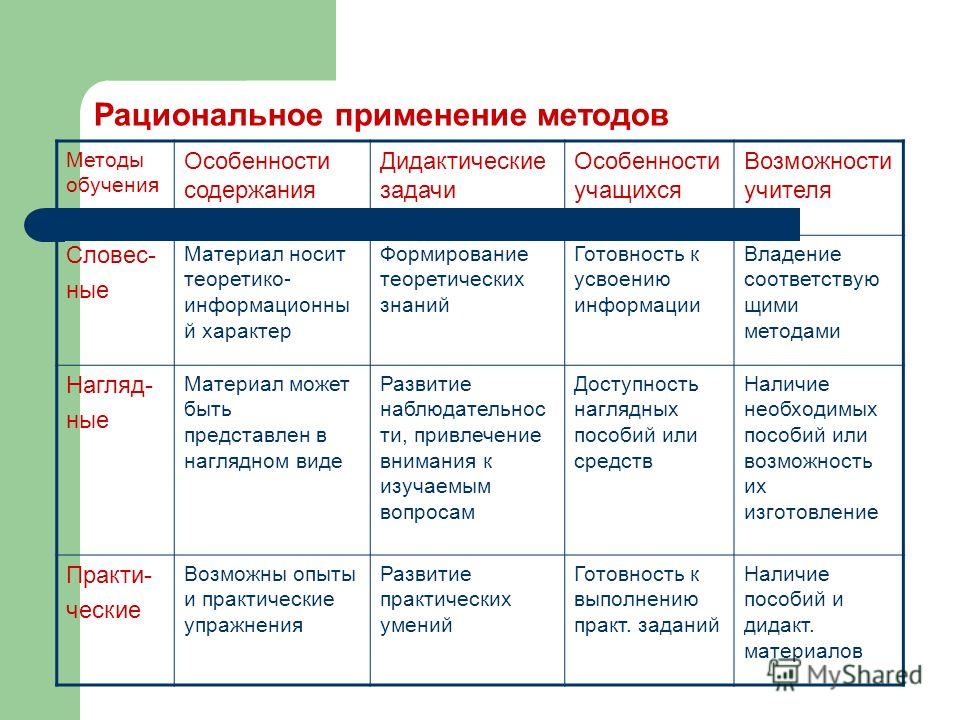 Отношения и пропорции
Отношения и пропорции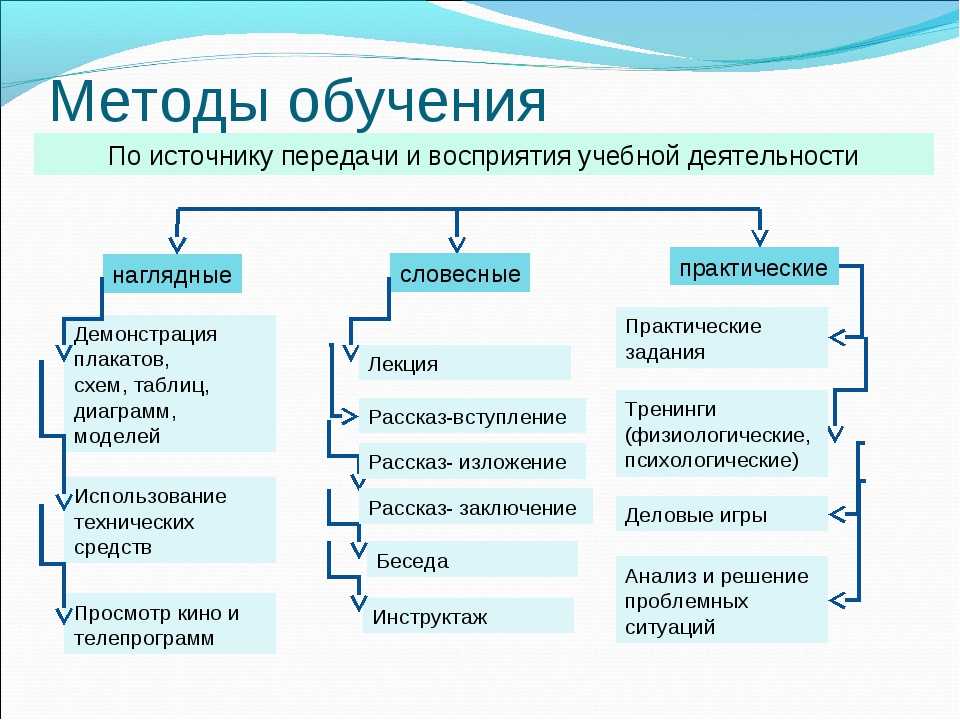 Умножение и деление положительных и отрицательных чисел.
Умножение и деление положительных и отрицательных чисел. 6. Упрощение вычислений.
6. Упрощение вычислений. Дроби.
Дроби. 5. Решение задач на пропорции.
5. Решение задач на пропорции.
 Учебник в 2 ч. / С.А. Козлова, А.Г. Рубин. — 2-е изд. — М.: Баласс, 2015. — Ч.1 — 208с., Ч.2 — 208с.
Учебник в 2 ч. / С.А. Козлова, А.Г. Рубин. — 2-е изд. — М.: Баласс, 2015. — Ч.1 — 208с., Ч.2 — 208с.  Тайная жизнь чисел. Любопытные разделы математики. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с.
Тайная жизнь чисел. Любопытные разделы математики. / Пер. с исп. – М.: Де Агостини, 2014. – 160 с. / И.В. Шаповаленко — М.: Гардарики, 2005. — 349 с.
/ И.В. Шаповаленко — М.: Гардарики, 2005. — 349 с. Рестон, Вирджиния: NCTM.
Рестон, Вирджиния: NCTM.
 Американский журнал исследований в области образования, 47 (4), 833–878.
Американский журнал исследований в области образования, 47 (4), 833–878. в их бумаге. Сохранение стоимости относится к функции денег как средства сохранения стоимости покупательной способности с течением времени. Средство обмена относится к функции денег как общепризнанного посредника при обмене товаров и услуг. Платежные средства подчеркивают активную роль денег как средства погашения долгов и выполнения обязательств. Расчетная единица относится к функции денег как эталона измерения или единицы стоимости, в которой выражаются цены, заработная плата и другие экономические ценности.
в их бумаге. Сохранение стоимости относится к функции денег как средства сохранения стоимости покупательной способности с течением времени. Средство обмена относится к функции денег как общепризнанного посредника при обмене товаров и услуг. Платежные средства подчеркивают активную роль денег как средства погашения долгов и выполнения обязательств. Расчетная единица относится к функции денег как эталона измерения или единицы стоимости, в которой выражаются цены, заработная плата и другие экономические ценности. Наконец, он объясняет, что «напротив, подход к« расчетной единице »сводит деньги к пассивной роли, эластично приспосабливаясь к потребностям реальной экономики».
Наконец, он объясняет, что «напротив, подход к« расчетной единице »сводит деньги к пассивной роли, эластично приспосабливаясь к потребностям реальной экономики». Такой подход исключает необходимость рытья туннеля под дном водоема, будь то река, озеро или море. Тем не менее, инженерные требования огромны, и любая такая конструкция должна быть устойчива к току и коррозии, а также к чрезвычайным происшествиям, таким как цунами.
Такой подход исключает необходимость рытья туннеля под дном водоема, будь то река, озеро или море. Тем не менее, инженерные требования огромны, и любая такая конструкция должна быть устойчива к току и коррозии, а также к чрезвычайным происшествиям, таким как цунами. Исследователи также рассмотрели различные политические выводы относительно этой новой транспортной технологии. Их вывод состоит в том, что такие туннели в конечном итоге произведут революцию в области связи и транспорта. Такие туннели могли бы оказать серьезное влияние, например, на объединение островных кластеров или соединение регионов, где пролетный мост был бы неуместен или невозможен.
Исследователи также рассмотрели различные политические выводы относительно этой новой транспортной технологии. Их вывод состоит в том, что такие туннели в конечном итоге произведут революцию в области связи и транспорта. Такие туннели могли бы оказать серьезное влияние, например, на объединение островных кластеров или соединение регионов, где пролетный мост был бы неуместен или невозможен. 58–78.
58–78. 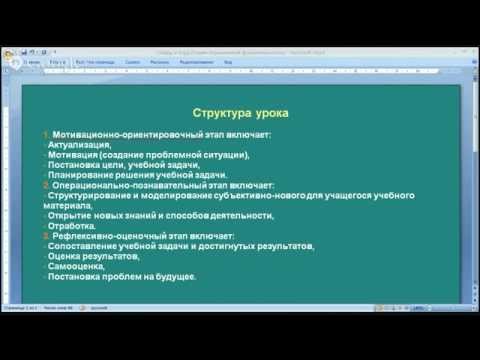
 Виртуальные приемы могут быть интегрированы в такое управление, сокращая количество поездок к врачу, которые необходимо совершить пациенту, тем самым избавляя их от неудобств, беспокойства и затрат. Виртуальные приемы также могут снизить риск инцидента или несчастного случая или даже риск заражения пациента неприятной инфекцией от третьего лица по пути в кабинет врача и обратно, что остается важным моментом в продолжающемся COVID-19.пандемия.
Виртуальные приемы могут быть интегрированы в такое управление, сокращая количество поездок к врачу, которые необходимо совершить пациенту, тем самым избавляя их от неудобств, беспокойства и затрат. Виртуальные приемы также могут снизить риск инцидента или несчастного случая или даже риск заражения пациента неприятной инфекцией от третьего лица по пути в кабинет врача и обратно, что остается важным моментом в продолжающемся COVID-19.пандемия. Люди использовали сонар, звуковую навигацию и дальномер еще со времен Леонардо да Винчи, который впервые описал технику акустического прослушивания в 149 году.0. Современные активные сонарные методы, конечно же, намного сложнее, чем его пассивная техника.
Люди использовали сонар, звуковую навигацию и дальномер еще со времен Леонардо да Винчи, который впервые описал технику акустического прослушивания в 149 году.0. Современные активные сонарные методы, конечно же, намного сложнее, чем его пассивная техника.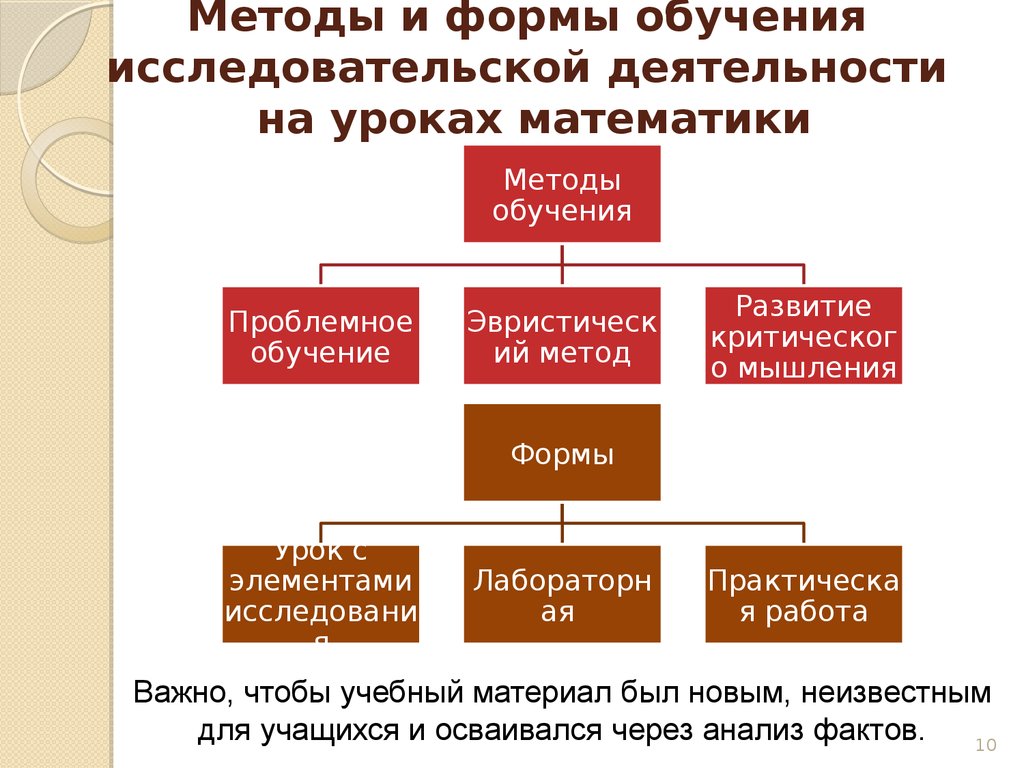 Команда показала, что в диапазоне от 1 до 3 килогерц (кГц) они могут передавать и получать информацию со скоростью 200 бит в секунду акустически через воду и могут отправлять необходимую информацию с веб-страницы, преобразованную в азбуку Морзе. , через воду, которую затем можно было бы расшифровать, а информацию использовать для отображения страницы на компьютере на принимающей стороне. Система построена на интернет-протоколе TCP/IP. Рабочее расстояние между передатчиком и приемником может составлять до 25 метров с текущей настройкой. Команда добавляет, что улучшения в технологии могут значительно увеличить радиус действия их системы, что сделает ее гораздо более полезной.
Команда показала, что в диапазоне от 1 до 3 килогерц (кГц) они могут передавать и получать информацию со скоростью 200 бит в секунду акустически через воду и могут отправлять необходимую информацию с веб-страницы, преобразованную в азбуку Морзе. , через воду, которую затем можно было бы расшифровать, а информацию использовать для отображения страницы на компьютере на принимающей стороне. Система построена на интернет-протоколе TCP/IP. Рабочее расстояние между передатчиком и приемником может составлять до 25 метров с текущей настройкой. Команда добавляет, что улучшения в технологии могут значительно увеличить радиус действия их системы, что сделает ее гораздо более полезной. А., Пэн, Ю. и Вей, С. (2022) «Подводная беспроводная связь с использованием TCP/IP», Int. J. Intelligent Internet of Things Computing, Vol. 1, № 4, с. 273–286.
А., Пэн, Ю. и Вей, С. (2022) «Подводная беспроводная связь с использованием TCP/IP», Int. J. Intelligent Internet of Things Computing, Vol. 1, № 4, с. 273–286.  Расширение также имеет встроенный инструмент напоминания. Команда отмечает, что она использует модель freemium, в которой базовые функции доступны бесплатно, но премиум-функции можно приобрести в браузере Chrome.
Расширение также имеет встроенный инструмент напоминания. Команда отмечает, что она использует модель freemium, в которой базовые функции доступны бесплатно, но премиум-функции можно приобрести в браузере Chrome. J. Система системной инженерии, Vol. 13, № 1, стр. 1–29.
J. Система системной инженерии, Vol. 13, № 1, стр. 1–29.  Фархан также показал, что предполагаемая польза для здоровья, а также гедонистические и социальные ценности положительно влияют на отношение потребителей к органическим продуктам питания. Это неизбежно привело к тому, что потребители с большей вероятностью стали покупать органические продукты питания. Результаты подчеркивают важность осведомленности и просвещения в отношении органических продуктов питания. Вполне вероятно, что в ближайшие несколько лет спрос продолжит расти, и производители и продавцы должны знать об этом, чтобы извлечь выгоду из повышения осведомленности своих потенциальных клиентов и найти способы удовлетворить растущий спрос.
Фархан также показал, что предполагаемая польза для здоровья, а также гедонистические и социальные ценности положительно влияют на отношение потребителей к органическим продуктам питания. Это неизбежно привело к тому, что потребители с большей вероятностью стали покупать органические продукты питания. Результаты подчеркивают важность осведомленности и просвещения в отношении органических продуктов питания. Вполне вероятно, что в ближайшие несколько лет спрос продолжит расти, и производители и продавцы должны знать об этом, чтобы извлечь выгоду из повышения осведомленности своих потенциальных клиентов и найти способы удовлетворить растущий спрос. Тем не менее, повышение осведомленности о еде и здоровье, а также просвещение всегда будут полезны, и те люди, которые выбирают органические продукты, могут также внести другие изменения в свои привычки питания и образ жизни во имя улучшения своего здоровья, что принесет дополнительные, более ощутимые преимущества.
Тем не менее, повышение осведомленности о еде и здоровье, а также просвещение всегда будут полезны, и те люди, которые выбирают органические продукты, могут также внести другие изменения в свои привычки питания и образ жизни во имя улучшения своего здоровья, что принесет дополнительные, более ощутимые преимущества. Большая часть вовлеченности и виральности контента в социальных сетях и других местах — это не что иное, как автоматизированная деятельность ботов и фермы кликов. Многое из этого делается как часть продвижения дезинформации в политических целях, и многое делается для того, чтобы обмануть рекламодателей, заставив их представить, что их платную рекламу видят реальные люди.
Большая часть вовлеченности и виральности контента в социальных сетях и других местах — это не что иное, как автоматизированная деятельность ботов и фермы кликов. Многое из этого делается как часть продвижения дезинформации в политических целях, и многое делается для того, чтобы обмануть рекламодателей, заставив их представить, что их платную рекламу видят реальные люди.
 данные. Учитывая недавнее публичное появление так называемых языковых моделей и инструментов, вполне вероятно, что мы будем видеть все больше и больше поддельных отзывов в Интернете. Однако те самые инструменты, которые генерируют такой вводящий в заблуждение контент, также могут использоваться для обнаружения его присутствия. Мы неизбежно увидим игру в кошки-мышки между сайтами электронной коммерции и мошенниками, а в центре внимания окажутся потребители, которые ищут достойный продукт по хорошей цене.
данные. Учитывая недавнее публичное появление так называемых языковых моделей и инструментов, вполне вероятно, что мы будем видеть все больше и больше поддельных отзывов в Интернете. Однако те самые инструменты, которые генерируют такой вводящий в заблуждение контент, также могут использоваться для обнаружения его присутствия. Мы неизбежно увидим игру в кошки-мышки между сайтами электронной коммерции и мошенниками, а в центре внимания окажутся потребители, которые ищут достойный продукт по хорошей цене. Стеганография предполагает сокрытие информации, а также существование этой информации, чтобы ее мог найти только предполагаемый получатель.
Стеганография предполагает сокрытие информации, а также существование этой информации, чтобы ее мог найти только предполагаемый получатель.