Мажорный лад
В музыке подавляющего большинства стран мира существуют два основных лада мажор и минор. Все остальные ладовые образования в итоге сводятся, как правило, к той или иной модификации мажорного или минорного ладов. Мажорным ладом (или просто мажором) называется семиступенный лад, устойчивые звуки которого образуют большое (мажорное) трезвучие.
Само слово «мажор» (ит. maggiore) в буквальном переводе означает: «больший», «старший». Этот термин используется в слоговой нотации, в буквенной же нотации слово «мажор» заменяется словом «dur» (от лат. durus, буквально твердый).
Главным характерным признаком мажорного
лада является интервал большой терции
между I и III ступенями, которая, собственно, и
определяет специфику (то есть мажорность)
совместного звучания как самих устойчивых
звуков, так и лада в целом.
Гамма. Ступени лада
Звуки лада могут быть расположены по-разному, но наиболее простым, естественным и удобным является расположение ступеней лада в виде гаммы. Гаммой называется поступенное восходящее или нисходящее мелодическое движение в пределах октавы (от нижней тоники до верхней и наоборот).
Мажорный лад имеет три основные разновидности: натуральный мажор, гармонический мажор и мелодический мажop.
Мажорный лад строится следующим образом: тон-тон-полутон-тон-тон-тон-полутон. Все ступени лада имеют свои порядковые номера, соответствующие их высотному положению в ладе, и, кроме того, специальные наименования, отражающие их функциональное значение.
I ступень —
называется тоникой, поскольку
является примой (основным тоном)
тонического трезвучия и определяет
наименование самой тональности. II ступень называется нисходящим
вводным тоном. III ступень называется медиантой, так как находится посредине между двумя
другими устойчивыми звуками (I и V ступенями). IV ступень называется субдоминантой(буквально
— нижняя доминанта), так как отстоит от
тоники тоже на квинту, но только вниз.
Обозначается буквой S. V ступень называется доминантой, так как
является наиболее высоким (по
местоположению) из всех устойчивых
звуков (от лат. dominans,
что значит — возвышаться, господствовать).
Обозначается буквой D. VI ступень называется субмедиантой (то
есть нижней медиантой), так как занимает
серединное положение между субдоминантой
и тоникой.
II ступень называется нисходящим
вводным тоном. III ступень называется медиантой, так как находится посредине между двумя
другими устойчивыми звуками (I и V ступенями). IV ступень называется субдоминантой(буквально
— нижняя доминанта), так как отстоит от
тоники тоже на квинту, но только вниз.
Обозначается буквой S. V ступень называется доминантой, так как
является наиболее высоким (по
местоположению) из всех устойчивых
звуков (от лат. dominans,
что значит — возвышаться, господствовать).
Обозначается буквой D. VI ступень называется субмедиантой (то
есть нижней медиантой), так как занимает
серединное положение между субдоминантой
и тоникой.
Все семь диатонических ступеней лада
(в данном случае — мажорного) являются
основными, а I, IV и V ступени, то
есть тоника, субдоминанта и доминанта
называются еще и главными ступенями
лада. Такое название они носят потому,
что строящиеся на этих ступенях трезвучия
отражают специфику лада, являясь, как
и тоническое, мажорными трезвучиями.
Такое название они носят потому,
что строящиеся на этих ступенях трезвучия
отражают специфику лада, являясь, как
и тоническое, мажорными трезвучиями.
Минорный лад
Минорным ладом (или просто минором) называется семиступенный лад, устойчивые звуки которого образуют малое (минорное) трезвучие.
Само слово «минор» (ит. — minore) в буквальном переводе означает «меньший». Этот термин используется в слоговой нотации, в буквенной же нотации слово «минор» заменяется словом
moll (от лат. molle, буквально — «мягкий»).Главным характерным признаком минорного лада является интервал малой терции (м. 3) между I и III ступенями, которая, собственно, и определяет специфику, то есть минорность совместного звучания, как самих устойчивых звуков, так и лада в целом при любом порядке исполнения его ступеней.
В принципе свойства и названия ступеней
лада в миноре будут те же, что и в мажоре,
меняются лишь — в ряде случаев —
интервальные соотношения между ними
и, соответственно, характер их звучания.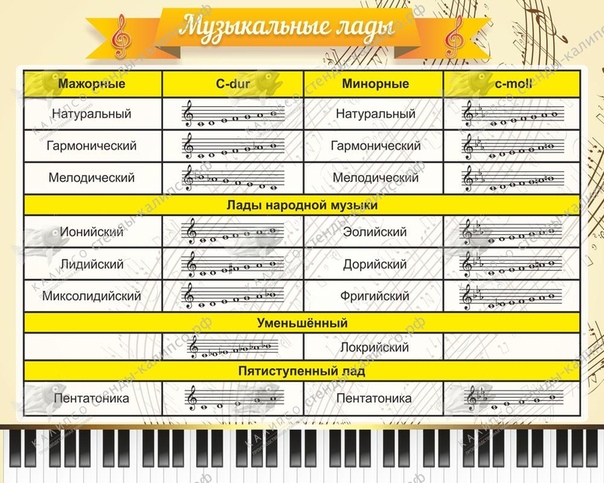
Минорный лад (как и мажорный) имеет три основных вида: натуральный, гармонический и мелодический
Минорный лад строится следующим образом: тон-полутон-тон-тон-полутон-тон-тон.
Страница не найдена |
Государственное бюджетное
профессиональное
образовательное учреждение
Республики Башкортостан
Учалинский колледж искусств и культуры
им.С.Низаметдинова
Учалинский колледж искусств и культуры им.С.Низаметдинова
Всероссийская акция «Окна Победы»
2023-05-05
В преддверии 78-ой годовщины Победы в Великой Отечественной войне Учалинский колледж искусств и культуры им. С. Низаметдинова принял участие в ежегодной Всероссийской акции «Окна Победы».
Окна Победы – это…
Читать далее…
«Светлой памяти павших в борьбе против фашизма»
5 мая Учалинский колледж искусств и культуры им. С. Низаметдинова принял участие в общереспубликанской общественной гражданско-патриотической церемонии «Светлой памяти павших в борьбе против фашизма» (Минута молчан…
С. Низаметдинова принял участие в общереспубликанской общественной гражданско-патриотической церемонии «Светлой памяти павших в борьбе против фашизма» (Минута молчан…
«Стена памяти»
Ко Дню Победы в Учалинском колледже искусств и культуры им. С. Низаметдинова оформлена «Стена памяти», на которой размещены портреты участников Великой Отечественной войны — дедов и прадедов студентов и работников …
Читать далее…
«Читать, чтобы помнить!»
К празднованию Дня Победы в библиотеке колледжа была подготовлена выставка: «Читать, чтобы помнить!». На ней были представлены следующие произведения башкирских и татарских писателей о Великой Отечественной войне: …
Читать далее…
Всероссийская акция «Георгиевская ленточка».
Волонтеры Учалинского колледжа искусств и культуры им. С. Низаметдинова приняли активное участие во Всероссийской акции «Георгиевская ленточка».
Читать далее…
Концерт «Весенний экспромт»
Стихи и музыка слились
И дальше…песня зазвучала
В ней просто отразилась Жизнь
Жизнь без конца и без начала.
3 мая 2023 года в ДШИ с. Учалы состоялся профориентационный концерт студентов отделений «Вокальное искус…
Читать далее…
Мастер-класс в технике канзаши
Георгиевская ленточка является символом героизма, воинской доблести и славы защитников России. «Георгиевская ленточка» – это эстафета от прошлых поколений к нынешним. Эстафета народной памяти, уважения к подвигам от…
Читать далее…
28 апреля в районном доме культуры с. Инзер состоялся семинар «Приоритетное направление в работе культурно — досуговых учреждений. Основные аспекты». В рамках семинара преподаватели и студенты Учалинского колледжа и…
Основные аспекты». В рамках семинара преподаватели и студенты Учалинского колледжа и…
Читать далее…
Конкурс «Победный май»
В 2023 году наша страна отмечает 78 годовщину Победы в Великой Отечественной войне. Этот праздник в России один из самых важных и трогательных. Победа в этой долгой и жестокой войне далась нашей стране ценой огром…
Читать далее…
XXII молодежные Дельфийские игры России
21 – 26 апреля в Саратове состоялись XXII молодежные Дельфийские игры России. Студенты отделения «Декоративно-прикладное искусство и народные промыслы» Мартиросян Ален, преподаватель Вершинина Юлия Александровна и Ха…
Поиск по сайту
Календарь
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Апр | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | ||||
Ссылки
Гамма мажор и минор
Эта статья предназначена для студентов моего фонда Understanding Music Theory, но доступна для всех, кто изучает композицию или постановку и хочет понять, как работает построение гаммы.
К концу этого вы должны быть в состоянии
- Вычислить мажорную гамму для любого заданного корня
- Вычислить минорную гамму, начинающуюся с того же корня
- Понять, как вырабатываются относительные мажор и минор
- Выяснить все диезы
- Вычислить все бемоли
В тональной музыке гаммы составляют основу мелодического письма. Шкала может иметь множество определений, но я хочу установить пару правил для шкал, которые мы будем обсуждать. Прежде чем сделать это, давайте разберемся, что такое полутона .
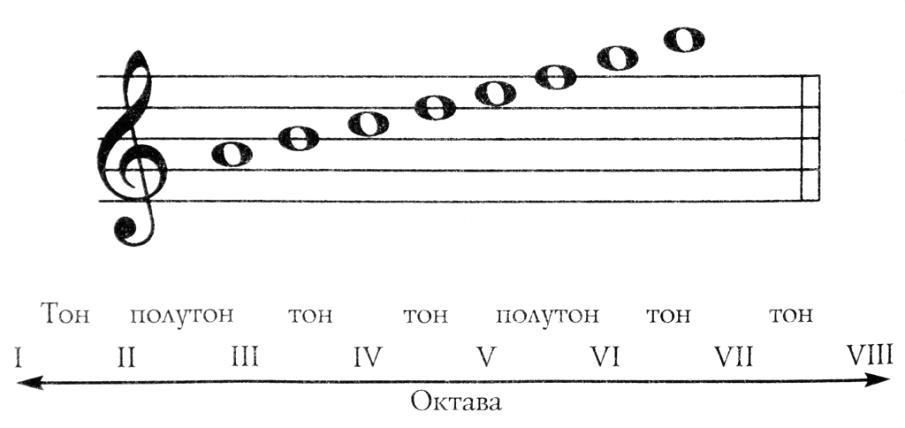
На фортепиано или гитаре полутон — это наименьшая музыкальная дискретная высота, на которую мы можем подняться или опуститься. На фортепиано они соответствуют ближайшей соседней клавише вверх или вниз, а на гитаре — на лады. Ниже мы видим клавиатуру, отображающую две октавы (двенадцать полутонов). Все гаммы сегодня существуют в пределах одной октавы, расстояния между C до C, D до D, F до F или чем-то еще.
Белые ноты на клавиатуре обозначают от A до G перед повторением. Это изображение обрезано с самой нижней нотой C, но принцип тот же. Черные ноты можно рассматривать как относительные к ноте выше или ниже. Например, черная нота между C и D может быть C# или Db в зависимости от контекста. Когда мы добавляем диез к ноте, мы указываем, что это черная клавиша над этой нотой, F# над F, G# над G и так далее. Когда мы добавляем бемоль, мы обозначаем, что это черная клавиша под ней. Bb ниже B, Ab ниже A и так далее.
Все гаммы, которые мы сегодня обсудим, имеют семь разных нот, прежде чем вернуться к основной ноте, или тонике . Есть гаммы с пятью нотами (пентатоника), шестью (блюз, цельный тон), восемью (октотоника/уменьшенная), но сегодня мы рассмотрим только мажор и минор.
Общее эмпирическое правило для диатонических гамм заключается в том, что вы не склонны смешивать диезы и бемоли в гамме. Кроме того, каждая диатоническая гамма содержит ноты от A до G, некоторые из которых либо диезы, либо бемоли. Например, у вас не было бы и D, и D#, потому что не было бы «E». Опять же, вне парадигмы мажоров и миноров эти правила могут быть нарушены.
Например, у вас не было бы и D, и D#, потому что не было бы «E». Опять же, вне парадигмы мажоров и миноров эти правила могут быть нарушены.
Помимо полутона, другой интервал, который нам понадобится, это тон . Тон — это просто два полутона. Все гаммы, которые мы сегодня рассмотрим, состоят из тонов (T) и полутонов (S). Повышение тона от C будет D, повышение тона от D будет E, а повышение тона от E будет F# (это потому, что между E и F нет черной клавиши). Гаммы, которые не являются мажорными или минорными (такие как гармоника , минор , блюз или пентатоника), могут содержать интервалы больше тона. Напомним эти правила для весов сегодня:
- Гаммы существуют между двумя одинаковыми нотами в пределах одной октавы (например, от C до C)
- Содержат семь разных нот
- Состоят из тонов и полутонов
- Содержат каждую букву от A до G один раз
- Содержат диезы или бемоли, но не оба
Построение мажорной гаммы
Начнем с мажорной гаммы. Все мажорные гаммы имеют одинаковую схему, начиная с корня мы двигаем тон, тон, полутон, тон, тон, тон, полутон (T T S T T T S). Вы можете думать об этом численно, если хотите (2 2 1 2 2 2 1) или с точки зрения полутонов от корня (0 2 4 5 7 911 12 – сюда входят основной тон и октава, 0 и 12 соответственно).
Все мажорные гаммы имеют одинаковую схему, начиная с корня мы двигаем тон, тон, полутон, тон, тон, тон, полутон (T T S T T T S). Вы можете думать об этом численно, если хотите (2 2 1 2 2 2 1) или с точки зрения полутонов от корня (0 2 4 5 7 911 12 – сюда входят основной тон и октава, 0 и 12 соответственно).
Начнем с до мажор. Он содержит все белые клавиши между C и C, поэтому C, D, E, F, G, A, B и C снова. Однако, если бы мы этого не знали, мы могли бы начать с C, подняться на тон вверх к D, на тон вверх к E, на полутон вверх к F и т. д. Полутона в мажорной гамме всегда попадают между ступенями гаммы 3 и 4 и 7 и 8.
Давайте попробуем еще раз, но начнем с D. Важно понимать, что теперь это не будут белые клавиши между D и D, так как шаблон теперь будет включать в себя несколько черных клавиш. Для следующих изображений я не включил поля тона и полутона на диаграммы.
Это дало нам диезы в третьей и седьмой ступенях, F# и C#. Если мы повторим тот же паттерн, начиная с ноты E, мы получим следующее:
Это дает четыре диеза: F#, G#, C# и D#. Однако не все основные клавиши будут иметь диезы. Если мы начнем наш паттерн со следующей белой ноты (F), то получим бемоль в четвертой ступени гаммы:
Однако не все основные клавиши будут иметь диезы. Если мы начнем наш паттерн со следующей белой ноты (F), то получим бемоль в четвертой ступени гаммы:
Я бы посоветовал вам также определить соль, ля и си мажор. Вы можете попробовать бемольные и диезные тональности (некоторые из них будут рассмотрены в этой статье), но есть некоторые аномалии с такими вещами, как двойные диезы, двойные бемоли и другие нестандартные энгармоники (Cb, E# и т. д.).
Построение минорной гаммы
Существует несколько различных типов минорной гаммы: гармонический, мелодический, дорийский и другие лады, но сегодня мы сосредоточимся на натуральном миноре. Натуральная минорная гамма имеет уплощенную третью, шестую и седьмую ступень по сравнению с мажорной гаммой, начинающейся с той же корневой ноты.
Давайте посмотрим на те же основные ноты, C, D, E и F. Хотя можно запомнить T, T, S-образный паттерн, я никогда этого не делал и всегда запоминаю гамму как модификацию крупный масштаб. Теперь у нас есть те же ноты, за исключением того, что Eb, Ab и Bb заменяют E, A и B. Обратите внимание, что полутона теперь появляются между двумя и тремя ступенями шкалы, а также между пятью и шестью.
Теперь у нас есть те же ноты, за исключением того, что Eb, Ab и Bb заменяют E, A и B. Обратите внимание, что полутона теперь появляются между двумя и тремя ступенями шкалы, а также между пятью и шестью.
Ре мажор содержит два диеза, F# и C#. Если мы опустим F# на один шаг, мы получим F natural, C# станет C, B natural станет Bb.
Однако не во всех минорных гаммах есть только бемоли. Ми-мажор содержит четыре диеза (F#, G#, C# и D#), но сглаживание G, C и D по-прежнему оставляет нам F#.
Наконец, фа минор, состоящий из четырех бемолей.
Повторите процесс для соль минор, ля минор и си минор. Опять же, диезные и бемольные тональности имеют смысл, но некоторые из них крайне редко используются для записи из-за их энгармонических нот.
Определение относительных миноров и мажоров
Все мажорные гаммы имеют минорную гамму, которая содержит те же ноты, которые называются относительными минорами. Минорные гаммы также имеют относительный мажор. Есть два способа получить относительный минор.
Относительный минор
Начнем с до мажор и его относительного минора, ля минор. Мы видим, что ля — это шестая ступень до мажор. Начав гамму с шестой ступени, мы можем получить относительный минор.
Шестая ступень ре мажор — си. Начиная с шестой ступени ре мажор, мы получаем си минор. Для тех из вас, кто читал о ладах, это тот же процесс, на самом деле мажорную и минорную гаммы можно рассматривать как лады, ионийский и эолийский соответственно.
Как узнать относительный минор, не выписывая всю гамму? Другой метод — начать с тоники и считать вниз по на три полутона. Всегда начинайте с ноля тоники, то есть E, D#, D, C#.
Наконец, фа мажор и ре минор.
Для каждой мажорной гаммы есть относительный минор, остальные можно вычислить, хотя я перечислил некоторые другие ниже.
Относительная мажорность
Давайте работать в обратном направлении и начать с минорной гаммы, а затем извлечь относительную 9Масштаб 0003 мажор . Мы можем использовать те же два метода, что и выше, инвертированные. Вместо того, чтобы считать три полутона в обратном порядке, мы можем считать три полутона в обратном порядке. Опять же важно начать с нуля в качестве вашего тонизирующего средства. До, Ре-бемоль, Ре, Ми-бемоль.
Мы можем использовать те же два метода, что и выше, инвертированные. Вместо того, чтобы считать три полутона в обратном порядке, мы можем считать три полутона в обратном порядке. Опять же важно начать с нуля в качестве вашего тонизирующего средства. До, Ре-бемоль, Ре, Ми-бемоль.
Нам не нужно играть ре минор, потому что мы рассмотрели его в разделе относительного минора, где фа является относительным мажором. Для ми минор относительным мажором является соль мажор.
Вместо подсчета мы можем начать шкалу с третьей ступени шкалы. Начиная с фа минор с третьей ступени гаммы (Ab), мы получаем Ab мажор.
Разобраться со всеми острыми ключами
Давайте разберемся со всеми острыми ключами. Меня научили очень простому методу отработки всех диезов. Начнем с до мажор. Запишите его с цифрами шкалы градусов над каждой буквой.
Затем начните шкалу с пятой ступени (G) и запишите это внизу. Это дало бы нам G A B C D E F G. Все, что нам нужно сделать, это повысить резкость до седьмой степени (F становится F #), и это дает вам гамму соль мажор. Соль мажор на одну чистую квинту выше до мажор. Повторение этого процесса даст нам ре мажор, который на чистую квинту выше соль мажор.
Соль мажор на одну чистую квинту выше до мажор. Повторение этого процесса даст нам ре мажор, который на чистую квинту выше соль мажор.
Ниже представлены ноты до, соль, ре, ля, ми и си мажор. Мы могли бы продолжить фа-диез мажор, но седьмая ступень была бы ми-бемоль (энгармонично фа на клавиатуре). В этом нет ничего плохого, но эта статья предназначена для начинающих, поэтому я не буду упоминать эти весы.
Разобраться со всеми плоскими ключами
Теперь давайте разберемся со всеми плоскими ключами. Это немного сложнее. Начинаем шкалу с четвертой ступени. Четвертая ступень до мажор — это фа. Запишите ноты от фа до фа (фа, соль, ля, си, до, ре, ми и фа), а затем сгладьте четвертую ступень.
Я дошел до Db (5 бемолей), так как Gb мажор содержит Cb (энгармонический си). Интересно, что Gb энгармоничен F#.
Масштаб 1461: «Мажор-минор»
Захватывающая Вселенная Музыкальной Теории
представляет
больше, чем вы когда-либо хотели знать о. ..
..
Идентичен Aeolian, но с приподнятой терцией; это называется эоловой доминантой, потому что ее члены 1-3-5-7 образуют доминирующий септаккорд.
Браслет Диаграмма
На браслете показаны тона этой шкалы, начиная сверху (12 часов) по часовой стрелке в восходящих полутонах. Значок «i» отмечает несовершенных тона, у которых нет тона на квинту выше. Пунктирные линии указывают оси симметрии.
Диаграмма Тоннеца
Диаграммы Тоннеца популярны в неоримановой теории. Ноты расположены в виде решетки, где чистые квинтовые интервалы расположены слева направо, большая терция — к северо-востоку, а основные квинтовые интервалы — к северо-западу. Другие направления обратны своим противоположностям. Эта диаграмма помогает визуализировать общие триады (треугольники) и отношения пятого круга (горизонтальные линии).
Общие названия
- Западный смешанный
- Большой-минорный
- Азербайджан
- Мугам Баяты Шираз
- 90 151 Карнатик
- Чарукеши
- Мела Чарукеши
- Рага Чарукеши
- Тарангини
- Вестерн
- Эолийская доминанта
- Западный модерн
- Мелодический мажор
- Шенкерийский
- Мишунг 6
- Западный альтерированный
- Миксолидийский плоский 6
- Миксолидийский плоский 13
- Альтерированный миксолидийский
- Экзотика
- Индуистский 901 54
- Hindustan
- Zeitler
- Stydian
- Dozenal
- JUSian
- Карнатик Мелакарта
- Чарукеси
- Карнатик Нумерованный Мелакарта
- 26-я Мелакарта рага
Анализ
Мощность Кардинальность — это число шагов в шкале. | 7 (гептатонический) |
Набор классов шагаТона этой шкалы, выраженные числами от 0 до 11 | {0,2,4,5,7,8,10} |
Форте НомерКод, присвоенный теоретиком Алленом Форте для этого набора классов основного тона и всех его транспозиционных (вращение) и инверсионных (отражение) преобразований. | 7-34 |
Вращательная симметрияНекоторые шкалы имеют вращательную симметрию, иногда называемую «ограниченной транспозицией». Если есть вращательные симметрии, то это интервалы периодичности. | нет |
Оси отраженияЕсли шкала имеет ось отражательной симметрии, то она может переходить в себя путем инверсии. Это также означает, что шкала имеет гребенчатые тона. Примечательно, что ось отражения может располагаться непосредственно на тоне или на полпути между двумя тонами. | [0] |
Палиндромность Палиндромная шкала имеет одинаковую структуру интервалов как по возрастанию, так и по убыванию. | да |
ХиральностьХиральная шкала не может быть преобразована в свою обратную путем вращения. Если шкала хиральна, то она имеет энантиоморф. | нет |
ГемитонияГемитон – это два тона, разделенные полутоновым интервалом. Гемитония описывает, сколько существует таких гемитонов. | 2 (дигемитонный) |
КогемитонияКогемитон — это экземпляр двух смежных полутонов. Когемитония описывает, сколько существует таких когемитонов. | 0 (анкогемитонический) |
НесовершенстваНесовершенство – это тон, над которым нет совершенной квинты в звукоряде. Это значение является количеством несовершенств в этой шкале. | 3 |
Режимы Моды — это вращательные преобразования этой шкалы. Это число включает саму шкалу, поэтому число обычно совпадает с его мощностью; если нет вращательной симметрии, то мод меньше. | 7 |
Основная формаОписывает, находится ли эта шкала в простой форме с использованием алгоритма Старра/Рана. | нет простой: 1371 |
ГенераторУказывает, можно ли построить шкалу с использованием генератора и начала координат. | нет |
Глубокая чешуяГлубокая шкала — это шкала, в которой вектор интервалов имеет 6 разных цифр, что является показателем максимальной иерархизации. | нет |
Интервальная структураОпределяет шкалу как последовательность интервалов между одним тоном и другим. | [2, 2, 1, 2, 1, 2, 2] |
Интервальный векторОписывает интервальное содержание шкалы, читаемое слева направо как количество вхождений каждого размера интервала от полутона до шести полутонов. | <2, 5, 4, 4, 4, 2> |
Вектор пропорциональной насыщенности Впервые описанный Майклом Бухлером (2001), это вектор, показывающий значимость интервалов относительно максимально и минимально возможного количества элементов шкалы. | <0, 0,75, 0,5, 0,333, 0,5, 0,5> |
Интервальный спектрТо же, что и интервальный вектор, но выраженный в синтаксисе, используемом Говардом Хэнсоном. | p 4 m 4 n 4 s 5 d 2 t 2 |
Распределительные спектры Описывает определенные размеры интервалов, которые существуют для каждого универсального размера интервала. Каждый общий | <1> = {1,2} <2> = {3,4} <3> = {4,5,6} <4> = {6,7,8} <5> = {8,9} <6> = {10,11} |
Вариант спектра Определено по спектрам распределения; это сумма всех ширин спектра, деленная на мощность шкалы. | 1,143 |
Максимально четныйМасштаб максимально ровный, если тона оптимально разнесены друг от друга. | нет |
Набор максимальной площадиМасштаб является набором максимальной площади, если многоугольник, описываемый вершинами, додециметрически расположенными вокруг окружности, дает максимальную внутреннюю площадь для масштабов одинаковой мощности. Все максимально четные множества имеют максимальную площадь, но не все множества максимальной площади максимально четные. | да |
Внутренняя зонаПлощадь многоугольника, описываемого вершинами, расположенными для каждого тона шкалы додециметрически вокруг единичной окружности, т. е. окружности радиусом 1, | 2,665 |
Периметр полигона Периметр многоугольника, описываемый вершинами, расположенными для каждого тона шкалы додециметрически вокруг единичной окружности. | 6.035 |
Недвижимость МайхиллШкала имеет свойство Myhill, если спектры распределения имеют ровно два конкретных интервала для каждого общего интервала. | № |
СбалансированныйШкала уравновешена, если распределение ее тонов удовлетворяет «задаче о центрифуге», т.е. они расположены так, что они уравновешиваются в своей центральной точке. | нет |
Ридж ТонсРидж-тона — это те, которые появляются во всех транспозициях гаммы на элементы этой гаммы. Ридж-тоны напрямую соответствуют осям рефлективной симметрии. | [0] |
ПриличияТакже известен как Rothenberg Propriety, названный в честь его изобретателя. Правильность описывает, однозначно ли каждый конкретный интервал отображается в общий интервал. Шкала бывает «Правильная», «Строго правильная» или «Неправильная». | Правильный |
Гетероморфный профиль Определенный Норманом Кэри (2002), гетероморфный профиль представляет собой упорядоченную тройку (c, a, d), где c — количество противоречий, a — количество неясностей, d — количество различий. | (0, 10, 72) |
Коэффициент когерентностиКоэффициент когерентности — это оценка от 0 до 1, указывающая долю нарушений когерентности (двусмысленности или противоречия) в шкале по отношению к максимально возможной мощности. Высокий коэффициент когерентности указывает на менее сложный масштаб, тогда как коэффициент 0 указывает на максимально сложный масштаб. | 0,929 |
Коэффициент одинаковостиКоэффициент сходства — это оценка от 0 до 1, указывающая пропорцию различий в гетероморфном профиле по отношению к максимально возможной кардинальности. Более высокое частное указывает на менее сложную шкалу, тогда как частное 0 указывает на шкалу с максимальной сложностью. | 0,429 |
Терцианские гармонические аккорды
Терцианские аккорды состоят из чередующихся членов гаммы, т. е. построены из «сложенных терций». Не все гаммы хорошо подходят для третичной гармонии.
е. построены из «сложенных терций». Не все гаммы хорошо подходят для третичной гармонии.
Генератор
У этих весов нет генератора.
Общие трезвучия
Это общие трезвучия (мажорное, минорное, увеличенное и уменьшенное), которые вы можете создать из членов этой гаммы.
* Высота тона показана с C в качестве корня
| Тип триады | Триада * | Классы высоты тона | Степень 906 04 | Эксцентриситет | Близость Центральность |
|---|---|---|---|---|---|
| Мажорные трезвучия | С | {0,4,7} | 2 | 3 | 1,71 |
| А♯ | {10,2, 5} | 2 | 3 | 1,71 | |
| Незначительное Триады | фм | {5,8,0} | 2 | 3 | 1,71 |
| гм | {7, 10,2} | 2 | 3 | 1,71 | |
| Расширенный Триады | C+ | {0,4,8} | 2 | 3 | 1. 71 71 |
| Уменьшенные триады | d° | {2,5,8} | 2 | 3 | 1,71 |
| e° | {4,7,10} | 2 | 3 | 1,71 |
Выше приведен график, показывающий возможности экономного залога между трезвучиями *. Каждая строка соединяет два трезвучия, которые имеют два общих тона, а третий тон изменяется на один общий шаг гаммы.
| Диаметр | 3 |
|---|---|
| Радиус | 3 |
| Самоцентрирующийся | да |
Режимы
Режимы представляют собой вращательное преобразование этой шкалы. Шкала 1461 может быть повернута в сделайте 6 других весов. 1-й режим сам по себе.
| 2-й режим: Масштаб 1389 | mp3″/> | Малый локр | |||
| 3-й вид: Масштаб 1371 9024 3 | Superlocrian | Это основной режим | |||
| 4-й режим: Гамма 2733 | Мелодический минор По возрастанию | ||||
| 5-й лад: Гамма 1707 | Дориан Флэт 2 | ||||
| 6-й режим: Масштаб 2901 | 9024 3 | Lydian Augmented | |||
| 7-й режим: Scale 1749 | Acoustic |
Prime
Основная форма этой шкалы — Scale 1371
| Scale 1371 | mp3″/> | Superlocrian |
Дополнение
Гептатоническая модальная семья [1461, 1389, 1371, 2733, 1707, 2901, 1749] (Forte: 7-34) является дополнением пентатонической модальной семьи [59 7, 681, 1173, 1317, 1353] (Forte: 5-34)
Инверсия
Инверсия шкалы — это отражение, использующее корень в качестве оси. Инверсия числа 1461 — это само число, потому что это палиндромная шкала!
| Шкала 1461 | Major-Minor |
Иерархизируемость
Основанная на работе Нильса Вероски, иерархичность — это мера повторяющихся паттернов с остаточными битами «нахождения места», рекурсивно применяемая к двоичному представлению шкалы. Для полного объяснения прочитайте статью Нильса «Иерархизируемость как предиктор масштабной кандидатуры». Переменная k — это максимальное количество остатков, разрешенных на каждом уровне рекурсии, чтобы они учитывались как приращение иерархичности. Высокий показатель иерархизируемости является хорошим индикатором кандидатуры шкалы, т. е. мерой полезности для создания приятной музыки. Существует сильная корреляция между гаммами с максимальной иерархичностью и гаммами, популярными в различных мировых музыкальных традициях.
Высокий показатель иерархизируемости является хорошим индикатором кандидатуры шкалы, т. е. мерой полезности для создания приятной музыки. Существует сильная корреляция между гаммами с максимальной иерархичностью и гаммами, популярными в различных мировых музыкальных традициях.
| k | Иерархизируемость | Шаблон разбивки | Диаграмма |
|---|---|---|---|
| 1 | 9 0238 1101011011010 | 1461k = 1h = 1 | |
| 2 | 2 | (10)( 10)1(10)1(10)(10) | 1461k = 2h = 2 |
| 3 | 3 | ([1]0[1])01([1]0[1])( [1]0[1])0 | 1461k = 3h = 3 |
| 4 | 2 | ([10][10])1101([10][10]) | 1461k = 4h = 2 |
| 5 | 2 | ([10][10])1101([10][ 10 ]) | 1461k = 5h = 2 |
. «I» означает инвертированный результат. Операция — это идентичный способ выразить одно и то же; синтаксис
 Примечание о множителях: умножение на 1 ничего не меняет, умножение на 11 дает тот же результат, что и инверсия. 5 — единственный невырожденный множитель, а множитель 7 дает значение, обратное 5.
Примечание о множителях: умножение на 1 ничего не меняет, умножение на 11 дает тот же результат, что и инверсия. 5 — единственный невырожденный множитель, а множитель 7 дает значение, обратное 5.| Аббревиатура | Операция | Результат | Аббревиатура | Операция | Результат | |||
|---|---|---|---|---|---|---|---|---|
| T 0 | 1461 | 9023 8 T 0 I | 1461 | |||||
| T 1 | 9 0238 2922 | T 1 I | 2922 | |||||
| T 2 9 0243 | 1749 | T 2 I | 1749 | 9 0238|||||
| T 3 | 3498 | T 3 I | 3498 | |||||
| Т 4 | 2901 | T 4 I | 90 238 2901 | |||||
| T 5 | 1707 | 902 43 | Т 5 Я | 1707 | ||||
| Т 6 | 3414 | T 6 I | 3414 | |||||
| Т 7 | 2733 | 9 0238 | T 7 I | 2733 | ||||
| T 8 902 43 | 1371 | T 8 I | 1371 | |||||
| 2742 | T 9 I | 2742 | ||||||
| T 909 73 10 | 1389 | T 10 I | 9023 8 1389 | |||||
| T 11 | 2778 | T 11 I 9024 3 | 2778 | |||||
| Аббревиатура | Операция | Результат | Аббревиатура | Операция | Результат | |||
| T 0 M | 3351 | T 0 МИ | 3351 | |||||
| Т 1 М | 2607 | Т 1 МИ | 2607 | |||||
| Т 2 М | 1119 | T 2 MI | 1119 | |||||
| T 3 9 0974 М | 2238 | T 3 MI | 2238 | 902 43 | ||||
| Т 4 М | 381 | T 4 MI | 381 | |||||
| T 5 M | 762 | T 5 MI | 9 0238762 | |||||
| T 6 M | 1524 | 902 38 Т 6 МИ | 1524 | |||||
| T 7 M | 3048 | T 7 9 0974 МИ | 3048 | |||||
| Т 8 М | 2001 | T 8 MI | 2001 | |||||
| T 9 M | 4002 | T 9 MI | 4002 | |||||
| T 10 M | 3909 | T 10 MI | 3909 | 902 46 | ||||
| Т 11 M | 3723 | T 11 MI | 902 43 | 3723 | ||||
Преобразования, которые сопоставляют этот набор с самим собой: T 0 , T 0 I
Ближайшие гаммы:
Это другие гаммы, похожие на эту, созданные путем добавления тона, удаления тона или перемещения на одну ноту вверх или вниз на полтона.
| Масштаб 1463 | Заптиллик | |||
| Масштаб 1457 902 43 | Рага Камаламанохари | |||
| Масштаб 1459 | Фригийский доминант | |||
| Масштаб 1465 9 0243 | Мела Рагавардхани | |||
| Масштаб 1469 | 90 243 | Эпириллит | ||
| Масштаб 1445 | Рага Наваманохари | |||
| Масштаб 1453 | Эолийский | |||
| Масштаб 1429 | mp3″/> | 9024 3 | Bythimic | |
| Масштаб 1493 | Малый лидийский | |||
| Весы 1525 | 1333902 38 | Липтимик | ||
| Масштаб 1397 | Большой локр | |||
| Масштаб 1205 9024 3 | Рага Шива Камбходжи | |||
| Весы 1717 | Mixolydian | |||
| Масштаб 1973 | Испанский октамод 6-е вращение | |||
| Масштаб 437 | mp3″/> | Ronimic | ||
| Шкала 949 | Мела Мараранджани | |||
| Гамма 2485 | Гармонический мажор | 9024 6|||
| Весы 3509 | Stogyllic |
Этот масштабный анализ был создан Яном Рингом, канадским композитором произведений для фортепиано и ботаником общей теории музыки. Обозначение масштаба, созданное VexFlow и Lilypond, визуализация графика с помощью Graphviz, звук с помощью TiMIDIty и FFMPEG. Все остальные схемы и визуализации принадлежат © Ian Ring. Некоторые названия весов, используемые на этой и других страницах, принадлежат Уильяму Цейтлеру, 2005 г. (http://allthescales.org), используются с разрешения.
Используемый здесь алгоритм написания тонов адаптирован из метода Узая Бора, Бариса Текина Тезеля и Альпера Вахаплара.



 Насыщенность 0 означает, что интервал присутствует минимально, насыщенность 1 означает, что он максимально возможный.
Насыщенность 0 означает, что интервал присутствует минимально, насыщенность 1 означает, что он максимально возможный.
 Когда c равно нулю, масштаб равен Правильный . Когда и также равны нулю, масштаб равен Strictly Proper .
Когда c равно нулю, масштаб равен Правильный . Когда и также равны нулю, масштаб равен Strictly Proper .