Глава 2 Эрнест Мах, как упоминалось ранее, был первым, кто ввел понятие «мысленный эксперимент». Он сделал это, оценивая работы Галилея. Мах охарактеризовал эксперименты Галилея как воображаемые и говорил об их большой значимости в формировании естествознания нового времени. Но это совсем не значит, что в более ранний период развития науки мысленный эксперимент не существовал. Вспомнить хотя бы эксперименты Аристотеля, доказывавшего невозможность в природе пустоты1. «Я и без опыта уверен, что результат будет такой, как я вам говорю, так как необходимо, чтобы он последовал». Галилео Галилей Предпосылки научно-технической революции зародились еще в эпоху Великих Географических Открытий, когда Америко Веспуччи3 доказал шарообразность Земли, подтверждая это своими заметками из Путешествия в «Индию». Серьезным ударом для Церкви стал выход в свет книги Николая Коперника 4 «О вращении небесных сфер», в которой он утверждал о гелиоцентрической системе мироздания. Геоцентрическая система устраивала католическую церковь, потому что могла служить философской основой для представления о человеке как венце божественного творения и потому помещенного в центр мироздания. Вселенная по Птолемею Вполне естественно, что в астрономии были принято, начиная с Тихо Браге1, пользоваться реальными экспериментами, а не мысленными, поэтому подробно разбирать прогресс астрономии в этой работе мы не будем. К середине XVI века наука начинает все больше опираться на объективные законы, а не на умозрительные концепции, как во времена античности и средневековья. Главной особенностью этого периода становится переход от латыни к живым языкам. Таким образом, именно Коперник своим трудом возвестил приход новой науки, свободной от идеологических догм, свободе исследований, идее о познаваемости мира. Прежде чем перейти к описанию мысленных экспериментов, следует сказать пару слов о представлении людей в средние века и античность о существенных понятиях в физике. Во-первых – движение. Движение разделялось на два типа: естественное и насильственное. До XV века считалось, что движение происходит в четырех случаях (категориях): субстанция, количество, качество и место. Движение включает в себя возникновение и уничтожение субстанции, изменение качества (сгущение, разрежение; в живых организмах – увеличение и уменьшение материи), изменение качества (увеличение или уменьшение интенсивности), изменение места. Все философы античности пытались ответить на вопрос: является ли движение отдельной категорией или происходит в одной из них? Во-вторых – сопротивление. Под сопротивлением понималось сопротивление среды. Это понятие было существенным, так как именно оно обусловливало факт совершения движения. Согласно общепринятой точке зрения любое насильственное движение на земле испытывало два вида сопротивления: внешнее сопротивление среды и внутреннее сопротивление. Последнее складывалось из тенденции к противоположно направленному движению и тенденции к покою. В-третьих – скорость. Как это ни странно, но определение понятия скорости представляло трудности для многих поколений исследователей вплоть до Галилея. Причина этих трудностей заключалась в том, что движение рассматривалось в широком смысле слова, в том, что любое отношение имело в глазах философов смысл только тогда, когда в него входили величины одного рода (т.е. путь сравнивался с путем, время — со временем и т. п.), поэтому отношение пути ко времени — а именно так мы определяем скорость сегодня — было им абсолютно чуждо. Ученые того времени считали, что скорость – это величина с градусной мерой. До XV века существовало много разных правил и теорий о соотношении равномерного и неравномерного движений, равномерного и равноускоренного движений. В-четвертых – импетус. Популярна была теория импетуса, созданная для облегчения объяснения ускорения. Эта теория гласила, что для поддержания движения небесных тел необходим нематериальный двигатель, выполняющий функцию первого импульса, который сохраняется в движении небесных тел, возрастает в свободном падении, но прерывается другими земными движениями (удар, бросок), так что движение прекращается. В-пятых – ускорение. Тяжелые тела имеют склонность стремиться вертикально вниз, но если освободиться от этой «склонности» и рассмотреть движение свободно падающих тел, тогда, согласно Жану Буридану3, тело будет ускоряться (в виду того, что движение лишено сопротивления). Буридан считал, что в начальный момент движения импетус не оказывает влияние на скорость. В дальнейшем изменение импетуса, а следовательно, и скорости идет скачками, а не совершается непрерывно. Графиком скорости такого ускоренного движения была ступенчатая функция. Для людей Средневековья была характерна существенная разница между физическим и математическим понятиями. Лучшим примером этого является проблема «первого мгновения» движения: «можно ли считать первое мгновение движения идентичным последнему мгновению покоя? Если да, то такое заключение содержит противоречие, ибо в таком случае тело будет одновременно находиться и в состоянии покоя, и в состоянии движения. Если мгновение мыслится математически, то задача не имеет смысла, однако физическое мгновение всегда имеет некоторую длительность, как бы мала она ни была. Галилео Галилей является одним из величайших ученых на протяжении всей истории человечества. Его труды поистине гениальны. Изобретения, эксперименты, и идея посмотреть через телескоп на небо – все это принадлежит ему. Конечно же, Галилей является создателем самых интересных мысленных экспериментов, о чем пойдет наша речь в дальнейшем. М ысленные эксперименты для Галилея всегда были очень важны. «Нетрудно установить ту же истину путем простого рассуждения», — говорил он, стараясь все же все свои теоретические выводы подкреплять реальными наблюдениями и реальными опытами. Кое-что Галилею не удавалось демонстрировать для подтверждения своей правоты, в основном потому, что еще не были изобретены многие точные приборы. Галилею для осуществления опытов необходимо было иметь инструменты, с помощью которых можно было бы измерить доли миллиметра. Поэтому Галилей во многих случаях прибегал к мысленному эксперименту. Чувствуется большая разница между мысленным экспериментом Галилея и Аристотеля. 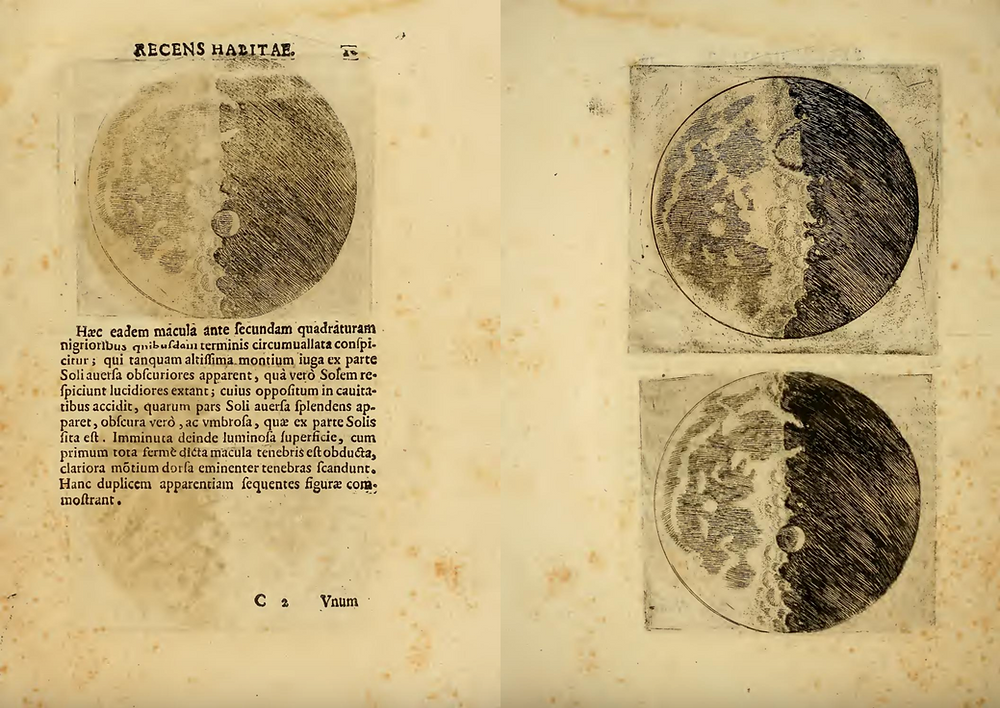 У этих людей он играл разные роли. Аристотель прибегал к нему для того, чтобы отвергнуть какую-либо возможность. Галилей же прибегал к воображаемому эксперименту для подтверждения своих допущений. Такое изменение значения мысленного эксперимента в физике связано у Галилея с перестройкой метода доказательства, со стремлением построить физику на базе математики У этих людей он играл разные роли. Аристотель прибегал к нему для того, чтобы отвергнуть какую-либо возможность. Галилей же прибегал к воображаемому эксперименту для подтверждения своих допущений. Такое изменение значения мысленного эксперимента в физике связано у Галилея с перестройкой метода доказательства, со стремлением построить физику на базе математикиНесмотря на все новые подходы Галилея к изучению физики, он не мог не прибегать к принципам, базировавшимся на характерном для античной и средневековой науки различении математического и физического подходов. Галилео Галилей стремился доказать, что между физическим движением и его математической моделью нет никакого различия. Галилей считал, что выводы, сделанные с помощью мысленного эксперимента, искажаются до такой степени, что «ни поперечное движение не будет равномерным, ни ускоренное движение при падении не будет соответствовать выведенной пропорции, ни траектория брошенного тела не будет параболой и т. Теперь непосредственно перейдем к мысленным экспериментам Галилео Галилея. В 1608 году был изобретен телескоп. Галилей обрадовался этому событию и начал думать, как именно он может быть устроен. В следующем году он создал свой телескоп с увеличением в 30 раз. Как это ни странно никто в то время не собирался смотреть через него на небо. И Галилей был первым, кто это сделал. С этого момента Галилея очаровала астрономия и вращение планет. Поэтому известны многие опыты Галилея, связанные с движением небесных тел. Галилей считал, что если в мире господствует совершенный порядок, то тела, составляющие Вселенную, должны по своей природе обладать круговыми движениями. Допустим, что они движутся прямолинейно, удаляясь от своей исходной точки и от всех тех мест, которые они последовательно прошли. Если такое движение им естественно присуще, то они с самого начала не находилось на своем естественном месте, и, значит, части Вселенной не расположены в совершенном порядке. Галилей занимался суточным вращением Земли. Птолемей отрицал возможность вращения Земли вокруг своей оси. Галилей считал возражения Птолемея самыми сильными. Действительно, говорит Галилей, «ведь если бы Земля обладала бы суточным обращением, то башня, с вершины которой дали упасть камню, перенесется обращением Земли, пока падает камень, на много сотен локтей к востоку, и на таком расстоянии от подножья башни камень должен был бы удариться о Землю». Аналогичное явление можно наблюдать, если бросать свинцовый шар с мачты движущегося корабля. «Когда корабль движется, то место падения шара должно будет находиться на таком удалении от первого, на какое корабль ушел вперед за время падения свинца». Так же Птолемей утверждал, что во-первых, птицы и облака не связанны с Землей, и поэтому не испытывают никакого влияния вследствие ее движения, хотя они, очевидно, должны были бы отставать от нее. Первый довод Птолемея опровергается Галилеем на том основании, что с физической точки зрения одушевленные предметы не отличаются от неодушевленных. Соответственно движение птиц не должно отличаться от движения камня – птица не может не касаться Земли, а как только это происходит, ей тотчас же передается суточное движение Земли2. В следующем за этим рассуждении описывается мысленный эксперимент, объясняющий также и движение облаков. «Уединитесь с кем-либо из друзей в просторное помещение под палубой какого-нибудь корабля, запаситесь мухами, бабочками и другими подобными мелкими летающими насекомыми; пусть будет у вас там также большой сосуд с водой и плавающими в нем маленькими рыбками; подвесьте, далее, наверху ведерко, из которого вода будет падать капля за каплей в другой сосуд с узким горлышком, поставленный внизу. Пока корабль стоит неподвижно, наблюдайте прилежно, как мелкие летающие животные с одной и той же скоростью движутся во все стороны помещения; рыбы, как вы увидите, будут плавать безразлично во всех направлениях; все падающие капли попадут в поставленный сосуд, и вам, бросая какой-либо предмет, не придется бросать его с большей силой в одну сторону, чем в другую, если расстояния будут одни и те же; и если вы будете прыгать сразу двумя ногами, то сделаете прыжок на одинаковое расстояние в любом направлении. Второй довод Птолемея вызывает у Галилея большие трудности. Здесь он предлагает объяснение, не являющееся ни полностью правильным, ни исчерпывающим. Галилей говорит, что тела на Земле удерживаются тяготением. Галилей называет это свойство тел тяжестью. По мнению Галилея, то, что тела не срываются с поверхности Земли, обусловлено фактом, что любое тело отлетает по касательной к окружности вращения: «Таким образом, если бы камень, отброшенный вращающимся с огромной скоростью колесом, имел такую же естественную склонность двигаться к центру этого колеса, с какой он движется к центру Земли, то ему нетрудно было бы вернуться к колесу или, скорее, вовсе не удаляться от него, ибо раз в начале отрыва удаление столь ничтожно из-за бесконечной остроты угла касания, малейшего уклонения по направлению к центру колеса было бы достаточно, чтобы удержать его на окружности». Итак, в процессе защиты коперниканства Галилей оказался вовлеченным в построение новой науки о движении. Ведь чтобы опровергнуть возражения против движения Земли, ему было необходимо создать, по крайней мере, интуитивно, новую механику, с помощью которой можно было бы проанализировать следствия, вытекающие из наличия такого движения. Галилей не создал цельной системы; может быть, он к этому и не стремился1. Галилео Галилей пытался познать суть свободного падения. Он всегда был уверен, что скорость падения тел на Землю не зависит от их массы. Галилею требовалось узнать, что же произойдет, если вообще убрать сопротивление среды. Галилей понимает, что полностью сопротивление среды убрать невозможно, поэтому «я придумал, — пишет Галилей, — заставлять тело двигаться по наклонной плоскости, поставленной под небольшим углом к горизонту; при таком движении совершенно так же, как и при отвесном падении, должна обнаружиться разница, происходящая от веса. Прибор Галилея (реконструкция) Идя далее, я захотел освободиться от того сопротивления, которое обусловливается соприкосновением движущихся тел с наклонной плоскостью. Для этого я взял, в конце концов, два шара — один из свинца, другой — из пробки, причем первый был в сто раз тяжелее второго, и прикрепил и подвесил их на двух одинаковых тонких нитях длиной в четыре или пять локтей; когда я затем выводил тот и другой шарик из отвесного положения и отпускал их одновременно, то они начинали двигаться по дуге круга одного и того же радиуса, переходили через отвес, возвращались тем же путем обратно и т. д.; после того, как шарики производили сто качаний туда и обратно, становилось ясным, что тяжелый движется столь согласованно с легким, что не только после ста, но после тысячи качаний не обнаруживается ни малейшей разницы во времени, и движение обоих происходит совершенно одинаково». Результат, полученный Галилеем, имел далеко идущие последствия. Понятно, что Галилей не мог достичь такого идеального результата с реальным эксперимента, но он допустил, что поскольку среду полностью устранить невозможно, тяжелый шарик движется согласованно с легким. Следующий эксперимент, подтверждающий тезис Галилея представлен в его работе «Диалоги1». Он гласит: представим пушечное ядро и мушкетную пулю. Если считать, что тяжёлые тела падают быстрее лёгких, то ядро должно падать с большей скоростью, а мушкетная пуля с меньшей. Если мы соединим их вместе перемычкой, то более тяжелое должно ускорять менее тяжелое, и менее тяжелое должно замедлять более тяжелое. Мы получим, что у нового тела скорость — среднее арифметическое двух изначальных. Таким образом, новое тело, по массе большее его составных частей будет падать с меньшей скоростью, чем его составная часть. Отсюда обнаруживается противоречие, из которого можно сделать вывод, что все тела падают с одинаковой скоростью. В Что касается пустоты Сальвиати в «Диалогах» говорит, что есть нечто связующее мельчайшие частицы вещества, наподобие клея. Сальвиати продолжает, что у природы есть «боязнь пустоты», которую легко проверить на опыте: «Если мы возьмем цилиндр воды и обнаружим в нем сопротивление его частиц разделению, то оно не может происходить от продолжение дискуссии Второго дня Галилей критикует представление Аристотеля, что среда является причиной движения брошенного тела. Он говорит, что среда может только препятствовать движению, а не вызывать его. Обложка книги Галилео Галилея «Диалоги о двух главнейших системах мира – Птолемеевой и Коперниковой» иной причины, кроме стремления не допустить образования пустоты». В «Беседах2» обсуждается вопрос о пустотах, держащих связанными частицы металла. В пример приводятся рассуждения Сагредо о муравьях, способных вытащить корабль, нагруженный зерном на берег. «Если сопротивление не бесконечно велико, то оно может быть преодолено множеством весьма малых сил, так что большое количество муравьев могло бы вытащить на землю судно, нагруженное зерном. Приведенный пример — специальная формулировка аксиомы непрерывности Архимеда1, которая устанавливает, какого рода величины могут находиться между собой в отношении и что это значит — находиться в отношении. Эту формулировку хочет опровергнуть Галилей своим доказательством о том, что конечная величина может представлять собой сумму бесконечного числа. Галилей обращается к «колесу Аристотеля». В средневековой механике эта задача выглядит так: почему при совместном движении двух кругов больший проходит такое же расстояние, как и меньший, в то время как при независимом движении этих двух кругов пройденные ими расстояния относились бы как их радиусы. Для решения этой задачи Галилей вводит допущение. Он рассматривает сначала движение равносторонних и равноугольных многоугольников. При движении большего многоугольника должен двигаться также и вписанный в него меньший. При этом меньший многоугольник пройдет пространство почти равное пройденному большим. При движение меньшего многоугольника, как показывает Галилей, происходят «скачки», число которых будет равно числу сторон обоих многоугольников. При возрастании числа сторон многоугольников размеры скачки пропорционально уменьшаются. Заметим, что число сторон многоугольника и «скачки» являются конечным числом. Но при рассмотрении случая, когда многоугольник превращается в круг, то дело существенно меняется. В многоугольнике с 1000 сторон путь измеряется обводом большего многоугольника. Путь меньшего равен 1000 его сторон с прибавлением 1000 «скачков». Затем Галилей делает еще одно допущение, что круг представляет собой многоугольник с бесконечно большим числом сторон. Такое допущение не принималось математиками ни в античности, ни в средние века, оно дозволялось только в логистике для упрощения расчетов, которые всегда принимались как приблизительные. Для ученых Средневековья было чрезвычайно характерно понимание различия между тем, что мы наблюдаем в действительности, и тем, как мы говорим о том, что наблюдаем. В связи с этим существовало два подхода к понятию скорости. С одной стороны, скорость можно было рассматривать как расстояние, проходимое в определенное время. С другой стороны, скорость могла рассматриваться в контексте теории качеств как интенсивность движения. С помощью противоречивого понятия «неделимого», или «бесконечно малого», Галилей вводит важное понятие в механике — «мгновенная скорость». При обсуждении вопроса о бесконечной медленности Симпличио возражает против введения этого понятия, указывая на возникающий здесь парадокс Зенона. Если степени медленности бесчисленны, то они никогда не могут быть все исчерпаны. Таким образом, подымающийся камень никогда не пришел бы в состояние покоя, но пребывал бы в бесконечном, постоянно замедляющемся движении, чего, однако, в действительности никогда не бывает. Но Сальвиати на это дает ответ, формулируя понятие мгновенной скорости: «Это случилось бы, синьор Симпличио, если бы тело двигалось с каждой степенью скорости некоторое определенное время; но оно только проходит через эти степени, не задерживаясь больше, чем на мгновение; а так как в каждом, даже в самом малом промежутке времени содержится бесконечное множество мгновений, то их число является достаточным для соответствия бесконечному множеству уменьшающихся степеней скорости». Галилей указывает на то, что высота существенно влияет на изменение действия силы падающего тела на Землю. В пример приводит падающий груз на сваю с разных высот, то есть с высоты четырех локтей груз вгонит сваю на четыре дюйма. При падении груза с высоты двух локтей он вгонит ее в землю меньше и, конечно, еще меньше при падении с высоты одного локтя, одной пяди. Галилей делает вывод, что если величина силы зависит прямо пропорционально от скорости, то движение и скорость очень малы при незаметном совершении удара. В первой половине XVII века самыми главными и крупнейшими учеными были Рене Декарт и Христиан Гюйгенс. Декарт всегда пытался постигнуть суть мироздания. Он критиковал Галилея, пытавшегося решать только частные проблемы, утверждал, что Галилей строил дом без фундамента. Главной идеей с точки зрения Декарта было понять мир в целом, описать его одним законом (законами). Проблема мысленного эксперимента в это время и его статуса неоднократно становилась темой дискуссий. Гюйгенс постоянно критиковал Декарта за созданные им мысленные эксперименты (два из которых мы приведем далее). Гюйгенс их отождествлял с теорией и не считал их достаточным для построения физики как науки о природе. На реальном, а не мысленном только эксперименте настаивал Ньютон в своей «Оптике». В качестве еще одного интересного мысленного эксперимента можно представить эксперимент о доказательстве в круговом движении прямолинейного. Декарт утверждает, что путь тела представляется криволинейной траекторией, «тем не менее, каждая из частиц тела по отдельности стремится продолжать свое движение по прямой линии». Далее Декарт поясняет: «Заставьте, например, колесо вращаться вокруг своей оси: все его части будут двигаться тогда по кругу, так как, будучи соединены друг с другом, они не могут перемещаться иначе; однако склонны они передвигаться не по кругу, а по прямой. Это ясно видно, когда одна из частиц его оторвется от других. Как только она очутится на свободе, движение ее перестает быть круговым и продолжается по прямой линии»1.
Каталог: files -> referat жүктеу/скачать 2.02 Mb. Достарыңызбен бөлісу: |
Мысленный эксперимент
При помощи блестящего мысленного эксперимента Галилей показал, что все тела падают с одинаковой скоростью.
Stanford Encyclopedia of Philosophy
James Robert Brown
Мысленный эксперимент — это средство исследования природы при помощи воображения. Достаточно вспомнить несколько известных мысленных экспериментов, чтобы увидеть их огромное влияние и важность для науки: демон Максвелла, лифт Эйнштейна, Гамма микроскоп Гейзенберга, кот Шредингера.
Ещё в 17 веке мысленный эксперимент применяли такие блестящие
умы, как Галилей, Декарт, Ньютон и Лейбниц. Создание квантовой
механики и теории относительности в наше время было бы немыслимо
без использования мысленных экспериментов. Галилей и Эйнштейн,
вероятно, были самыми известными «мысленными экспериментаторами»,
но они не были первыми. Мысленный эксперимент применялся и в средние
века и в древние времена.
Создание квантовой
механики и теории относительности в наше время было бы немыслимо
без использования мысленных экспериментов. Галилей и Эйнштейн,
вероятно, были самыми известными «мысленными экспериментаторами»,
но они не были первыми. Мысленный эксперимент применялся и в средние
века и в древние времена.
Один из наиболее красивых ранних мысленных экспериментов (Лукреций, De Rerum Natura ) пытался доказать, что пространство бесконечно. Если имеется граница Вселенной, то мы можем выстрелить в неё из лука. Если стрела пролетит насквозь, то это вообще не граница. Если стрела отскочит назад, как от стены, то у этой космической стены должна быть другая сторона, и, значит, что-то должно быть за предполагаемым краем пространства. В обоих случаях граница вселенной не достигается. Следовательно, пространство бесконечно.
Этот пример хорошо иллюстрирует многие общие особенности мысленного
эксперимента. Мы воображаем некоторую ситуацию; выполняем действия;
видим, что получается. Этот пример также показывает возможность
неверного вывода. В данном случае мы уже знаем, что пространство
может быть безграничным и конечным.
Этот пример также показывает возможность
неверного вывода. В данном случае мы уже знаем, что пространство
может быть безграничным и конечным.
Часто реальный аналог мысленного эксперимента невозможен по физическим, техническим или простым практическим причинам. Но эти условия не мешают проведению мысленного эксперимента. Главное в том, что мы, кажется, способны проникнуть в тайны природы при помощи одной только мысли. Вот это и представляет интерес для философии. Можно ли узнать что-то (явно) новое о природе без новых эмпирических данных?
Эрнст Мах (кажется, именно он начал использовать термин Gedankenexperiment ) приводит интересное эмпирическое рассуждение в своей классической «Науке Механики». Он говорит, что мы обладаем большим запасом полученных из опыта «инстинктивных знаний». Они совсем не обязательно должны быть ясно сформулированы, но они практически применяются в подходящей ситуации.
Рис.1a
Рис.1b
Один из его любимых примеров придумал Simon Stevin.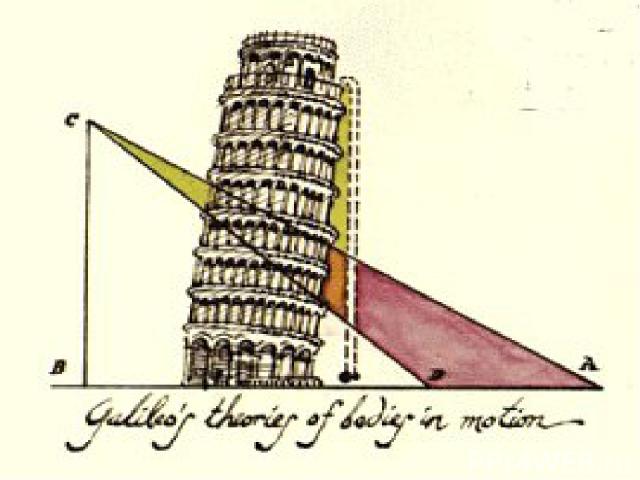
Рис.1a Если перевесить цепь через ребро несимметричной двойной наклонной плоскости без трения, как на рис.1a, то в какую сторону она соскользнёт? Мысленно добавьте несколько звеньев цепи как на рис.1b.
Рис.1b Теперь всё очевидно. С самого начала цепь находилась в статическом равновесии. Иначе, мы получили бы вечный двигатель, но, в соответствии с нашим основанным на опыте «инстинктивным знанием», говорит Мах, это невозможно.
По мнению Томаса Куна, хорошо убеждающий мысленный эксперимент может привести к кризису или, по крайней мере, к выявлению несогласованности в царствующей теории, и, таким образом, внести вклад в смену парадигмы. Итак, мысленный эксперимент способен научить нас чему-то новому о мире, даже если мы не используем новых данных, помогая нам более рационально перестроить наши представления о мире.
В последнее время интерес к мысленному эксперименту заметно
увеличился. Brown и Norton представляют предельные позиции от
платоновского рационализма до классического эмпиризма, соответственно. Norton утверждает, что любой мысленный эксперимент — это реальный
(возможно неявный) аргумент; он исходит из опыта и использует
логические или индуктивные правила вывода результата. Живописные
подробности любого мысленного эксперимента, делающие его похожим
на настоящий эксперимент, могут быть психологически полезными,
но они, строго говоря, излишни. Итак, говорит Norton, мы никогда
не выходим за рамки эмпирических предпосылок, против чего не стал
бы возражать ни один эмпирик.
Norton утверждает, что любой мысленный эксперимент — это реальный
(возможно неявный) аргумент; он исходит из опыта и использует
логические или индуктивные правила вывода результата. Живописные
подробности любого мысленного эксперимента, делающие его похожим
на настоящий эксперимент, могут быть психологически полезными,
но они, строго говоря, излишни. Итак, говорит Norton, мы никогда
не выходим за рамки эмпирических предпосылок, против чего не стал
бы возражать ни один эмпирик.
Brown придерживается другой позиции. В некоторых особых случаях мы всё же отбрасываем старые данные, чтобы получить новые априорные знания о природе. Галилей показал, что все тела падают с одинаковой скоростью при помощи блестящего мысленного эксперимента, что привело к крушению царствующих в то время Аристотелевских взглядов. Они заключались в том, что тяжелые тела падают быстрее, чем лёгкие (Т > Л).
Рис.2
Но рассмотрите Рис.2 , на котором тяжелое пушечное
ядро Т и легкая мушкетная пуля Л соединены вместе
и образуют новый более тяжёлый предмет
Т+Л . Он должен падать быстрее, чем пушечное ядро. Но
он же должен падать медленнее, чем пушечное ядро, так как лёгкая
мушкетная пуля должна тормозить движение тяжёлого ядра. Мы получили
противоречие:
Т + Л > Т и
Т > Т + Л . Это и конец теории Аристотеля,
и правильный очевидный вывод: все они падают с одинаковой скоростью
Т = Л = Т + Л .
Он должен падать быстрее, чем пушечное ядро. Но
он же должен падать медленнее, чем пушечное ядро, так как лёгкая
мушкетная пуля должна тормозить движение тяжёлого ядра. Мы получили
противоречие:
Т + Л > Т и
Т > Т + Л . Это и конец теории Аристотеля,
и правильный очевидный вывод: все они падают с одинаковой скоростью
Т = Л = Т + Л .
Говорят, что это априорные (выдуманные, а значит ненадёжные) знания о природе, так как не использовались никакие новые данные, не было сделано логического вывода из старых данных, и они не являются чисто логической истиной. Такое понимание мысленного эксперимента развивается далее путём привязывания априорной эпистемологии к прежним представлениям о законах природы как связях между существующими абстрактными сущностями. Этот вполне платоновский взгляд не слишком далёк от платоновского подхода к математике, который отстаивается и Гёделем.
Два представленных здесь взгляда могли бы расположиться на
противоположных концах спектра позиций, с которых рассматривается
мысленный эксперимент. Есть удачные новые альтернативные взгляды,
например, Sorensen в духе Маха считает, что мысленный эксперимент
— это «предельный случай» обычного эксперимента; он
способен достичь своей цели без фактического выполнения. В своей
книге Sorensen обсуждает мысленный эксперимент в философии разума,
в этике и других разделах философии и науки. Есть и другие перспективные
идеи. Gooding особо подчеркивает похожесть технологий в мысленном
и реальном экспериментах. Miscevic и Nersessian связывают мысленный
эксперимент с «ментальными моделями». Horowitz и Massey
(1991) тоже имеют несколько перспективных работ на эту тему.
Есть удачные новые альтернативные взгляды,
например, Sorensen в духе Маха считает, что мысленный эксперимент
— это «предельный случай» обычного эксперимента; он
способен достичь своей цели без фактического выполнения. В своей
книге Sorensen обсуждает мысленный эксперимент в философии разума,
в этике и других разделах философии и науки. Есть и другие перспективные
идеи. Gooding особо подчеркивает похожесть технологий в мысленном
и реальном экспериментах. Miscevic и Nersessian связывают мысленный
эксперимент с «ментальными моделями». Horowitz и Massey
(1991) тоже имеют несколько перспективных работ на эту тему.
Copyright © 1996 by
James Robert Brown
University of Toronto
Перевод Е.Корниенко
метод, который помогал Галилею принимать решения
Мысленные эксперименты являются классическим инструментом, которым пользуются многие великие мыслители. Он дает возможность изучения невозможных ситуаций. С его помощью можно предсказать, каковы будут их последствия и результаты. Используя мысленные эксперименты, можно решить сложные вопросы или предотвратить возможные проблемы.
Используя мысленные эксперименты, можно решить сложные вопросы или предотвратить возможные проблемы.
Что такое мысленный эксперимент
Его основная цель заключается в использовании размышлений, логического мышления и изменении парадигмы. Проводя такие изыскания, человек выходит из зоны комфорта, так как ему приходится искать ответы на очень сложные вопросы, ответы, которые не возникают сами собой. С их помощью можно обнаружить то, чего мы еще не знаем, осознать пределы своих возможностей.
Как это делали древние философы
Впервые к этому методу прибегли древние греки и римляне. Самым первым мысленным экспериментом считают рассказ философа Зенона об Ахиллесе и черепахе, который был составлен около 430 года до нашей эры. Цель Зенона при этом заключалась в выведении первых принципов, для чего нужно было устранить неверные концепции.
Он хотел доказать, что движение является иллюзией. Допустим, Ахиллес бежит в 10 раз быстрее черепахи и решил состязаться в беге с ней, при этом находится на тысячу шагов позади нее. Пока Ахиллес преодолеет это расстояние, черепаха проползет еще на сто шагов вперед. Когда Ахиллес продвинется на сто шагов, черепаха — еще на 10 шагов и так далее. Соответственно, по мнению Зенона, тот никогда не сможет выиграть у черепахи, так как расстояние между ними будет постоянно увеличиваться.
Пока Ахиллес преодолеет это расстояние, черепаха проползет еще на сто шагов вперед. Когда Ахиллес продвинется на сто шагов, черепаха — еще на 10 шагов и так далее. Соответственно, по мнению Зенона, тот никогда не сможет выиграть у черепахи, так как расстояние между ними будет постоянно увеличиваться.
Они всегда тщательно планируют будущее: 3 знака зодиака (Козерог среди них)
Конкуренция растёт. Болгария открыла границы для вакцинированных россиян
Страстная пятница — 30 апреля. Короткая и мощная молитва о спасении души своей
Декарт тоже мысленно экспериментировал: он поставил под сомнение существование практически всего, в результате не осталось ничего, что могло бы вызвать у него сомнения. Его размышления получили название «мозг в бочке».
Попытки Галилея
В 17-м веке итальянский физик, астроном и философ Галилео Галилей при помощи мысленных экспериментов пытался подтвердить свои теории. Один из таких примеров – два шара (тяжелый и легкий), падающие с Пизанской башни. До этого философы считали, что тяжелый шар окажется на земле раньше. Однако Галилей считал это утверждение неверным, так как ускорение не зависит от массы.
Один из таких примеров – два шара (тяжелый и легкий), падающие с Пизанской башни. До этого философы считали, что тяжелый шар окажется на земле раньше. Однако Галилей считал это утверждение неверным, так как ускорение не зависит от массы.
В ранней версии биографии ученого, которая датируется 1654 годом, сказано, что он действительно сбросил два предмета, которые упали одновременно и тем самым доказали его теорию. Однако в действительности нет достоверных сведений, проводил ли Галилей такой опыт, поэтому данный эксперимент считают мысленным.
Размышления Эйнштейна
Мысленные эксперименты Альберта Эйнштейна были связаны со многими его важными открытиями. Самыми известными считаются его размышления о луче света. «Что случилось бы, если бы вы могли поймать луч света, когда он двигался?» — спросил он себя. Отвечая на собственные вопросы, он перешел к проблеме времени и, как следствие, к теории относительности.
Роспотребнадзор не видит причин для ограничения передвижения по России
Надежный пароль: вопросы об интернете, которые стоит обсудить с детьми
Они нередко уводят чужих мужей: 3 женских знака зодиака
Естественный процесс
Известный философ и физик, живший в XIX веке, Эрнст Мах считал любознательность неотъемлемым качеством человека. Дети начинают изучать мир с рождения. Постепенно это процесс становится все глубже, и в определенный момент человек переходит к мысленным экспериментам. По его мнению, они не что иное, как планы и образы, которые мы создаем перед тем, как что-то сделать. Например, это может быть репетиция разговора перед его началом, планирование работы. По мнению ученого, это относится к нашей естественной способности решения сложных задач и творческого введения новшеств. Также он считает, что в ходе мысленных экспериментов можно получить настолько достоверные результаты, что физические уже становятся бессмысленными.
Дети начинают изучать мир с рождения. Постепенно это процесс становится все глубже, и в определенный момент человек переходит к мысленным экспериментам. По его мнению, они не что иное, как планы и образы, которые мы создаем перед тем, как что-то сделать. Например, это может быть репетиция разговора перед его началом, планирование работы. По мнению ученого, это относится к нашей естественной способности решения сложных задач и творческого введения новшеств. Также он считает, что в ходе мысленных экспериментов можно получить настолько достоверные результаты, что физические уже становятся бессмысленными.
Философский подход
Мысленные эксперименты использовались философами еще в древности. В первую очередь это объясняется субъективностью философских гипотез и невозможностью их эмпирического доказательства.
При помощи мысленных экспериментов философы представляют свои теории в понятной форме. Они помогают проиллюстрировать концепцию при помощи воображаемых сценариев. При этом они заняты не поисками правильного ответа, а созданием новых идей.
В качестве примера можно рассмотреть «Аллегорию пещеры», написанную Платоном. Группа людей постоянно проживает в темной пещере. Они не видят ничего другого, только тени, и не знают, как выглядит внешний мир. И не хотят покидать свое убежище. В какой-то момент они выходят из пещеры и видят мир, в котором есть много всего.
В двойном размере. Россиян предупредили о штрафе за выброс мусора
Что посадить, чтобы комары облетали ваш участок десятой дорогой: 7 растений
Индия: инженер создал прицеп «скорой помощи» к мотоциклу с кислородным баллоном
При помощи этого эксперимента Платон попытался показать, насколько неполным может быть наше представление о реальности. Только покинув пещеру, можно увидеть, насколько интересным может быть окружающий мир. Соответственно, стремление к познанию мира, по мнению Платона, — это первый шаг, ведущий к выходу из пещеры.
Научный взгляд
Хотя эмпирические данные обычно необходимы для науки, мысленные эксперименты могут использоваться для разработки гипотезы или подготовки к экспериментам. Некоторые гипотезы невозможно проверить (например, теорию струн), по крайней мере, с учетом наших нынешних возможностей. Ученые-теоретики могут обратиться к мысленным экспериментам, чтобы получить предварительный ответ, часто основанный на бритве Оккама.
Мысленные эксперименты можно рассматривать как ключевую часть науки. По своей значимости они не уступают физическим экспериментам. Кроме того, для их проведения все предположения необходимо предварительно подтвердить эмпирически. Контекст должен быть правдоподобным и давать полезные ответы на сложные вопросы.
Этические проблемы
Есть известный эксперимент, получивший название «проблема вагонетки». По условиям человек видит мчащийся по рельсам неуправляемый трамвай. Если он будет и дальше так двигаться, то погибнут пять человек – его пассажиры. Если зритель нажмет переключатель, то переведет трамвай на другие рельсы и погибнет только один человек. При этом у человека, принимающего участие в эксперименте, спрашивают, сможет ли он нажать на переключатель.
Если зритель нажмет переключатель, то переведет трамвай на другие рельсы и погибнет только один человек. При этом у человека, принимающего участие в эксперименте, спрашивают, сможет ли он нажать на переключатель.
С этой проблемой связано много дополнительных вопросов:
- Есть ли необходимость во вмешательстве?
- Что ценнее – одна жизнь или пять?
- Что бы изменилось, если бы надо было толкать человека на рельсы, а не использовать переключатель? Что бы изменилось, если бы этот человек был злодеем или близким наблюдателю?
Как показали исследования, люди скорее согласятся нажать на переключатель, чем вытолкнуть человека под трамвай. С другой стороны, злодеев готовы подтолкнуть гораздо охотнее. Несмотря на то что проблема вагонетки теоретическая, ее последствия значимы для реального мира.
Нашли нарушение? Пожаловаться на содержание
Механическая картина мира (стр. 2 из 4)
Сделав зрительную трубу с увеличением в 32 раза и направив ее на небо, Галилей обнаружил неровности Луны; Млечный Путь оказался состоящим из множества звезд, число которых росло с ростом увеличения трубы; у Юпитера были найдены четыре спутника. Все это не соответствовало учению Аристотеля о противоположности земного и небесного, а подтверждало систему Коперника.
Все это не соответствовало учению Аристотеля о противоположности земного и небесного, а подтверждало систему Коперника.
В 1612г Галилей издает “Рассуждения о телах, пребывающих в воде, и тех, которые в ней движутся”, эта работа была направлена против механики Аристотеля. Вслед за ней появляется письмо Галилея о солнечных пятнах. Это было тоже опровержение Аристотеля, но оно не могло пройти незамеченным церковью, церковь обвиняет Галилея в том, что он доказывает движение Земли и неподвижность Солнца; они пытаются добиться запрещения учения Коперника. В 1615г Галилей едет в Рим, чтобы защитить себя и предотвратить запрещение учения Коперника. Но 5 марта 1616г учение Коперника “как ложное и целиком противное Священному Писанию” было запрещено, Галилей получил от святой инквизиции негласный приказ молчать. В 1623г он снова едет в Рим, чтобы добиться отмены ограничений в своей научной деятельности, но официальной отмены ограничений ему добиться не удалось. Несмотря на ограничения Галилей готовит к опубликованию свою основную работу “Диалог о двух главнейших системах мира: Птолемеевой и Коперниковой”. В феврале 1632г книга вышла в свет, туда вошли все произведения Галилея , все то, что было создано им с 1590г по1625г. Цель ученого – представить не только асторономические, но и механические доводы в пользу истинности учения Коперника.
В феврале 1632г книга вышла в свет, туда вошли все произведения Галилея , все то, что было создано им с 1590г по1625г. Цель ученого – представить не только асторономические, но и механические доводы в пользу истинности учения Коперника.
Вращение Земли, по словам Птолемея, должно было бы рассеять находящиеся на ней тела; тела при падении должны были бы двигаться не вертикально, а наклонно, так как они будут отставать от движущейся Земли; птицы и облака должны были бы уноситься на запад. Опровергая эти аргументы Галилей приходит к открытию закона инерции. Открытием этого закона было ликвидировано многовековое заблуждение, выдвинутое Аристотелем, о необходимости постоянной силы для поддержания равномерного движения. Современная формулировка этого закона такова: Всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет его из этого состояния. Галилей определил механический принцип относительности: никакими механическими опытами, проведенными внутри замкнутой инерциальной системы, невозможно установить: покоится система или движется равномерно и прямолинейно.
Разговоры собеседников о различных астрономических открытиях (неровностях Луны, пятнах на Солнце, фазах Венеры, спутниках Юпитера) утверждает мысль о справедливости теории Коперника.
Успех “Диалога” был потрясающим, единомышленники восторженно приветствуют Галилея с открытием новой эры в изучении природы. Противники же в свою очередь пустили слух, что под маской защитника Аристотеля и Птолемея выведен сам Папа. Началась травля Галилея, в сентябре Галилею было передано повеление папской инквизиции явиться в Рим, но из –за болезни Галилея дают небольшую отсрочку. В феврале 1633г Галилей прибывает в Рим, на допросе он отрицал, что разделял Коперниково учение после того, как инквизиция объявила его еретическим. Галилей твердо стоял на том, что в дискуссионном порядке о гелиоцентрической системе Мира и писать, и говорить не запрещалось, а сама книга была выпущена с разрешения цензуры. После допроса Галилей был арестован и заключен в кандалы инквизиции. 22 июня 1633г в церкви Святой Марии при большом стечении народа состоялся последний акт судилища над Галилеем. По приговору его книга была запрещена, а сам он подлежит тюремному заключению, длительность, которого оставлена на усмотрение Святой службы. Унизительный акт судилища и отречения сильно подорвали здоровье больного Галилея, но несмотря не на все Галилей мысленно видел свое будущее произведение “Беседы и математические доказательства”, в котором идеи “Диалога” получали свое дальнейшее развитие. «Беседы» были закончены в 1637г. В книге обобщено все то, что сделал Галилей в области механики. В 1642г Галилея не стало. Ушел из жизни один из замечательных мыслителей, великий астроном, механик, физик, математик.
По приговору его книга была запрещена, а сам он подлежит тюремному заключению, длительность, которого оставлена на усмотрение Святой службы. Унизительный акт судилища и отречения сильно подорвали здоровье больного Галилея, но несмотря не на все Галилей мысленно видел свое будущее произведение “Беседы и математические доказательства”, в котором идеи “Диалога” получали свое дальнейшее развитие. «Беседы» были закончены в 1637г. В книге обобщено все то, что сделал Галилей в области механики. В 1642г Галилея не стало. Ушел из жизни один из замечательных мыслителей, великий астроном, механик, физик, математик.
Галилей считается одним из основоположников опытного естествознания и новой науки. Именно он сформулировал требования к научному эксперименту, состоящие в устранении побочных обстоятельств, в умении видеть главное. Путем эксперимента Галилей опроверг учение Аристотеля о пропорциональности скорости падения весу тела, показал, что воздух имеет вес и определил его плотность. Он был первым, кто направил зрительную трубу на небо в научных целях, тем самым, расширив сферу познания. Мысленные эксперименты Галилея построены на идеализации движения шаров, тележек и других материальных объектов по горизонтали и наклонной плоскости. Мысленный эксперимент получил в дальнейшем широкое распространение в физике и стал важнейшим методом познания, им пользовался Максвелл при создании теории электромагнитного поля. Мысленные эксперименты позволили многим ученым (Максвелл, Больцман, Карно и др.) установить закономерности в хаотическом тепловом движении и термодинамики. Таким образом, и принцип относительности Галилея, получивший свое дальнейшее развитие в теории относительности, и мысленный эксперимент, введенный в науку им же и ставший необходимым методом современной физики, свидетельствуют о чрезвычайно высоком методологическом уровне, на котором в своих исследованиях стоял великий итальянский ученый.
Мысленные эксперименты Галилея построены на идеализации движения шаров, тележек и других материальных объектов по горизонтали и наклонной плоскости. Мысленный эксперимент получил в дальнейшем широкое распространение в физике и стал важнейшим методом познания, им пользовался Максвелл при создании теории электромагнитного поля. Мысленные эксперименты позволили многим ученым (Максвелл, Больцман, Карно и др.) установить закономерности в хаотическом тепловом движении и термодинамики. Таким образом, и принцип относительности Галилея, получивший свое дальнейшее развитие в теории относительности, и мысленный эксперимент, введенный в науку им же и ставший необходимым методом современной физики, свидетельствуют о чрезвычайно высоком методологическом уровне, на котором в своих исследованиях стоял великий итальянский ученый.
4.Иоган Кеплер и открытие законов небесной механики.
Иоган Кеплер родился 27 декабря 1571г, отец его, Генрих Кеплер, разорившийся дворянин, служил простым солдатом, мать – дочь деревенского трактирщика, не умела читать и писать. При рождении мальчик чудом остался жив. Когда ему исполнилось четыре года родители бросили его, в 13 лет он умирал в третий раз, но жизнь не покидала его. Окончив в 1579г монастырскую школу, Кеплер перевелся в духовную трехгодичную школу, после которой остался в Тюбингенской семинарии, а после – в Тюбингенском университете. В университете он познакомился с учением Коперника, став его горячим сторонником. Работая учителем математики и философии в училище г. Граца, он вместе с преподаванием стал заниматься научной работой по астрономии, а также составлять календари и гороскопы. Кеплер был вынужден заниматься астрологией, чтобы не умереть с голоду, прокормить свою семью и вести исследования по астрономии.
При рождении мальчик чудом остался жив. Когда ему исполнилось четыре года родители бросили его, в 13 лет он умирал в третий раз, но жизнь не покидала его. Окончив в 1579г монастырскую школу, Кеплер перевелся в духовную трехгодичную школу, после которой остался в Тюбингенской семинарии, а после – в Тюбингенском университете. В университете он познакомился с учением Коперника, став его горячим сторонником. Работая учителем математики и философии в училище г. Граца, он вместе с преподаванием стал заниматься научной работой по астрономии, а также составлять календари и гороскопы. Кеплер был вынужден заниматься астрологией, чтобы не умереть с голоду, прокормить свою семью и вести исследования по астрономии.
За свою жизнь Кеплер написал много работ. Его первая книга, изданная в 1597г., вышла под интересным названием «Космографическая тайна». Кеплер поставил задачу найти числовые отношения между орбитами планет. Пробуя различные комбинации чисел, он пришел к геометрической схеме, по которой можно было отыскивать расстояния планет от Солнца.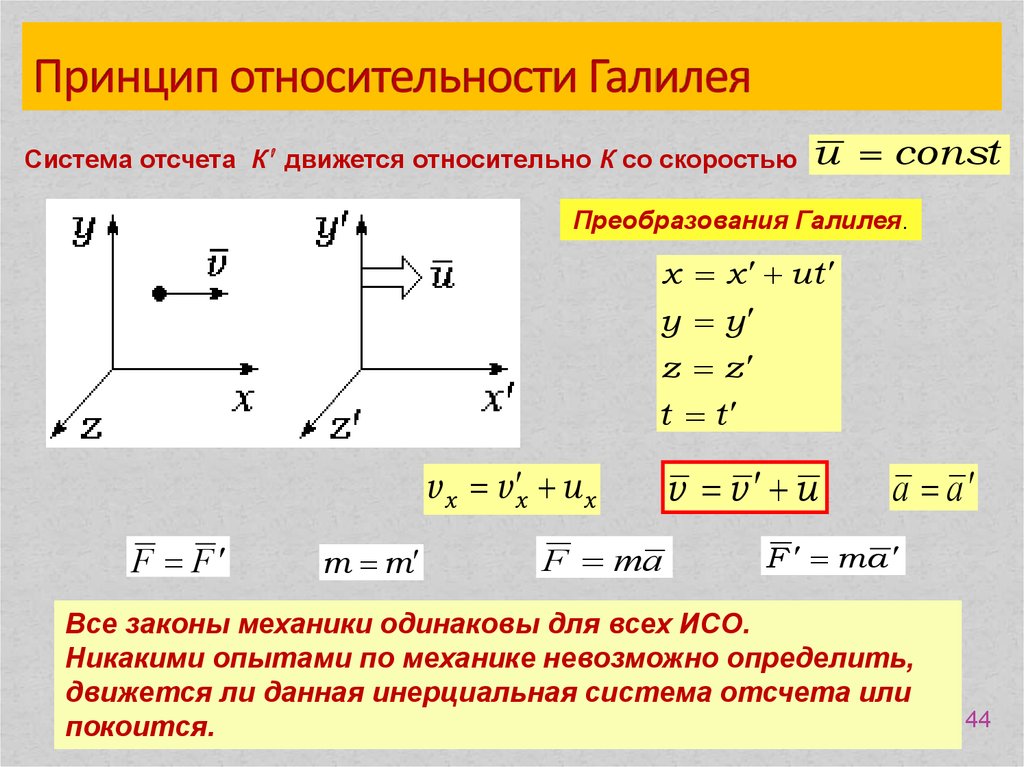 Свою работу Кеплер отослал датскому астроному Тихо Браге и Г.Галилею. Из-за преследования со стороны католической церкви жизнь на родине стала невыносимой, и Кеплер едет в Прагу. Там он был назначен имперским математиком и должен был работать под руководством Тихо Браге – имперского астронома. В 1601г умирает Тихо Браге и в руках Кеплера оказался журнал тридцатилетних наблюдений «короля астрономии».
Свою работу Кеплер отослал датскому астроному Тихо Браге и Г.Галилею. Из-за преследования со стороны католической церкви жизнь на родине стала невыносимой, и Кеплер едет в Прагу. Там он был назначен имперским математиком и должен был работать под руководством Тихо Браге – имперского астронома. В 1601г умирает Тихо Браге и в руках Кеплера оказался журнал тридцатилетних наблюдений «короля астрономии».
В 1609г появилась на свет книга Кеплера «Новая астрономия или Небесная физика с комментариями на движение планеты Марс по наблюдениям Тихо Браге». В течение восьми лет трудился он над расчетами, семьдесят раз пришлось повторять каждое вычисление, но, не смотря не на все он сформулировал первые два закона о движении планет:
1. Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
2. Радиус-вектор, проведенный от Солнца к планете, за равные промежутки времени описывает равные площади.
Нужда и несчастье продолжает преследовать его, в 1611г умерли его жена и сын, и он остался с двумя детьми на руках. Материальная нужда заставила его покинуть Прагу, и он уехал в Линц, где он занял место преподавателя математики. В 1615г он получает известие об обвинении его матери в колдовстве. Всю свою силу и находчивость он тратит, чтобы спасти мать от костра, в 1621 он добивается ее освобождения. Даже после таких ударов судьбы сила духа не покидает его, и он выпускает новую работу «Гармония мира», содержащую третий закон небесной механики: квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.
Материальная нужда заставила его покинуть Прагу, и он уехал в Линц, где он занял место преподавателя математики. В 1615г он получает известие об обвинении его матери в колдовстве. Всю свою силу и находчивость он тратит, чтобы спасти мать от костра, в 1621 он добивается ее освобождения. Даже после таких ударов судьбы сила духа не покидает его, и он выпускает новую работу «Гармония мира», содержащую третий закон небесной механики: квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.
Другие наиболее известные работы Кеплера это: «Рудольфовы таблицы» — астрономические планетные таблицы, над которыми Кеплер работал 20 лет. Названы были в честь императора Рудольфа 2. Эти таблицы служили морякам и астрономам, составителям календарей и астрологам и только в 19 веке были заменены более точными. Своими работами по математике Кеплер внес большой вклад в теорию конических
Сечений, в разработку теории логарифмов, способствовал разработке интегрального исчисления и изобретению первой вычислительной машины. В1618г начинается Тридцатилетняя война. Казна по прежнему пуста Кеплер живет случайными заработками, совершая многочисленные поездки в Регенсбург с хлопотами о выдаче жалованья. Во время одной из таких поездок Кеплер заболел и умер. В 1774г Петербургская Академия наук купила большую часть архива Кеплера.
В1618г начинается Тридцатилетняя война. Казна по прежнему пуста Кеплер живет случайными заработками, совершая многочисленные поездки в Регенсбург с хлопотами о выдаче жалованья. Во время одной из таких поездок Кеплер заболел и умер. В 1774г Петербургская Академия наук купила большую часть архива Кеплера.
Мысленный эксперимент: метод, который помогал Галилею принимать решения
fb.ru
Мысленные эксперименты являются классическим инструментом, которым пользуются многие великие мыслители. Он дает возможность изучения невозможных ситуаций. С его помощью можно предсказать, каковы будут их последствия и результаты. Используя мысленные эксперименты, можно решить сложные вопросы или предотвратить возможные проблемы.
Его основная цель заключается в использовании размышлений, логического мышления и изменении парадигмы. Проводя такие изыскания, человек выходит из зоны комфорта, так как ему приходится искать ответы на очень сложные вопросы, ответы, которые не возникают сами собой. С их помощью можно обнаружить то, чего мы еще не знаем, осознать пределы своих возможностей.
Впервые к этому методу прибегли древние греки и римляне. Самым первым мысленным экспериментом считают рассказ философа Зенона об Ахиллесе и черепахе, который был составлен около 430 года до нашей эры. Цель Зенона при этом заключалась в выведении первых принципов, для чего нужно было устранить неверные концепции.
Он хотел доказать, что движение является иллюзией. Допустим, Ахиллес бежит в 10 раз быстрее черепахи и решил состязаться в беге с ней, при этом находится на тысячу шагов позади нее. Пока Ахиллес преодолеет это расстояние, черепаха проползет еще на сто шагов вперед. Когда Ахиллес продвинется на сто шагов, черепаха — еще на 10 шагов и так далее. Соответственно, по мнению Зенона, тот никогда не сможет выиграть у черепахи, так как расстояние между ними будет постоянно увеличиваться.
Проводя такие изыскания, человек выходит из зоны комфорта, так как ему приходится искать ответы на очень сложные вопросы, ответы, которые не возникают сами собой. С их помощью можно обнаружить то, чего мы еще не знаем, осознать пределы своих возможностей.
Впервые к этому методу прибегли древние греки и римляне. Самым первым мысленным экспериментом считают рассказ философа Зенона об Ахиллесе и черепахе, который был составлен около 430 года до нашей эры. Цель Зенона при этом заключалась в выведении первых принципов, для чего нужно было устранить неверные концепции.
Он хотел доказать, что движение является иллюзией. Допустим, Ахиллес бежит в 10 раз быстрее черепахи и решил состязаться в беге с ней, при этом находится на тысячу шагов позади нее. Пока Ахиллес преодолеет это расстояние, черепаха проползет еще на сто шагов вперед. Когда Ахиллес продвинется на сто шагов, черепаха — еще на 10 шагов и так далее. Соответственно, по мнению Зенона, тот никогда не сможет выиграть у черепахи, так как расстояние между ними будет постоянно увеличиваться. Декарт тоже мысленно экспериментировал: он поставил под сомнение существование практически всего, в результате не осталось ничего, что могло бы вызвать у него сомнения. Его размышления получили название «мозг в бочке».
В 17-м веке итальянский физик, астроном и философ Галилео Галилей при помощи мысленных экспериментов пытался подтвердить свои теории. Один из таких примеров – два шара (тяжелый и легкий), падающие с Пизанской башни. До этого философы считали, что тяжелый шар окажется на земле раньше. Однако Галилей считал это утверждение неверным, так как ускорение не зависит от массы.
В ранней версии биографии ученого, которая датируется 1654 годом, сказано, что он действительно сбросил два предмета, которые упали одновременно и тем самым доказали его теорию. Однако в действительности нет достоверных сведений, проводил ли Галилей такой опыт, поэтому данный эксперимент считают мысленным.
Мысленные эксперименты Альберта Эйнштейна были связаны со многими его важными открытиями. Самыми известными считаются его размышления о луче света.
Декарт тоже мысленно экспериментировал: он поставил под сомнение существование практически всего, в результате не осталось ничего, что могло бы вызвать у него сомнения. Его размышления получили название «мозг в бочке».
В 17-м веке итальянский физик, астроном и философ Галилео Галилей при помощи мысленных экспериментов пытался подтвердить свои теории. Один из таких примеров – два шара (тяжелый и легкий), падающие с Пизанской башни. До этого философы считали, что тяжелый шар окажется на земле раньше. Однако Галилей считал это утверждение неверным, так как ускорение не зависит от массы.
В ранней версии биографии ученого, которая датируется 1654 годом, сказано, что он действительно сбросил два предмета, которые упали одновременно и тем самым доказали его теорию. Однако в действительности нет достоверных сведений, проводил ли Галилей такой опыт, поэтому данный эксперимент считают мысленным.
Мысленные эксперименты Альберта Эйнштейна были связаны со многими его важными открытиями. Самыми известными считаются его размышления о луче света. «Что случилось бы, если бы вы могли поймать луч света, когда он двигался?» — спросил он себя. Отвечая на собственные вопросы, он перешел к проблеме времени и, как следствие, к теории относительности.
Известный философ и физик, живший в XIX веке, Эрнст Мах считал любознательность неотъемлемым качеством человека. Дети начинают изучать мир с рождения. Постепенно это процесс становится все глубже, и в определенный момент человек переходит к мысленным экспериментам. По его мнению, они не что иное, как планы и образы, которые мы создаем перед тем, как что-то сделать. Например, это может быть репетиция разговора перед его началом, планирование работы. По мнению ученого, это относится к нашей естественной способности решения сложных задач и творческого введения новшеств. Также он считает, что в ходе мысленных экспериментов можно получить настолько достоверные результаты, что физические уже становятся бессмысленными.
Мысленные эксперименты использовались философами еще в древности. В первую очередь это объясняется субъективностью философских гипотез и невозможностью их эмпирического доказательства.
«Что случилось бы, если бы вы могли поймать луч света, когда он двигался?» — спросил он себя. Отвечая на собственные вопросы, он перешел к проблеме времени и, как следствие, к теории относительности.
Известный философ и физик, живший в XIX веке, Эрнст Мах считал любознательность неотъемлемым качеством человека. Дети начинают изучать мир с рождения. Постепенно это процесс становится все глубже, и в определенный момент человек переходит к мысленным экспериментам. По его мнению, они не что иное, как планы и образы, которые мы создаем перед тем, как что-то сделать. Например, это может быть репетиция разговора перед его началом, планирование работы. По мнению ученого, это относится к нашей естественной способности решения сложных задач и творческого введения новшеств. Также он считает, что в ходе мысленных экспериментов можно получить настолько достоверные результаты, что физические уже становятся бессмысленными.
Мысленные эксперименты использовались философами еще в древности. В первую очередь это объясняется субъективностью философских гипотез и невозможностью их эмпирического доказательства. При помощи мысленных экспериментов философы представляют свои теории в понятной форме. Они помогают проиллюстрировать концепцию при помощи воображаемых сценариев. При этом они заняты не поисками правильного ответа, а созданием новых идей.
В качестве примера можно рассмотреть «Аллегорию пещеры», написанную Платоном. Группа людей постоянно проживает в темной пещере. Они не видят ничего другого, только тени, и не знают, как выглядит внешний мир. И не хотят покидать свое убежище. В какой-то момент они выходят из пещеры и видят мир, в котором есть много всего.
При помощи этого эксперимента Платон попытался показать, насколько неполным может быть наше представление о реальности. Только покинув пещеру, можно увидеть, насколько интересным может быть окружающий мир. Соответственно, стремление к познанию мира, по мнению Платона, — это первый шаг, ведущий к выходу из пещеры.
Хотя эмпирические данные обычно необходимы для науки, мысленные эксперименты могут использоваться для разработки гипотезы или подготовки к экспериментам.
При помощи мысленных экспериментов философы представляют свои теории в понятной форме. Они помогают проиллюстрировать концепцию при помощи воображаемых сценариев. При этом они заняты не поисками правильного ответа, а созданием новых идей.
В качестве примера можно рассмотреть «Аллегорию пещеры», написанную Платоном. Группа людей постоянно проживает в темной пещере. Они не видят ничего другого, только тени, и не знают, как выглядит внешний мир. И не хотят покидать свое убежище. В какой-то момент они выходят из пещеры и видят мир, в котором есть много всего.
При помощи этого эксперимента Платон попытался показать, насколько неполным может быть наше представление о реальности. Только покинув пещеру, можно увидеть, насколько интересным может быть окружающий мир. Соответственно, стремление к познанию мира, по мнению Платона, — это первый шаг, ведущий к выходу из пещеры.
Хотя эмпирические данные обычно необходимы для науки, мысленные эксперименты могут использоваться для разработки гипотезы или подготовки к экспериментам. Некоторые гипотезы невозможно проверить (например, теорию струн), по крайней мере, с учетом наших нынешних возможностей. Ученые-теоретики могут обратиться к мысленным экспериментам, чтобы получить предварительный ответ, часто основанный на бритве Оккама.
Мысленные эксперименты можно рассматривать как ключевую часть науки. По своей значимости они не уступают физическим экспериментам. Кроме того, для их проведения все предположения необходимо предварительно подтвердить эмпирически. Контекст должен быть правдоподобным и давать полезные ответы на сложные вопросы.
Есть известный эксперимент, получивший название «проблема вагонетки». По условиям человек видит мчащийся по рельсам неуправляемый трамвай. Если он будет и дальше так двигаться, то погибнут пять человек – его пассажиры. Если зритель нажмет переключатель, то переведет трамвай на другие рельсы и погибнет только один человек. При этом у человека, принимающего участие в эксперименте, спрашивают, сможет ли он нажать на переключатель.
С этой проблемой связано много дополнительных вопросов:
Как показали исследования, люди скорее согласятся нажать на переключатель, чем вытолкнуть человека под трамвай.
Некоторые гипотезы невозможно проверить (например, теорию струн), по крайней мере, с учетом наших нынешних возможностей. Ученые-теоретики могут обратиться к мысленным экспериментам, чтобы получить предварительный ответ, часто основанный на бритве Оккама.
Мысленные эксперименты можно рассматривать как ключевую часть науки. По своей значимости они не уступают физическим экспериментам. Кроме того, для их проведения все предположения необходимо предварительно подтвердить эмпирически. Контекст должен быть правдоподобным и давать полезные ответы на сложные вопросы.
Есть известный эксперимент, получивший название «проблема вагонетки». По условиям человек видит мчащийся по рельсам неуправляемый трамвай. Если он будет и дальше так двигаться, то погибнут пять человек – его пассажиры. Если зритель нажмет переключатель, то переведет трамвай на другие рельсы и погибнет только один человек. При этом у человека, принимающего участие в эксперименте, спрашивают, сможет ли он нажать на переключатель.
С этой проблемой связано много дополнительных вопросов:
Как показали исследования, люди скорее согласятся нажать на переключатель, чем вытолкнуть человека под трамвай. С другой стороны, злодеев готовы подтолкнуть гораздо охотнее. Несмотря на то что проблема вагонетки теоретическая, ее последствия значимы для реального мира.
Нашли нарушение? Пожаловаться на содержание
С другой стороны, злодеев готовы подтолкнуть гораздо охотнее. Несмотря на то что проблема вагонетки теоретическая, ее последствия значимы для реального мира.
Нашли нарушение? Пожаловаться на содержание
Читать полностью…
- Последние
- Популярные
Больше новостей
Больше новостей
Новости по дням
Сегодня,
1 октября 2022
Другие новости
Больше новостей
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 23 из 39Следующая ⇒
Мыслительная деятельность исследователя в процессе научного познания включает в себя особый вид абстрагирования, который называют идеализацией. Идеализация представляет собой мысленное внесение определенных изменений в изучаемый объект в соответствии с целями исследований. В результате таких изменений могут быть, например, исключены из рассмотрения какие-то свойства, стороны, признаки объектов. Так, широко распространенная в механике идеализация, именуемая материальной точкой, подразумевает тело, лишенное всяких размеров. Такой абстрактный объект, размерами которого пренебрегают, удобен при описании движения. Причем подобная абстракция позволяет заменить в исследовании самые различные реальные объекты: от молекул или атомов при решении многих задач статистической механики и до планет Солнечной системы при изучении, например, их движения вокруг Солнца. Изменения объекта, достигаемые в процессе идеализации, могут производиться также и путем наделения его какими-то особыми свойствами, в реальной действительности неосуществимыми. Примером может служить введенная путем идеализации в физику абстракция, известная под названием абсолютно черного тела. Такое тело наделяется несуществующим в природе свойством поглощать абсолютно всю попадающую на него лучистую энергию, ничего не отражая и ничего не пропуская сквозь себя. Спектр излучения абсолютно черного тела является идеальным случаем, ибо на него не оказывает влияния природа вещества излучателя или состояние его поверхности. А если можно теоретически описать спектральное распределение плотности энергии излучения для идеального случая, то можно кое-что узнать и о процессе излучения вообще. Указанная идеализация сыграла важную роль в прогрессе научного познания в области физики, ибо помогла выявить ошибочность некоторых существовавших во второй половине XIX века представлений. Физики занялись проблемой излучения абсолютно черного тела в самом конце XIX столетия. Начав с предположений, основанных на законах классической термодинамики и оптики, они попытались вывести формулу энергетического спектра излучения. Эти попытки потерпели неудачу, так как привели к выводу, который стал известен как «ультрафиолетовая катастрофа». Из теории следовало, что абсолютно черное тело, нагретое до высоких температур, должно испускать бесконечно большое количество энергии в области высоких частот, т. е. в ультрафильтровой области спектра и за ее пределами. В случае абсолютно черного тела теория предсказывала катастрофу, которая в действительности не имеет места. Проблемой расчета количества излучения, испускаемого идеальным излучателем — абсолютно черным телом, серьезно занялся Макс Планк, который работал над ней долгих четыре года. Наконец, в 1900 году ему удалось найти решение в виде формулы, которая правильно описывала спектральное распределение энергии излучения абсолютно черного тела. Целесообразность использования идеализации определяется следующими обстоятельствами. Во-первых, идеализация целесообразна тогда, когда подлежащие исследованию реальные объекты достаточно сложны для имеющихся средств теоретического, в частности математического, анализа, а по отношению к идеализированному случаю можно, приложив эти средства, построить и развить теорию, в определенных условиях и целях эффективную, для описания свойств и поведения этих реальных объектов. Последнее, в сущности, и удостоверяет плодотворность идеализации, отличает ее от бесплодной фантазии. Во-вторых, идеализацию целесообразно использовать в тех случаях, когда необходимо исключить некоторые свойства, связи исследуемого объекта, без которых он существовать не может, но которые затемняют существо протекающих в нем процессов. Сложный объект представляется как бы в «очищенном» виде, что облегчает его изучение. На эту гносеологическую возможность идеализации обратил внимание Ф.Энгельс, который показал её на примере исследования, проведенного Сади Карно. Он изучил паровую машину, проанализировал её, нашел, что в ней основной процесс не выступает в чистом виде, а заслонен всякого рода побочными процессами, устранил эти безразличные для главного процесса побочные обстоятельства и сконструировал идеальную паровую машину (или газовую машину), которую, правда, нельзя осуществить, как нельзя, например, осуществить геометрическую линию или геометрическую плоскость, но которая оказывает, по-своему, такие же услуги, как эти математические абстракции: она представляет рассматриваемый процесс в чистом, независимом, неискаженном виде. В-третьих, применение идеализации целесообразно тогда, когда исключаемые из рассмотрения свойства, стороны, связи изучаемого объекта не влияют в рамках данного исследования на его сущность. Выше уже упоминалось, например, о том, что абстракция материальной точки позволяет в некоторых случаях представлять самые различные объекты — от молекул или атомов и до гигантских космических объектов. Следует отметить, что характер идеализации может быть весьма различным, если существуют разные теоретические подходы к изучению какого-то явления. В качестве примера можно указать на три разных понятия «идеального газа», сформировавшихся под влиянием различных теоретико-физических представлений: Максвелла — Больцмана, Бозе — Эйнштейна и Ферми — Дирака. Однако полученные при этом все три варианта идеализации оказались плодотворными при изучении газовых состояний различной природы: идеальный газ Максвелла — Больцмана стал основой исследований обычных молекулярных разреженных газов, находящихся при достаточно высоких температурах; идеальный газ Бозе — Эйнштейна был применен для изучения фотонного газа, а идеальный газ Ферми — Дирака помог решить ряд проблем электронного газа. Будучи разновидностью абстрагирования, идеализация допускает элемент чувственной наглядности (обычный процесс абстрагирования ведет к образованию мысленных абстракций, не обладающих никакой наглядностью). Эта особенность идеализации очень важна для реализации такого специфического метода теоретического познания, каковым является мысленный эксперимент (его также называют умственным, субъективным, воображаемым, идеализированным). Мысленный эксперимент предполагает оперирование идеализированным объектом (замещающим в абстракции объект реальный), которое заключается в мысленном подборе тех или иных положений, ситуаций, позволяющих обнаружить какие-то важные особенности исследуемого объекта. В этом проявляется определенное сходство мысленного (идеализированного) эксперимента с реальным. Более того, всякий реальный эксперимент, прежде чем быть осуществленным на практике, сначала «проигрывается» исследователем мысленно в процессе обдумывания, планирования. В этом случае мысленный эксперимент выступает в роли предварительного идеального плана реального эксперимента. Вместе с тем мысленный эксперимент играет и самостоятельную роль в науке. При этом, сохраняя сходство с реальным экспериментом, он в то же время существенно отличается от него. Эти отличия заключаются в следующем. Реальный эксперимент — это метод, связанный с практическим, предметно-манипулятивным, «орудийным» познанием окружающего мира. В мысленном же эксперименте исследователь оперирует не материальными объектами, а их идеализированными образами, и само оперирование производится в его сознании, т. е. чисто умозрительно. Возможность постановки реального эксперимента определяется наличием соответствующего материально-технического (а иногда и финансового) обеспечения. Мысленный эксперимент такого обеспечения не требует. В реальном эксперименте приходится считаться с реальными физическими и иными ограничениями его поведения, с невозможностью в ряде случаев устранить мешающие ходу эксперимента воздействия извне, с искажением в силу указанных причин получаемых результатов. В научном познании могут быть случаи, когда при исследовании некоторых явлений, ситуаций проведение реальных экспериментов оказывается вообще невозможным. Этот пробел в познании может восполнить только мысленный эксперимент. Научная деятельность Галилея, Ньютона, Максвелла, Карно, Эйнштейна и других ученых, заложивших основы современного естествознания, свидетельствует о существенной роли мысленного эксперимента в формировании теоретических идей. История развития физики богата фактами использования мысленных экспериментов. Примером могут служить мысленные эксперименты Галилея, приведшие к открытию закона инерции. Реальные эксперименты, в которых невозможно устранить фактор трения, казалось бы, подтверждали господствовавшую в течение тысячелетий концепцию Аристотеля, утверждавшую, что движущееся тело останавливается, если толкающая его сила прекращает свое действие. Результаты мысленных экспериментов могут ставить иногда серьезные проблемы перед наукой, разрешить которые бывает не так-то легко. Интересным примером в этом плане является мысленный эксперимент Максвелла, вызвавший сенсацию в начале 1870-х годов. Этот мысленный эксперимент, описанный в его работе «»Теория теплоты»», ставил под сомнение второе начало термодинамики. В своем мысленном эксперименте Максвелл допустил наличие особого существа — «демона», «… способности которого настолько изощрены, что оно может следить за каждой молекулой на её пути и в состоянии делать то, что в настоящее время для нас невозможно». «Предположим, — писал Максвелл, — что имеется сосуд, разделенный на две части А и В перегородкой с небольшим отверстием, и что существо, которое может видеть отдельные молекулы, открывает и закрывает это отверстие так, чтобы дать возможность только более быстрым молекулам перейти из А в В и только более медленным перейти из В в А. Сражение с «демоном» Максвелла заняло длительный период времени. Только в ХХ столетии американские физики Сцилард, Димерс и Гейбор доказали, что второе начало термодинамики остается незыблемым и что никакого «вечного двигателя», даже с помощью «демона», построить нельзя. Они сумели спроектировать и рассчитать машину-демона и убедились, что такая машина работать будет, но требует питания внешней энергией. Причем затраты энергии на ее работу окажутся больше, чем выход энергии в результате ее деятельности. Поиск ответа на проблему, поставленную мысленным экспериментом Максвелла, был, несомненно, полезен и способствовал приращению научных знаний. Мысленный эксперимент может иметь большую эвристическую ценность, помогая интерпретировать новое знание, полученное чисто математическим путем. Это подтверждается многими примерами из истории науки. Однако незнание некоторыми учеными материалистической диалектики помешало правильно понять этот вывод. В результате возникли многочисленные дискуссии по данному вопросу, которые особенно бурно развернулись на Сольвеевских конгрессах 1927 и 1930 гг. В этих дискуссиях, по свидетельству их участников, огромную роль играли идеализированные воображаемые эксперименты. В них, писал Гейзенберг, «подобные парадоксы (противоречия между волновыми и корпускулярными представлениями) проступали особенно резко, и мы старались разгадать, какой ответ на такие эксперименты, возможно, дала бы природа». Метод идеализации, оказывающийся весьма плодотворным во многих случаях, имеет в то же время определенные ограничения. Развитие научного познания заставляет иногда отказываться от принятых ранее идеализированных представлений. Так произошло, например, при создании Эйнштейном специальной теории относительности, из которой были исключены ньютоновские идеализации «абсолютное пространство» и «абсолютное время». Кроме того, любая идеализация ограничена конкретной областью явлений и служит для решения только определенных проблем. Это хорошо видно хотя бы на примере вышеуказанной идеализации «абсолютно черное тело». Сама по себе идеализация, хотя и может быть плодотворной и даже подводить к научному открытию, еще недостаточна для того, чтобы сделать это открытие. Здесь определяющую роль играют теоретические установки, из которых исходит исследователь. Основное положительное значение идеализации как метода научного познания заключается в том, что получаемые на ее основе теоретические построения позволяют затем эффективно исследовать реальные объекты и явления. Упрощения, достигаемые с помощью идеализации, облегчают создание теории, вскрывающей законы исследуемой области явлений материального мира. Если теория в целом правильно описывает реальные явления, то правомерны и положенные в ее основу идеализации. Формализация. Язык науки
Под формализацией понимается особый подход в научном познании, который заключается в использовании специальной символики, позволяющей отвлечься от изучения реальных объектов, от содержания описывающих их теоретических положений и оперировать вместо этого некоторым множеством символов (знаков). Ярким примером формализации являются широко используемые в науке математические описания различных объектов, явлений, основывающиеся на соответствующих содержательных теориях. При этом используемая математическая символика не только помогает закрепить уже имеющиеся знания об исследуемых объектах, явлениях, но и выступает своего рода инструментом в процессе дальнейшего их познания. Для построения любой формальной системы необходимо: а) задание алфавита, т. е. определенного набора знаков; б) задание правил, по которым из исходных знаков этого алфавита могут быть получены «слова», «формулы»; в) задание правил, по которым от одних слов, формул данной системы можно переходить к другим словам и формулам (так называемые правила вывода). В результате создается формальная знаковая система в виде определенного искусственного языка. Важным достоинством этой системы является возможность проведения в ее рамках исследования какого-либо объекта чисто формальным путем (оперирование знаками) без непосредственного обращения к этому объекту. Другое достоинство формализации состоит в обеспечении краткости и четкости записи научной информации, что открывает большие возможности для оперирования ею. Вряд ли удалось бы успешно пользоваться, например, теоретическими выводами Максвелла, если бы они не были компактно выражены в виде математических уравнений, а описывались бы с помощью обычного, естественного языка. Разумеется, формализованные искусственные языки не обладают гибкостью и богатством языка естественного. Зато в них отсутствует многозначность терминов (полисемия), свойственная естественным языкам. Они характеризуются точно построенным синтаксисом (устанавливающим правила связи между знаками безотносительно их содержания) и однозначной семантикой (семантические правила формализованного языка вполне однозначно определяют соотнесенность знаковой системы с определенной предметной областью). Таким образом, формализованный язык обладает свойством моносемичности. Возможность представить те или иные теоретические положения науки в виде формализованной знаковой системы имеет большое значение для познания. Поучительным примером формально полученного и на первый взгляд «бессмысленного» результата, который обнаружил впоследствии весьма глубокий физический смысл, являются решения уравнения Дирака, описывающего движение электрона. Среди этих решений оказались такие, которые соответствовали состояниям с отрицательной кинетической энергией. Позднее было установлено, что указанные решения описывали поведение неизвестной дотоле частицы — позитрона, являющегося антиподом электрона. В данном случае некоторое множество формальных преобразований привело к содержательному и интересному для науки результату. Расширяющееся использование формализации как метода теоретического познания связано не только с развитием математики. В химии, например, соответствующая химическая символика вместе с правилами оперирования ею явилась одним из вариантов формализованного искусственного языка. Все более важное место метод формализации занимал в логике по мере ее развития. Труды Лейбница положили начало созданию метода логических исчислений. Последний привел к формированию в середине XIX века математической логики, которая во второй половине ХХ столетия сыграла важную роль в развитии кибернетики, в появлении электронных вычислительных машин, в решении задач автоматизации производства и т. д. Язык современной науки существенно отличается от естественного человеческого языка. Он содержит много специальных терминов, выражений, в нем широко используются средства формализации, среди которых центральное место принадлежит математической формализации. Исходя из потребностей науки, создаются различные искусственные языки, предназначенные для решения тех или иных задач. Вместе с тем следует иметь в виду, что создание какого-то единого формализованного языка науки не представляется возможным. Дело в том, что даже достаточно богатые формализованные языки не удовлетворяют требованию полноты, т. е. некоторое множество правильно сформулированных предложений такого языка (в том числе и истинных) не может быть выведено чисто формальным путем внутри этого языка. Данное положение вытекает из результатов, полученных в начале 1930-х годов австрийским логиком и математиком Куртом Гёделем. Знаменитая теорема Гёделя утверждает, что каждая формальная система либо противоречива, либо содержит некоторую неразрешимую (хотя и истинную) формулу, т.е. такую формулу, которую в данной системе нельзя ни доказать, ни опровергнуть. Правда, то, что не выводимо в данной формальной системе, выводимо в другой системе, более богатой. Однако из невозможности создать единый для всех наук формализованный язык не следует делать вывод, умаляющий важность построения формализованных языков вообще. Из геделевской теоремы «о неполноте» следует, что точная формализованная система, выступающая в качестве языка науки, не может считаться совершенно адекватной системе объектов, ибо некоторые содержательно истинные предложения не могут быть получены средствами данного формализма, а это означает, что формализация языка науки не снижает, а, напротив, предполагает содержательные моменты в построении языковой системы. Формализованные языки не могут быть единственной формой языка современной науки, ибо стремление к максимальной адекватности требует использовать и неформализованные системы. Индукция и дедукция
Индукция (от лат. inductio — наведение, побуждение) есть метод познания, основывающийся на формально логическом умозаключении, которое приводит к получению общего вывода на основании частных посылок. Другими словами, это есть движение нашего мышления от частного, единичного к общему. Индукция широко применяется в научном познании. Обнаруживая сходные признаки, свойства у многих объектов определенного класса, исследователь делает вывод о присущности этих признаков, свойств всем объектам данного класса. Например, в процессе экспериментального изучения электрических явлений использовались проводники тока, выполненные из различных металлов. На основании многочисленных единичных опытов сформировался общий вывод об электропроводности всех металлов. Индукция, используемая в научном познании (научная индукция), может реализовываться в виде следующих методов: 1.Метод единственного сходства (во всех случаях наблюдения какого-то явления обнаруживается лишь один общий фактор, все другие — различны; следовательно, этот единственный сходный фактор есть причина данного явления). 2.Метод единственного различия (если обстоятельства возникновения какого-то явления и обстоятельства, при которых оно не возникает, почти во всем сходны и различаются лишь одним фактором, присутствующим только в первом случае, то можно сделать вывод, что этот фактор и есть причина данного явления). 3.Соединенный метод сходства и различия (представляет собой комбинацию двух вышеуказанных методов). 4. Метод сопутствующих изменений (если определенные изменения одного явления всякий раз влекут за собой некоторые изменения в другом явлении, то отсюда вытекает вывод о причинной связи этих явлений). 5.Метод остатков (если сложное явление вызывается многофакторной причиной, причем некоторые из этих факторов известны как причина какой-то части данного явления, то отсюда следует вывод: причина другой части явления — остальные факторы, входящие в общую причину этого явления). Родоначальником классического индуктивного метода познания является Ф. Бэкон. Но он трактовал индукцию чрезвычайно широко, считал ее важнейшим методом открытия новых истин в науке, главным средством научного познания природы. На самом же деле вышеуказанные методы научной индукции служат главным образом для нахождения эмпирических зависимостей между экспериментально наблюдаемыми свойствами объектов и явлений. В них систематизированы простейшие формальнологические приемы, которые стихийно использовались учеными-естествоиспытателями в любом эмпирическом исследовании. По мере развития естествознания становилось все более ясным, что методы классической индукции далеко не играют той всеохватывающей роли в научном познании, которую им приписывали Ф. Такое неоправданно расширенное понимание роли индукции в научном познании получило наименование всеиндуктивизма. Его несостоятельность обусловлена тем, что индукция рассматривается изолированно от других методов познания и превращается в единственное, универсальное средство познавательного процесса. С критикой всеиндуктивизма выступил Ф. Энгельс, указавший, что индукцию нельзя, в частности, отрывать от другого метода познания — дедукции. Дедукция (от лат. deductio — выведение) есть получение частных выводов на основе знания каких-то общих положений. Другими словами, это есть движение нашего мышления от общего к частному, единичному. Например, из общего положения, что все металлы обладают электропроводностью, можно сделать дедуктивное умозаключение об электропроводности конкретной медной проволоки (зная, что медь — металл). Если исходные общие положения являются установленной научной истиной, то методом дедукции всегда будет получен истинный вывод. Получение новых знаний посредством дедукции существует во всех естественных науках, но особенно большое значение дедуктивный метод имеет в математике. Оперируя математическими абстракциями и строя свои рассуждения на весьма общих положениях, математики вынуждены чаще всего пользоваться дедукцией. И математика является, пожалуй, единственной собственно дедуктивной наукой. В науке Нового времени пропагандистом дедуктивного метода познания был видный математик и философ Р. Декарт. Вдохновленный своими математическими успехами, будучи убежденным в безошибочности правильно рассуждающего ума, Декарт односторонне преувеличивал значение интеллектуальной стороны за счет опытной в процессе познания истины. Дедуктивная методология Декарта была прямой противоположностью эмпирическому индуктивизму Бэкона. Но, несмотря на имевшие место в истории науки и философии попытки оторвать индукцию от дедукции, противопоставить их в реальном процессе научного познания, эти два метода не применяются как изолированные, обособленные друг от друга. Более того, в процессе использования индуктивного метода зачастую в скрытом виде присутствует и дедукция. Обобщая факты в соответствии с какими-то идеями, мы тем самым косвенно выводим получаемые нами обобщения из этих идей, причем далеко не всегда отдаем себе в этом отчет. Кажется, что наша мысль движется прямо от фактов к обобщениям, т.е. тут присутствует чистая индукция. На самом же деле, сообразуясь с какими-то идеями, иначе говоря, неявно руководствуясь ими в процессе обобщения фактов, наша мысль косвенно идет от идей к этим обобщениям, и, следовательно, тут имеет место и дедукция. Можно сказать, что во всех случаях, когда мы обобщаем, сообразуясь с какими-либо философскими положениями, наши умозаключения являются не только индукцией, но и скрытой дедукцией. Подчеркивая необходимую связь индукции и дедукции, Ф. Энгельс настоятельно советовал ученым: «Вместо того, чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться каждую применять на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг другом».
⇐ Предыдущая18192021222324252627Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0. |
№ 166: ЭКСПЕРИМЕНТ ГАЛИЛЕЯ Щелкните здесь для прослушивания аудио эпизода 166.
|
Ускорительный эксперимент Галилея
Ускорительный эксперимент Галилеяпредыдущий индекс следующие
Майкл Фаулер, Факультет физики UVa
Обобщение взглядов Аристотеля
Аристотель считал, что существует два вида движения неживой материи:
естественные и неестественные. Неестественное (или «жестокое») движение — это когда
что-то толкается, и в этом случае скорость движения пропорциональна
к силе толчка. (Это, вероятно, было выведено из наблюдения за повозками с волами и
лодки.) Естественное движение — это когда что-то ищет свое естественное место в
Вселенной, например, падающий камень или поднимающийся огонь. (Мы говорим только здесь
о веществах, состоящих из земли, воды, воздуха и огня, «природных
круговое движение» планет, состоящее из обеих, считается
отдельно).
Неестественное (или «жестокое») движение — это когда
что-то толкается, и в этом случае скорость движения пропорциональна
к силе толчка. (Это, вероятно, было выведено из наблюдения за повозками с волами и
лодки.) Естественное движение — это когда что-то ищет свое естественное место в
Вселенной, например, падающий камень или поднимающийся огонь. (Мы говорим только здесь
о веществах, состоящих из земли, воды, воздуха и огня, «природных
круговое движение» планет, состоящее из обеих, считается
отдельно).
Для естественного движения тяжелых предметов, падающих на землю, Аристотель утверждал что скорость падения была пропорциональна весу , а обратно пропорционально пропорциональна плотности среды , через которую проваливается тело. Он также упомянул, что было некоторое ускорение, так как тело приближалось больше приблизился к своей стихии, его вес увеличился, и он ускорился. Однако эти замечания у Аристотеля очень кратки и расплывчаты и, конечно, не количественны.
На самом деле, эти взгляды Аристотеля не остались без внимания даже в древних Афинах. Примерно через тридцать лет после смерти Аристотеля Стратон указал, что камень
падение с большей высоты оказало большее воздействие на землю, что предполагает
что камень набирал большую скорость, когда падал с большей высоты.
Примерно через тридцать лет после смерти Аристотеля Стратон указал, что камень
падение с большей высоты оказало большее воздействие на землю, что предполагает
что камень набирал большую скорость, когда падал с большей высоты.
Две новые науки
Галилей изложил свои идеи о падающих телах и о снарядах в вообще, в книге под названием « Две новые науки ». Эти двое были наука о движении, ставшая краеугольным камнем физики, и наука о материалах и конструкции, важный вклад в инженерное дело.
Идеи представлены в живой форме в виде диалога с участием трех персонажи, Сальвиати, Сагредо и Симпличио. Официальная церковная точка зрения, то есть аристотелизм, выдвигается персонажем по имени Симпличио, и обычно сносят другие. Защита Галилея при обвинении в ересь в подобной книге заключалась в том, что он просто излагал все точки зрения, но это несколько неискренне — Симплицио почти всегда изображается как простодушный.
Например, на странице 62 TNS Сальвиати указывает:
Я очень сомневаюсь, что Аристотель когда-либо проверял экспериментально,
верно, что два камня, один из которых в десять раз тяжелее другого, если допустить
упасть в одно и то же мгновение с высоты, скажем, 100 локтей, было бы так
отличаются по скорости, что, когда более тяжелый достиг земли, другой
не упали более чем на 10 локтей.
Симпличио отвечает на это не думать с точки зрения выполнения испытать себя, чтобы ответить на вызов Сальвиати, но тщательно изучить ближе священное писание:
SIMP: Судя по его языку, он пробовал поэкспериментируйте, потому что он говорит: мы видим тяжелее ; теперь слово см. показывает, что он провел эксперимент.
Затем присоединяется Сагредо:
САГР: Но я, Симпличио, который сделал тест, могу заверить вас, что пушечное ядро весом в сто-двести фунтов, а то и больше не долетит землю на целых пяди впереди мушкетной пули весом всего в половину фунта, при условии, что оба они будут сброшены с высоты 200 локтей.
Это знаменует собой начало современной эры в науке — отношение что утверждения о физическом мире со стороны авторитетов, какими бы мудрыми или почитается, стоять или падать экспериментальным испытанием. Легенда гласит, что Галилей провел этот конкретный эксперимент с падающей башни в Пизе.
Галилей продолжает подробный анализ падающих тел. Он понимает
что для очень легких предметов, таких как перья, сопротивление воздуха становится
доминирующий эффект, тогда как в эксперименте он имеет лишь незначительное значение
изложено выше.
Он понимает
что для очень легких предметов, таких как перья, сопротивление воздуха становится
доминирующий эффект, тогда как в эксперименте он имеет лишь незначительное значение
изложено выше.
Естественно ускоренное движение
Экспериментально установив, что тяжелые предметы падают практически С той же скоростью Галилей продолжил рассмотрение центрального вопроса о скорости падения едва затронутый Аристотелем — как изменяется скорость при падении?
Проблема в том, что очень сложно ответить на этот вопрос
просто смотреть, как что-то падает — все кончается слишком быстро. Чтобы сделать любой вид
измерения скорости движение должно быть каким-то образом замедлено. Конечно,
некоторые падающие движения естественно медленные, например, перо или что-то другое
слишком тяжелое падение через воду. Наблюдая за этими движениями, можно увидеть, что после
при падении тело быстро набирает определенную скорость, а затем равномерно падает с
эта скорость. Ошибка, которую совершали люди, состояла в том, что они полагали, что все падающие
тела следовали той же схеме, так что большая часть падения происходила с постоянной скоростью. скорость. Галилей утверждал, что эта точка зрения ложна, повторяя
забытые слова Стратона почти две тысячи лет назад:
скорость. Галилей утверждал, что эта точка зрения ложна, повторяя
забытые слова Стратона почти две тысячи лет назад:
(ТНС, стр. 163) Но скажите мне, господа, не правда ли, что если блок будет позволено упасть на кол с высоты четырех локтей и вбить его в земли, скажем, в четыре пальца ширины, что, исходящее с высоты двух локтей, загонит кол на гораздо меньшее расстояние; и, наконец, если блок будет поднят всего на один палец, насколько больше он сделает, чем если просто наложить вершина кола без перкуссии? Конечно очень мало. Если его поднять только толщина листа, эффект будет совершенно незаметен. А также поскольку эффект удара зависит от скорости этого ударяющего тела, может ли кто-нибудь сомневаться в том, что движение очень медленное … всякий раз, когда эффект незаметно?
Гипотеза ускорения Галилея
Установив с помощью приведенных выше аргументов и экспериментов, что тело продолжает набирать скорость или ускоряться по мере падения, предположил Галилей простейшая возможная гипотеза (перефразируя обсуждение на странице 161 TNS):
Падающее тело равномерно ускоряется: оно набирает равные скорости
через равные промежутки времени, так что если он падает из состояния покоя, то движется в два раза быстрее
быстро через две секунды, так как он двигался через одну секунду, и двигался через три
раза быстрее через три секунды, чем через одну секунду.
Это привлекательная простая гипотеза, но Галилею не так-то просто ее обосновать. проверить опытным путем — как он мог дважды измерить скорость падающего камня осенью и сделать сравнение?
Замедление движения
Хитрость заключается в том, чтобы замедлить движение каким-то образом, чтобы скорость могла быть измерено, без изменения в то же время характера движения . Галилей знал, что падение в воду чего-либо, падающего довольно мягко, сделал изменить характер движения, он приземлился бы так же мягко на дно упал с десяти футов так же, как и с двух футов, поэтому замедлил движение падение чего-то через воду полностью изменило ситуацию.
Идея Галилея для замедления движения заключалась в том, чтобы катить мяч
вниз по пандусу, а не падать вертикально. Он утверждал, что скорость, набранная в
скатывание по пандусу заданной высоты не зависело от уклона. Его
аргумент был основан на эксперименте с маятником и гвоздем, показанном на стр. 171 из Две новые науки . Маятник состоит из нити и поводка
пуля. Его отводят в сторону, а нить натянута до некоторой точки C.
171 из Две новые науки . Маятник состоит из нити и поводка
пуля. Его отводят в сторону, а нить натянута до некоторой точки C.
Гвоздь вставлен в точку E непосредственно под верхним концом нити, так что
маятник качается в своей нижней точке, нить попадает в гвоздь и
маятник эффектно укорочен, благодаря чему пуля более круто качается вверх,
к G с гвоздем в E. Тем не менее маятник будет качаться назад
до почти такой же высоты он начался, то есть точки G и C
находятся на одной высоте над уровнем земли. Кроме того, когда он откидывается назад, он
снова поднимается до точки С, если пренебречь небольшой потерей воздуха
сопротивление. Отсюда можно сделать вывод, что скорость, с которой мяч проходит
через самую низкую точку одинакова в обоих направлениях. Чтобы увидеть это, представьте
сначала ситуация без гвоздя в E. Мяч будет качаться
назад и вперед симметричным образом, обычный маятник, и
конечно в этом случае скорость в нижней точке одинакова для обоих
направлениях (опять же игнорируя постепенное замедление от сопротивления воздуха). Когда мы
вбить гвоздь, однако, мы видим из эксперимента, что на качели назад,
мяч все же успевает попасть в начальную точку C. Делаем вывод, что он
должно быть, двигался с той же скоростью, с которой он качнулся назад через самую низкую точку
как тогда, когда гвоздя не было, потому что в тот момент, когда он оставляет гвоздь на
обратный ход это всего лишь обычный маятник, и как далеко он раскачивается
от вертикали зависит от того, как быстро он движется в самой нижней точке.
Когда мы
вбить гвоздь, однако, мы видим из эксперимента, что на качели назад,
мяч все же успевает попасть в начальную точку C. Делаем вывод, что он
должно быть, двигался с той же скоростью, с которой он качнулся назад через самую низкую точку
как тогда, когда гвоздя не было, потому что в тот момент, когда он оставляет гвоздь на
обратный ход это всего лишь обычный маятник, и как далеко он раскачивается
от вертикали зависит от того, как быстро он движется в самой нижней точке.
Галилей утверждает, что аналогичная картина будет наблюдаться, если мяч скатится вниз пандус, который плавно соединяется с другим более крутым пандусом, т. мяч скатится по второй рампе до уровня, практически равного уровню, на котором он начал в, даже если две рампы имеют разные наклоны. Тогда это будет продолжайте катиться назад и вперед между двумя пандусами, в конце концов останавливается из-за трения, сопротивления воздуха и т. д.
Размышляя об этом движении, становится ясно, что
вниз при последовательных проходах) он должен идти та же скорость отрывается
одна рампа, как она отрывается от другой. Затем Галилей предлагает представить себе
вторая рампа все круче и круче — и мы видим, что если она достаточно крутая,
мы можем думать о мяче как о простом падении! Он заключает, что на мяч
скатываясь по пандусу, скорость на различных высотах одинакова со скоростью
мяч достиг бы (гораздо быстрее!), просто упав вертикально с
его начальная точка на этой высоте . Но если мы сделаем пандус достаточно пологим,
движение будет достаточно медленным для измерения. (на самом деле разница есть
между катящимся мячом и плавно скользящим или падающим мячом, но не
влияют на характер увеличения скорости, поэтому мы не будем здесь останавливаться на этом.)
Затем Галилей предлагает представить себе
вторая рампа все круче и круче — и мы видим, что если она достаточно крутая,
мы можем думать о мяче как о простом падении! Он заключает, что на мяч
скатываясь по пандусу, скорость на различных высотах одинакова со скоростью
мяч достиг бы (гораздо быстрее!), просто упав вертикально с
его начальная точка на этой высоте . Но если мы сделаем пандус достаточно пологим,
движение будет достаточно медленным для измерения. (на самом деле разница есть
между катящимся мячом и плавно скользящим или падающим мячом, но не
влияют на характер увеличения скорости, поэтому мы не будем здесь останавливаться на этом.)
Эксперимент Галилея по ускорению
Теперь мы готовы рассмотреть эксперимент Галилея, в котором он испытал его гипотеза о том, как падающие тела набирают скорость. Мы цитируем счет из «Двух новых наук», стр. 178:
Кусок деревянного бруса длиной около 12 локтей,
была взята ширина в локоть и толщина в три пальца; по его краю была вырезана
канал шириной чуть больше одного пальца; сделав этот паз очень
прямой, гладкой и полированной, и выстлав ее пергаментом, также как
гладкой и отполированной, мы катили по ней твердую, гладкую и очень
круглый бронзовый шар. Разместив эту доску в наклонном положении, подняв
один конец на один-два локтя выше другого, мы катали мяч, как я
просто говорю вдоль канала, отмечая способом, который сейчас будет описан,
время, необходимое для спуска. Мы повторили этот эксперимент более
один раз, чтобы измерить время с такой точностью, чтобы отклонение
между двумя наблюдениями никогда не превышала одной десятой доли пульса. Имея
выполнили эту операцию и убедившись в ее надежности, мы
теперь катил мяч только четверть длина канала; а также
измерив время его спуска, мы нашли ровно половину бывшего. Далее пробовали другие дистанции, сравнивали время на весь
длина с той, что на половину, или с той, что на две трети, или на три четверти,
или действительно для любой дроби; в таких опытах, повторенных сто раз,
мы всегда находили, что пройденных пространств относились друг к другу как квадраты
времени , и это было справедливо для всех наклонов плоскости, т. е.
канал, по которому мы катили мяч. Мы также заметили, что времена
спуск, при различных наклонах самолета, относились друг к другу точно
то соотношение, которое, как мы увидим позже, автор предсказал и
продемонстрировано для них.
Разместив эту доску в наклонном положении, подняв
один конец на один-два локтя выше другого, мы катали мяч, как я
просто говорю вдоль канала, отмечая способом, который сейчас будет описан,
время, необходимое для спуска. Мы повторили этот эксперимент более
один раз, чтобы измерить время с такой точностью, чтобы отклонение
между двумя наблюдениями никогда не превышала одной десятой доли пульса. Имея
выполнили эту операцию и убедившись в ее надежности, мы
теперь катил мяч только четверть длина канала; а также
измерив время его спуска, мы нашли ровно половину бывшего. Далее пробовали другие дистанции, сравнивали время на весь
длина с той, что на половину, или с той, что на две трети, или на три четверти,
или действительно для любой дроби; в таких опытах, повторенных сто раз,
мы всегда находили, что пройденных пространств относились друг к другу как квадраты
времени , и это было справедливо для всех наклонов плоскости, т. е.
канал, по которому мы катили мяч. Мы также заметили, что времена
спуск, при различных наклонах самолета, относились друг к другу точно
то соотношение, которое, как мы увидим позже, автор предсказал и
продемонстрировано для них.
Для измерения времени мы использовали большой сосуд с водой, помещенный в возвышенном положении; ко дну этого сосуда была припаяна трубка из небольшой диаметр, дающий тонкую струю воды, которую мы собрали в небольшой стакан во время каждого спуска, будь то по всей длине канала или на часть своей длины; собранную таким образом воду взвешивали после каждого спуск, на очень точном равновесии; различия и соотношения этих веса дали нам различия и соотношения времен, и это при таком точность в том, что хотя операция повторялась много-много раз, нет заметных расхождений в результатах.
Фактически проводим эксперимент
Мы проводили эксперимент в классе в октябре 1996 года.
канал пергаментом, а мы использовали обычный большой стальной шарик (около
дюйма в диаметре). Мы использовали водяные часы, когда студент пустил струю воды.
воды в полистироловый(!) стаканчик в перерыве между
выпуская мяч на некоторое расстояние вверх по рампе, и он попадает в упор на
нижний. Мы провели эксперимент три раза для полной рампы и три раза
раз на четверть дистанции. Мы взвесили количество воды в чашке
с обычным балансом. К своему удивлению, мы обнаружили, что в среднем
сумма для полной рампы составила 56 граммов, для четверти рампы 28 граммов. Это было
отчасти повезло, был разброс в несколько граммов. Тем не менее, это предполагает, что
Галилей не преувеличивал в своих утверждениях о точности Две новые науки ,
поскольку он был гораздо более осторожен, чем мы, и повторял эксперимент много
больше раз.
Мы провели эксперимент три раза для полной рампы и три раза
раз на четверть дистанции. Мы взвесили количество воды в чашке
с обычным балансом. К своему удивлению, мы обнаружили, что в среднем
сумма для полной рампы составила 56 граммов, для четверти рампы 28 граммов. Это было
отчасти повезло, был разброс в несколько граммов. Тем не менее, это предполагает, что
Галилей не преувеличивал в своих утверждениях о точности Две новые науки ,
поскольку он был гораздо более осторожен, чем мы, и повторял эксперимент много
больше раз.
предыдущий индекс следующий
Пизанская башня Галилея. Эксперимент
Галилей и Пизанская башня научили нас многому о свободно падающих объектах. Да, та самая башня, которая из-за своего веса не могла стоять прямо, сыграла важную роль в открытии одной из основ физики. У Галилея было видение пойти против идей Аристотеля, и проведенный им эксперимент доказал его правоту. Итак, что это был за эксперимент? Продолжайте читать, чтобы узнать.
Пизанская башня Галилея. Объяснение эксперимента
Итальянский ученый Галилео Галилей провел знаменитый эксперимент, доказавший, что ускорение, с которым падают объекты, одинаково независимо от их массы. Этот эксперимент известен как Эксперимент Галилея с Пизанской башней. Его результатом было прямое нарушение теории гравитации Аристотеля, которая предполагала, что объекты падают со скоростью, прямо пропорциональной их массе.
Предсказание Архимеда об эксперименте (слева) и измерение Галилея (справа), Wikimedia Commons CC-BY-SA-3.0.
Хотя до сих пор неясно, был ли этот знаменитый эксперимент проведен в реальности или это был мысленный эксперимент, говорят, что Галилео Галилей провел его примерно в 1589 году. Он сбросил два шара разной массы с вершины Пизанской башни. потому что он хотел продемонстрировать, что объекты будут падать с одинаковой скоростью независимо от их массы. Действительно, две сферы упали на землю одновременно, подтверждая идею о том, что объекты падают с одинаковой скоростью независимо от их массы. Это снова подтвердилось много лет спустя, когда астронавт Аполлона-15 Дэвид Скотт сбросил с одной высоты на Луну молоток и перо, и они одновременно ударились о поверхность Луны. До эксперимента Галилея широкое распространение получила теория гравитации Аристотеля, согласно которой объекты падают со скоростью, пропорциональной их массам. Спустя некоторое время после опыта Галилея он дал теоретическое объяснение этому явлению.
Это снова подтвердилось много лет спустя, когда астронавт Аполлона-15 Дэвид Скотт сбросил с одной высоты на Луну молоток и перо, и они одновременно ударились о поверхность Луны. До эксперимента Галилея широкое распространение получила теория гравитации Аристотеля, согласно которой объекты падают со скоростью, пропорциональной их массам. Спустя некоторое время после опыта Галилея он дал теоретическое объяснение этому явлению.
Эксперимент Галилея с падающим телом, проведенный Дэвидом Скоттом на Луне, в котором перо и молоток одновременно достигают поверхности Луны, StudySmarter Originals.
Мысленный эксперимент Галилея с падением мяча
Мысленный эксперимент Галилея с падением мяча имел решающее значение для понимания влияния ускорения гравитации на падающий объект, и он раз и навсегда положил конец спорам. Это доказало, что теория гравитации Аристотеля была неверной. Давайте посмотрим, о чем думал Галилей!
Представьте, что вы стоите на вершине Пизанской башни. Предположим, что более тяжелые тела падают с большей скоростью, чем более легкие. Теперь вы бросаете сверху два шара разной массы, но есть одна загвоздка: шары связаны нитью. Согласно предположению, более тяжелый шар упадет быстрее, чем более легкий, поэтому нить будет натянута: натяжение нити тянет за собой более тяжелый мяч, что, следовательно, должно уменьшить его ускорение.
Предположим, что более тяжелые тела падают с большей скоростью, чем более легкие. Теперь вы бросаете сверху два шара разной массы, но есть одна загвоздка: шары связаны нитью. Согласно предположению, более тяжелый шар упадет быстрее, чем более легкий, поэтому нить будет натянута: натяжение нити тянет за собой более тяжелый мяч, что, следовательно, должно уменьшить его ускорение.
Все объекты падают с одинаковой скоростью, StudySmarter Originals.
Но это означало бы, что если мы уроним тяжелый шар без какого-либо крепления, его ускорение будет больше, чем у системы, в которой два шара связаны. Это противоречит нашему первоначальному предположению, согласно которому более тяжелое тело будет падать быстрее: вся система должна падать быстрее, чем любой отдельный шар. Таким образом, наше предположение неверно: единственное возможное объяснение состоит в том, что все тела будут падать с одинаковой скоростью независимо от их массы.
В этом мысленном эксперименте мы предполагаем, что объекты находятся в свободном падении, что означает, что мы не принимаем во внимание сопротивление воздуха.
Теория гравитации Галилея
Теория гравитации Галилея утверждает, что все объекты падают с одинаковой скоростью независимо от их массы.
Галилей в ходе своего эксперимента определил, что предметы падают с одинаковым ускорением, подтвердив свое предсказание и опровергнув теорию гравитации Аристотеля, которая утверждает, что тела падают со скоростью, пропорциональной их массе.
Теория движения Галилея
Все мы слышали о первом законе движения Ньютона, но знаете ли вы, что первый закон движения Ньютона был первоначально предложен Галилеем?
Закон инерции Галилея гласит, что объект будет продолжать двигаться по прямой линии с постоянной скоростью, если на него не действует внешняя сила.
К такому выводу он пришел во время одного из своих экспериментов. Он обнаружил, что если вы позволите металлическому шару соскользнуть вниз по пандусу, а затем подняться на другой пандус, шар всегда поднимется на свою первоначальную вертикальную высоту независимо от наклона обоих пандусов. Это навело его на мысль, что если бы наклон второй рампы был равен нулю, мяч продолжал бы катиться вечно, так как никогда не достиг бы своей первоначальной высоты. Много лет спустя Ньютон разработает свой первый закон движения на тех же принципах.
Это навело его на мысль, что если бы наклон второй рампы был равен нулю, мяч продолжал бы катиться вечно, так как никогда не достиг бы своей первоначальной высоты. Много лет спустя Ньютон разработает свой первый закон движения на тех же принципах.
Эксперимент Галилея вдохновил и поддержал его закон инерции, StudySmarter Originals.
Галилей и ускорение
Аристотель утверждал, что сила вызывает скорость, но это снова было опровергнуто Галилеем, который утверждал, что сила вызывает ускорение. Это снова было получено из его эксперимента с падающими телами. Он предсказал, что скорость тел, падающих на землю, постоянно увеличивается. Это увеличение скорости, также известное как ускорение, вызвано силой тяжести. Мы можем доказать это с помощью эксперимента.
Когда мяч падает с высоты, экспериментально можно определить, что расстояние, которое он проходит за первую секунду спуска, будет меньше, чем расстояние, которое он проходит в последующие секунды спуска. Это означает, что его скорость постоянно увеличивается. Эта увеличивающаяся скорость вызвана ничем иным, как гравитацией, которая является силой, что приводит нас к заключению, что сила производит ускорение.
Эта увеличивающаяся скорость вызвана ничем иным, как гравитацией, которая является силой, что приводит нас к заключению, что сила производит ускорение.
Эксперимент Галилея в Пизанской башне — основные выводы
- Галилео Галилей провел эксперимент с падающими телами, чтобы опровергнуть теорию гравитации Аристотеля.
- Согласно теории Аристотеля, объекты падают со скоростью, пропорциональной их массе.
- Теория гравитации Галилея утверждает, что все объекты падают с одинаковой скоростью независимо от их массы. Это и по сей день считается правдой.
- Галилей объяснил свои выводы мысленным экспериментом с двумя шарами, соединенными нитью.
- Закон инерции Галилея гласит, что объект продолжает двигаться прямолинейно с постоянной скоростью, пока на него не действует внешняя сила.
- То же, что и первый закон Ньютона.
- Свободное падение не учитывает силу трения сопротивления воздуха.
- Галилей обнаружил, что сила вызывает ускорение, а не скорость.

Галилео Галилей: эксперимент с падающими телами
|
Многие думают, что этот эксперимент никогда не проводился Галилеем и что это всего лишь легенда, поскольку не существует рассказа самого Галилея о таком эксперименте, проведенном им, и многие историки науки признают, что этот эксперимент был в самом разгаре. по большей части мысленный эксперимент, которого на самом деле не было. Чтобы узнать больше об этом споре, см. Раздел ссылок ниже.
по большей части мысленный эксперимент, которого на самом деле не было. Чтобы узнать больше об этом споре, см. Раздел ссылок ниже.
В своей книге Две новые науки (1634) Галилей обсуждает математику (впервые применившую математику для физического анализа) простого типа движения, которое мы сегодня называем равномерным ускорением или постоянным ускорением. Затем он предполагает, что тяжелые тела на самом деле падают именно таким образом и что, если бы было возможно создать вакуум, любые два падающих тела прошли бы одинаковое расстояние за одно и то же время. На основе этого предложения он предсказывает скатывание шаров по наклонной плоскости. Наконец, он описывает некоторые эксперименты с наклонной плоскостью, подтверждающие его теорию.
Галилей использовал в своем эксперименте наклонные плоскости, чтобы замедлить ускорение настолько, чтобы можно было измерить прошедшее время. Мячу позволяли катиться на известное расстояние вниз по пандусу, и измеряли время, необходимое для того, чтобы мяч переместился на известное расстояние. Время измерялось водяными часами.
Время измерялось водяными часами.
Галилей показал, что движение по наклонной плоскости имеет постоянное ускорение, зависящее только от угла наклона плоскости, а не от массы катящегося тела. Затем Галилей утверждал, но не мог доказать, что движение свободного падения ведет себя аналогичным образом, потому что движение свободного падения можно было описать как движение наклонной плоскости под углом 90°. Используя законы Ньютона, мы можем доказать теорию Галилея, разложив гравитационную силу, действующую на катящиеся шары, на два вектора, один перпендикулярный наклонной плоскости, а другой параллельный ей. http://www.physics.smu.edu…
После своих опытов Галилей сформулировал уравнение для падающего тела или объекта, движущегося с равноускорением: d=1/2gt 2 .
Выдающийся французский историк науки Александр Койре утверждает, что эксперименты, описанные в Две новые науки , чтобы определить закон ускорения падающих тел, требовали точных измерений времени, что оказалось невозможным с технологией 1600 года. Согласно Койре, закон был получен дедуктивно, а эксперименты были просто иллюстративными. мысленные эксперименты.
Согласно Койре, закон был получен дедуктивно, а эксперименты были просто иллюстративными. мысленные эксперименты.
Однако известность Галилея заключалась в том, что его теоретическая (или практическая?) работа, упомянутая выше, утвердила механику как науку и проложила путь Ньютону позже в этом веке, особенно его механике и его закону всемирного тяготения.
Теперь вернемся к нашему эксперименту с падающими телами. Некоторые данные показывают, что такие опыты действительно производились различными учеными и экспериментаторами, предшествовавшими теоретическим работам Галилея о падающих телах и тем самым опровергавшим утверждение Аристотеля о том, что более тяжелые тела падают быстрее легких.
Еще в 1544 году историк Бенедетто Варки сослался на фактические испытания, которые опровергли утверждение Аристотеля.
В 1576 г. Джузеппе Молетти, предшественник Галилея на кафедре математики в Падуанском университете, сообщил, что тела из одного и того же материала, но разного веса, а также тела одного объема, но из разного материала, сбрасываемые с высоты, достигают Земля одновременно.
В 1597 году Якопо Маццони из Пизанского университета сообщил, что он наблюдал объекты, падающие с одинаковой скоростью независимо от веса, и части объекта, падающие с той же скоростью, что и целое.
Самым известным из них является Саймон Стевин, который в 1586 году (за 3 года до Галилея) сообщил, что разные грузы падали на заданное расстояние за одно и то же время. Его эксперименты с помощью его друга Яна Корнеттса де Гроота проводились с использованием двух свинцовых шаров, один из которых был в десять раз тяжелее другого, которые он сбросил в тридцати футах от церковной башни в Делфте. по звуку ударов они сделали вывод, что шары падали с одинаковой скоростью, не такой, как утверждал Аристотель. Многие считают Стевина первым, кто провел эксперименты с падающими телами.
Тем не менее, есть некоторые свидетельства того, что Стивенс предшествовал Галилею, он не проводил свой эксперимент с научной точки зрения — он не измерял время, как это делал или предлагал Галилей, он не использовал математику как инструмент для обоснования своей теории, и как таковой неудивительно, что именно теории Галилея проложили путь Ньютону.
Подводя итог дискуссии, мы считаем, что Галилею следует приписать эксперименты с падающими телами и наклонной плоскостью, поскольку его работа привела к дальнейшему научному развитию, в то время как вклад других, который нельзя игнорировать, был если не бессмысленным, то в меньшей степени. наименее бесцельно.
Вместо этого мы предлагаем несколько безопасных экспериментов, чтобы продемонстрировать это явление.
1. Держите на кончиках пальцев разных рук монету и бумажный диск на высоте метра или более от пола. Выбросьте их обоих одновременно. Монета достигнет пола раньше бумажного диска. Из этого опыта можно сделать ошибочный вывод, что более тяжелые предметы падают быстрее.
2. Установите бумажный диск на монету и бросьте их вместе. Оба объекта достигнут земли одновременно. Смысл этого эксперимента в том, что не количество массы заставляет падающие тела падать быстрее или медленнее, а сопротивление/трение воздуха, потому что сопротивление воздуха здесь приложено только к монете, а не к бумажному диску, и отсюда мы можем сделать вывод, что сопротивление воздуха, а не количество массы мешало бумажному диску упасть быстрее — так же, как и монете.
Оба объекта достигнут земли одновременно. Смысл этого эксперимента в том, что не количество массы заставляет падающие тела падать быстрее или медленнее, а сопротивление/трение воздуха, потому что сопротивление воздуха здесь приложено только к монете, а не к бумажному диску, и отсюда мы можем сделать вывод, что сопротивление воздуха, а не количество массы мешало бумажному диску упасть быстрее — так же, как и монете.
Чтобы исключить возможность притяжения монеты и бумажного диска, можно показать, что они не слипаются ни в каком положении.
Эксперименты 1 и 2 взяты из:
Weiss Moshe, Physics by Experimental Demonstrations , vol II, Jerusalem: Rubin Mass, 1968, pp. 208-209 материалов, массы или формы в вакуумной камере (если она есть в вашей школе). Все предметы, брошенные с одной высоты, будут падать с одинаковой скоростью, независимо от их массы, потому что сопротивления воздуха нет.
4. Попробуйте поэкспериментировать с наклонными плоскостями и выясните, постоянно ли ускорение? Зависит ли ускорение от массы и диаметра катящегося тела, от угла наклона плоскости, от распределения массы тела, от того, является ли тело сферой или цилиндром, сплошным или полым? Попробуйте оценить влияние трения на ваши результаты, используя для своих экспериментов разные поверхности. http://collegeofsanmateo.edu…
http://collegeofsanmateo.edu…
5. Эксперимент с падающими телами может быть также экспериментально продемонстрирован путем сравнения движения маятника в воздухе с шариками из свинца и пробки, которые имеют разный вес, но в остальном похожи — период не зависит от веса боба.
Астронавт Аполлона-15 на Луне воссоздает знаменитый эксперимент Галилея.
Эксперимент Галилея по ускорению — Майкл Фаулер, Университет Вирджинии
Закон падения Галилея
Что такое объяснение Галилея? — Карл Мартикеан
Измерение ускорения гравитации — SMART
Аристотелевская физика — QuarkNet, FSU
Гравитация — Гиперфизика
Битва Галилея за небеса — PBS
Проводил ли Галилей эксперимент с Пизанской башней?
Битва Галилея за небеса — PBS
On Motion — The Galileo Project
Weights Make Haste: Lighter Linger — Новости науки Саймон Стевин Линкс
Саймон Стевин (1548—1620) — голландский инженер и математик.
 Его эксперименты по гидростатике показали, что давление, оказываемое жидкостью, зависит только от ее высоты по вертикали, а не от формы сосуда с жидкостью, и продемонстрировали принцип работы гидравлического пресса. Вероятно, он предвосхитил эксперименты Галилея с падающими телами. Стевину также приписывают введение десятичных знаков в обычное употребление.
Его эксперименты по гидростатике показали, что давление, оказываемое жидкостью, зависит только от ее высоты по вертикали, а не от формы сосуда с жидкостью, и продемонстрировали принцип работы гидравлического пресса. Вероятно, он предвосхитил эксперименты Галилея с падающими телами. Стевину также приписывают введение десятичных знаков в обычное употребление. Саймон Стевин — Проект «Галилео»
Саймон Стевин — Католическая энциклопедия
Саймон Стевин. Введение десятичных дробей — Филл Шульц, Университет Западной Австралии Стевинус — Британика 1911
Золотая нить в развитии механики
1История механики широко исследована в ряде исторических работ, в том числе классических книгах, таких как Мах (1960), Dugas (1988) и Clagett (1961), а также множество статей в различных академических журналах. Полная история от греков и средневековья через научную революцию до современной эпохи длинна и сложна. Тоже неполный. Исследования, проведенные на сегодняшний день, были на удивление тщательными, чтобы представить эмпирические открытия в надлежащей перспективе и прояснить огромную важность математических новшеств. Но на удивление мало внимания уделялось роли мысленных экспериментов в развитии механики. Конечно, многие историки справедливо подчеркивали важность реконцептуализации в истории науки и далее отмечали, что этот процесс был чем-то иным, чем наблюдение новых фактов. Но в центре внимания не были мысленные эксперименты как движущая сила таких концептуальных разработок. Ни в кинематике, ни в динамике мысленные эксперименты не получили своего исторического признания в их древней, средневековой, классической (ньютоновской) или современной (относительность и квантовая теория) формах, несмотря на их очевидную важность в развитии каждой из них. Мы надеемся, хотя бы частично, исправить это.
Тоже неполный. Исследования, проведенные на сегодняшний день, были на удивление тщательными, чтобы представить эмпирические открытия в надлежащей перспективе и прояснить огромную важность математических новшеств. Но на удивление мало внимания уделялось роли мысленных экспериментов в развитии механики. Конечно, многие историки справедливо подчеркивали важность реконцептуализации в истории науки и далее отмечали, что этот процесс был чем-то иным, чем наблюдение новых фактов. Но в центре внимания не были мысленные эксперименты как движущая сила таких концептуальных разработок. Ни в кинематике, ни в динамике мысленные эксперименты не получили своего исторического признания в их древней, средневековой, классической (ньютоновской) или современной (относительность и квантовая теория) формах, несмотря на их очевидную важность в развитии каждой из них. Мы надеемся, хотя бы частично, исправить это.
2Излишне говорить, что мы не можем надеяться быть исчерпывающими. Мы сосредоточимся только на одной теме — мысленных экспериментах в связи с инерцией и относительным движением. Даже в этом мы не начинаем с нуля. Эрнст Мах в процитированной выше книге воздал должное gedanken Experimenten , как он их назвал. А Александр Койре (1968) утверждал, что Галилей был прежде всего мысленным экспериментатором. Но эти исследования — только важное начало. Мы надеемся выйти за его пределы, но у нас нет иллюзий полноты даже в относительно узкой теме мысленных экспериментов и движения. Полное изучение даже одного периода в истории механики, конечно, должно включать в себя с трудом добытые эмпирические данные, разработку таких инструментов, как телескоп, и соответствующие математические инновации, а также мысленные эксперименты. Опять же, мы сосредоточимся только на последнем. Короче говоря, наша цель — представить краткую историю одного из аспектов механики с помощью мысленных экспериментов.
Даже в этом мы не начинаем с нуля. Эрнст Мах в процитированной выше книге воздал должное gedanken Experimenten , как он их назвал. А Александр Койре (1968) утверждал, что Галилей был прежде всего мысленным экспериментатором. Но эти исследования — только важное начало. Мы надеемся выйти за его пределы, но у нас нет иллюзий полноты даже в относительно узкой теме мысленных экспериментов и движения. Полное изучение даже одного периода в истории механики, конечно, должно включать в себя с трудом добытые эмпирические данные, разработку таких инструментов, как телескоп, и соответствующие математические инновации, а также мысленные эксперименты. Опять же, мы сосредоточимся только на последнем. Короче говоря, наша цель — представить краткую историю одного из аспектов механики с помощью мысленных экспериментов.
3Читатели могут захотеть, чтобы мы сначала дали определение мысленным экспериментам. Мы думаем, что лучше всего довольствоваться лишь грубой характеристикой. Мысленные эксперименты проводятся в «лаборатории разума». Это воображаемые ситуации, в которых мы обычно настраиваем вещи, запускаем их и смотрим, что происходит. Физики часто рассматривают гипотетические ситуации и рассуждают о них, но мысленные эксперименты более специализированы — гипотетическая ситуация должна быть визуализируемой; имеет экспериментальный характер. Как и в случае реальных экспериментов, результат мысленного эксперимента может опровергнуть одну теорию, поддержать другую или, возможно, проиллюстрировать какой-то сложный концептуальный вопрос. И опять же, как и настоящие эксперименты, они подвержены ошибкам.
Это воображаемые ситуации, в которых мы обычно настраиваем вещи, запускаем их и смотрим, что происходит. Физики часто рассматривают гипотетические ситуации и рассуждают о них, но мысленные эксперименты более специализированы — гипотетическая ситуация должна быть визуализируемой; имеет экспериментальный характер. Как и в случае реальных экспериментов, результат мысленного эксперимента может опровергнуть одну теорию, поддержать другую или, возможно, проиллюстрировать какой-то сложный концептуальный вопрос. И опять же, как и настоящие эксперименты, они подвержены ошибкам.
4Наша история, какой бы узкой она ни была, будет еще более усечена. Она должна начаться с греков и закончиться теорией относительности, но мы ограничимся, после некоторых греческих предположений, периодом позднего средневековья и ранней научной революции, годами, которые были решающими в развитии классической механики и идеи движения по инерции.
5 Как и во многих других случаях, нет лучшего места для начала, чем греки. Раннее представление о пространстве было запутанным и запутанным, но часто гениальным. Согласно Аристотелю (на которого мы опираемся во многом в наших знаниях о досократиках),
Раннее представление о пространстве было запутанным и запутанным, но часто гениальным. Согласно Аристотелю (на которого мы опираемся во многом в наших знаниях о досократиках),
- 1 1 Аристотель, Метафизика , А4, 985b4.
Левкипп и его сподвижник Демокрит считают, что элементы — это полнота и пустота; они называют их бытием и небытием соответственно. Бытие полно и твердо, небытие пусто и редко. Поскольку пустота существует не меньше, чем тело, отсюда следует, что небытие существует не меньше, чем бытие. Вместе они являются Материальными причинами существующих вещей1.
6 Сразу видно, почему пустота вызывала у греков столько споров. Само выражение идеи проблематично. Пустота — это ничто, это небытие. Итак, можно было бы естественно заключить, что, поскольку пустота вообще ничто, ее нет и не может быть. Именно к такому выводу пришли многие, включая Парменида. Идея пустоты была отвергнута как нелогичная бессмыслица. Тем не менее, для многих других пустота была необходима, иначе как могли бы вещи двигаться, если бы у них не было пустого места, куда можно было бы двигаться?
Идея пустоты была отвергнута как нелогичная бессмыслица. Тем не менее, для многих других пустота была необходима, иначе как могли бы вещи двигаться, если бы у них не было пустого места, куда можно было бы двигаться?
7Парменид и его последователи процветали примерно в то же время, что и ранние атомисты (5 век до н.э.). Их возражение было простым: пустота — это ничто, и ничто не может существовать как вещь. Все, что существует, должно быть непрерывным, недифференцированным целым. Изменение требует, чтобы вещи двигались, но это было бы невозможно, так как нет места для чего-либо, куда можно было бы двигаться. Следовательно, вселенная неизменна, а видимость изменений и различий — полная иллюзия — реальность сильно отличается от того, чем кажется.
8Вклад Зенона в мировоззрение Парменида был порожден несколькими известными мысленными экспериментами. Они приняли форму парадоксов, в которых он хотел показать, что предположение здравого смысла о движении приводит к абсурду. В одном из этих парадоксов Зенон утверждает, что невозможно пересечь стадион. Прежде чем перейти на другую сторону, нужно добраться до середины. Но прежде чем достичь середины, нужно пройти четверть пути, и так 90 436 до бесконечности 90 437. Таким образом, чтобы пересечь стадион, нужно было пройти бесконечно много расстояний за конечное время, а это считалось невозможным.
Прежде чем перейти на другую сторону, нужно добраться до середины. Но прежде чем достичь середины, нужно пройти четверть пути, и так 90 436 до бесконечности 90 437. Таким образом, чтобы пересечь стадион, нужно было пройти бесконечно много расстояний за конечное время, а это считалось невозможным.
9Другой парадокс Зенона показывает, что Ахиллес не может догнать черепаху, если у черепахи есть фора. Неважно, как быстро может бежать Ахиллес, как медленно движется черепаха или как короток промежуток между ними. Если Ахиллес пробегает расстояние до того места, где черепаха стартовала за заданный интервал времени, то черепаха немного продвинулась вперед. Теперь Ахиллес должен пробежать это второе расстояние, но за это время черепаха продвинулась еще немного вперед. Хотя пропасть между ними становится меньше, таких промежутков, которые нужно преодолеть, бесконечно много, и Ахиллес не сможет достичь этого за конечное время.
10Вывод, который Зенон хочет, чтобы мы сделали из его парадоксов, заключается в том, что наши обычные представления о пространстве, времени и движении спутаны и противоречивы. Его мысленные эксперименты поддерживают Парменида, показывая, что противоположная точка зрения абсурдна, хотя и непоколебима. Внешний вид и реальность резко расходятся.
Его мысленные эксперименты поддерживают Парменида, показывая, что противоположная точка зрения абсурдна, хотя и непоколебима. Внешний вид и реальность резко расходятся.
11Как это часто бывает при фундаментальных разногласиях, modus ponens одной стороны является modus tollens другой стороны. Парменид и его последователи считали пустоту абсурдной, поэтому они сделали вывод, что движение невозможно. Атомисты перевернули это, утверждая, что движение очевидно возможно, и поэтому они пришли к выводу, что пустота все-таки должна существовать. То, что разделяют две стороны, является общей предпосылкой: движение требует пустоты . Греческая мысль о пространстве и движении казалась тупиковой, по крайней мере, до Аристотеля (384–322 гг. до н. э.).
12Пространство и время являются частью общей теории движения и изменения Аристотеля. Аристотеля интересовало не только то, как объект меняется из одного пространственного положения в другое, но и то, как желудь превращается в дуб. Короче говоря, он интересовался движением или изменением в самом общем смысле и использовал понятия 9.0436 потенциальность и актуальность в его объяснении. В описании Аристотеля есть ряд важных ингредиентов.
Короче говоря, он интересовался движением или изменением в самом общем смысле и использовал понятия 9.0436 потенциальность и актуальность в его объяснении. В описании Аристотеля есть ряд важных ингредиентов.
- 2 2 Различие между актуальной и потенциальной бесконечностью лежит в основе всех так называемых конструктивных действий (…)
13Во-первых, небытие бесконечного . Принято говорить, что на прямой бесконечно много точек. Большой успех аналитической геометрии (которая ставит действительные числа во взаимно однозначное соответствие с точками на линии), несомненно, объясняет это широко распространенное мнение. Это стало непререкаемым здравым смыслом. Но так ли это? Аристотель, конечно, думал, что нет. На линии (или на плоскости, или в пространстве) нет точек, кроме тех, которые мы делаем. Линия, по Аристотелю, есть истинный континуум. Он бесконечно делим в том смысле, что его можно делить снова и снова без ограничений. Если мы делаем разрез по линии (скажем, циркулем), то мы строим точку. Мы можем делать это неоднократно и без ограничений; то есть мы никогда не приходим к ситуации, когда мы не можем сделать это снова. Но на любом данном этапе процесса построения точек мы делаем только конечное число разрезов на линии, никогда не делаем так называемых 9 разрезов.0436 актуальная (или завершенная) бесконечность . Единственная бесконечность для Аристотеля — это потенциальная бесконечность 2.
Если мы делаем разрез по линии (скажем, циркулем), то мы строим точку. Мы можем делать это неоднократно и без ограничений; то есть мы никогда не приходим к ситуации, когда мы не можем сделать это снова. Но на любом данном этапе процесса построения точек мы делаем только конечное число разрезов на линии, никогда не делаем так называемых 9 разрезов.0436 актуальная (или завершенная) бесконечность . Единственная бесконечность для Аристотеля — это потенциальная бесконечность 2.
14 Имея в виду это объяснение бесконечности, Аристотель мог заняться парадоксами Зенона. Важнейшей предпосылкой аргументов Зенона является допущение, что пространство состоит из действительной бесконечности точек, а время — из действительной бесконечности моментов. Теория потенциальной бесконечности Аристотеля категорически это отрицает. Итак, рассуждения Зенона даже не могут начаться, поскольку необходимых предпосылок для мысленных экспериментов не существует.
- 3 3 Аристотель, Физика , 212a20.

15Вторая, естественное место и естественное движение . Природа, по Аристотелю, есть причина движения и изменения. Место определяется как «самая внутренняя неподвижная граница того, что оно содержит»3. Место вина в бутылке; место лодки в воде, которая непосредственно ее окружает. Это релятивистский взгляд на пространственное положение, особенно когда рассматривается движение. Но есть иерархия локаций. Место движущейся лодки — в воде; место проточной воды находится в берегах рек; место берегов реки …, и так далее. В окончательной схеме вещей есть стационарный центр вселенной, высшая система отсчета.
16Эти идеи используются в сложной и далеко идущей доктрине Аристотеля о естественном месте . Вселенная конечна в размерах (поскольку пространство не может быть фактически бесконечным), но ее нет нигде (поскольку нет вместилища). Есть центр Вселенной, и именно там находится Земля. Есть цель «вверх» и «вниз», определяемые радиальными линиями от центра Вселенной. Природа направляет вещи на их естественное место. Камень падает к центру Земли не из-за действия Земли, а потому, что камень стремится попасть на свое естественное место, в центр Вселенной. Если бы мы могли каким-то образом отодвинуть Землю на несколько тысяч километров, а затем уронить камень, мы бы не увидели, как он падает на Землю, а скорее он двигался бы к центру Вселенной. Точно так же есть естественное место для воды, которое находится чуть выше естественного места для земли, воздух выше этого и огонь, но опять же естественно выше воздуха. Будучи удалены со своих естественных мест, они стремятся вернуться на них.
Природа направляет вещи на их естественное место. Камень падает к центру Земли не из-за действия Земли, а потому, что камень стремится попасть на свое естественное место, в центр Вселенной. Если бы мы могли каким-то образом отодвинуть Землю на несколько тысяч километров, а затем уронить камень, мы бы не увидели, как он падает на Землю, а скорее он двигался бы к центру Вселенной. Точно так же есть естественное место для воды, которое находится чуть выше естественного места для земли, воздух выше этого и огонь, но опять же естественно выше воздуха. Будучи удалены со своих естественных мест, они стремятся вернуться на них.
17Подобно тому, как Аристотель апеллирует к «естественности» в своем определении места, у него есть соответствующая идея движения. Материальные объекты более или менее определяются Аристотелем с точки зрения их естественного движения. Это может показаться чуждым современному уху, но мы должны напомнить себе, что подобные свойства присутствуют в современной физике. В то время как электроны не определяются в терминах скоростей (допускаются любые скорости ниже скорости света), фотоны, например, характеризуются тем, что в каждой инерциальной системе отсчета они всегда движутся со скоростью c , движение для них «естественное». Согласно ньютоновской механике, пока на тело не действует сила, оно движется прямолинейно с постоянной скоростью. Это движение, движение по инерции, естественно для любого тела. Различие Аристотеля между естественными и неестественными движениями (которые он называл насильственными) имеет решающее значение. Несмотря на то, что мы сильно расходимся в деталях с Аристотелем, мы все же принимаем нечто похожее в различении кинематики (свободного движения) и динамики (движения под действием силы).
В то время как электроны не определяются в терминах скоростей (допускаются любые скорости ниже скорости света), фотоны, например, характеризуются тем, что в каждой инерциальной системе отсчета они всегда движутся со скоростью c , движение для них «естественное». Согласно ньютоновской механике, пока на тело не действует сила, оно движется прямолинейно с постоянной скоростью. Это движение, движение по инерции, естественно для любого тела. Различие Аристотеля между естественными и неестественными движениями (которые он называл насильственными) имеет решающее значение. Несмотря на то, что мы сильно расходимся в деталях с Аристотелем, мы все же принимаем нечто похожее в различении кинематики (свободного движения) и динамики (движения под действием силы).
18В аристотелевской вселенной есть четыре элемента: земля, вода, воздух и огонь, и их естественное местонахождение находится в концентрических кольцах вокруг центра вселенной. Помимо этих элементов есть пятый, эфир. Естественное движение четырех элементов происходит по радиальным линиям, проходящим через центр вселенной к своему естественному месту. Естественное движение эфира круговое, опять же вокруг центра вселенной.
Естественное движение эфира круговое, опять же вокруг центра вселенной.
19Почему естественное движение эфира круговое? Ответ Аристотеля прозвучал бы правдой для любого разумного слушателя до 17 века. Круговое движение, по его словам, идеально. Оно не только совершенно, но круговое движение уникально тем, что оставляет совершенное небесное царство совершенно неизменным. Он вращается вокруг Земли (помните, это центр Вселенной), как жесткое, неизменное целое.
20Третий, небытие пустоты . Аристотель отрицал существование пустоты, пустого пространства. Вселенная полна; повсюду есть вещи того или иного рода. В разных местах он выдвинул несколько аргументов против пустоты или истинного вакуума. Один из них звучит следующим образом: между различными областями пустоты нет никакого различия; он полностью однороден. Но камень, например, перемещается на свое естественное место, и для того, чтобы это произошло, одно место должно быть объективно отличным от другого. Поскольку одно место не отличается от другого в пустоте, движение в пустоте должно быть проблематичным, если не невозможным. Камень в пустоте был бы полностью дезориентирован; он не знал бы, какой путь вниз, и поэтому не знал бы, в каком направлении двигаться и двигаться ли вообще. Аристотелевское место обладает своего рода причинной силой или, по крайней мере, способностью указывать объекту, как двигаться; пустота не имеет такой силы.
Поскольку одно место не отличается от другого в пустоте, движение в пустоте должно быть проблематичным, если не невозможным. Камень в пустоте был бы полностью дезориентирован; он не знал бы, какой путь вниз, и поэтому не знал бы, в каком направлении двигаться и двигаться ли вообще. Аристотелевское место обладает своего рода причинной силой или, по крайней мере, способностью указывать объекту, как двигаться; пустота не имеет такой силы.
21У Аристотеля была очень большая проблема, о которой нужно было беспокоиться. Вспомните спор между атомистами и Парменидом. Оба согласились, что пустота необходима для движения, но Парменид считал пустоту абсурдной, поэтому движение должно быть невозможным, в то время как атомисты считали, что движение очевидно, поэтому пустота должна существовать. Аристотель хотел, чтобы было и то, и другое: есть движение, и оно происходит в полном пространстве.
22Конечно, казалось, что если бы все было заполнено вещами, то не было бы места для движения чего бы то ни было. Аристотель возражал, что движение в полости возможно до тех пор, пока одно тело движется в сторону для другого. Идея действительно очень проста. Представьте рыбу, плывущую по воде, которая смещается вперед и отходит назад по мере того, как рыба плывет. Мы вернемся к этому моменту.
Аристотель возражал, что движение в полости возможно до тех пор, пока одно тело движется в сторону для другого. Идея действительно очень проста. Представьте рыбу, плывущую по воде, которая смещается вперед и отходит назад по мере того, как рыба плывет. Мы вернемся к этому моменту.
23Четвертый, естественное движение против насильственного . Когда камень подбрасывается вверх, он, конечно, движется, но не естественно в аристотелевском смысле. Такое движение называлось «насильственным движением», и Аристотелю и его последователям в средние века было ужасно трудно разобраться в этом. Когда камень или копье покидают наши руки, почему они какое-то время остаются в своем неестественном движении и почему естественное движение в конце концов настигает их? Как мы только что упомянули, объяснение, которое, по-видимому, предпочитал Аристотель, утверждало, что воздух, который уходил с пути движущегося объекта, устремлялся назад (чтобы предотвратить образование вакуума), и это давало объекту толчок. Таким образом, объект будет оставаться в сильном движении даже после того, как он покинет наши руки. Процесс называется антиперистаз .
Таким образом, объект будет оставаться в сильном движении даже после того, как он покинет наши руки. Процесс называется антиперистаз .
24Наконец, мы должны указать также, что вселенная Аристотеля конечна в пространстве. Атомисты, как ранние, так и поздние, считали пустоту бесконечной. Лукреций ( De rerum natura ) предложил следующий умный мысленный эксперимент, чтобы доказать это. Предположим, что пространство только конечно. Тогда, если мы подходим к краю или границе, мы можем метнуть копье. Если он пролетает мимо предполагаемого края, то это все-таки не край. С другой стороны, если дротик отскакивает назад, то за краем должно быть что-то, что заставляет его отскакивать назад. Итак, еще раз, предполагаемое преимущество на самом деле не является преимуществом. Таким образом, пространство не имеет края; это бесконечно.
25Элегантные мысленные эксперименты, подобные этому, всегда доставляют удовольствие, даже если они не работают. Самое большее, что показал Лукреций, это то, что пространство безгранично, то есть у него нет края. Двумерное существо могло бы двигаться вокруг сферы (например, поверхности земли), бросая копье вперед и никогда не доходя до края. Сфера не ограничена. Но оно не бесконечно. Чего не учел Лукреций, так это возможности другой топологии. Конечно, это анахронизм. В свое время аргумент Лукреция был вполне убедительным.
Двумерное существо могло бы двигаться вокруг сферы (например, поверхности земли), бросая копье вперед и никогда не доходя до края. Сфера не ограничена. Но оно не бесконечно. Чего не учел Лукреций, так это возможности другой топологии. Конечно, это анахронизм. В свое время аргумент Лукреция был вполне убедительным.
26Смысл этого краткого раздела, посвященного представлениям греков о пространстве и движении, состоял в том, чтобы подготовить почву для Средневековья и раннего Нового времени. Трудности, с которыми они столкнулись, и используемые ими концептуальные инструменты — наследие греков. Средневековье было во власти Аристотеля и аристотелевской структуры. Подводя итог, можно сказать, что основные составляющие средневековой системы, унаследованной от Аристотеля, включают:
Объекты, которые мы видим вокруг себя, состоят из смеси четырех элементов: земли, воды, воздуха и огня. Небеса полностью состоят из эфира (пятого элемента или квинтэссенции).

Каждый элемент имеет естественное место и стремится к нему переместиться.
Естественным движением четырех элементов являются радиальные линии, проходящие через центр Вселенной. Естественное движение эфира круговое.
Сильное движение объясняется антиперистазом, при котором среда, через которую перемещается объект, активно отвечает за сохранение движения объекта.
Вселенная полна; вакуума нет.
Все, что движется, нуждается в двигателе. Нет ничего похожего на сохранение энергии или импульса; вещи естественным образом останавливаются на своих естественных местах.

Бог (неподвижный движитель или движители) постоянно привносит движение во вселенную.
27 Ниже мы подробнее остановимся на некоторых из этих пунктов. А пока подчеркнем, что здесь нет ничего похожего на понятие относительного движения или инерции. Мы будем придерживаться либерального взгляда на то, что такое инерция, но, чтобы быть разумным приближением к нашей современной концепции, она должна включать возможность движения, а также покоя как «естественного состояния» бытия.
28Почему камень, брошенный горизонтально, продолжает свое горизонтальное движение после того, как он покинул руку метателя? Это была серьезная головоломка, так как ее движение не является естественным. С точки зрения Аристотеля, он должен двигаться вниз, к своему естественному месту в центре вселенной. Такое неестественное движение называется «насильственным», и его объяснение было одной из центральных проблем в физике Аристотеля. Почему бурное движение продолжается после того, как объект был оторван от источника его движения?
Почему бурное движение продолжается после того, как объект был оторван от источника его движения?
29Согласно аристотелевской динамике, каждое движение предполагает движущего. Чтобы удовлетворить это требование для случая отрывного движения, Аристотель поясняет, что первопричина движения сообщает движущую силу не только самому снаряду, но и среде, окружающей движущийся объект:
- 4 Аристотель, Физика VIII.10.266b,27-267a.20, Clagett (пер.) 506.
Если верно, что все, что движимо… чем-то движимо, то почему некоторые вещи постоянно движутся, хотя то, что заставило их двигаться, уже не соприкасается с ними, как, например, брошенные вещи «… Мы должны, следовательно, считать, что первоначальное движение дает способность вызывать движение воздуху, или воде, или чему-либо другому, что естественным образом приспособлено как к движущемуся [т.
- 5 Аристотель, Физика VIII.
 10.266b,27-267a.20, Clagett (пер.) 507.
10.266b,27-267a.20, Clagett (пер.) 507. - 6 Аристотель, Физика VIII.10.266b,27-267a.20, Clagett (пер.) 506.
- 7 Аристотель, Физика VIII.10.266b,27-267a.20, Clagett (пер.) 507.
30Аристотелевская теория антиперистаза предполагает, что среда, хотя и остается неподвижной при движении через нее объекта, тем не менее «одновременно [вместе с объектом] получает силу или силу действовать как движущее»5. Таким образом, частицы воздуха, находящиеся ближе всего к первоначальному двигателю, например, получают полную движущую силу — часть этой силы они передают соседним частицам, которые затем передают уменьшенную часть движущей силы другим частицам, и так далее. Каждая последующая «волна» воздуха активно толкает снаряд благодаря «способности вызывать движение»6, которую он получает от соседней воздушной волны. Сопротивление заставляет эту движущую силу постепенно расходоваться. Движение объекта «наконец прекращается, когда член ряда [частиц в среде], непосредственно предшествующий, уже не делает следующий движущимся, а только вызывает его движение»7.
Движение объекта «наконец прекращается, когда член ряда [частиц в среде], непосредственно предшествующий, уже не делает следующий движущимся, а только вызывает его движение»7.
31 Важно отметить, что в аристотелевской динамике сопротивление играет фундаментальную роль. Без него не могло бы иметь место никакое движение.
- 8 Анонимная трактовка перипатетической динамики , 460, Clagett (пер.) 451.
Без сопротивления движение не происходит, а отсутствие сопротивления является причиной того, что простое тело не движется в вакууме. Так как простое тело не имеет собственного сопротивления, а в вакууме нет внешнего сопротивления, и [далее] нет никакого сопротивления, кроме внутреннего или внешнего [сопротивления], то и простое тело не имеет сопротивления и, следовательно, не движется в вакууме. Так как без сопротивления движение не происходит, кроме бесконечно быстрого, то чистое простое тело не может двигаться в вакууме, если только оно не должно двигаться бесконечно быстро; потому что если бы это было так, то он сразу же пересек бы пространство, что невозможно8.
32Динамика антиперистаза (при резком движении среда толкает движущееся тело) оставалась доминирующей в глубоком Средневековье, но страдала от концептуальных и эмпирических проблем. Некоторые из наиболее эффективных и влиятельных критических замечаний пришли в форме мысленных экспериментов, особенно предложенных Жаном Буриданом.
- 9 Некоторые доходят до того, что говорят: «Едва ли можно сомневаться в том, что импульс аналогичен позднейшей инертности (…)
33Натурфилософия XIV века была отмечена переходным периодом. Такие мыслители, как Жан Буридан (ок. 1300–ок. 1361) и его ученица Николь Орем (1323–1382), подвергли серьезной критике господствующую аристотелевскую теорию динамики. Вместо этого они предложили теорию импульса, которая объясняет, что источник движения находится не в среде (т. е. перемещение в естественное место или толкание среды), а скорее в самом движущемся объекте. В некотором смысле это развитие предвосхищает открытие законов инерции9. Галилео Галилея (1564–1642) и Рене Декарта (1596–1650) два века спустя. Что объединяет Буридана, Орема и Галилея, так это их совместное использование мысленных экспериментов, многие из которых являются одними из самых блестящих из когда-либо задуманных.
Галилео Галилея (1564–1642) и Рене Декарта (1596–1650) два века спустя. Что объединяет Буридана, Орема и Галилея, так это их совместное использование мысленных экспериментов, многие из которых являются одними из самых блестящих из когда-либо задуманных.
34Каждый из мысленных экспериментов, которые мы обсудим, идентифицирует некоторый пример отстраненного (т. е. насильственного) движения (будь то поступательное или круговое), которое предположительно происходит из опыта и тем не менее не может быть объяснено принципами аристотелевской динамики. В каждом случае предполагается, что читатель сделает вывод, что теория Аристотеля имеет серьезные недостатки.
35Комментарий Буридана к книге Аристотеля «Физика » содержит следующие разрушительные мысленные эксперименты, некоторые из которых близки к сообщениям о реальном опыте, а другие более гипотетичны. Все они направлены против аристотелевской теории антиперистаза.
- 10 Буридан, Вопросы физики Аристотеля , VIII.
12.2, Clagett (пер.) 533.
Копье, имеющее коническую заднюю часть, такую же острую, как и передняя, будет двигаться после выброса так же быстро, как и без острой конической задней части. Но, конечно, следующий воздух не мог бы толкнуть таким образом острый конец, потому что воздух был бы легко разделен остротой10.
- 11 Буридан, Вопросы физики Аристотеля, VIII.12.2, Clagett (пер.) 533.
Корабль, стремительно тянущийся по реке даже против течения реки, после прекращения рисования не может быть быстро остановлен, а продолжает движение длительное время. И все же матрос на палубе не чувствует толкающего его сзади воздуха. Он чувствует только воздух спереди, сопротивляющийся ему11.
- 12 Буридан, Вопросы физики Аристотеля , VIII.12.2, Clagett (пер.) 533.
36 Опять же, предположим, что упомянутое судно было загружено зерном или лесом, а человек находился в задней части груза. Тогда, если бы воздух имел такой импульс, что мог бы толкать корабль так сильно, человек был бы очень сильно зажат между этим грузом и воздухом, следующим за ним. Опыт показывает, что это неверно12.
Тогда, если бы воздух имел такой импульс, что мог бы толкать корабль так сильно, человек был бы очень сильно зажат между этим грузом и воздухом, следующим за ним. Опыт показывает, что это неверно12.
- 13 Буридан, Вопросы физики Аристотеля , VIII.12.2, Clagett (пер.) 533.
Или, по крайней мере, если бы корабль был нагружен зерном или соломой, следующий и толкающий воздух сложил бы стебли, которые были в корме. Все это ложь13.
37Мораль ясна. В любом случае воздух не может двигать те самые объекты, для перемещения которых он предназначен. Если бы это было так, мы бы заметили эффекты, явно противоречащие обычному опыту и ожиданиям. Антиперистаз не может объяснить эти случаи насильственного движения.
38В другом мысленном эксперименте Буридана используется очень прямая аналогия между запуском снаряда вместе с окружающим воздухом и толканием окружающего воздуха самим по себе.
- 14 Буридан, Вопросы физики Аристотеля, VIII.12.3, Clagett (пер.) 534.
Вы могли бы, толкая свою руку, перемещать соседний воздух, если в вашей руке ничего нет, так же быстро или быстрее, как если бы вы держали в руке камень, который хотите спроецировать. Следовательно, если этот воздух благодаря скорости своего движения имеет достаточно сильное побуждение, чтобы быстро двигать камень, то кажется, что если бы я гнал к вам воздух с такой же скоростью, то воздух должен был бы толкать вас стремительно и с силой. ощутимая сила. [Тем не менее] мы бы этого не восприняли14.
39Этим мысленным экспериментом Буридан делает доводы против антиперистаза еще более разрушительными. Если я брошу в тебя большой камень, будет больно. Но если я выброшу такое же количество воздуха, которое толкает камень, вам это покажется пустяком. Этот мысленный эксперимент имеет тот же эмпирический оттенок, что и любой великий эксперимент, но вывод настолько очевидно абсурден, что мы не чувствуем необходимости его проводить.
40Структура этих мысленных экспериментов обычная. Мы создаем условия, но обнаруживаем, что все идет не так, как требует теория. Вывод, который мы делаем, состоит в том, что теория неверна. Многие из знаменитых мысленных экспериментов Галилея, как мы увидим, имеют именно такую форму. И некоторые из Эйнштейна тоже. Известно, что он представил себе погоню за световым лучом, чтобы увидеть, как будет выглядеть фронт электромагнитной волны. Это привело к абсурду. Такие негативные мысленные эксперименты часто очень эффективны, говоря нам, что ложно, но не говорят нам, что правда. Так обстоит дело с Буриданом до сих пор. Мы можем видеть, что неправильно, но еще не можем видеть, что правильно. Так будет и в следующих нескольких примерах. Позже мы увидим мысленные эксперименты, которые сыграют положительную роль в приходе к новой теории.
41Теперь мы обратимся к круговому движению, которое представляет особенно сложную задачу для антиперистаза . В этом мысленном эксперименте мы должны рассмотреть волчок и кузнечную мельницу (тяжелое каменное колесо для измельчения зерна),
- 15 Буридан, Вопросы физики Аристотеля , VIII.
12.2, Clagett (пер.) 533.
которые долго перемещаются и не покидают своих мест. Следовательно, нет необходимости, чтобы воздух следовал за ним, чтобы заполнить место отправления такого волчка и кузнечной мельницы. Таким образом, нельзя сказать [что волчок и кузнечная мельница приводятся в движение воздухом] таким образом15.
42Воздуху нет необходимости заполнять места, освобождаемые вращающимся объектом, так как эти места заполняются другими частями самого объекта. И все же колесо движется. Антиперистаз в лучшем случае беспричинен в таких случаях, а в худшем — совершенно ложный.
43Еще один мысленный эксперимент, связанный с движением в отрыве, особенно интересен, потому что, как и другие, он кажется выполнимым, но на самом деле выполнить его довольно сложно. Тем не менее, результат кажется совершенно очевидным, если просто представить себе ситуацию.
- 16 Буридан, Вопросы физики Аристотеля, VIII.
12.3, Clagett (пер.) 534.
Если перекрыть воздух со всех сторон возле кузнечной мельницы тканью, то мельница от этого не останавливается, а еще долго продолжает двигаться. Поэтому он не перемещается по воздуху16.
44Этот мысленный эксперимент отличается от предыдущих примеров тем, что представляет собой попытку Буридана создать идеализированный или полностью «контролируемый» экспериментальный сценарий. Все мысленные эксперименты, с которыми мы сталкивались до сих пор, опровергают теорию о том, что воздух (или среда в целом) отвечает за метательное или круговое движение. Однако все, чего достигают предыдущие контрпримеры Буридана, — это демонстрация того, что воздух не «толкает» или «взаимно замещает» себя позади движущегося объекта. Однако примеры вполне реалистичны и предполагают, что объекты остаются погруженными в воздух. Таким образом, умный аристотелевец мог бы выдвинуть какую-то динамическую теорию, которая по-прежнему включает среду — возможно, как таинственный «невоспринимаемый» или «ненаблюдаемый» двигатель. Последний мысленный эксперимент Буридана — единственный, который может противостоять этому неоаристотелевскому возражению. Это потому, что он на самом деле предлагает полностью удаляет воздух из сценария, что делает невозможным, чтобы среда отвечала за поддержание автономного движения. В отличие от предыдущих мысленных экспериментов, которые включали обычные повседневные действия, такие как метание копий и наблюдение за проплывающими кораблями, Буридан предлагает абстрагироваться от обычного сценария «просто» прялки. Правда, далеко не ясно, к чему приведет «перекрытие воздуха со всех сторон около кузнечной мельницы тканью». Неужели Буридан хочет, чтобы мы представили себе колесо, вращающееся в полном вакууме? Возможно, все, что он имеет в виду, это то, что ткань должна облегать прялку как можно плотнее, фактически не касаясь ее. В любом случае ясно, что Буридан строит этот последний мысленный эксперимент так, что воздух может играть никакой роли в движении колеса.
Последний мысленный эксперимент Буридана — единственный, который может противостоять этому неоаристотелевскому возражению. Это потому, что он на самом деле предлагает полностью удаляет воздух из сценария, что делает невозможным, чтобы среда отвечала за поддержание автономного движения. В отличие от предыдущих мысленных экспериментов, которые включали обычные повседневные действия, такие как метание копий и наблюдение за проплывающими кораблями, Буридан предлагает абстрагироваться от обычного сценария «просто» прялки. Правда, далеко не ясно, к чему приведет «перекрытие воздуха со всех сторон около кузнечной мельницы тканью». Неужели Буридан хочет, чтобы мы представили себе колесо, вращающееся в полном вакууме? Возможно, все, что он имеет в виду, это то, что ткань должна облегать прялку как можно плотнее, фактически не касаясь ее. В любом случае ясно, что Буридан строит этот последний мысленный эксперимент так, что воздух может играть никакой роли в движении колеса. Этот шаг к идеализации устраняет все сомнения в несостоятельности аристотелевской динамики.
Этот шаг к идеализации устраняет все сомнения в несостоятельности аристотелевской динамики.
45Забегая вперед к Галилею, мы видим такую же реакцию на антиперистаз. В следующем мысленном эксперименте Галилей использует аналогию, чтобы выдвинуть аргумент против аристотелевской теории движения снарядов.
- 17 Галилей, Диалог , 153.
САГРЕДО: Если бы я положил на этот стол две стрелы, когда дул сильный ветер, одну в направлении ветра, а другую поперек, ветер бы быстро унес последнюю и оставил первую. Теперь, по-видимому, то же самое должно было бы произойти с двумя выстрелами из лука, если бы учение Аристотеля было верно, потому что выстрел в сторону был бы пришпорен большим количеством воздуха, приводимого в движение тетивой, — на всю длину стрелы — тогда как другая стрела получит импульс только от того количества воздуха, которое находится в крошечном круге ее толщины. 907:47 Симплицио: Я никогда не видел, чтобы стрела была выпущена вбок, но я думаю, что она не прошла бы и одной двадцатой расстояния одного острия выстрела17.
46Этот мысленный эксперимент вполне мог исходить от Буридана. И Галилей чувствовал бы себя как дома на любом из примеров Буридана. Нападая на Аристотеля, они во многом взаимозаменяемы. Но то, как они реагировали на проблемы с Аристотелем, как мы увидим, совершенно другое.
47 Продолжая тему воздуха, ответственного за движение, Галилей указывает на другой тип проблемы, на этот раз касающейся относительного веса различных вещей и того факта, что сам воздух имеет наименьший вес из всех.
- 18 Галилей, Диалог , 152.
САЛЬВИАТИ: [Подумайте, что произойдет], если две веревки одинаковой длины будут подвешены… к концу одной из них прикреплен свинцовый шарик, а к другому – ватный тампон. Как вы думаете, какой из этих маятников будет двигаться дольше, прежде чем остановится вертикально?
SIMPLICIO: Свинцовый шар ходил туда-сюда очень много раз; ватный тампон, максимум два или три.
САЛЬВИАТИ: Если маятники только что показали нам, что чем меньше движущееся тело имеет часть веса, тем меньше оно способно сохранять движение, то как же может быть, что воздух, который вообще не имеет веса в воздухе, является единственной вещью? что сохраняет приобретенное движение?18
48 Галилей дает нам начало положительного объяснения того, почему тяжелый маятник качается дольше, чем легкий (и что вообще вызывает бурное движение). Согласно приведенной выше аналогии, плотные твердые объекты способны «сохранять движение», а газообразный воздух — нет. Таким образом, Галилей утверждает, что все, что может быть источником движения снаряда, находится не в среде, через которую движется объект, а в самом объекте. Мысленный эксперимент не только представляет правдоподобный феномен, с помощью которого можно опровергнуть конкурирующую динамическую теорию Аристотеля, но и начинает развивать положительное объяснение движения снаряда.
- 19 Галилео, Диалог , 154.

49Некоторые из наиболее важных мысленных экспериментов Галилея по теме движения по инерции можно найти в контексте его рассуждений о суточном вращении Земли. На самом деле «Диалог о двух главнейших мировых системах» главным образом посвящен опровержению теории Аристотеля о том, что земля стоит на месте, а небеса вращаются вокруг нее. Обсуждение Галилея несколько предваряется в «9» Орема.0436 Le Livre du ciel et du monde , где автор также сталкивается с геоцентрической моделью Вселенной Птолемея с неподвижной Землей. Оказывается, и Птолемей, и Аристотель аргументируют свою позицию посредством мысленных экспериментов, включающих аналогии. Таким образом, Ореме и Галилею не хватает работы. Каждый указывает на ошибочность аналогий своих предшественников и пересматривает их мысленные эксперименты, чтобы явно включить то, что позже стало известно как принцип относительности Галилея (т. ускоренный, манера). Конечный результат, по словам Галилея Сальвиати, несколько неубедителен: «[Я утверждал] только для того, чтобы показать, что из экспериментов, предложенных [аристотелианцами] в качестве одного из аргументов в пользу неподвижности [Земли], нельзя сделать никаких выводов»19. . Поскольку на локальное кинематическое поведение объектов не повлияло бы равномерное вращение Земли (строго говоря, поскольку Земля ускоряется за счет вращения, ее нельзя считать инерциальной системой отсчета), мы не можем использовать мысленные эксперименты, чтобы решить вопрос одним способом. или другое. Хотя Орем и Галилей не смогли предоставить нам успешный положительный аргумент в пользу вращения Земли, опираясь на принцип относительности Галилея, они имплицитно принимают новую динамическую теорию: закон инерции .
. Поскольку на локальное кинематическое поведение объектов не повлияло бы равномерное вращение Земли (строго говоря, поскольку Земля ускоряется за счет вращения, ее нельзя считать инерциальной системой отсчета), мы не можем использовать мысленные эксперименты, чтобы решить вопрос одним способом. или другое. Хотя Орем и Галилей не смогли предоставить нам успешный положительный аргумент в пользу вращения Земли, опираясь на принцип относительности Галилея, они имплицитно принимают новую динамическую теорию: закон инерции .
50 Вот два мысленных эксперимента аналогического типа, которые претендуют на доказательство неподвижности Земли. В первом примере Птолемей проводит аналогию между движущимся кораблем и землей.
- 20 Орем, Le Livre du ciel et du monde , Самбурский (пер.) 161.
Если бы кто-то был на корабле, быстро движущемся на восток, и если бы он выпустил стрелу прямо вверх, она бы упала не в корабль, а очень далеко, на запад.
И точно так же, если бы земля двигалась очень быстро, поворачиваясь с запада на восток, предположим, что кто-то бросил бы камень прямо вверх, то он упал бы не в том месте, откуда он стартовал, а далеко к западу; а бывает и наоборот20.
51И, таким образом, Земля не может двигаться. В свое время этот мысленный эксперимент был столь же впечатляющим, сколь и простым.
52 Второй мысленный эксперимент, который Галилей приписывает последователям Аристотеля, несколько более основательно делает тот же самый вывод.
- 21 Галилей, Диалог , 126.
- 22 Галилей, Диалог , 144.
САЛЬВИАТИ: [Вот что] считается неопровержимым аргументом в пользу того, что Земля неподвижна. Ибо если бы он совершал дневное вращение, то башня, с вершины которой упал бы камень, увлекаемый вращением земли, переместилась бы на многие сотни ярдов на восток за то время, когда камень сгорит при падении, и камень должен удариться о землю на таком расстоянии от основания башни.
Этот эффект [аристотелевцы] подтверждают другим экспериментом, заключающимся в том, чтобы сбросить свинцовый шар с вершины мачты покоящейся лодки, отметив место, где он ударяется, близкое к подножию мачты; но если тот же самый мяч будет брошен из того же места во время движения лодки, он ударится на том расстоянии от подножия мачты, которое лодка прошла за время падения грузила, и ни по какой другой причине, кроме что естественное движение выпущенного мяча происходит по прямой к центру земли31.
Итак, вы говорите, что, поскольку, когда корабль стоит на месте, камень падает к подножию мачты, а когда корабль движется, он разваливается оттуда, то, наоборот, от падения камня к подножию сделал вывод, что корабль стоит на месте, и по его падению можно заключить, что этот корабль движется. А так как то, что происходит на земле, то из падения камня у подножия башни необходимо сделать вывод о неподвижности земного шара22.
- 23 Галилей, Диалог , 144.
В обоих мысленных экспериментах аналогии между движущейся лодкой и «движущейся землей» кажутся вполне уместными. Таким образом, единственный шанс опровергнуть их заключается в оспаривании центрального предположения. Ведь почему снаряд, выпущенный из движущегося объекта, должен «отставать»? Согласно аристотелевской динамике, это «не по какой другой причине, кроме того, что естественное движение выпущенного на свободу мяча происходит по прямой линии к центру земли»23.
53Оресме и Галилей расходятся во мнениях. Оба оспаривают это предположение и предлагают альтернативную схему, в которой снаряд, выпущенный из движущегося объекта, в некотором смысле сохраняет движение, которое было ему ранее сообщено.
54Оресме прямо опровергает основное предположение о том, куда упадет тело, утверждая, что если бы Земля вращалась, она увлекла бы за собой атмосферу. (Это предвосхищает предположения об «эфирном сопротивлении», которые будут сделаны в конце 19 века. -го -го века, чтобы объяснить неожиданные результаты в оптических экспериментах.) Следовательно, если бы стрела была выпущена вертикально вверх, движущийся воздух отвечал бы за удержание стрелы на пути, пока она падает обратно к исходной точке. Таким образом, только по тому, что камень возвращается к месту своего происхождения, мы не можем заключить ничего о движении Земли.
-го -го века, чтобы объяснить неожиданные результаты в оптических экспериментах.) Следовательно, если бы стрела была выпущена вертикально вверх, движущийся воздух отвечал бы за удержание стрелы на пути, пока она падает обратно к исходной точке. Таким образом, только по тому, что камень возвращается к месту своего происхождения, мы не можем заключить ничего о движении Земли.
- 24 Орем, Le Livre du ciel et du monde , Самбурский (пер.) 162.
О стреле или камне, брошенном вверх и т. д., можно сказать, что выпущенная стрела очень быстро движется на восток вместе с воздухом, через который она проходит, и со всей массой нижней части мира, которая движется с суточным движением; и по этой причине стрела падает обратно на то место на земле, откуда она стартовала24.
55 Сам факт того, что снаряд, запущенный вертикально вверх, возвращается в исходное положение, ничего не подтверждает. Это может быть результатом того, что Земля стоит на месте, или это может быть так же легко объяснено в модели Коперника с атмосферным сопротивлением. Дело в том, что мысленный эксперимент Птолемея терпит неудачу, потому что он не принимает во внимание что-то вроде принципа относительности Галилея. Орем, однако, явно обладает по крайней мере интуитивным пониманием относительного движения, если не полноценным движением по инерции.
Это может быть результатом того, что Земля стоит на месте, или это может быть так же легко объяснено в модели Коперника с атмосферным сопротивлением. Дело в том, что мысленный эксперимент Птолемея терпит неудачу, потому что он не принимает во внимание что-то вроде принципа относительности Галилея. Орем, однако, явно обладает по крайней мере интуитивным пониманием относительного движения, если не полноценным движением по инерции.
56Настоящая проблема здесь заключается в относительности движения, а не в антиперистазе. Даже если признать, ради аргумента, что Аристотель прав в своей динамике, проблема вращения Земли все еще не решена. Галилей делает то же самое. Коперниканская модель Вселенной как таковая вполне совместима с принципами аристотелевской динамики. Все, что нужно сделать, это постулировать среду, которая обычно отвечает за движение снаряда, который также вращается вместе с землей. Следовательно, сам движущийся воздух гарантирует, что камень «следует» за горизонтальным движением башни.
- 25 Галилей, Диалог , 143.
САЛЬВИАТИ: Я мог бы добавить по крайней мере ту часть воздуха, которая ниже самых высоких гор, должна быть унесена и унесена шероховатостью земной поверхности или должна естественным образом следовать суточному движению, потому что представляет собой смесь различных земные пары и выделения. Тот [объект], который покидает вершину башни, оказывается в среде, движущейся так же, как и весь земной шар, так что он не только не сталкивается с препятствиями из-за воздуха, но скорее следует общему курсу земли с помощью земного шара. воздух25.
57Чтобы сделать этот тезис более правдоподобным, следующий мысленный эксперимент Галилея опирается на аналогию между летящим орлом и движущейся землей. Согласно Галилею, если ветер сообщает некоторое горизонтальное движение сброшенному орлом полезному грузу, он также может быть ответственен за «наклонную» параболическую траекторию камня, сброшенного с башни. Обратите внимание, что Галилей говорит об использовании «мысленного зрения», чтобы представить себе эту аналогию — он явно представляет этот аргумент как мысленный эксперимент.
Обратите внимание, что Галилей говорит об использовании «мысленного зрения», чтобы представить себе эту аналогию — он явно представляет этот аргумент как мысленный эксперимент.
- 26 Галилей, Диалог , 143.
САЛЬВИАТИ: Если вы хотите представить более подходящий опыт, вы должны сказать, что можно было бы наблюдать (если не реальными глазами, то хотя бы глазами ума), если бы орел, носимый силой ветра, должен был выронить камень из своих когтей. Так как этот камень уже летел наравне с ветром, а затем вошел в среду, движущуюся с той же скоростью, я почти уверен, что он не будет виден падающим перпендикулярно, а, следуя направлению ветра и добавляя к этому, что собственного веса, будет двигаться по наклонной траектории36.
58 Важно отметить, что сам Галилей не намерен слишком полагаться на эту последнюю аналогию. В конце концов, как мы вскоре увидим, он категорически возражает против того, что среда ответственна за движение снаряда. Скорее, Галилей просто хочет указать, что траектория не всегда такая, какой кажется. Таким образом, даже убежденный сторонник Аристотеля должен признать, что, хотя с точки зрения орла кажется, что сброшенный полезный груз падает по прямой вертикальной линии вниз, земной наблюдатель видит, как камень очерчивает параболический путь. Если аристотелевец хочет, он может приписать это движение ветру, несущемуся за орлом.
Скорее, Галилей просто хочет указать, что траектория не всегда такая, какой кажется. Таким образом, даже убежденный сторонник Аристотеля должен признать, что, хотя с точки зрения орла кажется, что сброшенный полезный груз падает по прямой вертикальной линии вниз, земной наблюдатель видит, как камень очерчивает параболический путь. Если аристотелевец хочет, он может приписать это движение ветру, несущемуся за орлом.
59Ответ Орема Птолемею включает в себя несколько коротких мысленных экспериментов, подтверждающих его тезис по аналогии.
- 27 Орем, Le Livre du ciel et du monde , Самбурский (пер.) 162-163.
И [траектория стрелы] кажется возможной, если рассмотреть аналогичный случай; предположим, что человек находится на корабле, плывущем очень быстро на восток, не замечая этого движения, и предположим, что он быстро опускает руку на мачту корабля, ему покажется, что его рука двигалась только в прямая линия; и таким образом, согласно этому мнению, случай со стрелой, которая поднимается или падает прямо вверх или прямо вниз, кажется нам сходным27.
60Оресме выявляет ошибку в центральном предположении Птолемея и Аристотеля: только в системе отсчета, «абсолютно» покоящейся, законы движения могут соответствовать нашему опыту. Неверная посылка должна быть заменена, настаивает Орем, пониманием движения как чисто относительного явления. Таким образом, Орем оставляет нас в агностическом состоянии, не имея возможности выбирать между соперничающими версиями — птолемеевскими или коперниковскими. Он предлагает нам контрмысленный эксперимент, в результате которого первая нейтрализуется, но не решается вопрос в пользу альтернативы. Когда дело доходит до вращения Земли, вина не столько в динамической теории (включая антиперистаз), сколько в неспособности признать необходимость чего-то вроде относительности движения.
61Контрмысленные эксперименты имеют довольно сложную структуру. Экспериментальная часть находится посередине. Как правило, есть установка, за которой следует заявление о каком-то явлении, за которым следует объяснение, которое мы склонны считать результатом мысленного эксперимента. На самом деле контрмысленные эксперименты подрывают некоторые другие мысленные эксперименты, которые ранее считались убедительными. Таким образом, впервые появился мысленный эксперимент Ньютона с ведром, который он использовал для аргументации в пользу абсолютного пространства. 1Начнем с ведра, наполовину наполненного водой. Его привязывают к скрученной веревке, отпускают и начинают крутить. Поверхность воды, изначально плоская и покоящаяся по отношению к ведру, со временем становится вогнутой. Чем это вызвано? Ответ Ньютона заключается в том, что система ведра с водой (каждая часть которой покоится по отношению к любой другой части) должна двигаться — вращаться — по отношению к самому пространству. Итак, пространство должно быть самостоятельным.
На самом деле контрмысленные эксперименты подрывают некоторые другие мысленные эксперименты, которые ранее считались убедительными. Таким образом, впервые появился мысленный эксперимент Ньютона с ведром, который он использовал для аргументации в пользу абсолютного пространства. 1Начнем с ведра, наполовину наполненного водой. Его привязывают к скрученной веревке, отпускают и начинают крутить. Поверхность воды, изначально плоская и покоящаяся по отношению к ведру, со временем становится вогнутой. Чем это вызвано? Ответ Ньютона заключается в том, что система ведра с водой (каждая часть которой покоится по отношению к любой другой части) должна двигаться — вращаться — по отношению к самому пространству. Итак, пространство должно быть самостоятельным.
62Мах позже провел контрмысленный эксперимент, утверждая, что вода в ведре с очень толстыми стенками а не поднялась бы по стенкам, если бы ведро вращалось. Конечно, у нас нет оснований верить утверждению Маха, но из его контрмысленного эксперимента мы видим, что утверждения Ньютона о том, что произойдет с ведром в пустом пространстве, не столь очевидны и неизбежны, как мы думали раньше. Нам не нужно принимать положительное заключение Маха о том, что всякое движение должно быть движением относительным, но мы находим, что его встречный мысленный эксперимент подорвал ньютоновский. И именно это мысленный эксперимент Орема сделал с Птоломеем. (Подробнее об экспериментах с контрмыслью см. Brown 2007.)
Нам не нужно принимать положительное заключение Маха о том, что всякое движение должно быть движением относительным, но мы находим, что его встречный мысленный эксперимент подорвал ньютоновский. И именно это мысленный эксперимент Орема сделал с Птоломеем. (Подробнее об экспериментах с контрмыслью см. Brown 2007.)
63 Теперь обратимся к Галилею. Мы увидим, что, хотя мысленные эксперименты Галилея во многом аналогичны экспериментам Орема, они обеспечивают более строгое обоснование своих предположений. Первый мысленный эксперимент не вводит новую аналогию, а вместо этого, подобно первому аргументу Орема, ставит под сомнение лежащее в основе динамическое предположение Аристотеля (то есть, что если бы Земля вращалась, снаряд, запущенный вертикально вверх, «отставал бы» от своей точки происхождения). Это тоже контрмысленный эксперимент.
- 28 Галилей, Диалог , 139-140.
САЛЬВИАТИ: Но если бы случилось так, что земля вращалась и, следовательно, несла бы башню, и если бы было видно, что падающий камень точно так же касается края башни, то каким должно было бы быть его движение?… Движение было бы быть соединением двух движений; тот, которым он измеряет башню, и другой, которым он следует за ней.
Из этого соединения следовало бы, что скала описывает уже не эту простую прямую перпендикулярную линию, а косую, а может быть, и не прямую… Следовательно, только по тому, что падающий камень задел башню, нельзя было с уверенностью сказать, что она описывает прямой и перпендикулярной линии, если вы сначала не предположили, что земля стоит на месте28.
64 Галилей ясно объясняет, что простое наблюдение за падающим камнем само по себе не дает результатов. Он явно поддерживает относительность движения. Движение можно воспринимать только относительно собственной инерциальной системы отсчета. То есть никакой объект, движущийся с той же скоростью, что и наблюдатель, не может помочь этому наблюдателю определить, действительно ли он движется. Никаких «странных» кинематических эффектов не возникает в системах отсчета, движущихся с постоянной скоростью. Чтобы проиллюстрировать относительность движения и, по аналогии, бесполезность использования земных экспериментов для определения того, вращается ли сама Земля, Галилей представляет следующий мысленный эксперимент, один из самых эффективных:0014
- 29 Галилей, Диалог , 186.
САЛЬВИАТИ: Запритесь с каким-нибудь другом в главной каюте под палубой на каком-нибудь большом корабле и возьмите с собой мух, бабочек и других мелких летающих животных. Возьмите большую миску с водой и положите в нее рыбу; повесьте бутылку, которая опустошается по капле, в широкий сосуд под ней. Пока корабль стоит на месте, внимательно наблюдайте, как зверушки разлетаются с одинаковой скоростью во все стороны кабины. Рыбы равнодушно плавают во все стороны; капля падает в сосуд под ним; и, бросая что-то своему другу, вам нужно бросать не сильнее в одном направлении, чем в другом, при равных расстояниях; прыгая ногами вместе, вы проходите равные расстояния во всех направлениях. Когда вы внимательно наблюдаете за всем этим (хотя нет сомнения, что когда корабль стоит на месте, все должно происходить именно так), пусть корабль движется с любой скоростью, какой вам угодно, лишь бы движение было равномерным и не колебалось этой скорости. способ и то. Вы не обнаружите ни малейшего изменения во всех названных эффектах, и ни по одному из них вы не сможете сказать, движется ли корабль или стоит на месте29.
.
65Какой замечательный мысленный эксперимент. Это порождает столь желанный Aha! эффект или момент Эврики, когда все кажется кристально чистым. Этот мысленный эксперимент, возможно, больше, чем любой другой, приводит к идее относительности инерциальных систем отсчета, которую стали называть относительностью Галилея.
66Вооруженный этим принципом относительности, Галилей теперь способен обратить вспять первоначальную аналогию, на которую опирался аристотелевский мысленный эксперимент, пытаясь установить неподвижность Земли.
- 30 Галилей, Диалог , 144.
САЛЬВИАТИ: Если бы камень, упавший с вершины мачты, когда корабль быстро плыл, упал точно в то же самое место на корабле, куда он упал, когда корабль стоял на месте, какая польза от этого падения в отношении определить, стоит судно на месте или движется?30
67 На собственный вопрос он снова дает агностический ответ:
- 31 Галилей, Диалог , 145.
САЛЬВИАТИ: Та же причина, действующая на земле, что и на корабле, ничего не может заключить о движении или покое земли из камня, падающего всегда перпендикулярно подножию башни31.
68Ключевым изменением постаристотелевского мировоззрения является перенос источника движения со среды на сам объект. В следующем мысленном эксперименте Галилей утверждает, что движущийся корабль сам сообщает горизонтальное движение скале, стоящей на вершине мачты. Когда камень падает, он сохраняет это горизонтальное движение (поскольку ему ничто не препятствует) и, следовательно, приземляется прямо под точкой своего отправления.
- 32 Галилей, Диалог , 148.
SALVIATI: Что касается того камня, который находится на вершине мачты; разве он не движется, носимый кораблем…? И, следовательно, нет ли в нем неустранимого движения, когда все внешние препятствия устранены? И разве это движение не такое же быстрое, как у корабля?
Симплицио: Под окончательным выводом ты имеешь в виду, что камень, двигаясь с неизгладимо впечатленным движением, не собирается покидать корабль, а будет следовать за ним и, наконец, упадет на то же место, куда он упал, когда корабль оставался неподвижным32.
69Что к этому привело? Мы начнем с подборки замечаний Буридана, составляющих его теорию импульса. Согласно Буридану, импульс — это движущая сила, отвечающая за поддержание отстраненного движения, будь то поступательное или круговое.
Если легкое дерево и тяжелое железо одинакового объема и одинаковой формы перемещаются метателем с одинаковой скоростью, то железо будет перемещаться дальше, потому что в него вложен более интенсивный толчок, который не так быстро разрушается, как меньший импульс был бы поврежден.
70Вот и причина того, почему большую кузнечную мельницу, движущуюся быстро, остановить труднее, чем маленькую, очевидно, потому, что в большой, при прочих равных условиях, больше толчка.
- 33 Буридан, Вопросы физики Аристотеля VIII.12.5, Clagett (пер.) 535.
И по этой причине вы могли бы бросить камень весом в полфунта дальше, чем тысячную его часть.
Ибо толчок в этой тысячной доле настолько мал, что тотчас же преодолевается сопротивляющимся воздухом33.
71Мы хотели бы подчеркнуть именно то, что подчеркивает Буридан, а именно, что источник движения находится в объекте, а не в окружающей среде. На самом деле среда оказывает некоторое сопротивление, которое истощает импульс. Буридан доходит до того, что говорит, что произойдет, если из прялки убрать все источники сопротивления.
- 34 Буридан, Вопросы к книге Аристотеля «О небесах» , Клагетт (пер.) 561.
Если вы заставите вращаться большую и очень тяжелую кузнечную мельницу [т. Более того, вы не можете немедленно остановить его, но из-за сопротивления гравитации мельницы импульс будет постоянно уменьшаться, пока мельница не перестанет двигаться. И если бы мельница существовала вечно, без какого-либо уменьшения или изменения ее, и не было бы сопротивления, искажающего побуждение, возможно, мельница постоянно приводилась бы в движение этим побуждением34.
72Теперь Буридан может окончательно заключить, что аристотелевская динамика ложна. Ведь напомним, что в теории Аристотеля движение без сопротивления невозможно, потому что тогда объект двигался бы с бесконечной скоростью. Таким образом, Буридан представляет логически правдоподобный сценарий, который, как он дает нам основания полагать, привел бы к движению вечной продолжительности, что действительно несовместимо с аристотелевской динамикой.
73Буридан развивает аналогичный мысленный эксперимент, чтобы объяснить движение небесных тел, которые существуют в среде, полностью свободной от сопротивления. Опять же, мысленный эксперимент состоит из вывода о наилучшем объяснении: причина, по которой движение небесных тел кажется бесконечным, заключается в том, что они не встречают сопротивления, чтобы «испортить» первоначально приданный им импульс.
- 35 Буридан, Вопросы метафизики Аристотеля , XII.
9, Maier (1982a) (пер.) 89.
Вы знаете, что многие утверждают, что снаряд, покинув метателя, движется под действием импульса, сообщаемого метателем, и движется до тех пор, пока импульс остается сильнее сопротивления; и что импульс будет длиться вечно, если он не будет уменьшен и уничтожен противодействующим сопротивлением или тенденцией к противоположному движению. И в небесных движениях нет противодействующего сопротивления; поэтому, когда Бог при Сотворении двигал каждую небесную сферу именно с той скоростью, которую Он желал, он [затем] перестал двигать их сам, и с тех пор эти движения продолжаются вечно из-за импульса, приложенного к этим сферам35.
74 В особенно похожем на бритву маневре Оккама Буридан утверждает, что небесные тела сами по себе содержат причину своего постоянного движения. Нет необходимости постулировать дополнительные причины или «разумы», чтобы объяснить космологическое движение.
- 36 Буридан, Вопросы физики Аристотеля , VIII.
12, Clagett (пер.) 524-525.
Не представляется необходимым постулировать разумы такого рода, потому что можно было бы ответить, что Бог, когда Он сотворил мир, двигал каждую из небесных сфер по Своему желанию и, двигая их, вкладывал в них импульсы, которые двигали их без Ему надо было их больше двигать… И эти импульсы, которые Он вкладывал в небесные тела, не уменьшались и не искажались впоследствии, потому что не было склонности небесных тел к другим движениям. Не было и сопротивления, которое могло бы развратить или подавить этот импульс36.
75Обратимся к Орему и к паре мысленных экспериментов в том же духе, что и у Буридана, в поддержку теории импетуса. Колесо, которое приводится в движение:
- 37 Oresme, Questiones super De cœlo , II.7, Grant (2002) (пер.) 155.
не может быть немедленно остановлен без большого труда, но движим некоторым толчком, хотя и отделенным от первого движущегося агента и [не движимым] окружающим воздухом37.
76Постепенно устранив все возможные источники движения, Орем приходит к выводу, что прялка должна была получить импульс, который эффективно «поддерживает ее движение». Ибо это лучшее из оставшихся возможных объяснений.
77Второй мысленный эксперимент Орема более сложен, но и более успешен, потому что он устанавливает идеализированный сценарий в среде без сопротивления. Таким образом, это позволяет Орему более тщательно исследовать следствия теории импетуса. Как и его предшественник Буридан, Орем делает вывод, что при отсутствии сопротивления импульс, приданный объекту, будет поддерживать его движение вечно. Этот отрывок появляется в 9-м романе Орема.0436 Le Livre du ciel et du monde , где он обсуждает несоизмеримое круговое движение.
Теперь я хотел бы показать далее, что возможно и в действительности, и в неопровержимой теории, что некоторое движение имеет начало и длится вечно. Во-первых, что касается кругового движения: я предполагаю, что колесо из любого материала подобно колесу часов [ см.
рисунок Оресме ниже ]; это мы обозначим как и назовем его центр а.б. . Далее поместим в a другое колесо, меньшее, чем первое, наподобие эпицикла, с центром, обозначенным b . Добавим третье колесо, установленное на второе, с центром на окружности второго, подобно луне в ее эпицикле, и назовем это третье колесо c . Теперь поместим четвертое колесо вне этих трех так, чтобы c могли касаться его, и пусть его центр будет отмечен как d . Тогда я утверждаю, что a перемещаться вокруг своего центра, b перемещаться вместе с движением a , на котором он установлен, и при этом b также перемещаться своим собственным движением вокруг своего центра, а c не имеет собственного движения, но движется с движением a и b …
Ingrandisci Originale (jpeg, 598k)
- 38 Орем, Le Livre du ciel et du monde , 1.
29.46a-46d, Grant (1971) (пер.) 38. Наша репродукция h(…)
Теперь я утверждаю, что d может регулироваться или контролироваться противовесами и иным образом, чтобы он был склонен двигаться, но не двигался до тех пор, пока к нему не прикоснется c ; этот контакт убирает помеху и d начинает двигаться регулярно. Что-то в этом роде или подобное ему могло быть выполнено искусственно или искусным мастером. Далее, я утверждаю, что два движения числа a и b должны быть несоизмеримы, правильны и вечны… В настоящий момент я утверждаю, что колесо c касается колеса d , и я говорю, что невозможно, чтобы оно касалось его ранее или должен коснуться его снова, ибо он может коснуться его только тогда, когда центры b , c и d находятся в соединении ровно на одной линии; и это не могло произойти прежде, не снова в будущем… Из этого с необходимостью следует, что колесо d теперь начнет двигаться и никогда не остановится; и хотя такой ряд событий не может произойти в природе, не может быть показан материальным искусством или в разрушаемой материи и не может длиться так долго [как вечность], тем не менее он не содержит и не подразумевает никакого противоречия и не находится в своей собственной структуре.
ссылки несовместимы с разумом, но это возможно, если мы допускаем природу движений. Все несоответствия возникают из-за материала или из-за чего-то вне системы отсчета 38 .
78Возможно, наиболее эффективный пример вывода наилучшего объяснения представлен в мысленном эксперименте, который Галилей использует для иллюстрации закона инерции. Поскольку пример настолько абстрактен, Галилей может свести к минимуму и упростить предположения, необходимые для вывода.
- 39 Галилей, Диалог, 145-147.
САЛЬВИАТИ: Предположим, у вас есть плоская поверхность, гладкая, как зеркало, и сделанная из твердого материала, например стали. Он не параллелен горизонту, а несколько наклонен, и вы поместили на него шар совершенной сферической формы из какого-то твердого и тяжелого материала, такого как бронза. Как вы думаете, что это будет делать после освобождения?
СИМПЛИСИО: [Он катится вниз.]
САЛЬВИАТИ: Теперь, как долго будет катиться мяч и как быстро?
SIMPLICIO: Шар будет продолжать двигаться бесконечно, насколько простирается наклон поверхности, и с постоянно ускоряющимся движением.
САЛЬВИАТИ: Если бы кто-нибудь захотел, чтобы мяч двигался вверх по той же самой поверхности, как вы думаете, он бы пошел?
SIMPLICIO: Не спонтанно, нет; но нарисованный или брошенный силой, это было бы.
САЛЬВИАТИ: Теперь скажите мне, что произошло бы с тем же подвижным телом, помещенным на поверхность без наклона вверх или вниз?
SIMPLICIO: Нет склона вниз, не может быть и естественной тенденции к движению; а поскольку нет наклона вверх, не может быть и сопротивления движению, поэтому между склонностью и сопротивлением движению будет безразлично. Поэтому мне кажется, что она естественно должна оставаться стабильной.
САЛЬВИАТИ: Но что было бы, если бы ей дали толчок в любом направлении?
SIMPLICIO: Из этого должно следовать, что он будет двигаться в этом направлении.
САЛЬВИАТИ: Как далеко вы хотите, чтобы мяч продолжал двигаться?
SIMPLICIO: До тех пор, пока расширение поверхности продолжалось без подъема или опускания.
САЛЬВИАТИ: Значит, если бы такое пространство было безграничным, то и движение на нем было бы безграничным? То есть вечный?
Симпличио: Мне кажется, что да, если бы подвижное тело было из прочного материала39.
79В этом сократовском диалоге Сальвиати выводит из Simplicio вывод, что в отсутствие сопротивления или даже какой-либо внешней силы объекту нет необходимости изменять свое движение. В своем мысленном эксперименте Галилей использует пошаговый метод для постепенного устранения всех влияний, которые окружающая среда может реально оказывать на мяч. Прежде всего, он просит нас представить шар и плоскую поверхность совершенно гладкими и свободными от каких-либо препятствий, чтобы исключить из мысленного эксперимента все источники трения. Затем Галилей держит поверхность под таким углом, чтобы нейтрализовать любое влияние гравитации на шар. Наконец, нам говорят, что поверхность неограничена и простирается на бесконечное расстояние во всех направлениях. Абстрагируясь от всех сопротивлений и динамических воздействий на мяч, Галилей заключает, что скорость мяча навсегда останется неизменной. Этот результат явно противоречит аристотелевской динамике, но благодаря искусному манипулированию Галилеем динамических переменных на шаре мы не можем не сделать вывод, что он должен быть верным. Заметьте, что динамическое объяснение явления движения по инерции, данное Галилеем, просто говорит о том, что мяч не имеет ни склонности, ни сопротивления движению. Таким образом, Галилей переворачивает столы в вопросе, который занимал как Аристотеля, так и его средневековых критиков. Вместо того, чтобы предположить, что естественное состояние мяча — это состояние покоя, и спрашивать, «что удерживает мяч в равномерном движении», он предполагает, что естественным состоянием мяча является равномерное движение, и спрашивает: «Что мешает мячу оставаться в равномерном движении».
Наконец, нам говорят, что поверхность неограничена и простирается на бесконечное расстояние во всех направлениях. Абстрагируясь от всех сопротивлений и динамических воздействий на мяч, Галилей заключает, что скорость мяча навсегда останется неизменной. Этот результат явно противоречит аристотелевской динамике, но благодаря искусному манипулированию Галилеем динамических переменных на шаре мы не можем не сделать вывод, что он должен быть верным. Заметьте, что динамическое объяснение явления движения по инерции, данное Галилеем, просто говорит о том, что мяч не имеет ни склонности, ни сопротивления движению. Таким образом, Галилей переворачивает столы в вопросе, который занимал как Аристотеля, так и его средневековых критиков. Вместо того, чтобы предположить, что естественное состояние мяча — это состояние покоя, и спрашивать, «что удерживает мяч в равномерном движении», он предполагает, что естественным состоянием мяча является равномерное движение, и спрашивает: «Что мешает мячу оставаться в равномерном движении».
80Вывод наилучшего объяснения в целом кажется очень эффективным стилем мысленного эксперимента. Хотя все это идет как пакет, строго говоря, мысленный эксперимент устанавливает какое-то явление, а затем следует его объяснение. Эффективность этой формы рассуждений, возможно, неудивительна, учитывая, насколько близко этот вид мысленного эксперимента напоминает стиль научных рассуждений, используемых в реальных эмпирических экспериментах.
81История движения по инерции на этом не заканчивается, но все, что осталось, нужно оставить для другого случая. Мы дадим лишь самые краткие наброски, начиная с примера из Галилея.
- 40 Галилей, Две новые науки , 170.
Я мысленно представляю некое подвижное спроецированное на горизонтальную плоскость, при этом все препятствия устранены. Теперь из того, что было сказано в другом месте более подробно, очевидно, что равномерное движение на этой плоскости было бы вечным, если бы эта плоскость имела бесконечную протяженность40.
82Под бесконечной протяженностью Галилей может подразумевать не что иное, как неограниченную, т. е. отсутствие препятствий для дальнейшего движения объекта. Он не имеет в виду бесконечную прямую линию, поскольку инерция Галилея круговая. Все центры тяжести важны в его концепции того, как и почему все движется. Представив тело в горизонтальном движении, он заявляет:
- 41 Галилей, Две новые науки , 172.
невозможно, чтобы тяжелое тело… естественно двигалось вверх, удаляясь от общего центра, к которому взаимно сходятся все тяжелые тела; и, следовательно, невозможно, чтобы они двигались спонтанно, кроме как с тем движением, при котором их собственный центр тяжести приближается к упомянутому общему центру. Следовательно, на горизонтали, которая здесь означает поверхность [везде], равноудаленную от упомянутого [общего] центра и, следовательно, совершенно лишенную наклона, толчок или импульс движущегося будет равен нулю41.
83 Декарт заслуживает похвалы за современную концепцию инерции, а именно, состояния движения, которое включает в себя постоянную скорость по прямой линии.
- 42 Декарт, Основы философии , II, 37.
Первый закон природы: каждая вещь, насколько она в ее силах, всегда остается в одном и том же состоянии; и что, следовательно, когда он был однажды перемещен, он всегда продолжает двигаться42.
- 43 Декарт, Принципы , II, 39.
Второй закон природы: всякое движение само по себе происходит по прямым линиям; и, следовательно, тела, движущиеся по кругу, всегда стремятся удалиться от центра круга, который они описывают43.
84Декарт в этих пассажах ввел две принципиально важные вещи. Во-первых, идея состояние . Даже если тело может менять свое местоположение, его состояние может быть постоянным. Во-вторых, идея о прямолинейном движении по инерции.
Даже если тело может менять свое местоположение, его состояние может быть постоянным. Во-вторых, идея о прямолинейном движении по инерции.
85К тому времени, когда мы доберемся до Ньютона, движение по инерции прочно укоренилось и проявляется как первый закон Ньютона в Principia . Примечательно, с нашей точки зрения, то, что к тому времени, когда Ньютон сформулировал свою точку зрения, он задействовал инерцию в своих мысленных экспериментах с абсолютным пространством. Почему вода поднимается по стенкам ведра? Части воды вращаются, то есть ускоряются относительно самого пространства. Пространство является причиной движения тела по инерции, то есть его постоянной скорости по прямой, когда к нему не приложена никакая сила. С Ньютоном мы вернулись к идее, что некоторые аспекты движения обусловлены средой, а не телом. Само пространство является причиной постоянных скоростей, когда никакие силы не действуют.
86 После Ньютона следующим большим событием является подтверждение принципа относительности в специальной теории относительности после того, как ему серьезно угрожала электродинамика 19 -го -го века. Вслед за этим общая теория относительности ввела свободное падение, то есть движение по геодезическим пространствам-временям как движение по инерции, естественное состояние любого тела.
Вслед за этим общая теория относительности ввела свободное падение, то есть движение по геодезическим пространствам-временям как движение по инерции, естественное состояние любого тела.
[PDF] Галилей и незаменимость научного мысленного эксперимента
- ID корпуса: 147952283
@inproceedings{Szab1998GalileoAT,
title={Галилей и незаменимость научного мысленного эксперимента},
автор={Тамар Сзаб},
год = {1998}
} - Tamar Szab
- Опубликовано в 1998 г.
- Философия, физика
Тщательно изучив один из самых известных мысленных экспериментов в истории науки, с помощью которого, как говорят, Галилей опроверг аристотелевскую теорию падения более тяжелых тел. быстрее, чем более легкие — я пытаюсь показать, что мысленные эксперименты играют особую роль в научных исследованиях. Рассуждения о конкретных сущностях в контексте воображаемого сценария могут привести к рационально обоснованным выводам, которые при той же исходной информации не были бы рационально…
unige. ch
ch
Переосмысление мысленных экспериментов
Изучение двух мысленных экспериментов в современной физике показывает, что один и тот же мысленный эксперимент может быть переанализирован с точки зрения разных и несовместимых теорий. Этот факт…
Нортон и логика мыслительных экспериментов
- М. Стюарт
Философия
- 2016
Джон Д. Нортон защищает мысль о том, что центральная тема экспериментов – эмпирический эпизис, не более чем аргументы. Философы пытались…
Annus Mirabilis 1986 года: мысленные эксперименты и научный плюрализм
Эта статья о значительном взрыве литературы о мысленных экспериментах с 1980-х годов. Он входит в неизведанную территорию. Особый интерес представляет 1986 год: Джеймс Р. Браун…
Шаг к рациональности: эффективность мысленных экспериментов в науке, этике и свободе воли
- Р. Шепард
Физика
Познание. науч.
- 2008
Эволюционное появление у людей глубоко усвоенных имплицитных знаний об абстрактных принципах преобразования и симметрии, возможно, имело решающее значение для шага человечества к рациональности, включая открытие универсальных принципов математики, физики, этики и объяснение свободы воли, которое совместим с детерминизмом.
Мысленные эксперименты в науке
- М. Стюарт
Образование, физика
- 2015
Мысленные эксперименты — это средство творческого мышления с опытом работы более двух с половиной тысяч лет. Используемые Аристотелем, Галилеем, Ньютоном, Дарвином, Максвеллом и Эйнштейном, они…
Заглянуть в небеса Платона
Представлены примеры классических мысленных экспериментов и приведены некоторые моральные принципы. Мнения моих товарищей по симпозиуму Тамар Гендлер, Джона Нортона и Джеймса Макаллистера оцениваются. Отчет о мысли…
Галилей и предшествующая философия
- Дэвид Аткинсон, Дж. Пейненбург
Философия, физика
- 2004
Об истоках философии мысли Эксперименты: Предыстория мысленных экспериментов в настоящее время привлекает большое внимание, история мыслительных экспериментов и это связано с возобновившимся интересом философов к этому предмету. В этой статье исследуется история…
GALILEO VS .
 АРИСТОТЕЛЬ О СВОБОДНОПАДАЮЩИХ ТЕЛАХ в логическом анализе и истории философии
АРИСТОТЕЛЬ О СВОБОДНОПАДАЮЩИХ ТЕЛАХ в логическом анализе и истории философии- Падающие тела
Физика, философия
В этом эссе делается попытка продемонстрировать, что знаменитый мысленный эксперимент Галилея относительно падающих тел в его «Диалогах о двух новых науках» (Galileo 1954: 61-64) сомнительный. …
«Платонические» мысленные эксперименты: как, черт возьми?
- Р. Урбаниак
Философия
Синтез
- 2011
используемый Брауном, ТЭ Галилея с участием падающих тел.
SHOWING 1-10 OF 73 REFERENCES
SORT BYRelevanceMost Influenced PapersRecency
The Laboratory of the Mind: Thought Experiments in the Natural Sciences
- J. Brown
Philosophy, Education
- 1993
Thought experiments выполняются в лаборатории разума. Помимо этой метафоры, трудно сказать, что представляют собой эти замечательные устройства для исследования природы и как они работают. Хотя…
Хотя…
Логика научных открытий.
- К. Поппер
Философия
- 1934
Каждый из этих этапов исследовательского проекта оценивается для выяснения источников неясностей и неопределенностей, и вносятся предложения для уменьшения ошибок и ускорения научного прогресса.
Являются ли мысленные эксперименты именно тем, что вы думали?
- Дж. Нортон
Образование, философия
Canadian Journal of Philosophy
- 1996
Каковы бы ни были первоначальные намерения, введение термина «мысленный эксперимент» оказалось одним из величайших пиар-переворотов в научной литературе. Для поколений читателей научных…
Почему эмпиризм не работает
Мысленные эксперименты дают нам научное понимание и теоретические достижения, которые иногда весьма значительны, но они делают это без новых эмпирических данных и, возможно, без каких-либо…
Мысленные эксперименты после научной революции
- Дж.
 Браун
Браун Физика, образование
- 1986
дела были сделаны. Наиболее распространенный взгляд на научный…
Мысленные эксперименты и эпистемология законов
Цель этой статьи — показать, как мысленные эксперименты помогают нам узнать о законах. Приведя примеры такого рода номического освещения в первом разделе, я привожу объяснения нашей…
Мысленные эксперименты в работах Эйнштейна
- Дж. Нортон
Философия, образование
- 1991
- T. Horowitz, Gerald J. Massey
Философия, образование
- 1991
Предисловие: Этот том создан на конференции «Место мысленных экспериментов в науке и философии», которая была организована нами и проводилась в Центре философии науки в…
О чем эксперимент Мысленные эксперименты?
Я утверждаю, что мысленные эксперименты — это форма экспериментальных рассуждений, сходная с реальными экспериментами.
 К сожалению, устройство мира по Копернику в XVI веке не нашло признания. Оно трактовалась как сугубо математическая теория, призванная облегчить описание движения планет. Церковь с негодованием относилась к книге Коперника, потому что, исходя из гелиоцентрической модели мироздания, Человек не оказывался венцом творения природы, что противоречило всем христианским догмам. В это время все люди, ученые в том числе, были глубоко верующими людьми, поэтому теологические принципы в сознаниях большинства людей были главенствующими. Несмотря на то, что Церковь признала учение Коперника несовместимым со Священным Писанием, у Коперника нашлось много последователей. Это было связано с тем, что многие ученые заинтересовались его работой, никто раньше не пытался так «посмотреть» на физику, как это сделал Коперник. Большинство людей отвергло такую новую физику по многим причинам. Во-первых, в один момент им нужно было отказаться от всех Аристотелевских принципах, которые, по сути дела, считались аксиомами.
К сожалению, устройство мира по Копернику в XVI веке не нашло признания. Оно трактовалась как сугубо математическая теория, призванная облегчить описание движения планет. Церковь с негодованием относилась к книге Коперника, потому что, исходя из гелиоцентрической модели мироздания, Человек не оказывался венцом творения природы, что противоречило всем христианским догмам. В это время все люди, ученые в том числе, были глубоко верующими людьми, поэтому теологические принципы в сознаниях большинства людей были главенствующими. Несмотря на то, что Церковь признала учение Коперника несовместимым со Священным Писанием, у Коперника нашлось много последователей. Это было связано с тем, что многие ученые заинтересовались его работой, никто раньше не пытался так «посмотреть» на физику, как это сделал Коперник. Большинство людей отвергло такую новую физику по многим причинам. Во-первых, в один момент им нужно было отказаться от всех Аристотелевских принципах, которые, по сути дела, считались аксиомами.
 Идеи Коперника нуждались в теоретическом обосновании, дающим ответ на вопрос о том, что связывает планеты между собой, как и почему они движутся. Для этого было необходимо и развитие механики, сводившейся к новой науке. Именно в эти века начинается новая динамика, кинематика и т.д.
Идеи Коперника нуждались в теоретическом обосновании, дающим ответ на вопрос о том, что связывает планеты между собой, как и почему они движутся. Для этого было необходимо и развитие механики, сводившейся к новой науке. Именно в эти века начинается новая динамика, кинематика и т.д. Такое представление удовлетворяло объяснения всех движений, кроме двух: свободного падения тел и полета снарядов. В аристотелевской физике падение тел объяснялось их стремлением к естественному месту, к центру Земли. Считалось, что свободное падение является движением, которое содержит движущую силу внутри себя, что оно может быть только равномерным и зависеть только от массы. Что касается полета снарядов, то многие философы Средневековья были убеждены, что снаряд сначала ускоряется, достигает максимума скорости, а затем уже его скорость начинает убывать.
Такое представление удовлетворяло объяснения всех движений, кроме двух: свободного падения тел и полета снарядов. В аристотелевской физике падение тел объяснялось их стремлением к естественному месту, к центру Земли. Считалось, что свободное падение является движением, которое содержит движущую силу внутри себя, что оно может быть только равномерным и зависеть только от массы. Что касается полета снарядов, то многие философы Средневековья были убеждены, что снаряд сначала ускоряется, достигает максимума скорости, а затем уже его скорость начинает убывать.


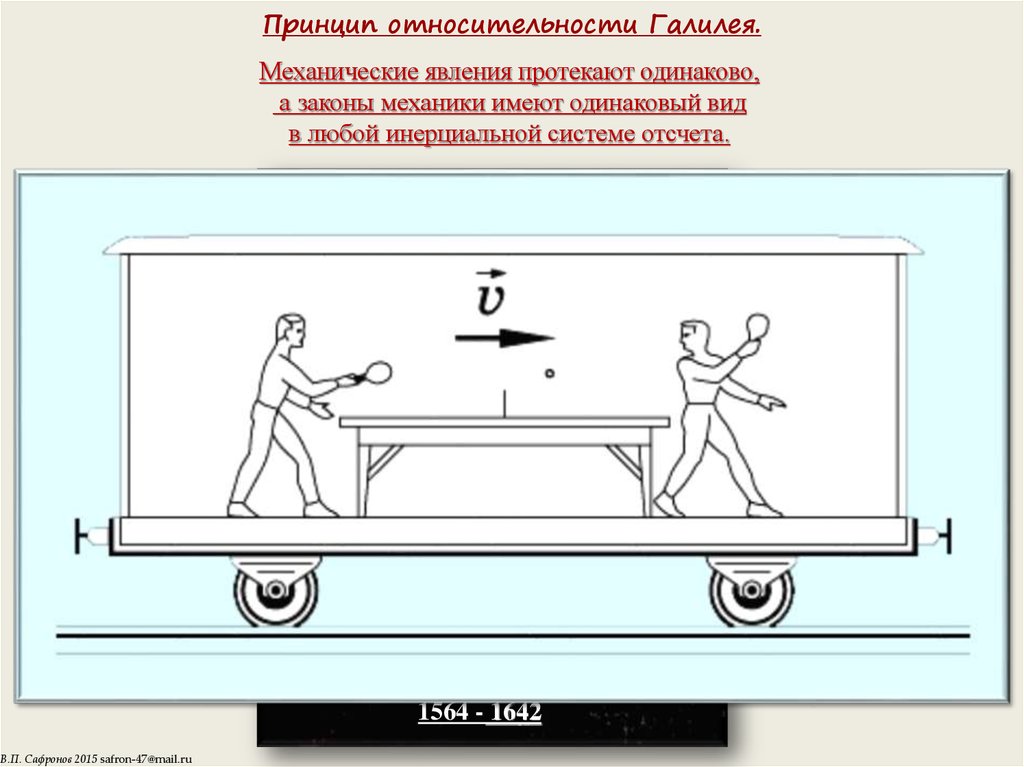 д.1»
д.1» Отсюда получается противоречие, потому что мы исходим из того, что в мире есть совершенный порядок, соответственно движения небесных тел могут быть только круговыми.
Отсюда получается противоречие, потому что мы исходим из того, что в мире есть совершенный порядок, соответственно движения небесных тел могут быть только круговыми. Во-вторых, скалы, здания и целые города должны были бы разрушиться вследствие центробежного эффекта при вращении.
Во-вторых, скалы, здания и целые города должны были бы разрушиться вследствие центробежного эффекта при вращении. Прилежно наблюдайте все это, хотя у вас не возникает никакого сомнения в том, что, пока корабль стоит неподвижно, все должно происходить именно так. Заставьте теперь корабль двигаться с любой скоростью, и тогда (если только движение будет равномерным и без качки в ту или другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно. Прыгая, вы переместитесь на полу на то же расстояние, что и раньше, н не будете делать больших прыжков в сторону кормы, чем в сторону носа, на том основании, что корабль быстро движется, хотя за то время, что вы будете в воздухе, пол под вами будет двигаться в сторону, противоположную вашему прыжку, и, бросая какую-нибудь вещь товарищу, вы не должны будете бросать ее с большей силой, когда он будет находиться на носу, чем когда ваше взаимное положение будет обратным; капли, как и — ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей; рыбы в воде не с большим усилием будут плыть к передней, чем к задней части сосуда; настолько же проворно они бросятся к пище, положенной в какой-угодно части сосуда; наконец, бабочки и мухи по-прежкему будут летать во всех направлениях, и никогда не случится того, чтобы они собрались у стенки, обращенной к корме, как если бы устали, следуя за быстрым движением корабля, от которого они были совершенно обособлены, держась долгое время I воздухе; и если от капли зажженного ладана образуется немного дыма, то видно будет, как он восходит вверх и держится наподобие облачка, двигаясь безразлично в одну сторону не более, чем в другую.
Прилежно наблюдайте все это, хотя у вас не возникает никакого сомнения в том, что, пока корабль стоит неподвижно, все должно происходить именно так. Заставьте теперь корабль двигаться с любой скоростью, и тогда (если только движение будет равномерным и без качки в ту или другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно. Прыгая, вы переместитесь на полу на то же расстояние, что и раньше, н не будете делать больших прыжков в сторону кормы, чем в сторону носа, на том основании, что корабль быстро движется, хотя за то время, что вы будете в воздухе, пол под вами будет двигаться в сторону, противоположную вашему прыжку, и, бросая какую-нибудь вещь товарищу, вы не должны будете бросать ее с большей силой, когда он будет находиться на носу, чем когда ваше взаимное положение будет обратным; капли, как и — ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей; рыбы в воде не с большим усилием будут плыть к передней, чем к задней части сосуда; настолько же проворно они бросятся к пище, положенной в какой-угодно части сосуда; наконец, бабочки и мухи по-прежкему будут летать во всех направлениях, и никогда не случится того, чтобы они собрались у стенки, обращенной к корме, как если бы устали, следуя за быстрым движением корабля, от которого они были совершенно обособлены, держась долгое время I воздухе; и если от капли зажженного ладана образуется немного дыма, то видно будет, как он восходит вверх и держится наподобие облачка, двигаясь безразлично в одну сторону не более, чем в другую. И причина согласованности всех этих явлений заключается в том, что движение корабля обще всем находящимся на нем предметам, так же как и воздуху».
И причина согласованности всех этих явлений заключается в том, что движение корабля обще всем находящимся на нем предметам, так же как и воздуху».

 Галилей подразумевает, что для науки совсем необязательным является достижение идеала на опыте — достаточно к нему приблизиться как можно ближе. Нарисовав впечатляющую картину мысленного эксперимента, Галилей не проводит его, а лишь подробно рассказывает, как его можно провести.
Галилей подразумевает, что для науки совсем необязательным является достижение идеала на опыте — достаточно к нему приблизиться как можно ближе. Нарисовав впечатляющую картину мысленного эксперимента, Галилей не проводит его, а лишь подробно рассказывает, как его можно провести.
 В самом деле, мы ежедневно наблюдаем, как муравей тащит зерно, а так как зерен в судне ограниченное число, то, увеличив это число даже в четыре или в шесть раз, мы все же найдем, что соответственно большое количество муравьев, принявшихся за работу, может вытащить на землю и зерно, и корабль. Мне кажется, что именно так обстоит дело и с пустотами, держащими связанными частицы металла».
В самом деле, мы ежедневно наблюдаем, как муравей тащит зерно, а так как зерен в судне ограниченное число, то, увеличив это число даже в четыре или в шесть раз, мы все же найдем, что соответственно большое количество муравьев, принявшихся за работу, может вытащить на землю и зерно, и корабль. Мне кажется, что именно так обстоит дело и с пустотами, держащими связанными частицы металла».
 Линия, образуемая непрерывным наложением бесконечно большого числа сторон большого круга, приблизительно равна по длине линии, образованной наложением бесконечно большого числа сторон меньшего круга, если включить в нее и промежутки между «скачками». В виду того что число сторон не ограниченно, а бесконечно, то и число промежутков между ними также бесконечно2.
Линия, образуемая непрерывным наложением бесконечно большого числа сторон большого круга, приблизительно равна по длине линии, образованной наложением бесконечно большого числа сторон меньшего круга, если включить в нее и промежутки между «скачками». В виду того что число сторон не ограниченно, а бесконечно, то и число промежутков между ними также бесконечно2. Галилей был первым, кому пришла в голову мысль объединить эти два подхода.
Галилей был первым, кому пришла в голову мысль объединить эти два подхода.
 Предположим, говорит Декарт, что теннисный мяч, посланный ракеткой в точке А, двигается равномерно по линии АВ и попадает на поверхность СЕ в точке В. Разложим его стремление на две составляющие — АС, которая перпендикулярна поверхности, и АН, ей параллельную. Так как мяч, ударившись о поверхность СЕ, не сообщит ей никакого движения, скорость его после отскока не изменится по величине, и он по прошествии времени, равному тому, которое ему потребовалось для прохождения отрезка АВ, окажется где-то на окружности, описанной радиусом АВ вокруг точки В. После отскока составляющая стремления АН, параллельная поверхности СЕ, останется без изменений (АН=НР), а вертикальная составляющая АС изменит свой знак на противоположный. Итак, горизонтальная составляющая определит прямую РЕ, находящуюся от вертикали НВ на расстоянии НР. Ясно, что по прошествии нужного времени мяч должен будет находиться на пересечении этой прямой с окружностью, т.
Предположим, говорит Декарт, что теннисный мяч, посланный ракеткой в точке А, двигается равномерно по линии АВ и попадает на поверхность СЕ в точке В. Разложим его стремление на две составляющие — АС, которая перпендикулярна поверхности, и АН, ей параллельную. Так как мяч, ударившись о поверхность СЕ, не сообщит ей никакого движения, скорость его после отскока не изменится по величине, и он по прошествии времени, равному тому, которое ему потребовалось для прохождения отрезка АВ, окажется где-то на окружности, описанной радиусом АВ вокруг точки В. После отскока составляющая стремления АН, параллельная поверхности СЕ, останется без изменений (АН=НР), а вертикальная составляющая АС изменит свой знак на противоположный. Итак, горизонтальная составляющая определит прямую РЕ, находящуюся от вертикали НВ на расстоянии НР. Ясно, что по прошествии нужного времени мяч должен будет находиться на пересечении этой прямой с окружностью, т. е. в точке Р. Отсюда с необходимостью следует, что угол падения АВН равен углу отражение НВР.
е. в точке Р. Отсюда с необходимостью следует, что угол падения АВН равен углу отражение НВР. В пустоте никаких сил нет, и не может быть, соответственно скорость тела становится мгновенной, чего не может произойти. Следовательно, пустоты нет.
В пустоте никаких сил нет, и не может быть, соответственно скорость тела становится мгновенной, чего не может произойти. Следовательно, пустоты нет. 
 1638.
1638.  Задачи типа «наименьшее количество предметов»
Задачи типа «наименьшее количество предметов»
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 Эти представления, приложенные к исследованию абсолютно черного тела, приводили к парадоксальной ситуации.
Эти представления, приложенные к исследованию абсолютно черного тела, приводили к парадоксальной ситуации. Так работа с идеализированным объектом помогла заложить основы квантовой теории, ознаменовавшей радикальный переворот в науке.
Так работа с идеализированным объектом помогла заложить основы квантовой теории, ознаменовавшей радикальный переворот в науке.
 При этом правильный выбор допустимости подобной идеализации играет очень большую роль. Если в ряде случаев возможно и целесообразно рассматривать атомы в виде материальных точек, то такая идеализация становится недопустимой при изучении структуры атома. Точно так же можно считать материальной точкой нашу планету при рассмотрении её вращения вокруг Солнца, но отнюдь не в случае рассмотрения её собственного суточного вращения.
При этом правильный выбор допустимости подобной идеализации играет очень большую роль. Если в ряде случаев возможно и целесообразно рассматривать атомы в виде материальных точек, то такая идеализация становится недопустимой при изучении структуры атома. Точно так же можно считать материальной точкой нашу планету при рассмотрении её вращения вокруг Солнца, но отнюдь не в случае рассмотрения её собственного суточного вращения.

 В этом плане мысленный эксперимент имеет явное преимущество перед экспериментом реальным. В мысленном эксперименте можно абстрагироваться от действия нежелательных факторов, проведя его в идеализированном, «чистом» виде.
В этом плане мысленный эксперимент имеет явное преимущество перед экспериментом реальным. В мысленном эксперименте можно абстрагироваться от действия нежелательных факторов, проведя его в идеализированном, «чистом» виде. Такое утверждение основывалось на простой констатации фактов, наблюдаемых в реальных экспериментах (шар или тележка, получившие силовое воздействие, а затем катящиеся уже без него по горизонтальной поверхности, неизбежно замедляли свое движение и в конце концов останавливались). В этих экспериментах наблюдать равномерное непрекращающееся движение по инерции было невозможно. Галилей, проделав мысленно указанные эксперименты с поэтапным идеализированием трущихся поверхностей и доведением до полного исключения из взаимодействия трения, опроверг аристотелевскую точку зрения и сделал единственно правильный вывод. Этот вывод мог быть получен только с помощью мысленного эксперимента, обеспечившего возможность открытия фундаментального закона механики движения. «… Закон инерции, — писали А. Эйнштейн и Л. Инфельд (1966), — нельзя вывести непосредственно из эксперимента, его можно вывести умозрительно — мышлением, связанным с наблюдением. Этот эксперимент никогда нельзя выполнить в действительности, хотя он ведет к глубокому пониманию действительных экспериментов».
Такое утверждение основывалось на простой констатации фактов, наблюдаемых в реальных экспериментах (шар или тележка, получившие силовое воздействие, а затем катящиеся уже без него по горизонтальной поверхности, неизбежно замедляли свое движение и в конце концов останавливались). В этих экспериментах наблюдать равномерное непрекращающееся движение по инерции было невозможно. Галилей, проделав мысленно указанные эксперименты с поэтапным идеализированием трущихся поверхностей и доведением до полного исключения из взаимодействия трения, опроверг аристотелевскую точку зрения и сделал единственно правильный вывод. Этот вывод мог быть получен только с помощью мысленного эксперимента, обеспечившего возможность открытия фундаментального закона механики движения. «… Закон инерции, — писали А. Эйнштейн и Л. Инфельд (1966), — нельзя вывести непосредственно из эксперимента, его можно вывести умозрительно — мышлением, связанным с наблюдением. Этот эксперимент никогда нельзя выполнить в действительности, хотя он ведет к глубокому пониманию действительных экспериментов».
 Это существо, таким образом, без затраты работы повысит температуру в В и понизит в А вопреки второму началу термодинамики».
Это существо, таким образом, без затраты работы повысит температуру в В и понизит в А вопреки второму началу термодинамики». Одним из них является мысленный эксперимент В. Гейзенберга, направленный на разъяснение соотношения неопределенности. «»В этом мысленном эксперименте соотношение неопределенности было найдено благодаря абстрагированию, разделившему целостную структуру электрона на две противоположности: волну и корпускулу. Тем самым совпадение результата мысленного эксперимента с результатом, достигнутым математическим путем, означало доказательство объективно существующей противоречивости электрона как цельного материального образования и дало возможность понять это классически»».
Одним из них является мысленный эксперимент В. Гейзенберга, направленный на разъяснение соотношения неопределенности. «»В этом мысленном эксперименте соотношение неопределенности было найдено благодаря абстрагированию, разделившему целостную структуру электрона на две противоположности: волну и корпускулу. Тем самым совпадение результата мысленного эксперимента с результатом, достигнутым математическим путем, означало доказательство объективно существующей противоречивости электрона как цельного материального образования и дало возможность понять это классически»». Эти мысленные эксперименты способствовали пониманию новых научных положений, помогали объяснить причины отказа от старых представлений.
Эти мысленные эксперименты способствовали пониманию новых научных положений, помогали объяснить причины отказа от старых представлений. Рассмотренная выше идеализация паровой машины, удачно осуществленная Сади Карно, подвела его к открытию механического эквивалента теплоты, которого, однако, «… он не мог открыть и увидеть лишь потому, — отмечает Ф. Энгельс, — что верил в теплород. Это является также доказательством вреда ложных теорий».
Рассмотренная выше идеализация паровой машины, удачно осуществленная Сади Карно, подвела его к открытию механического эквивалента теплоты, которого, однако, «… он не мог открыть и увидеть лишь потому, — отмечает Ф. Энгельс, — что верил в теплород. Это является также доказательством вреда ложных теорий».

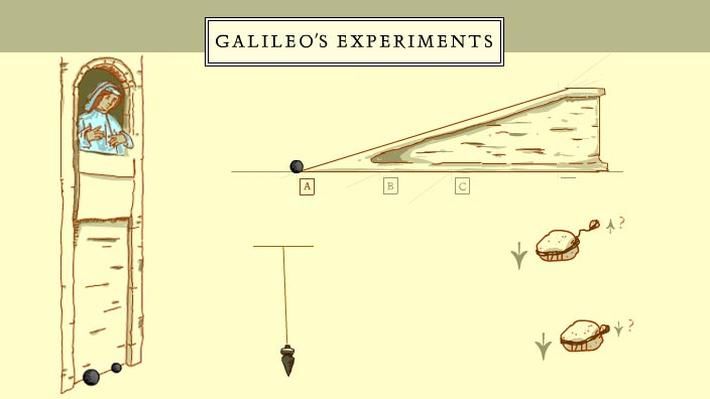 Но при этом следует иметь в виду, что формализация той или иной теории возможна только при учете ее содержательной стороны. Только в этом случае могут быть правильно применены те или иные формализмы. «Голое математическое уравнение еще не представляет физической теории, чтобы получить физическую теорию, необходимо придать математическим символам конкретное эмпирическое содержание» (Васильев, 1967).
Но при этом следует иметь в виду, что формализация той или иной теории возможна только при учете ее содержательной стороны. Только в этом случае могут быть правильно применены те или иные формализмы. «Голое математическое уравнение еще не представляет физической теории, чтобы получить физическую теорию, необходимо придать математическим символам конкретное эмпирическое содержание» (Васильев, 1967).
 Все множество созданных и создаваемых искусственных формализованных языков входит в язык науки,образуя мощное средство научного познания.
Все множество созданных и создаваемых искусственных формализованных языков входит в язык науки,образуя мощное средство научного познания. Но тем не менее все более полная формализация содержания никогда не может достигнуть абсолютной полноты, т. е. возможности любого формализованного языка остаются принципиально ограниченными. Таким образом, Гёдель дал строго логическое обоснование невыполнимости идеи Р. Карнапа о создании единого, универсального, формализованного «физикалистского» языка науки.
Но тем не менее все более полная формализация содержания никогда не может достигнуть абсолютной полноты, т. е. возможности любого формализованного языка остаются принципиально ограниченными. Таким образом, Гёдель дал строго логическое обоснование невыполнимости идеи Р. Карнапа о создании единого, универсального, формализованного «физикалистского» языка науки. Но в той мере, в какой адекватность немыслима без точности, тенденция к возрастающей формализации языков всех и особенно естественных наук является объективной и прогрессивной.
Но в той мере, в какой адекватность немыслима без точности, тенденция к возрастающей формализации языков всех и особенно естественных наук является объективной и прогрессивной. Наряду с другими методами познания, индуктивный метод сыграл важную роль в открытии некоторых законов природы (всемирного тяготения, атмосферного давления, теплового расширения тел и др.).
Наряду с другими методами познания, индуктивный метод сыграл важную роль в открытии некоторых законов природы (всемирного тяготения, атмосферного давления, теплового расширения тел и др.).
 Бэкон и его последователи вплоть до конца XIX века.
Бэкон и его последователи вплоть до конца XIX века. Общие принципы и законы не дают ученым в процессе дедуктивного исследования сбиться с пути: они помогают правильно понять конкретные явления действительности.
Общие принципы и законы не дают ученым в процессе дедуктивного исследования сбиться с пути: они помогают правильно понять конкретные явления действительности. Каждый из них используется на соответствующем этапе познавательного процесса.
Каждый из них используется на соответствующем этапе познавательного процесса.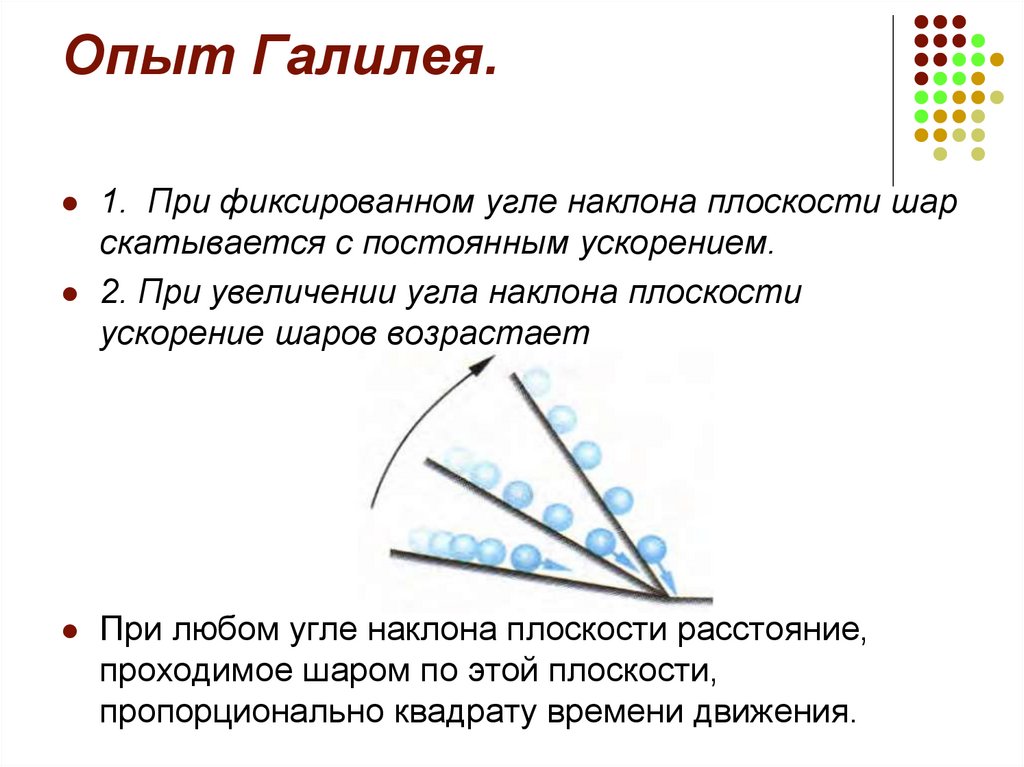
 016 с.)
016 с.)
 Кажется, он бросил разные мячи
с башни. Но какие веса? Какая башня? Мы можем
быть уверенным, что это была Пизанская башня.
Но в конечном итоге мы сомневаемся, действительно ли он это сделал.
эксперимент. Может быть, он просто сообщил, что он
мысль должна была произойти.
Кажется, он бросил разные мячи
с башни. Но какие веса? Какая башня? Мы можем
быть уверенным, что это была Пизанская башня.
Но в конечном итоге мы сомневаемся, действительно ли он это сделал.
эксперимент. Может быть, он просто сообщил, что он
мысль должна была произойти. Он говорит
более легкий мяч всегда стартовал немного быстрее
чем тяжелый мяч. Затем настиг тяжелый мяч.
Это звучит безумно.
Он говорит
более легкий мяч всегда стартовал немного быстрее
чем тяжелый мяч. Затем настиг тяжелый мяч.
Это звучит безумно.
 3-20.
3-20.