Основной психофизический закон: основной психофизический закон — это… Что такое основной психофизический закон?

Содержание

основной психофизический закон — это… Что такое основной психофизический закон?

ОСНОВНОЙ ПСИХОФИЗИЧЕСКИЙ ЗАКОН — функция зависимости величины ощущения от величины раздражителя. Единой формулы О. п. з. нет, но есть его варианты: логарифмический (Фехнера), степенной (Стивенса), обобщенные (Бэрда, Экмана, Забродина и др.). Наибольшую степень обобщения имеет закон Забродина, включающий не только логарифмическую и степенную функции, но и все промежуточные между ними.

Закон Стивенса — вариант О. п. з. (С. Стивене, 1957) — степенная зависимость величины ощущения от величины стимула. Он установлен эмпирически на материале субъективного шкалирования, а также выводится теоретически аналогично закону Фехнера. Степенной закон Стивенса получил широкое распространение по той же причине, что и логарифмический закон Фехнера: он хорошо описывает многие эмпирические данные. По Сти-венсу, его закон справедлив для любых раздражителей: как измеряемых объективно (интенсивность звука или света, вес, температура, длина или наклон линий и т.

п.), так и не измеряемых (разборчивость почерков, серии рисунков и т.п.). Закон экспериментально проверен для более чем 20 стимульных признаков. Установлено, что показатели степени варьировали от 0, 3 (громкость) до 3, 5 (электрический удар). Степенная функция в логарифмическом масштабе на обеих осях координат имеет линейный вид с наклоном, зависящим от показателя степени.

Все же обнаружено, что данный закон индивидуально варьирует, зависит от диапазона стимулов, плотности их расположения в диапазоне, вероятности их предъявления; крутизна степенной функции в двойных логарифмических координатах неодинакова в разных участках стимульной оси. Предложен ряд модификаций закона Стивенса, но неясно, какая из них лучше. На сегодня установлено, что он хорошо описывает в первом приближении субъективные оценки сенсорных стимулов. Однако он не универсален, так как не охватывает обнаружение и различение сигналов, неудовлетворительно описывает интервальное и категориальное шкалирование и т.

д.

Закон Фехнера — вариант О. п. з. ( Г. Фехнер, 1860) — логарифмическая зависимость величины ощущения от величины стимула, выраженной в единицах порога.

Он выведен автором теоретически на основе ряда априорных постулатов (за недоказанность которых не раз подвергнут критике) и закона Вебера. Несмотря на критику, закон Фехнера сохраняет свое значение и сегодня, так как хорошо соответствует многим экспериментальным фактам, особенно полученным для простых функций, близких к биологическим, а также для шкал едва заметных различий, накопленных над абсолютным порогом.

В.А. Барабанщиков

Энциклопедия эпистемологии и философии науки. М.: «Канон+», РООИ «Реабилитация». И.Т. Касавин. 2009.

Психофизический закон — это… Что такое Психофизический закон?

Психофизический закон: закон, устанавливающий связь между силой раздражения какого-либо органа чувств и интенсивностью ощущения; при средних значениях интенсивности раздражителя интенсивность ощущения прямо пропорциональна натуральному логарифму силы раздражителя.

Психофармакологи́ческие сре́дства
Психофизи́ческий параллели́зм

Смотреть что такое «Психофизический закон» в других словарях:

ПСИХОФИЗИЧЕСКИЙ ЗАКОН — (основной) см. Закон Фехнера, Закон Стивенса, Психофизика, Г. Т. Фехнер. Большой психологический словарь. М … Большая психологическая энциклопедия
психофизический закон — (син.: Вебера Фехнера закон, Фехнера закон) закон, устанавливающий связь между силой раздражения какого либо органа чувств и интенсивностью ощущения: при средних значениях интенсивности раздражителя интенсивность ощущения прямо пропорциональна… … Большой медицинский словарь
Психофизический закон — см. Вебера Фехнера закон … Большая советская энциклопедия
Психофизический закон Вебера — Этот закон гласит, что степень изменения стимула, при которой он становится различимым (порог различения) прямо пропорциональна интеенсивности этого стимула. Так, более мощные стимулы должны уусиливаться в большей степени, чем слабые стимулы,… … Большая психологическая энциклопедия
ОСНОВНОЙ ПСИХОФИЗИЧЕСКИЙ ЗАКОН — (англ. psychophysical function) функциональная зависимость величины ощущения от величины раздражителя. Син. психофизический закон, психофизическая функция (не следует путать с психометрической кривой, или функцией). Нет единой формулы О. п. з.,… … Большая психологическая энциклопедия
основной психофизический закон — ОСНОВНОЙ ПСИХОФИЗИЧЕСКИЙ ЗАКОН функция зависимости величины ощущения от величины раздражителя. Единой формулы О. п. з. нет, но есть его варианты: логарифмический (Фехнера), степенной (Стивенса), обобщенные (Бэрда, Экмана, Забродина и др. ) … Энциклопедия эпистемологии и философии науки
основной психофизический закон — закономерность, экспериментально установленная немецким физиком Фехнером. Согласно О.п.з., интенсивность возникающих у человека ощущений пропорционально логарифму силы воздействующих раздражителей … Энциклопедический словарь по психологии и педагогике
Закон сравнительных суждений — психофизический закон, определяющий отношение между двумя объектами в психическом пространстве человека. Сформулирован Л. Л. Терстоуном. Содержание 1 Основные положения 2 В … Википедия
закон Фехнера — закон психофизиологии, уточняющий закон Вебера и выражающий математическую зависимость между субьективным восприятием раздражителя и его физической величиной в виде логарифма. В 1858 г. немецкий физик Г. Фехнер математически обработал результаты… … Энциклопедический словарь по психологии и педагогике
закон Фехнера — 1. Сформулированный в 1860 г. Г. Т. Фехнером закон, согласно коему величина ощущения прямо пропорциональна логарифму интенсивности раздражителя то есть возрастание силы раздражения в геометрической прогрессии соответствует росту ощущения в… … Большая психологическая энциклопедия
Закон Вебера — Фехнера — Закон Вебера Фехнера эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула. В ряде экспериментов, начиная с 1834 года, Э. Вебер показал, что новый… … Википедия

Закон Фехнера | Мир Психологии

ЗАКОН ФЕХНЕРА

Закон ФЕХНЕРА (англ. Fechner’s law) — основной психофизический закон, утверждающий, что интенсивность ощущения прямо пропорциональна логарифму интенсивности раздражителя. Сформулирован Г. Фехнером в его основополагающем труде «Элементы психофизики» (1860). Исходя из постулата, что человек лишен способности непосредственно оценивать величину своих ощущений, Фехнер предложил косвенный способ определения величины любого ощущения посредством подсчета пороговых единиц.

Это позволило ему математически вывести формулу измерения ощущений, базируясь

на эмпирическом законе Вебера о постоянстве относительной величины приращения (или уменьшения) раздражителя, вызывающего ощущение едва заметного различия, и
собственном постулате о том, что едва заметный прирост ощущения величина постоянная, вследствие чего м. б. использован в качестве единицы измерения любой величины ощущения.

С помощью математики Фехнер теоретически обосновал тот известный факт, что ощущение изменяется гораздо медленнее, чем растет сила раздражения.

Согласно закону Фехнера, возрастанию силы раздражения в геометрической прогрессии соответствует рост ощущения в арифметической прогрессии (напр., если сила раздражителя возрастет в 100 раз, то сила ощущения возрастет только в 2 раза). Долгое время Закон Фехнера считался единственно возможной теоретической конструкцией основного психофизического закона. В настоящее время предложены многочисленные варианты последнего, но существенных преимуществ по сравнению с З.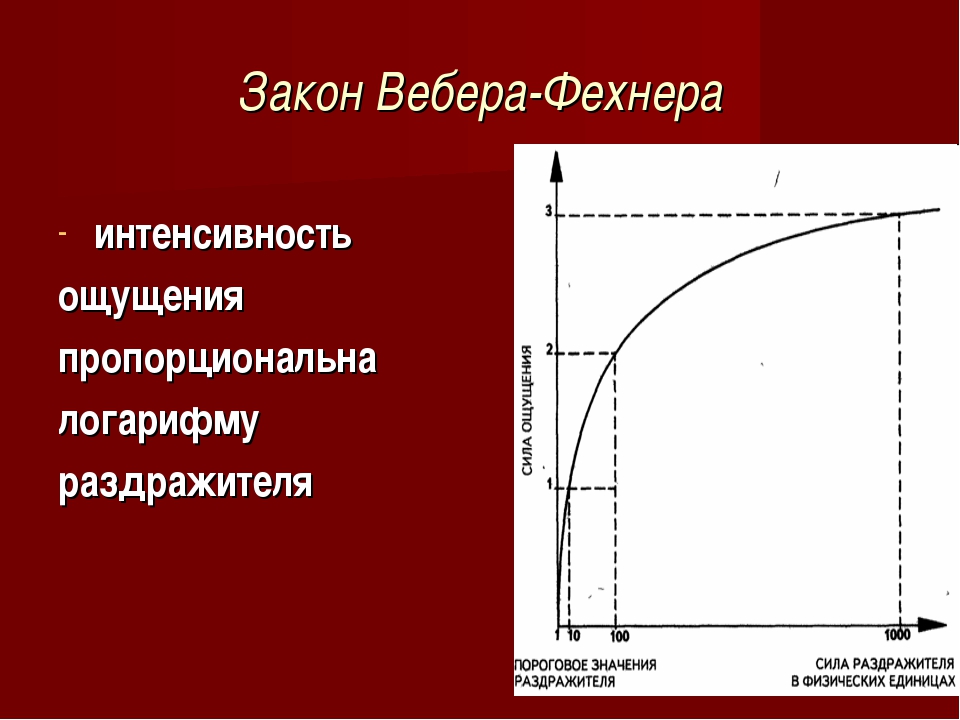

Ф. у них нет. См. Закон Стивенса, Психофизика.

Словарь практического психолога. С.Ю. Головин

Закон Фехнера

Сформулированный в 1860г. Г.Т. Фехнером закон, согласно коему величина ощущения прямо пропорциональна логарифму интенсивности раздражителя — то есть возрастание силы раздражения в геометрической прогрессии соответствует росту ощущения в арифметической прогрессии. Эта формула измерения ощущений была выведена на основе исследований Вебера, где было показано постоянство относительной величины приращения раздражителя, вызывающего ощущение едва заметного различия. При этом был введен его собственный постулат о том, что едва заметный прирост ощущения является величиной постоянной и его можно применять использовать как единицу измерения ощущения.

Так иногда называют закон Вебера-Фехнера.

Словарь психиатрических терминов. В.М. Блейхер, И.В. Крук

нет значения и толкования слова

Неврология. Полный толковый словарь. Никифоров А.С.

Закон Вебера-Фехнера — син.: Закон психофизический. Закон, устанавливающий связь между силой раздражения какого-либо органа чувств и интенсивностью ощущения. При средней интенсивности раздражения выраженность ощущения прямо пропорциональна натуральному логарифму силы раздражения.

Описали немецкий анатом и физиолог Е.Н. Weber (1795–1878) и немецкий физик G. Fechner (1801–1887).

Оксфордский толковый словарь по психологии

нет значения и толкования слова

предметная область термина

назад в раздел : словарь терминов / глоссарий / таблица

Научная суббота «Закон Э. Вебера – Г. Фехнера в жизни человека»

11 апреля 2020 года в Российской академии образования состоится интерактивная лекция «Закон Э. Вебера – Г. Фехнера в жизни человека. В чём сила маркетинга, рекламы и эргономики?»

Ведущие: Варвара Ильинична Моросанова, член-корреспондент РАО, доктор психологических наук, профессор; Сергей Владимирович Молчанов, кандидат психологических наук.

Участники узнают, как применяется на практике основной психофизический закон Вебера – Фехнера, и каким образом особенности человеческих ощущений и восприятия используются в эргономике, охране труда, маркетинге, рекламе. Во время обсуждения слушатели смогут найти ответы на вопросы о том, почему однообразная реклама быстро приедается и не замечается; почему на концертах и в вещании музыкальных телеканалов чередуются быстрые и медленные композиции, и почему сладкое лучше есть после первого и второго блюда, а не наоборот?

Вход на мероприятие по предварительной регистрации на сайте проекта «Субботы московского школьника» в соответствии с правилами регистрации и обозначенной для мероприятия целевой аудиторией.

Обучающиеся, прошедшие регистрацию, получат материалы занятий в видеоформате на адрес электронной почты, указанной при регистрации.

Лекция организована в рамках проекта “Субботы московского школьника”. Она станет одной из “Научных суббот”, которую организует РАО. Встречи с известными учеными и популяризаторами науки, которые показывают исследовательские будни изнутри, служат качественным дополнением к основной школьной программе. Каждый подросток сможет соприкоснуться с миром большой науки и увидеть связь теорий, теорем и гипотез с реальной жизнью.

Время проведения: с 14:45 до 16:20

Формат участия: дистанционный

Закон Вебера-Фехнера – основной психофизический закон. Основные психофизические законы (по Веккеру)

раздражителя к базовой величине раздражения; то же самое с ощущениями (слева)

Закон Вебера — Фехнера

установлены закономерные функциональные взаимосвязи между величиной силовой характеристики физического раздражения и соответствующей ей субъективной величиной ощущения: интенсивность ощущения пропорциональна логарифму интенсивности стимула (раздражителя).

Закон Стивенса – это модификация закона Вебера — Фехнера. Между рядом ощущений и рядом физических раздражителей существует не логарифмическая, а степенная зависимость.

где R – сила ощущения;

с – константа;

I – интенсивность раздражителя;

Iο — величина абсолютного порога ощущения;

n – показатель степени, зависящий от модальности ощущений

Обобщенный психофизический закон Ю. Забродина:

Характер зависимости между ощущениями и воздействующими раздражителями обусловлен осведомленностью человека о процессах ощущения.

Введение показателя z, характеризующего степень осведомленности.

Основные психофизические законы (по Веккеру).

Оказалось, что интенсивность как универсальная количественная энергетическая характеристика явлений природы была распространена на сферу психических процессов и были установлены закономерные функциональные взаимосвязи между величиной силовой характеристики физического раздражения и соответствующей ей субъективной величиной ощущения. В этом выражается содержание психофизического логарифмического закона Вебера — Фехнера. Принимая R=О при интенсивности раздражителя, равной абсолютному порогу (Iο)], получается следующее уравнение:

R=clog Iο/I,

где R – величина ощущения; с – константа, величина которой зависит от основания логарифма и от отношения Вебера; I – интенсивность раздражителя; Iο — величина абсолютного порога интенсивности.

По данному уравнению ощущение описывается кривой уменьшающегося прироста. Вывод логарифмического закона Фехнера основывается, как известно, на допущении о субъективном равенстве <едва заметных различий> раздражителей.

Интенсивность является универсальной характеристикой, она, конечно, не может не быть представленной на уровне нервного возбуждения, что и находит свое прямое выражение в нейрофизиологических фактах (прежде всего, например, в амплитудной характеристике градуальных сигналов).

Между ощущением как <первым> психическим сигналом и сигналом <чисто> нервным особый интерес представляет соотношение между психологической и нейрофизиологической величинами интенсивности (в их отношении к исходной интенсивности раздражения).

Современные психофизические исследования Стивенса и его школы открывают доступ к сущности психофизиологического <порога> или границы в рамках общих психофизических отношений. Он выявил степенной характер зависимости между силой ощущения и интенсивностью раздражителя (психофизический закон Стивенса).

, где R – сила ощущения; с – константа; I – интенсивность раздражителя; Iο — величина абсолютного порога ощущения; n – показатель степени, зависящий от модальности ощущений

Многочисленные данные свидетельствуют о том, что периферическая реакция анализатора действительно является именно логарифмической функцией интенсивности раздражителя. Периферическая реакция анализатора на раздражение есть реакция кодирования, преобразующего физическое воздействие источника информации в нервный сигнал-код, то сделанное Экманом заключение фактически означает

Психологический смысл психофизических законов — конспект — Психология

ПСИХОЛОГИЧЕСКИЙ СМЫСЛ ПСИХОФИЗИЧЕСКИХ ЗАКОНОВ Основной психофизический закон. Исходя из закона Вебера, Фехнер 0 0 1 Fсделал допущение, что едва заметные раз ницы в ощущениях можно 0 0 1 Fрассматривать как равные, поскольку все они — ве личины бесконечно малые, и принять их как единицу меры, при помощи которой можно численно выразить интенсивность ощущений как сумму (или интеграл) едва заметных (бесконечно малых) увеличений, считая от порога абсолютной чувствительности. В результате он получил два ряда переменных величин — величины раздражителей и соответствующие им величины ощущений. 0 0 1 FОщуще ния растут в арифметической прогрессии, когда раздражители 0 0 1 Fрастут в гео метрической прогрессии. Отношение этих двух переменных 0 0 1 Fвеличин можно вы разить в логарифмической формуле: Е = KlogJ + С, где К и С суть некоторые константы. Эта формула, определяющая зависимость интенсивности ощущений (в единицах едва заметных перемен) от интенсивности соответственности раздражителей, и представляет собой так называемый психофизический закон Вебера-Фехнера. Порогу чувствительности соответствует точка в сенсорном пространстве. В этой точке отражается значение стимула, при котором сенсорная система переходит из одного состояния в другое. В случае абсолютного порога она переходит от отсутствия ощущения к появлению едва заметного ощущения, В случае разностного порога — от отсутствия ощущения разницы к появлению ощущения различия. Таким образом, пороговые измерения — измерения точечные. Их результаты могут очертить границы (диапазон изменений величины стимулов), в которых действует сенсорная система, но они ничего не говорят о ее структуре. Следующим шагом в решении психофизической проблемы было построение функциональных зависимостей между психофизическими коррелятами, другими словами, построение психофизических шкал. Раздел психофизики, который занимается задачами построения психофизических шкал (психофизическим шкалированием), получил название психофизика-2. Решение этих задач нашло отражение в формулировке психофизических законов. Три самых известных психофизических закона представляют собой теоретические модели структуры сенсорного пространства. В основе этих моделей лежит эмпирический закон Бугера — Вебера. На границе XVIII — XIX вв. французский физик Бугер открыл некий эффект для зрительной 0 0 1 Fмодальности, а немецкий физиолог Вебер проверил его дей ствие для других модальностей. Этот эффект заключается в том, что отношение величины едва заметного увеличения стимула к исходному его значению остается 0 0 1 Fпостоянным в весьма широком диапазоне значе ний величины стимула, т.е. R/R=k Это соотношение получило название закона Бугера — Вебера. Закон Фехнера. Решая свою задачу о взаимоотношении 0 0 1 Fсубъектив ного и объективного, Фехнер рассуждал примерно следующим образом. Предположим, что наше сенсорное пространство состоит из очень 0 0 1 Fма леньких дискретных элементов е — едва заметных различений. Эти 0 0 1 Fэле менты равны между собой, т. е. постоянны: e=k, где k — константа. С учетом коэффициента пропорциональности две константы можно приравнять друг другу. Таким образом, постоянное отношение закона Бугера 0 0 1 F- Вебера можно приравнять константе, связанной с едва замет ным различением: R/R=Ke, где К — коэффициент пропорциональности. Далее Фехнер сделал шаг, за который его до сих пор ругают 0 0 1 Fматема тики (Фехнер сам был прекрасным математиком, следовательно, 0 0 1 Fсозна тельно пошел на это «преступление»). От этого уравнения, 0 0 1 Fсвязывающе го малые величины е и R, он перешел к дифференциальному 0 0 1 Fуравне нию dR/R=K×dE где dE — дифференциал, соответствующий очень маленькой величине е. Решением этого уравнения будет соотношение E=C1×LnR+C2 где C1 и C2 — константы интегрирования. Определим C2. Ощущение начинается с какого-то значения стимула, соответствующего пороговому (R1). При R=R1 ощущение отсутствует и появляется только при малейшем превышении R над R1, т.е. в этом случае Е=0. Подставим в полученное решение: О = C1 x InR1+C2, отсюда C2 = — C1 x InR1, следовательно, Е = C1 x InR- C1x In R1 = C1 x ln(R/ R1). Соотношение E = C1x ln (R/ R1) называется законом Фехнера или иногда 0 0 1 Fзаконом Вебера — Фехнера. Отметим, что закон Фехнера актив но использует понятие порога. R1 — это, очевидно, абсолютный порог; е- элементарные ощущения, аналог порога различения. Закон Стивенса. Американский психофизик Стивенс предложил свое решение задачи. Исходным пунктом для него был также закон Бугера — Вебера. Но модель сенсорного пространства он представлял себе иначе. Стивенс предположил, что в сенсорном пространстве действует отношение, 0 0 1 Fаналогичное закону Бугера — Вебера в пространстве стиму лов: E/E=k т.е. оглашение едва заметного приращения ощущения к его исходной величине является постоянной величиной. Опять же с точностью до 0 0 1 Fко эффициента пропорциональности мы можем приравнять две постоянные величины: E/E=K R/R Так как Стивенс не постулировал дискретность сенсорного 0 0 1 Fпро странства, он вполне корректно мог перейти к дифференциальному уравнению dE/E=dR/R

Астраномія. Астрафізіка і нябесная механіка

Мощность световой энергии обычно характеризуют потоком излучения (световым потоком), который является основным понятием фотометрии.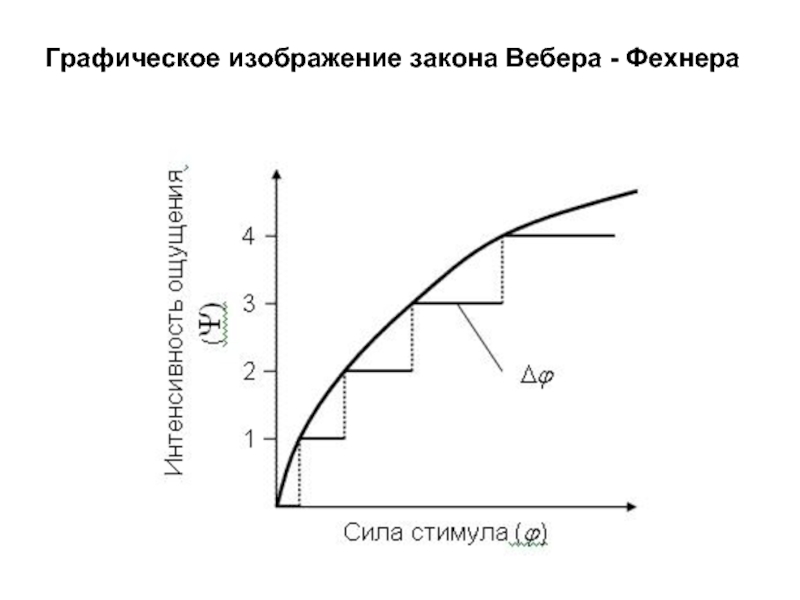 Потоком излучения Ф называется количество световой энергии, проходящей за единицу времени через данную площадку (например, входное отверстие телескопа). Освещённостью Е называется плотность светового потока, т. е. световой поток, приходящийся на единицу площади освещаемой поверхности: E = Ф/S. Поток излучения (а также освещённость) могут характеризовать излучение во всем спектре (полный или интегральный поток) или в каком-то определённом его участке. Если этот участок очень узок, то излучение, а вместе с ним и поток, называют монохроматическим. В последнем случае мощность излучения должна быть отнесена к единичному интервалу частот или длин волн. Вся энергия, проходящая в единицу времени через замкнутую поверхность, окружающую данный источник излучения, называется его светимостью L. Интенсивность излучения – энергетическая характеристика электромагнитного излучения, пропорциональная квадрату амплитуды колебаний. Мерой интенсивности служит вектор Пойнтинга. В фотометрии понятие интенсивности оптического излучения эквивалентно понятиям облучённости, освещённости и поверхностной плотности мощности излучения. В астрофизике под термином «интенсивность излучения» I понимают плотность потока излучения, создаваемого элементом среды в данном направлении: I = dФ/(dωdScosθ), где dФ – поток излучения в пределах бесконечно малого телесного угла dω, dS – площадь участка диафрагмы, нормаль к которой составляет угол θ с направлением распространения излучения. Если dS непосредственно является элементом излучающей поверхности, то определённая таким образом величина называется яркостью В этой поверхности в данной точке и в заданном направлении.

Густав Фехнер (1801 – 1887)

Эрнст Вебер (1795 – 1878)

Закон Вебера – Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула. Эрнст Вебер (1834): новый раздражитель, чтобы отличаться по ощущениям от предыдущего, должен отличаться от исходного на величину, пропорциональную исходному раздражителю.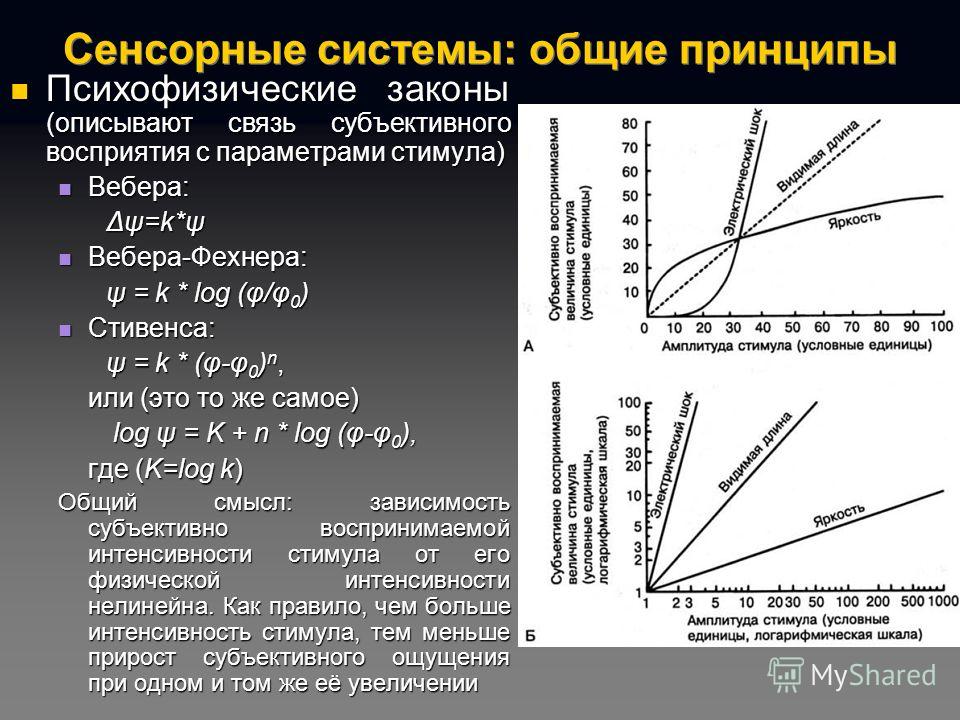 Густав Фехнер (1860): сила ощущения p пропорциональна логарифму интенсивности раздражителя S (основной психофизический закон): p = k log(S/S₀), где S₀ — граничное значение интенсивности раздражителя. Если S 0, раздражитель совсем не ощущается.

Создаваемая звёздами освещённость – (как правило) единственная о них фотометрическая информация. Во II веке до н. э. Гиппарх ввёл звёздную шкалу величин. Самые яркие звёзды были отнесены к первой величине, а находящиеся на границе видимости невооружённым глазом – к шестой величине. Звёздные величины обозначают индексом m, который ставится вверху после числового значения: 5^m. Глаз реагирует на световую энергию, прошедшую через зрачок и которая пропорциональна освещённости. При этом, согласно закону Вебера – Фехнера, при изменении внешнего раздражения в геометрической прогрессии, органы чувств передают соответствующие ощущения в арифметической прогрессии. Поэтому в шкале, введённой Гиппархом, освещённости от звёзд 1-й, 2-й, …, 6-й величин оказались в убывающей геометрической прогрессии, знаменатель q которой (по аналогии с октавой), должен был быть равен ½. Тогда освещённость E_m от звезды, у которой звёздная величина m, определяется через освещённость от звезды первой величины E₁ и знаменатель прогрессии q: E_m = E₁q^{m – 1}. Измерения, проведённые в середине XIX века, показали, что разности в 5 звёздных величин по шкале Гиппарха соответствует отношение освещённостей почти 1/100.

Норман Погсон (1829 – 1891)

В 1857 году Норман Погсон предложил использовать для шкалы звёздных величин следующее значение q: q = 100^–1/5 = 10^–0.4 ≈ 1/2.512, при котором разность в 5 звёздных величин точно соответствует отношению освещённостей в 100 раз. Число 2.512 показывает, во сколько раз освещённость от объекта со звёздной величиной m больше, чем от объекта со звёздной величиной m + 1. Таким образом, освещённости, создаваемые двумя объектами со звёздными величинами m₁ и m₂, связаны соотношениями: E_m₁/E_m₂ = (2.

512…)^{–(m₁ – m₂)} и lg(E_m₁/E_m₂) = –0.4(m₁ – m₂), или формулой Погсона: m₁ – m₂ = –2.5lg(E_m₁/E_m₂). Формула Погсона служит для определения шкалы звёздных величин (или видимых звёздных величин): звёздной величиной называется отсчитываемый от некоторого нуль-пункта десятичный логарифм освещённости, создаваемой данным объектом в месте наблюдения, умноженный на коэффициент –2,5. Формула Погсона позволяет определять звёздные величины объектов, более ярких, чем с m = 1. Для таких объектов m 2 = 0 соответствует E₂ = 1.

Венера

Звезда нулевой звёздной величины (0^m) создаёт на границе земной атмосферы освещённость E₀ = 2.48 × 10^–12 Вт/м². Примеры значений видимых (визуальных) звёздных величин: Солнце: –26,8^m Луна в полнолуние: –12,7^m Венера в элонгации: –4,4^m Юпитер в противостоянии: –2,7^m Марс в противостоянии: –2,0^m

Сириус

Меркурий в элонгации: –1,9^m Сириус: –1,5^m Вега: 0,0^m Проксима: 0,0^m Сатурн без колец: +0,7^m Полярная звезда: +2,0^m Туманность Андромеды: +3,4^m 1 квадратный градус ясного безлунного ночного неба: +3,5^m Уран в противостоянии: +5,5^m Нептун: +7,8^mДополнительная литература: П.

П. Лазарев. Основной психо-физический закон и его современная формулировка

границ | Единая теория психофизических законов восприятия силы звука

Введение

Психофизические законы пытаются связать амплитуду физического стимула с его воспринимаемой величиной, например громкость как функцию звукового давления или яркость как функцию яркости. Классический подход к раскрытию психофизических законов был предложен Фехнером (1966) в середине 18 века (оригинальная работа опубликована в 1860 году). Фехнер предположил, что едва заметная разница (jnd), выраженная как доля Вебера (Δ I / I ), где I — стандартная интенсивность звука, а Δ I — изменение интенсивности, необходимое для jnd, производит такое же приращение ощущения громкости (Δ L ).Интегрируя это уравнение, а именно Δ L = Δ I / I , он получил так называемый закон Фехнера: громкость является логарифмической функцией интенсивности звука ( L = log I ).

Мало того, что логарифмический закон Фехнера был заменен степенным законом Стивенса или L = I ^θ, где θ — константа (Stevens, 1961), его общий подход был также подвергнут сомнению из-за невозможности интегрировать jnd-функции два разных звука, чтобы предсказать их соответствующие функции громкости (Newman, 1933; Miller, 1947).Таким образом, неудивительно, что некоторые исследователи отказались от фехнеровского подхода к установлению связи между стимулом jnd и субъективной величиной. Что удивительно, так это основания отказа от фехнеровского подхода. Например, Стивенс (1961) утверждал, что метод прямой оценки величины устарел различение интенсивности в качестве меры связи между стимулом и ощущением. Он рассматривал меру дискриминации как «инженер говорит… разброс некоторых настроек шкалы».«В совершенно противоположной точке зрения Вимейстер и Бэкон (1988) заявили, что данные оценки громкости были мерой с« вероятно сильным участием несенсорных факторов, (и) мы не пытались связать эти данные с данными для различения интенсивности ».

Были и другие исследователи, которые продолжали продвигать фехнеровский подход в поисках единой теории, связывающей различение интенсивности с функцией громкости. Первоначальное предположение Фехнера иногда называли теорией «наклона», потому что оно предсказывало, что чем круче функция громкости, тем меньше jnd или доля Вебера для постоянного увеличения громкости.Это простое предсказание наклона оказалось неверным, по крайней мере, в случаях набора громкости, когда потеря слуха улитки или частичная маскировка повышали порог слышимости, но вызывали аномально резкий рост громкости, так что нормальная громкость воспринималась при высоких уровнях звука (Fowler, 1937). . Чтобы объяснить несостоятельность теории наклона Фехнера, несколько исследователей предложили теорию «пропорционального jnd», в которой размер jnd необходимо нормировать на общее число jnd в динамическом диапазоне стимула (Riesz, 1933; Teghtsoonian, 1971; Lim и другие., 1977). С другой стороны, теория «равной громкости, равной-jnd» утверждала, что jnd не имеет никакого отношения к наклону функции громкости, а скорее определяется общей громкостью (Zwislocki and Jordan, 1986). Несмотря на значительные усилия по проверке этих соотношений громкость-jnd, консенсуса пока не достигнуто (Houtsma et al., 1980; Hellman et al., 1987; Schlauch and Wier, 1987; Rankovic et al., 1988; Johnson et al., 1993; Стиллман и др., 1993; Шлаух и др., 1995; Аллен и Нили, 1997; Хеллман и Хеллман, 2001).

Здесь я представляю единую теорию, начиная с общей формы функции громкости Zwislocki (1965), чтобы вывести общую форму закона Брентано, и я приду к общей форме отношения громкость-jnd, которая объединяет предыдущие теории громкости-jnd. . В частности, я считаю, что предыдущие теории «наклона», «пропорционального jnd» и «равной громкости, равного jnd» являются тремя дополнительными терминами в новой единой теории. Я также показываю, что новая теория способна предсказывать громкость и jnd-данные в широком диапазоне слуховых ситуаций, включая нейросенсорную тугоухость, одновременную маскировку, прямую маскировку и электрический слух.

Вывод единой теории

Вывод общей формы закона Брентано или Экмана

Я начинаю с общей формы функции громкости, предложенной Zwislocki (1965; уравнение 212):

L = k [(I + cI0) θ- (cI0) θ] (1)

, где I ₀ — порог обнаружения для определенного типа звука, c представляет масштабный коэффициент внутреннего шума, а k — постоянная величина.

Общность и симметрия — две причины выбора функции громкости Цвислока.Во-первых, при высоких интенсивностях ( I I _o) функцию Цвислока можно упростить до степенного закона Стивенса, а именно: L = kI ^θ. При низкой интенсивности Цвислоки сделал неявное, но важное предположение для учета набора громкости вблизи порога: наклон (θ) функции громкости не увеличивается, как первоначально предполагалось (Fowler, 1937), вместо этого увеличивается громкость на пороге. Установка I = I _o в уравнении.(1), громкость на пороге, или L _o = k [( I _o + cI _o) ^θ — ( cI _o) ^θ] = k [( 1 / c + 1 ) ^θ — 1)] ( cI _o) ^θ ∼ k [θ ( 1 / c ) ^{1 – θ} ] ( I _o) ^θ, прямо пропорционально пороговому значению и «должно быть больше нуля (Zwislocki, 1965; p. .87) ». Математически громкость на пороге бесконечна, когда внутренний шум равен нулю ( c = 0), и наоборот. Это фундаментальный аргумент в пользу того, почему мозг имеет или нуждается во внутреннем шуме, потому что бесконечная громкость явно биологически неприемлема. Концепция внутреннего шума Цвислоки также была расширена, чтобы сформировать основу для рассмотрения набора громкости как «невосприятия мягкости» (Buus and Florentine, 2002), а тиннитуса как «дополнительного центрального шума» (Zeng, 2013). В интересах простоты я определяю громкость на пороге как: L _o = k ( cI _o) ^θ (или c = 0.125 для θ = 0,27).

Во-вторых, математическую симметрию можно показать, дифференцируя уравнение. (1):

ΔLΔI = θk (I + cI0) θ-1 = θk (I + cI0) θI + cI0 (2)

Складывая и вычитая тот же компонент в приведенном выше уравнении, я получаю:

ΔLΔI = θk (I + cI0) θ- (cI0) θ + (cI0) θI + cI0 = θL + L0I + cI0 (3)

Переписывая приведенное выше уравнение, я получаю общую форму закона Брентано или закона Экмана, а именно ΔLL = ΔII (обсуждение этих законов см. В Stevens, 1961):

ΔLL + L0 = θΔII + cI0 (4)

Уравнение (4) математически симметрично и сбалансировано, имеет общую форму закона Вебера, включающую пороговый поправочный член как в области ощущений ( L _o), так и в области стимулов (c I _{). o}).

В первом приближении закон Вебера в области стимулов был «воспроизведен в сотнях исследований по всем сенсорным модальностям и многим видам животных за последние два столетия (Pardo-Vazquez et al., 2019)». При распознавании интенсивности звука доля Вебера постоянна для широкополосного шума, но немного уменьшается с увеличением интенсивности, что приводит к «близкому нарушению» закона Вебера (McGill and Goldberg, 1968). Следовательно, уравнение. (4) можно записать как:

ΔLL + L0 = wIα (5)

, где w и α — константы, причем α = 0 указывает на полное соответствие закону Вебера.

Согласно теории «пропорционального jnd» (Лим и др., 1977), константа w обратно пропорциональна количеству jnds ( N ) в динамическом диапазоне стимула. Другими словами, w = 1/ N , что можно рассматривать как коэффициент масштабирования, чтобы учесть тот факт, что разные субъекты или разные типы стимулов могут иметь разное количество различимых шагов в их соответствующем динамическом диапазоне (например, , у слушателя с нормальным слухом есть 100 шагов, а у пользователя кохлеарного импланта — только 10), но все они имеют одинаковый рост громкости от тихого на пороговом уровне до неприятно громкого на верхнем пределе диапазона.Теория «пропорционального jnd» утверждает, что 10 шагов jnd у слушателя с нормальным слухом вызовут такое же изменение громкости, как и шаг jnd у пользователя кохлеарного имплантата. Хотя теория «пропорционального jnd» не предполагала и не требовала какой-либо конкретной функции jnd-громкости, Лим и др. (1977) намекнули, что закон Брентано «почти правильный» (см. Сноску 7 на стр. 1264 в Lim et al., 1977). В этом случае относительное изменение громкости обратно пропорционально количеству jnds с поправкой на интенсивность, происхождение которой будет рассмотрено в разделе «Обсуждение»:

ΔLL + L0 = 1NIα (6)

Прогнозирование функции jnd на основе функции баланса громкости

Предположим, что функция громкости для тихого тона равна: L = f (I) , и что получена функция баланса громкости между тихим тоном и тоном в маскировке: I = г (Я _м). По определению, при I = g (I _m) громкость сбалансирована, так что функция громкости может быть получена для частично замаскированного тона:

Lm = L = f (I) = f [g (Im)] (7)

Из приведенного выше уравнения получаем:

ΔLmΔIm = f ′ (I) g ′ (Im) = ΔLΔIg ′ (Im) (8)

Запишите приведенное выше уравнение:

ΔIm = ΔI1g ′ (Im) ΔLmΔL (9)

Заменить Δ L _м и Δ L формулой.(6) чтобы получить:

ΔIm = ΔI1g ′ (Im) NNmImαIαLm + LmoL + Lo (10)

Для прогнозирования jnd в форме доли Вебера при той же интенсивности, то есть I _м = I , чтобы можно было исключить поправочный член интенсивности (Imα / Iα) и разделить вышеприведенное уравнение по ( I ):

ΔImI = ΔII1g ′ (Im) NNmLm + LmoL + Lo (11)

Используя логарифмическое преобразование, можно вычислить jnd через долю Вебера в дБ (WFdB):

WFmdB (I) = WFdB (I) -10log⁡g ′ (Im) + 10logNNm + 10logLm + LmoL + Lo (12)

, где WF _м дБ (I) = 10log (Δ I _m / I ), что является долей Вебера для маскированного тона и WFdB (I) = 10log ( Δ I / I ), которая является долей Вебера для тона в тишине.

Уравнение (12) показывает, что, если известно WFdB (I) при данной интенсивности ( I ), то можно предсказать WF _м дБ (I) при той же интенсивности из трех дополнительных измеряет: (1) локальный наклон функции баланса громкости [ g ‘ ( I _m)], (2) коэффициент масштабирования ( N / N _m ) и (3) локальное соотношение громкости между замаскированным тоном и тоном в тишине [( L _{м +} L _мес) / (L + L _o)].Интересно, что теоретически нет необходимости точно знать порог обнаружения, точную форму увеличения громкости или функцию распознавания интенсивности для тона в тишине.

Я рассматриваю уравнение. (12) в качестве единой теории психофизических законов восприятия интенсивности звука, потому что последние три члена в уравнении содержат три предыдущие теории, которые пытались связать функцию jnd с функцией громкости. Член 10log g ’ ( I _м) представляет собой первоначальную теорию« наклона »Фехнера; термин 10log ( N / N _m ) представляет собой «пропорциональную» теорию Рисса; а последний термин представляет теорию Цвислоцкого «равной громкости, равной громкости».

Подтверждение единой теории

Прогнозирование jnd-функций при одновременном маскировании

Одновременное маскирование не только повышает порог чистого тона, но также влияет на восприятие его громкости, подобно набору громкости при нейросенсорной тугоухости. Функции баланса громкости и распознавания интенсивности были измерены в одной и той же группе слушателей для чистых тонов в тишине и при одновременном маскировании шума (Houtsma et al., 1980; Rankovic et al., 1988; Schlauch et al., 1995).

Здесь я использую Schlauch et al. (1995) данные для предсказания замаскированного jnd из тихого jnd, поскольку Schlauch et al. (1995) имел наиболее полный набор данных. Рисунок 1 иллюстрирует относительные вклады трех специальных членов в уравнении. (12) к предсказаниям jnd-данных при одновременном маскировании. На рисунке 1A показаны три функции баланса громкости: сплошная линия представляет гипотетическое состояние, при котором один и тот же тон идеально сбалансирован по громкости (т.е., соотношение 1: 1) между двумя ушами в тишине, пунктирная линия представляет измеренную функцию баланса для замаскированного тона в широкополосном шуме 15-SPL / Гц, а пунктирная линия для замаскированного тона в SPL / 40-дБ / Широкополосный шум Гц (из рисунка 3 в Schlauch et al., 1995). Затем дифференцируется интерполяция функции баланса громкости для получения наклонов в зависимости от интенсивности (X представляют маскировку 15 дБ SPL / Гц, а O представляют условие маскировки 40 дБ SPL / Гц). На рисунке 1B показана функция увеличения громкости для тона 1000 Гц в тишине (сплошная линия) на основе модели Цвислока [уравнение.(1), используя k = 3,1; θ = 0,27; c = 2,5; I _o = 10 ^— ¹² Вт / м ² или 0 дБ SPL], а также две функции замаскированного увеличения громкости, полученные путем применения функций баланса громкости на рисунке 1A к функция увеличения громкости в тишине. Значки X и O представляют собой соотношение громкости между соответствующими условиями тишины и маскировки. На рисунке 1C показаны измеренные jnd-функции в тихом режиме (сплошная линия), маскировке 15 дБ (пунктирная линия) и маскировке 40 дБ (пунктирная линия).Значки X и O представляют собой предсказанные значения jnd в двух вышеупомянутых условиях маскирования на основе уравнения. (12). В дополнение к использованию значений наклона на рисунке 1A и значений отношения громкости на рисунке 1B, уравнение. (12) использует коэффициент нормализации 4 дБ и 8 дБ для условий маскирования 15 дБ и 40 дБ соответственно. Коэффициенты нормализации 4 дБ и 8 дБ были оценены как по динамическому диапазону, так и по значениям jnd (Nelson et al., 1996; см. Их рисунок 9), при этом тихое состояние было в 2,5 раза больше и 6.В 3 раза больше шагов jnd, чем при условии маскирования 15 дБ и 40 дБ соответственно. В этом прогнозе не было свободного параметра. Что касается относительного вклада в успешное предсказание, теория «равной громкости, равной-jnd» была существенной для предсказания общей тенденции (та же нисходящая картина на рисунках 1B, C), в то время как теория наклона (относительно пологая Образец символов X и O на рисунке 1A) ведет себя аналогично теории пропорционального jnd в качестве константы для сдвига предсказанной функции вверх или вниз.

Рис. 1. Прогнозы при одновременном маскировании с данными (линиями), полученными Schlauch et al. (1995). Панель (A) показывает функции баланса громкости между тоном в тишине (ось y ) и тоном в шуме (ось x ): сплошная линия представляет состояние управления, при котором один и тот же тон был сбалансирован между два уха в тишине, пунктирная линия представляет функцию баланса для тона, маскируемого широкополосным шумом 15 дБ SPL / Гц, а пунктирная линия представляет функцию баланса громкости для тона шумом 40 дБ SPL / Гц.Символы представляют значения наклона для функции баланса. Значения наклона используют тот же масштаб, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны. Панель (B) показывает производные функции роста громкости. Символы представляют значения отношения громкости между тихими и замаскированными тонами и тонами в тихом режиме. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).

Прогнозирование функции jnd при прямом маскировании

На громкость и ее jnd-функции стимула также может влиять прямая и обратная маскировка.Увеличивается громкость и снижается различение интенсивности при прямом и обратном маскировании, особенно при средней интенсивности (Zeng et al., 1991; Plack and Viemeister, 1992; Zeng and Turner, 1992). Хотя ранняя попытка связать «горб среднего уровня» (функция jnd) с повышением громкости не увенчалась успехом (Zeng, 1994), Оберфельд (2008) обнаружил значительную корреляцию между повышенным jnd и повышенной громкостью при широком диапазоне маскирующих звуков. разность уровней сигнала.

Используя те же шаги обработки, что и на рисунках 1, 2, показана функция баланса громкости между тоном длительностью 25 мс в тишине и при наличии 90 дБ УЗД, 100 мс прямого маскера (рисунок 2A), полученное увеличение громкости функция (рисунок 2B), а также измеренные и прогнозируемые функции jnd в тихом режиме и с маскированием (рисунок 2C).Теория наклона (рис. 2A) предсказывала, что прямое маскирование будет давать меньшие, чем нормальные jnds для стандартных уровней ниже 50 дБ SPL, но большие jnds для уровней выше 50 дБ SPL. Теория «равной громкости, равного jnd» (рис. 2B) предсказала среднеуровневую функцию горба jnd из-за повышенной громкости при прямом маскировании. Коэффициент нормализации 7 дБ, или в пять раз меньше jnd шагов при прямом маскировании, был использован в окончательном успешном прогнозе (рис. 2C), который объединил все три специальные теории в формуле. (12).Подобная картина на рисунках 2B, C в целом согласуется с наблюдаемой корреляцией между повышенной громкостью и повышенным jnd (Oberfeld, 2008), но количественный прогноз требует дальнейшего изучения. Было бы также интересно узнать, может ли существующая объединенная теория предсказать аналогичную функцию jnd, наблюдаемую для коротких высокочастотных тонов в условиях режекторного шума (Carlyon and Moore, 1984). Оксенхэм и Мур (1995) намекнули на такую возможность, предложив «новую теорию, [объясняющую] резкое отклонение от закона Вебера с точки зрения как дисперсии…, так и громкости частично замаскированных сигналов.”

Рис. 2. Прогнозы при прямой маскировке с данными (линиями) из Zeng (1994). На панели (A) показаны функции баланса громкости между тоном в тишине ( по оси ) и тоном с прямой маскировкой (ось x ): сплошная линия представляет состояние управления, при котором один и тот же тон был сбалансирован между два уха в тишине, а пунктирная линия представляет функцию баланса для тона при прямой маскировке. Символы * представляют значения наклона для функции баланса, которая использует ту же шкалу, что и функция баланса от 0 до 100, за исключением того, что наклоны безразмерны.Панель (B) показывает производные функции роста громкости. Символы представляют значения отношения громкости между замаскированным тоном и тоном в тишине. Панель (C) показывает измеренные функции jnd (линии) и прогнозируемые значения jnd (символы).

Прогнозирование jnd-функций в электрическом слухе

В электрическом слухе, где волосковые клетки отсутствуют, а волокна слухового нерва напрямую стимулируются электрическим током, громкость обычно имеет узкий динамический диапазон 10–20 дБ (Zeng and Galvin, 1999).Зенг и Шеннон (1994) обнаружили, что у пользователей кохлеарных имплантатов громкость растет как традиционная степенная функция электрического тока для частот стимула ниже 300 Гц, но как экспоненциальная функция для частот стимула выше 300 Гц. Эти две разные функции увеличения громкости будут производить функцию логарифмического баланса громкости между низко- и высокочастотными электрическими стимулами. На рисунке 3A действительно показана такая функция логарифмического баланса (сплошные линии) между стимулом 100 Гц (синусоида или амплитуда импульса на оси y ) и синусоидой 1000 Гц (ось x ).

Рис. 3. Баланс громкости (A) и функции JND (B) у пользователей кохлеарных имплантатов. (A) Функции баланса громкости были получены между синусоидальным электрическим стимулом 100 Гц или импульсом 100 Гц и синусоидальным электрическим стимулом 1000 Гц, адаптированным из рисунков 2D, E в Zeng and Shannon (1994). Печатается с разрешения AAAS. Символы представляют индивидуальные данные, а сплошная линия представляет функцию логарифмического баланса. Пунктирная линия представляет функцию линейного баланса, которая явно не соответствовала действительности. (B) Данные JND (символы) и предсказанные функции (линии) с использованием одних и тех же стимулов от одних и тех же субъектов в (A) , адаптированном из рисунка 4 в Zeng and Shannon (1999). Печатается с разрешения Wolters Kluwer Health.

E1000 Гц = θlog⁡E100 Гц (13)

, где θ — наклон функции логарифмического баланса громкости. Дифференцируя приведенное выше уравнение, чтобы получить следующую функцию JND между высокочастотными и низкочастотными электрическими стимулами:

ΔE1000 Гц = θΔE100 ГцE100 Гц (14)

Зенг и Шеннон (1999) измерили jnds этих стимулов у тех же пациентов с имплантатом (символы на рисунке 3B) и обнаружили, что не только эта функция jnd сохраняется, но, что более важно, функция jnd была почти постоянной (сплошная линия на рисунке 3B). .Учитывая ту же функцию увеличения громкости мощности для электрических стимулов с частотой 100 Гц, неудивительно, что их доля Вебера также была постоянной. Но почему абсолютная разница (Δ E _{1000 Гц}) была постоянной для стимула с частотой 1000 Гц? Зенг и Шеннон (1999) показали, что эта постоянная абсолютная разница является результатом функции экспоненциального роста громкости.

L1000Hz = exp⁡ (E1000Hz) (15)

Из приведенного выше уравнения получаем:

ΔL1000HzΔE1000Hz = exp⁡ (E1000Hz) = L1000Hz (16)

Переписывая приведенное выше уравнение, получаем:

ΔL1000ГцL1000Гц = ΔE1000Гц (17)

Уравнение (17) означает, что коэффициент Брентано также постоянен при электростимуляции.Единственная разница между уравнениями. (17) и (4) состоит в том, что (17) не содержит порогового члена, вероятно, из-за отсутствия спонтанной нервной активности в глухом ухе (Kiang and Moxon, 1972).

Обсуждение

Ни один из отдельных компонентов существующей единой теории не является новым. Предыдущие исследования предлагали эти отдельные теории и оценивали их по отдельности (например, Zwislocki and Jordan, 1986; Hellman and Hellman, 1990, 2001; Schlauch, 1994; Schlauch et al., 1995; Allen and Neely, 1997).Настоящее исследование является новым в двух отношениях. Во-первых, настоящее исследование объединяет ранее отключенные отдельные компоненты с помощью единой теоретической основы, а именно общей формы закона Брентано в формуле. (4). Во-вторых, настоящее исследование предлагает новую формулу, а именно уравнение. (12), который специально сочетает эти отдельные термины для успешного прогнозирования соотношений громкости и jnd при одновременной и прямой маскировке, а также у пользователей кохлеарных имплантатов. Настоящая единая теория и ее успешные применения предполагают, что, хотя закон Вебера необходимо заменить общей формой закона Брентано, первоначальная идея Фехнера об использовании jnds для вывода психофизических законов действительна, по крайней мере, в широком диапазоне рассматриваемых здесь слуховых ситуаций.

Общая форма закона Брентано может быть использована для проверки того, насколько близко фактические данные jnd соответствуют закону Вебера и его потенциальным механизмам, путем комбинирования уравнений. (4) и (5):

ΔLL + L0 = θΔII + cI0 = wIαилиΔII + cI0 = w′Iα (18)

, где как w ’ (= w / θ), так и α являются свободными параметрами, подлежащими оценке, причем α = 0 указывает на полное соответствие закону Вебера. На рисунке 4 показаны данные jnd и оценка модели для тона 1 кГц (Schlauch et al., 1995), широкополосного шума 8 кГц (6–14 кГц) и того же шума на фоне шума с зазубринами (Viemeister, 1983). .Все три набора данных могут быть смоделированы двухэтапной функцией, с крутым первым этапом (∼10–20 дБ SPL), отражающим пороговое влияние, и более мелким вторым этапом (∼20–100 дБ SPL) с наклоном α в формуле. (16). Все три набора данных подчиняются закону Вебера (McGill and Goldberg, 1968), где α составляет -0,09 для тона, -0,03 для шума и 0,04 для шума на фоне шума с зазубринами. Ближний промах колеблется от -9% до 4% и составляет в среднем 3% для трех рассмотренных здесь стимулов.

Рисунок 4. Прогноз JND для шумовых и тональных стимулов. Данные JND для широкополосного шума (сплошные треугольники) и того же шума на фоне шума с надрезом (сплошные квадраты) были взяты из Viemeister (1983; те же символы на его рисунке 1) и данных JND тона 1000 Гц (светлые кружки) ) взяты из Schlauch et al. (1995; кружки на рис. 2 в правом нижнем углу). Пунктирная линия представляет собой прогноз функции JND шума, пунктирная линия представляет шум на фоне шума с выемками, а сплошная линия представляет функцию JND тона.

Чтобы найти решение для почти пропуска закона Вебера, Макгилл и Голдберг использовали процесс, подобный Пуассону, в котором среднее значение громкости ( L ) и его дисперсия (σ ²) равны, где σ — величина среднеквадратичное отклонение. Для достижения 75% правильного обнаружения в jnd задаче теория обнаружения сигналов требует: d ′ = ΔLσ = ΔLL0,5 = 1 (Green and Swets, 1966). Замена Δ L = L ^0,5 в уравнении. (19) произвести:

ΔLL + L0 = L0.5L + L0∝L-0.5∝ (I0,27) -0,5∝I-0,14 (19)

По сравнению с крутизной -0,14, предсказанной пуассоновским процессом, расчетная крутизна составляла 5% для тона, 11% для шума и 18% для шума на фоне режекторного шума. В качестве чрезмерной коррекции решение Макгилла и Голдберга создало гораздо большую разницу (в среднем = 11%), чем исходная проблема, то есть почти полное отсутствие (в среднем = 3%) закона Вебера. С другой стороны, использование распространения сигнала возбуждения является более вероятным механизмом, лежащим в основе почти несоблюдения закона Вебера (Florentine and Buus, 1981; Viemeister, 1983), но количественная обработка его предсказательной точности все еще отсутствует.По крайней мере, в первом приближении закон Вебера справедлив для различения интенсивности звука.

Несмотря на то, что это непросто, поиск единого психофизического закона продолжает привлекать внимание, особенно его биологическая основа (например, Shepard, 1987; Nieder and Miller, 2003; Dehaene et al., 2008; Джафаров и Колониус, 2011; Техцунян, 2012; Pardo-Vazquez et al., 2019). Во влиятельной статье, которая привлекла 30 открытых комментариев коллег, Крюгер (1989) попытался примирить Фехнера и Стивенса, предложив единый психофизический закон, в котором (1) «каждый jnd имеет одинаковую субъективную величину для данной модальности» (2). ) «Субъективная величина увеличивается приблизительно как степенная функция физической величины» и (3) «субъективная величина зависит в первую очередь от периферических сенсорных процессов, то есть не происходит никаких нелинейных центральных преобразований.Что касается (1), Крюгер предпочел Δ S или в настоящем термине Δ L = c (константа) для закона экономии, но был готов принять Δ L / L = c (закон Брентано) или даже Δ L / L = L ^−0,5 (процесс Пуассона Макгилла и Голдберга). Настоящее исследование отдает предпочтение закону Брентано с пороговым поправочным коэффициентом. Второй момент был главной задачей единого закона Крюгера, в котором он не только пытался согласовать различные способы измерения величины ощущений (например,g., оценка величины по сравнению с категориальным рейтингом), но также вывести функцию субъективной величины из данных jnd. Он подробно исследовал «теорию пропорционального jnd» (стр. 260), неявно обсуждал теорию «наклона» (его таблица 1 на стр. 261), но, вероятно, не знал о «равной громкости, равном jnd». теории, не говоря уже о том, чтобы рассматривать их как три независимых фактора, которые вместе вносят вклад в функцию jnd-громкости (настоящее исследование). Третий пункт Крюгера, относящийся к мозгу как к линейному устройству, неверен, потому что настоящее исследование (B3) не только показывает, что электрическая стимуляция слухового нерва, которая обходит слуховые волосковые клетки, вызывает экспоненциальную функцию громкости у пользователей кохлеарных имплантатов, но и что еще более важно, многие исследования нейропластичности обнаружили аномально повышенный прирост в головном мозге в ответ на снижение входного сигнала на периферии (например,г., Qiu et al., 2000; Норена, 2011; Chambers et al., 2016).

Заявление о доступности данных

Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.

Заявление об этике

Этическое одобрение для этого исследования не требовалось, поскольку данные на людях были взяты из ранее опубликованных исследований. Пациенты / участники предоставили письменное информированное согласие на участие в этом исследовании.

Авторские взносы

F-GZ несет полную ответственность за представленные здесь работы.

Конфликт интересов

Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.

Благодарности

Джо Цвислоки стимулировал мой интерес к этому предмету, когда я был аспирантом, посещающим его классы в Сиракузском университете. Я многому научился, а также получил пользу от интеллектуальных дискуссий с Крисом Тернером, Нилом Вимейстером, Бертом Шлаухом, Адрианом Хаутсмой, Бобом Шенноном, Уолтом Джестедтом, Джонтом Алленом, Брайаном Муром, Бобом Карлайоном, Крисом Плэком, Дунканом Люсом, Биллом МакГиллом, Бертом. Шарф, Рона и Билл Хеллман.Маике ван Экхаутте мотивировала обсуждение закона Вебера (рис. 4), Даниэль Оберфельд и Вольфганг Эллермайер сделали критические комментарии, которые помогли связать несколько неясных концов и расширить рамки обсуждения в этой статье. Однако я несу полную ответственность за представленные здесь работы.

Список литературы

Аллен, Дж. Б., и Нили, С. Т. (1997). Моделирование отношения между едва заметной разницей в интенсивности и громкостью для чистых тонов и широкополосного шума. Дж.Акуст. Soc. Являюсь. 102, 3628–3646. DOI: 10.1121 / 1.420150

CrossRef Полный текст | Google Scholar

Buus, S., и Florentine, M. (2002). Рост громкости у слушателей с улитковой тугоухостью: пересмотр набора. J. Assoc. Res. Отоларингол. 3, 120–139. DOI: 10.1007 / s101620010084

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Карлайон Р. П. и Мур Б. С. (1984). Дискриминация по интенсивности: серьезный отход от закона Вебера. J. Acoust. Soc. Являюсь. 76, 1369–1376. DOI: 10.1121 / 1.3

CrossRef Полный текст | Google Scholar

Чемберс, А. Р., Резник, Дж., Юань, Ю., Уиттон, Дж. П., Эдж, А. С., Либерман, М. С. и др. (2016). Усиление по центру восстанавливает слуховую обработку после почти полной денервации улитки. Neuron 89, 867–879. DOI: 10.1016 / j.neuron.2015.12.041

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Дехаэн, С., Изард, В., Спелке, Э., и Пика, П. (2008). Логарифмический или линейный? Четкое интуитивное понимание числовой шкалы в культурах коренных народов Запада и Амазонки. Наука 320, 1217–1220. DOI: 10.1126 / science.1156540

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Фехнер, Г. Т. (1966). Elemente der Psychophysik [Элементы психофизики]. Нью-Йорк, Нью-Йорк: Холт, Райнхарт и Уинстон, Инк.

Google Scholar

Florentine, M., and Buus, S. (1981). Модель возбуждающего паттерна для распознавания интенсивности. J. Acoust. Soc. Являюсь. 70, 1646–1654. DOI: 10.1121 / 1.387219

CrossRef Полный текст | Google Scholar

Фаулер, Э. П. (1937). Измерение ощущения громкости — новый подход к физиологии слуха, функциональным и дифференциально-диагностическим тестам. Arch. Отоларингол. 26, 514–521. DOI: 10.1001 / archotol.1937.00650020568002

CrossRef Полный текст | Google Scholar

Грин Д. М. и Светс Дж. А. (1966). Теория обнаружения сигналов и психофизика. Нью-Йорк, Нью-Йорк: Wiley.

Google Scholar

Хеллман Р., Шарф Б., Техцунян М. и Техцунян Р. (1987). О связи между ростом громкости и различением интенсивности чистых тонов. J. Acoust. Soc. Являюсь. 82, 448–453. DOI: 10.1121 / 1.395445

CrossRef Полный текст | Google Scholar

Хеллман, В. С., и Хеллман, Р. П. (1990). Дискриминация по интенсивности как движущая сила громкости. Применение к чистым тонам в тишине. J. Acoust. Soc. Являюсь. 87, 1255–1265. DOI: 10.1121 / 1.398801

CrossRef Полный текст | Google Scholar

Хеллман, У. С., и Хеллман, Р. П. (2001). Пересмотр отношений между громкостью и различением интенсивности. J. Acoust. Soc. Являюсь. 109 (5 Pt 1), 2098–2102. DOI: 10.1121 / 1.1366373

CrossRef Полный текст | Google Scholar

Хаутсма, А. Дж., Дурлах, Н. И., и Брейда, Л. Д. (1980). Восприятие интенсивности XI. Экспериментальные результаты по отношению разрешения по интенсивности к согласованию громкости. J. Acoust. Soc. Являюсь. 68, 807–813. DOI: 10.1121 / 1.384819

CrossRef Полный текст | Google Scholar

Джонсон, Дж. Х., Тернер, К. У., Цвислоки, Дж. Дж. И Марголис, Р. Х. (1993). Просто заметные различия в интенсивности и их отношении к громкости. J. Acoust. Soc. Являюсь. 93, 983–991. DOI: 10.1121 / 1.405404

CrossRef Полный текст | Google Scholar

Кианг, Н. Ю. и Моксон, Э. К. (1972). Психологические соображения при искусственной стимуляции внутреннего уха. Ann. Отол. Ринол. Ларингол. 81, 714–730. DOI: 10.1177 / 000348947208100513

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Крюгер, Л. Э. (1989). Примирение Фехнера и Стивенса — к единому психофизическому закону. Behav. Brain Sci. 12, 251–267. DOI: 10.1017 / S0140525x0004855x

CrossRef Полный текст | Google Scholar

Лим, Дж. С., Рабиновиц, В. М., Брейда, Л. Д., и Дурлах, Н. И. (1977). Восприятие интенсивности.VIII. Сравнение громкости между разными типами стимулов. J. Acoust. Soc. Являюсь. 62, 1256–1267. DOI: 10.1121 / 1.381641

CrossRef Полный текст | Google Scholar

МакГилл, У. Дж., И Голдберг, Дж. (1968). Исследование близких к неудачам с участием закона Вебера и дискриминации по интенсивности тона. Восприятие. Психофизика. 4, 105–109. DOI: 10.3758 / bf03209518

CrossRef Полный текст | Google Scholar

Миллер, Г. (1947). Чувствительность к изменениям интенсивности белого шума и его отношение к маскировке и громкости. J. Acoust. Soc. Являюсь. 19, 609–619. DOI: 10.1121 / 1.18