Закон сохранения энергии — Эко Энергия
Закон сохранения энергии
Открытие закона сохранения энергии
Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.
Фундаментальный смысл закона
Закон сохранения энергии — «фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени». Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени и в этом смысле является универсальным, то есть присущим системам самой разной физической природы. Другими словами, для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.
Другими словами, для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.
Однако в различных разделах физики по историческим причинам закон сохранения энергии формулируется по-разному, в связи с чем говорится о сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии выражается в виде первого начала термодинамики.
Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то более правильным является его именование не законом, а принципом сохранения энергии.
С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.
Согласно теореме Нётер каждому закону сохранению ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.
Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид:
Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).
История открытия закона сохранения и превращения энергии
В 1841 г. русский ученый Ленц и англичанин Джоуль почти одновременно и независимо друг от друга экспериментально доказали, что теплота может быть создана за счет механической работы. Джоуль определил механический эквивалент тепла. Эти и другие исследования подготовили открытие закона сохранения и превращения энергии. В 1842—1845 г.г. немецкий ученый Р. Майер сформулировал этот закон на основе обобщения данных естествознания о механическом движении, электричестве, магнетизме, химии и даже физиологии человека. Одновременно в Англии (Гров) и в Дании (Кольдинг) были высказаны аналогичные идеи. Несколько позднее этот закон разрабатывал Гельмгольц (Германия)
Эти и другие исследования подготовили открытие закона сохранения и превращения энергии. В 1842—1845 г.г. немецкий ученый Р. Майер сформулировал этот закон на основе обобщения данных естествознания о механическом движении, электричестве, магнетизме, химии и даже физиологии человека. Одновременно в Англии (Гров) и в Дании (Кольдинг) были высказаны аналогичные идеи. Несколько позднее этот закон разрабатывал Гельмгольц (Германия)
Воззрения на теплоту как форму движения мельчайших «нечувствительных» частиц материи высказывались еще в XVII в. Ф. Бэкон, Декарт, Ньютон, Гук и многие другие приходили к мысли, что теплота связана с движением частиц вещества []. Но со всей полнотой и определенностью эту идею разрабатывал и отстаивал Ломоносов. Однако он был в одиночестве, его современники переходили на сторону концепции теплорода, и, как мы видели, эта концепция разделялась многими выдающимися учеными XIX столетия.
Успехи экспериментальной теплофизики, и прежде всего калориметрии, казалось, свидетельствовали в пользу теплорода. Но тот же XIX в. принес наглядные доказательства связи теплоты с механическим движением. Конечно, факт выделения тепла при трении был известен с незапамятных времен. Сторонники теплоты усматривали в этом явлении нечто аналогичное электризации тел трением — трение способствует выжиманию теплорода из тела. Однако в 1798 г. Бенжамен Томпсон (1753―1814), ставший с 1790 г. графом Румфордом, сделал в мюнхенских военных мастерских важное наблюдение: при высверливании канала в пушечном стволе выделяется большое количество тепла. Чтобы точно исследовать это явление, Румфорд проделал опыт по сверлению канала в цилиндре, выточенном из пушечного металла. В высверленный канал помещали тупое сверло, плотно прижатое к стенкам канала и приводившееся во вращение. Термометр, вставленный в цилиндр, показал, что за 30 минут операции температура поднялась на 70 градусов Фаренгейта. Румфорд повторил опыт, погрузив цилиндр и сверло в сосуд с водой. В процессе сверления вода нагревалась и спустя 2,5 часа закипала.
Но тот же XIX в. принес наглядные доказательства связи теплоты с механическим движением. Конечно, факт выделения тепла при трении был известен с незапамятных времен. Сторонники теплоты усматривали в этом явлении нечто аналогичное электризации тел трением — трение способствует выжиманию теплорода из тела. Однако в 1798 г. Бенжамен Томпсон (1753―1814), ставший с 1790 г. графом Румфордом, сделал в мюнхенских военных мастерских важное наблюдение: при высверливании канала в пушечном стволе выделяется большое количество тепла. Чтобы точно исследовать это явление, Румфорд проделал опыт по сверлению канала в цилиндре, выточенном из пушечного металла. В высверленный канал помещали тупое сверло, плотно прижатое к стенкам канала и приводившееся во вращение. Термометр, вставленный в цилиндр, показал, что за 30 минут операции температура поднялась на 70 градусов Фаренгейта. Румфорд повторил опыт, погрузив цилиндр и сверло в сосуд с водой. В процессе сверления вода нагревалась и спустя 2,5 часа закипала. Этот опыт Румфорд считал доказательством того, что теплота является формой движения.
Этот опыт Румфорд считал доказательством того, что теплота является формой движения.
Опыты по получению теплоты трением повторил Дэви. Он плавил лед трением двух кусков друг о друга. Дэви пришел к выводу, что следует оставить гипотезу о теплороде и рассматривать теплоту как колебательное движение частиц материи.
По Майеру, все движения и изменения в мире порождаются «разностями», вызывающими силы, стремящиеся уничтожить эти разности. Но движение не прекращается, потому что силы неуничтожаемы и восстанавливают разности. «Таким образом, принцип, согласно которому раз данные силы количественно неизменны, подобно веществам, логически обеспечивает нам продолжение существования разностей, а значит, и материального мира». Эта формулировка, предложенная Майером, легко уязвима для критики. Не определено точно понятие «разность», неясно, что понимается под термином «сила». Это предчувствие закона, а не самый еще закон. Но из дальнейшего изложения понятно, что под силой он понимает причину движения, которое измеряется произведением массы на скорость. «Движение, теплота и электричество представляют собою явления, которые могут быть сведены к одной силе, которые измеряются друг другом и переходят друг в друга по определенным законам». Это вполне определенная и ясная формулировка закона сохранения и превращения силы, т.е. энергии.
«Движение, теплота и электричество представляют собою явления, которые могут быть сведены к одной силе, которые измеряются друг другом и переходят друг в друга по определенным законам». Это вполне определенная и ясная формулировка закона сохранения и превращения силы, т.е. энергии.
Задавшись целью применить идеи механики в физиологии, Майер начинает с выяснения понятия силы. И здесь он вновь повторяет мысль о невозможности возникновения движения из ничего, сила — причина движения, а причина движения является неразрушимым объектом. Эта формулировка поразительно напоминает формулировку «всеобщего закона» Ломоносова, распространяемого им «и на самые правила движения». Заметим, что выдвижение Ломоносовым и Майером всеобщего закона сохранения в качестве «верховного закона природы» принято современной наукой, которая формулирует многочисленные конкретные законы сохранения в качестве основной опоры научного исследования.
Майер подробно подсчитывает механический эквивалент теплоты из разности теплоемкостей газа (этот подсчет нередко воспроизводится в школьных учебниках физики) и находит его, опираясь на измерения Делароша и Берара, а также Дюлонга, определивших отношение теплоемкостей для воздуха равным 367 кгс-м/ккал. Он закончил развитие своих идей к 1848 г., когда в брошюре «Динамика неба в популярном изложении» он поставил и сделал попытку решить важнейшую проблему об источнике солнечной энергии. Майер понял, что химическая энергия недостаточна для восполнения огромных расходов энергии Солнца. Но из других источников энергии в его время была известна только механическая энергия. И Майер сделал вывод, что теплота Солнца восполняется бомбардировкой его метеоритами, падающими на него со всех сторон непрерывно из окружающего пространства. Он признает, что открытие сделано им случайно (наблюдение на Яве), но «оно все же моя собственность, и я не колеблюсь защищать свое право приоритета». Майер указывает далее, что закон сохранения энергии, «а также численное выражение его, механический эквивалент теплоты, были почти одновременно опубликованы в Германии и Англии». Он указывает на исследования Джоуля и признает, что Джоуль «открыл безусловно самостоятельно» закон сохранения и превращения энергии и что «ему принадлежат многочисленные важные заслуги в деле дальнейшего обоснования и развития этого закона».
Он закончил развитие своих идей к 1848 г., когда в брошюре «Динамика неба в популярном изложении» он поставил и сделал попытку решить важнейшую проблему об источнике солнечной энергии. Майер понял, что химическая энергия недостаточна для восполнения огромных расходов энергии Солнца. Но из других источников энергии в его время была известна только механическая энергия. И Майер сделал вывод, что теплота Солнца восполняется бомбардировкой его метеоритами, падающими на него со всех сторон непрерывно из окружающего пространства. Он признает, что открытие сделано им случайно (наблюдение на Яве), но «оно все же моя собственность, и я не колеблюсь защищать свое право приоритета». Майер указывает далее, что закон сохранения энергии, «а также численное выражение его, механический эквивалент теплоты, были почти одновременно опубликованы в Германии и Англии». Он указывает на исследования Джоуля и признает, что Джоуль «открыл безусловно самостоятельно» закон сохранения и превращения энергии и что «ему принадлежат многочисленные важные заслуги в деле дальнейшего обоснования и развития этого закона». Но Май ер не склонен уступать свое право на приоритет и указывает, что из самих его работ видно, что он не гонится за эффектом. Это, однако, не означает отказа от прав на свою собственность.
Но Май ер не склонен уступать свое право на приоритет и указывает, что из самих его работ видно, что он не гонится за эффектом. Это, однако, не означает отказа от прав на свою собственность.
Задолго до Джоуля исследования были начаты петербургским академиком Э.Х. Ленцем, который опубликовал свою работу в 1843 г. под заглавием «О законах выделения тепла гальваническим током». Упоминает Ленц о работе Джоуля, публикация которого опередила публикацию Ленца, но считает, что, хотя его результаты в «основном совпадают с результатами Джоуля», они свободны от тех обоснованных возражений, которые вызывают работы Джоуля.
Ленц тщательно продумал и разработал методику эксперимента, испытал и проверил тангенс-гальванометр, служивший у него измерителем тока, определил применяемую им единицу сопротивления (напомним, что закон Ома к этому времени еще не вошел во всеобщее употребление), а также единицы тока и электродвижущей силы, выразив последнюю через единицы тока и сопротивления. Он тщательно изучил поведение сопротивлений, в частности исследовал вопросе существовании так называемого «переходного сопротивления» при переходе из твердого тела в жидкость. Это понятие вводилось некоторыми физиками в эпоху, когда закон Ома еще не был общепризнанным. Затем он перешел к основному эксперименту, результаты которого сформулировал в следующих двух положениях: нагревание проволоки гальваническим током пропорционально сопротивлению проволоки; нагревание проволоки гальваническим током пропорционально квадрату служащего для нагревания тока. Точность и обстоятельность опытов Ленца обеспечили признание закона, вошедшего в науку под названием закона Джоуля — Ленца.
Это понятие вводилось некоторыми физиками в эпоху, когда закон Ома еще не был общепризнанным. Затем он перешел к основному эксперименту, результаты которого сформулировал в следующих двух положениях: нагревание проволоки гальваническим током пропорционально сопротивлению проволоки; нагревание проволоки гальваническим током пропорционально квадрату служащего для нагревания тока. Точность и обстоятельность опытов Ленца обеспечили признание закона, вошедшего в науку под названием закона Джоуля — Ленца.
Джоуль сделал свои эксперименты по выделению тепла электрическим током исходным пунктом дальнейших исследований выяснения связи между теплотой и работой. Уже на первых опытах он стал догадываться, что теплота, выделяемая в проволоке, соединяющей полюсы гальванической батареи, порождается химическими превращениями в батарее, т. е. стал прозревать энергетический смысл закона. Чтобы выяснить далее вопрос о происхождении «джоулева тепла» (как теперь называется теплота, выделяемая электрическим током), он стал исследовать теплоту, выделяемую индуцированным током. В работе «О тепловом эффекте магнитоэлектричества и механическом эффекте теплоты», доложенной на собрании Британской Ассоциации в августе 1843 г., Джоуль сформулировал вывод, что теплоту можно создавать с помощью механической работы, используя магнитоэлектричество (электромагнитную индукцию), и эта теплота пропорциональна квадрату силы индукционного тока.
В работе «О тепловом эффекте магнитоэлектричества и механическом эффекте теплоты», доложенной на собрании Британской Ассоциации в августе 1843 г., Джоуль сформулировал вывод, что теплоту можно создавать с помощью механической работы, используя магнитоэлектричество (электромагнитную индукцию), и эта теплота пропорциональна квадрату силы индукционного тока.
Вращая электромагнит индукционной машины с помощью падающего груза, Джоуль определил соотношение между работой падающего груза и теплотой, выделяемой в цепи. Он нашел в качестве среднего результата из своих измерений, что «количество тепла, которое в состоянии нагреть один фунт воды на один градус Фаренгейта, может быть превращено в механическую силу, которая в состоянии поднять 838 фунтов на вертикальную высоту в один фут». Переводя единицы фунт и фут в килограммы и метры и градус Фаренгейта в градус Цельсия, найдем, что механический эквивалент тепла, вычисленный Джоулем, равен 460 кгс-м/ккал. Этот вывод приводит Джоуля к другому, более общему выводу, который он обещает проверить в дальнейших экспериментах: «Могучие силы природы… неразрушимы, и… во всех случаях, когда затрачивается механическая сила, получается точное эквивалентное количество теплоты». Он утверждает, что животная теплота возникает в результате химических превращений в организме и что сами химические превращения являются результатом действия химических сил, возникающих из «падения атомов» Таким образом, в работе 1843 г. Джоуль приходит к тем же выводам, к которым ранее пришел Майер.
Он утверждает, что животная теплота возникает в результате химических превращений в организме и что сами химические превращения являются результатом действия химических сил, возникающих из «падения атомов» Таким образом, в работе 1843 г. Джоуль приходит к тем же выводам, к которым ранее пришел Майер.
Джоуль продолжал свои эксперименты и в 60-х и в 70-х годах. В 1870 г. он вошел в состав комиссии по определению механического эквивалента теплоты. В состав этой комиссии входили В. Томсон, Максвелл и другие ученые. Но Джоуль не ограничился работой экспериментатора. Он решительно встал на точку зрения кинетической теории теплоты и стал одним из основоположников кинетической теории газов. Об этой работе Джоуля будет сказано позднее.
В отличие от своих предшественников Гельмгольц связывает закон с принципом невозможности вечного двигателя (peгрetuum mobile). Этот принцип принимал еще Леонардо да Винчи, ученые XVII в. (вспомним, что Стевин обосновал закон наклонной плоскости невозможностью вечного движения), и, наконец, в XVIII в. Парижская Академия наук отказалась рассматривать проекты вечного двигателя. Гельмгольц считает принцип невозможности вечного двигателя тождественным принципу, что «все действия в природе можно свести на притягательные или отталкивательные силы». Материю Гельмгольц рассматривает как пассивную и неподвижную. Для того чтобы описать изменения, происходящие в мире, ее надо наделить силами как притягательными, так и отталкивательными. «Явления природы, — пишет Гельмгольц, — должны быть сведены к движениям материи с неизменными движущими силами, которые зависят только от пространственных взаимоотношений».
Парижская Академия наук отказалась рассматривать проекты вечного двигателя. Гельмгольц считает принцип невозможности вечного двигателя тождественным принципу, что «все действия в природе можно свести на притягательные или отталкивательные силы». Материю Гельмгольц рассматривает как пассивную и неподвижную. Для того чтобы описать изменения, происходящие в мире, ее надо наделить силами как притягательными, так и отталкивательными. «Явления природы, — пишет Гельмгольц, — должны быть сведены к движениям материи с неизменными движущими силами, которые зависят только от пространственных взаимоотношений».
Разными путями шли открыватели закона сохранения и превращения энергии к его установлению. Майер, начав с медицинского наблюдения, сразу рассматривал его как глубокий всеобъемлющий закон и раскрывал цепь энергетических превращений от космоса до живого организма. Джоуль упорно и настойчиво измерял количественное соотношение теплоты и механической работы. Гельмгольц связал закон с исследованиями великих механиков XVIII в. Идя разными путями, они наряду со многими другими современниками настойчиво боролись за утверждение и признание закона вопреки противодействию цеховых ученых. Борьба была нелегкой и порой принимала трагический характер, но она окончилась полной победой. Наука получила в свое распоряжение великий закон сохранения и превращения энергии.
Идя разными путями, они наряду со многими другими современниками настойчиво боролись за утверждение и признание закона вопреки противодействию цеховых ученых. Борьба была нелегкой и порой принимала трагический характер, но она окончилась полной победой. Наука получила в свое распоряжение великий закон сохранения и превращения энергии.
Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.
Однако в различных разделах физики по историческим причинам закон сохранения энергии формулируется по-разному, в связи с чем говорится о сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии выражается в виде первого начала термодинамики. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то более правильным является его именование не законом, а принципом сохранения энергии.
В 1841 г. русский ученый Ленц и англичанин Джоуль почти одновременно и независимо друг от друга экспериментально доказали, что теплота может быть создана за счет механической работы. Джоуль определил механический эквивалент тепла. Эти и другие исследования подготовили открытие закона сохранения и превращения энергии. В 1842—1845 г.г. немецкий ученый Р. Майер сформулировал этот закон на основе обобщения данных естествознания о механическом движении, электричестве, магнетизме, химии и даже физиологии человека. Одновременно в Англии (Гров) и в Дании (Кольдинг) были высказаны аналогичные идеи. Несколько позднее этот закон разрабатывал Гельмгольц (Германия) Разными путями шли открыватели закона сохранения и превращения энергии к его установлению.
Закон сохранения энергии — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
история открытия закона
сохранения энергии
презентацию подготовили ученицы 10 класса
кремер виола и вибе ангелина
как же открыл закон?
сначала следует сказать, что закон открыл
доктор, а не физик.
В 1840 году на острове Ява судовой врач
немец Роберт Майер вскрыл больному вену
и… к своему ужасу обнаружил, что потекла
вены попал в артерию?! Испуг врача
объяснялся тем, что алая кровь течет по
артериям от сердца — это кровь,
наполненная кислородом. А обратно, к
сердцу кровь течет по венам. В венозной
крови остается мало кислорода, поэтому
цвет у нее темно-красный. Кровотечение же
из артерии смертельно опасно.
«Почему же так происходит? — задумывается
Майер. — Может, дело в том, что температура
воздуха здесь почти равна температуре
человеческого тела… Организму не нужно
расходовать силу (в то время энергию еще
называли силой!) на поддержание
температуры тела, поэтому кислород остается
в крови — ведь силу дает именно сгорание
кислорода. Но это значит, что сила
сохраняется: она только превращается из
одного вида в другой, но никогда не исчезает и
не появляется из ничего».

Английский ученый Джемс Джоуль
ничего не зная о работах Майера, решил
поставить ряд опытов чтобы доказать
что при различных процессах, при
которых совершается работа и
выделяется теплота, для получения
единицы количества теплоты надо
затратить одно и то же количество
работы. Уже в 1841 году он опубликовал
выводы из своих опытов по
исследованию превращения работы
электрического тока в теплоту.
Задолго до открытий Майера, Джоуля и
Гельмгольца очень близко к открытию
закона сохранения энергии подошел
выдающийся российский ученый Михаил
Васильевич Ломоносов. Но, к сожалению,
труды Ломоносова долгое время оставались
неизвестными для европейских ученых.
Независимо от Майера, но
несколькими годами позже закон
сохранения энергии был открыт
английским физиком Джеймсом
Джоулем и немецким
естествоиспытателем Германом
Гельмгольцем.
Все эти ученые были очень молоды,
когда они совершили свое великое
Джоулю — 25, а Гельмгольцу — 26.

Герман Гельмгольц первым ввёл
представление о потенциальной
энергии. Рассуждения Майера и
опыты Джоуля доказали
эквивалентность механической
работы и теплоты, показав, что
количество выделяемой теплоты
равно совершённой работе и
наоборот, однако, формулировку в
точных терминах закону
сохранению энергии первым дал
Герман Гельмгольц.
главным нововведением Гельмгольца стало введение
понятия потенциальных сил и потенциальной энергии,
что позволило в дальнейшем обобщить закон
сохранения энергии на все разделы физики. В
частности, опираясь на закон сохранения энергии, он
вывел закон электромагнитной индукции Фарадея.
сам закон звучит так
люди, о которых было рассказано ранее,
внесли огромный вклад в развитие нашего
понимания окружающего мира.
Универсальный закон сохранения энергии
в жизни человека занимает важную роль.
Сама энергия не может возникнуть из
ниоткуда и уйти в никуда. Эти знания
получают ещё в средней школе на уроке
физики.
 Для людей закон сохранения
Для людей закон сохраненияэнергии выглядит немного по-другому, но не
меняет своей сути.
СПАСИБО ЗА
ВНИМАНИЕ!!!
English Русский Правила
Сохранение энергии — Энциклопедия Нового Света
- Эта статья о законе сохранения энергии в физике.
В физике закон сохранения энергии утверждает, что общее количество энергии в изолированной системе остается постоянным. На основании этого закона ученые пришли к выводу, что в изолированной системе энергия не создается и не уничтожается, но может менять форму. Например, потенциальная энергия может быть преобразована в кинетическую энергию, а кинетическая энергия может стать тепловой энергией.
Содержание
- 1 История
- 2 Первый закон термодинамики
- 3 Механика
- 3.1 Теорема Нётер
- 3.2 Относительность
- 3.3 Квантовая теория
- 4 См. также
- 5 Примечания
- 6 Каталожные номера
- 7 кредитов
Понимая этот закон, инженеры могут проектировать машины, которые могут использовать энергию для производства работы. Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии. Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не отдают энергию в окружающую среду, а устройства, производящие больше энергии, чем в них вложено, невозможны. Однако с формулировкой Альбертом Эйнштейном специальной теории относительности ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».
Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии. Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не отдают энергию в окружающую среду, а устройства, производящие больше энергии, чем в них вложено, невозможны. Однако с формулировкой Альбертом Эйнштейном специальной теории относительности ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».
История
Древние философы догадывались о сохранении некой основной субстанции, из которой все сделано. Например, Фалес Милетский думал, что это вода.
В 1638 году Галилей опубликовал свой анализ нескольких ситуаций, включая знаменитый «прерванный маятник», которые можно описать (на современном языке) как консервативное преобразование потенциальной энергии в кинетическую и обратно. Однако Галилей не изложил этот процесс в современных терминах, и ему снова нельзя приписать решающее понимание. Это был Готфрид Вильгельм Лейбниц в 1676–1689 гг.{2}}
Однако Галилей не изложил этот процесс в современных терминах, и ему снова нельзя приписать решающее понимание. Это был Готфрид Вильгельм Лейбниц в 1676–1689 гг.{2}}
сохранялся до тех пор, пока массы не взаимодействовали. Он назвал это количество
- ∑imivi{\displaystyle \,\!\sum _{i}m_{i}v_{i}}
был законсервированным vis viva . Позже было показано, что при соответствующих условиях обе величины сохраняются одновременно, например, при упругих столкновениях.
Главным образом инженеры, такие как Джон Смитон, Питер Юарт, Карл Хоцманн, Гюстав-Адольф Хирн и Марк Сеген, возражали против того, что одного сохранения импульса недостаточно для практических расчетов, и использовали принцип Лейбница. Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие академики, как Джон Плейфер, поспешили указать, что кинетическая энергия явно не сохраняется. Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии была еще неизвестна. Постепенно возникло подозрение, что теплота, неизбежно генерируемая движением при трении, представляет собой другую форму vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. [1] Наблюдения графа Румфорда в 1798 г. за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие академики, как Джон Плейфер, поспешили указать, что кинетическая энергия явно не сохраняется. Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии была еще неизвестна. Постепенно возникло подозрение, что теплота, неизбежно генерируемая движением при трении, представляет собой другую форму vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. [1] Наблюдения графа Румфорда в 1798 г. за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
, который можно понимать как нахождение точного значения константы преобразования кинетической энергии в работу, в значительной степени является результатом работы Гаспара-Гюстава Кориолиса и Жана-Виктора Понселе в период 1819–1839 гг.
В газете, Über die Natur der Wärme, , опубликованном в Zeitschrift für Physik в 1837 году, Карл Фридрих Мор дал одно из первых общих утверждений доктрины сохранения энергии в следующих словах: «Кроме 54 известных химических элементов, в физическом мире существует только один агент , и это называется Kraft [энергия или работа]. В зависимости от обстоятельств она может проявиться как движение, химическое сродство, сцепление, электричество, свет и магнетизм, и из любой из этих форм она может быть преобразована в любую из другие.»
Ключевым этапом в развитии современного принципа сохранения стала демонстрация механического эквивалента тепла . Калорическая теория утверждала, что теплота не может быть ни создана, ни уничтожена, но сохранение энергии влечет за собой противоположный принцип, согласно которому теплота и механическая работа взаимозаменяемы.
Принцип механической эквивалентности был впервые сформулирован в его современной форме немецким хирургом Юлиусом Робертом фон Майером. [2] Майер пришел к такому выводу во время путешествия в Голландскую Ост-Индию, где он обнаружил, что кровь его пациентов была более ярко-красной, потому что они потребляли меньше кислорода и, следовательно, меньше энергии для поддержания температуры тела в более жарких условиях. климат. Он обнаружил, что и теплота, и механическая работа являются формами энергии, а позже, улучшив свои познания в физике, вычислил количественную связь между ними.
Прибор Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к веревке, заставляет вращаться весло, погруженное в воду.
Между тем, в 1843 году Джеймс Прескотт Джоуль независимо открыл механический эквивалент в серии экспериментов. В самом известном из них, ныне называемом «аппаратом Джоуля», опускающийся груз, прикрепленный к струне, заставлял вращаться лопасть, погруженную в воду. Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), приобретаемой водой при трении о весло.
Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), приобретаемой водой при трении о весло.
В период 1840–1843 гг. подобную работу выполнял инженер Людвиг А. Колдинг, хотя она была малоизвестна за пределами его родной Дании.
Работа Джоуля и Майера страдала от сопротивления и пренебрежения, но именно работа Джоуля, возможно, несправедливо, в конечном итоге получила более широкое признание.
В 1844 году Уильям Роберт Гроув постулировал связь между механикой, теплотой, светом, электричеством и магнетизмом, рассматривая их все как проявления единой «силы» ( энергия по современным меркам). Гроув опубликовал свои теории в своей книге «Корреляция физических сил ». [3] В 1847 году, опираясь на более ранние работы Джоуля, Сади Карно и Эмиля Клапейрона, Герман фон Гельмгольц пришел к выводам, сходным с выводами Гроува, и опубликовал свои теории в своей книге Über die Erhaltung der Kraft ( On the Conservation Силы, 1847). Общее современное признание этого принципа проистекает из этой публикации.
Общее современное признание этого принципа проистекает из этой публикации.
В 1877 году Питер Гатри Тейт утверждал, что этот принцип был создан сэром Исааком Ньютоном на основе творческого прочтения предложений 40 и 41 из Philosophiae Naturalis Principia Mathematica . Сейчас это обычно рассматривается как не более чем пример истории вигов.
Первый закон термодинамики
Энтропия есть функция количества теплоты, которая показывает возможность преобразования этого тепла в работу.
Для термодинамической системы с фиксированным числом частиц первый закон термодинамики можно сформулировать так:
- δQ = dU + δW {\ displaystyle \ delta Q = \ mathrm {d} U + \ delta W \,} или эквивалентно, dU = δQ−δW {\ displaystyle \ mathrm {d} U = \ delta Q- \ delta W \,},
, где δQ {\ displaystyle \ delta Q} — количество энергии, добавляемой в систему в процессе нагрева, δ W {\ displaystyle \ delta W} — количество энергии, теряемой системой. из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
Значения δ перед терминами тепла и работы используются для обозначения того, что они описывают приращение энергии, которое следует интерпретировать несколько иначе, чем приращение внутренней энергии. Работа и тепло равны обрабатывает , которые добавляют или вычитают энергию, в то время как внутренняя энергия представляет собой конкретную форму энергии, связанную с системой. Таким образом, термин «тепловая энергия» для δQ {\ displaystyle \ delta Q} означает «количество энергии, добавленное в результате нагрева», а не относится к конкретной форме энергии. Точно так же термин «рабочая энергия» для δW {\ displaystyle \ delta W} означает «то количество энергии, которое теряется в результате работы». Наиболее важным результатом этого различения является тот факт, что можно ясно указать количество внутренней энергии, которой обладает термодинамическая система, но нельзя сказать, сколько энергии поступило в систему или вышло из нее в результате ее нагревания или охлаждения. , ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
, ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
Для простой сжимаемой системы работа, выполненная системой, может быть записана
- δW=PdV{\displaystyle \delta W=P\,\mathrm {d} V},
где P{\displaystyle P} — давление, а dV{\displaystyle dV} — небольшое изменение объем системы, каждый из которых является системной переменной. Тепловая энергия может быть записана
- δQ = TdS {\ displaystyle \ delta Q = T \, \ mathrm {d} S},
, где T {\ displaystyle T} — температура, а dS {\ displaystyle \ mathrm {d} S} — небольшое изменение энтропии системы. Температура и энтропия также являются системными переменными. 9{N} p_ {i} {\ dot {q}} _ {i} -L = const} и pi = ∂L ∂q˙i {\ displaystyle p_ {i} = {\ frac {\ partial L} {\ частичное {\dot {q}}_{i}}}}
, где L — функция Лагранжа. Чтобы эта конкретная форма была действительной, должно выполняться следующее:
- Система является склерономной (ни кинетическая, ни потенциальная энергия не являются явной функцией времени)
- Кинетическая энергия представляет собой квадратичную форму относительно скоростей
- Потенциальная энергия не зависит от скорости
Теорема Нётер
Сохранение энергии является общей чертой многих физических теорий. С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени.
С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени. Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Относительность
С формулировкой Альбертом Эйнштейном специальной теории относительности было предложено, чтобы энергия была одним компонентом 4-вектора энергии-импульса. Каждая из четырех составляющих (одна из энергии и три из импульса) этого вектора отдельно сохраняется в любой заданной инерциальной системе отсчета. Также сохраняется длина вектора (норма Минковского), которая является массой покоя. Релятивистская энергия одиночной массивной частицы содержит член, связанный с ее массой покоя, в дополнение к ее кинетической энергии движения. В пределе нулевой кинетической энергии (или, что то же самое, в системе покоя массивной частицы или в системе центра импульса для объектов или систем) полная энергия частицы или объекта (включая внутреннюю кинетическую энергию в системах) связана к его массе покоя через известное уравнение E=mc2{\displaystyle E=mc^{2}}. Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0009 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0009 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
В общей теории относительности сохранение энергии-импульса выражается с помощью псевдотензора напряжения-энергии-импульса.
Квантовая теория
В квантовой механике энергия определяется как пропорциональная производной по времени волновой функции. Отсутствие коммутации оператора производной по времени с самим оператором времени математически приводит к принципу неопределенности для времени и энергии: чем больше период времени, тем точнее можно определить энергию (энергия и время становятся сопряженной парой Фурье).
Однако существует глубокое противоречие между исторической оценкой квантовой теорией плотности энергии вакуума во Вселенной и энергией вакуума, предсказанной космологической постоянной. Расчетная разница плотности энергии порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
Расчетная разница плотности энергии порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
См. также
- Теория хаоса
- Термодинамика
- Принцип неопределенности
- Закон сохранения
- Сохранение массы
- Энергетический баланс подземных вод
- Законы термодинамики
- Теорема Нётер
- Основы энергетики
- Преобразование энергии
- Качество энергии
Примечания
- ↑ А.Л. Лавуазье и П.С. Лаплас, Мемуары о тепле, Académie Royale des Sciences (1780): 4-355.
- ↑ Дж. Р. фон Майер, Замечания о силах неорганической природы, Annalen der Chemie und Pharmacie 43 (1842): 233.

- ↑ В. Р. Гроув, Корреляция физических сил, 6-е изд. (Лондон, Великобритания: Longmans, Green, 1874 г.).
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Brown, T.M. 1965. Информационное письмо EEC-1 об эволюции энергетических концепций от Галилея до Гельмгольца. Американский журнал физики . 33: 759–765.
- Кардвелл, Д.С.Л. 1971. От Ватта до Клаузиуса: рост термодинамики в раннеиндустриальную эпоху . Лондон, Великобритания: Хайнеманн. ISBN 0435541501.
- Colding, LA 1864. К истории принципа сохранения энергии. Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 27: 56–64.
- Гольдштейн, Мартин и Ф. Инге Ф. 1993. Холодильник и Вселенная . Кембридж, Массачусетс: Гарвардский ун-т. Нажимать. ISBN 9780674753242.
- Guillen, M. 1999. Пять уравнений, которые изменили мир . Лондон, Великобритания: Абакус. ISBN 0349110646.

- Хиберт, Э.Н. 1981. Исторические корни принципа сохранения энергии . Мэдисон, Висконсин: Паб Ayer Co. ISBN 0405138806.
- Кремер, Герберт и Чарльз Киттель. 1980. Теплофизика, 2-е изд. Сан-Франциско, Калифорния: W.H. Компания Фримен. ISBN 0716710889.
- Кун, Т.С. 1957. «Сохранение энергии как пример одновременного открытия». В М. Клагетт (ред.), Критические проблемы истории науки . Мэдисон, Висконсин: Издательство Висконсинского университета.
- Ланцос, Корнелиус. 1970. Вариационные принципы механики . Торонто, Калифорния: University of Toronto Press. ISBN 0802017436.
- Мах, Э. 1872. История и корни принципов сохранения энергии . Анн-Арбор, Мичиган: University Microfilms International.
- Нолан, Питер Дж. 1996. Основы физики колледжа, 2-е изд. Дубьюк, Айова: Издательство Уильяма К. Брауна. ISBN 9780697121455.
- Окстоби, Дэвид В. и Норман Х. Нахтриб. 1996. Основы современной химии, 3-е изд.
 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049. - Папино, Д. 2002. Размышление о сознании . Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN 9780199271153.
- Пуанкаре, Х. 1905. Наука и гипотеза . Нью-Йорк, штат Нью-Йорк: репринт Дувра, 1952. ISBN 0486602214.
- Сартон, Г. 1929. Открытие закона сохранения энергии. Исида 13: 18–49.
- Серуэй, Рэймонд А. и Джон В. Джуэтт. 2004. Физика для ученых и инженеров, 6-е изд. Бельмонт, Калифорния: Брукс/Коул. ISBN 0534408427.
- Smith, C. 1998. Наука об энергии: культурная история физики энергии в викторианской Британии . Лондон, Великобритания: Хайнеманн. ISBN 0485114313.
- Стенгер, Виктор Дж. 2000. Вневременная реальность . Амхерст, Нью-Йорк: Книги Прометея. ISBN 9781573928595.
- Типлер, Пол. 2004. Физика для ученых и инженеров: механика, колебания и волны, термодинамика, 5-е изд.
 Сан-Франциско, Калифорния: W.H. Фриман. ISBN 0716708094.
Сан-Франциско, Калифорния: W.H. Фриман. ISBN 0716708094.
Авторы
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статьи Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Кредит должен соответствовать условиям этой лицензии, которая может ссылаться как на Энциклопедия Нового Света участников и самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
- Сохранение энергии история
История этой статьи с момента ее импорта в Энциклопедию Нового Света :
- История «Энергосбережения»
Примечание. На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.
На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.
Сохранение энергии — Энциклопедия Нового Света
- Эта статья о законе сохранения энергии в физике.
В физике закон сохранения энергии утверждает, что общее количество энергии в изолированной системе остается постоянным. На основании этого закона ученые пришли к выводу, что в изолированной системе энергия не создается и не уничтожается, но может менять форму. Например, потенциальная энергия может быть преобразована в кинетическую энергию, а кинетическая энергия может стать тепловой энергией.
Содержание
- 1 История
- 2 Первый закон термодинамики
- 3 Механика
- 3.1 Теорема Нётер
- 3.2 Относительность
- 3.3 Квантовая теория
- 4 См. также
- 5 Примечания
- 6 Каталожные номера
- 7 кредитов
Понимая этот закон, инженеры могут проектировать машины, которые могут использовать энергию для производства работы. Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии. Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не отдают энергию в окружающую среду, а устройства, производящие больше энергии, чем в них вложено, невозможны. Однако с формулировкой Альбертом Эйнштейном специальной теории относительности ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».
Например, тепловая энергия (или тепло, выделяемое при сжигании топлива) может использоваться для привода турбины, которая, в свою очередь, может использоваться для выработки электроэнергии. Кроме того, на основании этого закона можно сделать вывод, что вечные двигатели могут работать только в том случае, если они не отдают энергию в окружающую среду, а устройства, производящие больше энергии, чем в них вложено, невозможны. Однако с формулировкой Альбертом Эйнштейном специальной теории относительности ученые теперь рассматривают сохранение энергии как часть более крупного закона, а именно сохранения «массы-энергии».
История
Древние философы догадывались о сохранении некой основной субстанции, из которой все сделано. Например, Фалес Милетский думал, что это вода.
В 1638 году Галилей опубликовал свой анализ нескольких ситуаций, включая знаменитый «прерванный маятник», которые можно описать (на современном языке) как консервативное преобразование потенциальной энергии в кинетическую и обратно. Однако Галилей не изложил этот процесс в современных терминах, и ему снова нельзя приписать решающее понимание. Это был Готфрид Вильгельм Лейбниц в 1676–1689 гг.{2}}
Однако Галилей не изложил этот процесс в современных терминах, и ему снова нельзя приписать решающее понимание. Это был Готфрид Вильгельм Лейбниц в 1676–1689 гг.{2}}
сохранялся до тех пор, пока массы не взаимодействовали. Он назвал это количество vis viva или жизненной силы системы. Принцип представляет собой точную формулировку приблизительного сохранения кинетической энергии в ситуациях, когда нет трения. Многие физики того времени считали, что закон сохранения импульса, сохраняющийся даже в системах с трением, определяемый импульсом:
- ∑imivi{\displaystyle \,\!\sum _{i}m_{i}v_{i}}
был законсервированным vis viva . Позже было показано, что при соответствующих условиях обе величины сохраняются одновременно, например, при упругих столкновениях.
Главным образом инженеры, такие как Джон Смитон, Питер Юарт, Карл Хоцманн, Гюстав-Адольф Хирн и Марк Сеген, возражали против того, что одного сохранения импульса недостаточно для практических расчетов, и использовали принцип Лейбница. Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие академики, как Джон Плейфер, поспешили указать, что кинетическая энергия явно не сохраняется. Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии была еще неизвестна. Постепенно возникло подозрение, что теплота, неизбежно генерируемая движением при трении, представляет собой другую форму vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. [1] Наблюдения графа Румфорда в 1798 г. за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
Этот принцип также отстаивали некоторые химики, такие как Уильям Хайд Волластон. Такие академики, как Джон Плейфер, поспешили указать, что кинетическая энергия явно не сохраняется. Это очевидно для современного анализа, основанного на втором законе термодинамики, но в восемнадцатом и девятнадцатом веках судьба потерянной энергии была еще неизвестна. Постепенно возникло подозрение, что теплота, неизбежно генерируемая движением при трении, представляет собой другую форму vis viva . В 1783 году Антуан Лавуазье и Пьер-Симон Лаплас рассмотрели две конкурирующие теории vis viva и теорию калорийности. [1] Наблюдения графа Румфорда в 1798 г. за выделением тепла во время сверления пушек добавили веса мнению о том, что механическое движение может быть преобразовано в тепло, и (что не менее важно) что преобразование было количественным и его можно было предсказать (с учетом универсальная константа преобразования между кинетической энергией и теплотой). 9{2}}
, который можно понимать как нахождение точного значения константы преобразования кинетической энергии в работу, в значительной степени является результатом работы Гаспара-Гюстава Кориолиса и Жана-Виктора Понселе в период 1819–1839 гг. Первый назвал количество quantité de travail (количество работы), а второй travail mécanique (механическая работа), и оба отстаивали его использование в инженерных расчетах.
Первый назвал количество quantité de travail (количество работы), а второй travail mécanique (механическая работа), и оба отстаивали его использование в инженерных расчетах.
В газете, Über die Natur der Wärme, , опубликованном в Zeitschrift für Physik в 1837 году, Карл Фридрих Мор дал одно из первых общих утверждений доктрины сохранения энергии в следующих словах: «Кроме 54 известных химических элементов, в физическом мире существует только один агент , и это называется Kraft [энергия или работа]. В зависимости от обстоятельств она может проявиться как движение, химическое сродство, сцепление, электричество, свет и магнетизм, и из любой из этих форм она может быть преобразована в любую из другие.»
Ключевым этапом в развитии современного принципа сохранения стала демонстрация механического эквивалента тепла . Калорическая теория утверждала, что теплота не может быть ни создана, ни уничтожена, но сохранение энергии влечет за собой противоположный принцип, согласно которому теплота и механическая работа взаимозаменяемы.
Принцип механической эквивалентности был впервые сформулирован в его современной форме немецким хирургом Юлиусом Робертом фон Майером. [2] Майер пришел к такому выводу во время путешествия в Голландскую Ост-Индию, где он обнаружил, что кровь его пациентов была более ярко-красной, потому что они потребляли меньше кислорода и, следовательно, меньше энергии для поддержания температуры тела в более жарких условиях. климат. Он обнаружил, что и теплота, и механическая работа являются формами энергии, а позже, улучшив свои познания в физике, вычислил количественную связь между ними.
Прибор Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к веревке, заставляет вращаться весло, погруженное в воду.
Между тем, в 1843 году Джеймс Прескотт Джоуль независимо открыл механический эквивалент в серии экспериментов. В самом известном из них, ныне называемом «аппаратом Джоуля», опускающийся груз, прикрепленный к струне, заставлял вращаться лопасть, погруженную в воду. Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), приобретаемой водой при трении о весло.
Он показал, что гравитационная потенциальная энергия, теряемая весом при спуске, равна тепловой энергии (теплу), приобретаемой водой при трении о весло.
В период 1840–1843 гг. подобную работу выполнял инженер Людвиг А. Колдинг, хотя она была малоизвестна за пределами его родной Дании.
Работа Джоуля и Майера страдала от сопротивления и пренебрежения, но именно работа Джоуля, возможно, несправедливо, в конечном итоге получила более широкое признание.
В 1844 году Уильям Роберт Гроув постулировал связь между механикой, теплотой, светом, электричеством и магнетизмом, рассматривая их все как проявления единой «силы» ( энергия по современным меркам). Гроув опубликовал свои теории в своей книге «Корреляция физических сил ». [3] В 1847 году, опираясь на более ранние работы Джоуля, Сади Карно и Эмиля Клапейрона, Герман фон Гельмгольц пришел к выводам, сходным с выводами Гроува, и опубликовал свои теории в своей книге Über die Erhaltung der Kraft ( On the Conservation Силы, 1847). Общее современное признание этого принципа проистекает из этой публикации.
Общее современное признание этого принципа проистекает из этой публикации.
В 1877 году Питер Гатри Тейт утверждал, что этот принцип был создан сэром Исааком Ньютоном на основе творческого прочтения предложений 40 и 41 из Philosophiae Naturalis Principia Mathematica . Сейчас это обычно рассматривается как не более чем пример истории вигов.
Первый закон термодинамики
Энтропия есть функция количества теплоты, которая показывает возможность преобразования этого тепла в работу.
Для термодинамической системы с фиксированным числом частиц первый закон термодинамики можно сформулировать так:
- δQ = dU + δW {\ displaystyle \ delta Q = \ mathrm {d} U + \ delta W \,} или эквивалентно, dU = δQ−δW {\ displaystyle \ mathrm {d} U = \ delta Q- \ delta W \,},
, где δQ {\ displaystyle \ delta Q} — количество энергии, добавляемой в систему в процессе нагрева, δ W {\ displaystyle \ delta W} — количество энергии, теряемой системой. из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
из-за работы, совершаемой системой над ее окружением, и представляет собой увеличение внутренней энергии системы.
Значения δ перед терминами тепла и работы используются для обозначения того, что они описывают приращение энергии, которое следует интерпретировать несколько иначе, чем приращение внутренней энергии. Работа и тепло равны обрабатывает , которые добавляют или вычитают энергию, в то время как внутренняя энергия представляет собой конкретную форму энергии, связанную с системой. Таким образом, термин «тепловая энергия» для δQ {\ displaystyle \ delta Q} означает «количество энергии, добавленное в результате нагрева», а не относится к конкретной форме энергии. Точно так же термин «рабочая энергия» для δW {\ displaystyle \ delta W} означает «то количество энергии, которое теряется в результате работы». Наиболее важным результатом этого различения является тот факт, что можно ясно указать количество внутренней энергии, которой обладает термодинамическая система, но нельзя сказать, сколько энергии поступило в систему или вышло из нее в результате ее нагревания или охлаждения. , ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
, ни в результате работы, выполняемой системой или системой. Проще говоря, это означает, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую.
Для простой сжимаемой системы работа, выполненная системой, может быть записана
- δW=PdV{\displaystyle \delta W=P\,\mathrm {d} V},
где P{\displaystyle P} — давление, а dV{\displaystyle dV} — небольшое изменение объем системы, каждый из которых является системной переменной. Тепловая энергия может быть записана
- δQ = TdS {\ displaystyle \ delta Q = T \, \ mathrm {d} S},
, где T {\ displaystyle T} — температура, а dS {\ displaystyle \ mathrm {d} S} — небольшое изменение энтропии системы. Температура и энтропия также являются системными переменными. 9{N} p_ {i} {\ dot {q}} _ {i} -L = const} и pi = ∂L ∂q˙i {\ displaystyle p_ {i} = {\ frac {\ partial L} {\ частичное {\dot {q}}_{i}}}}
, где L — функция Лагранжа. Чтобы эта конкретная форма была действительной, должно выполняться следующее:
- Система является склерономной (ни кинетическая, ни потенциальная энергия не являются явной функцией времени)
- Кинетическая энергия представляет собой квадратичную форму относительно скоростей
- Потенциальная энергия не зависит от скорости
Теорема Нётер
Сохранение энергии является общей чертой многих физических теорий.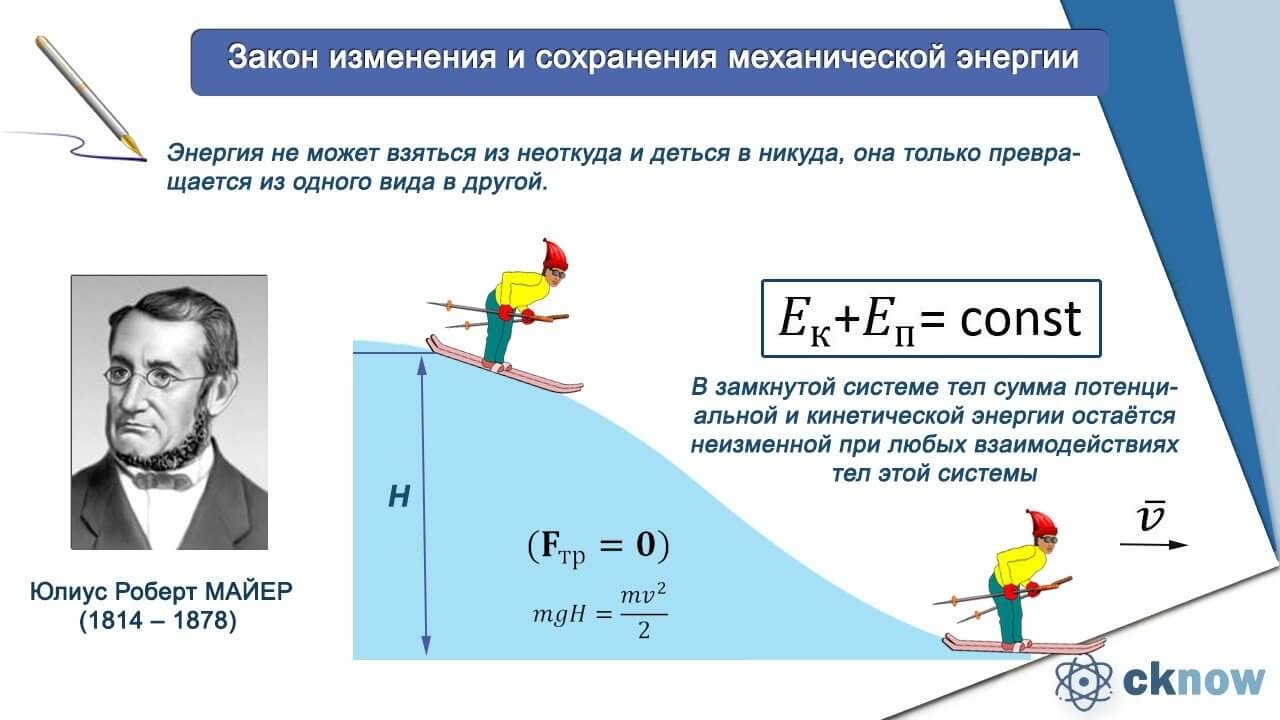 С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени.
С математической точки зрения это понимается как следствие теоремы Нётер, которая утверждает, что каждой симметрии физической теории соответствует сохраняющаяся величина; если симметрия теории инвариантна во времени, то сохраняющаяся величина называется «энергией». Закон сохранения энергии является следствием сдвиговой симметрии времени; сохранение энергии подразумевается эмпирическим фактом, что законы физики не меняются с течением времени. Философски это можно сформулировать так: «ничто не зависит от времени как такового».
Другими словами, если теория инвариантна относительно непрерывной симметрии переноса времени, то ее энергия (которая является канонической величиной, сопряженной времени) сохраняется. И наоборот, теории, не инвариантные относительно сдвигов во времени (например, системы с зависящей от времени потенциальной энергией), не обнаруживают сохранения энергии, если только не считать, что они обмениваются энергией с другой, внешней системой, так что теория расширенной системы становится снова инвариантен во времени. Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Поскольку любая меняющаяся во времени теория может быть встроена в инвариантную во времени метатеорию, сохранение энергии всегда можно восстановить путем подходящего переопределения того, что такое энергия. Таким образом, сохранение энергии для конечных систем справедливо во всех современных физических теориях, таких как специальная и общая теория относительности и квантовая теория (включая квантовую электродинамику).
Относительность
С формулировкой Альбертом Эйнштейном специальной теории относительности было предложено, чтобы энергия была одним компонентом 4-вектора энергии-импульса. Каждая из четырех составляющих (одна из энергии и три из импульса) этого вектора отдельно сохраняется в любой заданной инерциальной системе отсчета. Также сохраняется длина вектора (норма Минковского), которая является массой покоя. Релятивистская энергия одиночной массивной частицы содержит член, связанный с ее массой покоя, в дополнение к ее кинетической энергии движения. В пределе нулевой кинетической энергии (или, что то же самое, в системе покоя массивной частицы или в системе центра импульса для объектов или систем) полная энергия частицы или объекта (включая внутреннюю кинетическую энергию в системах) связана к его массе покоя через известное уравнение E=mc2{\displaystyle E=mc^{2}}. Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0009 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
Таким образом, в специальной теории относительности было показано, что правило сохранения энергии является частным случаем более общего правила, также называемого 9-м правилом.0009 сохранение массы и энергии, сохранение массы-энергии, сохранение энергии-импульса, сохранение инвариантной массы, или сейчас обычно просто называют сохранением энергии.
В общей теории относительности сохранение энергии-импульса выражается с помощью псевдотензора напряжения-энергии-импульса.
Квантовая теория
В квантовой механике энергия определяется как пропорциональная производной по времени волновой функции. Отсутствие коммутации оператора производной по времени с самим оператором времени математически приводит к принципу неопределенности для времени и энергии: чем больше период времени, тем точнее можно определить энергию (энергия и время становятся сопряженной парой Фурье).
Однако существует глубокое противоречие между исторической оценкой квантовой теорией плотности энергии вакуума во Вселенной и энергией вакуума, предсказанной космологической постоянной. Расчетная разница плотности энергии порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
Расчетная разница плотности энергии порядка 10 120 раз. Складывается консенсус в отношении того, что полученная квантовой механикой плотность энергии поля в нулевой точке не сохраняет полную энергию Вселенной и не соответствует нашему пониманию расширения Вселенной. За кулисами в физике предпринимаются интенсивные усилия, чтобы решить эту дилемму и привести ее в соответствие с расширяющейся Вселенной.
См. также
- Теория хаоса
- Термодинамика
- Принцип неопределенности
- Закон сохранения
- Сохранение массы
- Энергетический баланс подземных вод
- Законы термодинамики
- Теорема Нётер
- Основы энергетики
- Преобразование энергии
- Качество энергии
Примечания
- ↑ А.Л. Лавуазье и П.С. Лаплас, Мемуары о тепле, Académie Royale des Sciences (1780): 4-355.
- ↑ Дж. Р. фон Майер, Замечания о силах неорганической природы, Annalen der Chemie und Pharmacie 43 (1842): 233.

- ↑ В. Р. Гроув, Корреляция физических сил, 6-е изд. (Лондон, Великобритания: Longmans, Green, 1874 г.).
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Brown, T.M. 1965. Информационное письмо EEC-1 об эволюции энергетических концепций от Галилея до Гельмгольца. Американский журнал физики . 33: 759–765.
- Кардвелл, Д.С.Л. 1971. От Ватта до Клаузиуса: рост термодинамики в раннеиндустриальную эпоху . Лондон, Великобритания: Хайнеманн. ISBN 0435541501.
- Colding, LA 1864. К истории принципа сохранения энергии. Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 27: 56–64.
- Гольдштейн, Мартин и Ф. Инге Ф. 1993. Холодильник и Вселенная . Кембридж, Массачусетс: Гарвардский ун-т. Нажимать. ISBN 9780674753242.
- Guillen, M. 1999. Пять уравнений, которые изменили мир . Лондон, Великобритания: Абакус. ISBN 0349110646.

- Хиберт, Э.Н. 1981. Исторические корни принципа сохранения энергии . Мэдисон, Висконсин: Паб Ayer Co. ISBN 0405138806.
- Кремер, Герберт и Чарльз Киттель. 1980. Теплофизика, 2-е изд. Сан-Франциско, Калифорния: W.H. Компания Фримен. ISBN 0716710889.
- Кун, Т.С. 1957. «Сохранение энергии как пример одновременного открытия». В М. Клагетт (ред.), Критические проблемы истории науки . Мэдисон, Висконсин: Издательство Висконсинского университета.
- Ланцос, Корнелиус. 1970. Вариационные принципы механики . Торонто, Калифорния: University of Toronto Press. ISBN 0802017436.
- Мах, Э. 1872. История и корни принципов сохранения энергии . Анн-Арбор, Мичиган: University Microfilms International.
- Нолан, Питер Дж. 1996. Основы физики колледжа, 2-е изд. Дубьюк, Айова: Издательство Уильяма К. Брауна. ISBN 9780697121455.
- Окстоби, Дэвид В. и Норман Х. Нахтриб. 1996. Основы современной химии, 3-е изд.
 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049. - Папино, Д. 2002. Размышление о сознании . Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN 9780199271153.
- Пуанкаре, Х. 1905. Наука и гипотеза . Нью-Йорк, штат Нью-Йорк: репринт Дувра, 1952. ISBN 0486602214.
- Сартон, Г. 1929. Открытие закона сохранения энергии. Исида 13: 18–49.
- Серуэй, Рэймонд А. и Джон В. Джуэтт. 2004. Физика для ученых и инженеров, 6-е изд. Бельмонт, Калифорния: Брукс/Коул. ISBN 0534408427.
- Smith, C. 1998. Наука об энергии: культурная история физики энергии в викторианской Британии . Лондон, Великобритания: Хайнеманн. ISBN 0485114313.
- Стенгер, Виктор Дж. 2000. Вневременная реальность . Амхерст, Нью-Йорк: Книги Прометея. ISBN 9781573928595.
- Типлер, Пол. 2004. Физика для ученых и инженеров: механика, колебания и волны, термодинамика, 5-е изд.



 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049. Сан-Франциско, Калифорния: W.H. Фриман. ISBN 0716708094.
Сан-Франциско, Калифорния: W.H. Фриман. ISBN 0716708094.

 Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.
Форт-Уэрт, Техас. Издательство Saunders College. ISBN 9780030059049.