| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| © 2006-2023 Издательство ГРАМОТА разработка и создание сайта, поисковая оптимизация: krav.  ru | ||||||||||
Бесплатный просмотрщик PDF-файлов можно скачать здесь.
И. Герцена, 1975. Ч. 1. С. 89-98.
Сер. Филологические науки. Вып. 75. Уфа, 1973. № 25. С. 19-26.Говорим по-русски: как выбрать между «ни» и «не»?
Свежий номер
РГ-Неделя
Родина
Тематические приложения
Союз
Свежий номер
Общество
19.05.2010 23:21
Поделиться
Марина Королева
Не или ни? Ни или не? Кто только ни задавался этим вопросом, кто (да что уж там, сознаемся!) ни проклинал все на свете, пытаясь вспомнить правило из школьной программы: что же, что именно здесь надо написать, не или ни?..
А поскольку ошибки все-таки встречаются, причем и в рекламе, и в журнальных текстах, не говоря уж об Интернете, можно сделать вывод, что вспомнить удается далеко не всегда. Тогда в силу вступает правило, известное всем как «русский авось». Вот исходя из этого правила обычно и выбирают: не или ни.
Чтобы этого не происходило, давайте все-таки припомним иные правила — а они есть!
Итак, ни.
Существуют случаи, которые смело можно назвать простыми.
Мы пишем ни, и только ни в устойчивых выражениях (таких, как ни свет ни заря, ни днем ни ночью, ни жив ни мертв, ни рыба ни мясо). Ни с места! Ни шагу назад! Ни один человек не пришел на акцию (то есть никто). Он ни разу мне не позвонил (то есть нисколько). Это запомнить просто.
Но есть и непростые ситуации, куда же без них!
О, это «ни для усиления отрицания»… Со школьных времен мы думаем о тебе с содроганием. А напрасно, между прочим. И это можно попробовать запомнить. Итак, в предложениях, где ни используется для усиления отрицания, обычно уже имеется отрицание (нет или не): Нет ни копейки денег. Он не дал мне ни рубля. Иногда отрицание только подразумевается: Ни копеечки (не было) в кармане.
Существует, правда, двойное отрицание с не (ты не мог меня не заметить). Но это двойное отрицание придает предложению смысл утверждения, а вовсе не отрицания! Что такое не мог не заметить? Это значит «заметил».
Как сказали бы математики, «минус на минус дает плюс».
Однако вернемся к ни.
Особый случай — употребление ни при местоимениях и наречиях. Кто ни пройдет, оставит свой след (кто ни — то же, что всякий). Где бы ни появился, всюду его узнают (где бы ни — то есть где угодно). Как видите, здесь местоимения и наречия с ни легко заменяются синонимическими конструкциями.
Если же речь идет о независимом восклицательном или вопросительном предложении, то пишется не: Кто не восхищался ею! Что он только не передумал!
И еще раз о ни.
Ни, и только ни мы напишем в так называемых уступительных придаточных, чтобы усилить утверждение.
Тут будет уместно вспомнить шлягер Аллы Пугачевой: «Я отправлюсь за тобой, что бы путь мне ни пророчил». Да, знаю, сама она поет не пророчил. Но это ошибка, увы… Ни пророчил, и только ни!
Российская газета — Неделя — Федеральный выпуск: №108(5187)
Поделиться
ОбразованиеКолонка Марины Королёвой
Логические и математические операторы — рабочие примеры
Иногда в математике важно определить, что является противоположностью данному математическому утверждению.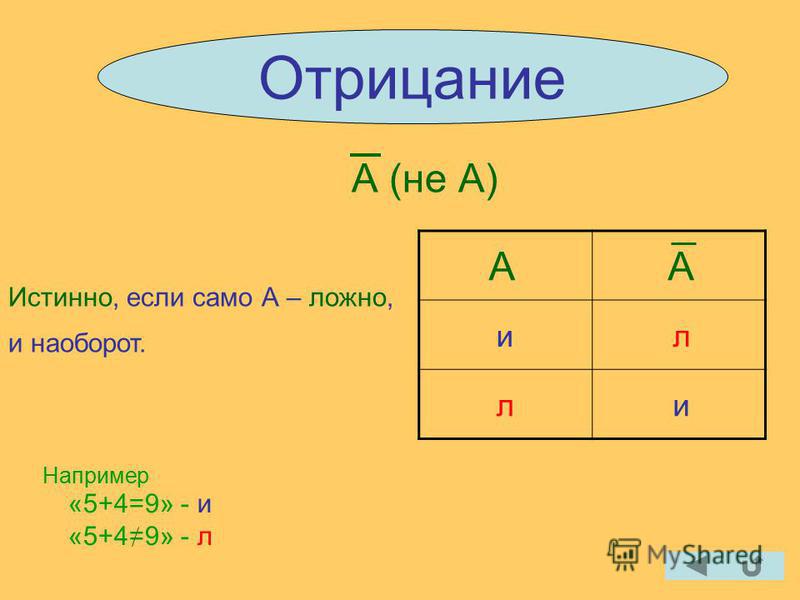
Это обычно называют «отрицанием» утверждения. Следует иметь в виду, что если утверждение истинно, то его отрицание ложно (а если утверждение ложно, то его отрицание истинно).
Давайте рассмотрим некоторые из наиболее распространенных отрицаний.
Отрицание «A
или B».Прежде чем дать ответ, попробуем сделать это для примера.
Рассмотрим утверждение «Вы либо богаты, либо счастливы». Чтобы это утверждение было ложным, вы не можете быть богатым и вы не можете быть счастливым. Другими словами, наоборот, быть не богатым и не счастливым. Или, если мы перепишем его в терминах исходного утверждения, мы получим «Вы не богаты и не счастливы».
Если мы допустим, что А будет утверждением «Вы богаты», а В будет утверждением «Вы счастливы», то отрицание «А или В» станет «Не А и не В».
В общем случае мы имеем одно и то же утверждение: Отрицание «А или В» есть утверждение «Не А и Не В».
Отрицание «A
и B».Опять же, давайте сначала проанализируем пример.
Рассмотрим утверждение «Я и богат, и счастлив». Чтобы это утверждение было ложным, я мог быть либо небогатым , либо несчастливым. Если мы допустим, что А будет утверждением «я богат», а В будет утверждением «я счастлив», то отрицание «А и В» станет «я не богат».0013 или Я недоволен» или «Не А и не Б».
Отрицание «
Если А, , то В».Чтобы опровергнуть утверждение вида «Если А, то В», мы должны заменить его утверждением « А и не В ». Сначала это может показаться запутанным, поэтому давайте рассмотрим простой пример, чтобы понять, почему это правильно.
Рассмотрим утверждение «Если я богат, то я счастлив». Для этого
Если бы утверждение было ложным, мне нужно было бы быть богатым и несчастливым. Если
— это утверждение «Я богат», а Б — это утверждение «Я счастлив»,
тогда отрицание «A $\Rightarrow$ B» есть «я богат» = A, и «я
я недоволен» = не Б.
Таким образом, отрицание «, если А, , затем В» становится «А , а не В».
Пример.
Теперь давайте рассмотрим утверждение, включающее некоторую математику. Возьмем утверждение «Если n четно, то $\frac{n}{2}$ — целое число». Чтобы это утверждение было ложным, нам нужно было бы найти четное целое число $n$, для которого $\frac{n}{2}$ не было целым числом. Таким образом, противоположным этому утверждению является утверждение, что «$n$ четно, а $\frac{n}{2}$ не является целым числом».
Отрицание «Для каждого…», «Для всех…», «Существует…»
Иногда встречаются такие фразы, как «для каждого», «для любого», «для любого». все» и «существует» в математических утверждениях.
Пример.
Рассмотрим утверждение «Для всех целых чисел $n$ либо $n$ четно, либо
$n$ нечетно».
Хотя формулировка немного отличается, это утверждение формы «Если А, то Б».
Мы можем переформулировать это предложение следующим образом: «Если $n$ — любое целое число, то либо $n$ четно, либо $n$ нечетно».
Как бы мы опровергли это утверждение? Чтобы это утверждение было ложным, все, что нам нужно, это найти единственное целое число, которое не является четным и не нечетным. Другими словами, отрицание — это утверждение «Существует целое число $n$, такое, что $n$ нечетно и $n$ нечетно».
В общем, при отрицании утверждения, включающего «для всех», «для каждого», фраза «для всех» заменяется на «существует». Точно так же при отрицании утверждения, включающего «существует», фраза «существует» заменяется на «для каждого» или «для всех».
Пример. Отрицайте утверждение «Если все богатые люди счастливы, то все бедные несчастны».
Во-первых, это высказывание имеет форму «Если А, то В», где А — высказывание «Все богатые люди счастливы», а В — высказывание «Все бедняки грустны». Таким образом, отрицание имеет форму «А, а не В».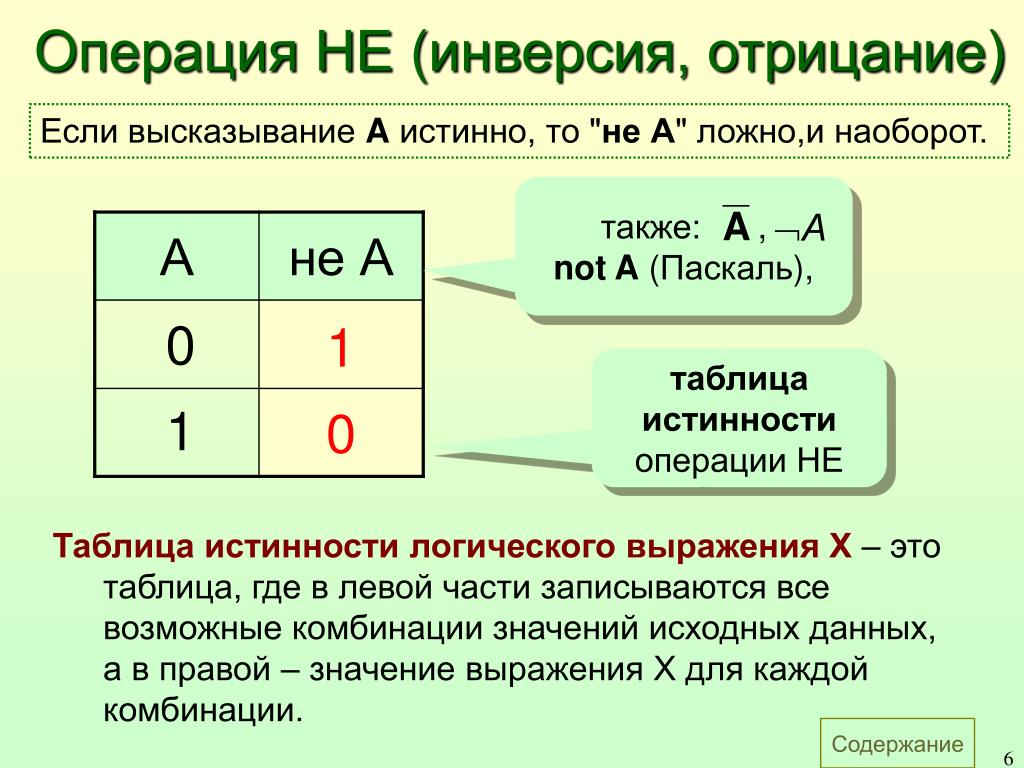
Итак, нам нужно будет отрицать B. Отрицание утверждения B таково: «Существует бедный человек, который не грустит».
Соединив это вместе, мы получим: «Все богатые люди счастливы, но существует бедняк, который не грустит» как отрицание «Если все богатые люди счастливы, то все бедные люди грустны».
Резюме.| Выписка | Отрицание |
| «А или Б» | «не А и не Б» |
| «А и Б» | «не А и не Б» |
| «если А, то Б» | «А, а не Б» |
| «Для всех х, А(х)» | «Существуют x такие, что не A(x)» |
| «Существует x такой, что A(x)» | «Для каждого x, кроме A(x)» |
элементарная теория множеств — Что такое отрицание «$A\subseteq B$»?
$\begingroup$
Я пытаюсь что-то доказать с помощью косвенного доказательства, поэтому мне нужно знать отрицание $A\subseteq B$.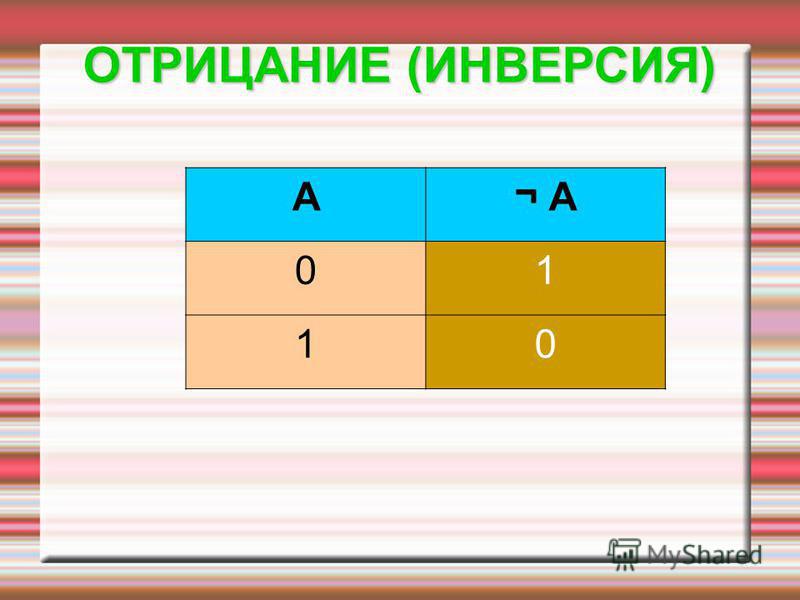
Я предполагаю, что это $A\nsubseteq B$, но что это означает симантически? Это $\forall x\in A,\x\notin B$? Можно ли с уверенностью сказать, что $A$ и $B$ не пересекаются в этой точке?
- элементарная теория множеств
$\endgroup$
1
$\begingroup$
К сожалению, нет. $A \subset B$ означает $\forall x \in A, x \in B$, поэтому отрицание равно $\exists x \in A, x \not \in B$, т.е. существует некоторый элемент $A$, который не находится в $B$.
Интуитивно, поскольку $A \subset B$ означает, что $A$ «полностью содержится в $B$». $A$, не являющееся подмножеством $B$, означает, что $A$ равно , а не полностью 9.0014 содержится в $B$. Это включает в себя ситуацию, когда они не пересекаются, но также включает ситуацию, когда некоторые элементы $A$ находятся в $B$, но не все из них (т. е. $A$ — это , частично содержащихся в $B$).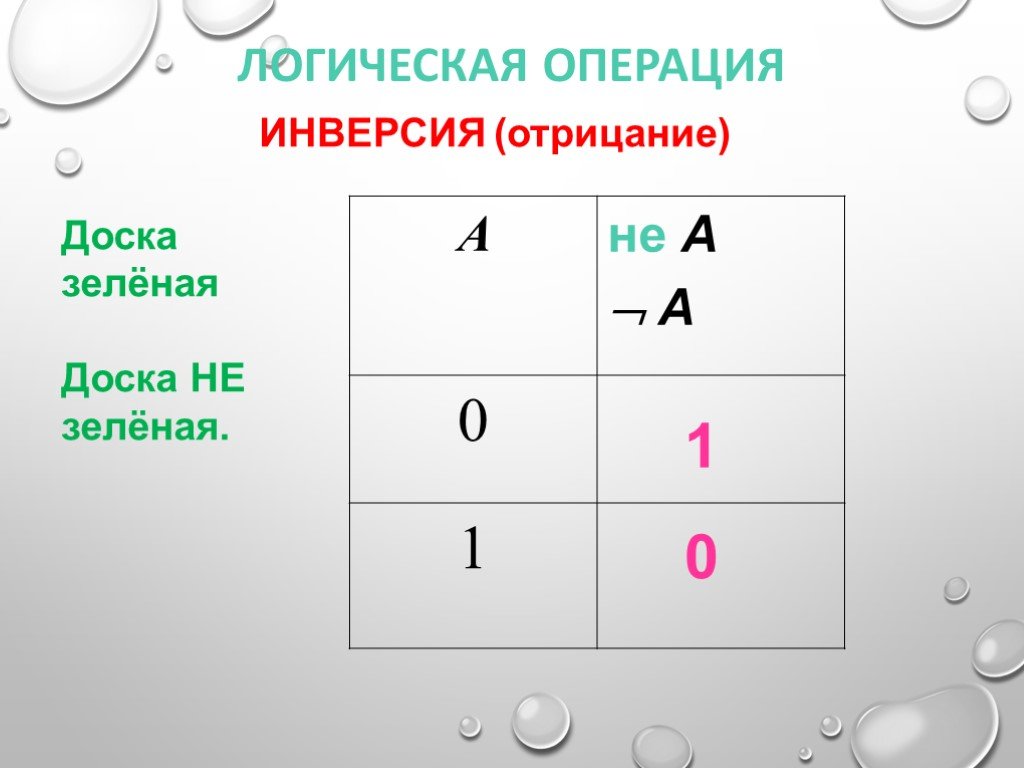
$\endgroup$
2
$\begingroup$
$$A \subseteq B \equiv \forall x( x \in A \rightarrow x \in B)\tag{1}$$
Отрицание $(1)$ дает нам:
$$ \begin{align} A \not\subseteq B & \equiv \lnot \forall x(x\in A \rightarrow x \in B) \\ \\ & \equiv\exists x \lnot(x\in A \rightarrow x \in B) \\ \\ & \equiv \exists x \lnot[\lnot(x \in A) \lor (x \in B)] \tag{$p \to q \equiv \lnot p \lor q$}\\ \\ & \equiv \exists x [\lnot\lnot(x \in A) \land \lnot (x \in B)] \tag{DeMorgan’s}\\ \\ & \equiv \exists x [x \in A \land \lnot (x \in B)] \\ \\ & \equiv \exists x (x\in A \land x \notin B) \tag{$A\not \subseteq B$} \end{выравнивание}$$
$\endgroup$
1
$\begingroup$
Вспомните определение подмножества: если $A \subseteq B$, то каждый элемент A является элементом $B$.
Отрицание таких утверждений, как «каждый объект есть» или «все объекты есть», есть утверждение «по крайней мере один объект не является». Таким образом, $A \not \subseteq B$ означает, что хотя бы один элемент A не является элементом $B$.
$\endgroup$
$\begingroup$
Подсказка: используйте $$A\subseteq B\equiv \forall x(x\in A\Longrightarrow x\in B)$$, чтобы увидеть, что это не так, как вы сказали.
$\endgroup$
3
$\begingroup$
Чтобы ответить на последнюю часть, которая не была вашим основным вопросом: ваше утверждение «$\forall x\in A$, $x\notin B$» действительно эквивалентно тому, что $A$ и $B$ непересекающийся. Но совершенно очевидно, что $A$, не являющееся подмножеством $B$, намного слабее, чем непересекающиеся $A$ и $B$, например, $B$ может быть даже правильным подмножеством $A$.