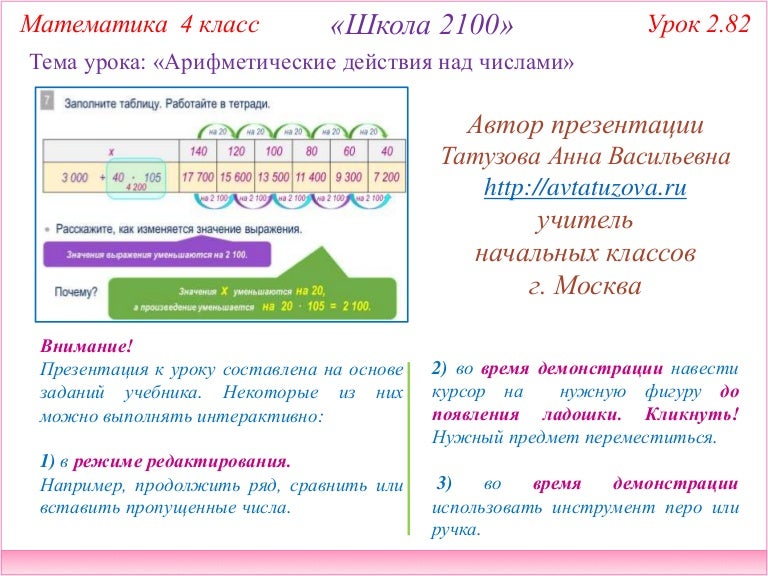
Практическая работа арифметические действия над числами: Урок. Практическая работа. «Арифметические действия над числами в разных системах счисления.»

Практическая работа «Действия с действительными числами» | Методическая разработка по алгебре (10 класс):

Практическая работа «Действия с действительными числами»

1. Выполните сложение и вычитание: 1) -16- 24= — 40 2) -6,78-0,3= — 7,08 3) 19-45= — 26 4) -2,5-(-2,8)= 0,3 5) -4,5+5,4-8,7+4,9= -2,9 6) -8,7-2,3+5,4-4,9= -10,5 7) 59-(-47)= 106	8) 5,68-9,12= -3,44 9) -5,68-(-18,2)= 12,52 10) -124+36-76-36+78=122 11) -7.8+8,1=0,3 12) -9.73-8,5= — 18.23 13) -15.6-(-2.04)= 13,59 14) 97-(-6,7)= 103,7
2. Умножение и деление: 1) 2,45*(-3)= — 0,81 2) -5,9*(-0,4)= 2,36 3) -8,02*0,7= — 5,61 4) -0,01*(-76,2)= 0,76 5) 276-138=138 6) 0,98:1,4=0,7 7) -56,4:(-0,01)=5640	8) 24,11:(-0,09)= — 267.88 9)-5,6*(-0,5)-7,4:(-6,3+2,60)=2,8-7,4(-3,7)=2,8+27,38 = 30,18 10) 2,7:(-0,3)= — 9 11) -57:1,9= — 30 12) -0,207*(-0,1)= 0,02 13) -4. 5*(0.2)*(-2)*0,5= 0,9 14) -6.54:(-0.2)= 32,7
3. Решить уравнения: 1) х-3,4=-6,8 Х= — 3,4 2) у:(-0,5)=-1,1 У= 2,2 3) 6,4:у=-0,04 У= — 0,00625 4) Х+2,5=0,5 Х= -2 5) -0,02*х=-0,1 Х=5 6) -12,8:у=-0,001 У=0,000078125 7) -3,12-х=-0,2 Х= — 2,92 8) -8,2*(х+1)*(х-6)*х=0 Х= — 1   Х = 6   Х=0 9) – х *(х+5)*(х-3)=0 Х=0  Х= — 5  Х = 3	10) (х-5,4)(0,6-х)(3х+1)=0 Х = 5,4   Х = 0,6   Х= — 1/3 11) -3,12-х=-0,2 Х= — 2,92 12) -0,03+у=-0,3 У = — 0,27 13) х:(-2)=-0,08 Х = 0,16 14) 0,3*у=-6,03 У = — 20,1 15) х+6,05=-0.4 Х= — 6,45 16) 8,3-у=12,3 У = — 4 17) 0,1(х+5,8)(х-6,05)х=0 Х=0   Х= — 5,8   Х = 6,05 18) (6,04-х)(х+7)(3х-0,6)(2х+7)=0 Х= 6,04   Х= — 7   Х=0,2   Х= — 3,5
4. Вычислить: 1)-2,1*(-4)-6,8:(-8,9+7,2)= 8,4-6,8(-1,7)=19,96 2) -3,5*(-0,4)*(-2)*25=1,4*(-50)= — 70	3) -1,2*(-3)-6,4:(-7,8+6,2)=3,6-6,4(-1,6)=13,84 4) -4,5*(-0,2)*(-2)*5= — 9
5.Упростить выражение и найти его значение:      при ; -а- 2  5/6+2= -а – 5/6 = -7/4-5/6 = -62/44= — 31/12 = — 2   7/12	при ; Х +10 – 10  7/13 = х-7/13= 8/13-7/13=1/13
6. Вычислите:  = 2,5	=6,6
7. Вычислите: =(6+6) /(6-6) делить на 0 нельзя!	= (2+6)/(2-6)=8/(-4) = -2

ГАПОУ ТО «Тобольский медицинский колледж им. В.Солдатова»  34.02.01 Сестринское дело
ОУД. 03 Математика: алгебра и начала математического анализа; геометрия
Практическая работа	Действия над действительными числами

1. Выполните сложение и вычитание: 1) -16- 24= 2) -6,78-0,3= 3) 19-45= 4) -2,5-(-2,8)= 5) -4,5+5,4-8,7+4,9= 6) -8,7-2,3+5,4-4,9= 7) 59-(-47)=	8) 5,68-9,12= 9) -5,68-(-18,2)= 10) -124+36-76-36+78= 11) -7.8+8,1= 12) -9.73-8,5= 13) -15.6-(-2.04)= 14) 97-(-6,7)=
2. Выполните умножение и деление: 1) 2,45*(-3)= 2) -5,9*(-0,4)= 3) -8,02*0,7= 4) -0,01*(-76,2)= 5) 276-138= 6) 0,98:1,4= 7) -56,4:(-0,01)=	8) 24,11:(-0,09)= 9) -5,6*(-0,5)-7,4:(-6,3+2.60)= 10) 2,7:(-0,3)= 11) -57:1,9= 12) -0,207*(-0,1)= 13) -4. 5*(0.2)*(-2)*0,5= 14) -6.54:(-0.2)=
3. Решите уравнения: 1) х-3,4=-6,8 2) у:(-0,5)=-1,1 3) 6,4:у=-0,04 4) Х+2,5=0,5 5) -0,02*х=-0,1 6) -12,8:у=-0,001 7) -3,12-х=-0,2 8) -8,2*(х+1)*(х-6)*х=0 9) – х *(х+5)*(х-3)=0	10) (х-5,4)(0,6-х)(3х+1)=0 11) -3,12-х=-0,2 12) -0,03+у=-0,3 13) х:(-2)=-0,08 14) 0,3*у=-6,03 15) х+6,05=-0.4 16) 8,3-у=12,3 17) 0,1(х+5,8)(х-6,05)х=0 18) (6,04-х)(х+7)(3х-0,6)(2х+7)=0
4. Вычислите: 1)-2,1*(-4)-6,8:(-8,9+7,2)= 2) -3,5*(-0,4)*(-2)*25=	3) -1,2*(-3)-6,4:(-7,8+6,2)= 4) -4,5*(-0,2)*(-2)*5=
5.Упростите выражение и найти его значение:      при ;	при ;
6. Вычислите:
7. Вычислите: .	.

Практическое занятие 1. Выполнение арифметических действий над числами. | План-конспект занятия:

Практическое занятие№3

 по теме: 

Взаимное расположение прямых в пространстве.

Маршрутный лист занятия:

1. Выполните тест.  За каждый правильный ответ – 1 балл. Письменно в тетради.

1. Стереометрия – это раздел геометрии, изучающий

а)  свойства фигур на плоскости    

б) свойства фигур в пространстве    

в) различные фигуры

2. Что может принадлежать плоскости

а) точка       б) точка и  прямая        в) плоскость  

3. Через две пересекающиеся прямые можно провести только

а) одну плоскость

б) две плоскости

4. Через любые две точки пространства проходит

а) единственная прямая       б) единственная плоскость         в) две плоскости

5. Если две плоскости имеют общую точку, то они

а) не пересекаются

б) пересекаются

в) пересекаются по прямой

6. Через прямую и не лежащую на ней точку можно провести только

а) одну плоскость

б) две плоскости

в) три плоскости

2. Заполните таблицу. Письменно в тетради.

В голубой строке заполните:

Как расположены прямые      a и b?  

Как расположены прямые   c и d?  

Как расположены прямые   k и m?

В красной строке заполните:

Какие прямые лежат в одной плоскости?

Какие прямые не лежат в одной плоскости?

Проверьте себя с нижеприведенной таблицей.

ab (прямые параллельны)	cd=А (прямые пересекающиеся)	k∸m (прямые  скрещивающиеся)
лежат в одной плоскости	лежат в одной плоскости	не лежат в одной плоскости

3. Определите взаимное расположение прямых. Письменно в тетради.

АB ? CD AD ? DD1 DC ? A1D1 A1B1 ? A1D1 B1C1 ?  BC B1C1 ? AA1 DC1 ? AB

4. Решите задачи устно.

	1) Дано: PABC – тетраэдр. Параллельны ли его ребра PB и AC?  Пересекаются ли прямые PC и AB?
2) Дано: АВ  CD. Могут ли быть прямые АC и ВD скрещивающимися ? Могут ли быть прямые АC и ВD пересекающимися?		а)

5. Решите задачи. Письменно в тетради.

    1. Задача  

Нарисуйте плоскость . Нарисуйте две параллельные прямые a и b, пересекающую  данную плоскость. Нарисуйте  прямую c лежащую в  данной плоскости и пересекающую прямую b в точке K. Каково взаимное расположение прямых a и c?

2. Задача. За каждый правильный ответ – 1 балл.

Дано: ABCDA1B1C1D1 — куб.

Определите взаимное расположение прямых:

АВ и D1C1,  

BC и CC1,

АB1 и  B1C,  

AD и BB1,  

A1B и  AD

6. Математический диктант. Ответьте «Да» или «Нет» на данные утверждения. За каждый правильный ответ – 1 балл.

1.Две прямые не имеющие общих точек  могут быть только                    параллельными.                                                                                        Да или нет?

2.Две прямые, имеющие лишь одну  общую точку, называются

 пересекающимися.                                                                                  Да или нет?

3. Две прямые, которые не лежат в одной плоскости, называются

скрещивающимися.                                                                                 Да или нет?

4.Если две прямые скрещивающиеся, то они лежат в одной                      

 плоскости.                                                                                                Да или нет?

5.Если две прямые не пересекаются и не лежат в одной плоскости,                               то они параллельные.                                                                               Да или нет?

По результатам выполненной работы будут выставлены следующие оценки:

15-16 баллов  – оценка «5»

13-14 баллов  – «4»

11-12  баллов  – «3»

Арифметические операции — Примеры | Основные арифметические операции

Арифметические операции являются основой математики. В основном он состоит из таких операций, как сложение, вычитание, умножение и деление. Они также известны как математические операции. В нашей повседневной жизни мы используем арифметические операции, чтобы узнать общие доходы и расходы бизнеса, составить месячный или годовой бюджет, измерить длину и т. д. Мы используем их почти в любое время дня, например, при расчете общего числа вопросов, заданных в домашнем задании, при подсчете времени, денег, количества съеденных конфет, количества полученных баллов по всем предметам и т. д.

1.	Определение арифметических операций
2.	Четыре основных арифметических операции
3.	Арифметические операции с целыми числами
4.	Арифметические операции с рациональными числами
5.	Часто задаваемые вопросы по арифметическим операциям

Определение арифметических операций

Арифметические операции представляют собой набор из четырех основных операций, которые необходимо выполнить для сложения, вычитания, умножения или деления двух или более величин. Они включают изучение чисел, включая порядок операций, которые полезны во всех других частях математики, таких как алгебра, обработка данных и геометрия. Мы не можем решить задачу без использования правил арифметических действий. Арифметические операции включают четыре основных правила: сложение, вычитание, умножение и деление. Для каждой из четырех арифметических операций, показанных на изображении ниже, используется определенный символ.

Четыре основных арифметических операции

Здесь мы обсуждаем четыре основных правила арифметических операций для всех действительных чисел.

• Дополнение (сумма; «+»)
• Вычитание (разница; «-»)
• Умножение (произведение; ‘×’ )
• Отдел (÷)

Давайте подробно обсудим приведенные выше арифметические операции.

Сложение

Сложение — это базовый математический навык нахождения или вычисления суммы двух или более чисел, или мы можем сказать простыми словами сложение вещей. Обозначается символом «+». Когда мы складываем два или более чисел, получается один термин. Порядок цифр в сложении не имеет значения.

Например: 367 + 985 = 1352

Вычитание

Арифметическая операция вычитания показывает разницу между двумя числами. Обозначается символом «-». Вычитание в основном используется, чтобы узнать, что останется, когда вещи уберут, или, другими словами, вычитание одного числа из другого числа.

Например: 20 — 9 = 11

Умножение

Повторное сложение называется умножением. Он представлен символом «×». Умножение как арифметическая операция помогает нам узнать сумму, когда число повторяется несколько раз. Например, 2 умножить на 3 равно 6. Математически мы можем записать это как 2 × 3 = 6. Множитель и множитель — это термины, используемые в процессе умножения. Произведение — это термин, который мы используем для обозначения результата умножения множимого и множителя.

Например: 20 × 31 = 620

В приведенном выше примере «20» — это множитель, «31» — множимое, а результат «620» известен как произведение.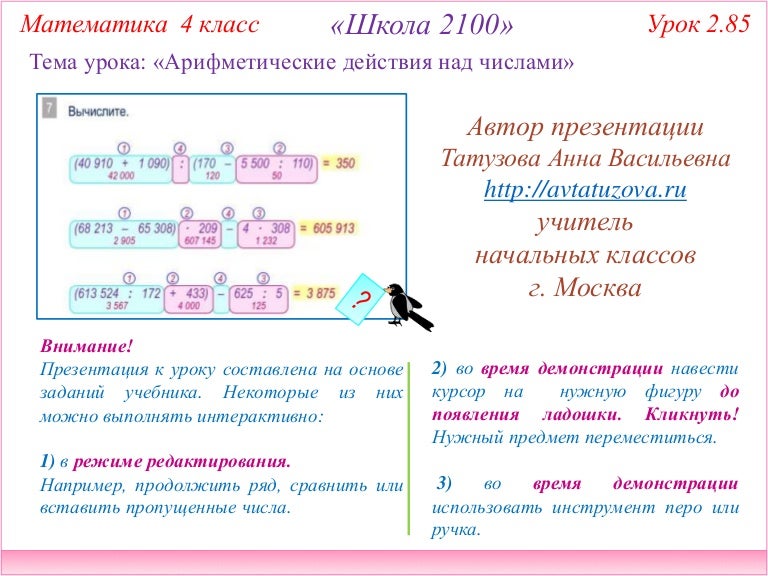

Деление

Деление — это акт деления чего-либо на равные части или группы. Это одна из четырех основных арифметических операций, которая дает справедливый результат равного распределения. Деление является обратным умножению. Например, 2 группы по 3 карандаша в каждой дают при умножении 6 карандашей (2×3), а в случае деления 6 карандашей, разделенных на 2 равные группы, дают по 3 карандаша в каждой группе. Обозначается символом «÷». Итак, здесь мы можем записать это как 6 ÷ 2 = 3,

Арифметические операции с целыми числами

С целыми числами мы можем легко выполнять четыре основных арифметических действия. Целые числа — это набор чисел, который начинается с 0 и продолжается до бесконечности. Такие числа не имеют дробных или десятичных частей. Сложение двух и более целых чисел всегда приводит к увеличению конечной суммы. Например, если мы сложим три числа 4, 5 и 6, то получим 4 + 5 + 6 = 9 + 6 = 15. Итак, здесь 15 больше, чем все три слагаемых.

Добавление любого числа к 0 всегда приводит к одному и тому же числу, и если мы добавляем 1 к любому целому числу, мы получаем его последовательный номер или преемник.

В случае целых чисел мы всегда вычитаем меньшую величину из большей, чтобы получить разность, которая меньше уменьшаемого. Вычитание 0 из любого числа всегда приводит к одному и тому же числу, а вычитание 1 из числа дает его предшественник. Умножение двух и более целых чисел можно выполнить с помощью таблицы умножения. Произведение всегда больше обоих чисел, за исключением случая умножения на 1 и 0. Число, умноженное на 0, всегда дает 0, а умножение на 1 дает нам то же число, что и произведение.

Деление двух целых чисел может дать или не дать целые числа. Если частное является целым числом, это означает, что делимое кратно делителю. Если это не так, то в качестве частного будет десятичное число.

Арифметические операции с рациональными числами

Арифметические операции с рациональными числами такие же, как и с целыми числами. Единственное отличие состоит в том, что рациональные числа представлены в виде p/q, где p и q — целые числа, а q не равно 0. При сложении или вычитании двух рациональных чисел мы должны взять НОК знаменателей. Чтобы узнать об арифметических операциях над рациональными числами, нажмите здесь.

Связанные статьи по арифметическим операциям

Ознакомьтесь со следующими страницами, посвященными арифметическим операциям.

• Арифметика
• Порядок действий
• правило PEMDAS
• Сложение и вычитание дробей

Часто задаваемые вопросы по арифметическим операциям

Каковы основные правила арифметических операций?

В математике сложение (+), вычитание (-), умножение (×) и деление — четыре основных арифметических действия.

Что представляют четыре арифметические операции?

Четыре арифметических действия — сложение, вычитание, умножение и деление представляют собой:

• Сложения представляют собой сумму двух значений.
• Вычитание представляет разницу между двумя числами
• Умножение показывает произведение двух чисел.
• Деление — это процесс деления одного числа на другое и получения значений частного и остатка.

Каков порядок арифметических операций?

Порядок, в котором должны выполняться арифметические операции в выражении, известен как PEMDAS или BODMAS. В этом правиле четко указано, что порядок выполнения операций следующий: круглые скобки, возведения в степень, умножение или деление, сложение или вычитание.

Является ли вычитание арифметической операцией?

Да, вычитание — это арифметическая операция, показывающая процесс удаления объектов из коллекции. Вычитание предполагает вычитание одного числа из другого числа. Символ вычитания выглядит так «-«. Имя символа представляет собой знак минус. Например, у Рэйчел 6 яблок, и из них 2 яблока она отдала своему брату Джону. Значит, чтобы найти оставшиеся яблоки с Рэйчел, отнимем от 6 2. Разница и будет ответом, то есть 6 — 2 = 4.

Является ли сложение арифметической операцией?

Да, сложение — одно из правил арифметической операции. Сложение означает подсчет суммы или нахождение суммы двух или более чисел. Символ добавления выглядит так: «+». Например, 25 + 10 + 4 = 39.

Каковы символы основных арифметических операций?

Символы основных арифметических операций:

• Символ сложения ⇒ «+»
• Символ вычитания ⇒ ‘-’
• Символ умножения ⇒ «×»
• Символ деления ⇒ «÷»

Арифметические операторы — основы программирования

Кеннет Лерой Басби и Дэйв Брауншвейг

Обзор

Основными арифметическими операциями являются сложение, вычитание, умножение и деление. Арифметика выполняется в соответствии с порядком операций.

[1]

Обсуждение

Оператор выполняет действие над одним или несколькими операндами. Общие арифметические операторы:

Действие	Общий символ
Дополнение	+
Вычитание	-
Умножение	*
Отдел	/
Модуль (связанный с целыми числами)	%

Эти арифметические операторы являются бинарными, то есть имеют два операнда. Операнды могут быть как константами, так и переменными.

возраст + 1

Это выражение состоит из одного оператора (сложения), который имеет два операнда. Первый представлен переменной с именем age, а второй — буквальной константой. Если бы age имел значение 14, то выражение оценивало бы (или равнялось) 15.

Эти операторы работают так, как вы их выучили на протяжении всей жизни, за исключением деления и модуля. Обычно мы думаем о делении как о результате результата, который может иметь дробную часть (тип данных с плавающей запятой). Однако деление, когда оба операнда имеют целочисленный тип данных, может действовать по-разному. Пожалуйста, обратитесь к следующему разделу «Целочисленное деление и модуль».

Арифметические операторы присваивания

Многие языки программирования поддерживают комбинацию операций присваивания ( = ) и арифметических операций ( + , - , * , /,

% ). В различных учебниках они называются «составными операторами присваивания» или «комбинированными операторами присваивания». Их использование можно объяснить с точки зрения оператора присваивания и арифметических операторов. В таблице мы будем использовать переменную age и можно предположить, что она имеет целочисленный тип данных.

 

Примеры арифметических назначений:	Эквивалентный код:
возраст += 14;	возраст = возраст + 14;
возраст -= 14;	возраст = возраст - 14 лет;
возраст *= 14;	возраст = возраст * 14;
возраст /= 14 лет;	возраст = возраст / 14 лет;
возраст %= 14;	возраст = возраст % 14;

Псевдокод

 Основная функция
 .
No related posts.