4 примера использования линейной регрессии в реальной жизни
Линейная регрессия является одним из наиболее часто используемых методов в статистике. Он используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика.
Самая основная форма линейной регрессии известна как простая линейная регрессия , которая используется для количественной оценки взаимосвязи между одной переменной-предиктором и одной переменной-ответом.
Если у нас есть более одной переменной-предиктора, мы можем использовать множественную линейную регрессию, которая используется для количественной оценки взаимосвязи между несколькими переменными-предикторами и переменной отклика.
В этом руководстве представлены четыре различных примера использования линейной регрессии в реальной жизни.
Реальный пример линейной регрессии №1Компании часто используют линейную регрессию, чтобы понять взаимосвязь между расходами на рекламу и доходами.
Например, они могут соответствовать простой модели линейной регрессии, используя расходы на рекламу в качестве переменной-предиктора и доход в качестве переменной-отклика. Регрессионная модель будет иметь следующий вид:
доход = β 0 + β 1 (расходы на рекламу)
Коэффициент β 0 будет представлять общий ожидаемый доход, когда расходы на рекламу равны нулю.
Коэффициент β 1 будет представлять собой среднее изменение общего дохода, когда расходы на рекламу увеличиваются на одну единицу (например, на один доллар).
Если β 1 отрицательное, это будет означать, что большие расходы на рекламу связаны с меньшими доходами.
Если β 1 близко к нулю, это будет означать, что расходы на рекламу мало влияют на доход.
И если β 1 положителен, это будет означать, что чем больше расходов на рекламу, тем больше доход.
В зависимости от значения β 1 компания может решить уменьшить или увеличить свои расходы на рекламу.
Медицинские исследователи часто используют линейную регрессию, чтобы понять взаимосвязь между дозировкой лекарств и артериальным давлением пациентов.
Например, исследователи могут вводить пациентам различные дозы определенного препарата и наблюдать за реакцией их кровяного давления. Они могут соответствовать простой модели линейной регрессии, используя дозировку в качестве предиктора и артериальное давление в качестве переменной отклика. Регрессионная модель будет иметь следующий вид:
кровяное давление = β 0 + β 1 (дозировка)
Коэффициент β 0 будет представлять ожидаемое кровяное давление, когда доза равна нулю.
Коэффициент β 1 будет представлять собой среднее изменение артериального давления при увеличении дозы на одну единицу.
Если β 1 отрицательный, это будет означать, что увеличение дозы связано со снижением артериального давления.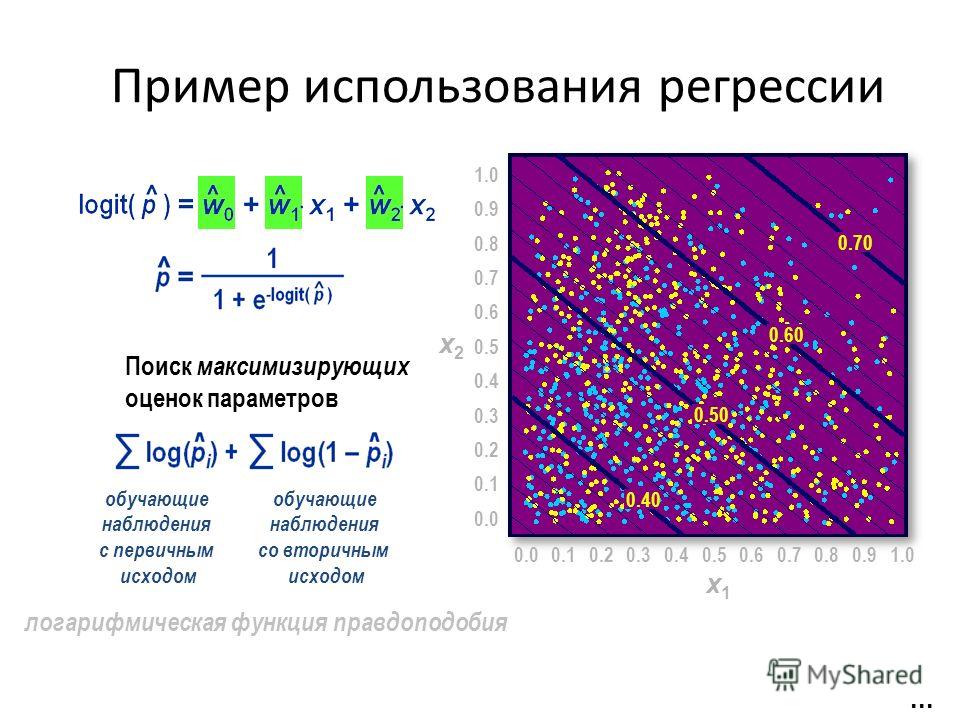
Если β 1 близок к нулю, это будет означать, что увеличение дозы не связано с изменением артериального давления.
Если β 1 положительный, это будет означать, что увеличение дозы связано с повышением артериального давления.
В зависимости от значения β 1 исследователи могут принять решение об изменении дозировки, данной пациенту.
Реальный пример линейной регрессии № 3Ученые-агрономы часто используют линейную регрессию для измерения влияния удобрений и воды на урожайность.
Например, ученые могут использовать разное количество удобрений и воды на разных полях и посмотреть, как это повлияет на урожайность. Они могут соответствовать модели множественной линейной регрессии, используя удобрения и воду в качестве переменных-предикторов и урожайность в качестве переменной отклика. Регрессионная модель будет иметь следующий вид:
урожайность = β 0 + β 1 (количество удобрений) + β 2 (количество воды)
Коэффициент β 0 будет представлять ожидаемую урожайность без удобрений и воды.
Коэффициент β 1 будет представлять собой среднее изменение урожайности при увеличении количества удобрений на одну единицу при условии, что количество воды остается неизменным.
Коэффициент β 2 будет представлять собой среднее изменение урожайности при увеличении количества воды на одну единицу при условии, что количество удобрений остается неизменным.
В зависимости от значений β 1 и β 2 ученые могут изменить количество удобрений и воды, используемых для получения максимальной урожайности.
Реальный пример линейной регрессии № 4Исследователи данных для профессиональных спортивных команд часто используют линейную регрессию для измерения влияния различных режимов тренировок на производительность игроков.
Например, специалисты по данным в НБА могут проанализировать, как разное количество еженедельных занятий йогой и тяжелой атлетикой влияет на количество очков, набранных игроком. Они могут соответствовать модели множественной линейной регрессии, используя занятия йогой и занятия тяжелой атлетикой в качестве переменных-предикторов и общее количество баллов, набранных в качестве переменной отклика. Регрессионная модель будет иметь следующий вид:
Регрессионная модель будет иметь следующий вид:
набранные баллы = β 0 + β 1 (занятия йогой) + β 2 (занятия тяжелой атлетикой)
Коэффициент β 0 будет представлять собой ожидаемое количество очков, набранных игроком, который участвует в нулевых занятиях йогой и нулевых занятиях тяжелой атлетикой.
Коэффициент β 1 будет представлять собой среднее изменение в баллах, набранных при увеличении количества еженедельных занятий йогой на единицу, при условии, что количество еженедельных занятий тяжелой атлетикой остается неизменным.
Коэффициент β 2 будет представлять собой среднее изменение в баллах, набранных при увеличении количества еженедельных занятий тяжелой атлетикой на единицу, при условии, что количество еженедельных занятий йогой остается неизменным.
В зависимости от значений β 1 и β 2 исследователи данных могут порекомендовать игроку участвовать в более или менее еженедельных занятиях йогой и тяжелой атлетикой, чтобы максимизировать свои очки.
Линейная регрессия используется в самых разных реальных ситуациях в самых разных отраслях. К счастью, статистическое программное обеспечение позволяет легко выполнять линейную регрессию.
Не стесняйтесь изучить следующие учебные пособия, чтобы узнать, как выполнять линейную регрессию с использованием различных программ:
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить множественную линейную регрессию в R
Как выполнить множественную линейную регрессию в Stata
Как выполнить линейную регрессию на калькуляторе TI-84
Примеры линейной регрессии
Если вы считаете регрессионное моделирование недоступным для понимания, или если у вас были проблемы с алгеброй в старшей школе, то эта статья для вас. Конечно, всем остальным она тоже не повредит.
Загрузить программу ВІ
Демонстрации решений
Оглавление
Если вы считаете регрессионное моделирование недоступным для понимания, или если у вас были проблемы с алгеброй в старшей школе, то эта статья для вас. Конечно, всем остальным она тоже не повредит.
Конечно, всем остальным она тоже не повредит.Представьте, что вам дали базу данных, содержащую возраст и доход каждого жителя определенного района. Ваш начальник хочет, чтобы вы использовали эти данные, чтобы создать модель, предсказывающую доход человека на основании его возраста. И вот вы звоните с просьбой о срочной статистической помощи некоему Доктору Иванову из Информационных Систем. Удача вам сопутствует – доктор на связи. Док Иванов мудро удостоверяется, что среди данных нет аномальных значений, способных исказить анализ. Затем он колдует над данными и добросовестно представляет вам математическую модель: «Умножьте возраст в годах на 971.4, приплюсуйте 1536.2 и получите годовой доход в долларах. Вот ваша оптимальная модель».
Вы как следует благодарите Доктора Иванова и спешите подготовить отчет своему начальнику. Вы используете формулу, чтобы построить график с доходом по вертикальной оси и возрастом по горизонтальной, и восхищаетесь простотой, с которой это правило связывает возраст и доход.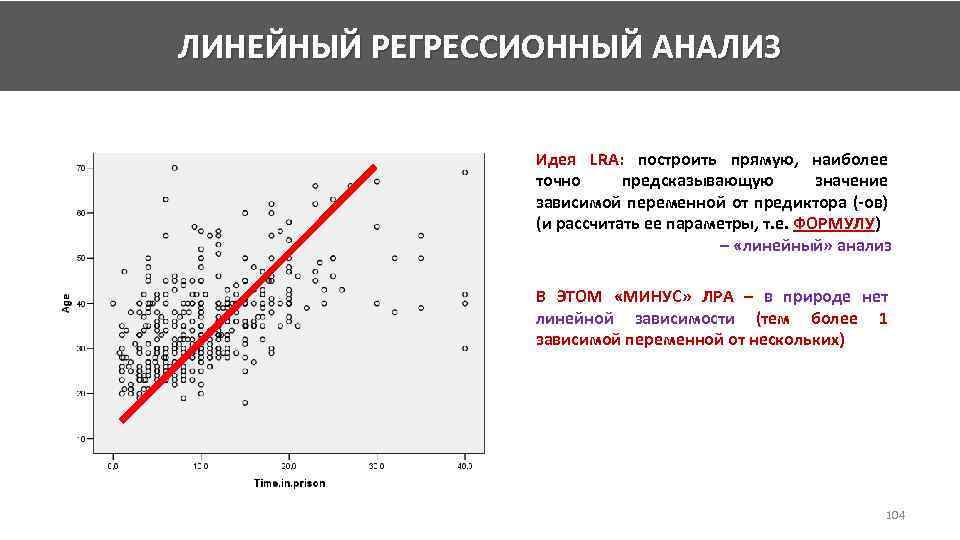 Это прямая линия – и к тому же, оптимальная. Но ее блеск чуть меркнет, когда вы замечаете, что по этой модели доход 18-летних составляет $19,021 (этим юнцам следовало бы делать домашние задания, а не грести такие суммы!) И он исчезает окончательно, когда вы видите, что предполагаемый доход 70-летних составляет $69,534, и каждый последующий год жизни добавляет автоматический бонус в $971 (и вряд ли за счет надбавок к государственной пенсии).
Это прямая линия – и к тому же, оптимальная. Но ее блеск чуть меркнет, когда вы замечаете, что по этой модели доход 18-летних составляет $19,021 (этим юнцам следовало бы делать домашние задания, а не грести такие суммы!) И он исчезает окончательно, когда вы видите, что предполагаемый доход 70-летних составляет $69,534, и каждый последующий год жизни добавляет автоматический бонус в $971 (и вряд ли за счет надбавок к государственной пенсии).
Так почему же формула доктора Иванова выглядит подозрительной? Потому что она плохая. Но как модель может быть плохой, когда она «оптимальна»? Она будет оптимальна только в том случае, если Иванов сделал правильное предположение о ее форме. Он предположил, что правильная форма модели – это прямая линия. Компьютер сделал свою часть работы, выбрав наиболее подходящую прямую линию из всех возможных с помощью применения многоуважаемой техники, созданной еще Карлом Гауссом (1777-1855).
Уловка-22
Если вам кажется, что здесь есть Уловка-22, то вы правы. Если бы вы знали верную форму модели с самого начала, вам бы не понадобился Доктор Иванов. Док тоже не знал, какая форма является верной, так что из-за своей занятости он выбрал самое простое и предположил, что это прямая линия. Уравнение прямой линии выглядело научным, по крайней мере, в тот момент, но по сути научным не являлось. Прямые линии зачастую отражают невероятные физические законы в науке и инженерии, и нет никаких оснований полагать, что они применимы к экономическим ситуациям. Алгебраическая формула, и впрямь, проста и удобна, но кому нужно простое описание плохой модели?
Если бы вы знали верную форму модели с самого начала, вам бы не понадобился Доктор Иванов. Док тоже не знал, какая форма является верной, так что из-за своей занятости он выбрал самое простое и предположил, что это прямая линия. Уравнение прямой линии выглядело научным, по крайней мере, в тот момент, но по сути научным не являлось. Прямые линии зачастую отражают невероятные физические законы в науке и инженерии, и нет никаких оснований полагать, что они применимы к экономическим ситуациям. Алгебраическая формула, и впрямь, проста и удобна, но кому нужно простое описание плохой модели?
Действительно ли объединенные силы математики и процессора Pentiumвытянули именно то, что было нужно, из данных? Вот и нет. То, что сделал Док, случается слишком часто, потому что всегда есть искушение бездумно применить повсеместно используемый инструмент, называемый линейной регрессией.
Линейная регрессия
Формула, которую дал вам Док, умножает возраст на 971.4 и добавляет 1536. 2 к результату. Он получил 971.4 и 1536.2 с помощью компьютерной программы линейной регрессии, которая выполнила все трудоемкие вычисления, чтобы найти эти числа. Данные числа определяют конкретную прямую, на которую ложатся исходные данные.
2 к результату. Он получил 971.4 и 1536.2 с помощью компьютерной программы линейной регрессии, которая выполнила все трудоемкие вычисления, чтобы найти эти числа. Данные числа определяют конкретную прямую, на которую ложатся исходные данные.
Линейная регрессия – это математический метод оценивания некоего количественного значения (например, суммы в долларах), посредством «взвешивания» одного или нескольких прогнозирующих параметров, таких как возраст, число детей, средний счет в боулинге и так далее. Он был разработан задолго до цифровых компьютеров, и его вечная слава обусловлена привлекательностью для академических исследований.
Если предположить, что линейная регрессия была единственным моделирующим инструментом в арсенале Дока, то мы можем увидеть, как его созданная из подручных средств модель появилась на свет. Подобные инструменты делают допущение, что прямая линия является правильной формой, определяющей отношение каждого из прогнозирующих параметров к искомому количественному показателю. Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Давайте предположим, что в дополнение к возрасту, ваши данные включали бы «число детей» как прогнозирующий параметр дохода. Введение обоих параметров в регрессию даст формулу вида:
Доход = 1007.8*Возраст -752.35*Число детей +933.6
Звездочка – знак умножения.Влияние нашей новой переменной «число детей», тоже линейное. Это происходит потому, что предполагаемый доход прямолинейно уменьшается на $752.35 за каждого дополнительного ребенка. Мы используем эту формулу, показывающую отношение возраста и числа детей к доходу, чтобы проиллюстрировать то, что важно знать о числах, предоставляемых линейной регрессией.
1) Довольно часто, некорректно полагают, что 1007.8 – это «вес» возраста, а -752.35 – «вес» числа детей. Если бы возраст выражался в месяцах, а не в годах, то новый «вес» был бы разделен на 12 лишь для того, чтобы отразить изменение шкалы. Таким образом, величина «веса» не является мерой важности прогнозирующего параметра, к которому он относится. Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Называйте эти множители коэффициентами, и вы не ошибетесь и избежите семантической опасности «веса». В модели будет столько же коэффициентов, сколько и прогнозирующих параметров.
Единственное предназначение коэффициентов и, в сущности, всех чисел (технически, значений параметров), производимых регрессией – это сделать так, чтобы формула хорошо сходилась с исходными данными.
2) Обратите внимание, что коэффициент (-752.35), множитель числа детей, имеет отрицательно значение. В реальности это вовсе не означает, что если число детей растет, то предполагаемый доход обязательно уменьшается. Знак перед коэффициентом будет достоверно указывать направление только в том случае, когда он является единственным прогнозирующим параметром. Если имеется два и более прогнозирующих параметра, и между ними существует корреляция, то вполне вероятно, что один параметр будет иметь положительный коэффициент, а другой – отрицательный, вопреки здравому смыслу. Для нашего примера, на самом деле, если бы число детей было бы единственным прогнозирующим параметром, то тогда коэффициент перед ними оказался бы положительным. Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
Но если соединить число детей с возрастом, между которыми существует некоторая корреляция, то получится сбивающий с толку отрицательный коэффициент.
3) Последний параметр регрессии, константа +933.6 существует для того, чтобы удостоверится, что если каждый параметр принимает среднее значение, то результирующий предполагаемый доход тоже окажется средним. Линейная регрессия всегда так работает. Допустим, средний возраст равен 45.67, а среднее число детей – 1.41. Мы можем подставить эти значения в формулу следующим образом:
1007.8*45.67 -752.35*1.41 +933.56 = 45899
И 45899 – действительно, средний доход в исходных данных. После того как коэффициенты умножены на свои соответствующие параметры и просуммированы, в итоге всегда останется добавить эту константу (даже если она равна нулю).
Математический подвиг
До этого момента мы говорили о том, как линейная регрессия делает допущение о линейности отношений, и о том, как интерпретировать параметры, которые она находит. Но что делать, если отношения не линейны? Вы можете, не задумываясь, подставить данные в линейную регрессию, но то, что вы получите, будет линейным округлением для верной формы. Чем больше верная форма отличается от прямой линии, тем менее точным будет результат.
Но что делать, если отношения не линейны? Вы можете, не задумываясь, подставить данные в линейную регрессию, но то, что вы получите, будет линейным округлением для верной формы. Чем больше верная форма отличается от прямой линии, тем менее точным будет результат.
Из-за того, что процедура линейной регрессии выбита в граните классики, ответственность за выпрямление данных в нечто напоминающее прямую линию ложится на сознательного пользователя. Технический термин для выпрямления – это «трансформирование». Из своих предпочтений Док Иванов, скорее всего, использует что-то математическое, чтобы выполнять трансформирование. Например, если между возрастом и доходом не существует линейных отношений, возможно, они существуют между квадратным корнем возраста и доходом. Нет ничего волшебного в квадратном корне. Это всего лишь одна из множества математических функций, которая может использоваться в попытке трансформировать возраст во что-то новое, что будет более сопоставимо с линейной регрессией. Пара трансформаций тут и там может оказаться делом веселым и интересным, но что если вам приходится иметь дело с сотней потенциальных прогнозирующих параметров?
Пара трансформаций тут и там может оказаться делом веселым и интересным, но что если вам приходится иметь дело с сотней потенциальных прогнозирующих параметров?
Книга 1995 года, адресованная индустрии прямого маркетинга, говорит о трансформировании следующее [наши комментарии – в квадратных скобках]:
«…довольно просто взглянуть на диаграмму рассеяния [точечный график, в котором горизонтальная ось – прогнозирующие параметры, а вертикальная – прогнозируемые] для определения, являются ли отношения линейными, или же они должны быть выпрямлены с помощью какой-либо трансформации».
Предыдущее утверждение верно, если рассматривается небольшое число параметров, и отношения настолько сильны, что очевидны при первом взгляде. Но если слабые отношения погребены под грудой из 50,000 параметров, тогда бы и Шерлок Холмс, вооруженный своей лупой, их бы не нашел. Другой подход с такой же сложностью – это построить график с ошибками («погрешностью») линейной модели, чтобы обнаружить очевидные закономерности упущенной информации.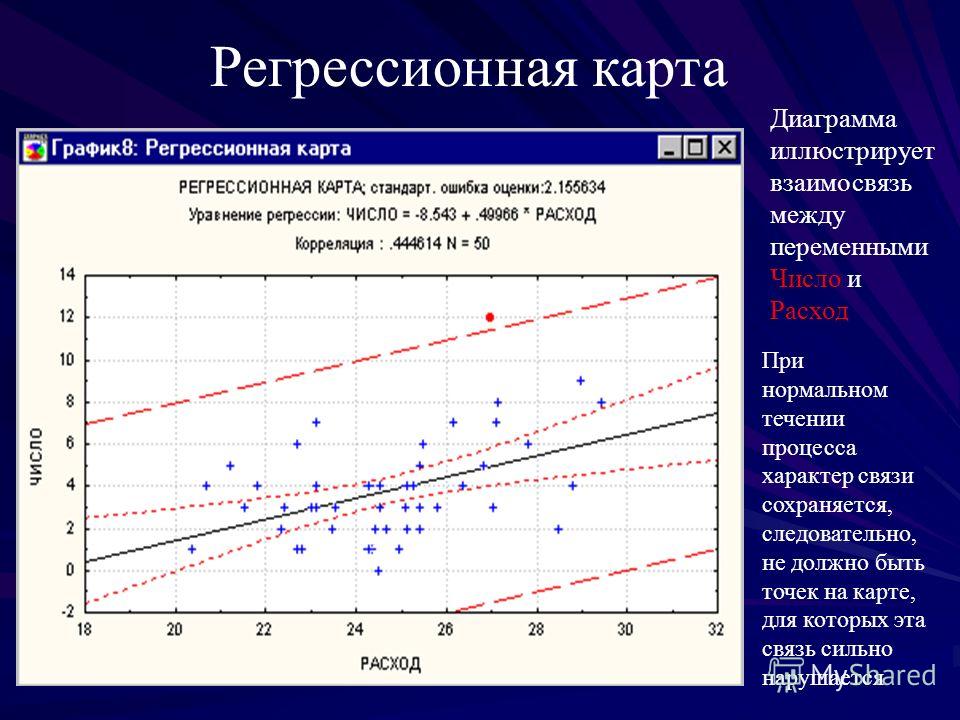 Недавно была продемонстрирована работа очень медленной (но упорной) компьютерной программы, которая испытывает одно уравнение трансформации за другим, усердно строя графики каждой найденной формулы на экране. Вы буквально можете оставить эту штуку работать всю ночь. Столь фанатичную преданность аналитическим функциям сложно оправдать, потому что пользователь, тот, кто платит по счетам, без сомнений, не обладает способностью интуитивно интерпретировать любую из них.
Недавно была продемонстрирована работа очень медленной (но упорной) компьютерной программы, которая испытывает одно уравнение трансформации за другим, усердно строя графики каждой найденной формулы на экране. Вы буквально можете оставить эту штуку работать всю ночь. Столь фанатичную преданность аналитическим функциям сложно оправдать, потому что пользователь, тот, кто платит по счетам, без сомнений, не обладает способностью интуитивно интерпретировать любую из них.
Давайте вернемся к изначальной проблеме предсказания дохода на основе возраста. Чтобы проиллюстрировать нашу позицию, давайте предположим, что следующая героическая модель наиболее соответствует вашим данным:
Доход = 46001 -exp(0.01355*(Возраст-46)**2)
Спорим, что она не вызовет у вашего начальника теплых и нежных чувств. У этого уравнения нет никакого смысла, кроме того, что эта гладкая кривая больше соответствует вашим данным, чем прямая линия. Можно найти еще более экзотичные уравнения, которые будут еще лучше соответствовать данным. Но эти упражнения по поиску наиболее соответствующей кривой не только лишены всякого смысла, но и полученная в результате кривая может подойти чересчур хорошо, внушив ложную уверенность в том, что было совершено некое научное достижение.
Но эти упражнения по поиску наиболее соответствующей кривой не только лишены всякого смысла, но и полученная в результате кривая может подойти чересчур хорошо, внушив ложную уверенность в том, что было совершено некое научное достижение.
Повседневный подвиг
Давайте начнем с того, что такое модель и что ей не является. Модель – это просто набор правил, который позволит вам оттолкнуться от того, что вы уже знаете, и предсказать то, что вы желаете узнать. Возвращаясь к нашей исходной гипотетической проблеме. Вы хотите оттолкнуться от того, что вы уже знаете (возраст), и предсказать то, что вы хотите узнать (доход). Здесь, разумеется, будут возникать ошибки, но вы хотели бы в среднем оказываться правым, при этом постоянно не завышая и не занижая оценку дохода для возрастных диапазонов. Нужен набор правил, который точно описывает отношения между возрастом и доходом, и будет действительно моделью.
Начать вам лучше с составления собственной табличной модели со следующими строчками:
| Возраст | Доход |
|---|---|
| 18-22 | $7,500 |
| 23-33 | $25,000 |
| 34-44 | $38,000 |
| 45-55 | $58,000 |
| 56-60 | $30,000 |
| 61 и больше | $21,000 |
По крайней мере, эта таблица отражает реальность, в которой студенты и пенсионеры в среднем получают меньше остальных. Это может быть не алгебраично и не оптимально, но это модель и, к тому же, хорошая и нелинейная. Существует естественная разница между линейной моделью Дока и вашей прагматичной таблицей. Уравнение Дока «глобально»: это означает, что оно делает оценки для любого возраста от нуля до бесконечности. Если из-за ошибки ввода или программирования, в формулу будет подставлено значение возраста 999, то она радостно определит предполагаемый доход как $971,965. Помните, что многие математические формулы безжалостно проецируются в прекрасное далеко, если в них подставляют значения прогнозирующего параметра абсурдно далекие от их разумных пределов. Не всегда легко найти математические выражения, которые подстраиваются под данные в рамках разумного диапазона.
Это может быть не алгебраично и не оптимально, но это модель и, к тому же, хорошая и нелинейная. Существует естественная разница между линейной моделью Дока и вашей прагматичной таблицей. Уравнение Дока «глобально»: это означает, что оно делает оценки для любого возраста от нуля до бесконечности. Если из-за ошибки ввода или программирования, в формулу будет подставлено значение возраста 999, то она радостно определит предполагаемый доход как $971,965. Помните, что многие математические формулы безжалостно проецируются в прекрасное далеко, если в них подставляют значения прогнозирующего параметра абсурдно далекие от их разумных пределов. Не всегда легко найти математические выражения, которые подстраиваются под данные в рамках разумного диапазона.
Ко всей этой затее с трансформированием есть более практичный подход. Его можно осуществить на основе таблицы, в которой доход для диапазона возрастов 56-60 превосходил бы доход для диапазона 18-22 примерно в четыре раза – лучше или хуже группируя разные диапазоны возрастов и наблюдая, как изменяется средний доход. Такая компьютерная процедура называется локальным сглаживаем. При локальном сглаживании предполагается, что прогнозируя, скажем, доход для 35-, 34- и 36-летних мы получим значение, схожее со значением дохода для 35-летних, и таким образом, это значение будет обладать почти одним с ним весом при округлении. Доходы для 18-летних или 70-летних не будут иметь ничего общего с доходом 35-летних, и поэтому получат нулевой вес при взвешивании. Более разумно использовать компьютер для нахождения этой локальной информации, чем пускаться в охоту за формой (математической функцией), которая по счастливой случайности будет иметь изгибы в нужных местах.
Такая компьютерная процедура называется локальным сглаживаем. При локальном сглаживании предполагается, что прогнозируя, скажем, доход для 35-, 34- и 36-летних мы получим значение, схожее со значением дохода для 35-летних, и таким образом, это значение будет обладать почти одним с ним весом при округлении. Доходы для 18-летних или 70-летних не будут иметь ничего общего с доходом 35-летних, и поэтому получат нулевой вес при взвешивании. Более разумно использовать компьютер для нахождения этой локальной информации, чем пускаться в охоту за формой (математической функцией), которая по счастливой случайности будет иметь изгибы в нужных местах.
Прогнозирующие параметры
Линейная регрессия делает допущение, что прогнозирующие параметры что-то измеряют. Предположим, у нас есть прогнозирующий параметр – семейное положение, и он кодируется так: 1 = состоит в браке, 2 = не состоит в браке, 3 = разведен(а), 4 = вдова(ец). Эти четыре числовых кода ничего не измеряют; они произвольно выбраны, чтобы обозначать категории. Пользователю линейной регрессии приходится обходить эту проблему с помощью создания дополнительных прогнозирующих параметров, называемых вспомогательными переменными. Мы не станем в это углубляться, но рекомендуем вам учесть, что это другой неудобный аспект попытки приспособиться к допущениям линейной регрессии. Мы не завидуем тем, кому приходится иметь дело с дюжиной потенциальных прогнозирующих параметров, которые требуют применения уловки с трансформацией или же со вспомогательными переменными.
Пользователю линейной регрессии приходится обходить эту проблему с помощью создания дополнительных прогнозирующих параметров, называемых вспомогательными переменными. Мы не станем в это углубляться, но рекомендуем вам учесть, что это другой неудобный аспект попытки приспособиться к допущениям линейной регрессии. Мы не завидуем тем, кому приходится иметь дело с дюжиной потенциальных прогнозирующих параметров, которые требуют применения уловки с трансформацией или же со вспомогательными переменными.
Значима ли модель?
В оценке того, насколько модель хороша, только одна вещь имеет значение – насколько хорошо модель делает предположения на основе данных, которых никогда не встречала. Всегда придерживайте некоторые данные в стороне в процессе моделирования как раз на этот случай. Когда значения внешних данных отсортированы от меньшего к большему, очевидна ли разница между возможностями и рисками? Сравнение различий между нижними 10 процентами значений и верхними 10 процентами – это распространенная проверка качества модели. Нет ничего особенного в группировке по десяткам. Общее правило – сделать группы настолько маленькими, насколько возможно, чтобы при этом сохранялась закономерность ступенчатого различия между группами. Если градация сохраняется, а результаты, полученные на основе данных, не входящих в выборку, выглядят хорошо, то модель значима. Точка.
Нет ничего особенного в группировке по десяткам. Общее правило – сделать группы настолько маленькими, насколько возможно, чтобы при этом сохранялась закономерность ступенчатого различия между группами. Если градация сохраняется, а результаты, полученные на основе данных, не входящих в выборку, выглядят хорошо, то модель значима. Точка.
Повседневный семантический смысл слова «значимый» – это «имеющий смысл» или «важный». Статистическое значение слова – это оценка того, является ли отхождение от гипотезы достаточно большим, чтобы обоснованно считаться не случайным. «Значимость» в статистическом смысле не имеет ничего общего с тем, является ли результат хорошим или плохим, а означает, что результат является не случайным.
Охраняя храм
Если вы посмотрите на линейную регрессию с точки зрения математики, то она прекрасна. Если вы взгляните на нее как на инструмент моделирования и оценки, то у нее обнаружится множество недостатков. Чтобы приблизится к математическому храму, вам потребуется жрец, который знает, как манипулировать данными, чтобы они соответствовали линейному канону, говорит о F-тестах и делает такого рода предупреждения (все та же книга):
«…нам следует не забывать тот факт, что финальная модель регрессии может быть применена к клиентскому файлу, содержащему миллионы имен, и что чем сложнее модель, тем больше трудностей она может вызывать у программистов, которые не являются специалистами по статистике и у которых может не оказаться программных инструментов, необходимых для работы с логарифмами и оценки базы данных».
Это невероятное заявление! После всей суеты вокруг модели, может оказаться, что у бедного программиста нет необходимых инструментов, чтобы с ней работать!
Заключение
Можно еще многое сказать о линейной регрессии. В статье представлены наиболее практичные советы, потому что регрессия находится повсюду и обладает такой богатой историей, что она будет использоваться еще долго. Линейная регрессия – это наследие тех дней, когда компьютеров не существовало, и нужен эксперт, чтобы грамотно ей воспользоваться. Это контрпродуктивно и дорого. Программное обеспечение должно помогать людям. Если вы действительно знаете, чего хотите, вы можете выполнить это в компьютерной программе. Современные компьютерно-ориентированные методы могут позаботиться о тех ограничениях линейной регрессии, которые требуют затратных услуг эксперта, вроде выявления аномальных значений, проведения трансформаций и манипуляций с категориями. Когда дело касается предсказаний, они тоже могут выполняться с помощью компьютерных программ, используя в основе данные, использованные при создании модели.
Оригинал статьи www.quirks.com
Перевод статьи Агентство маркетинговых исследований FDFgroup
Почитать еще
Скользкий склон безудержной семантики
Недавняя статья под названием «Спящее будущее визуализации данных? Фотография »расширяет определение визуализации данных до нового предела.
Data mining средства обнаружения данных могут создавать ценность для бизнеса?
Мы живем во время, когда данные вокруг нас. В эпоху цифровых технологий те, кто может выжать
Что такое гипер-персонализация? Преимущества, структура и примеры
Представьте себе сценарий встречи с кем-то много раз: Представьте, что человек узнает ваше имя, ваши
Введение в анализ временных рядов
Хотя для анализа данных используются все многочисленные передовые инструменты и методы, такие как наука о
Визуализация данных и виртуальная реальность
Время от времени кто-то заявляет, что визуализация данных может быть улучшена при просмотре в виртуальной
Структурированные и неструктурированные данные
Из-за всей шумихи вокруг больших данных и способов их использования компаниями вы можете спросить: «Какие
Что может сделать машинное обучение для вашего бизнеса прямо сейчас?
Этим вопросом задается множество бизнес-лидеров, поскольку ежедневно новшества в сфере ИИ и машинного обучения расширяют
История развития моделей данных
Итак, прыгайте на борт и наслаждайтесь путешествиями во времени наших попыток справиться с временностью в
Информационный шум
Чтобы тщательно, точно и четко информировать, мы должны определить предполагаемый сигнал, а затем усилить его,
Читайте о всех решениях
Какие бы задачи перед Вами не стояли, мы сможем предложить лучшие инструменты и решения
Смотреть
Проиграть видео
Презентация аналитической платформы Tibco Spotfire
Проиграть видео
Отличительные особенности Tibco Spotfire 10X
Проиграть видео
Как аналитика данных помогает менеджерам компании
Что такое нелинейная регрессия? Сравнение с линейной регрессией
Уилл Кентон
Полная биография
Уилл Кентон — эксперт в области экономики и инвестиционного законодательства. Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.
Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.
Узнайте о нашем редакционная политика
Обновлено 29 мая, 2022
Рассмотрено
Сомер Андерсон
Рассмотрено Сомер Андерсон
Полная биография
Сомер Дж. Андерсон является дипломированным бухгалтером, доктором бухгалтерского учета и профессором бухгалтерского учета и финансов, который работает в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.
Узнайте о нашем Совет по финансовому обзору
Нелинейная регрессия — это форма регрессионного анализа, в которой данные подгоняются к модели, а затем выражаются в виде математической функции. Простая линейная регрессия связывает две переменные (X и Y) прямой линией (y = mx + b), а нелинейная регрессия связывает две переменные нелинейной (кривой) связью.
Простая линейная регрессия связывает две переменные (X и Y) прямой линией (y = mx + b), а нелинейная регрессия связывает две переменные нелинейной (кривой) связью.
Цель модели — сделать сумму квадратов как можно меньше. Сумма квадратов — это мера, которая отслеживает, насколько сильно наблюдения Y отличаются от нелинейной (кривой) функции, используемой для прогнозирования Y.
Он вычисляется путем нахождения разницы между подобранной нелинейной функцией и каждой точкой Y данных в наборе. Затем каждая из этих разностей возводится в квадрат. Наконец, все квадраты цифр складываются вместе. Чем меньше сумма этих квадратов, тем лучше функция соответствует точкам данных в наборе. Нелинейная регрессия использует логарифмические функции, тригонометрические функции, экспоненциальные функции, степенные функции, кривые Лоренца, функции Гаусса и другие методы подбора.
Ключевые выводы
- Как линейная, так и нелинейная регрессия предсказывают отклики Y от переменной (или переменных) X.

- Нелинейная регрессия представляет собой кривую функцию переменной X (или переменных), которая используется для прогнозирования переменной Y.
- Нелинейная регрессия может показывать прогноз роста населения с течением времени.
Моделирование нелинейной регрессии похоже на моделирование линейной регрессии в том смысле, что оба стремятся графически отследить конкретный ответ от набора переменных. Нелинейные модели сложнее разработать, чем линейные модели, потому что функция создается посредством серии приближений (итераций), которые могут возникать в результате проб и ошибок. Математики используют несколько установленных методов, таких как метод Гаусса-Ньютона и метод Левенберга-Марквардта.
Часто модели регрессии, которые на первый взгляд кажутся нелинейными, на самом деле являются линейными. Процедуру оценки кривой можно использовать для определения характера функциональных взаимосвязей в ваших данных, чтобы вы могли выбрать правильную модель регрессии, линейную или нелинейную. Модели линейной регрессии, хотя они обычно образуют прямую линию, также могут образовывать кривые, в зависимости от формы уравнения линейной регрессии. Точно так же можно использовать алгебру для преобразования нелинейного уравнения, чтобы оно имитировало линейное уравнение — такое нелинейное уравнение называется «внутренне линейным».
Модели линейной регрессии, хотя они обычно образуют прямую линию, также могут образовывать кривые, в зависимости от формы уравнения линейной регрессии. Точно так же можно использовать алгебру для преобразования нелинейного уравнения, чтобы оно имитировало линейное уравнение — такое нелинейное уравнение называется «внутренне линейным».
Линейная регрессия связывает две переменные прямой линией; нелинейная регрессия связывает переменные с помощью кривой.
Одним из примеров использования нелинейной регрессии является прогнозирование роста населения с течением времени. Диаграмма рассеяния изменения данных о населении с течением времени показывает, что связь между временем и ростом населения, по-видимому, существует, но это нелинейная связь, требующая использования модели нелинейной регрессии. Логистическая модель роста населения может предоставить оценки населения за периоды, которые не были измерены, и прогнозы будущего роста населения.
Независимые и зависимые переменные, используемые в нелинейной регрессии, должны быть количественными. Категориальные переменные, такие как регион проживания или религия, должны быть закодированы как бинарные переменные или другие типы количественных переменных.
Категориальные переменные, такие как регион проживания или религия, должны быть закодированы как бинарные переменные или другие типы количественных переменных.
Чтобы получить точные результаты от модели нелинейной регрессии, вы должны убедиться, что указанная вами функция точно описывает взаимосвязь между независимыми и зависимыми переменными. Также необходимы хорошие начальные значения. Плохие начальные значения могут привести к тому, что модель не будет сходиться, или решение будет оптимальным только локально, а не глобально, даже если вы указали правильную функциональную форму для модели.
Источники статей
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем
редакционная политика.
Университет Отаго, Новая Зеландия. «Нелинейный регрессионный анализ».
Определение, принцип работы и расчет
Что такое линия наилучшего соответствия?
Линия наилучшего соответствия относится к линии, проходящей через точечную диаграмму точек данных, которая лучше всего выражает взаимосвязь между этими точками. Статистики обычно используют метод наименьших квадратов (иногда известный как обычный метод наименьших квадратов или OLS), чтобы получить геометрическое уравнение для линии либо путем ручных расчетов, либо с помощью программного обеспечения.
Прямая линия будет результатом простого линейного регрессионного анализа двух или более независимых переменных. Множественная регрессия, включающая несколько связанных переменных, в некоторых случаях может давать кривую линию.
Ключевые выводы
- Линия наилучшего соответствия — это прямая линия, минимизирующая расстояние между ней и некоторыми данными.

- Линия наилучшего соответствия используется для выражения отношения на точечной диаграмме различных точек данных.
- Это результат регрессионного анализа, который можно использовать в качестве инструмента прогнозирования индикаторов и ценовых движений.
- В финансах линия наилучшего соответствия используется для выявления тенденций или корреляций в рыночных доходах между активами или во времени.
Линия наилучшего соответствия
Понимание линии наилучшего соответствия
Линия наилучшего соответствия оценивает прямую линию, которая минимизирует расстояние между собой и местом, где наблюдения попадают в некоторый набор данных. Линия наилучшего соответствия используется для отображения тенденции или корреляции между зависимой переменной и независимой переменной (переменными). Его можно изобразить визуально или в виде математического выражения.
Линия наилучшего соответствия является одним из наиболее важных понятий в регрессионном анализе. Регрессия относится к количественному показателю связи между одной или несколькими независимыми переменными и результирующей зависимой переменной. Регрессия полезна профессионалам в самых разных областях, от науки и государственной службы до финансового анализа.
Регрессия относится к количественному показателю связи между одной или несколькими независимыми переменными и результирующей зависимой переменной. Регрессия полезна профессионалам в самых разных областях, от науки и государственной службы до финансового анализа.
Линия наилучшего соответствия и регрессионного анализа
Чтобы выполнить регрессионный анализ, статистик собирает набор точек данных, каждая из которых включает полный набор зависимых и независимых переменных. Например, зависимой переменной может быть цена акций фирмы, а независимыми переменными могут быть индекс Standard and Poor’s 500 и уровень безработицы в стране, при условии, что акции не котируются в S&P 500. Набором выборки может быть каждая из этих три набора данных за последние 20 лет.
На диаграмме эти точки данных будут отображаться в виде точечной диаграммы, набора точек, которые могут быть организованы, а могут и не располагаться вдоль какой-либо линии. Если линейный узор очевиден, можно нарисовать линию наилучшего соответствия, которая сводит к минимуму расстояние этих точек от этой линии. Если организующая ось не видна визуально, регрессионный анализ может создать линию на основе метода наименьших квадратов. Этот метод строит линию, которая минимизирует квадрат расстояния каждой точки от линии наилучшего соответствия.
Если организующая ось не видна визуально, регрессионный анализ может создать линию на основе метода наименьших квадратов. Этот метод строит линию, которая минимизирует квадрат расстояния каждой точки от линии наилучшего соответствия.
Чтобы определить формулу для этой строки, статистик вводит эти три результата за последние 20 лет в программу регрессии. Программное обеспечение выводит линейную формулу, которая выражает причинно-следственную связь между индексом S&P 500, уровнем безработицы и ценой акций рассматриваемой компании. Это уравнение является формулой для линии наилучшего соответствия. Это инструмент прогнозирования, предоставляющий аналитикам и трейдерам механизм прогнозирования будущей цены акций фирмы на основе этих двух независимых переменных.
Как рассчитать линию наилучшего соответствия
Регрессия с двумя независимыми переменными, такая как рассмотренный выше пример, даст формулу со следующей базовой структурой:
y= c + b 1 (x 1 ) + b 2 (x 2 )
В этом уравнении y — зависимая переменная, c — константа, b 1 — первый коэффициент регрессии, а x 1 — первая независимая переменная.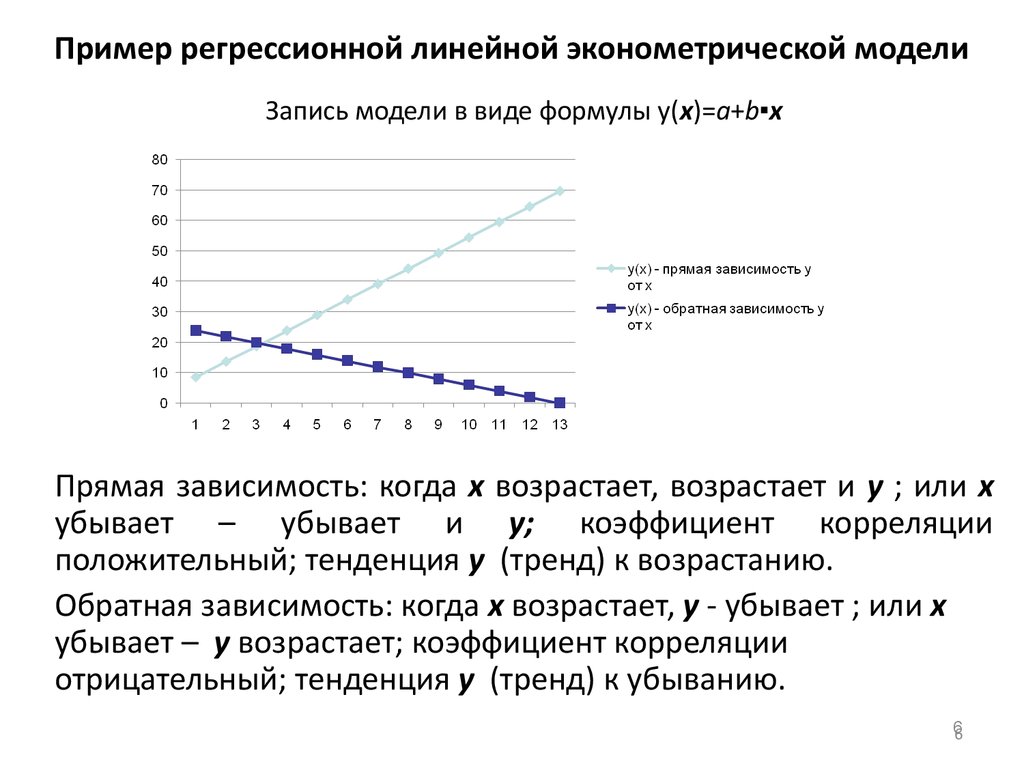 Второй коэффициент и вторая независимая переменная равны b 2 и х 2, соответственно. Исходя из приведенного выше примера, цена акции будет равна y, S&P 500 будет равна x 1 , а уровень безработицы будет равен x 2 . Коэффициент каждой независимой переменной представляет собой степень изменения y для каждой дополнительной единицы этой переменной.
Второй коэффициент и вторая независимая переменная равны b 2 и х 2, соответственно. Исходя из приведенного выше примера, цена акции будет равна y, S&P 500 будет равна x 1 , а уровень безработицы будет равен x 2 . Коэффициент каждой независимой переменной представляет собой степень изменения y для каждой дополнительной единицы этой переменной.
Если S&P 500 увеличится на единицу, результирующая цена y или акции вырастет на величину коэффициента. То же самое верно и для второй независимой переменной, уровня безработицы. В простой регрессии с одной независимой переменной этот коэффициент представляет собой наклон линии наилучшего соответствия. В этом примере или любой регрессии с двумя независимыми переменными наклон представляет собой сочетание двух коэффициентов. Константа c представляет собой точку пересечения оси Y с линией наилучшего соответствия.
Как найти линию наилучшего соответствия?
Существует несколько подходов к оценке линии наилучшего соответствия некоторым данным. Самый простой и грубый способ заключается в том, чтобы визуально оценить такую линию на точечной диаграмме и изобразить ее как можно лучше.
Самый простой и грубый способ заключается в том, чтобы визуально оценить такую линию на точечной диаграмме и изобразить ее как можно лучше.
Более точный метод включает метод наименьших квадратов. Это статистическая процедура для нахождения наилучшего соответствия набору точек данных путем минимизации суммы смещений или невязок точек на построенной кривой. Это основной метод, используемый в регрессионном анализе.
Всегда ли линия наилучшего соответствия прямая?
По определению линия всегда прямая, поэтому линия наилучшего соответствия является линейной. Однако кривая также может использоваться для описания наилучшего соответствия набору данных. Действительно, кривая наилучшего соответствия может быть квадратной (x 2 ), кубической (x 3 ), квадратичной (x 4 ), логарифмической (ln), квадратным корнем (√) или чем-либо еще, что может быть математически описывается уравнением. Обратите внимание, однако, что часто предпочтение отдается более простым объяснениям подгонки.

