Линейная регрессия с примерами на R
Меня давно преследует идея пройтись по ключевым алгоритмам data mining, систематизировать имеющиеся знания и составить некий обзор с примерами. Собственно, этой статьей и ознаменую начало данной серии. Для примеров будет использоваться программная среда R, о которой я уже писал в одном из прошлых постов.Линейная регрессия
Строго говоря, линейная регрессия не является алгоритмом data mining. Это один из методов пришедших из статистики. В статистике, под регрессией, обычно подразумевают прогнозирование, в той или иной форме. Существует множество различных типов регрессий, но в основе любого из них лежит одна и та же идея: построить модель, связывающую предсказываемое значение с исходными данными (предикторами), минимизируя ошибку.Линейная регрессия это простейший вариант регрессии. Рассмотрим, для примера, линейную регрессию с одним предиктором и одним предсказываемым значением. Такую регрессию легко нарисовать на графике X-Y. Для этого по оси абсцисс X мы отмечаем значения предиктора, а по оси ординат Y значения предсказываемой величины. Тогда простая линейная регрессия это прямая, проведенная таким образом, чтобы минимизировать расхождение между истинными значениями предсказываемой величины и точками на линии, соответствующими значениям предикторов.
 На языке математики, мы можем описать нашу линейную модель в виде уравнения: Y = a+b*X, где X – это предиктор или исходные данные, а Y – это предсказываемая величина. А саму задачу переформулировать в виде: найти коэффициенты a и b минимизирующие величину ошибки.
На языке математики, мы можем описать нашу линейную модель в виде уравнения: Y = a+b*X, где X – это предиктор или исходные данные, а Y – это предсказываемая величина. А саму задачу переформулировать в виде: найти коэффициенты a и b минимизирующие величину ошибки. Когда модель построена, а коэффициенты найдены мы можем использовать полученное уравнение для предсказания неизвестных нам значений.
Пример:
Возьмем пример из области финансов. Ни для кого не секрет, что цены акций нефтедобывающих компаний сильно зависят от цен на нефть. В нулевом приближении, мы можем считать чтоЦена Акции = K * Цена барреля нефти + Некая константа
Если мы можем определить константу и коэффициент, то мы можем по цене на нефть предсказывать цену акции. Если возникает отклонение, то можно купить спред и на этом заработать, в теории, естественно.
А теперь практика, возьмем R, и проведем линейную регрессию цен акций компании Роснефть по цене на нефть. Исходные данные можно взять здесь:
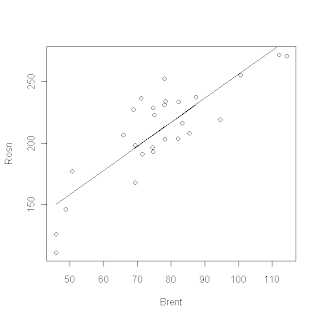
data Результат:На рисунке, интересующие нас коэффициенты, обозначены (1). Подставив их в уравнение регрессии, получим выражение: ROSN = 61.405 + 1.944*Brent Помимо значений, собственно, коэффициентов, R показывает нам величины ошибок, или стандартного отклонения, для каждого коэффициента. Но это не все... Например, нам может быть интересно, объясняют ли вообще хоть что-нибудь наши коэффициенты. Чтобы проверить это, мы, выдвигаем нулевую гипотезу, что, к примеру, коэффициент 61.405 является лишь результатом погрешности и его значением можно пренебречь. Для проверки такой гипотезы, используется t-критерий Стьюдента. Здесь R за нас делает всю работу, вычисляя как саму величину t так и степень значимости нашей гипотезы Pr(>|t|). Так, в нашем случае величина (2) 0.0036 означает что мы на 100*(1-0.0036) = 99.64% уверены в том, что свободный член в нашем выражении отличен от нуля. Далее мы можем проверить, насколько точно наша модель описывает данные. Для этого используются коэффициенты R
2 (3). Чем ближе величина этих значений к 1, тем лучше. 1 это идеальный результат, означающий, что модель на 100% описывает данные. И, наконец, последнее, что мы можем проверить, это то, насколько предсказываемая величина зависит от предикторов. Для этого выдвигается нулевая гипотеза, что предсказываемая величина вообще не зависит от предикторов. Для этой гипотезы определяется p-значение (4). В нашем случае, оно получилось равным 2.65*10^-8. Т.е. мы можем быть уверенны на 99.99999735%, что предсказываемая величина действительно зависит от предикторов. Обычно, имеет смысл смотреть на этот параметр в первую очередь, ведь он определяет, насколько вообще наша модель адекватна. Да, кстати, график чуть выше, как раз показывает наши данные и результат линейной регрессии. Что если мои данные не описываются прямой линией?
Линейная регрессия с одним предиктором это простейший вариант регрессии, на практике возможен целый ряд усложнений позволяющих решать гораздо более сложные задачи: 1) добавление нескольких предикторов – дополнительные предикторы могут добавить в модель больше информации и, тем самым, улучшить результаты. Уравнение линейной регрессии, в таком случае может иметь следующий вид: Y = a + b1*X1 + … bn*Xn 2)предварительное преобразование предикторов - Возведение предикторов в степень либо извлечение корней является одним из способов увеличить возможности линейной регрессии. На практике, нередко приходится проводить большое количество различных преобразований с целью выяснить, какое из них даст наилучшую оценку. 3)в уравнение модели могут быть добавлены члены содержащие произведение предикторов 4)часто возникает задача предсказания вероятности возникновения события. Т.е. предсказываемая величина принимает лишь два значения 1 и 0 или да и нет. Для решения такого рода задач применяется логистическая регрессия. К счастью, все эти и множество других дополнений реализованы в R и готовы к использованию. Информацию о том, как ими пользоваться можно почерпнуть набрав> ?lmв командном интерфейсе R.
www.algorithmist.ru
Множественная линейная регрессия
Пример: множественный регрессионный анализ
Коэффициенты регрессии
Значимость эффектов предиктора
Построчный график выбросов
Расстояния Махаланобиса
Удаленные остатки
Задачей множественной линейной регрессии является построение линейной модели связи между набором непрерывных предикторов и непрерывной зависимой переменной. Часто используется следующее регрессионное уравнение:
(1)
Здесь аi — регрессионные коэффициенты, b0 — свободный член(если он используется), е — член, содержащий ошибку — по поводу него делаются различные предположения, которые, однако, чаще сводятся к нормальности распределения с нулевым вектором мат. ожидания и корреляционной матрицей .
Такой линейной моделью хорошо описываются многие задачи в различных предметных областях, например, экономике, промышленности, медицине. Это происходит потому, что некоторые задачи линейны по своей природе.
Приведем простой пример. Пусть требуется предсказать стоимость прокладки дороги по известным ее параметрам. При этом у нас есть данные о уже проложенных дорогах с указанием протяженности, глубины обсыпки, количества рабочего материала, числе рабочих и так далее.
Ясно, что стоимость дороги в итоге станет равной сумме стоимостей всех этих факторов в отдельности. Потребуется некоторое количество, например, щебня, с известной стоимостью за тонну, некоторое количество асфальта также с известной стоимостью.
Возможно, для прокладки придется вырубать лес, что также приведет к дополнительным затратам. Все это вместе даст стоимость создания дороги.
При этом в модель войдет свободный член, который, например, будет отвечать за организационные расходы (которые примерно одинаковы для всех строительно-монтажных работ данного уровня) или налоговые отчисления.
Ошибка будет включать в себя факторы, которые мы не учли при построении модели (например, погоду при строительстве — ее вообще учесть невозможно).
Пример: множественный регрессионный анализ
Для этого примера будут анализироваться несколько возможных корреляций уровня бедности и степень, которая предсказывает процент семей, находящихся за чертой бедности. Следовательно мы будем считать переменную характерезующую процент семей, находящихся за чертой бедности, — зависимой переменной, а остальные переменные непрерывными предикторами.
Коэффициенты регрессии
Чтобы узнать, какая из независимых переменных делает больший вклад в предсказание уровня бедности, изучим стандартизованные коэффициенты (или Бета) регрессии.
Рис. 1. Оценки параметров коэффициентов регрессии.
Коэффициенты Бета это коэффициенты, которые вы бы получили, если бы привели все переменные к среднему 0 и стандартному отклонению 1. Следовательно величина этих Бета коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в зависимую переменную. Как видно из Таблицы, показанной выше, переменные изменения населения с 1960 года (POP_ CHING), процент населения, проживающего в деревне (PT_RURAL) и число людей, занятых в сельском хозяйстве (N_Empld) являются самыми главными предикторами уровня бедности, т.к. только они статистически значимы (их 95% доверительный интервал не включает в себя 0). Коэффициент регрессии изменения населения с 1960 года (Pop_Chng) отрицательный, следовательно, чем меньше возрастает численность населения, тем больше семей, которые живут за чертой бедности в соответствующем округе. Коэффициент регрессии для населения (%), проживающего в деревне (Pt_Rural) положительный, т.е., чем больше процент сельских жителей, тем больше уровень бедности.
Значимость эффектов предиктора
Просмотрим Таблицу с критериями значимости.
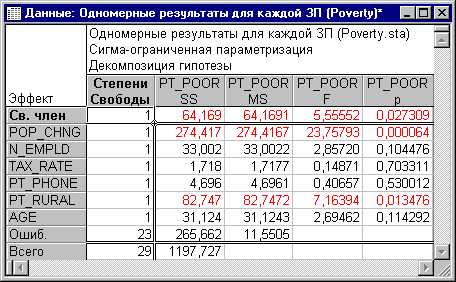
Рис. 2. Одновременные результаты для каждой заданной переменной.
Как показывает эта Таблица, статистически значимы только эффекты 2 переменных: изменение населения с 1960 года (Pop_Chng) и процент населения, проживающего в деревне (Pt_Rural), p < .05.
Анализ остатков. После подгонки уравнения регрессии, почти всегда нужно проверять предсказанные значения и остатки. Например, большие выбросы могут сильно исказить результаты и привести к ошибочным выводам.
Построчный график выбросов
Обычно необходимо проверять исходные или стандартизованные остатки на большие выбросы.
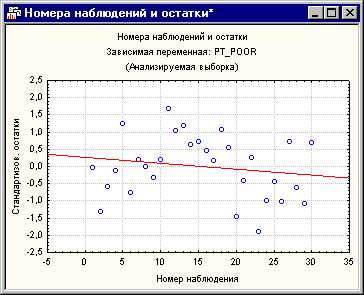
Рис. 3. Номера наблюдений и остатки.
Шкала вертикальной оси этого графика отложена по величине сигма, т.е., стандартного отклонения остатков. Если одно или несколько наблюдений не попадают в интервал ± 3 умноженное на сигма, то, возможно, стоит исключить эти наблюдения (это можно легко сделать через условия выбора наблюдений) и еще раз запустить анализ, чтобы убедится, что результаты не изменяются этими выбросами.
Расстояния Махаланобиса
Большинство статистических учебников уделяют много времени выбросам и остаткам относительно зависимой переменной. Тем не менее роль выбросов в предикторах часто остается не выявленной. На стороне переменной предиктора имеется список переменных, которые участвуют с различными весами (коэффициенты регрессии) в предсказании зависимой переменной. Можно считать независимые переменные многомерным пространством, в котором можно отложить любое наблюдение. Например, если у вас есть две независимых переменных с равными коэффициентами регрессии, то можно было бы построить диаграмму рассеяния этих двух переменных и поместить каждое наблюдение на этот график. Потом можно было отметить на этом графике среднее значение и вычислить расстояния от каждого наблюдения до этого среднего (так называемый центр тяжести) в двумерном пространстве. В этом и заключается основная идея вычисления расстояния Махаланобиса. Теперь посмотрим на гистограмму переменной изменения населения с 1960 года.
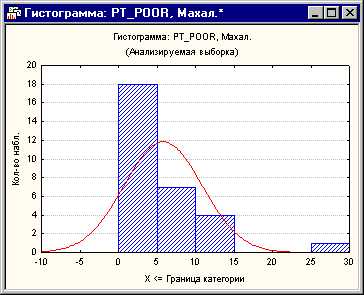
Рис. 4. Гистограмма распределения расстояний Махаланобиса.
Из графика следует, что есть один выброс на расстояниях Махаланобиса.
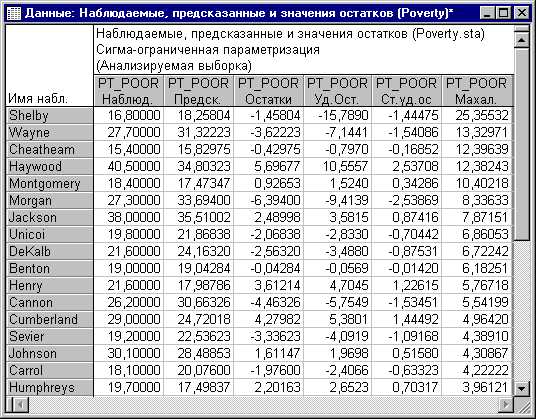
Рис. 5. Наблюдаемые, предсказанные и значения остатков.
Обратите внимание на то, что округ Shelby (в первой строке) выделяется на фоне остальных округов. Если посмотреть на исходные данные, то вы обнаружите, что в действительности округ Shelby имеет самое большое число людей, занятых в сельском хозяйстве (переменная N_Empld). Возможно, было бы разумным выразить в процентах, а не в абсолютных числах, и в этом случае расстояние Махаланобиса округа Shelby, вероятно, не будет таким большим на фоне других округов. Очевидно, что округ Shelby является выбросом.
Удаленные остатки
Другой очень важной статистикой, которая позволяет оценить серьезность проблемы выбросов, являются удаленные остатки. Это стандартизованные остатки для соответствующих наблюдений, которые получаются при удалении этого наблюдения из анализа. Помните, что процедура множественной регрессии подгоняет поверхность регрессии таким образом, чтобы показать взаимосвязь между зависимой и переменной и предиктором. Если одно наблюдение является выбросом (как округ Shelby), то существует тенденция к «оттягиванию» поверхности регрессии к этому выбросу. В результате, если соответствующее наблюдение удалить, будет получена другая поверхность (и Бета коэффициенты). Следовательно, если удаленные остатки очень сильно отличаются от стандартизованных остатков, то у вас будет повод считать, что регрессионный анализа серьезно искажен соответствующим наблюдением. В этом примере удаленные остатки для округа Shelby показывают, что это выброс, который серьезно искажает анализ. На диаграмме рассеяния явно виден выброс.
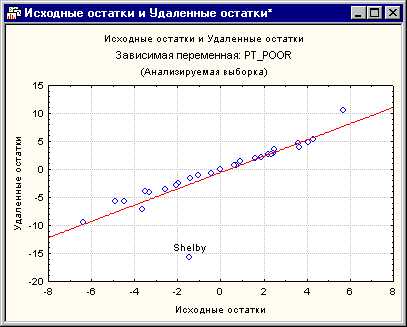
Рис. 6. Исходные остатки и Удаленные остатки переменной, означающей процент семей, проживающих ниже прожиточного минимума.
Большинство из них имеет более или менее ясные интерпретации, тем не менее обратимся к нормальным вероятностным графикам.
Как уже было упомянуто, множественная регрессия предполагает, что существует линейная взаимосвязь между переменными в уравнении и нормальное распределение остатков. Если эти предположения нарушены, то вывод может оказаться неточным. Нормальный вероятностный график остатков укажет вам, имеются ли серьезные нарушения этих предположений или нет.
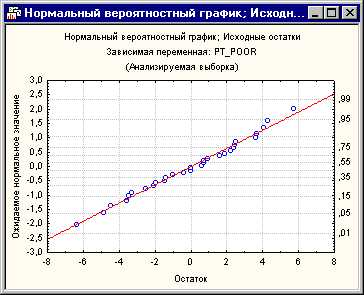
Рис. 7. Нормальный вероятностный график; Исходные остатки.
Этот график был построен следующим образом. Вначале стандартизованные остатки ранжируюся по порядку. По этим рангам можно вычислить z значения (т.е. стандартные значения нормального распределения) на основе предположения, что данные подчиняются нормальному распределению. Эти z значения откладываются по оси y на графике.
Если наблюдаемые остатки (откладываемые по оси x) нормально распределены, то все значения легли бы на прямую линию на графике. На нашем графике все точки лежат очень близко относительно кривой. Если остатки не являются нормально распределенными, то они отклоняются от этой линии. Выбросы также становятся заметными на этом графике.
Если имеется потеря согласия и кажется, что данные образуют явную кривую (например, в форме буквы S) относительно линии, то зависимую переменную можно преобразовать некоторым способом (например, логарифмическое преобразование для «уменьшения» хвоста распределения и т.д.). Обсуждение этого метода находится за пределами этого примера (Neter, Wasserman, и Kutner, 1985, pp. 134-141, представлено обсуждение преобразований, убирающих ненормальность и нелинейность данных). Однако исследователи очень часто просто проводят анализ напрямую без проверки соответствующих предположений, что ведет к ошибочным выводам.
Связанные определения:
Линейная регрессия
Матрица плана
Общая линейная модель
Регрессия
В начало
Содержание портала
statistica.ru
Простая линейная регрессия
16.1 Простая линейная регрессия
Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze… (Анализ) ► Regression… (Регрессия). Откроется соответствующее подменю.
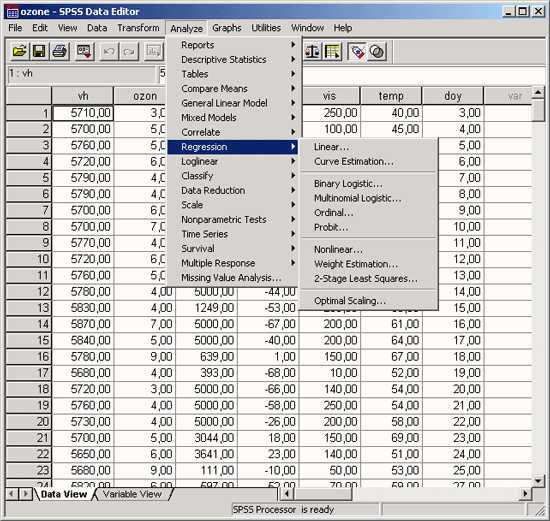
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
При изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим пример из раздела корреляционный анализ с зависимостью показателя холестерина спустя один месяц после начала лечения от исходного показателя. Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей, явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.
у = b • х + а,
где b — регрессионные коэффициенты, a — смещение по оси ординат (OY).
Смещение по оси ординат соответствует точке на оси Y (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение:
b = tg(a) — указывает на угол наклона прямой.
При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.
Если мы рассмотрим показатель холестерина через один месяц (переменная chol1) как зависимую переменную (у), а исходную величину как независимую переменную (х),
то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения:
chol1 = b • chol0 + a
После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.
Расчёт уравнения регрессии
Откройте файл hyper.sav.
Выберите в меню Analyze… (Анализ) ► Regression…(Регрессия) ► Linear… (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия).
Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.
Ничего больше не меняя, начните расчёт нажатием ОК.
Рис.16.2: Диалоговое окно Линейная регрессия
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
| Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Скорректир. R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
| 1 | ,861а | ,741 | ,740 | 25,26 |
а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
ANOVA b
| Model (Модель) | Sum of Squares (Сумма Квадратов) | df | Mean Square (Среднее значение квадрата) | F | Sig. (Значимость) | |
| 1 | Regression (Регрессия) | 314337,948 | 1 | 314337,9 | 492,722 | ,000a |
| Residual (Остатки) | 109729,408 | 172 | 637,962 | |||
| Total (Сумма) | 424067,356 | 173 |
a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина).
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
Coefficients (Коэффициенты) а
| Model (Модель) | Unstandardized Coefficients (Не стандартизированные коэффициенты) | Standardized Coefficients (Стандартизированные коэффициенты) | t | Sig. (Значимость) | ||
| B | Std: Error (Станд. ошибка) | ß (Beta) | ||||
| 1 | (Constant) (Константа) | 34,546 | 9,416 | 3,669 | ,000 | |
| Cholesterin, Ausgangswert | ,863 | ,039 | ,861 | 22,197 | ,000 | |
a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем «константа». То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0,863 • chol0 + 34,546
Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента ß будет рассмотрено при изучении многомерного анализа.
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется «коэфициентом детерминации». В таблице результатов это частное выводится под именем «R-квадрат». В нашем примере мера определённости равна:
314337,948 / 424067,356 = 0,741
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый «R», равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэфициент детерминации. Величина «Cмещенный R-квадрат» всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots…(Графики) зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.
Сохранение новых переменных
Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.
Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить). Откроется диалоговое окно Linear Regression: Save (Линейная регрессия: Сохранение) как изображено на рисунке 16.3.

Рис. 16.3: Диалоговое окно Линейная регрессия: Сохранение
Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values (Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии. При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того, рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.
Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения).
Подтвердите нажатием Continue (Далее) и в заключение ОК.
В редакторе данных будет образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1, возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от реального показателя содержания холестерина, взятого через один месяц (chol1) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1, так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.
Если мы в уравнение регрессии:
chol1 = 0,863 • chol0 + 34,546
подставим исходное значение для chol0 (265), то получим: chol1 = 0,863 • 265 + 34,546 = 263,241
Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов.
Добавьте для этого в конец файла hyper.sav, ещё два случая, используя фиктивные значения для переменной chol0. Пусть к примеру, это будут значения 282 и 314.
Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1.
В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 — значение 305,37620.
Построение регрессионной прямой
Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:
Выберите в меню следующие опции Graphs … (Графики) / Scatter plots… / Диаграммы рассеяния. Откроется диалоговое окно Scatter plots… (Диаграмма рассеяния) — (рис. 16.4).
В диалоговом окне Scatter plots…(Диаграмма рассеяния) оставьте предварительную установку Simple (Простая) и щёлкните на кнопке Define (Определить). Откроется диалоговое окно Simple Scatter plot (Простая диаграмма рассеяния) (рис. 16.5).
Перенесите переменную chol1 в поле оси Y, а переменную chol0 в поле оси X.
Подтвердите щелчком на ОК. В окне просмотра результатов появится диаграмма рассеяния (рис. 16.6).
Щёлкните дважды на этом графике, чтобы перенести его в редактор диаграмм.
Выберите в редакторе диаграмм меню Chart… (Диаграмма) / Options… (Опции). Откроется диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния) (рис. 16.7).
В рубрике Fit Line (Приближенная кривая) поставьте флажок напротив опции Total (Целиком для всего файла данных) и щёлкните на кнопке Fit Options (Опции для приближения). Откроется диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния: приближенная кривая) (см. рис. 16.8).
Подтвердите предварительную установку Linear Regression (Линейная регрессия) щелчком Continue (Далее) и затем на ОК.
Закройте редактор диаграмм и щёлкните один раз где-нибудь вне графика. Теперь в диаграмме рассеяния отображается регрессионная прямая (рис. 16.9).
Рис. 16.4: Диалоговое окно Scatter plots… (Диаграмма рассеяния)
Рис. 16.5: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния).
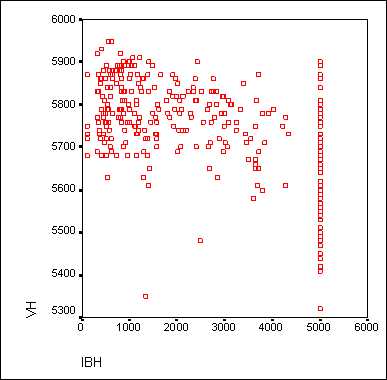
Рис. 16.6: Диаграмма рассеяния в окне просмотра
Рис. 16.7: Диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния)

Рис. 16.8: Диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния:

Рис. 16.9: Диаграмма рассеяния с регрессионной прямой
Выбор осей
Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день, а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее, постройте диаграмму рассеяния с внедрённой регрессионной прямой.
В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum — в поле оси X. После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.
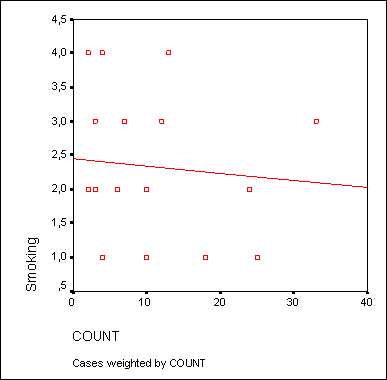
Рис. 16.10: Диаграмма рассеяния с регрессионной прямой до коррекции осей
Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому эту ось необходимо откорректировать.
Дважды щёлкните на графике и в меню редактора диаграмм вберите опции Chart… (Диаграмма) / Axis… (Оси). Откроется диалоговое окно Axis Selection (Выбор оси) (рис. 16.11).
Подтвердите предварительный выбор оси X нажатием кнопки ОК. Откроется диалоговое окно X-Scale Axis (Ось X) (рис. 16.12).
В редактируемом поле Displayed (Отображаемый) в рубрике Range (Диапазон) измените минимальное значение на 0.
Подтвердите нажатием на ОК.
Выберите вновь в меню редактора диаграмм опции Chart… (Диаграмма* Axis… (Оси)
Активируйте в диалоговом окне Axis Selection (Выбор оси) опцию Y Scale (Ось Y). Откроется диалоговое окно Y-Scale Axis (Ось Y).
И здесь в рубрике Range (Диапазон) в редактируемом поле Displayed (Отображаемый) измените минимальное значение на «0».
Подтвердите нажатием на ОК.
Рис. 16.11: Диалоговое окно Axis Selection (Выбор оси)
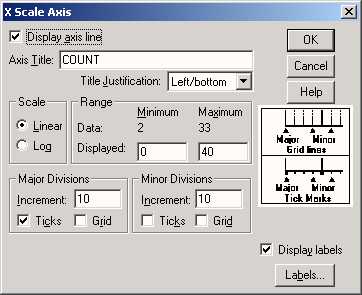
Рис. 16.12: Диалоговое окно X-Scale Axis (Ось X)
В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).
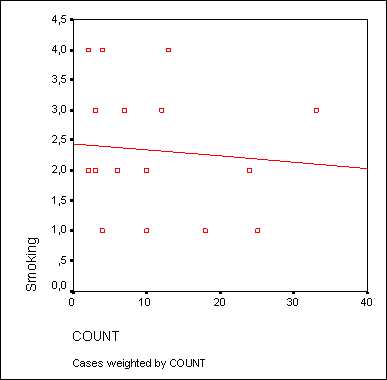
Рис. 16.13: Диаграмма рассеяния с регрессионной прямой после корректировки осей
На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:
Coefficients (Коэффициенты)а
| Model (Модель) | Unstandardized Coefficients (Не стандартизированные коэффициенты) | Standardized Coefficients (Стандартизированные коэффициенты) | t | Sig. (Значимость) | ||
| B | Std: Error (Станд. ошибка) | ß (Beta) | ||||
| 1 | (Constant) (Константа) | 2,871 | ,639 | 4,492 | ,002 | |
| tgl. Zigarettenkonsum | ,145 | ,038 | ,804 | 3,829 | ,005 | |
a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)
Что дает следующее уравнение регрессии:
puls = 0,145 • konsum + 2,871
Константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.
www.datuapstrade.lv
 На рисунке, интересующие нас коэффициенты, обозначены (1). Подставив их в уравнение регрессии, получим выражение:
ROSN = 61.405 + 1.944*Brent
Помимо значений, собственно, коэффициентов, R показывает нам величины ошибок, или стандартного отклонения, для каждого коэффициента. Но это не все...
Например, нам может быть интересно, объясняют ли вообще хоть что-нибудь наши коэффициенты. Чтобы проверить это, мы, выдвигаем нулевую гипотезу, что, к примеру, коэффициент 61.405 является лишь результатом погрешности и его значением можно пренебречь. Для проверки такой гипотезы, используется t-критерий Стьюдента. Здесь R за нас делает всю работу, вычисляя как саму величину t так и степень значимости нашей гипотезы Pr(>|t|). Так, в нашем случае величина (2) 0.0036 означает что мы на 100*(1-0.0036) = 99.64% уверены в том, что свободный член в нашем выражении отличен от нуля.
Далее мы можем проверить, насколько точно наша модель описывает данные. Для этого используются коэффициенты R
На рисунке, интересующие нас коэффициенты, обозначены (1). Подставив их в уравнение регрессии, получим выражение:
ROSN = 61.405 + 1.944*Brent
Помимо значений, собственно, коэффициентов, R показывает нам величины ошибок, или стандартного отклонения, для каждого коэффициента. Но это не все...
Например, нам может быть интересно, объясняют ли вообще хоть что-нибудь наши коэффициенты. Чтобы проверить это, мы, выдвигаем нулевую гипотезу, что, к примеру, коэффициент 61.405 является лишь результатом погрешности и его значением можно пренебречь. Для проверки такой гипотезы, используется t-критерий Стьюдента. Здесь R за нас делает всю работу, вычисляя как саму величину t так и степень значимости нашей гипотезы Pr(>|t|). Так, в нашем случае величина (2) 0.0036 означает что мы на 100*(1-0.0036) = 99.64% уверены в том, что свободный член в нашем выражении отличен от нуля.
Далее мы можем проверить, насколько точно наша модель описывает данные. Для этого используются коэффициенты R