Метод проб и ошибок
Метод проб и ошибок
в решении текстовых задач.
При решении текстовых задач многие учащиеся испытывают затруднения. Главная задача учителя научить решать ученика различные типы текстовых задач. Процесс решения текстовых задач развивает у учащихся логическое мышление, учат находить выход из проблем реальной жизни, дает почувствовать уверенность в своих силах.
Текстовые задачи можно разбить на два основных класса:
Причем это разделение довольно условно. Многие текстовые арифметические задачи можно решить с помощью уравнений, а задачи на составление уравнений (систем уравнений) часто решают по действиям, а если это не получается, то используют метод проб и ошибок или метод перебора.
Мне бы хотелось продемонстрировать решение ряда задач этими методами.
Задача №1
Одна сторона прямоугольного участка земли на 3 м больше другой его стороны. Площадь участка равна 70 м².
Найти размеры этого участка.
Пусть x м ширина участка, (x+3) м – длина участка, а площадь x·(x+3) м²,
что по условию задачи равно 70 м². Чтобы найти размеры участка надо составить уравнение x·(x+3)=70 и решить его. Но в 5ом классе такие учащиеся решать еще не могут. Поэтому попробуем подобрать решение «экспериментально», так называемым методом проб и ошибок.
пусть x=4, т.е. 4·(4+3)=28, 28≠70;
x=6, т.е. 6·(6+3)=54, 54≠70;
x=7, т.е. 7·(7+3)=70, 70=70 верно.
Т.е. мы увидели, что метод проб и ошибок позволяет найти ответ даже в случае, когда математический модель представляет собой новый, не изученный еще объект. Но, решая задачи этим способом, следует помнить, что подбор одного решения не гарантирует полноты решения. Поэтому необходимы обоснования того, что найдены все возможные решения.
В нашей задаче, если бы x было больше 7,то x+310 и x·(x+3)70, если наоборот xx+3 x·(x+3)
Задачи для учащихся.
Переведи условие задачи на математический язык и найди решение методом проб и ошибок.
Площадь прямоугольника равна 68 дм², а длина больше ширины на 13 дм. Каковы стороны этого прямоугольника?
Ширина прямоугольника на 9 см меньше длины, а площадь равна 90 см². Найти стороны прямоугольника.
Найти периметр прямоугольника, площадь которого составляет 18 м², а ширина в 2 раза меньше длины.
Площадь прямоугольника равна 64 дм², а его длина в 4 раза больше ширины. Чему равен периметр прямоугольника?
Длину прямоугольника уменьшили на 3 см, а ширину увеличили на 4 см и получили квадрат. Найти сторону квадрата, если площадь прямоугольника равна 30 см².
После того как ширину прямоугольника увеличили на 1 м, а длину уменьшили на 5 м, получили квадрат. Чему равна площадь квадрата, если площадь прямоугольника 91 м².
Длина прямоугольника на 5 м больше ширины, а площадь составляет 24 м².
каковы стороны этого прямоугольника?Длину прямоугольника уменьшили в 2 раза, а ширину увеличили на 1 дм и получили квадрат. Найти сторону квадрата, если площадь прямоугольника 60 дм².
Найти периметр прямоугольника, у которого ширина на 4 см меньше длины, а площадь составляет 32 см².
каковы стороны этого прямоугольника?10)Одна из сторон прямоугольника на 20 см больше другой. Если
большую сторону уменьшить в 3 раза, а меньшую сторону увеличить
в 2 раза, то площадь нового прямоугольника будет равна 200 см².
Найти стороны данного прямоугольника.
Метод перебора при
нахождении НОД.
Рассмотрим еще один метод – метод перебора. Т.к. предыдущий метод решения задач – метод проб и ошибок не дает уверенности в том, что найдены все искомые значения. Поэтому для обоснования полноты решения требуются дополнительные, иногда очень непростые рассуждения. В этом недостаток метода проб и ошибок. Но он исключен в методе полного перебора.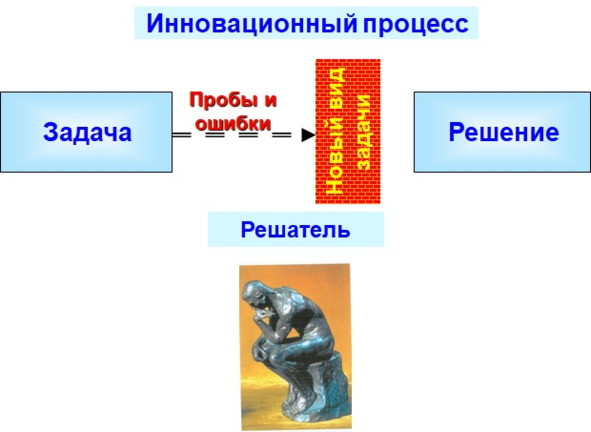
Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем «лобовой» перебор.
Задача. На экскурсию едут 252 ученика школы. Для них заказаны
несколько автобусов. Однако выяснилось, что если заказать
автобусы, вмещающие на 6 человек больше, то автобусов
потребуется на один меньше. Сколько больших автобусов надо
заказать?
Составим таблицу.
Кол-во детей в одном автобусе | Количество автобусов | Общее кол-во детей | |
Большие автобусы | 252 : x | x | 252 |
Маленькие автобусы | 252 : (x+1) | x+1 | 252 |
Т.
к. по условию в большой автобус вмещается на 6 детей больше, чем в маленький, то разность 252 : x — 252 : (x+1) = 6. Значит решением задачи является число X, удовлетворяющее равенству: 252 : x — 252 : (x+1) = 6.
Но можно получить более простую математическую модель этой задачи, обозначив дополнительно буквой Y число детей, которых можно разместить в большом автобусе.
Кол-во детей в одном автобусе | Количество автобусов | Общее кол-во детей | |
Большие автобусы | y | x | 252 |
Маленькие автобусы | y-6 | x+1 | 252 |
Очевидно, что в этом случае математической моделью задачи являются два равенства:
xy = 252;
(x+1)·(y-6) = 252.
Искомые числа x и y должны удовлетворять как первому, так и
второму равенству. Найдем эти числа x и y.
Из равенства xy = 252 можно заметить, что числа x и y не могут быть
больше, чем 252. Однако и в этом случае «лобовой» перебор потребовал бы рассмотрения огромного числа вариантов. Но более внимательный анализ первого равенства показывает, что числа x и y – это парные делители 252: при делении 252 на x получается y, и наоборот. Следовательно, достаточно рассмотреть лишь парные делители числа 252, причем для случая, когда y6 (y-60).
Составим таблицу:
+1
x | 1 | 2 | 3 | 4 | 6 | 7 | 9 | 14 | 18 | 28 | 36 |
y | 252 | 126 | 84 | 63 | 42 | 36 | 28 | 18 | 14 | 9 | 7 |
— 6
Анализ второго равенства позволяет еще больше сократить число возможных вариантов.
Оно означает, что число (x+1) и (y-6) так же являются парными делителями 252. Из таблицы видно, что такими свойствами обладает только пара x=6, y=42.
Ответ: для экскурсии надо заказать 6 больших автобусов.
Задачи для учащихся.
Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 меньше исходного. Найти эти числа.
Сумма цифр двузначного числа равна 12. число, записанное теми же цифрами, но в обратном порядке, составляет 4 /7 исходного числа. Найти эти числа.
Одно из двух натуральных чисел на 4 больше другого. Найди эти числа, если их произведение равно 96.
У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и трехместных лодок было у причала?
Прямоугольный газон обнесен изгородью, длинна которой 30 м.
Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.В несколько посылок упаковали 36 книг и 54 журнала, распределив их между посылками поровну. В каждой посылке книг на 2 меньше, чем журналов. Сколько получилось посылок?
Произведение двух натуральных чисел равно 72. Найти эти числа, если одно из них больше другого на 6.
На турбазе имеются палатки и домики, общее число которых равно 25. в каждом домике живут 4 человека, а в палатке – 2 человека. Сколько на турбазе палаток и сколько домиков, если всего на этой турбазе отдыхают 70 человек?
Прямоугольный участок земли обнесен забором, длина которого 40 м. Площадь участка 96 м². Найти длины сторон этого участка, если известно, что они выражаются натуральными числами.
Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.Еще один тип задач, которые решаются методом перебора.
Задумано двузначное число, которое на 52 больше произведения своих цифр. Какое число задумано?
Пусть xy – задуманное двузначное число, где x – цифра десятков, а y – цифра единиц.
Тогда их произведение равно xy. Само двузначное число можно записать как 10x+y. По условию 10x+y на 52 больше произведения своих цифр xy. Т.е. должно выполняться равенство 10x+y= xy+52, которое является математической моделью данной задачи.
Решается это уравнение методом перебора. Полный перебор можно провести, рассматривая последовательно все значения x от 1 до 9 и подбирая в каждом случае соответствующее значение y от 0 до 9.
Однако этот перебор можно сократить, если заметить, что первая часть данного равенства больше 52. Значит, и первая его часть, т.е. задуманное число, больше 52. Поэтому неизвестное число x не меньше 5, и можно рассматривать только пять значений x – от 5 до 9.
При x=5 будем иметь равенство 50+y=5y+52, оно невозможно, т.к. 50+yy+52.
При x=6 60+y=6y+52 | -y
60=5y+52
5y=8 невозможно для натурального y.
При x=7 70+y=7y+52
70=6y+52
6y=18
y=3 Число 73
При x=8 80+y=8y+52
80=7y+52
7y=28
y=4 Число 87
При x=9 90+y=9y+52
38=8y невозможно
Таким образом, задумано либо 73, либо 84.
Условие задачи не дает возможности ответить на этот вопрос. Поэтому два ответа: 73 или 84.
Задачи для учащихся.
Метод перебора используется при доказательстве общих утверждений, где необходимо вводить буквенные обозначения.
Например: Доказать, что сумма любых трех последовательных натуральных чисел делится на 3.
1 сл. 1,2,3 1+2+3=6, 6:3=2
2 сл. 5,6,7 5+6+7=18, 18:3=6
3 сл. 21,22,23 21+22+23=66 66:3=22
и т.д.
Возьмем произведение натурального числа и обозначим его n. Тогда следующие за ним два числа соответственно равны n+1 и n+2.
Их сумма: n+(n+1)+(n+2)=3n+3=3(n+1) делится на 3, т.к. один из множителей делится на 3.
Метод проб и ошибок: достоинства и недостатки
Человечество берет свое начало несколько тысяч лет назад. И на протяжении всего этого времени оно неустанно развивается. Причин на это было всегда много, но без изобретательности человека это просто не представлялось бы возможным.
Метод проб и ошибок был и является в настоящее время одним из основных.
Описание способа
Четко зафиксированного в исторических документах применения данного метода мало. Но, несмотря на это, он заслуживает особого внимания.
Метод проб и ошибок – это способ, при котором решение задачи достигается подбором вариантов до тех пор, пока результат не станет правильным (например, в математике) или приемлемым (при изобретении новых методов в науке).
Человечество всегда пользовалось данным методом. Ориентировочно век назад психологи пытались найти общее между людьми, которые использовали данный способ познания. И им это удалось. Человек, который ищет ответ на поставленную задачу, вынужден подбирать варианты, ставить эксперименты и смотреть на результат. Это продолжается до тех пор, пока не приходит озарение по данному вопросу. Экспериментатор выходит на новую ступень мышления в данном вопросе.
Методы решения проблем: обзор способов и рекомендации
Различные методы решения проблем направлены на преодоление трудностей в учебной, социальной,.
..
Метод в мировой истории
Одним из самых известных людей, кто применял данный способ, был Эдисон. Все знают его историю изобретения лампочки. Он экспериментировал до тех пор, пока не получилось. Но Эдисон усовершенствовал данный метод. При поиске решения он разделял задачи между людьми, которые работали на него. Соответственно материала по теме получалось намного больше, чем при работе одного человека. И на основании полученных данных метод проб и ошибок имел большой успех в деятельности Эдисона. Благодаря этому человеку появились исследовательские институты, которые применяют, в том числе, и этот метод.
Степени трудности
У данного метода есть несколько уровней сложности. Они были так разделены для лучшего усвоения. Задача первого уровня считается легкой, и на поиск ее решения затрачивается немного сил. Но и вариантов ответов она имеет не так много. С повышением степени трудности растет и сложность поставленной задачи. Метод проб и ошибок 5 класса – самый труднорешаемый и затратный по времени.
Методика Счет по Крепелину: краткое описание и…
Методика «Счет по Крепелину» очень известна, востребована и информативна для…
Необходимо учитывать, что при возрастании уровня сложности растет и объем знаний, которыми обладает человек. Чтобы лучше понимать, о чем идет речь, рассмотрим технику. Первый и второй уровни позволяют изобретателям ее усовершенствовать. На последней ступени сложности создается совершенно новый продукт.
Например, известен случай, когда молодые люди темой дипломной работы взяли труднорешаемую задачу из аэронавигации. Студенты не обладали такими же знаниями, как многие ученые, которые работали в данной области, но благодаря широкому спектру знаний ребят у них получилось найти ответ. И причем область решения оказалась в самом далеком от науки кондитерском деле. Казалось бы, что это невозможно, но это факт. Молодым людям было даже выдано авторское свидетельство на их изобретение.
Преимущества метода
Первым достоинством можно по праву считать творческий подход.
Задачи методом проб и ошибок решаемые позволяют задействовать оба полушария головного мозга для поиска ответа.
Стоит привести в пример, как строились лодки. Раскопки показывают, как на протяжении столетий деталь за деталью менялась форма. Исследователи постоянно пробовали что-то новое. Если лодка тонула, то эту форму вычеркивали, если оставалась держаться на воде, то принимали это к сведению. Таким образом, в итоге было найдено компромиссное решение.
Методы отбора проб: правила, методика, основные показатели
Отбор проб является важнейшей составляющей качественно проведенного анализа взятых для исследования…
Если поставленная задача не слишком сложная, то данный метод занимает немного времени. У некоторых возникающих проблем может быть десять вариантов, один или два из которых окажутся правильными. Но если рассматривать, например, робототехнику, то в данном случае без применения других методов исследования могут затянуться на десятки лет и принесут миллионы вариантов.
Разделение задач на несколько уровней позволяет оценить, насколько быстрым и возможным представляется поиск решения. Это сокращает время для принятия решения. И при сложных задачах можно использовать метод проб и ошибок параллельно с другими.
Недостатки метода
С развитием технологий и науки данный метод начал терять свою популярность.
В некоторых областях просто нерационально создавать тысячи образцов, чтобы менять по одному элементу. Поэтому зачастую теперь используют другие методы, основанные на конкретных знаниях. Для этого стали изучаться природа вещей, взаимодействие элементов друг с другом. Стали использоваться математические расчеты, научные обоснования, эксперименты и опыт прошлого.
Метод проб и ошибок все так же отлично используется в творчестве. Но строить автомобиль таким способом уже кажется глупым и неактуальным. Поэтому теперь, при нынешнем уровне развития цивилизации, нужно в точных науках по большей части использовать другие методы.
Часто при рассматриваемом способе задача может описывать много совершенно незначительных вещей и не учитывать априори важные вещи. Например, изобретатель пенициллина (антибиотик) утверждал, что при правильном подходе лекарство могли изобрести лет на двадцать раньше его. Это поспособствовало бы спасению огромного количества жизней.
При сложных задачах часто бывают ситуации, когда сам вопрос лежит в одной области знаний, а его решение — совершенно в другой.
Не всегда исследователь уверен, что ответ вообще будет найден.
Автор метода проб и ошибок
Кто конкретно изобрел это способ познания, мы никогда не узнаем. Точнее мы знаем, что это явно был изобретательный человек, которым, скорее всего, руководило желание улучшить свою жизнь.
В древности люди были достаточно ограничены во многих вещах. Все изобреталось именно этим методом. Тогда еще не было каких-то фундаментальных знаний в области физики, математики, химии и прочих важных наук. Поэтому приходилось действовать наугад.
Именно так добыли огонь, чтобы защищаться от хищников, готовить пищу и обогревать жилище. Оружие, чтобы добывать пропитание, лодки — для передвижения по рекам. Все было изобретено при столкновении человека с трудностью. Но каждый раз решаемая проблема приводила к более качественному уровню жизни.
Известно, что многие ученые использовали этот метод в своих трудах.
Однако именно описание метода и активное использование мы наблюдаем у физиолога Торндайка в конце девятнадцатого века.
Исследования Торндайка
Пример метода проб и ошибок можно рассмотреть в научных трудах ученого-физиолога. Он ставил различные поведенческие эксперименты с животными, помещая их в специальные коробки.
Один из экспериментов выглядел приблизительно следующим образом. Кошка, помещенная в ящик, ищет выход. Сама коробка может иметь 1 вариант открытия: нужно было нажать на пружинку — и дверца распахивалась. Животное применяло много действий (так называемых проб), и большинство из них оказывались неудачными.
Кошка так и оставалась в коробке. Но после некоторого набора вариантов животному удавалось нажать на пружинку и выбраться из ящика. Таким образом, кошка, попадая в коробку, с течением времени запоминала варианты развития событий. И выбиралась из ящика за более короткое время.
Торндайк доказал, что метод действителен, и хоть результат не линеен, но со временем, при повторении аналогичных действий, решение приходит практически моментально.
Решение задач методом проб и ошибок
Примеров этого способа великое множество, однако стоит привести один очень интересный.
В начале двадцатого века жил известный конструктор двигателей для авиации Микулин. В то время наблюдалось огромное количество авиакатастроф из-за магнето, то есть искра зажигания через некоторое время полета исчезала. Много было экспериментов и размышлений о причине, но ответ пришел в совершенно неожиданной ситуации.
Александр Александрович встретил на улице мужчину с подбитым глазом. В тот момент к нему и пришло озарение, что человек без одного глаза видит намного хуже.
Он поделился этим наблюдением с авиатором Уточкиным. Когда установили в самолеты второе магнето, количество авиакатастроф значительно уменьшилось. А Уточкин некоторое время выплачивал после каждого показательного полета Микулину денежные вознаграждения.
Применение способа в математике
Достаточно часто метод проб и ошибок в математике применяется в школах как способ развития логического мышления и проверки скорости поиска вариантов. Это позволяет разнообразить процесс обучения и внести элементы игры.
Часто можно встретить в школьных учебниках задания с формулировкой «реши уравнение методом проб и ошибок». В данном случае необходимо подбирать варианты ответа. Когда найден правильный ответ, он просто доказывается уже практически, то есть проводятся необходимые расчеты. В итоге мы удостоверяемся, что это единственно верный ответ.
Пример практической задачи
Метод проб и ошибок в математике 5 класса (в последних изданиях) часто фигурирует. Приведем пример.
Необходимо назвать, какие стороны могут быть у прямоугольника.
При условии, что площадь (S) = 32 см, а периметр (P) = 24 см.
Решение данной задачи: предположим, что длина одной стороны 4. Значит и длина еще одной стороны такая же.
Получаем следующее уравнение:
24 – 4 – 4 = 16
16 делим на 2 = 8
8 см – это ширина.
Проверяем по формуле площади. S = A*B = 8*4 = 32 сантиметра. Как мы видим, решение верное. Так же можно вычислить и периметр. По формуле получается следующий расчет Р = 2* (А + В) = 2* (4 + 8) = 24.
В математике метод проб и ошибок не всегда отлично подходит для поиска решений. Зачастую можно использовать более подходящие способы, при этом затрачивается меньше времени. Но для развития мышления данный метод имеется в арсенале каждого педагога.
Теория решения изобретательских задач
В ТРИЗ метод проб и ошибок считается одним из самых неэффективных. Когда человек попадает в необычную для него затруднительную ситуацию, то действия наугад, скорее всего, будут безрезультатными. Можно потратить много времени и в результате не добиться успеха.
Теория решения изобретательских задач основана на уже известных закономерностях, и обычно используются другие методы познания. Часто ТРИЗ используют в воспитании детей, делая этот процесс интересным и увлекательным для ребенка.
Выводы
Рассмотрев данный метод, можно с уверенностью сказать, что он достаточно интересный. Несмотря на недостатки, он часто используется в решении творческих задач.
Однако не всегда он позволяет добиться нужного результата. Никогда исследователь не знает, когда стоит прекратить поиски или, может, стоит сделать еще пару усилий и гениальное изобретение появится на свет. Также непонятно, сколько времени будет затрачено.
Если вы решили использовать данный метод для решения какой-либо проблемы, то должны понимать, что ответ порой может находиться в совершенно неожиданной области. Но это позволяет взглянуть на поиск с разных точек зрения. Возможно, придется набросать несколько десятков вариаций, а может, и тысячи. Но лишь упорство и вера в успех приведут к нужному результату.
Иногда этот метод используют как дополнительный. Например, на начальном этапе для сужения поиска. Либо когда исследование было проведено многими способами и зашло в тупик. В этом случае творческая составляющая метода позволит найти компромиссное решение проблемы.
Метод проб и ошибок часто применяют в педагогической деятельности. Он позволяет детям на собственном опыте находить решения в различных жизненных ситуациях. Это учит их запоминать правильные типы поведения, которые приняты в обществе.
Художники используют данный способ для поиска вдохновения.
Метод стоит опробовать в обыденной жизни при решении проблем. Возможно, какие-то вещи предстанут вам по-другому.
Использование метода проб и ошибок для решения проблем
К Эксфорсис | 20 июля 2006 г. |
Решение проблем
Использование метода проб и ошибок для решения проблем
Некоторые сложные проблемы можно решить методом проб и ошибок.
Метод проб и ошибок обычно хорош для проблем, когда у вас есть несколько шансов найти правильное решение. Однако это не лучший метод для проблем, которые не дают вам многократных шансов найти решение.
Примером ситуаций, когда вы не хотели бы использовать метод проб и ошибок, является обезвреживание бомбы или выполнение операции на пациенте. В таких случаях ошибка может привести к катастрофе. Метод проб и ошибок лучше всего использовать, когда он применяется к ситуациям, которые дают вам много времени и безопасности, чтобы найти решение.
Кроме того, метод проб и ошибок также является отличным способом получения знаний. По сути, человек, который использует метод проб и ошибок, попытается найти метод, чтобы убедиться, что это хорошее решение. Если это не очень хорошее решение, они пробуют другой вариант. Если метод работает, человек, использующий его, получил правильное решение проблемы. Однако бывают ситуации, когда вариантов слишком много, и человек не может просмотреть их все, чтобы выяснить, какой из них работает лучше всего.
В этом случае человек захочет использовать тот вариант, который имеет наилучшие шансы на успех. Если это не сработает, они могут попробовать следующий лучший вариант, пока не найдут хорошее решение.
Существует ряд важных факторов, которые делают метод проб и ошибок хорошим инструментом для решения проблем. Цель проб и ошибок не в том, чтобы выяснить, почему проблема была решена. Он в основном используется для решения проблемы. Хотя это может быть хорошо в некоторых областях, это может не сработать в других. Например, хотя метод проб и ошибок может быть полезен при поиске решений механических или инженерных проблем, он может оказаться бесполезным для определенных областей, где возникает вопрос, «почему» решение работает. Метод проб и ошибок в первую очередь хорош для областей, где решение является наиболее важным фактором. Это часто имеет место в математических курсах, которые преподаются в средней школе или колледже.
Большинство учителей математики уделяют особое внимание методу проб и ошибок при поиске решения задач, и многие из них не тратят много времени на объяснение того, «почему» решение работает.
Одна из причин этого заключается в том, что у большинства учителей математики есть ограничения по времени. Тем не менее, некоторые студенты, посещающие курсы математики в колледже, могут узнать больше о том, почему те или иные решения работают. Еще одним хорошим аспектом метода проб и ошибок является то, что он не пытается использовать решение как способ решения более чем одной проблемы. Метод проб и ошибок в основном используется для поиска единственного решения одной проблемы.
Метод проб и ошибок — это не метод поиска наилучшего решения и не метод поиска всех решений. Это метод решения проблем, который просто используется для поиска решения. Одним из самых мощных преимуществ этой техники является то, что она не требует от вас больших знаний. Однако это может потребовать от вас большого терпения. Метод проб и ошибок обычно используется для открытия новых лекарств, и он также играет важную роль в научном методе. Некоторые также считают, что органическая эволюция — это форма проб и ошибок, потому что случайные мутации будут происходить до тех пор, пока они не принесут успеха.
Метод проб и ошибок также является отличным инструментом для изобретателей. Изобретатель сначала представит устройство, которое он хотел бы изобрести, а затем он может пройти через процесс проб и ошибок, чтобы найти наилучшие способы изобретения устройства. Хотя метод проб и ошибок является чрезвычайно мощным инструментом, который можно использовать для решения проблем, он также имеет некоторые недостатки. Я кратко упомянул об этом в первом абзаце. Метод проб и ошибок неэффективен в ситуациях, когда ошибка может привести к серьезной травме или смерти. Хорошим примером тому могут служить попытки преодоления звукового барьера, которые предпринимались авиационными инженерами. Хотя им это удалось, многие пилоты погибли, потому что использовали метод проб и ошибок. В ситуации и ошибка часто приводила к крушению самолета.
Решение инженерных задач | Метод проб и ошибок против математического подхода
Брюс Бартлетт Брюс Бартлетт рассматривает два подхода к решению инженерных задач: математический и метод проб и ошибок. Наша задача как инженеров — создавать решения, решающие проблемы. Например, спроектируйте звуковую систему, чтобы свести к минимуму обратную связь, или определите звуковой эффект объекта, помещенного рядом с микрофоном. Два метода решения проблем — это метод проб и ошибок и предсказание с использованием математики. Методом проб и ошибок вы интуитивно придумываете решение, пробуете его и смотрите, что получится. Это проба и проба. Это повторяющиеся разнообразные попытки, которые вы продолжаете, пока не достигнете успеха. В качестве альтернативы вы предсказываете результат, используя математические уравнения или используя известные свойства объекта. Затем проверьте свой прогноз с помощью реальных измерений. Метод проб и ошибок не обязательно приводит к наилучшему результату, но часто этого достаточно. Фото 1: Решение инженерных задач – метод проб и ошибок Физические свойства и геометрия объектов создают математические законы физики. Иногда, используя методы проб и ошибок, мы можем позволить законам физики выполнять тяжелую работу сложной математики, чтобы получить желаемый результат. Методом проб и ошибок вы проводите эксперимент — меняете одну переменную в системе — и измеряете результаты. Вместо того, чтобы использовать математику для расчета и предсказания результатов этого эксперимента, вы позволяете законам природы «вычислять» или формировать результат, как это сделал бы аналоговый компьютер. Природа прекрасно «считает», когда выдает результат эксперимента. Иногда природа слишком сложна математически, чтобы мы могли предсказать результат, используя наши ограниченные знания о том, что происходит физически. Например, как небольшой предмет или открытая щель рядом с капсюлем микрофона влияет на его частотную характеристику? Если бы вы попытались предсказать это с помощью математики, вам нужно было бы знать о гидродинамике, геометрии, точной форме выступа или щели, резонансе, влиянии препятствий различной формы на звуковые волны (дифракция) и т. д. Но если вы просто создаете объект или щель и измеряете результат (дельту или изменение частотной характеристики), природа «вычислила» за вас легко и точно. Если хотите, можете составить уравнения и попытаться сопоставить их с данными, которые природа уже «подсчитала» за вас. Вот пример. Предположим, у вас есть P.A. системы, и вы хотите создать максимально громкий звук без обратной связи. Вы размещаете микрофон и динамик в определенных местах относительно источника звука. Вы увеличиваете громкость до тех пор, пока не начнется обратная связь. Затем измените одну переменную. Например, увеличить расстояние громкоговорителя от микрофона. Если обратная связь прекратится, вы можете немного увеличить громкость, пока обратная связь не начнется снова. Из того, что вы только что узнали, вы можете написать уравнение: громкость до обратной связи пропорциональна расстоянию от динамика до микрофона. SPL ∝ D1*X , где SPL — громкость, 
Другими словами, реальность дает тот же результат, что и правильные математические уравнения.
Иногда метод проб и ошибок дает полезные результаты намного быстрее, чем расчеты.
X — неизвестная константа или переменная, а 
Затем вы измените другую переменную и посмотрите, что произойдет. Вы приближаете микрофон к источнику звука. Громкость звуковой системы увеличивается, не вызывая обратной связи. Таким образом, вы составляете другое уравнение:
SPL ∝ X/Ds
, где
L — громкость,
X — неизвестная константа или переменная, а
Ds — расстояние от микрофона до источника.
Объединив эти два уравнения, вы получите SPL ∝ D1*X/Ds. Вы начинаете составлять уравнение, которое предсказывает усиление до обратной связи.
Теперь вы изменяете другую переменную. Вы приближаете громкоговоритель к слушателю. Звуковая система становится громче для слушателя, не вызывая обратной связи. В качестве математического выражения вы могли бы сказать
SPL ∝ X/D2
, где
SPL — громкость,
D2 — расстояние от громкоговорителя до слушателя.
Объединив эти три уравнения, вы получите
SPL ∝ D1*X/(Ds*D2)
Наше уравнение для прогнозирования коэффициента усиления до обратной связи становится все более полным.
Он говорит вам следующее: если вы хотите увеличить громкость, увеличьте расстояние от динамика до микрофона, уменьшите расстояние от микрофона до источника и уменьшите расстояние от динамика до слушателя. Другими словами, поместите динамик далеко от микрофона, поместите микрофон ближе к источнику, а динамик поместите ближе к аудитории.
Фото 2: Решение инженерных задач – использование математики
X в этом уравнении могут быть другие переменные, такие как частотная характеристика и чувствительность микрофона в направлении динамика, отклик и чувствительность динамика в направлении микрофон, диаграмма направленности микрофона, диаграмма направленности динамика, живость комнаты, громкость источника звука и т. д.
X также может быть уравнением. Мы могли бы начать с закона обратных квадратов, связывающего SPL с расстоянием, и вывести из него наше уравнение обратной связи.
Реальность не следует уравнениям. Он просто реагирует на обстоятельства единственным доступным ему способом.