Тавтология скрытая: что это такое? Примеры тавтологий.

Плеоназм и тавтология

1.06.2015

Точность словоупотребления не допускает появления речевой избыточности, выражением которой является плеоназм и тавтология.

Плеоназм (в переводе с греч. — излишество) — оборот речи, содержащий однозначные или близкие по смыслу слова (лично я, вернуться в апреле месяце, написать свою автобиографию).

Надо помнить, что если «краткость — сестра таланта» (А. Чехов), то многословие — враг ясности. М. Горький в советах начинающим писателям неоднократно приводил примеры того, как можно одну и ту же мысль выразить короче, экономнее. Так, рассматривая предложение «Не суй своего носа, куда не следует», он на полях рукописи заметил: «А разве можно совать чужой нос?» В сочетаниях «своя родная семья», «молча, без слов», «слизывая капельки с волос усов» М. Горький отметил повторение одного и того же понятия: своя — это и есть родная, молча — значит без слов, усы — это волосы на верхней губе.

Крайней формой плеоназма является тавтология (в переводе с греч. — то же самое слово) — оборот речи, содержащий повторение одних и тех же или однокоренных слов: следует отметить следующие факты, изображаемый образ наглядно показывает.

Речевую избыточность порождает и соединение иностранного слова с русским, дублирующим его значение: памятные сувениры, необычный феномен, биография жизни, своя автобиография, мизерные мелочи, в конечном итоге, ведущий лидер, ответная контратака, демобилизоваться из армии, народный фольклор.

В таких случаях говорят о скрытой тавтологии, так как русское слово повторяет значение заимствованного. Например, сувенир -французское слово, означающее «подарок на память», «вещь, связанная с воспоминаниями», а к нему ещё добавляют памятный; биография — греческое слово, означающее «жизнеописание», автобиография — жизнеописание какого-либо лица, составленное им самим, поэтому добавление слова «жизнь» неуместно.

Однако некоторые сочетания подобного типа все же закрепляются в языке, что обычно связано с изменением значений входящих в них слов. Примером утраты тавтологичности может быть сочетание период времени. Лингвисты раньше считали это выражение избыточным, так как греческое по происхождению слово период означает «время». Однако постепенно это слово стало означать «промежуток времени», что сделало возможным его употребление в качестве второго варианта. Из других, ранее считавшихся избыточными, словосочетаний также вошли в обиход следующие: реальная действительность, экспонаты выставки, букинистическая книга и некоторые другие. В них определения перестали быть простым повторением основного признака, заключённого в существительном.

Не только скрытую, но и явную тавтологию порой приходится признать допустимой, потому что в речи могут столкнуться одно-коренные слова, не имеющие синонимов, например: словарь иностранных слов, бригадир первой бригады, загадать загадку, постелить постель и т. д.

Экономное, точное выражение мысли — важнейшее требование стилистики.

Ключевые слова: Слово

Источник: Жилина О. А., Романова Н.Н. — Русский язык и культура речи. ч.1. Основы культуры речи — 2008

Материалы по теме
Иностранные слова в русской лексике Жилина О.А., Романова Н.Н. — Русский язык и культура речи. ч.1. Основы культуры речи — 2008…
Вводные слова и предложения Русский язык и культура речи. Синтаксис: Учеб. пособие для студентов вузов / Под ред. Г. Я….
Особенности использования устойчивых глагольно-именных словосочетаний Жилина О.А., Романова Н.Н. — Русский язык и культура речи. ч.1. Основы культуры речи — 2008…
Порядок слов в простом предложении, его актуальное членение Русский язык и культура речи. Синтаксис: Учеб. пособие для студентов вузов / Под ред. Г. Я….
Полная и краткая формы имён прилагательных в роли синонимов Жилина О. А., Романова Н.Н. — Русский язык и культура речи. ч.1. Основы культуры речи — 2008…
Средства связи частей сложноподчиненного предложения Русский язык и культура речи. Синтаксис: Учеб. пособие для студентов вузов / Под ред. Г. Я….
Числительные в составе сложных слов Жилина О.А., Романова Н.Н. — Русский язык и культура речи. ч.1. Основы культуры речи — 2008…
Стилистическая окраска слов Стилистика русского языка и культура речи : учебник для академического бакалавриата / И. Б….

6. Перепишите по предложению, подчеркните ошибочное слово,формы, выражения. Назовите тип ошибки. Дайте исправленный вариант.А) В…

А) В печати отмечалось об ограниченном ассортименте товаров.

В печати отмечалось, что ассортимент товаров ограничен.

Ошибка в построении словосочетаний. Глагол отмечать – переходный, поэтому требует после себя либо прямое дополнение без предлога (отмечалось что?), либо придаточное предложение.

Б) Впервые он дебютировал на сцене нашего города.

Впервые он выступил на сцене нашего города. / Он дебютировал на сцене нашего города.

Скрытая тавтология. Дебют – это и есть первое выступление. Оставляем что-то одно.

В) Ни один из них не отвечал ему ни слова, они только безмолвно пялили на него очи.

Ни один из них не отвечал ему ни слова, они только безмолвно пялили на него глаза.

Ошибка в употреблении фразеологизма. Пялить глаза – фразеологизм, а, как известно, фразеологизм – это устойчивый оборот, который разрывать нельзя.  

Г) Я сломала каблук у правого туфля.

Я сломала каблук у правой туфли.

Ошибка в определении рода слова. Слово туфля – женского рода.

Д) Он занимал выборочную должность.

Он занимал выборную должность.

Ошибка в употреблении паронимов (слов, близких по звучанию, но разных по смыслу)

Е) Жизненный уровень сотрудников отдела возрос.

Жизненный уровень сотрудников отдела вырос.

Тоже ошибка в употреблении паронимов.

Ж) Указанный признак проявляет себя здесь более сильнее.

Указанный признак проявляет себя здесь сильнее./ Указанный признак проявляет себя здесь более сильно.

Ошибка в образовании степени сравнения наречия. Возможна либо простая форма сравнительной степени, либо составная, смешивать их нельзя.

З) Следует различать различные подходы к данной проблеме.

Следует различать возможные подходы к данной проблеме.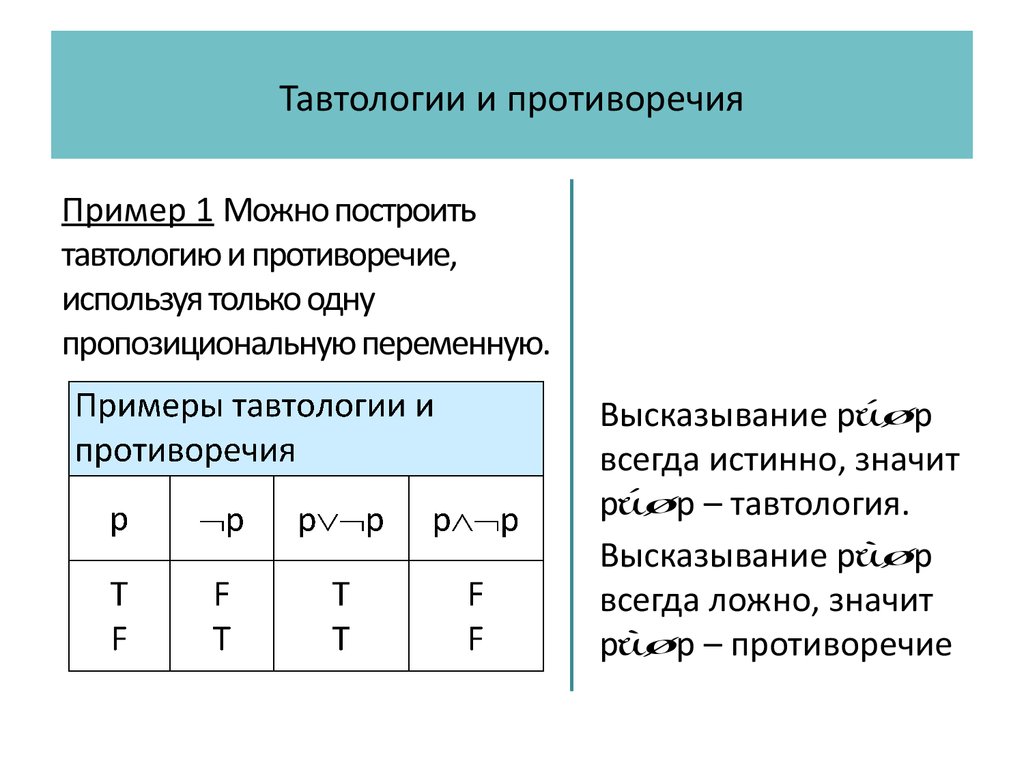

Ошибка в употреблении паронимов, в результате которой получается тавтология: повтор однокоренных слов.

И) Наряжая ёлку, мне вспомнилось детство.

Когда я наряжал ёлку, мне вспомнилось детство./Наряжая елку, я вспомнил детство.

Ошибка в употреблении деепричастного оборота. Деепричастный оборот должен согласовываться исключительно с подлежащим, т.к. он выражает добавочное действие этого подлежащего при основном. В данном примере подлежащее вообще отсутствует, поэтому деепричастные обороты здесь невозможны. Либо перестраиваем предложение из безличного в определенно-личное, либо заменяем простое предложение на сложноподчиненное.

1.6: Тавтологии и противоречия — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

23876

• Дэйв Витте Моррис и Джой Моррис
• Летбриджский университет

Большинство утверждений истинны в одних ситуациях и ложны в других.

Но одни утверждения верны во всех ситуациях, а другие ложны во всех ситуациях.

Определение \(1.6.1\).

• A тавтология — это утверждение логики высказываний, истинное во всех ситуациях; то есть верно для всех возможных значений его переменных.
• противоречие — это утверждение логики высказываний, ложное во всех ситуациях; то есть оно ложно для всех возможных значений его переменных.

Пример \(1.6.2\).

Утверждение \(A\или B\) истинно, когда \(A\) истинно (или \(B\) истинно), но ложно, когда \(A\) и \(B\) оба ложные. Таким образом, утверждение иногда верно, а иногда ложно; это не противоречие и не тавтология.

Пример \(1.6.3\).

Покажите, что утверждение \(\bigl( P \& (\lnot Q \lor \lnot R) \bigr) \Rightarrow (P \Rightarrow \lnot Q)\) не является ни тавтологией, ни противоречием.

Нацарапанный.

Нам нужно найти значения переменных, которые делают утверждение верным, и другие значения, которые делают утверждение ложным.

Легко сделать утверждение истинным, потому что импликация истинна, когда верен ее вывод, поэтому нам просто нужно сделать \(P \Rightarrow \lnot Q\) истинным. И мы можем сделать это истинным, сделав \(\lnot Q\) истинным. Итак, мы допускаем, что \(Q\) ложно. Тогда мы можем позволить \(P\) и \(R\) быть тем, чем захотим: вероятно, проще всего сделать их обоих ложными (так же, как \(Q\)).

Чтобы сделать утверждение ложным, нужно сделать его гипотезу верной, а вывод ложным.

• Начнем с вывода \(P \Стрелка вправо\lnot Q\). Чтобы сделать это ложным, нам нужно сделать \(P\) истинным, а \(\lnot Q\) ложным. Таким образом, мы полагаем \(P = \mathsf{T}\) и \(Q = \mathsf{T}\).
• Теперь рассмотрим гипотезу \(P \& (\lnot Q \lor \lnot R)\). К счастью, мы уже решили сделать \(P\) истинным, но нам также нужно сделать \(\lnot Q \или \lnot R\) истинным. Так как мы уже решили сделать \(Q\) истинным, нам нужно сделать \(\lnot R\) истинным, так что пусть \(R = \mathsf{F}\).

Решение

Если \(P\), \(Q\) и \(R\) ложны, то \[\begin{aligned} \bigl( P \& (\lnot Q \lor \lnot R) \bigr) \Rightarrow (P \Rightarrow \lnot Q) & \quad = \quad \bigl( \mathsf{F} \& (\lnot \mathsf{F} \lor \lnot \mathsf{F} ) \bigr) \Rightarrow (\mathsf{F} \Rightarrow \lnot \mathsf{F}) \\& \quad = \quad \bigl( \mathsf{F} \& (\mathsf{T} \lor \mathsf {T}) \bigr) \Rightarrow (\mathsf{F} \Rightarrow \mathsf{T}) \\& \quad = \quad \bigl( \mathsf{F} \& \mathsf{T} \bigr) \ Стрелка вправо (\mathsf{T}) \\& \quad = \quad \mathsf{F} \Rightarrow \mathsf{T} \\& \quad = \quad \mathsf{T} , \end{aligned}\]
тогда как если \(P\) и \(Q\) истинны, но \(R\) ложно, то \[\begin{aligned} \bigl( P \& (\lnot Q \lor \lnot R) \bigr) \Rightarrow (P \Rightarrow \lnot Q) & \quad = \quad \bigl( \mathsf{T} \& (\lnot \mathsf{T} \lor \lnot \mathsf{F}) \bigr) \Rightarrow (\mathsf{T} \Rightarrow \lnot \mathsf{T}) \\& \quad = \quad \bigl( \mathsf{T} \& (\mathsf{F} \lor \mathsf{T}) \bigr) \Rightarrow (\mathsf{T} \Rightarrow \mathsf{F}) \\& \quad = \quad \bigl( \mathsf{T} \& \mathsf{T} \bigr) \Rightarrow (\mathsf {F}) \\& \quad = \quad \mathsf{T} \Rightarrow \mathsf{F} \\& \quad = \quad \mathsf{F} .

\конец{выровнено}\]
Таким образом, утверждение иногда верно, а иногда ложно, поэтому оно не является ни тавтологией, ни противоречием.

Упражнение \(1.6.4\).

Покажите, что каждое из следующих утверждений не является ни тавтологией, ни противоречием.

1. \(A \Стрелка вправо (A \& B)\)
2. \((A \или B) \Стрелка вправо A\)
3. \((A \Leftrightarrow B) \lor (A \& \lnot B)\)
4. \((X \Стрелка вправо Z) \Стрелка вправо (Y \Стрелка вправо Z)\)
5. \(\bigl( P \& \lnot(Q \& R) \bigr) \lor (Q {\Rightarrow} R)\)

Пример \(1.6.5\) (Закон исключенного третьего).

Легко видеть, что утверждение \(А \или \lне А\) истинно, когда \(А\) истинно, а также когда \(А\) ложно. Таким образом, утверждение верно для обоих возможных значений переменной \(A\), так что это тавтология:

Решение

\[\begin{aligned} A \lor \lnot A \text{ есть тавтология} \end{aligned}\]

Замечание \(1.

6.6\).

Вышеупомянутая тавтология называется «Законом исключенного третьего», потому что в ней говорится, что каждое утверждение либо истинно, либо ложно: нет золотой середины, где утверждение частично истинно, а частично ложно.

Пример \(1.6.7\).

Легко видеть, что утверждение \(A \& \lnot A\) ложно, когда \(A\) истинно, а также когда \(A\) ложно. Таким образом, утверждение неверно для обоих возможных значений переменной \(A\), так что это противоречие:

Решение

\[\begin{aligned} A \& \lnot A \text{ является противоречие} \end{выравнивание}\]

Замечание \(1.6.8\).

Утверждения \(A \lor \lnot A\) и \(A \& \lnot A\) являются наиболее важными (и наиболее распространенными) примерами тавтологий и противоречий. Однако они обычно возникают, когда в переменную \(A\) вставляется какое-либо другое выражение. Например, полагая \(A\) утверждением \((P \lor Q) \Rightarrow R\), мы получаем тавтологию \[\bigl( (P \lor Q) \Rightarrow R \bigr) \lor \lnot \bigl( (P \lor Q) \Rightarrow R \bigr) ,\]
, что является более сложным примером закона исключенного третьего, и мы также получаем противоречие \[\bigl( (P \lor Q) \Rightarrow R \bigr) \& \lnot \bigl( (P \lor Q) \Rightarrow R \bigr) . \]

Пример \(1.6.9\).

Мы также можем привести примеры на английском языке, а не в символах; рассмотрите эти утверждения:

27. Идет дождь.
28. Либо идет дождь, либо нет.
29. Идет дождь, и не идет дождь.

Чтобы узнать, верно ли утверждение 27, нужно проверить погоду. С логической точки зрения оно может быть либо истинным, либо ложным, так что это не тавтология и не противоречие.

Утверждение 28 отличается. Вам не нужно выглядывать наружу, чтобы знать, что это правда, независимо от того, какая погода. Так что это тавтология.

Вам также не нужно смотреть прогноз погоды, чтобы узнать об Утверждении 29. Это должно быть ложным, просто с точки зрения логики. Дождь может идти здесь, а не в другом городе, или может идти дождь сейчас, но дождь прекращается, даже когда вы читаете это, но невозможно, чтобы одновременно шел дождь и не шел дождь в любой конкретной ситуации (в любое конкретное время и в любом месте).

). Таким образом, третье утверждение ложно во всех возможных ситуациях; это противоречие.

Упражнение \(1.6.10\).

Что из следующего возможно? Для тех, что можно, приведите пример. Для тех, кто не знает, объясните, почему.

1. Верный вывод, вывод которого является противоречием.
2. Правильный вывод, вывод которого является тавтологией.
3. Действительная дедукция, одной из гипотез которой является тавтология.
4. Верный вывод, одна из гипотез которого содержит противоречие.
5. Неверный вывод, вывод которого является противоречием.
6. Неверный вывод, вывод которого является тавтологией.
7. Неверный вывод, одной из гипотез которого является тавтология.
8. Неверный вывод, одна из гипотез которого содержит противоречие.

---

Эта страница под названием 1.6: Тавтологии и противоречия распространяется в соответствии с лицензией CC BY-NC-SA 2. 0, ее авторами, ремиксами и/или кураторами являются Дэйв Витте Моррис и Джой Моррис.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэйв Витте Моррис и Джой Моррис

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   2,0

   Показать страницу TOC

   нет

2. Теги

   1. тавтология

00_Criticism52-3-4_FM_pi-ii.