Тавтология в логике: Tautology | What Is Tautology?

Содержание

Тавтология (логика)

Эта статья посвящена тавтологии формальной логики. Для использования в других целях см. Тавтология (значения).

В логика, а тавтология (из Греческий: ταυτολογία) это формула или утверждение, которое истинно во всех возможных интерпретация. Пример: «x = y или x ≠ y». Менее абстрактный пример: «Мяч полностью зеленый, или мяч не весь зеленый». Это было бы тавтологией независимо от цвета мяча.

Философ Людвиг Витгенштейн впервые применил этот термин к дублированию логика высказываний в 1921 г., заимствуя риторика, где тавтология является повторяющимся заявлением. В логике формула удовлетворительный если это верно хотя бы при одной интерпретации, и, следовательно, тавтология — это формула, отрицание которой неудовлетворительно. Неудовлетворительные утверждения, выраженные как через отрицание, так и через подтверждение, формально известны как противоречия. Формула, не являющаяся ни тавтологией, ни противоречием, называется логически случайный. Такая формула может быть сделана либо истинной, либо ложной на основе значений, присвоенных ее пропозициональным переменным. В двойной турникет обозначение ⊨S{displaystyle vDash S} используется, чтобы указать, что S это тавтология. Тавтология иногда обозначается буквой «V».pq«, и противоречие» Opq«. тройник символ ⊤{displaystyle op} иногда используется для обозначения произвольной тавтологии с двойным символом ⊥{displaystyle ot} (ложь) представляющее произвольное противоречие; в любом символизме значение истинности может быть заменено тавтологией «правда», что обозначается, например,» 1 «.^[1]^[2]

Тавтологии — ключевое понятие в логика высказываний, где тавтология определяется как пропозициональная формула, истинная при любых возможных Логическая оценка своего пропозициональные переменные.^[3] Ключевым свойством тавтологий в логике высказываний является то, что эффективный метод существует для проверки того, всегда ли выполняется данная формула (эквивалентно, является ли ее отрицание невыполнимым).

Определение тавтологии можно распространить на предложения в логика предикатов, который может содержать кванторы- признак, отсутствующий в предложениях логики высказываний. В самом деле, в логике высказываний нет различия между тавтологией и тавтологией. логически действительный формула. В контексте логики предикатов многие авторы определяют тавтологию как предложение, которое можно получить, взяв тавтологию логики высказываний и равномерно заменив каждую пропозициональную переменную формулой первого порядка (одна формула на пропозициональную переменную). Набор таких формул представляет собой правильное подмножество набора логически верных предложений логики предикатов (т. е. предложений, истинных в каждом модель).

История

Слово тавтология использовалось древними греками для описания утверждения, которое считалось истинным только на основании повторения одного и того же дважды, уничижительный это означает, что все еще используется для риторические тавтологии. Между 1800 и 1940 годами это слово приобрело новое значение в логике и в настоящее время используется в математическая логика для обозначения определенного типа пропозициональной формулы без уничижительных коннотаций, которыми она изначально обладала.

В 1800 г. Иммануил Кант написал в своей книге Логика:

Идентичность концепций в аналитических суждениях может быть либо явный (эксплицита) или неявный (имплицита). В первом случае аналитические предложения тавтологический.

Вот, аналитическое предложение относится к аналитическая правда, утверждение на естественном языке, истинное исключительно из-за задействованных терминов.

В 1884 г. Готтлоб Фреге предложил в своем Grundlagen что истина аналитична именно тогда, когда ее можно вывести с помощью логики. Однако он проводил различие между аналитическими истинами (то есть истинами, основанными только на значениях их терминов) и тавтологиями (т.е. утверждениями, лишенными содержания).

В его Логико-философский трактат в 1921 году Людвиг Витгенштейн предположил, что утверждения, которые могут быть выведены с помощью логической дедукции, являются тавтологическими (бессмысленными), а также являются аналитическими истинами. Анри Пуанкаре сделал аналогичные замечания в Наука и гипотеза в 1905 году. Хотя Бертран Рассел сначала выступал против этих замечаний Витгенштейна и Пуанкаре, утверждая, что математические истины не только нетавтологичны, но и синтетический, позже он высказался в их пользу в 1918 году:

Все, что является утверждением логики, должно быть в том или ином смысле похоже на тавтологию. Это должно быть что-то, имеющее какое-то особое качество, которое я не знаю, как определить, что принадлежит логическим предложениям, но не другим.

Вот, логическое предложение относится к утверждению, которое можно доказать с помощью законов логики.

В течение 1930-х годов была разработана формализация семантики логики высказываний в терминах присвоения истинности. Термин «тавтология» стал применяться к тем пропозициональным формулам, которые истинны независимо от истинности или ложности их пропозициональных переменных. Некоторые ранние книги по логике (например, Символическая логика от К. И. Льюис и Langford, 1932) использовали этот термин для обозначения любого предложения (в любой формальной логике), которое является универсально допустимым. После этого обычно в презентациях (например, Стивен Клини 1967 и Герберт Эндертон 2002) использовать тавтологию для обозначения логически действительной пропозициональной формулы, но поддерживать различие между «тавтологией» и «логически действительным» в контексте логики первого порядка. (увидеть ниже).

Задний план

Логика высказываний начинается с пропозициональные переменные, атомарные единицы, которые представляют конкретные предложения. А формула состоит из пропозициональных переменных, связанных логическими связками, построенных таким образом, что истинность общей формулы может быть выведена из истинности или ложности каждой переменной. А оценка — это функция, которая присваивает каждой пропозициональной переменной либо T (для истины), либо F (для ложности). Итак, используя пропозициональные переменные А и B, бинарные связки ∨{displaystyle lor} и ∧{displaystyle land} представляющий дизъюнкция и соединение соответственно, а унарная связка ¬{displaystyle lnot} представляющий отрицание, может быть получена следующая формула:(А∧B)∨(¬А)∨(¬B){displaystyle (Aland B) lor (lnot A) lor (lnot B)}.

Оценка здесь должна быть назначена каждому из А и B либо T, либо F. Но как бы это ни было сделано, общая формула окажется верной. Ведь если первое соединение (А∧B){displaystyle (Aland B)} не удовлетворен конкретной оценкой, то один из А и B присваивается F, что делает один из следующих дизъюнктов присвоенным T.

Определение и примеры

Формула логики высказываний — это тавтология если сама формула всегда верна, независимо от того, какая оценка используется для пропозициональные переменные.Тавтологий бесконечно много. Примеры включают:

(А∨¬А){displaystyle (Alor lnot A)} («А или нет А«), закон исключенного среднего. Эта формула имеет только одну пропозициональную переменную, А. Любая оценка по этой формуле должна по определению присваивать А одна из истинных ценностей правда или ложный, и назначить ¬{displaystyle lnot}А другое значение истины.
(А→B)⇔(¬B→¬А){displaystyle (A o B) Leftrightarrow (lnot B o lnot A)} («если А подразумевает B, то не-B подразумевает не-А«, и наоборот), что выражает закон противопоставление.
((¬А→B)∧(¬А→¬B))→А{displaystyle ((lnot A o B) land (lnot A o lnot B)) o A} («если не-А подразумевает как B и его отрицание не-B, то не-А должно быть ложным, тогда А должно быть правдой «), принцип, известный как сокращение до абсурда.
¬(А∧B)⇔(¬А∨¬B){displaystyle lnot (Aland B) Leftrightarrow (lnot Alor lnot B)} («если не оба А и B, то не-А или нет-B«, и наоборот), который известен как Закон де Моргана.
((А→B)∧(B→C))→(А→C){displaystyle ((A o B) земля (B o C)) o (A o C)} («если А подразумевает B и B подразумевает C, тогда А подразумевает C«), который известен как принцип силлогизм.
((А∨B)∧(А→C)∧(B→C))→C{displaystyle ((Alor B) земля (A o C) земля (B o C)) o C} («если хотя бы один из А или B верно, и каждый подразумевает C, тогда C также должно быть правдой «), который известен как принцип доказательство по делам.

Минимальная тавтология — это тавтология, которая не является примером более короткой тавтологии.

(А∨B)→(А∨B){displaystyle (Alor B) o (Alor B)} это тавтология, но не минимальная, потому что это реализация C→C{displaystyle C o C}.

Проверка тавтологий

Проблема определения того, является ли формула тавтологией, является фундаментальной в логике высказываний. Если есть п переменные, входящие в формулу, то есть 2^п различные оценки формулы. Следовательно, задача определения того, является ли формула тавтологией, является конечной и механической задачей: нужно только оценить значение истины формулы под каждой из ее возможных оценок. Один из алгоритмических методов проверки того, что каждая оценка делает формулу истинной, — это сделать таблица истинности это включает в себя всевозможные оценки.^[3]

Например, рассмотрим формулу

((А∧B)→C)⇔(А→(B→C)).{displaystyle ((Aland B) o C) Leftrightarrow (A o (B o C)).}

Есть 8 возможных оценок пропозициональных переменных А, B, C, представленный первыми тремя столбцами следующей таблицы. Остальные столбцы показывают истинность подформул приведенной выше формулы, а кульминацией является столбец, показывающий значение истинности исходной формулы для каждой оценки.

Поскольку каждая строка последнего столбца показывает Т, рассматриваемое предложение проверяется на тавтологию.

Также можно определить дедуктивная система (т.е. система доказательств) для логики высказываний как более простой вариант дедуктивных систем, используемых для логики первого порядка (см. Клини 1967, раздел 1.9 для одной такой системы). Доказательство тавтологии в соответствующей дедуктивной системе может быть намного короче, чем полная таблица истинности (формула с п пропозициональные переменные требуют таблицы истинности с 2^п линий, что быстро становится невозможным, поскольку п увеличивается). Системы доказательства также требуются для изучения интуиционистский логика высказываний, в которой метод таблиц истинности не может быть использован, потому что не предполагается закон исключенного третьего.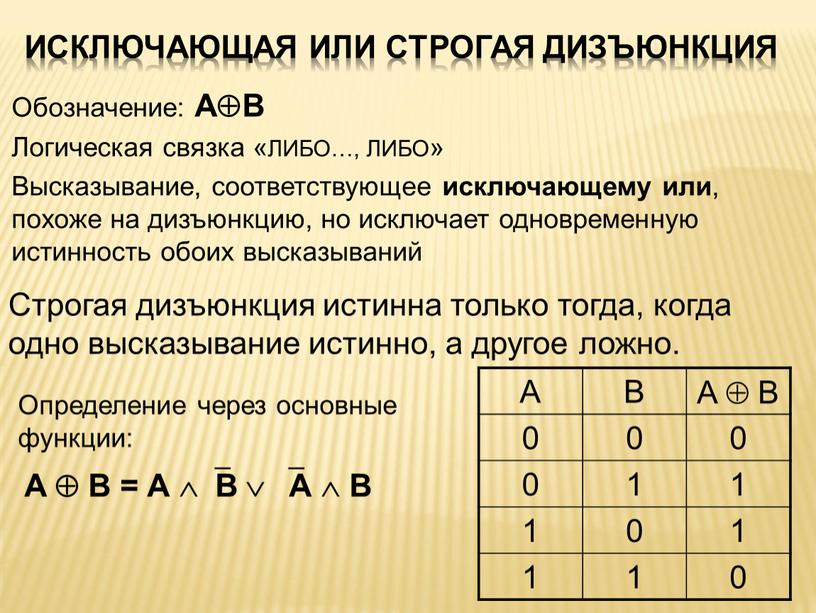

Тавтологический смысл

Формула р говорят тавтологически подразумевают формула S если каждая оценка, которая вызывает р быть правдой также вызывает S быть правдой. Эта ситуация обозначается р⊨S{displaystyle Rmodels S}. Это эквивалентно формуле р→S{displaystyle R o S} быть тавтологией (Клини, 1967, с. 27).

Например, пусть S{displaystyle S} быть А∧(B∨¬B){displaystyle Aland (Blor lnot B)}. потом S{displaystyle S} не тавтология, потому что любая оценка, которая делает А{displaystyle A} ложь сделает S{displaystyle S} ложный. Но любая оценка, которая делает А{displaystyle A} правда сделает S{displaystyle S} правда, потому что B∨¬B{displaystyle Blor lnot B} это тавтология. Позволять р{displaystyle R} быть формулой А∧C{displaystyle Aland C}. потом р⊨S{displaystyle Rmodels S}, потому что любая оценка, удовлетворяющая S{displaystyle S} сделаю А{displaystyle A} правда — и таким образом делает S{displaystyle S} правда.

Из определения следует, что если формула р{displaystyle R} противоречие, то р{displaystyle R} тавтологически подразумевает каждую формулу, потому что нет оценки истины, которая вызывает р{displaystyle R} быть истинным, и поэтому определение тавтологической импликации тривиально выполняется. Аналогично, если S{displaystyle S} это тавтология, то S{displaystyle S} тавтологически подразумевается каждой формулой.

Замена

Есть общая процедура, правило замены, что позволяет построить дополнительные тавтологии из данной тавтологии (Kleene 1967 sec. 3). Предположим, что S является тавтологией и для каждой пропозициональной переменной А в S фиксированный приговор S_А выбран. Тогда предложение, полученное заменой каждой переменной А в S с соответствующим предложением S_А тоже тавтология.

Например, пусть S быть тавтологией

(А∧B)∨¬А∨¬B{displaystyle (Aland B) lor lnot Alor lnot B}.

Позволять S_А быть C∨D{displaystyle Clor D} и разреши S_B быть C→E{displaystyle C o E}.

Из правила подстановки следует, что предложение

((C∨D)∧(C→E))∨¬(C∨D)∨¬(C→E){displaystyle ((Clor D) land (C o E)) lor lnot (Clor D) lor lnot (C o E)}

это тоже тавтология. В свою очередь, значение истинности может быть заменено тавтологией »правда».

Семантическая полнота и обоснованность

An аксиоматическая система является полный если каждая тавтология является теоремой (выводимой из аксиом). Аксиоматическая система звук если каждая теорема является тавтологией.

Эффективная проверка и проблема логической выполнимости

Проблема построения практических алгоритмов для определения того, являются ли предложения с большим числом пропозициональных переменных тавтологией, является областью современных исследований в области автоматическое доказательство теорем.

Методика таблицы истинности проиллюстрированный выше, доказуемо верен — таблица истинности для тавтологии будет заканчиваться столбцом только с Т, в то время как таблица истинности для предложения, не являющегося тавтологией, будет содержать строку, последний столбец которой F, и оценка, соответствующая этой строке, является оценкой, не удовлетворяющей проверяемому предложению. Этот метод проверки тавтологий является эффективная процедура, что означает, что при неограниченных вычислительных ресурсах его всегда можно использовать для механистического определения того, является ли предложение тавтологией. Это означает, в частности, что множество тавтологий над фиксированным конечным или счетным алфавитом является разрешимый набор.

Как эффективная процедураОднако таблицы истинности ограничены тем фактом, что количество оценок, которые необходимо проверить, увеличивается как 2^k, где k количество переменных в формуле. Этот экспоненциальный рост длины вычислений делает метод таблицы истинности бесполезным для формул с тысячами пропозициональных переменных, поскольку современное вычислительное оборудование не может выполнить алгоритм за допустимый период времени.

Проблема определения того, существует ли какая-либо оценка, которая делает формулу верной, заключается в Проблема логической выполнимости; проблема проверки тавтологий эквивалентна этой проблеме, потому что проверка того, что предложение S тавтология эквивалентна проверке того, что не существует оценки, удовлетворяющей ¬S{displaystyle lnot S}. Известно, что проблема булевой выполнимости имеет вид НП завершена, и широко распространено мнение, что нет полиномиальный алгоритм который может это выполнить. Следовательно, тавтология совместно NP-полный. Текущие исследования сосредоточены на поиске алгоритмов, которые хорошо работают с определенными классами формул или в среднем быстро завершаются, даже если некоторые входные данные могут потребовать гораздо больше времени.

Тавтологии и валидности в логике первого порядка

Фундаментальное определение тавтологии находится в контексте логики высказываний. Однако определение может быть расширено на предложения в логика первого порядка (см. Enderton (2002, стр. 114) и Kleene (1967 secs 17–18)). Эти предложения могут содержать кванторы, в отличие от предложений логики высказываний. В контексте логики первого порядка сохраняется различие между логическая достоверность, предложения, которые верны в каждой модели, и тавтологии, которые являются надлежащим подмножеством логических значений первого порядка. В контексте логики высказываний эти два термина совпадают.

Тавтология в логике первого порядка — это предложение, которое можно получить, взяв тавтологию логики высказываний и равномерно заменив каждую пропозициональную переменную формулой первого порядка (одна формула на пропозициональную переменную). Например, потому что А∨¬А{displaystyle Alor lnot A} тавтология логики высказываний, (∀Икс(Икс=Икс))∨(¬∀Икс(Икс=Икс)){displaystyle (forall x (x = x)) lor (lnot forall x (x = x))} является тавтологией в логике первого порядка. Точно так же в языке первого порядка с унарными символами отношения р,S,Тследующее предложение является тавтологией:

(((∃ИксрИкс)∧¬(∃ИксSИкс))→∀ИксТИкс)⇔((∃ИксрИкс)→((¬∃ИксSИкс)→∀ИксТИкс)).{displaystyle (((существует xRx) land lnot (exists xSx)) o forall xTx) Leftrightarrow ((существует xRx) o ((lnot exists xSx) o forall xTx)).}

Получается заменой А{displaystyle A} с ∃ИксрИкс{displaystyle существует xRx}, B{displaystyle B} с ¬∃ИксSИкс{displaystyle lnot существует xSx}, и C{displaystyle C} с ∀ИксТИкс{displaystyle forall xTx} в пропозициональной тавтологии ((А∧B)→C)⇔(А→(B→C)){displaystyle ((Aland B) o C) Leftrightarrow (A o (B o C))}.

Не все логические обоснования являются тавтологиями в логике первого порядка. Например, предложение

(∀ИксрИкс)→¬∃Икс¬рИкс{displaystyle (forall xRx) o lnot существует xlnot Rx}

верно в любой интерпретации первого порядка, но соответствует пропозициональному предложению А→B{displaystyle A o B} что не является тавтологией логики высказываний.

На естественном языке

В естественных языках некоторые очевидные тавтологии, как в некоторых банальности, на практике может иметь нетавтологическое значение.^[4] В английском языке «это то, что есть» используется в значении «это невозможно изменить».^[5] В Тамильский, поверхностная тавтология вантаал варуваан буквально означает «если он придет, он придет», но обычно означает «он просто может прийти».^[6]

Смотрите также

Нормальные формы

Связанные логические темы

использованная литература

дальнейшее чтение

Бохенский, Я. М. (1959) Краткое изложение математической логики, перевод с французского и немецкого изданий Отто Берда, Дордрехт, Южная Голландия: Д. Рейдел.
Эндертон, Х. (2002) Математическое введение в логику, Harcourt/Академическая пресса, ISBN 0-12-238452-0.
Клини, С. (1967) Математическая логика, перепечатано в 2002 г., Dover Publications, ISBN 0-486-42533-9.
Райхенбах, Х. (1947). Элементы символической логики, переиздано 1980 г., Дувр, ISBN 0-486-24004-5
Витгенштейн, Л. (1921). «Logisch-философский Abhandlung», Annalen der Naturphilosophie (Leipzig), v. 14, pp. 185–262, перепечатано в английском переводе как Логико-философский трактат, Нью-Йорк и Лондон, 1922.

внешняя ссылка

ЛОГИЧЕСКИЕ ТАВТОЛОГИИ. По законам логики

ЛОГИЧЕСКИЕ ТАВТОЛОГИИ

В обычном языке слово «тавтология» означает повторение того, что уже было сказано; «Жизнь есть жизнь» или «Не повезет так не повезет».

Тавтологии бессодержательны и пусты, они не несут никакой информации.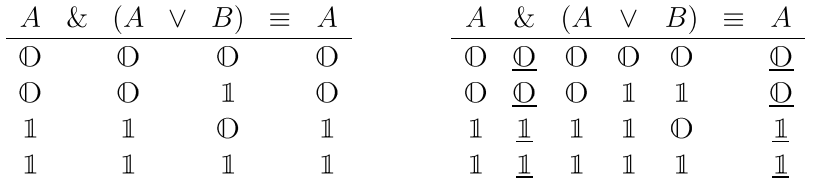 От них стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.

Иногда, правда, случается, что тавтология наполняется вдруг каким-то чужим содержанием. Попадая в определенный контекст, она как бы принимается светить отраженным светом.

Французский капитан Ла Паллис пал в битве при Павии в 1525 году. В его честь солдаты сложили дошедшую до наших дней песню «За четверть часа до смерти он был еще живой…». Понятая буквально, эта строка песни, ставшая ее названием, является тавтологией. Как таковая она совершенно пуста. Всякий человек до самой своей смерти жив. Сказать о ком-то, что он был жив за день до своей смерти или за четверть часа до нее, значит, ровным счетом ничего о нем не сказать.

И тем не менее какая-то мысль, какое-то содержание за этой строкой стоит. Оно каким-то образом напоминает о бренности человеческой жизни и особенно жизни солдата, о случайности и, так сказать, неожидаемости момента смерти и о чем-то еще другом.

Один писатель сказал о своем герое: он дожил до самой смерти, а потом умер. Козьме Пруткову принадлежит афоризм: «Не будь цветов, все ходили бы в одноцветных одеяниях». Буквально говоря, это тавтологии и пустота. Но на самом деле смысл здесь все-таки есть, хотя это и не собственный смысл данных фраз, а отражаемый или навеваемый ими смысл.

С легкой руки Л. Витгенштейна слово «тавтология» стало широко использоваться для характеристики законов логики.

Став логическим термином, оно получило строгие определения применительно к отдельным разделам логики. В общем случае логическая тавтология — это выражение, остающееся истинным независимо от того, о какой области объектов идет речь, или «всегда истинное выражение».

Все законы логики являются логическими тавтологиями. Если в формуле, представляющей закон, заменить переменные любыми постоянными выражениями соответствующей категории, эта формула превратится в истинное высказывание.

Например, в формулу «А или не-А», представляющую закон исключенного третьего, вместо переменной А должны подставляться высказывания, то есть выражения языка, являющиеся истинными или ложными. Результаты таких подстановок: «Дождь идет или не идет», «Два плюс два равно нулю или не равно нулю», «Бог существует или его нет» и тому подобное. Каждое из этих сложных высказываний является истинным. И какие бы дальнейшие высказывания ни подставлялись вместо А — как истинные, так и ложные, — результат будет тем же — полученное высказывание будет истинным.

Аналогично в случае формул, представляющих закон противоречия, закон тождества, закон двойного отрицания и т. д. «Неверно, что бог существует и не существует; что дождь идет и не идет; что я иду быстро и не иду быстро» — все это высказывания, полученные из формулы: «Неверно, что А и не-А», и все они являются истинными. «Если бога нет, то его нет; если я иду быстро, то я иду быстро; если два равно нулю, то два равно нулю» — это результаты подстановок в формулу «Если А, то А» и опять-таки истинные высказывания.

Тавтологический характер законов логики послужил отправным пунктом для многих спекуляций по их поводу.

Из тавтологии «Дождь идет или не идет» мы ничего не можем узнать о погоде. Тавтология «Неверно, что бог есть и его нет» ровным счетом ничего не говорит о существовании бога. Ни одна тавтология не несет содержательной информации о мире.

Тавтология не описывает никакого реального положения вещей. Она совместима с любым таким положением. Немыслима ситуация, сопоставлением с которой можно было бы тавтологию опровергнуть.

Эти специфические особенности тавтологий были истолкованы как несомненное доказательство отсутствия какой-либо связи законов логики с действительностью.

Такое «исключительное положение» законов логики среди всех предложений подразумевает прежде всего, что законы логики представляют собой априорные, известные до всякого опыта истины. Они не являются бессмысленными, но вместе с тем не имеют и содержательного смысла. Их невозможно ни подтвердить, ни опровергнуть ссылкой на опыт.

Действительно ли законы логики не несут никакой информации?

Если бы это было так, они по самой своей природе решительно отличались бы от законов других наук, описывающих действительность и что-то говорящих о ней.

Мысль об информационной пустоте логических законов является, конечно, ошибочной. В основе ее лежит крайне узкое истолкование опыта, способного подтверждать научные утверждения и законы. Этот опыт сводится к фрагментарным, изолированным ситуациям или фактам. Они достаточны для проверки истинности элементарных описательных утверждений типа «Идет дождь» или «Я иду быстро». Но явно недостаточны для суждения об истинности абстрактных теоретических обобщений, опирающихся не на отдельные, разрозненные факты, а на совокупный, систематический опыт. Даже законы опытных наук, подобных биологии или физике, нельзя обосновать простой ссылкой на факты и конкретику. Тем более это невозможно сделать в случае самых абстрактных из всех законов — законов логики. Они должны черпать свое обоснование из предельно широкого опыта мыслительной, теоретической деятельности. За законами логики стоит, конечно, опыт, и в этом они сходны со всеми иными научными законами. Но опыт не в форме каких-то изолированных, доступных наблюдению ситуаций, а конденсированный опыт всей истории человеческого познания.

Тавтологии обычного языка нередко наполняются содержанием, пришедшим со стороны, и светят отраженным светом. Так же обстоит дело и с логическими тавтологиями.

Изолированная от других тавтологий, оторванная от языка и от истории познания, логическая тавтология блекнет и создает впечатление отсутствия всякого содержания.

Это еще раз подтверждает мысль, что рассуждения о смысле и значении отдельных выражений языка, изъятых из среды своего существования, допустимы и справедливы только в ограниченных пределах. Нужно постоянно иметь в виду, что язык — это единый, целостный организм, части которого взаимосвязаны, взаимообусловлены и не способны действовать вне его.

Кроме того, сам язык не является некой самодостаточной системой. Он погружен в более широкую среду — среду познания и социальной жизни, когда-то создавшей его и с тех пор постоянно его воссоздающей.

How to make tautologies clear?

References

Боброва, 2016 – Боброва А.С. Графы Пирса: особенности их построения и прочтения // Логико-философские штудии. Ежегодник Ассоциации логиков СанктПетербурга. Т. 14. СПб.: Изд-во РХГА, 2016. С. 76–90.

Боброва, 2018 – Боброва А.С. Диаграмматические теории (Дж. Венн, Ч.С. Пирс) и логическое следование. Учебное пособие. М.: ВАВТ, 2018. 48 с.
Боброва, 2019 – Боброва А.С. Обучение графами. Диаграммы Ч.С. Пирса и преподавание логики (в печати).
Витгенштейн, 1994 – Витгенштейн Л. Витгенштейн Л. Логико-философский трактат //Витгенштейн Л. Философские работы (часть I) / Пер. с нем. М.С. Козловой и Ю.А. Асеева. Ч. I. М.: Гнозис, 1994. С. 3–73. Цитируется как Тр. с последующим указанием номера части и параграфа.
Лихтарников, 1999 – Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. М., 1999.
Bellucci, Pietarinen, 2016 – Bellucci F., Pietarinen A.-V. Existential Graphs As an Instrument of Logical Analysis: Part I. Alpha // The Review of Symbolic Logic. Vol. 9. No. 2. 2016. P. 209–237.

Bellucci, Pietarinen, 2017 – Bellucci F., Pietarinen A.-V. Two Dogmas of Diagrammatic Reasoning: a View from Existential Graphs // Peirce on Perception and Reasoning: From Icons to Logic /Ed. by K.A. Hull, R.K. Atkins. New York. NY: Routledge, 2017. P. 174–196.
D¨orﬂer, 2016 – D¨orﬂer W. Signs and Their Use: Peirce and Wittgenstein. Springer, Cham, 2016.
Kauﬀman, 2001 – Kauﬀman L. The Mathematics of Charles Sanders Peirce // Cybernetics & Human Knowing. Vol. 8. No. 1–2. 2001. P. 79–110.
Misak, 2016 – Misak C. Cambridge Pragmatism: From Peirce and James to Ramsey and Wittgenstein. Oxford University Press, 2016.
Nubiola, 1996 – Nubiola J. Scholarship On the Relations Between Ludwig Wittgenstein and Charles S. Peirce // Studies on the History of Logic. Proceedings of the III Symposium on History of Logic / Ed. by I. Angelelli y M. Cerezo. Berlin: Gruyter, 1996. P. 281–294.
Peirce, 1931–1958 – Peirce C.S. Collected Papers. Vols. 1–8. Cambridge: Belknap Press of Harvard University Press, 1931–1958. Цитируется как СР с номером тома и параграфа.
Peirce, 1967 – Peirce C.S. Peirce C.S. Manuscripts in the Houghton Library of Harvard University, as identiﬁed by Richard Robin // Annotated Catalogue of the Papers of Charles S. Peirce. Amherst. 1967. Цитируется как MS или R с номером манускрипта.
Pietarinen, 2005 – Pietarinen A.-V. Compositionality, Relevance and Peirce’s Logic of Existential Graphs // Axiomathes. No. 15, 2005. P. 513–540.
Pietarinen, 2006 – Pietarinen A.-V. Signs of Logic. Peircean Themes on the Philosophy of Language, Games, and Communication. Dordrecht: Springer, 2006. Pietarinen, 2015 – Pietarinen A.-V. Two Papers on Existential Graphs by Charles Peirce // Synthese. Vol. 192. No. 4. 2015. P. 881–922.
Roberts, 1973 – Roberts D. The Existential Graphs of Charles S. Peirce. The Hague: Mouton, 1973.
Wittgenstein, 2012 – Wittgenstein L. Wittgenstein in Cambridge. Letters and documents 1911–1951 / Ed. by B. McGuinness. Oxford: Blackwell, 2012.

Zeman, 1964 – Zeman J. The Graphical Logic of C.S. Peirce, dissertation, University of Chicago, 1964. Online edition, 2002. URL: users.clas.ufl.edu/jzeman/ (дата обращения: 15.01.2019).

2.6. Тавтологии логики предикатов

A не явля-

Решение. Имеем

x (¬ A(x) → y (¬ B(y)))→(B(z) → A(z)) ≡

≡x (A(x) y (¬ B(y)))→(¬ B(z) A(z)) ≡

≡¬ x (A(x) y (¬ B(y))) (¬ B(z) A(z)) ≡

≡ x (¬ A(x) y B(y)) (¬ B(z) A(z)) ≡

≡ x y (¬ A(x) B(y)) (¬ B(z) A(z)) ≡

≡ x y (¬ A(x)¬ B(z) A(z)) (B(y)¬ B(z) A(z)) .

Напомним, что формула алгебры высказываний, принимающая значение 1 (истина) при любом наборе значений входящих в нее переменных, называется тождественно истинной или тавтологией.

Формулу логики предикатов называют общезначимой (или

тождественно истинной, или тавтологией), если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в тождественно истинный предикат. Общезначимую формулу называют также логическим законом.

Формулу A назовем выполнимой, если формула ется тождественно истинной.

Формулу логики предикатов называют тождественно ложной (или противоречием), если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в тождественно ложный предикат.

Напомним, что проблемой разрешения для алгебры высказываний называется следующий вопрос: существует ли алгоритм,

позволяющий для произвольной логической формулы в конечное число шагов выяснить, является ли она тождественно истин-

ной? Как отмечалось, этот вопрос имеет положительное решение (подробно о понятии алгоритма будет рассказано ниже, на с. 63).

Проблема распознавания общезначимости формул логики предикатов существенно сложнее. Она также называется проблемой разрешения. Метод перебора всех вариантов здесь не применим, так как вариантов может быть бесконечно много. В 1936 году А. Чёрч доказал, что в общем виде проблема разрешения для логики предикатов не имеет алгоритмического решения. Сформулируем соответствующую теорему:

Теорема Чёрча. Не существует алгоритма, который для любой формулы логики предикатов устанавливает, общезначима она или нет.

Примеры

1. Доказать общезначимость следующей формулы логики предикатов:

x(P(x) → Q(x))→( x P(x) → x Q(x)).

Решение. Упростим формулу, используя равносильные преобразования:

x(P(x) → Q(x))→( x P(x) → x Q(x)) ≡

≡x (P(x) Q(x)) ( x P(x) x Q(x)) ≡

≡x (P(x) Q(x)) ( x P(x)) ( x Q(x)) ≡

≡x ((P(x) Q(x)) P(x) ) ( x Q(x)) ≡

≡x (Q(x) P(x)) ( x Q(x)) ≡

≡x (P(x) Q(x)) ( x Q(x)) ≡

≡( x P(x)) ( x Q(x)) ( x Q(x)) ≡

≡ ( x P(x)) 1 ≡ 1.

Таким образом, общезначимость формулы доказана.

2.Доказать тождественную ложность следующей формулы:

x y ((F(x)→F(y)) (F(x)→F(y)) F(x)).

Решение. Упростим формулу, используя равносильные преобразования:

x y ((F(x)→F(y)) (F(x)→F(y)) F(x)) ≡

≡A → B ≡ A B ≡

≡x y ((F(x) F(y)) (F(x) F(y)) F(x)) ≡

≡(A B) C ≡ (A C) (B C) ≡

≡x y ((F(x) F(y)) ((F(x) F(x)) (F(y) F(x)))) ≡

≡x y ((F(x) F(y)) (0 (F(y) F(x)))) ≡

≡A A ≡ 0 ≡

≡x y ((F(x) F(y)) (F(y) F(x))) ≡

≡x y (F(x) F(y) F(x)) (F(y) F(y) F(x)) ≡

≡x y (0 0) ≡ 0.

Таким образом, формула тождественно ложна, то есть является противоречием.

3.Доказать общезначимость следующей формулы:

x (A(x) (S → B(x)))→( x (A(x) → ¬ B(x)) → ¬ S ).

Решение. Проведем доказательство методом от противного. Предположим, что

x (A(x) (S → B(x)))→( x (A(x) → ¬ B(x)) → ¬ S ) ≡ 0.

Но произвольная импликация P →Q ложна в том и только в том случае, когда P истинно, а Q ложно. Следовательно, мы имеем

x (A(x) (S → B(x))) ≡ 1

x (A(x) → ¬ B(x)) → ¬ S ≡ 0.

Рассуждая аналогично, из последнего равенства получаем, что

¬ S ≡ 0 (т. е. S ≡ 1) и x (A(x) → ¬ B(x)) ≡ 1.

Из того, что x (A(x) (S → B(x))) ≡ 1, следует, что в об-

ласти определения предметной переменной x найдется константа a, для которой

A(a) (S → B(a)) ≡ 1.

Но тогда A(a) ≡ 1 и (S → B(a)) ≡ 1, а поскольку S ≡ 1, мы видим, что B(a) ≡ 1. Следовательно,

(A(a) → ¬ B(a)) ≡ 0,

что противоречит равенству x (A(x) → ¬ B(x)) ≡ 1.

тавтологий | Определение и факты

Тавтология , в логике, утверждение, составленное таким образом, что его нельзя отрицать без противоречий. Таким образом, утверждение «Все люди — млекопитающие» должно утверждать в отношении чего бы то ни было, что это либо не человек, либо млекопитающее. Но эта универсальная «истина» следует не из каких-либо фактов о реальных людях, а только из фактического использования человека и млекопитающего и, таким образом, является чисто вопросом определения.

Подробнее по этой теме

эпистемология: тавтологические и значимые суждения

Предложение называется тавтологическим, если составляющие его члены повторяются или если их можно свести к повторяющимся терминам, так что…

В исчислении высказываний — логика, в которой целые предложения связаны такими связками, как ⊃ («если… то»), · («и»), ∼ («не») и ∨ («или»), даже сложные выражения, такие как [( A B ) · ( C ⊃ ∼ B )] ⊃ ( C ⊃ ∼ A ), могут быть показаны как тавтологии, отображая в таблице истинности каждые возможная комбинация истинностных значений — T (истина) и F (ложь) — ее аргументов A, B, C и после вычисления с помощью механического процесса истинностного значения всей формулы, отмечая, что , для каждой такой комбинации формула T .Тест эффективен, потому что в любом конкретном случае общее количество различных присвоений истинностных значений переменным конечно, и вычисление истинностного значения всей формулы может выполняться отдельно для каждого присвоения истинности. значения.

Понятие тавтологии в исчислении высказываний было впервые разработано в начале 20 века американским философом Чарльзом Сандерсом Пирсом, основателем школы прагматизма и крупным логиком. Сам термин, однако, был введен британским философом австрийского происхождения Людвигом Витгенштейном, который утверждал в Logisch-Philosophische Abhandlung (1921; Tractatus Logico-Philosophicus , 1922), что все необходимые предложения являются тавтологиями и что они существуют. следовательно, в смысле, в котором все необходимые предложения говорят одно и то же, а именно, вообще ничего.

Использование Витгенштейном термина требует его расширения от исчисления высказываний до исчисления предикатов первого порядка (с функциями), которое может распространяться на классы, множества и отношения, а также на отдельные переменные (переменные, которые могут обозначать индивидов) . Это расширенное понятие тавтологии, далее объясненное английским логиком Фрэнком П. Рэмси в 1926 году, на самом деле является менее точным предшественником того, что сейчас обычно называют валидностью.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас

Позже некоторые логические позитивисты, особенно Рудольф Карнап, внесли поправки в доктрину Витгенштейна в свете того различия, что существует эффективный тест на тавтологию в исчислении высказываний, но нет такой проверки достоверности даже в низшем исчислении предикатов. Логические позитивисты считали, что в целом всякая необходимая истина (и, следовательно, всякая тавтология) выводится из некоторого правила языка; его единственная необходимость — это быть предписанным правилом определенной системы.Однако, поскольку такие выводы трудно выполнить на обычном языке — как в случае с утверждением «Все, что имеет начало во времени, должно иметь причину» — предпринимались попытки, как в книге Карнапа Der logische Aufbau der Welt (1928; The Logical Structure of the World: Pseudoproblems in Philosophy , 1967), чтобы построить искусственный язык, на котором можно было бы продемонстрировать все необходимые утверждения, обращаясь к формулам.

Таблицы истинности, тавтологии и логические эквивалентности

Математики обычно используют двузначное число . логика : Каждый оператор равен Истина или Неверно .Это называется . Закон Исключенного Среднего .

Утверждение в логике предложений строится из простых утверждений с использованием логические связки,,, и. Правда или ложь утверждения, построенного с помощью этих связок, зависит от истины или ложность его составляющих.

Например, составной оператор строится с использованием логических связок, и. Правда или ложь зависит от правды или ложность P, Q и R.

Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.

Вот таблица для отрицания:

Эта таблица проста для понимания. Если P равно истинно , его отрицание ложно . Если P ложно , то истинно .

должно быть истинно , когда и P, и Q равны истина и ложь иначе:

равно истинно , если либо P равно истинно , либо Q равно правда (или оба — помните, что мы используем «или» в инклюзивном смысле). Только ложно , если и P, и Q равны ложь .

Вот таблица для логического вывода:

Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие пример:

«Если вы получите пятерку, я дам вам доллар.»

Утверждение будет истинным , если я сдержу свое обещание и ложно , если я этого не сделаю.

Предположим, что это истинное , что вы получаете A, и это истинное что я даю вам доллар. Поскольку я сдержал свое обещание, подразумевается правда . Это соответствует первой строке в таблице.

Предположим, что истинно , что вы получили пятерку, но это ложно что я даю вам доллар. Поскольку я не сдержал обещание , подразумевается ложь .Это соответствует второму строка в таблице.

Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам доллар, я не нарушил свое обещание. Таким образом, значение не может быть false, поэтому (поскольку это двузначная логика) должно быть истинным. Этот объясняет последние две строки таблицы.

означает, что P и Q равны эквивалент . Таким образом, двойное значение истинно , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.

Вы должны помнить — или уметь составлять — таблицы истинности для логических связок. Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Проще продемонстрировать что делать, чем описывать словами, чтобы вы увидели порядок действий отработано в примерах.

Замечание. (а) Когда вы конструируете истину таблице, вы должны рассмотреть все возможные назначения True (T) и Ложь (F) для операторов компонентов.Например, предположим, что операторы компонентов — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, значит, есть возможности.

Когда вы перечисляете возможности, вы должны присваивать значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографическая упорядоченность . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:

(б) Существуют разные способы составления таблиц истинности.Вы можете для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно наращивая столбец для «первичной» связки.

Я напишу подробности, построив столбцы для каждого «кусок» составного высказывания и постепенно наращивая к составному оператору. Любой стиль хорош, пока ты показываешь достаточно работы, чтобы оправдать ваши результаты.

Пример. Постройте таблицу истинности для формула.

Сначала я перечисляю все альтернативы для P и Q.

Затем в третьем столбце я перечисляю значения на основе значений P. Я использую таблицу истинности для отрицание: когда P истинно ложно, а когда P ложно, правда.

В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь («F»), если P истинно («T») и Q ложно («F»).

Пятый столбец дает значения для моего составного выражения.Это «и» (третий столбец) и (четвертый столбец). «И» верно, только если обе части «и» верны; в противном случае это ложь. Итак, я смотрю на третья и четвертая колонки; если оба верны («T»), я положил T в пятом столбце, иначе я поставил F.

Тавтология — это формула, которая «всегда истина «— то есть верно для каждого присвоения истины ценности к его простым компонентам. Вы можете думать о тавтологии как о правило логики .

Противоположность тавтологии — . противоречие , формула, которая «всегда ложна». В другими словами, противоречие ложно для каждого приписывания истины ценности к его простым компонентам.

Пример. Показать, что это тавтология.

Я составляю таблицу истинности и показываю, что формула всегда верна.

Последний столбец содержит только буквы T. Следовательно, формула представляет собой тавтология.

Пример. Постройте таблицу истинности для.

Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством связок или множества простых утверждений довольно утомительно и подвержен ошибкам. Хотя могут быть некоторые применения этого (например, для цифровых схем), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).

Дело здесь в том, чтобы понять, как истинное значение сложного утверждение зависит от значений истинности его простых утверждений и его логические связки.В большинстве работ математики обычно не используйте операторы, которые очень сложны с логической точки зрения Посмотреть.

Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинным значение не может быть определено.

(b) Предположим, что это неверно. Расскажи истинно ли Q, ложно или его истинное значение не может быть определено.

(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно.Следовательно, Q должно быть ложным.

(b) Утверждение «если-то» неверно, когда часть «если» истина, а часть «тогда» — ложь. Поскольку ложно, верно. Утверждение «и» верно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.

Пример. Предположим

» » правда.

«» ложно.

«У Кэлвина Баттерболла фиолетовые носки» — правда.

Определите истинность утверждения

Для простоты пусть

P = «».

Q = «».

R = «У Кэлвина Баттерболла фиолетовые носки».

Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q, и R, я установил таблицу истинности с единственной строкой, используя данный значения для P, Q и R:

Следовательно, утверждение верно .

Пример. Определите истинное значение утверждение

Утверждение «» ложно.Ты не можешь сказать есть ли в заявлении «Икабод Ксеркс шоколад» кексы «верно или неверно, но это не имеет значения. Если «если» часть утверждения «если-то» ложна, тогда утверждение «если-то» верно. (Проверить правду таблица, если вы не уверены в этом!) данное утверждение должно быть верным.

Два оператора X и Y логически равны . эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простому элементу операторы , составляющие X и Y, операторы X и Y имеют идентичные значения истинности.

С практической точки зрения вы можете заменить выражение в доказательство любым логически эквивалентным утверждением.

Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтология — это есть ли «все ли Т в его столбце». Однако проще создать таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.

Пример. Покажите, что и логически эквивалентны.

Поскольку столбцы для и идентичны, два оператора логически эквивалент. Эта тавтология называется условной . Дизъюнкция . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.

Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.

Когда тавтология имеет форму двоякого условия, два утверждения составляющие двусмысленность, логически эквивалентны.Следовательно, вы может заменить одну сторону на другую без изменения логического имея в виду.

Вам часто нужно будет отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое заявления.

Пример. Запишите отрицание следующие утверждения, упрощающие так, чтобы только простые утверждения отрицается.

(а)

(б)

(а) Я отвергаю данное утверждение, а затем упрощаю, используя логические эквивалентности.Я дал названия логических эквивалентов на так что вы можете видеть, какие из них я использовал.

(б)

Я показал это и логически эквивалентен в предыдущем примере.

В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать по математике. В идея состоит в том, чтобы преобразовать слово-утверждение в символическое утверждение, тогда используйте логические эквивалентности, как в предыдущем примере.

Пример. Используйте закон ДеМоргана, чтобы написать отрицание следующего утверждения, упрощая так, чтобы отрицаются только простые утверждения:

«Кальвина нет дома, или Бонзо в кино».

Пусть C будет утверждением «Кальвин дома» и пусть B будет заявление «Бонзо в движении». Данное заявление . Я должен опровергнуть это утверждение, затем упростите:

Результат: «Кальвин дома, а Бонзо нет в доме. кино».

«Если Фиби покупает пиццу, то Кэлвин покупает попкорн».

Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет заявление «Кэлвин покупает попкорн». Данное заявление . Чтобы упростить отрицание, я буду использовать тавтологию Conditional Disjunction , которая гласит:

То есть я могу заменить на (или наоборот).

Итак, вот отрицание и упрощение:

Результат: «Фиби покупает пиццу, а Кэлвин не покупает. попкорн ».

Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к задачи, связанные с построением обратного, обратного и противоположность утверждению «если-то».

Пример. Заменить следующую инструкцию на его противоположность:

«Если x и y рациональны, значит рационально.»

В силу контрапозитивной эквивалентности это утверждение совпадает с утверждением «Если нерационально, значит, это не так. что и x, и y рациональны «.

Этот ответ верен в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей легче понять положительное утверждение, чем отрицательное заявление.

По определению действительное число иррациональное , если это не рационально.Так что я мог бы заменить часть «если» в противоположно выражению «иррационально».

«Тогда» часть контрапозитива — это отрицание «и» заявление. Вы могли бы повторить это так: «Это не случай, когда и x рационально, и y рационально «. (Слово «оба» гарантирует, что отрицание применимо ко всему «И», а не только «х рационально».)

По закону ДеМоргана это эквивалентно: «x нерационально или y не рационально «. В качестве альтернативы я мог бы сказать:» x есть иррационально или y иррационально ».

Объединив все вместе, я мог бы выразить контрапозитив как: «Если иррационально, то либо x иррационально или y иррационально «.

(Как обычно, я добавил слово «либо», чтобы было ясно, что часть «затем» — это целое «или».)

Пример. Покажите, что обратное и обратное условному выражению логически эквивалентны.

Позвольте быть условным. Обратное. Обратное.

Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.

Начнем с:

Помните, что я могу заменить выражение логическим эквивалент. Например, на последнем шаге я заменил Q, потому что два оператора эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление

«Если, тогда.»

Постройте обратное, обратное и противоположное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и противоположное — используя свои знания алгебры.

Обратное — «Если, то».

Контрапозитив — «Если, то».

Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно контрапозитивный, контрапозитивный тоже должен быть ложным.

Верно и обратное. Обратное логически эквивалентно наоборот, поэтому верно и обратное.

\новая страница

\ centerline {\ bigssbold Список тавтологий}

Контактная информация

Домашняя страница Брюса Икенаги

Авторские права 2019 Брюс Икенага

Тавтология (логика) | Психология вики

Индекс философии: Эстетика · Эпистемология · Этика · Логика · Метафизика · Сознание · Философия языка · Философия разума · Философия науки · Социальная и политическая философия · Философия · Философы · Список списков

В логике высказываний тавтология (от греческого слова ταυτολογία) — это утверждение, которое функционально истинно истинно — i.е. это универсально верно или верно в любой интерпретации (или модели, или оценке). Например, утверждение «Если идет дождь, значит, идет дождь» — тавтология. Каждая теорема логики высказываний является тавтологией, и поэтому мы можем эквивалентно определить «тавтологию» как любую теорему логики высказываний, т. Е. любое утверждение, которое выводится из пустого множества в некоторой системе вывода логики высказываний, такой как естественная система вывода. Этот термин часто ошибочно применяется к любой достоверности (или теореме) логики первого порядка, хотя он применяется только к надлежащему подмножеству таких достоверностей.Термин был первоначально введен Людвигом Витгенштейном.

Отрицание тавтологии — это явно противоречие, а отрицание противоречия — явно тавтология. Иногда произвольная тавтология обозначается через, а произвольное противоречие — через, последнее из которых можно определить как, т. Е. Отрицание первого. (Конечно, первое можно определить как отрицание второго.) Предложение, которое не является ни тавтологией (всегда истинным), ни противоречием (всегда ложным), является логически случайным, т.е.е., может быть истинным или ложным, в зависимости от интерпретации его нелогических символов.

Тавтологии против валидности [править | править источник]

Однако использование «тавтологии» можно распространить на логику первого порядка, поскольку она включает логику высказываний. Его можно расширить, включив в него предложения, количественно выраженные в следующем смысле. Назовите любое утверждение, которое не является функциональным составом истинности (т. Е. Не конъюнкцией, дизъюнкцией, условием и т. Д.), Булевым атомом.Тогда каждое атомарное предложение является булевым атомом, как и каждое количественное предложение, т. Е. те из формы или. Например, и являются логическими атомами, а пока — нет. Тогда утверждение логики первого порядка является тавтологией, если единообразное изменение названия каждого из его булевых атомов дает тавтологию в пропозициональном смысле. Таким образом, это не тавтология, так как ее булевское изменение букв дает, в то время как это тавтология. Можно было бы дополнительно расширить это понятие, приняв утверждения как классы эквивалентности утверждений, каждое из которых замкнуто в силу того, что его элементы являются вариантами друг друга (например,грамм. ∀xP (x) является вариантом ∀yP (y) , и аналогичным образом при замене любой другой переменной на x в первом случае). Тогда булевское изменение букв дает тавтологию, поскольку каждый дизъюнкт попадает в один и тот же класс эквивалентности.

Эффективная процедура проверки того, является ли пропозициональная формула тавтологией, осуществляется с помощью таблиц истинности. Однако в качестве эффективной процедуры таблицы истинности ограничены тем фактом, что количество логических интерпретаций (или присвоений истинностных значений), которые должны быть проверены, увеличивается как 2 ^k, где k — число переменных в формуле.Алгебраические, символьные или трансформационные методы упрощения формул быстро становятся практической необходимостью для преодоления «грубой силы», исчерпывающий поиск стратегий табличных процедур принятия решений.

Эта статья кажется необъективной или не имеет ссылок.
Вы можете помочь Psychology Wiki, цитируя соответствующие ссылки.
См. Соответствующее обсуждение на странице обсуждения.

Нормальные формы [править | править источник]

Связанные логические темы [edit | править источник]

Связанные темы [править | править источник]

Определение тавтологии Merriam-Webster

тау · тол · о · гы | \ tȯ-ˈtä-lə-jē \
1а : ненужное повторение идеи, утверждения или слова Риторическое повторение, тавтология («всегда и навсегда»), банальные метафоры и короткие абзацы — это часть жаргона.- Филип Ховард
б : пример такого повторения Фраза «новичок, который только начал» — тавтология.
2 логика : утверждение, которое истинно только в силу своей логической формы. Логическая комбинация предложений, которая всегда истинна, независимо от истинности или ложности составляющих предложений, известна как «тавтология».«- Руди Ракер… теперь было выдвинуто возражение, что вся теория естественного отбора опиралась на тавтологию:« Кто выживает? Самый приспособленный. Кто лучше всех? Те, кто выживают », — Эрнст Майр.
Тавтология и логическая эквивалентность | Бесплатная помощь с домашним заданием
В письменной форме утверждения можно оценивать относительно друг друга.В зависимости от их отношения они могут рассматриваться как тавтология или логическая эквивалентность.
Тавтология:
Если мы рассмотрим предложение, Это круто или это не круто , это дизъюнкция утверждения и его отрицания. Этот тип предложений может быть представлен дизъюнкцией pv ~ p. Поскольку дизъюнкция истинна, если хотя бы одна из ее составляющих истинна, pv ~ q всегда истинно, потому что одно из p и ~ q всегда истинно. Таблица истинности для pv ~ q следующая.
Здесь все значения истинности составного утверждения pv ~ q истинны для всех возможных значений истинности утверждения p. Здесь pv ~ q называется тавтологией.
Таким образом, тавтология является составным суждением, которое истинно для всех возможных комбинаций значений истинности его компонентов.
Логический эквивалент:
Рассмотрим два утверждения.
р: Я много работаю
в: Я проиграю
Если мы рассмотрим два предложения, Если я не буду много работать, я проиграю и Я много работаю или проиграю означают то же самое.Заметим то же самое символически с помощью таблиц истинности.
~ p -> q: Если я не буду много работать, то проиграю
pvq: Я много работаю или проиграю
Здесь, если мы можем заметить, что значения истинности как ~ p-> q, так и pvq одинаковы для всех возможных комбинаций значений истинности p и q. Итак, эти два предложения логически эквивалентны.
Таким образом, два составных оператора называются логически эквивалентными , если все их значения истинности одинаковы для всех возможных комбинаций его компонентов.
Вам также нужна помощь с вашими учебными навыками? Взгляните на наши репетиторские услуги по обучению навыкам.
SchoolTutoring Academy — ведущая компания в области образовательных услуг для школьников и школьников. Мы предлагаем репетиторские программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Вашингтоне, посетите: Репетиторство в Вашингтоне.
2.5: Логические эквивалентности — математика LibreTexts
Тавтология и противоречие
Определение
A тавтология — суждение, которое всегда истинно, независимо от значений истинности содержащихся в нем пропозициональных переменных.
Определение
Утверждение, которое всегда ложно, называется противоречием .
Утверждение, которое не является ни тавтологией, ни противоречием, называется случайностью . Термин «случайность» не так широко используется, как термины тавтология и противоречие.
Пример \ (\ PageIndex {1} \ label {например: logiceq-01} \)
Из следующей таблицы истинности \ [\ begin {array} {| c | c | c | c |} \ hline p & \ overline {p} & p \ vee \ overline {p} & p \ wedge \ overline {p } \\ \ hline \ text {T} & \ text {F} & \ text {T} & \ text {F} \\ \ text {F} & \ text {T} & \ text {T} & \ text {F} \\ \ hline \ end {array} \] мы получаем, что \ (p \ vee \ overline {p} \) — тавтология, а \ (p \ wedge \ overline {p} \) — противоречие.
На словах \ (p \ vee \ overline {p} \) говорит, что либо утверждение \ (p \) истинно, либо утверждение \ (\ overline {p} \) истинно (то есть \ (p \) ложно). Это утверждение всегда верно.
Составной оператор \ (p \ wedge \ overline {p} \) утверждает, что \ (p \) истинно, и в то же время \ (\ overline {p} \) также истинно (что означает \ (p \) ложно). Это явно невозможно. Следовательно, \ (p \ wedge \ overline {p} \) должно быть ложным.
Пример \ (\ PageIndex {2} \ label {например: logiceq-02} \)
Покажите, что \ ((p \ Rightarrow q) \ Leftrightarrow (\ overline {q} \ Rightarrow \ overline {p}) \) является тавтологией.
Ответ
Мы можем использовать таблицу истинности для проверки утверждения. \ [\ begin {array} {| * {7} {c |}} \ hline p & q & p \ Rightarrow q & \ overline {q} & \ overline {p} & \ overline {q} \ Rightarrow \ overline {p} & (p \ Rightarrow q) \ Leftrightarrow (\ overline {q} \ Rightarrow \ overline {p}) \\ \ hline \ text {T} & \ text {T} & \ text {T} & \ text {T} & \ text {T} & \ text {F} & \ text {T} \\ \ text {T} & \ text {F} & \ text {F} & \ text {T} & \ text { F} & \ text {F} & \ text {T} \\ \ text {F} & \ text {T} & \ text {T} & \ text {F} & \ text {T} & \ text {T } & \ text {T} \\ \ text {F} & \ text {F} & \ text {T} & \ text {T} & \ text {T} & \ text {T} & \ text {T} \\ \ hline \ end {array} \] Обратите внимание, как мы работаем над каждым компонентом составного оператора отдельно, прежде чем объединить их для получения окончательного ответа.
Пример \ (\ PageIndex {3} \ label {например: logiceq-03} \)
Покажите, что аргумент
«Если \ (p \) и \ (q \), то \ (r \). Следовательно, если не \ (r \), то не \ (p \) или не \ (q \) ».
действителен. Другими словами, покажите, что логика, использованная в аргументе, верна.
Ответ
Символически аргумент гласит: \ [[(p \ wedge q) \ Rightarrow r] \ Rightarrow [\ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q})].\ label {eqn: tautology} \] Мы хотим показать, что это тавтология. Это легко проверить с помощью таблицы истинности. Мы также можем утверждать, что это составное утверждение всегда верно, показывая, что оно никогда не может быть ложным.
Предположим, напротив, что ([eqn: tautology]) ложно для некоторых вариантов \ (p \), \ (q \) и \ (r \). Тогда \ [(p \ wedge q) \ Rightarrow r \ quad \ mbox {должно быть истинным}, \ qquad \ mbox {и} \ qquad \ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q }) \ quad \ mbox {должно быть ложным}. \] Чтобы второе утверждение было ложным, нам нужно, чтобы \ [\ overline {r} \ quad \ mbox {было истинным}, \ qquad \ mbox {и} \ qquad \ overline {p} \ vee \ overline {q} \ quad \ mbox {неверно}.\] Они, в свою очередь, подразумевают, что \ (r \) ложно, и оба \ (\ overline {p} \) и \ (\ overline {q} \) ложны; следовательно, и \ (p \), и \ (q \) истинны. Это сделало бы \ ((p \ wedge q) \ Rightarrow r \) ложным, что противоречит предположению, что это правда. Таким образом, ([eqn: тавтология]) не может быть ложным, это должна быть тавтология.
практическое упражнение \ (\ PageIndex {1} \ label {he: logiceq-01} \)
Используйте таблицу истинности, чтобы показать, что \ [[(p \ wedge q) \ Rightarrow r] \ Rightarrow [\ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q})] \] является тавтология.
Ответ
Нам нужно восемь комбинаций значений истинности в \ (p \), \ (q \) и \ (r \). Мы перечисляем значения истинности в соответствии со следующим соглашением. В первом столбце для значений истинности \ (p \) заполните верхнюю половину буквой T, а нижнюю половину — F. В следующем столбце для значений истинности \ (q \) повторите тот же шаблон отдельно, с верхней половиной и нижней половиной. Итак, мы разделим верхнюю половину второго столбца на две половины, заполним верхнюю половину буквой Т, а нижнюю половину буквой F.Аналогичным образом разделите нижнюю половину второго столбца на две половины, заполните верхнюю половину буквой T, а нижнюю половину F. Повторите тот же шаблон с третьим столбцом для значений истинности \ (r \), и так далее, если у нас есть больше пропозициональных переменных.
Заполните следующую таблицу: \ [\ begin {array} {| * {11} {c |}} \ hline p & q & r & p \ wedge q & (p \ wedge q) \ Rightarrow r & \ overline { r} & \ overline {p} & \ overline {q} & \ overline {p} \ vee \ overline {q} & \ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q}) & [(p \ wedge q) \ Rightarrow r] \ Rightarrow [\ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q})] \\ \ hline \ text {T} & \ text {T } & \ text {T} &&&&&&&& \\ \ text {T} & \ text {T} & \ text {F} &&&&&&&& \\ \ text {T} & \ text {F} & \ text {T} &&&&&&&&& \\ \ text {T} & \ text {F} & \ text {F} &&&&&&&& \\ \ text {F} & \ text {T} & \ text {T} &&&&&&&& \\ \ text {F} & \ text {T } & \ text {F} &&&&&&&& \\ \ text {F} & \ text {F} & \ text {T} &&&&&&&& \\ \ text {F} & \ text {F} & \ text {F} &&&&&&&&& \\ \ hline \ end {array} \] Вопрос: Если в предложении четыре пропозициональные переменные, сколько строк в таблице истинности?
Биконусность и эквивалентность
Примечание
Две логические формулы \ (p \) и \ (q \) — это , логически эквивалентные , обозначенные \ (p \ Equiv q, \) (определены в разделе 2.2) тогда и только тогда, когда \ (p \ Leftrightarrow q \) — тавтология.
Мы равны , а не , говоря, что \ (p \) равно \ (q \). Поскольку \ (p \) и \ (q \) представляют два разных утверждения, они не могут быть одинаковыми. Мы говорим, что они всегда производят одно и то же значение истинности, независимо от значений истинности лежащих в основе пропозициональных переменных. Вот почему мы пишем \ (p \ Equiv q \) вместо \ (p = q \).
Пример \ (\ PageIndex {4} \ label {например: logiceq-04} \)
Мы узнали, что \ [p \ Leftrightarrow q \ Equiv (p \ Rightarrow q) \ wedge (q \ Rightarrow p), \], поэтому мы называем \ (p \ Leftrightarrow q \) двухусловным утверждением.
Пример \ (\ PageIndex {5} \ label {например: logiceq-05} \)
Используйте таблицы истинности для проверки следующих эквивалентных утверждений.
\ (p \ Rightarrow q \ Equiv \ overline {p} \ vee q \). [эквивалент1]
\ (п \ клин (д \ ви г) \ экв (р \ клин д) \ ви (р \ клин г) \). [эквивалент2]
Ответ
Таблицы истинности для (a) и (b) показаны ниже. \ [\ begin {array} {| * {5} {c |}} \ hline p & q & p \ Rightarrow q & \ overline {p} & \ overline {p} \ vee q \\ \ hline \ text { T} & \ text {T} & \ text {T} & \ text {F} & \ text {T} \\ \ text {T} & \ text {F} & \ text {F} & \ text {F } & \ text {F} \\ \ text {F} & \ text {T} & \ text {T} & \ text {T} & \ text {T} \\ \ text {F} & \ text {F } & \ text {T} & \ text {T} & \ text {T} \\ \ hline \ end {array} \] \ [% \ arraygap {1.25} \ begin {array} {| * {8} {c |}} \ hline p & q & r & q \ vee r & p \ wedge (q \ vee r) & p \ wedge q & q \ wedge r & (p \ wedge q) \ vee (p \ wedge r) \\ \ hline \ text {T} & \ text {T} & \ text {T} & \ text {T} & \ text {T} \ phantom {(q \ vee {})} & \ text {T} & \ text {T} & \ text {T} \\ \ text {T} & \ text {T} & \ text {F} & \ text { T} & \ text {T} \ phantom {(q \ vee {})} & \ text {T} & \ text {F} & \ text {T} \\ \ text {T} & \ text {F} & \ text {T} & \ text {T} & \ text {T} \ phantom {(q \ vee {})} & \ text {F} & \ text {T} & \ text {T} \\ \ текст {T} & \ text {F} & \ text {F} & \ text {F} & \ text {F} \ phantom {(q \ vee {})} & \ text {F} & \ text {F } & \ text {F} \\ \ text {F} & \ text {T} & \ text {T} & \ text {T} & \ text {F} \ phantom {(q \ vee {})} & \ text {F} & \ text {F} & \ text {F} \\ \ text {F} & \ text {T} & \ text {F} & \ text {T} & \ text {F} \ phantom {(q \ vee {})} & \ text {F} & \ text {F} & \ text {F} \\ \ text {F} & \ text {F} & \ text {T} & \ text { T} & \ text {F} \ phantom {(q \ vee {})} & \ text {F} & \ text {F} & \ text {F} \\ \ text {F} & \ text {F} & \ text {F} & \ text {T} & \ text {F} \ phantom {(q \ vee {})} & \ text {F} & \ text {F} & \ text {F} \\ \ hline \ end {array} \] Пример ([Equiv1]) — важный результат.Он говорит, что \ (p \ Rightarrow q \) истинно, когда происходит одно из этих двух событий: (i) когда \ (p \) ложно, (ii) в противном случае (когда \ (p \) истинно) \ (q \) должно быть правдой.
практическое упражнение \ (\ PageIndex {2} \ label {he: logiceq-02} \)
Используйте таблицы истинности, чтобы установить эти логические эквивалентности.
\ (p \ Rightarrow q \ Equiv \ overline {q} \ Rightarrow \ overline {p} \)
\ (п \ ви п \ эквив \)
\ (p \ wedge q \ Equiv \ overline {\ overline {p} \ vee \ overline {q}} \)
\ (p \ Leftrightarrow q \ Equiv (p \ Rightarrow q) \ wedge (q \ Rightarrow p) \)
Ответ
Мы накрыли стол для (а), а остальное оставляем вам.
\ [\ begin {array} [t] {| c | c | c | c | c | c |} \ hline p & q & p \ Rightarrow q & \ overline {q} & \ overline {p} & \ overline {q} \ Rightarrow \ overline {p} \\ \ hline \ text {T} & \ text {T} &&&& \\ \ text {T} & \ text {F} &&&& \\ \ text {F} & \ текст {T} &&&& \\ \ text {F} & \ text {F} &&&& \\ \ hline \ end {array} \]
практическое упражнение \ (\ PageIndex {3} \ label {he: logiceq-03} \)
Логическая связка исключающая или, обозначаемая \ (p \ veebar q \), означает либо \ (p \), либо \ (q \), но не то и другое вместе.Следовательно, \ [p \ veebar q \ Equiv (p \ vee q) \ wedge \ overline {(p \ wedge q)} \ Equiv (p \ wedge \ overline {q}) \ vee (\ overline {p} \ wedge q). \] Постройте таблицу истинности, чтобы проверить это утверждение
Недвижимость
Свойства логической эквивалентности. Обозначим через \ (T \) и \ (F \) тавтологию и противоречие соответственно. У нас есть следующие свойства для любых пропозициональных переменных \ (p \), \ (q \) и \ (r \).
Коммутативные свойства : \ (\ begin {array} [t] {l} p \ vee q \ Equiv q \ vee p, \\ p \ wedge q \ Equiv q \ wedge p.\ end {array} \)
Ассоциативные свойства : \ (\ begin {array} [t] {l} (p \ vee q) \ vee r \ Equiv p \ vee (q \ vee r), \\ (p \ wedge q) \ клин г \ эквив р \ клин (д \ клин г). \ конец {массив} \)
Распределительные законы : \ (\ begin {array} [t] {l} p \ vee (q \ wedge r) \ Equiv (p \ vee q) \ wedge (p \ vee r), \\ p \ клин (q \ vee r) \ эквив (p \ wedge q) \ vee (p \ wedge r). \ end {array} \)
Идемпотентные законы : \ (\ begin {array} [t] {l} p \ vee p \ Equiv p, \\ p \ wedge p \ Equiv p.\ end {array} \)
Законы Де Моргана : \ (\ begin {array} [t] {l} \ overline {p \ vee q} \ Equiv \ overline {p} \ wedge \ overline {q}, \\ \ overline { p \ wedge q} \ Equiv \ overline {p} \ vee \ overline {q}. \ end {array} \)
Законы исключенного среднего или обратные законы : \ (\ begin {array} [t] {l} p \ vee \ overline {p} \ Equiv T, \\ p \ wedge \ overline {p} \ Equiv F. \ end {array} \)
Законы идентичности : \ (\ begin {array} [t] {l} p \ vee F \ Equiv p, \\ p \ wedge T \ Equiv p.\ end {array} \)
Законы господства : \ (\ begin {array} [t] {l} p \ vee T \ Equiv T, \\ p \ wedge F \ Equiv F. \ end {array} \)
Эквивалентность импликации и ее контрапозитива: \ (p \ Rightarrow q \ Equiv \ overline {q} \ Rightarrow \ overline {p} \).
Запись импликации как дизъюнкции: \ (p \ Rightarrow q \ Equiv \ overline {p} \ vee q \).
Отрицание импликации: \ (\ overline {p \ Rightarrow q} \ Equiv p \ wedge \ overline {q} \)
Убедитесь, что вы поняли и запомнили последние три эквивалента, потому что мы будем часто использовать их в оставшейся части курса.
Может быть нелегко запомнить названия всех этих свойств; однако все они должны иметь для вас смысл. Важное имя — законы Де Моргана. Объясним их словами и сравним с аналогичными операциями над действительными числами,
Коммутативные свойства : Короче говоря, они говорят, что «порядок работы не имеет значения». Неважно, какое из двух логических утверждений идет первым, результат конъюнкции и дизъюнкции всегда дает одно и то же значение истинности.Сравните это со сложением действительных чисел: \ (x + y = y + x \). Вычитание не коммутативно, потому что не всегда верно, что \ (x-y = y-x \). Это объясняет, почему мы должны убедиться, что операция коммутативна.
Ассоциативные свойства : грубо говоря, эти свойства также говорят, что «порядок работы не имеет значения». Однако между ними и коммутативными свойствами есть ключевое различие.
Коммутативные свойства применяются к операциям с двумя логическими операторами , но ассоциативные свойства включают трех логических операторов .Поскольку \ (\ wedge \) и \ (\ vee \) — это двоичных операций, мы можем работать только с парой операторов за раз. Учитывая три утверждения \ (p \), \ (q \) и \ (r \), появляющиеся в этом порядке, с какой парой операторов мы должны работать в первую очередь? Ответ: неважно. Порядок , объединяющий (отсюда и термин ассоциативный), не имеет значения для ассоциативных свойств.
Важным следствием ассоциативности является следующее: поскольку не имеет значения, с какой парой операторов мы должны выполнить операцию первой, мы можем убрать круглые скобки и написать, например, \ [p \ vee q \ vee r \] не беспокоясь о путанице.
Не все операции ассоциативны. Вычитание не ассоциативно. Учитывая три числа 5, 7 и 4 в указанном порядке, как нам провести два вычитания? Какую интерпретацию мы должны использовать: \ [(5-7) -4, \ qquad \ mbox {или} \ qquad 5- (7-4)? \] Поскольку они приводят к разным результатам, мы должны быть осторожны, где размещать круглые скобки.
Законы распределения : Когда мы смешиваем две различных операций с тремя логическими операторами, одна из них должна сначала работать с парой операторов, образуя «внутреннюю» операцию.2 = x \), где \ (x \) — действительное число. Это верно только тогда, когда \ (x = 0 \) или \ (x = 1 \). Но логические эквивалентности \ (p \ vee p \ Equiv p \) и \ (p \ wedge p \ Equiv p \) верны для всех \ (p \).
Законы Де Моргана : Когда мы отрицаем дизъюнкцию (соответственно, конъюнкцию), мы должны отрицать два логических утверждения и изменять операцию с дизъюнкции на конъюнкцию (соответственно, с конъюнкции на дизъюнкцию).
Законы исключенного среднего или обратные законы : Любое утверждение либо истинно, либо ложно, следовательно, \ (p \ vee \ overline {p} \) всегда истинно.Точно так же утверждение не может быть одновременно истинным и ложным, поэтому \ (p \ wedge \ overline {p} \) всегда ложно.
Законы идентичности : Сравните их с уравнением \ (x \ cdot1 = x \): значение \ (x \) не изменится после умножения на 1. Мы называем число 1 мультипликативным тождеством. Для логических операций идентичность дизъюнкции — F, а идентичность конъюнкции — T.
Законы доминирования : Сравните их с уравнением \ (x \ cdot0 = 0 \) для действительных чисел: результат всегда равен 0, независимо от значения \ (x \).«Ноль» для дизъюнкции — T, а «ноль» для конъюнкции — F.
Пример \ (\ PageIndex {6} \ label {например: logiceq-07} \)
Что такое отрицание \ (2 \ leq x \ leq 3 \)? Дайте логическое объяснение, а также графическое объяснение.
Ответ
Неравенство \ (2 \ leq x \ leq 3 \) означает \ [(x \ geq 2) \ wedge (x \ leq 3). \] Его отрицание, согласно законам Де Моргана, равно \ [(x <2 ) \ vee (x> 3). \] Неравенство \ (2 \ leq x \ leq 3 \) дает замкнутый интервал.Его отрицание дает два открытых интервала. Их графическое изображение на числовой прямой показано ниже.
(130,60) (- 20, -45) (-20,0) (1,0) 130 (30, 0) (30,0) 2 (20, -25) (20,20) \ (2 \) (50, -25) (20,20) \ (3 \) (0, -50) (90,20) \ ((x \ geq 2) \ клин (x \ leq 3) \) (30, 0) (1,0) 30
(130,60) (- 20, -45) (-20,0) (1,0) 130 (30, 0) (30,0) 2 (20, -25) (20,20) \ (2 \) (50, -25) (20,20) \ (3 \) (0, -50) (90,20) \ ((x <2) \ vee (x> 3) \) (-20, 0 ) (1,0) 48 (62, 0) (1,0) 48
Обратите внимание на две конечные точки 2 и 3.Когда мы принимаем отрицание, они меняются от включения к исключению.
практическое упражнение \ (\ PageIndex {4} \ label {he: logiceq-04} \)
Поскольку \ (0 \ leq x \ leq 1 \) означает «\ (x \ geq 0 \) и \ (x \ leq 1 \)», его отрицание должно быть «\ (x <0 \) или \ (x > 1 \) ». Объясните, почему неуместно и действительно неправильно писать «\ (0> x> 1 \)».
практическое упражнение \ (\ PageIndex {5} \ label {he: logiceq-05} \)
Разверните \ ((p \ vee q) \ wedge (r \ vee s) \).
Пример \ (\ PageIndex {7} \ label {например: logiceq-09} \)
Мы использовали таблицу истинности, чтобы проверить, что \ [[(p \ wedge q) \ Rightarrow r] \ Rightarrow [\ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q})] \] это тавтология.Мы можем использовать свойства логической эквивалентности, чтобы показать, что этот составной оператор логически эквивалентен \ (T \). За такими доказательствами обычно труднее следовать, поэтому рекомендуется давать объяснения на каждом этапе. Вот полное доказательство: \ [% \ arraygap {1.2} \ begin {array} {lcl @ {\ quad} l} [(p \ wedge q) \ Rightarrow r] \ Rightarrow [\ overline {r} \ Rightarrow ( \ overline {p} \ vee \ overline {q})] & \ Equiv & \ overline {(p \ wedge q) \ Rightarrow r} \ vee [\ overline {r} \ Rightarrow (\ overline {p} \ vee \ overline {q})] & \ mbox {(импликация как дизъюнкция)} \\ & \ Equiv & \ overline {(p \ wedge q) \ Rightarrow r} \ vee [\ overline {\ overline {p} \ vee \ overline {q }} \ Rightarrow r] & \ mbox {(импликация как дизъюнкция)} \\ & \ Equiv & \ overline {(p \ wedge q) \ Rightarrow r} \ vee [(p \ wedge q) \ Rightarrow r] & \ mbox {(Закон Де Моргана)} \\ & \ Equiv & T & \ mbox {(обратный закон)} \ end {array} \] Это именно то, что мы назвали методом слева направо для доказательства идентичности (в данном случае , логическая эквивалентность).
Пример \ (\ PageIndex {8} \ label {например: logiceq-10} \)
Запишите \ (\ overline {p \ Rightarrow q} \) как союз.
Ответ
Важно помнить, что \ [\ overline {p \ Rightarrow q} \ not \ Equiv q \ Rightarrow p, \] и \ [\ overline {p \ Rightarrow q} \ not \ Equiv \ overline {p} \ Rightarrow \ overline {q} \] тоже. Вместо этого, поскольку \ (p \ Rightarrow q \ Equiv \ overline {p} \ vee q \), из закона Де Моргана следует, что \ [\ overline {p \ Rightarrow q} \ Equiv \ overline {\ overline {p} \ vee q} \ Equiv p \ wedge \ overline {q}.\] В качестве альтернативы мы можем рассуждать следующим образом. Интерпретировать \ (\ overline {p \ Rightarrow q} \) как высказывание \ (p \ Rightarrow q \) неверно. Для этого требуется, чтобы \ (p \) было истинным, а \ (q \) — ложным, что переводится в \ (p \ wedge \ overline {q} \). Таким образом, \ (\ overline {p \ Rightarrow q} \ Equiv p \ wedge \ overline {q} \).
Упражнения \ (\ PageIndex {} \)
Упражнение \ (\ PageIndex {1} \ label {ex: logiceq-01} \)
Используйте таблицу истинности, чтобы проверить закон Де Моргана \ (\ overline {p \ vee q} \ Equiv \ overline {p} \ wedge \ overline {q} \).
Ответ
\ (\ begin {array} [t] {{| c | c | c | c | c | c |}} \ hline p & q & p \ vee q & \ overline {p \ vee q} & \ overline {p} & \ overline {q} & \ overline {p} \ wedge \ overline {q} \\ \ hline T & T & T & F & F & F & F \\ T & F & T & F & F & T & F \\ F & T & T & F & T & F & F \\ F & F & F & T & T & T & T \\ \ hline \ end {array} \)
Упражнение \ (\ PageIndex {2} \ label {ex: logiceq-02} \)
Используйте таблицы истинности для проверки двух ассоциативных свойств.
Упражнение \ (\ PageIndex {3} \ label {ex: logiceq-03} \)
Создайте таблицу истинности для каждой формулы ниже. Какие из них являются тавтологиями?
\ ((\ overline {p} \ vee q) \ Rightarrow p \)
\ ((p \ Rightarrow q) \ vee (p \ Rightarrow \ overline {q}) \)
\ ((p \ Rightarrow q) \ Rightarrow r \)
Ответ
Only (b) — это тавтология, как указано в таблицах истинности ниже.
(a) \ (\ begin {array} [t] {| * {5} {c |}} \ hline p & q & \ overline {p} & \ overline {p} \ vee q & (\ overline { p} \ vee q) \ Rightarrow p \\ \ hline T & T & F & T & \ qquad \; T \\ T & F & F & F & \ qquad \; T \\ F & T & T & T & \ qquad \; F \\ F & F & T & T & \ qquad \; F \\ \ hline \ end {array} \)
(b) \ (\ begin {array} [t] {| * {6} {c |}} \ hline p & q & p \ Rightarrow q & \ overline {q} & p \ Rightarrow \ overline {q} & (p \ Rightarrow q) \ vee (p \ Rightarrow \ overline {q}) \\ \ hline T & T & T & F & F & T \\ T & F & F & T & T & T \\ F & T & T & F & T & T \\ F & F & T & T & T & T \\ \ hline \ end {array} \)
(c) \ (\ begin {array} [t] {| * {5} {c |}} \ hline p & q & r & p \ Rightarrow q & (p \ Rightarrow q) \ Rightarrow r \\ \ hline T & T & T & T & \ qquad \ quad T \\ T & T & F & T & \ qquad \ quad F \\ T & F & T & F & \ qquad \ quad T \\ T & F & F & F & \ qquad \ quad T \\ F & T & T & T & \ qquad \ quad T \\ F & T & F & T & \ qquad \ quad F \\ F & F & T & T & \ qquad \ quad T \\ F & F & F & T & \ qquad \ quad F \\ \ hline \ end {array} \)
Упражнение \ (\ PageIndex {4} \ label {ex: logiceq-04} \)
Используйте таблицы истинности для проверки этих логических эквивалентностей.
\ ((p \ клин q) \ Leftrightarrow p \ Equiv p \ Rightarrow q \)
\ ((p \ wedge q) \ Rightarrow r \ Equiv p \ Rightarrow (\ overline {q} \ vee r) \)
\ ((p \ Rightarrow \ overline {q}) \ wedge (p \ Rightarrow \ overline {r}) \ Equiv \ overline {p \ wedge (q \ vee r)} \)
Упражнение \ (\ PageIndex {5} \ label {ex: logiceq-05} \)
Используйте только свойства логической эквивалентности для проверки (b) и (c) в задаче 4.
Ответ
Доказательства представлены ниже без пояснений.Обязательно заполните их.
(b) \ (\ begin {array} [t] {lcl @ {\ quad (\ hskip1.5in)}} (p \ wedge q) \ Rightarrow r & \ Equiv & \ overline {p \ wedge q} \ vee r \\ & \ Equiv & (\ overline {p} \ vee \ overline {q}) \ vee r \\ & \ Equiv & \ overline {p} \ vee (\ overline {q} \ vee r) \\ & \ Equiv & p \ Rightarrow (\ overline {q} \ vee r) \ end {array} \)
(c) \ (\ begin {array} [t] {lcl @ {\ quad (\ hskip1.5in)}} (p \ Rightarrow \ overline {q}) \ wedge (p \ Rightarrow \ overline {r}) & \ Equiv & (\ overline {p} \ vee \ overline {q}) \ wedge (\ overline {p} \ vee \ overline {r}) \\ & \ Equiv & \ overline {p} \ vee (\ overline {q } \ wedge \ overline {r}) \\ & \ Equiv & \ overline {p} \ vee \ overline {q \ vee r} \\ & \ Equiv & \ overline {p \ wedge (q \ vee r)} \ end { массив} \)
Упражнение \ (\ PageIndex {6} \ label {ex: logiceq-06} \)
Определите, являются ли формулы \ (u \) и \ (v \) логически эквивалентными (вы можете использовать таблицы истинности или свойства логических эквивалентностей).
\ (u: \; (p \ Rightarrow q) \ wedge (p \ Rightarrow \ overline {q}) \) \ (v: \; \ overline {p} \)
\ (u: \; p \ Rightarrow q \) \ (v: \; q \ Rightarrow p \)
\ (u: \; p \ Leftrightarrow q \) \ (v: \; q \ Leftrightarrow p \)
\ (u: \; (p \ Rightarrow q) \ Rightarrow r \) \ (v: \; p \ Rightarrow (q \ Rightarrow r) \)
Упражнение \ (\ PageIndex {7} \ label {ex: logiceq-07} \)
Найдите обратное, обратное и противоположное этим значениям.
Если треугольник \ (ABC \) равнобедренный и содержит угол 45 градусов, то \ (ABC \) — прямоугольный треугольник.
Если четырехугольник \ (ABCD \) квадрат, то это и прямоугольник, и ромб.
Если у четырехугольника \ (ABCD \) две стороны равной длины, то это либо прямоугольник, либо ромб.
Ответ
(а)
Конверс: Если треугольник \ (ABC \) прямоугольный, то \ (ABC \) равнобедренный
и содержит угол 45 градусов.
Обратное: Если треугольник \ (ABC \) не является равнобедренным или не содержит угла
из 45 градусов, то \ (ABC \) не является прямоугольным треугольником.
Контрапозитивные: Если треугольник \ (ABC \) не является прямоугольным, то \ (ABC \) не является равнобедренным
или не содержит угла в 45 градусов.
(б)
Конверс: Если четырехугольник \ (ABCD \) одновременно является прямоугольником и ромбом,
, то \ (ABCD \) квадрат.
Обратное: Если четырехугольник \ (ABCD \) не квадрат,
то это не прямоугольник или не ромб.
Контрапозитивные: Если четырехугольник \ (ABCD \) не прямоугольник или не ромб,
, то \ (ABCD \) не квадрат.
(в)
Конверс: Если четырехугольник \ (ABCD \) является прямоугольником или ромбом,
, то \ (ABCD \) имеет две стороны равной длины.
Обратное: Если четырехугольник \ (ABCD \) не имеет двух сторон одинаковой длины,
, то это не прямоугольник и не ромб.
Контрапозитивные: Если четырехугольник \ (ABCD \) не прямоугольник и не ромб,
, то \ (ABCD \) не имеет двух сторон равной длины.2> 0 \ Rightarrow x> 0 \).
Если \ (PQRS \) — квадрат, то \ (PQRS \) — параллелограмм.
Если \ (n> 1 \) простое число, то \ (n + 1 \) составное.
Если \ (x \) и \ (y \) — целые числа, такие что \ (xy \ geq1 \), то либо \ (x \ geq1 \), либо \ (y \ geq1 \).
Упражнение \ (\ PageIndex {9} \ label {ex: logiceq-09} \)
Определите, верны ли следующие формулы:
\ (\ overline {p \ Leftrightarrow q} \ Equiv \ overline {p} \ Leftrightarrow \ overline {q} \)
\ ((p \ Rightarrow q) \ wedge (p \ Rightarrow \ overline {q}) \ Equiv \ overline {p} \)
\ (p \ Rightarrow q \ Equiv q \ Rightarrow p \)
Ответ
(а) ложь (б) правда (в) ложь
Упражнение \ (\ PageIndex {10} \ label {ex: logiceq-10} \)
Определите, верны ли следующие формулы:
\ ((p \ Rightarrow q) \ Rightarrow r \ Equiv p \ Rightarrow (q \ Rightarrow r) \)
\ (p \ Rightarrow (q \ vee r) \ Equiv (p \ Rightarrow q) \ vee (p \ Rightarrow r) \)
\ (p \ Rightarrow (q \ wedge r) \ Equiv (p \ Rightarrow q) \ wedge (p \ Rightarrow r) \)
Упражнение \ (\ PageIndex {11} \ label {ex: logiceq-11} \)
Какое из следующих утверждений эквивалентно утверждению «если \ (x ^ 2> 0 \), то \ (x> 0 \)»?
Если \ (x> 0 \), то \ (x ^ 2> 0 \).2 \ not> 0 \), то \ (x \ not> 0 \).
Ответ
Только
(б).
Упражнение \ (\ PageIndex {12} \ label {ex: logiceq-12} \)
Определите, являются ли следующие формулы тавтологиями, противоречиями или нет:
\ ((p \ Rightarrow q) \ wedge \ overline {p} \)
\ ((p \ Rightarrow \ overline {q}) \ wedge (p \ wedge q) \)
\ ((p \ Rightarrow \ overline {q}) \ wedge q \)
Упражнение \ (\ PageIndex {13} \ label {ex: logiceq-13} \)
Упростите следующие формулы:
\ (p \ клин (p \ клин q) \)
\ (\ overline {\ overline {p} \ vee q} \)
\ (\ overline {p \ Rightarrow \ overline {q}} \)
Ответ
(a) \ (p \ wedge q \)
(b) \ (p \ wedge \ overline {q} \)
(c) \ (p \ wedge q \)
Упражнение \ (\ PageIndex {14} \ label {ex: logiceq-14} \)
Упростите следующие формулы:
\ ((p \ Rightarrow \ overline {q}) \ wedge (\ overline {q} \ Rightarrow p) \)
\ (\ overline {p \ wedge \ overline {q}} \)
\ (p \ wedge (\ overline {p} \ vee q) \)
Упражнение \ (\ PageIndex {15} \)
T означает тавтологию, а F означает противоречие.
Верно или неверно?
а. \ (F \ rightarrow \ overline {q} \)
г. \ (п \ вее Т \)
г. \ (F \ клин p \)
г. \ (\ overline {T} \ vee F \)
Ответ
(а) верно (б) верно (в) ложно (г) неверно
Упражнение \ (\ PageIndex {16} \)
T означает тавтологию, а F означает противоречие.
Упростите до эквивалентного выражения, которое представляет собой одну букву ( T , F , p или ~ p )
а.\ (\ overline {T} \ vee F \ Equiv \)
г. \ (Т \ клин р \ эквив \)
г. \ (F \ wedge \ overline {p} \ Equiv \)
г. \ (F \ vee \ overline {p} \ Equiv \)
e. \ ((F \ vee T) \ vee F \ Equiv \)
ф. \ ((F \ vee T) \ клин T \ Equiv \)
Define Tautology — Cuemath
Если я скажу: «Я дам вам 5 долларов или не дам вам 5 долларов». Что вы подумаете об этом комментарии?
Я всегда буду правдой, независимо от того, даю я вам немного денег или нет.
Знаменитая фраза Джорджа Вашингтона «Я не могу солгать» также является еще одним примером таких заявлений.
Такие утверждения хорошо объяснены и подпадают под тавтологию.
Итак, приступим к изучению примеров тавтологии, определения тавтологии в математике и таблицы истинности тавтологии.
План урока
Что такое тавтология в математике?
Определение
Логическая комбинация предложений, которая всегда истинна, независимо от истинности или ложности составляющих предложений, известна как «тавтология».«
— Руди Ракер
Тавтология — это составное утверждение, которое всегда истинно, независимо от того, являются ли отдельные утверждения ложными или истинными.
Слово тавтология происходит от греческого слова, где «тауто» означает «тот же», а «логия» означает «логика».
Чтобы узнать, является ли данное утверждение тавтологией, нам нужно построить таблицу истинности и посмотреть на значение истинности в последнем столбце.
Если все значения верны, то это тавтология.
Вот несколько простых примеров тавтологии:
Либо прыгнешь, либо не прыгнешь.
Генри худощавый или Генри не стройный.
Эмануэль будет танцевать или Эмануэль не будет танцевать.
Все эти утверждения верны, несмотря ни на что.
Логические символы в математике
Поскольку математика является логическим предметом, она использует логические утверждения для определения ответов.
Чтобы узнать, является ли данное утверждение тавтологическим или нет, логика тавтологии должна быть истинной.
В тавтологии для представления составных утверждений используются разные логические символы.
Вот логические символы, которые используются в тавтологическом высказывании:
Операторы Условные обозначения Представительство
И \ (\ земля \) A \ (\ земля \) B
Или \ (\ lor \) A \ (\ lor \) B
Отрицание \ (\ lnot \) \ (\ lnot \) А
Не \ (\ sim \) \ (\ sim \) А
Если и только если \ (\ iff \) А \ (\ iff \) В
Подразумевает или если-то \ (\ longrightarrow \) A \ (\ longrightarrow \) B
Эквивалент = А = В
Аналитический центр
В чем отрицание этих утверждений?
Если экзамен сложный, то сдашь, если учишься.
Если я стану врачом, то открою больницу.
Таблица истинности
Таблица истинности тавтологических утверждений приведена ниже:
Для этого:
X Y \ (\ sim \) X X \ (\ земля \) Y X \ (\ lor \) Y X \ (\ longrightarrow \) Y X \ (\ iff \) Y
Т Т F Т Т Т Т
Т F F F Т F F
Ф Т Т F Т Т F
Ф F Т F F Т Т
Важные примечания
Примеры тавтологии и математики
Пример 1. Проверить, является ли P \ (\ longrightarrow \) (P \ (\ land \) Q) тавтологическим или нет.
П квартал (П \ (\ земля \) Q) P \ (\ longrightarrow \) (P \ (\ land \) Q)
Т Т Т Т
Т F F F
Ф Т F Т
Ф F F Т
Это не тавтологическое утверждение, потому что все значения в последнем столбце не истинны (T).
Пример 2. Проверьте, является ли \ (\ sim \) X \ (\ lor \) Y тавтологическим или нет.
х \ (\ sim \) Х Y \ (\ sim \) X \ (\ lor \) Y
Т F F F
Т F F F
Ф Т Т Т
Ф Т Т Т
Это не тавтологическое утверждение, потому что все значения в последнем столбце не истинны (T).
Разница между тавтологией и противоречием?
Тавтология — это составное утверждение, которое всегда истинно, независимо от того, являются ли отдельные утверждения ложными или истинными.
Тогда как противоречие противоположно тавтологии или просто отрицание тавтологии есть противоречие.
Противоречие также известно как заблуждение.
Противоречие — это составное утверждение, которое всегда ложно, независимо от того, являются ли отдельные утверждения ложными или истинными.
П В (П \ (\ lor \) V) P \ (\ longrightarrow \) (P \ (\ lor \) V) \ (\ sim \) (P \ (\ longrightarrow \) (P \ (\ lor \) V))
Т Т Т Т F
Т F Т Т F
Ф Т Т Т F
Ф F F Т F
Глядя на таблицу истинности, P \ (\ longrightarrow \) (P \ (\ lor \) V) является тавтологией, тогда как \ (\ sim \) (P \ (\ longrightarrow \) (P \ ( \ lor \) V)) противоречивое утверждение.
Решенные примеры
Эшли было поручено построить таблицу истинности для {A \ (\ iff \) B} \ (\ lor \) {B \ (\ iff \) A}. Можете ли вы помочь ей сделать то же самое?
Решение
А Б (А \ (\ iff \) B) (В \ (\ iff \) А) {A \ (\ iff \) B} \ (\ lor \) {B \ (\ iff \) A}
Т Т Т Т Т
Т F F F F
Ф Т F F F
Ф F Т Т Т
Ян не понимает, является ли N \ (\ lor \) {\ (\ sim \) N} тавтологическим утверждением или нет.Вы можете помочь ему в этом разобраться?
Решение
№ \ (\ sim \) N N \ (\ lor \) {\ (\ sim \) N}
Т F Т
Ф Т Т
Это тавтологическое утверждение, поскольку все значения в последнем столбце верны.
Можете ли вы помочь Полу построить таблицу истинности для {Y \ (\ land \) Z} \ (\ longrightarrow \) Z?
Решение
Таблица истинности {Y \ (\ land \) Z} \ (\ longrightarrow \) Z может быть составлена следующим образом:
Y Z Y \ (\ land \) Z {Y \ (\ land \) Z} \ (\ longrightarrow \) Z
Т Т Т Т
Т F F Т
Ф Т F Т
Ф F F Т
Интерактивные вопросы
Вот несколько занятий для вас.Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги!
Мини-урок был посвящен увлекательной концепции тавтологии, примеру тавтологии, как определять тавтологию в математике и таблице истинности тавтологии. Математическое путешествие по тавтологии начинается с того, что ученик уже знает, и продолжается творческим развитием новой концепции в молодых умах.Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Как вы определяете тавтологию?
Если вы хотите знать, что данное утверждение является тавтологией, то все, что вам нужно сделать, это построить таблицу истинности и посмотреть на значение истинности в последнем столбце.
Если все значения верны, это тавтология.
2. Что означают P и Q?
Утверждение от P до Q означает, что если P истинно, то Q также должно быть истинным.
3. Является ли тавтология заблуждением?
Тавтология — это составное утверждение, которое всегда истинно, независимо от того, истинны ли отдельные утверждения или нет.
А противоречие — противоположность тавтологии. Другими словами, отрицание тавтологии есть противоречие.
Противоречие также известно как заблуждение. Следовательно, тавтология — это не заблуждение.
.
No related posts.
Оставить Комментарий на Тавтология в логике: Tautology | What Is Tautology?
Навигация по записям
Дети избалованы: Избалованный ребенок: рекомендации родителям
Почему матерные слова называются матерными: Русский мат: история, происхождение, употребление.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Искать для:
Рубрики
Взрослен
Взросление
Ответствен
Ответственность
Правил
Правила
Привязан
Привязанность
Разное
Самовоспитан
Самовоспитание
Совет
Советы психолога
2019 © Все права защищены. Карта сайта(C) МКОУ СОШ №1 с.п.Аргудан