| Методика «Лесенка»В.Г.Щур Описание методики Цель методики — исследование самооценки детей старшего дошкольного и младшего школьного возраста. Процедура проведения Ребенку показывают нарисованную лесенку с семью ступеньками, и объясняют задание. Стимульныйматериал Инструкция «Если всех детей рассадить на этой лесенке, то на трех верхних ступеньках окажутся хорошие дети: умные, добрые, сильные, послушные – чем выше, тем лучше (показывают: «хорошие», «очень хорошие», «самые хорошие»). А на трех нижних ступеньках окажутся плохие дети – чем ниже, тем хуже («плохие», «очень плохие», «самые плохие»). На средней ступеньке дети не плохие и не хорошие. Покажи, на какую ступеньку ты поставишь себя. Объясни почему?» После ответа ребенка, его спрашивают: «Ты такой на самом деле или хотел бы быть таким? Пометь, какой ты на самом деле и каким хотел бы быть». Процедура проведения Используется стандартный набор характеристик: «хороший – плохой», «добрый – злой», «умный – глупый», «сильный – слабый», «смелый – трусливый», «самый старательный – самый небрежный». Количество характеристик можно сократить. В процессе обследования необходимо учитывать, как ребенок выполняет задание: испытывает колебания, раздумывает, аргументирует свой выбор. Если ребенок не дает никаких объяснений, ему следует задать уточняющие вопросы: «Почему ты себя сюда поставил? Ты всегда такой?» и т.д.
Интерпретация результатов Неадекватно завышенная самооценка Не раздумывая, ставит себя на самую высокую ступеньку; считает, что мама оценивает его также; аргументируя свой выбор, ссылается на мнение взрослого: «Я хороший. Хороший и больше никакой, это мама так сказала». Завышенная самооценка После некоторых раздумий и колебаний ставит себя на самую высокую ступеньку, объясняя свои действия, называет какие-то свои недостатки и промахи, но объясняет их внешними, независящими от него, причинами, считает, что оценка взрослых в некоторых случаях может быть несколько ниже его собственной: «Я, конечно, хороший, но иногда ленюсь. Адекватная самооценка Обдумав задание, ставит себя на 2-ю или 3-ю ступеньку, объясняет свои действия, ссылаясь на реальные ситуации и достижения, считает, что оценка взрослого такая же либо несколько ниже. Заниженная самооценка Ставит себя на нижние ступеньки, свой выбор не объясняет либо ссылается на мнение взрослого: «Мама так сказала». Если ребенок ставит себя на среднюю ступеньку, это может говорить о том, что он либо не понял задание, либо не хочет его выполнять. Дети с заниженной самооценкой из-за высокой тревожности и неуверенности в себе часто отказываются выполнять задание, на все вопросы отвечают: «Не знаю». Дети с задержкой развития не понимают и не принимают это задание, действуют наобум. Неадекватно завышенная самооценка свойственна детям младшего и среднего дошкольного возраста: они не видят своих ошибок, не могут правильно оценить себя, свои поступки и действия. Самооценка детей 6-7-летнего возраста становится уже более реалистичной, в привычных ситуациях и привычных видах деятельности приближается к адекватной. В незнакомой ситуации и непривычных видах деятельности их самооценка завышенная.
Выбор нижних ступенек свидетельствует о заниженной самооценке. Для таких детей, как правило, характерны тревожность, неуверенность в себе. Если значимые люди (по мнению ребенка) оценивают его так же, как он оценил себя, или дают более высокую оценку — ребенок защищен психологически, эмоционально благополучен. Дата ______ Ф.И._______________ Класс__________ Дата ______ Ф.И._______________ Класс__________ Дата ______ жүктеу/скачать 27.48 Kb. Достарыңызбен бөлісу: |
Мама говорит, что я неаккуратный».
Тест на самооценку детей
Детская психология0
Психологи утверждают, что решающее значение для формирования успешной личности играет самооценка ребенка. При рождении она безупречна, но по мере роста и развития сильно изменяется. На нее влияет множество факторов, событий, отношения внутри семьи и со сверстниками.
Если на всех этапах роста самооценка развивается гармонично, ребенок оценивает себя положительно, он с легкостью идет по жизни, строит карьеру и личные отношения. При заниженном восприятии собственного «Я» ему сложно преодолевать трудности и кризисы, реагировать на обиды и разочарования.
Как формируется самооценка ребенка
При рождении дети имеют здоровую самооценку, которая меняется с каждым новым событием в его жизни. Психологи условно выделяют несколько основных этапов, когда происходят кардинальные изменения:
От рождения до 1,5 лет. При положительной атмосфере в семье у крохи зарождается любовь и уважение к себе.
До 4 лет. Если родители поощряют самостоятельность, активность и инициативу, формируется завышенная самооценка и любознательность.
До 6 лет. Идет активный процесс социализации, первое осознание своей роли в обществе. Ребенок понимает, что хочет вырасти успешным и быть лучше сверстников.
До 14 лет. Важнейший этап формирования самооценки на фоне общения со старшими, школьными друзьями.
В детском возрасте родители любовью и правильным воспитанием могут заложить в голове ребенка уважение к себе. В дальнейшем он будет больше тянуться к людям, которые относятся к нему тепло, сможет уверенно отсеивать недоброжелателей и недостойных друзей.
Чем выше самооценка, тем к большему стремится человек. Поэтому дети с заниженным восприятием собственного «Я» стараются не выделяться, не развивают талант, не участвуют в конкурсах и соревнованиях. Они не умеют ставить цели и планировать будущее, не стремятся к саморазвитию.
Методика диагностики «Лесенка»
Психологи разработали интересный и простой способ проверить, на каком уровне находится самооценка ребенка, как он представляет себя в глазах окружающих людей. Методика «Лесенка» (автор В.Г.Щур) помогает выявить проблему на ранней стадии и подобрать оптимальные пути решения.
Для проведения теста необходим лист бумаги с нарисованной лестницей, маленький бумажный человечек и карандаш. Ребенку объясняют, что на верхней ступени стоят лучшие и самые успешные дети, на нижней – плохие, непослушные, глупые. На середину необходимо поставить «ни плохих, ни хороших» малышей. Затем просят его разместить фигурку, которая обозначает его самого.
Во время работы психолог предлагает показать ступеньки, на которые ребенка бы поставила мама, воспитатель, учитель, друзья.
Специалист наблюдает за скоростью реакции, колебаниями и сомнениями детей, может уточнить, почему такое положение человечка на лестнице.
Понять самооценку можно по результату выполненного задания:
Если ребенок быстро поставил фигурку на самый верх, он переоценивает себя, считает гораздо лучше остальных детей. Это говорит о завышенной самооценке.
Адекватное отношение к себе выдает попытка поставить себя на 2 или 3 ступень после небольшого раздумья.
Если малыш размещает фигурку на самой последней ступени, его самооценка сильно и часто неоправданно занижена.
Еще один признак несправедливого отношения к себе – отказ от выполнения задания «Лесенка». Дети с заниженной самооценкой сильно переживают, испытывают стресс, не желают отвечать на вопросы психолога. Иногда тест с лестницей проводят в группах, чтобы проверить восприятие собственного «Я» у нескольких малышей одновременно.
При заниженной самооценке необходима длительная и кропотливая работа взрослых, которые окружают ребенка.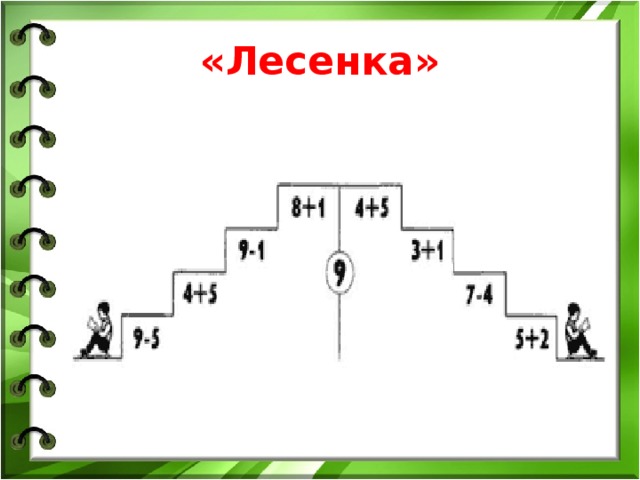
Родителям следует давать малышу больше внимания, тепла и поддержки, чаще обсуждать с ним интересные занятия, увлечения, поступки других детей. Это поможет сформировать уверенность в силах, желание достигать цели и преодолевать трудности.
Родители должны знать, как ребенок относится к себе, на каком уровне его самооценка. Во многом заниженное восприятие – результат неправильного воспитания, недостатка любви и взаимопонимания. Только взрослые могут научить его правильно ставить цели, достигать результата.
Поделиться:Выпуклость Шура и положительная определенность полных однородных симметричных многочленов четной степени
Полный однородный симметричный многочлен переменных и степени может быть определен как
, например,
2 и
9 2000032 и
9 определить все полные однородные симметричные многочлены переменных одновременно с помощью производящей функции Мы будем думать о переменных как о принимающих значения в действительных числах.
Когда кто-то делает это, можно заметить, что многочлен второй степени является положительно определенной квадратичной формой, поскольку он имеет представление суммы квадратов
В частности, если . Это можно сравнить с внешне похожей квадратичной формой
, где независимые случайно выбранные знаки. Закон полуокружности Вигнера говорит, что для больших собственные значения этой формы будут в основном распределены в интервале с использованием распределения полуокружности, поэтому, в частности, форма довольно далека от положительно определенной, несмотря на наличие первых положительных членов. Таким образом, положительная определенность исходит из более тонкой алгебраической структуры , а не только из величин ее коэффициентов.
Можно было бы спросить, верна ли та же положительность для других степеней, кроме двух. Для нечетных степеней ответ явно нет, так как в таком случае. Но можно было бы надеяться, например, что
также имеет представление суммы квадратов, демонстрирующее положительную определенность.
Теорема 1 Пусть , пусть четные и пусть вещественные.
- (i) (Положительная определенность) Есть , со строгим неравенством, если только .
- (ii) (Выпуклость Шура) Каждый имеет всякий раз, когда мажорирует , с равенством тогда и только тогда, когда является перестановкой .
- (iii) (Критерий Шура-Островского для выпуклости Шура) Для любого , со строгим неравенством, если только .
Доказательство: Проведем индукцию по (допущение произвольности). Утверждение тривиально верно для и легко проверяется для , поэтому предположим, что и утверждения (i), (ii), (iii) уже доказаны для (и для произвольного ).
Если мы применим дифференциальный оператор к правилу произведения, то после кратких вычислений получим
Используя (1) и извлекая коэффициент, мы получаем тождество
Отсюда следует утверждение (iii).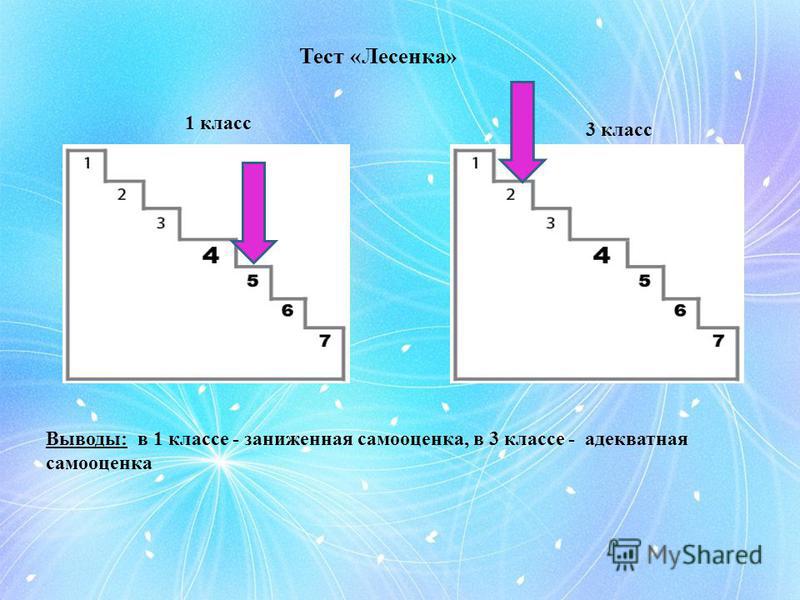
из (i) и предположения индукции.
Чтобы получить (ii), мы используем более общее утверждение (известное как критерий Шура-Островского ), что (ii) следует из (iii), если мы заменим его произвольной симметричной непрерывно дифференцируемой функцией. Чтобы установить этот критерий, мы индуцируем по (это рассуждение можно провести независимо от существующей индукции по ). Если мажорируется , он лежит в перестановке . Если лежит на грани этой перестановки, то после перестановки обоих и мы можем считать, что мажорируется на , а мажорируется на для некоторого , и тогда утверждение следует из двух применений предположения индукции. Если вместо этого лежит внутри перестановки, то можно проследить его до границы с помощью одного из векторных полей , и утверждение следует из граничного случая.
Наконец, чтобы получить (i), мы наблюдаем, что мажорирует , где среднее арифметическое . Но явно положительно кратно , и теперь утверждение следует из (ii).
Если переменные ограничены неотрицательностью, тот же аргумент дает выпуклость Шура и для нечетных степеней.
Доказательство положительной определенности в Хантере устроено несколько иначе, чем приведенное выше, но все же в конечном счете опирается на тождество (2). Интересно, существует ли действительно другой способ установить положительную определенность, который не проходит через это тождество.
Например:
Нравится нагрузка …
[PDF] плавильный ледяной хроматический @article{Huh3018MeltingLC, title={Хроматические квазисимметричные функции плавления леденцов и разложение Шура одноклеточных полиномов LLT}, автор={ЧжиСун Ха, Нам Сун-Ён и Мису Ю}, журнал={Дискретный. мат.}, год = {2018}, объем={343}, страницы={111728} }
- JiSun Huh, Sun-Young Nam, Meesue Yoo
- Опубликовано 9 декабря 2018 г.
- Математика
- Discret. Мат.
Посмотреть PDF на arXiv
Полиномы ЛЛТ, элементарные симметричные функции и плавящиеся леденцы на палочке
Мы предполагаем явную положительную комбинаторную формулу для разложения одноклеточных полиномов ЛЛТ в элементарном симметричном базисе.
Это аналог гипотезы Шарешяна–Вакса…
Полиномы LLT, элементарные симметрические функции и плавящиеся леденцы на палочке
Мы выдвинули гипотезу о явной положительной комбинаторной формуле для разложения одноклеточных полиномов ЛЛТ в элементарном симметричном базисе. Это аналог гипотезы Шарешяна–Вакса…
Расширенные хроматические симметричные функции и равенство ленточных функций Шура
- Ф. Алиниэйфард, В. Ван, С. Виллигенбург
Математика
Adv. заявл. Мат.
- 2021
Комбинаторное разложение Шура горизонтальных полиномов ЛЛТ без треугольников
В последние годы Александерссон и другие доказали комбинаторные формулы для разложения по функции Шура горизонтально-полосного многочлена LLT $G_\lambda(x;q)$ в некоторых частных случаях. Сопоставим…
Комбинаторное разложение вертикальных полосовых полиномов ЛЛТ по базису элементарных симметрических функций
- П. Александерсон, Робин Сульцгрубер
Математика
- 2020
- Мацей Доленга, Мацей Ковальски
Математика
Электрон. Дж. Комб.
- 2022
- Мацей Ковальски
Математика
- 204530
А РЕЗЮМЕ . Мы доказываем комбинаторную формулу для кумулянтов LLT тающих леденцов как положительную комбинацию полиномов LLT, индексированных остовными деревьями. Результат дает утвердительный ответ на…
Нисходящие алгебры и хроматические симметрические функции
- Филипп Надо, Васу Тевари
Математика
- 2022
Мы устанавливаем неопубликованную линейную связь Гуэ-Паке между некоторыми хроматическими симметрическими функциями, связывая его алгебру на путях с q-алгеброй Клячко. Коэффициенты в этом отношении равны…Унипотентная реализация хроматической квазисимметричной функции
- Л. Ганьон
Математика
- 2022
F q q : хроматические квазисимметричные функции и…
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 26 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантностиНаиболее влиятельные статьиНедавность
Полиномы LLT, хроматические квазисимметричные функции и графики с циклами
- П. Александерссон, Г. Панова
Математика
Дискрет. Мат.
- 2018
Симметричные функции Lollipop и Lariat
Выводится, что существуют счетно бесконечные различные $e-положительные, а значит, по Шуру положительные базисы алгебры симметрических функций, образующими которых являются хроматические асимметричные функции.
Графики с равными хроматическими симметричными функциями
- Р. Орельяна, Г. Скотт
Математика
Дискрет. Мат.
- 2014
Эйлеровые квазимметричные функции
- .
Mathematics
- 2001
- Э. Эгге, Н. Лоер, Г. Уоррингтон
Математика
Eur. Дж. Комб.
- 2010
- Samantha Dahlberg
Mathematics
- 2018
- А.
Вертикальную характеристику 20 9004 -полосные многочлены ЛЛТ $\mathrm{LLT}_P(x;q)$ как единственное семейство симметрических функций, удовлетворяющих некоторым комбинаторным соотношениям.
Это… 9. Для естественного единичного интервального порядка P мы опишем правильные раскраски графа несравнимости P на языке куч. После этого мы вводим комбинаторную операцию, называемую локальным флипом…
LLT Кумулянты и раскраска графа
Целью этой заметки является введение нового семейства квазисимметричных функций, называемых LLT-кумулянтами, и обсуждение его свойств. Мы определяем кумулянты LLT, используя алгебраическую основу для…
Комбинаторная формула для кумулянтов LLT плавящихся леденцов в терминах остовных деревьев
Мы устанавливаем неопубликованную линейную связь Гуэ-Паке между некоторыми хроматическими симметрическими функциями, связывая его алгебру на путях с q-алгеброй Клячко. Коэффициенты в этом отношении равны…
AbstractStanley (Advanced in Math.111, 1995, 166–194), ассоциированная с графом G симметричная функция XG, которая сводится к хроматическому многочлену G $${\mathcal{X}_G \влево( п \вправо)}$$ под…
От квазисимметричных разложений к разложениям Шура через модифицированную обратную матрицу Костки
Треугольные лестницы $ p_ {D, 2} $ $ e $ -позитивные
. графы $P_{d,2}$, которые мы называем треугольными лестницами, являются $e$-положительными. В данной работе мы подтверждаем эту гипотезу, которая также…
