Закон сохр энергии: Закон сохранения энергии

Законы сохранения энергии — Электронный учебник по законам сохранения

Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от  до  то силы совершили определенную работу A. Работа всех приложенных сил равна работе равнодействующей силы  Работа равнодействующей силы. .A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы  В этом случае векторы силы  перемещения  скорости  и ускорения  направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой  Отсюда следует, что  Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости). Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:  Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.   Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:  Если тело движется со скоростью  то для его полной остановки необходимо совершить работу  В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел. Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рисунок ниже Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии. Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траекторииA = A1a2 + A2b1 = A1a2 – A1b2 = 0 Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести  Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения  на ось OY, направленную вертикально вверх:  ΔA = Fт Δs cos α = –mgΔs y, где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY , то сила тяжести совершила работу  A = –mg (h2 – h1) = –(mgh2 – mgh1). Работа силы тяжести Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести  Eр = mgh. Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготени). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии rот центра Земли, имеет вид:  где M – масса Земли, G – гравитационная постоянная. Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :  где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину  Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:  Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости. Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя. Ek1 + Ep1 = Ek2 + Ep2. 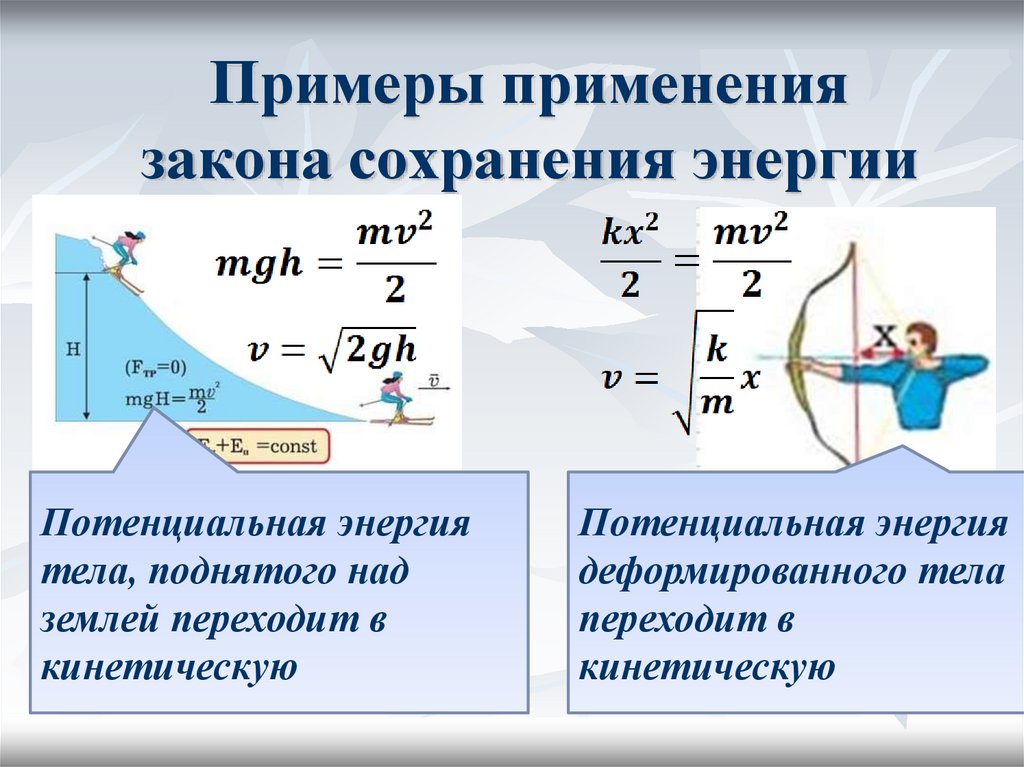Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии. Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи. К задаче Христиана Гюйгенса.   – сила натяжения нити в нижней точке траектории Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:  Обратим внимание на то, что сила  натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы. При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:  Из этих соотношений следует:  Центростремительное ускорение в нижней точке создается силами  и  направленными в противоположные стороны:  Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно  F = 6mg. Прочность нити должна, очевидно, превышать это значение. Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач. В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды. Сила трения не является консервативной. Работа силы трения зависит от длины пути. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии Один из проектов «вечного двигателя». Почему эта машина не будет работать? История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.

§6. Задачи на столкновения и законы сохранения импульса и энергии — ЗФТШ, МФТИ

В физике под столкновениями понимают процессы взаимодействия  между телами (частицами) в широком смысле слова, а не только в буквальном — как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы — тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения)  импульсами и энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.

Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль. С такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.

Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. ‘)`.

Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц).

Сохранение энергии и сохранение массы – Изучение физического мира: введение в химию и физику

Химические изменения и сопровождающие их изменения энергии являются важной частью нашего повседневного мира (рис. 5.1). Макроэлементы в пище (белки, жиры и углеводы) подвергаются метаболическим реакциям, которые обеспечивают энергию для поддержания функционирования нашего организма. Мы сжигаем различные виды топлива (бензин, природный газ, уголь) для производства энергии для транспорта, отопления и производства электроэнергии. Промышленные химические реакции требуют огромного количества энергии для производства сырья (например, железа и алюминия). Затем энергия используется для производства из этого сырья полезных продуктов, таких как автомобили, небоскребы и мосты.

 

Рис. 5.1 Энергия, связанная с химическими изменениями, важна для нашей повседневной жизни: (a) чизбургер на обед дает энергию, необходимую вам до конца дня; (б) сжигание бензина обеспечивает энергию, которая перемещает вашу машину (и вас) между домом, работой и школой; и (c) кокс, переработанная форма угля, обеспечивает энергию, необходимую для преобразования железной руды в железо, что необходимо для производства многих продуктов, которые мы используем ежедневно. (кредит a: модификация работы «Pink Sherbet Photography»/Flickr; кредит b: модификация работы Джеффри Тернера)

Более 90% энергии, которую мы используем, исходит от солнца. Каждый день солнце поставляет Земле почти в 10 000 раз больше энергии, чем необходимо для удовлетворения всех мировых энергетических потребностей в этот день. Наша задача состоит в том, чтобы найти способы преобразования и хранения поступающей солнечной энергии, чтобы ее можно было использовать в реакциях или химических процессах, которые были бы одновременно удобными и не загрязняющими окружающую среду.

Растения и многие бактерии улавливают солнечную энергию посредством фотосинтеза. Мы высвобождаем энергию, хранящуюся в растениях, когда сжигаем древесину или продукты растительного происхождения, такие как этанол. Мы также используем эту энергию для подпитки нашего тела, употребляя в пищу пищу, полученную непосредственно из растений или животных, которые получают энергию, поедая растения. Сжигание угля и нефти также высвобождает накопленную солнечную энергию: это топливо представляет собой ископаемые растения и животные вещества.

Сохранение энергии

Энергия может быть определена как способность производить тепло или выполнять работу. Один тип работы (w) — это процесс, в результате которого материя движется против противодействующей силы. Например, мы совершаем работу, когда накачиваем велосипедную шину, — мы перемещаем материю (воздух в насосе) против противодействующей силы воздуха, уже находящегося в шине.

Как и материя, энергия бывает разных типов. Одна схема классифицирует энергию на два типа; потенциальная и кинетическая энергия. Потенциальная энергия — это энергия, которой обладает объект из-за его относительного положения, состава или состояния. Кинетическая энергия – это энергия, которой объект обладает благодаря своему движению. Вода в верхней части водопада или плотины обладает потенциальной энергией из-за своего положения; когда он течет вниз через генераторы, он обладает кинетической энергией, которую можно использовать для выполнения работы и производства электроэнергии на гидроэлектростанции (рис. 5.2). Батарея обладает потенциальной энергией, потому что содержащиеся в ней химические вещества могут производить электричество, которое может совершать работу.

 

Рисунок 5.2 (a) Вода на большей высоте, например, на вершине водопада Виктория, имеет более высокую потенциальную энергию, чем вода на более низкой высоте. Когда вода падает, часть ее потенциальной энергии преобразуется в кинетическую энергию.

(b) Если вода течет через генераторы на дне плотины, такой как показанная здесь плотина Гувера, ее кинетическая энергия преобразуется в электрическую энергию. (кредит a: модификация работы Стива Джурветсона; кредит b: модификация работы curimedia/Wikimedia commons)

Энергия может быть преобразована из одной формы в другую, но вся энергия, имевшаяся до того, как произошло изменение, всегда существует в той или иной форме после того, как изменение завершено. Это наблюдение выражается в законе сохранения энергии: при химическом или физическом изменении энергия не может ни создаваться, ни уничтожаться, хотя и может изменяться по форме. Это также одна из версий первого закона термодинамики.

Когда одно вещество превращается в другое, всегда происходит связанное с этим преобразование одной формы энергии в другую. Тепло обычно выделяется или поглощается, но иногда преобразование включает свет, электрическую энергию или какую-либо другую форму энергии. Например, химическая энергия (разновидность потенциальной энергии) хранится в молекулах, из которых состоит бензин. Когда бензин сгорает в цилиндрах двигателя автомобиля, быстро расширяющиеся газообразные продукты этой химической реакции генерируют механическую энергию (разновидность кинетической энергии), когда они перемещают поршни цилиндров.

Сохранение массы

Масса объекта является мерой количества вещества в нем. Одним из способов измерения массы объекта является измерение силы, необходимой для ускорения объекта. Для ускорения автомобиля требуется гораздо больше усилий, чем для велосипеда, потому что автомобиль имеет гораздо большую массу. Более распространенным способом определения массы объекта является использование весов для сравнения его массы с эталонной массой.

Хотя вес связан с массой, это не одно и то же. Вес относится к силе, с которой гравитация действует на объект. Эта сила прямо пропорциональна массе объекта. Вес объекта изменяется при изменении силы тяжести, а его масса — нет. Масса космонавта не меняется только потому, что он летит на Луну. Но ее вес на Луне составляет лишь одну шестую от ее земного веса, потому что гравитация Луны составляет лишь одну шестую от земной. Она может чувствовать себя «невесомой» во время своего путешествия, когда на нее действуют ничтожные внешние силы (гравитационные или любые другие), хотя она, конечно, никогда не бывает «безмассовой».

Закон сохранения материи обобщает многие научные наблюдения о материи. В нем говорится:

нет никакого заметного изменения в общем количестве присутствующей материи, когда материя переходит из одного типа в другой (химическое изменение) или изменяется между твердым, жидким или газообразным состоянием (физическое изменение). Приготовление пива и работа батареек являются примерами сохранения материи (рис. 5.3). Во время варки пива ингредиенты (вода, дрожжи, злаки, солод, хмель и сахар) превращаются в пиво (вода, спирт, карбонизация и ароматизирующие вещества) без фактической потери вещества. Наиболее ярко это видно в процессе розлива, когда глюкоза превращается в этанол и углекислый газ, а общая масса веществ не меняется. Это также можно увидеть в свинцово-кислотном автомобильном аккумуляторе: исходные вещества (свинец, оксид свинца и серная кислота), способные производить электричество, превращаются в другие вещества (сульфат свинца и воду), которые не производят электричество. , без изменения фактического количества материи.

Рисунок 5.3 (a) Масса материалов-предшественников пива такая же, как и масса произведенного пива: сахар превратился в спирт и углекислый газ. б) Масса свинца, оксида свинца и серной кислоты, израсходованных на производство электроэнергии, в точности равна массе образующегося сульфата свинца и воды.

Хотя этот закон сохранения верен для всех преобразований материи, убедительных примеров очень мало, потому что вне контролируемых условий в лаборатории мы редко собираем весь материал, который производится во время определенного преобразования. Например, когда вы едите, перевариваете и усваиваете пищу, все вещества исходной пищи сохраняются. Но поскольку некоторые вещества входят в состав вашего тела, а многие выводятся из организма в виде различных видов отходов, это сложно проверить с помощью измерений.

Сохранение энергии

Закон сохранения энергии является фундаментальным понятием физики.

вместе с сохранение массы и сохранение импульса. В некоторой проблемной области количество энергии остается постоянным и энергия не создается и не уничтожается. Энергия может быть преобразована из из одной формы в другую (потенциальная энергия может быть преобразована в кинетическую энергия), но полная энергия внутри домена остается фиксированной.

Термодинамика — это раздел физики который имеет дело с энергией и работой системы. Как упоминалось на слайд со свойствами газа, термодинамика занимается только с крупномасштабной реакцией системы, которую мы можем наблюдать и измерить в опытах. В ракетостроении мы наиболее интересуется термодинамикой при изучении двигательные установки и понимание высокоскоростных потоков.

На отдельных слайдах мы обсудили состояние статического газа, свойства которые определяют состояние и первый закон термодинамики применительно к любой системе в целом. На этом слайде мы выводим полезную форму уравнения сохранения энергии для газа, начиная с первого начала термодинамики.

Если мы назовем внутреннюю энергию газа E , то работа, совершаемая газом W , и теплота, переданная газу Q , то первый закон термодинамики указывает, что между состоянием «1» и состояние «2»:

E2 — E1 = Q — W

Аэрокосмические инженеры обычно упрощают термодинамический анализ с использованием интенсивных переменных; переменные, не зависящие от масса газа. Мы называем эти переменные конкретный переменные. Мы создаем «конкретную» переменную, взяв свойство, чье величина зависит от массы системы и деления ее на массу системы. Многие из государственных свойств, перечисленных на этом слайде, Например, работа и внутренняя энергия зависят от общей массы газа. Мы будем использовать «конкретные» версии этих переменных. Инженеры обычно используют строчную букву для «конкретного» версия переменной. Тогда наше первое уравнение закона принимает вид: 92) / 2

и уравнение первого закона принимает вид:

e2 — e1 + k2 — k1 = q — w

Есть две части конкретной работы для подвижный газ.