Закон сохранения энергии как звучит – Универсальный Закон Сохранения Энергии

Закон сохранения энергии

Полная механическая энергия замкнутой системы тел остается неизменной.

Во всех явлениях, происходящих в природе, энергия не возникает и не исчезает. Она только превращается из одного вида в другой, при этом ее значение сохраняется.

Закон сохранения энергии — фундаментальный закон природы, заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

Закон сохранения механической энергии

В механике закон сохранения энергии утверждает, что в замкнутой системе частиц, полная энергия, которая является суммой кинетической и потенциальной энергии и не зависит от времени, то есть является интегралом движения. Закон сохранения энергии справедлив только для замкнутых систем, то есть при отсутствии внешних полей или взаимодействий.

Силы взаимодействия между телами, для которых выполняется закон сохранения механической энергии называются консервативными силами. Закон сохранения механической энергии не выполняется для сил трения, поскольку при наличии сил трения происходит преобразование механической энергии в тепловую.

Математическая формулировка

Эволюция механической системы материальных точек с массами \( m_i\) по второму закону Ньютона удовлетворяет системе уравнений

\[ m_i\dot{\mathbf{v}_i} = \mathbf{F}_i \]

где
\( \mathbf{v}_i \) — скорости материальных точек, а \( \mathbf{F}_i \) — силы, действующие на эти точки.

Если подать силы, как сумму потенциальных сил \( \mathbf{F}_i^p \) и непотенциальных сил \( \mathbf{F}_i^d \), а потенциальные силы записать в виде

\[ \mathbf{F}_i^p = — \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) \]

то, домножив все уравнения на \( \mathbf{v}_i \) можно получить

\[ \frac{d}{dt} \sum_i \frac{mv_i^2}{2} = — \sum_i \frac{d\mathbf{r}_i}{dt}\cdot \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) + \sum_i \frac{d\mathbf{r}_i}{dt} \cdot \mathbf{F}_i^d \]

Первая сумма в правой части уравнения является ни чем иным, как производной по времени от сложной функции, а следовательно, если ввести обозначения

\[ E = \sum_i \frac{mv_i^2}{2} + U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) \]

и назвать эту величину механической энергией, то, интегрируя уравнения с момента времени t=0 до момента времени t, можно получить

\[ E(t) — E(0) = \int_L \mathbf{F}_i^d \cdot d\mathbf{r}_i \]

где интегрирование проводится вдоль траекторий движения материальных точек.

Таким образом, изменение механической энергии системы материальных точек со временем равно работе непотенциальных сил.

Закон сохранения энергии в механике выполняется только для систем, в которых все силы потенциальные.

Закон сохранения энергии для электромагнитного поля

В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойтинга.

Изменение электромагнитной энергии, заключенной в неком объеме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объем, и количеству тепловой энергии, выделившейся в данном объеме, взятой с обратным знаком.

$ \frac{d}{dt}\int_{V}\omega_{em}dV=-\oint_{\partial V}\vec{S}d\vec{\sigma}-\int_V \vec{j}\cdot \vec{E}dV $

Электромагнитное поле обладает энергией, которая распределяется в пространстве, занятом полем. При изменении характеристик поля меняется и распределение энергии. Она перетекает из одной области пространства в другую, переходя, возможно, в другие формы. Закон сохранения энергии для электромагнитного поля является следствием полевых уравнений.

Внутри некоторой замкнутой поверхности S, ограничивающей объем пространства V, занятого полем, содержится энергия W — энергия электромагнитного поля:

W = Σ(εε₀E_i² / 2 + μμ₀H_i² / 2)ΔV_i.

Если в этом объеме имеются токи, то электрическое поле производит над движущимися зарядами работу, за единицу времени равную

N = Σ_ij̅_i ×E̅_i • ΔV_i.

Это величина энергии поля, которая переходит в другие формы. Из уравнений Максвелла следует, что

ΔW + NΔt = -Δt∮_SS̅ × n̅ • dA, [1]

где ΔW — изменение энергии электромагнитного поля в рассматриваемом объеме за время Δt, а вектор S̅ = E̅ × H̅ называется вектором Пойнтинга.

Это закон сохранения энергии в электродинамике.

Через малую площадку величиной ΔA с единичным вектором нормали n̅ за единицу времени в направлении вектора n̅ протекает энергия S̅ × n̅ • ΔA, где S̅ — значение вектора Пойнтинга в пределах площадки. Сумма этих величин по всем элементам замкнутой поверхности (обозначена знаком интеграла), стоящая в правой части равенства [1], представляет собой энергию, вытекающую из объема, ограниченного поверхностью, за единицу времени (если эта величина отрицательна, то энергия втекает в объем). Вектор Пойнтинга определяет поток энергии электромагнитного поля через площадку, он отличен от нуля всюду, где векторное произведение векторов напряженности электрического и магнитного полей отлично от нуля.

Можно выделить три главных направления практического применения электричества: передача и преобразование информации (радио, телевидение, компьютеры), передача импульса и момента импульса (электродвигатели), преобразование и передача энергии (электрогенераторы и линии электропередачи). И импульс, и энергия переносятся полем через пустое пространство, наличие среды приводит лишь к потерям. Энергия не передается по проводам! Провода с током нужны для формирования электрического и магнитного полей такой конфигурации, чтобы поток энергии, определяемый векторами Пойнтинга во всех точках пространства, был направлен от источника энергии к потребителю. Энергия может передаваться и без проводов, тогда ее переносят электромагнитные волны. (Внутренняя энергия Солнца убывает, уносится электромагнитными волнами, в основном светом. Благодаря части этой энергии поддерживается жизнь на Земле.)

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

calcsbox.com

Зако́н сохране́ния эне́ргии — фундаментальный закон природы

Закон сохранения энергии – фундаментальный закон природы

Содержание этого закона в наиболее краткой формулировке формулируется так : “Энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной. Энергия может только превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение/уменьшение ее энергии равно убыли/возрастанию энергии взаимодействующих с ней тел и физических полей.”

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.

Некоторые авторы не согласны с тем, что энергия является скалярной величиной. Ведь энергия — это физическая величина, характеризующая движение материи, а понятие движение очевидно связано с понятием направления. Закон сохранения энергии в современной трактовке ничего не говорит о сохранении направления движения, так как энергия трактуется как скалярная величина. Поскольку энергия является характеристикой движения, то закон сохранения энергии является частным случаем более общего закона сохранения движения, учитывающего не только сохранение количества энергии, но и сохранение направления движения. Именно закон сохранения движения отражает не только вечное существование материи, но и вечное ее движение. Впрочем, наш сайт — не место для научных споров и мы ограничимся наиболее распространенным понятием энергии как скалярной величины.

Закон сохранения энергии говорит, что энергия не создается из ничего и не теряется бесследно. При всех происходящих в природе процессах один вид энергии превращается в другой. Химическая энергия батареек фонарика превращается в электрическую, в лампочке электрическая энергия превращается в тепловую и световую — это простой пример «энергетической цепочки», показывающий как один вид энергии превращается в другой.

Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

Коэффициент полезного действия

На первый взгляд закон сохранения энергии как бы утверждает, что энергия при любых преобразованиях не должна теряться. Но все мы знакомы с понятием коэффициента полезного действия, то есть знаем, что превращение энергии одного вида в другой связано с потерями энергии. Противоречия тут нет, поскольку речь идет о «полезном действии». Когда мы говорим о коэффициенте полезного действия мы всегда, явно или неявно, имеем в виду некоторый процесс преобразования энергии в работу, причем сравниваем при этом количество затраченной энергии с полученной работой. Но коэффициент полезного действия ни одного реального (необратимого) процесса не может быть 100% при преобразовании энергии в работу (этот принцип известен как второй закон термодинамики). Причина в том, что в ходе любого такого процесса имеют место неизбежные потери энергии, в основном на трение и нагревание участвующих в процессе тел. Трение — это в результате тоже нагревание, то есть часть затраченной энергии всегда переходит в теплоту.

Коэффициент полезного действия (КПД) выражают в процентах.

КПД механизма тем больше, чем большая часть потребляемой энергии превращается в необходимую энергию. Например, а среднем автомобиль преобразует лишь 15% химической энергии бензина в кинетическую энергию. Вся остальная энергия превращается в тепло. КПД флуоресцентных ламп выше КПД обычных электрических лампочек, поскольку во флуоресцентных лампах больше электричества превращается в свет и меньше уходит на производство тепла.

Но при описании таких устройств как тепловые насосы мы встречаемся с утверждениями, что их КПД превышает 100%. На первый взгляд может показаться, что тут есть какое-то противоречие с законом сохранения энергии. В действительности же тут просто некорректно используется понятие КПД. Действительно, достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса. Но для характеристики эффективности теплового насоса нужно применять не КПД, а коэффициент преобразования или отопительный коэффициент СОР (coefficient of performance), равный отношению энергии, отдаваемой потребителю теплоты к мощности, потребляемой компрессором. Поскольку энергия, отдаваемая потребителю перекачивается от источника этой теплоты, значение коэффициэнта преобразования может быть и больше 100%.

Энтропия

Итак, мы видим, что при любом преобразовании энергии в работу количество «полезной» энергии уменьшается, то есть количество энергии для преобразования в работу или теплоту непрерывно уменьшается со временем, так как теплота спонтанно переходит из более теплой области к более холодной. Но первый закон термодинамики гласит, что энергию невозможно создать или уничтожить. Следовательно, количество энергии во вселенной всегда такое же, как было и при ее создании. Другими словами, количество энергии во вселенной остается постоянным, но возможность использования ее для того, чтобы проделать полезную работу, уменьшается при каждой теплопередаче и выполнении работы. Это явление в науке принято характеризовать величиной, которая называется энтропией.

Энтропия — это сокращение доступной энергии вещества в результате передачи энергии. Энтропия используется для измерения уменьшения пригодности энергии в результате процесса.

Термин «энтропия» используется для описания количества хаотичности в любой системе. В термодинамике энтропия указывает расположение молекул вещества или организацию энергии системы. Системы или вещества с высоким значением энтропии более дезорганизованы, чем с низким. Например, у молекул в твердых телах определенная кристаллическая структура, благодаря чему они лучше организованы, и у них ниже значение энтропии. При сообщении телу теплоты и изменении его состояния на жидкое увеличивается уровень его энтропии, так как кинетическая энергия увеличивает колебания молекул, в результате чего их положение становится случайным.

Энтропия увеличивается, когда жидкость изменяет состояние на газообразное при потреблении большего количества тепловой энергии. Такая же аналогия существует при описании порядка источников энергии. Если энергия заключена в ограниченном источнике, у нее низкое значение энтропии. Если она распределена среди большого количества молекул, ее интенсивность уменьшается, увеличивая энтропию. Например, если 1,05 кДж энергии у 1000 молекул передать 1 миллиону молекул, интенсивность энергии уменьшится, а энтропия возрастет.

Энтропию трудно понять, так как это абстрактное понятие беспорядка энергии во вселенной. Этот беспорядок связан с уменьшением пригодности энергии для преобразования в работу. Энергия всегда становится недоступной, если процессы уменьшают ее интенсивность, распространяя ее по вселенной. Если энергия распределена среди бесчисленных молекул вселенной, разница температур самых холодных и самых теплых участков уменьшается. Если разница температур уменьшается, тепловая энергия, которую можно преобразовать в полезную работу, также уменьшается. Следовательно, любой процесс, который производит увеличение энтропии, уменьшает энергию для будущих процессов. В конечном счете наступит момент, когда энтропия вселенной приблизится к максимальному значению, и преобразование теплоты в работу станет невозможным.

Абсолютная энтропия (S) вещества или процесса — это изменение доступной энергии при теплопередаче при данной температуре (Btu/R, Дж/К). Математически энтропия равняется теплопередаче, деленной на абсолютную температуру, при которой происходит процесс. Следовательно, процессы передачи большого количества теплоты больше увеличивают энтропию. Также изменения энтропии увеличатся при передаче теплоты при низкой температуре. Так как абсолютная энтропия касается пригодности всей энергии вселенной, температуру обычно измеряют в абсолютных единицах (R, К).

Удельную энтропию (S) измеряют относительно единицы массы вещества. Температурные единицы, которые используются при вычислении разниц энтропии состояний, часто приводятся с температурными единицами в градусах по Фаренгейту или Цельсию. Так как различия в градусах между шкалами Фаренгейта и Ренкина или Цельсия и Кельвина равные, решение в таких уравнениях будет правильным независимо от того, выражена энтропия в абсолютных или обычных единицах.

Все процессы преобразования энергии в конечном счете увеличивают энтропию вселенной. Вывод отсюда — полезная работа может производиться только до тех пор, пока не иссякли запасы доступной нам энергии.

Вечный двигатель

Люди веками мечтали (некоторые все еще мечтают) создать устройство, способное бесконечно совершать работу без затрат топлива или других энергетических ресурсов. Но согласно закону сохранения энергии, все попытки создать такой двигатель обречены на провал. К выводу о невозможности создания вечного двигателя ученые пришли после того, как многочисленные попытки создать такой двигатель оказались безуспешными.

Проекты вечных двигателей разделяют на два типа по характеру совершаемой работы:

Вечный двигатель первого рода (физический \ механический, гидравлический, магнитный) — непрерывно действующая машина, которая, будучи запущенной один раз, совершает работу без получения энергии извне. Это устройства механического характера, принцип действия которых основывается на использовании некоторых физических явлений, например, на действии силы тяжести, законе Архимеда, капиллярных явлениях в жидкостях. Возможность работы такой машины неограниченное время означала бы получение энергии из ничего.

Вечный двигатель второго рода (естественный) — тепловая машина, которая в результате совершения цикла полностью преобразует в работу тепло, получаемое от какого- либо одного «неисчерпаемого» источника (океана, атмосферы и т. п.). Классический вечный двигатель второго рода предусматривает возможность накопления тепла за счет работы, затраты которой меньше полученного тепла, и использования части этого тепла для повторного совершения работы в новом цикле. Таким образом, должен образоваться избыток работы. Другой вариант этого двигателя подразумевает упорядочение хаотического теплового движения молекул, в результате чего возникает направленное движение вещества, сопровождаемое понижением его термодинамической температуры.

В результате бесконечных попыток создать вечный двигатель были сформулированы так называемые первое и второе начала термодинамики, которые являются следствиями закона сохранения энергии:

Первое начало термодинамики гласит: изменение внутренней энергии термодинамической системы при переходе ее из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход, т. е. Q = ΔU + A. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Второе начало термодинамики утверждает: невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему. Что также означает, что в замкнутой системе энтропия при любом реальном процессе либо возрастает, либо остается неизменной (т. е. ΔS ≥ 0). Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Несмотря на то, что наука давно и окончательно пришла к выводу о невозможности создания вечного двигателя, существует множество энтузиастов, которые продолжают разрабатывать различные проекты такого рода. Чтобы убедиться в этом, достаточно создать запрос на Youtube.com на тему «вечный двигатель».

altenergiya.ru

Закон сохранения энергии — Традиция

Материал из свободной русской энциклопедии «Традиция»

Закон сохранения энергии — основной закон природы, заключающийся в том, что энергия замкнутой системы сохраняется во времени. Говоря проще, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую.^[1]

Закон сохранения энергии встречается во всех областях жизни, в различных разделах физики и проявляется в сохранении различных её форм. Например, в классической механике закон проявляется в сохранении механической энергии (суммы потенциальной и кинетической энергий). В термодинамике закон сохранения энергии называется первым началом термодинамики и говорит о сохранении энергии в сумме с тепловой энергией.

Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую закономерность в природе во всех явлениях, то правильнее называть его не законом, а принципом сохранения энергии.

Частный случай — Закон сохранения механической энергии — механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии сил типа трения (диссипативных сил) механическая энергия не возникает из ничего и не может никуда исчезнуть.

Ек1+Еп1=Ек2+Еп2

Закон сохранения энергии — это интегральный закон. Это значит, что он складывается из действия дифференциальных законов и является свойством их совокупного действия. Например, иногда говорят, что невозможность создать вечный двигатель обусловлена законом сохранения энергии. Но это не так. На самом деле, в каждом проекте вечного двигателя срабатывает один из дифференциальных законов и именно он делает двигатель неработоспособным. Закон сохранения энергии просто обобщает этот факт.

Сократ о законе сохранения энергии[править]

«Ничего не возникает из ничего и не исчезает в никуда».

Ломоносов о законе сохранения энергии[править]

«Ежели где-то что-то убыло, то где-то что-то прибыть должно непременно».

Эйнштейн о релятивистском законе сохранения энергии[править]

«Дорелятивистская физика знала два фундаментальных закона сохранения, а именно: закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один».

Эйнштейн А. Собрание научных трудов. том 1. М. 1965 г. стр. 553.

Согласно теореме Нётер, закон сохранения механической энергии является следствием однородности времени.^[2]

traditio.wiki

Закон сохранения энергии — Циклопедия

Закон сохранения энергии // Первый образовательный телеканал [4:39] 15.04 Закон сохранения полной механической энергии [38:08]

Закон сохранения энергии в физике, принцип, согласно которому полная энергия замкнутой системы сохраняется на протяжении времени. Энергия не возникает из ничего и не исчезает в никуда, а может только превращаться из одной формы в другую. Из-за этого закона невозможны вечные двигатели первого рода. Закон был изобретен независимо для разных видов энергии многими учеными, среди которых Готфрид Лейбниц — для кинетической энергии, Джеймс Джоуль — для внутренней энергии, Джон Пойнтинг — для электромагнитной энергии. Предвосхитивший закон сохранения энергии общий принцип, что материя всегда сохраняется, был сформулирован М. В. Ломоносовым в письме к Л. Эйлеру (5 июля 1748 года).

[править] Закон сохранения механической энергии

В механике закон сохранения энергии утверждает, что в замкнутой системе частиц, полная энергия, которая является суммой кинетической и потенциальной энергии и не зависит от времени, то есть является интегралом движения. Закон сохранения энергии справедлив только для замкнутых систем, то есть при отсутствии внешних полей или взаимодействий.

Силы взаимодействия между телами, для которых выполняется закон сохранения механической энергии называются консервативными силами. Закон сохранения механической энергии не выполняется для сил трения, поскольку при наличии сил трения происходит преобразование механической энергии в тепловую.

[править] Математическая формулировка

Эволюция механической системы материальных точек с массами [math] m_i[/math] по второму закону Ньютона удовлетворяет системе уравнений

[math] m_i\dot{\mathbf{v}_i} = \mathbf{F}_i [/math],

где [math] \mathbf{v}_i [/math] — скорости материальных точек, а [math] \mathbf{F}_i [/math] — силы, действующие на эти точки.

Если подать силы, как сумму потенциальных сил [math] \mathbf{F}_i^p [/math] и непотенциальных сил [math] \mathbf{F}_i^d [/math], а потенциальные силы записать в виде

[math] \mathbf{F}_i^p = — \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) [/math],

то, домножив все уравнения на [math] \mathbf{v}_i [/math] можно получить

[math] \frac{d}{dt} \sum_i \frac{mv_i^2}{2} = — \sum_i \frac{d\mathbf{r}_i}{dt}\cdot \nabla_i U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) + \sum_i \frac{d\mathbf{r}_i}{dt} \cdot \mathbf{F}_i^d [/math]

Первая сумма в правой части уравнения является ни чем иным, как производной по времени от сложной функции, а следовательно, если ввести обозначения

[math] E = \sum_i \frac{mv_i^2}{2} + U(\mathbf{r}_1, \mathbf{r}_2, \ldots \mathbf{r}_N) [/math]

и назвать эту величину механической энергией, то, интегрируя уравнения с момента времени t=0 до момента времени t, можно получить

[math] E(t) — E(0) = \int_L \mathbf{F}_i^d \cdot d\mathbf{r}_i[/math],

где интегрирование проводится вдоль траекторий движения материальных точек.

Таким образом, изменение механической энергии системы материальных точек со временем равно работе непотенциальных сил.

Закон сохранения энергии в механике выполняется только для систем, в которых все силы потенциальные^[1].

[править] Однородность времени

Закон сохранения энергии связан с однородностью времени, а именно с принципом, согласно которому ни одно мгновение никоим образом не отличается от другого, поэтому одинаковые физические системы при одинаковых условиях всегда эволюционируют одинаково. В этом закон сохранения энергии является частным случаем общей теоремы Нётер.

С точки зрения аналитической механики, однородность времени сводится к утверждению, что механика Лагранжа или Гамильтона классической системы не зависит от времени непосредственно, а только опосредованно, через обобщенные координаты.

[править] Закон сохранения энергии в термодинамике

В термодинамике закон сохранения энергии устанавливает соотношение между внутренней энергией тела, количеством теплоты, переданного телу и проделанной работой.

Термодинамика изучает в основном неподвижные тела, кинетическая и потенциальная энергия которых остается неизменной. Однако, эти тела могут выполнять работу над другими телами, если, например, изменять их температуру. Итак, поскольку нагретое тело может выполнять работу, оно имеет определенную энергию. Эта энергия получила название внутренней энергии. С точки зрения физики микромира — физики атомов и молекул, внутренняя энергия тела является суммой кинетических и потенциальных энергий частиц, из которых это тело состоит. Однако, учитывая большое количество и малые размеры частиц и вообще неизвестные законы их взаимодействия, внутреннюю энергию тела определить трудно, исходя из его строения. Однако очевидно, что она зависит от температуры тела.

Определяющим моментом для установления закона сохранения энергии стало установление эквивалентности между теплом, количественной характеристикой которого является количество теплоты, и механической работой. Если телу предоставить определенное количество теплоты Q, то часть ее пойдет на выполнение механической работы A, а часть на увеличение внутренней энергии тела:

[math] Q = A + \Delta E [/math],

Эта формула составляет основу первого закона термодинамики.

Аналогичным образом при выполнении механической работы, часть энергии теряется в виде тепла, то есть идет на повышение температуры тела и окружающей среды.

В общем суммарный приток энергии в систему должен быть равен суммарному оттоку энергии из системы, плюс изменение энергии тел, из которых состоит сама система. Другими словами, энергия может быть преобразована из одной формы в другую, но не может быть создана или уничтожена.

[править] Уравнение непрерывности

В неизолированных физических системах энергия может переплывать с одной пространственной части системы к другой. В таком случае закон сохранения энергии принимает вид уравнения непрерывности

[math] \frac{dw}{dt} + \text{div}\, \mathbf{J}_E = 0[/math],

где [math] w [/math] — плотность энергии, [math] \mathbf{J}_E [/math] — плотность потока энергии.

Это уравнение означает, что изменение энергии определенного элементарного объема со временем равно разнице между притоком энергии в этот элементарный объем и оттоком энергии из него.

Так выглядит, в частности уравнение теплопроводности.

[править] Преобразование энергии

Энергия одного вида может превращаться в энергию другого вида, например, химическая энергия может превращаться в тепловую, а тепловая энергия в механическую и тому подобное.

В молекуле химического соединения атомы связаны между собой химическими связями. Для того, чтобы разорвать химическую связь нужно затратить определенную энергию, значение которой определяется типом связи. В одних молекулах энергия связи больше, в других меньше. Так, энергия связи в молекуле углекислого газа СО₂ больше, чем суммарная энергия атома углерода в угле и атомов кислорода в молекуле кислорода O₂. Поэтому возможна химическая реакция горения, в результате которой образуется углекислый газ, а остатки химической энергии передаются поступательному, тепловому движению молекул, то есть превращаются в тепло. Выделенное в результате горения тепло можно использовать, например, для нагрева пара в паровой турбине, которая, вращаясь, создает электродвижущую силу в генераторе, производя электроэнергию. Электроэнергия может, в свою очередь использоваться для выполнения механической работы, например, подъема лифта, или же для освещения, где электрическая энергия превращается в энергию электромагнитных волн — света.

1. ↑ Хотя сила Лоренца, которая действует на движущиеся электрические заряды не является потенциальной, она не выполняет работы, поэтому в магнитном поле закон сохранения энергии тоже выполняется

• Залевски К. Феноменологическая и статистическая термодинамика. — М.: Мир, 1973. — 168 с.

cyclowiki.org

Закон сохранения энергии | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Закон сохранения энергии — один из наиболее важных законов, согласно которому физическая величина — энергия сохраняется в изолированной системе. Этому закону подчиняются все без исключения известные процессы в природе. В изолированной системе энергия может только превращаться из одной формы в другую, но ее количество остается постоянным.

Для того, чтоб понять что же представляет из себя закон и откуда это получается возьмем тело массой m, которое уроним на Землю. В точке 1 тело у нас находится на высоте h и покоится (скорость равна 0). В точке 2 тело тело имеет некоторую скорость v и находится на расстоянии h-h2. В точке 3 тело имеет максимальную скорость и оно почти лежит на нашей Земле, то есть h=0

В точке 1 тело имеет только потенциальную энергию, так как скорость тела равно 0,так что полная механическая энергия равна.

После того как мы тело отпустили, оно стало падать. При падении потенциальная энергия тела уменьшается, так как уменьшается высота тела над Землей, а его кинетическая энергия увеличивается, так как увеличивается скорость тела. На участке 1-2 равном h2 потенциальная энергия будет равна

А кинетическая энергия будет равная в тот момент ( — скорость тела в точке 2):

Чем ближе тело становится к Земле, тем меньше его потенциальная энергия, но в тот же момент увеличивается скорость тела, а из-за этого и кинетическая энергия. То есть в точке 2 работает закон сохранения энергии: потенциальная энергия уменьшается, кинетическая растет.

В точке 3 (на поверхности Земли) потенциальная энергия равна нулю (так как h = 0), а кинетическая максимальна (где v3 — скорость тела в момент падения на Землю). Так как , то кинетическая энергия в точке 3 будет равна Wk=mgh. Следовательно, в точке 3 полная энергия тела W3=mgh и равна потенциальной энергии на высоте h. Конечная формула закона сохранения механической энергии будет иметь вид:

Формула выражает закон сохранения энергии в замкнутой системе, в которой действуют только консервативные силы: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию и обратно.

В Формуле мы использовали :

— Полная энергия тела

— Потенциальная энергия тела

— Кинетическая энергия тела

— Масса тела

— Ускорение свободного падения

— Высота на которой находится тело

— Скорость тела

xn--b1agsdjmeuf9e.xn--p1ai

Закон сохранения энергии — Научно-популярный журнал: «Как, зачем и почему»

Энергия ветра

Возможно, вы думаете, что энергия, это что – то такое, что можно до конца использовать, исчерпать. Например, если в баке кончился бензин, то энергия, которая движет машину, иссякла. Ученые смотрят на этот вопрос иначе. Они бы сказали в случае с машиной, что энергия перешла из одной формы в другую.

Законе сохранения энергии

Такое убеждение основано на законе сохранения энергии, который утверждает, что энергию нельзя создать из ничего и нельзя уничтожить: ее можно только перевести из одной формы в другую

Это утверждение равносильно тому, что вся энергия Вселенной присутствовала в ней с самого начала и останется до тех пор, пока Вселенная будет существовать.

Потенциальная и кинетическая энергия

Представьте себе горное озеро. Озеро сообщается с долиной узким ущельем. Это ущелье перегорожено плотиной. Шлюз плотины закрыт, и вода, поэтому не может стечь в долину. Если шлюз открыть, то вода немедленно потечет, но при закрытом шлюзе она спокойно стоит. В таком случае говорят, что вода обладает потенциальной энергией. То есть такой энергией, которую только предстоит использовать.

Но вот шлюз открыт, вода хлынула вниз, увлекаемая земным притяжением. Энергия тяжести воды может перейти в механическую энергию, если на пути воды поставить ротор электростанции. Вода производит работу — она вращает турбину. Потенциальная энергия воды перешла в кинетическую энергию — энергию движения турбины.

Вращение турбины электростанции заставляет генератор вырабатывать электрический ток. То есть электрическая энергия в виде электрического тока приходит в наши дома и заставляет гореть лампы, работать холодильники и стиральные машины. Когда вы зажигаете лампу, то возникают свет (электромагнитная энергия) и тепло (тепловая энергия).

Таким образом, потенциальная энергия воды не исчезла, а превратилась в свет и тепло в вашем доме. Сквозь стены и окна остатки этой энергии рассеиваются во Вселенной, но ни в коем случае не исчезают.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

kipmu.ru

Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы

Тестирование онлайн

Закон сохранения энергии

Полная механическая энергия замкнутой системы тел остается неизменной

Закон сохранения энергии можно представить в виде

Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения

Рассмотрим свободное падение тела с некоторой высоты h2. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.

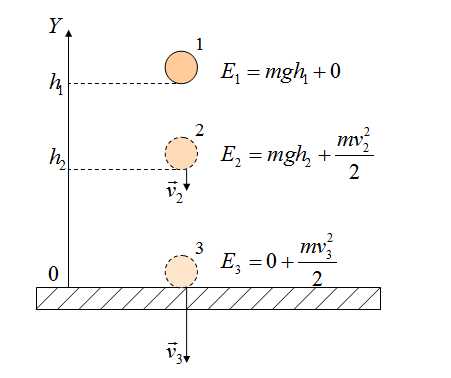
В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h3 меньше h2. Часть потенциальной энергии перешло в кинетическую.

Состояние 3 — это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).

Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.

А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.

Главное запомнить

1) Суть закона сохранения энергии

fizmat.by

No related posts.