Закон сохранения энергии кратко и понятно – Закон сохранения энергии

Закон сохранения энергии в механике

Закон сохранения энергии в механике

«Физика — 10 класс»

Как изменяются потенциальная, кинетическая и полная механическая энергии тела при его свободном падении вниз? если тело брошено вверх?

Обратимся к простой системе тел, состоящей из земного шара и поднятого над поверхностью Земли тела, например камня.

Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Изменение кинетической энергии камня равно работе сил тяжести:

ΔЕ_к = A_т         (5.23)

Изменение потенциальной энергии равно работе силы тяжести, взятой с обратным знаком:

ΔЕ_п = -А_т       (5.24)

Работа силы тяжести, действующей со стороны камня на земной шар, практически равна нулю. Из-за большой массы земного шара его перемещением и изменением скорости можно пренебречь. Из формул (5.23) и (5.24) следует, что

ΔЕ_к = -ΔЕ_п.         (5.25)

Равенство (5.25) означает, что увеличение кинетической энергии системы равно убыли её потенциальной энергии (или наоборот). Отсюда следует, что

ΔЕ_к + ΔЕ_п = 0,

или

Δ (Е_к + Е_п) = 0.         (5.26)

Изменение суммы кинетической и потенциальной энергий системы равно нулю.

Полная механическая энергия Е равна сумме кинетической и потенциальной энергий тел, входящих в систему:

Е = Е_к + Е_п.         (5.27)

Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (5.26) равно нулю, то энергия остаётся постоянной:

Е = Е_к + Е_п = const.         (5.28)

,BR.

Закон сохранения механической энергии:

В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.

Закон сохранения механической энергии является частным случаем общего закона сохранения энергии.

Общий закон сохранения энергии:

Энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.

Учитывая, что в рассматриваемом конкретном случае Е_п = mgh и закон сохранения механической энергии можно записать так:

или

Это уравнение позволяет очень просто найти скорость υ₂ камня на любой высоте h₂ над землёй, если известна начальная скорость камня на исходной высоте h₁.

Чем мы пренебрегаем, когда говорим, что механическая энергия падающего камня сохраняется? Какие превращения энергии реально происходят при падении камня в воздухе?

Закон сохранения механической энергии (5.28) легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под Е

к нужно понимать сумму кинетических энергий всех тел, а под Е_п — полную потенциальную энергию системы. Для системы, состоящей из тела массой m и горизонтально расположенной пружины (см. рис. 5.13), закон сохранения механической энергии имеет вид

Уменьшение механической энергии системы под действием сил трения.

Рассмотрим влияние сил трения на изменение механической энергии системы.

Если в изолированной системе силы трения совершают работу при движении тел относительно друг друга, то её механическая энергия не сохраняется. В этом легко убедиться, толкнув книгу, лежащую на столе. Из-за действия силы трения книга почти сразу останавливается. Сообщённая ей механическая энергия исчезает.

Сила трения совершает отрицательную работу и уменьшает кинетическую энергию. Но потенциальная энергия при этом не увеличивается.

Поэтому полная механическая энергия убывает. Кинетическая энергия не превращается в потенциальную.

Нагревание при действии сил трения легко обнаружить. Для этого, например, достаточно энергично потереть монету о стол. С повышением температуры, как известно из курса физики основной школы, повышается кинетическая энергия теплового движения молекул или атомов. Следовательно, при действии сил трения кинетическая энергия тела превращается в кинетическую энергию хаотично движущихся молекул.

Силы трения (сопротивления) неконсервативны.

Отличие сил трения от консервативных сил становится особенно наглядным, если рассмотреть работу тех и других на замкнутом пути. Работа силы тяжести, например, на замкнутом пути всегда равна нулю. Она положительна при падении тела с высоты h и отрицательна при подъёме на ту же высоту. Работа же силы сопротивления воздуха отрицательна как при подъёме тела вверх, так и при движении его вниз. Поэтому на замкнутом пути она обязательно меньше нуля.

В любой системе, состоящей из больших макроскопических тел, действуют силы трения. Следовательно, даже в изолированной системе движущихся тел механическая энергия обязательно убывает. Постепенно затухают колебания маятника, останавливается машина с выключенным двигателем и т. д.

Но убывание механической энергии не означает, что эта энергия исчезает бесследно. В действительности происходит переход энергии из механической формы в другие. Обычно при работе сил трения происходит нагревание тел, или, как говорят, увеличение их внутренней энергии.

Во всех процессах, происходящих в природе, как и в создаваемых приборах, устройствах, всегда выполняется закон сохранения и превращения энергии: энергия не исчезает и не появляется вновь, она может только перейти из одного вида в другой.

В двигателях внутреннего сгорания, паровых турбинах, электродвигателях и т. д. механическая энергия появляется за счёт убыли энергии других форм: химической, электрической и т. д.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика

Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»

class-fizika.ru

Закон сохранения механической энергии. Видеоурок. Физика 9 Класс

Темой урока является один из фундаментальных законов природы – закон сохранения механической энергии.

Мы ранее говорили о потенциальной и кинетической энергии, а также о том, что тело может обладать вместе и потенциальной, и кинетической энергией. Прежде чем говорить о законе сохранения механической энергии вспомним, что такое полная энергия. Полной механической энергией называют сумму потенциальной и кинетической энергий тела.

Также вспомним, что называют замкнутой системой. Замкнутая система – это такая система, в которой находится строго определенное количество взаимодействующих между собой тел и никакие другие тела извне на эту систему не действуют.

Когда мы определились с понятием полной энергии и замкнутой системы, можно говорить о законе сохранения механической энергии. Итак, полная механическая энергия в замкнутой системе тел, взаимодействующих друг с другом посредством сил тяготения или сил упругости (консервативных сил), остается неизменной при любом движении этих тел.

Мы уже изучали закон сохранения импульса (ЗСИ):

Очень часто случается так, что поставленные задачи можно решить только с помощью законов сохранения энергии и импульса.

Рассмотреть сохранение энергии удобно на примере свободного падения тела с некоторой высоты. Если некоторое тело находится в состоянии покоя на некоторой высоте относительно земли, то это тело обладает потенциальной энергией. Как только тело начинает свое движение, высота тела уменьшается, уменьшается и потенциальная энергия. При этом начинает нарастать скорость, появляется энергия кинетическая. Когда тело приблизилось к земле, то высота тела равна 0, потенциальная энергия тоже равна 0, а максимальной будет являться кинетическая энергия тела. Вот здесь и просматривается превращение потенциальной энергии в кинетическую (рис. 1). То же самое можно сказать о движении тела наоборот, снизу вверх, когда тело бросают вертикально вверх.

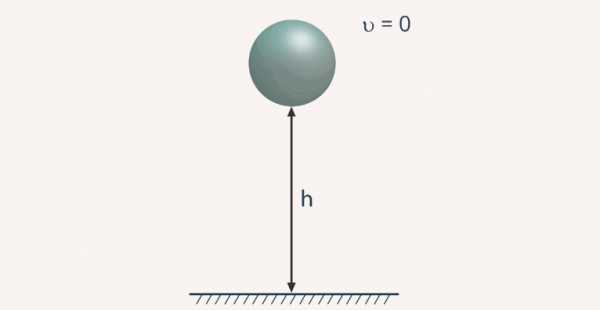
Рис. 1. Свободное падение тела с некоторой высоты

---

Дополнительная задача 1. «О падении тела с некоторой высоты»

Задача 1

Условие

Тело находится на высоте  от поверхности Земли и начинает свободно падать. Определите скорость тела в момент соприкосновения с землей.

Решение 1:

Начальная скорость тела . Нужно найти .

Рассмотрим закон сохранения энергии.

Рис. 2. Движение тела (задача 1)

В верхней точке тело обладает только потенциальной энергией:

. Когда тело приблизится к земле, то высота тела над землей будет равна 0, а это означает, что потенциальная энергия у тела исчезла, она превратилась в кинетическую:

Согласно закону сохранения энергии можем записать:

Масса тела сокращается. Преобразуя указанное уравнение, получаем: .

Окончательный ответ будет: . Если подставить все значение, то получим:.

Ответ:.

Пример оформления решения задачи:

Рис. 3. Пример оформления решения задачи № 1

Данную задачу можно решить еще одним способом, как движение по вертикали с ускорением свободного падения.

Решение 2:

Запишем уравнение движения тела в проекции на ось :

Когда тело приблизится к поверхности Земли, его координата будет равна 0:

Перед ускорением свободного падения стоит знак «-», поскольку оно направлено против выбранной оси .

Подставив известные величины, получаем, что тело падало на протяжении времени . Теперь запишем уравнение для скорости:

Полагая ускорение свободного падения равным  получаем:

Знак минус означает, что тело движется против направления выбранной оси.

Ответ:.

Пример оформления решения задачи № 1 вторым способом.

Рис. 4. Пример оформления решения задачи № 1 (способ 2)

Также для решения данной задачи можно было воспользоваться формулой, которая не зависит от времени:

---

Конечно, нужно отметить, что данный пример мы рассмотрели с учетом отсутствия сил трения, которые в реальности действуют в любой системе. Обратимся к формулам и посмотрим, как записывается закон сохранения механической энергии:

---

Дополнительная задача 2

Тело свободно падает с высоты . Определите, на какой высоте  кинетическая энергия равна трети потенциальной ().

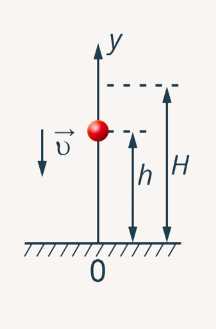
Рис. 5. Иллюстрация к задаче № 2

Решение:

Когда тело находится на высоте , оно обладает потенциальной энергией, и только потенциальной. Эта энергия определяется формулой: . Это и будет полная энергия тела.

Когда тело начинает двигаться вниз, уменьшается потенциальная энергия, но вместе с тем нарастает кинетическая. На высоте, которую нужно определить, у тела уже будет некоторая скорость V. Для точки, соответствующей высоте h, кинетическая энергия имеет вид: 

Потенциальная энергия на этой высоте будет обозначена следующим образом: .

По закону сохранения энергии, у нас полная энергия сохраняется. Эта энергия  остается величиной постоянной. Для точки  мы можем записать следующее соотношение:  (по З.С.Э.).

Вспоминая, что кинетическая энергия по условию задачи составляет , можем записать следующее: .

Обратите внимание: масса и ускорение свободного падения сокращается, после несложных преобразований мы получаем, что высота, на которой такое соотношение выполняется, составляет .

Ответ: 

Пример оформления задачи 2.

Рис. 6. Оформление решения задачи № 2

---

 

Представьте себе, что тело в некоторой системе отсчета обладает кинетической и потенциальной энергией. Если система замкнутая, то при каком-либо изменении произошло перераспределение, превращение одного вида энергии в другой, но полная энергия остается по своему значению той же самой (рис. 7).

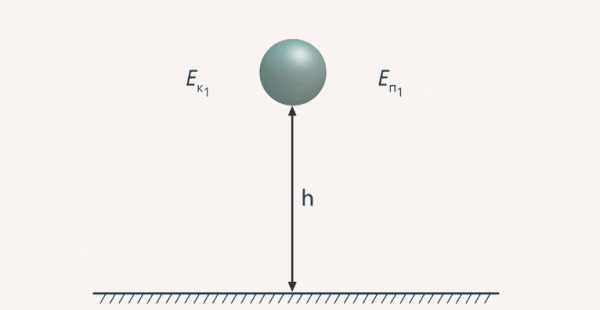
Рис. 7. Закон сохранения энергии

Представьте себе ситуацию, когда по горизонтальной дороге движется автомобиль. Водитель выключает мотор и продолжает движение уже с выключенным мотором. Что в этом случае происходит (рис. 8)?

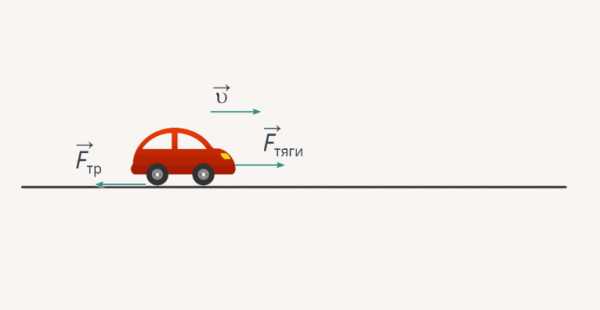
Рис. 8. Движение автомобиля

В данном случае автомобиль обладает кинетической энергией. Но вы прекрасно знаете, что с течением времени автомобиль остановится. Куда девалась в этом случае энергия? Ведь потенциальная энергия тела в данном случае тоже не изменилась, она была какой-то постоянной величиной относительно Земли. Как произошло изменение энергии? В данном случае энергия пошла на преодоление сил трения. Если в системе встречается трение, то оно также влияет на энергию этой системы. Посмотрим, как записывается в данном случае изменение энергии.

Изменяется энергия, и это изменение энергии определяется работой против силы трения. Определить работу силы трения мы можем с помощью формулы, которая известна из 7 класса (сила и перемещение направлены противоположно): 

Итак, когда мы говорим об энергии и работе, то должны понимать, что каждый раз мы должны учитывать и то, что часть энергии расходуется на преодоление сил трения. Совершается работа по преодолению сил трения. Работа является величиной, которая характеризует изменение энергии тела.

В заключение урока хотелось бы сказать, что работа и энергия по сути своей связанные величины через действующие силы.

---

Дополнительная задача 3

Два тела – брусок массой  и пластилиновый шарик массой  – движутся навстречу друг другу с одинаковыми скоростями (). После столкновения пластилиновый шарик прилип к бруску, два тела продолжают движение вместе. Определить, какая часть механической энергии  превратилась во внутреннюю энергию этих тел, с учетом того что масса бруска в 3 раза больше массы п

interneturok.ru

Закон сохранения механической энергии

Закон сохранения механической энергии

Внимание! Zaochnik не продает дипломы, аттестаты об образовании и иные документы об образовании. Все услуги на сайте предоставляются исключительно в рамках законодательства РФ.

Внимание! Zaochnik не продает дипломы, аттестаты и иные документы об образовании. Все услуги на сайте предоставляются в рамках законодательства РФ.

Мы помогаем студентам с дипломными, курсовыми, контрольными Узнать стоимость

При имеющейся замкнутой механической системе тела взаимодействуют посредством сил тяготения и упругости, тогда их работа равняется изменению потенциальной энергии тел с противоположным знаком:

A=–(Eр2–Eр1).

Следуя из теоремы о кинетической энергии, формула работы примет вид

A=Ek2-Ek1.

Отсюда следует, что

Ek2-Ek1=–(Eр2–Eр1) или Ek1+Ep1=Ek2+Ep2.

Кинетическая и потенциальная энергии

Определение 1

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Данное утверждение выражает закон сохранения энергии в замкнутой системе и в механических процессах, являющийся следствием законов Ньютона.

Определение 2

Сумма E=Ek+Ep— это полная механическая энергия.

Закон сохранения энергии выполняется при взаимодействии сил с потенциальными энергиями в замкнутой системе.

Пример N

Примером применения такого закона служит нахождение минимальной прочности легкой нерастяжимой нити, которая удерживает тесло с массой m, вращая его вертикально относительно плоскости (задачи Гюйгенса). Подробное решение изображено на рисунке 1.20.1.

Рисунок 1.20.1. К задаче Гюйгенса, где F→ принимаетс

zaochnik.com

Закон сохранения энергии | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Электромагнитное поле обладает энергией, которая рас­пределяется в пространстве, занятом полем. При изме­нении характеристик поля меняется и распределение энергии. Она перетекает из одной области пространства в другую, переходя, возможно, в другие формы. Закон со­хранения энергии для электромагнитного поля является следствием полевых уравнений.

Внутри некоторой замкнутой поверхности S, ограничивающей объем пространства V, занятого полем, содержится энергия W — энергия электромагнитного поля:

W = Σ(εε₀E_i² / 2 + μμ₀H_i² / 2)ΔV_i.

Если в этом объеме имеются токи, то электрическое поле производит над движущимися зарядами работу, за единицу времени равную

N = Σ_ij̅_i ×E̅_i • ΔV_i.

Это величина энергии поля, которая переходит в другие формы. Из уравнений Максвелла следует, что

ΔW + NΔt = -Δt∮_SS̅ × n̅ • dA, [1]

где ΔW — изменение энергии электромагнитного поля в рассматриваемом объеме за время Δt, а вектор S̅ = E̅ × H̅ называется вектором Пойнтинга.

Это закон сохранения энергии в электродинамике.

Через малую площадку величиной ΔA с единичным вектором нормали n̅ за единицу времени в направлении вектора n̅ про­текает энергия S̅ × n̅ • ΔA, где S̅ — значение вектора Пойнтин­га в пределах площадки. Сумма этих величин по всем элемен­там замкнутой поверхности (обозначена знаком интеграла), стоящая в правой части равенства [1], представляет собой энергию, вытекающую из объема, ограниченного поверхно­стью, за единицу времени (если эта величина отрицательна, то энергия втекает в объем). Вектор Пойнтинга определяет поток энергии электромаг­нитного поля через площадку, он отличен от нуля всюду, где векторное произведение векторов напряженности электрического и магнитного полей отлично от нуля. Материал с сайта http://worldofschool.ru

Можно выделить три глав­ных направления практи­ческого применения элек­тричества: передача и преобразование инфор­мации (радио, телевиде­ние, компьютеры), пере­дача импульса и момента импульса (электродвига­тели), преобразование и передача энергии (элек­трогенераторы и линии электропередачи). И им­пульс, и энергия перено­сятся полем через пустое пространство, наличие среды приводит лишь к потерям. Энергия не пе­редается по проводам! Провода с током нужны для формирования элек­трического и магнитного полей такой конфигура­ции, чтобы поток энергии, определяемый векторами Пойнтинга во всех точках пространства, был на­правлен от источника энергии к потребителю. Энергия может переда­ваться и без проводов, тогда ее переносят электромагнитные вол­ны. (Внутренняя энергия Солнца убывает, уносится электромагнитными вол­нами, в основном светом. Благодаря части этой энергии поддерживается жизнь на Земле.)

На этой странице материал по темам:

• Шпаргалки закон сохранения энергии

• Законы сохранения шпора

• Закон сохранения энергии сообщение кратко

• Шпаргалка закон сохранения энергии

• Закон сохранения энергии в электродинамике

worldofschool.ru