Что такое циклоидный психоз? — Центр «Феникс»
Известный уже более 100 лет, циклоидный психоз сочетает в себе симптомы как шизофрении, так и биполярного расстройства, но при этом, является другим заболеванием.
Циклоидный психоз в основном описан в европейской литературе. Это не широко признанное психотическое заболевание, но в большинстве исследований оно клинически и биологически отличается как от тяжелых расстройств настроения, так и от шизофрении.
Термин «циклоидный психоз» был впервые введен в 1926 году для описания случаев, которые не соответствовали типичной форме шизофрении или биполярного аффективного расстройства. Среди этих состояний было много случаев острых психотических заболеваний, характеризующихся ограниченной продолжительностью и восстановлением между рецидивами. Хотя острые проявления носят психотический характер, напоминающий шизофрению, течение носит эпизодический характер, как и при биполярном расстройстве.
Симптомы циклоидного психоза.
Циклоидный психоз начинается очень внезапно. Одна из ключевых вещей в этом заключается в том, что вы можете быть в порядке сегодня и быть в состоянии психоза уже на следующий день, а затем, в течение четырех дней после приема лекарств, психоз может купироваться.
Это состояние может сопровождаться симптомами, сходными с шизофренией, шизоаффективным расстройством. Но есть некоторые ключевые особенности:
- быстрое начало,
- быстрое прекращение,
- отличное состояние между эпизодами (качественные ремиссии),
- схожее проявление от эпизода к эпизоду (эпизоды по типу клише).
Циклоидный психоз, который чаще встречается у молодых женщин, редко сопровождается галлюцинациями.
Варианты лечения.
Электросудорожная терапия (ЭСТ) является эффективным методом лечения циклоидного психоза, но также эффективным является и медикаментозное лечение. Лечение антипсихотическими препаратами полезно в острой фазе, хотя неясно, предотвратит ли это рецидив.
Стабилизатор настроения литий, по-видимому, помогает предотвратить рецидив.
Как и при любом психическом заболевании, циклоидный психоз может быть вызван нарушениями в ежедневном ритме жизни. Физическая болезнь, изменения в вашей социальной жизни, даже смена времен года могут быть триггерами для некоторых людей.
Другая проблема заключается в том, что когда пациентам дают антипсихотическое лекарство, оно может иметь тяжелые побочные эффекты. Антипсихотическое лекарство может ослабить инициативу и мотивацию, и заставить человека чувствовать себя так, как будто на него «набросили тяжелое одеяло». Лекарства должны быть скорректированы с течением времени по мере изменения симптомов болезни и функционирования организма.
Долгосрочная перспектива.
В целом циклоидный психоз менее серьезен и меньше меняет жизнь, чем шизофрения. Циклоидный психоз обычно довольно хорошо и быстро поддается лечению и почти всегда реагирует на терапию лучше, чем шизофрения и аффективные расстройства.
Как правило, это приводит к хорошим результатам, и пациенты быстро возвращаются к привычной жизни.
БЕРЕГИТЕ СВОЕ ЗДОРОВЬЕ И ЗДОРОВЬЕ СВОИХ БЛИЗКИХ!
ВОВРЕМЯ ОБРАЩАЙТЕСЬ К ПСИХИАТРАМ!
Что такое Циклоида, определение термина в Энциклопедический словарь, Ударение в слове Циклоида
- Циклоида — (от греч. kykloeides — кругообразный) — плоская кривая,описываемая точкой Р окружности, катящейся без скольжения по неподвижнойпрямой. Циклоида — трансцендентная кривая. См. также Гипоциклоида,Эпициклоида.
-
Ударение в слове «Циклоида»
цикло́ида
Ударение падает на 2-й слог (с буквой о).
Тест для самопроверки:
Ivanov Alex
Предложения со словом Циклоида
Во-вторых, данная система в процессе трансформации может быть закрытой или открытой, находиться в состоянии, близком к равновесию или далёком от него, двигаться в историческом времени равномерно или ускоренно; соответственно своим социопространственным координатам, характеру социального движения и качеству системы она может находиться в параметрах действия закономерностей одного из циклов социального движения: синергетического, диалектического или в границах переходного периода, сочетая пропорции обеих циклоид.
В. И.
Карасев, Коррупция как механизм социальной деградации, 2005
Типичные циклоиды в детстве обычно производят впечатление гипертимических, но затем проявляется вялость, упадок сил, то, что раньше давалось легко, теперь требует непомерных усилий.
Коллектив авторов, Психологическая диагностика в практике врача, 2008
Ганнушкин выделил следующие типы психопатических личностей: циклоиды, астеники, шизоиды, параноики, эпилептоиды, истерические характеры, неустойчивые, антисоциальные и конституционально глупые.
Н. А. Дзеружинская, Диагностика, военно-врачебная экспертиза и принципы оказания помощи при расстройствах личности: методическое пособие, 2010
Непривычная для нас кривая проявления пассионарности равно не похожа ни на линию прогресса производительных сил — экспоненту, ни на синусоиду, где ритмично сменяются подъёмы и упадки, повторяясь, как времена года, ни на симметричную циклоиду биологического развития.
Л. Н. Гумилев, Тысячелетие вокруг Каспия, 1990
Циклоид — находчивый, но немного грустный, активный, но умеет отдыхать, общительный, но способен слушать.
С. Н. Савинков, Характеры. Как изучить и приручить, 2013
Для этого он изготовил соответствующие металлические поверхности и взвесил их: оказалось, что площадь циклоиды приблизительно в три раза больше площади круга.
Б. Н. Тарасов, «Мыслящий тростник». Жизнь и творчество Паскаля в восприятии русских философов и писателей, 2009
Он не собирается даже записывать полученные результаты, так как
Б. Н. Тарасов, «Мыслящий тростник». Жизнь и творчество Паскаля в восприятии русских философов и писателей, 2009
Выберите букву
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
- Значение слова Циклоида в других словарях:
-
- Значение слова циклоида — Толковый словарь Ушакова
- Что такое ЦИКЛОИДА — Словарь иностранных слов
- Определение термина Циклоида ж. — Словарь Ефремовой
- Что означает слово циклоидальный — Толковый словарь Ушакова
- Что означает термин Циклоидальный прил. — Словарь Ефремовой
— Словарь ЕфремовойПопулярные слова
Хвост
Фанаберия
Манто
Сват
Наст
Тауз
Парад
Бати
Янтарь
Ш
Небо
Табло
Нано.
Праздник циклоиды. Недавно я обнаружил новую форму — … | Рай Салливан
Недавно я открыл для себя новую форму — циклоиду. Никогда не слышал об этом? Теперь у вас есть шанс учиться вместе со мной и удивляться.
[ПРИМЕЧАНИЕ: этот пост не такой длинный, как кажется. Там много картинок.]
Не так уж часто можно обнаружить новую форму. Я думаю, что большинство из нас полагает, что наши знания о формах уже давно исчерпаны. Мы знаем наши квадраты, круги и треугольники из начальной школы, а позже в старшей школе добавили параболы, эллипсы и синусоиды.
Но никто не изучает новую форму в свои 30, верно? Неправильный!
Недавно я обнаружил новую интересную форму: циклоиду. Да, вы правильно прочитали — новая форма. В этом блоге я стремился представить себя (и горстку моих читателей) этой форме. В итоге получилось намного веселее (и зануднее), чем я ожидал. 🧠 🤙
Что такое циклоида?
Согласно Википедии, циклоида определяется как «кривая, описываемая точкой на окружности, когда она катится по прямой без проскальзывания». Возможно, это проще представить с помощью следующей анимированной гифки:
Они видят, как я катаюсь… Циклоид. Магистерский.Циклоида — это красная кривая, описываемая точкой за пределами круга, когда она катится по линии. Вот именно — это циклоида. Просто, верно? Опять неправильно.
История циклоиды
Циклоиду иногда называют «Еленой геометров», потому что за многие годы она вызвала так много споров среди математиков. Один спор вокруг того, кто открыл форму. Самый древний цитируемый кандидат — биограф Пифагора Ямвлих (ок.
245 г. н.э. — ок. 325 г. н.э.). Среди других упоминается множество эрудитов, включая немца Николая Кузанского (1401–1464), француза Шарля де Бовеля (1475–1566), итальянца Галилео Галилея (1564–1642) и француза Марина Мерсенна (1588–1648). Никто точно не знает, кто заслуживает признания.
Я полагаю, что большинство людей, как и я, слышали только о Галилее, который, как оказалось, был первым человеком, серьезно изучившим циклоиды и давшим им свое имя. Он зашел так далеко, что построил модели циклоид из листового металла, пытаясь понять площадь под кривой циклоиды. Вероятно, ему было бы полезно исчисление. Евангелисте Торричелли (1608–1647), изобретшему ртутный барометр, приписывают правильное вычисление площади под одной дугой циклоиды BTW.
Со временем циклоиды привлекли внимание известных математиков, включая Рене Декарта (1596–1650), Пьера де Ферма (1607–1626), Блеза Паскаля (1623–1662), Исаака Ньютона (1642–1726), Готфрида Лейбница.
(1646–1716), Гийом де л’Опиталь (1661–1704), Иоганн Бернулли (1667–1748), Леонард Эйлер (1707–1783) и Жозеф Луи Лагранж (1736–1813). Это, безусловно, имена, которые я узнаю.
Видимо, им нравилось создавать конкурсы и задачи, связанные с циклоидами, которые заканчивались драками и обзыванием. Например, Паскаль организовал соревнование по вычислению (1) центра тяжести, (2) площади и (3) объема циклоиды с испанским золотом в качестве приза. Трое судей посчитали, что никто не выиграл, что звучит не очень весело. Кристофер Рен (1632–1723), знаменитый проектировщик собора Святого Павла в Лондоне, представил доказательство для определения длины циклоиды во время конкурса, что на самом деле не входило в число вопросов конкурса, но все же довольно круто. Судьи конкурса утверждали, что он уже решил эту задачу много лет назад, но так и не записал ее. Это привело к публичным дракам. Еще менее весело. (Рен опубликовал свою работу и получил признание FWIW.)
Еще одна математическая задача была предложена Бернулли в 1696 году и закончилась мелочностью, но об этом мы еще услышим позже.
Знакомство с циклоидами с помощью математики
Теперь, когда мы познакомились с историей циклоидов, вы можете задать себе те же вопросы геометрии, что и наши мертвые друзья-математики Галилей и Рен: какова площадь под циклоидой? Какова длина пути циклоиды? Другими словами, расскажи мне об этой форме, чувак.
У нас (к счастью) есть математика (и YouTube), чтобы помочь нам.
Существуют параметрические уравнения, отображающие путь циклоиды относительно времени (t) по мере того, как круг катится вперед по осям x и y. Я нашел этот вывод YouTube особенно полезным для визуализации его синусоидальной природы. Имеется два уравнения, поскольку положения x и y не зависят друг от друга:
- x(t) = r(t−sin(t))
- y(t) = r(1−cos(t))
Чтобы увидеть эти уравнения в действии, давайте представим, что t = π. В этот момент x(π) = r(π−sin(π)). Поскольку sin(π) = 0, то x(π) = πr. Это половина пути вращения круга, поскольку длина окружности, по которой будет вращаться круг, равна 2πr.
Высота будет y(π) = r(1−cos(π)). Поскольку cos(π) = -1, то r(1-(-1))=2 и y(π) = 2r. Это имеет смысл, так как наша точка на окружности будет в самой высокой точке на полпути к рулону, на два полных радиуса выше линии.
Теперь, когда у нас есть уравнения, мы можем использовать вычисления, чтобы найти площадь и длину циклоиды. Да, я поставил перед собой задачу посчитать (не без помощи YouTube и Google). У меня были воспоминания о тригонометрии и исчислении AP с половинными тождествами углов и интегралами. Вот моя работа, со вкусом выполненная маркерами разных цветов:
Как и в большинстве случаев, связанных с кругами, решения просты. Площадь под циклоидой равна 3πr². Удивительно, но Галилей очень близко подошел к соотношению 3:1 между площадью циклоиды (3πr²) и площадью круга (πr²), используя суперстаромодный метод листового металла, упомянутый ранее. Длина циклоиды всего 8r. Это ответ, который Рен получил ранее. Никаких π или чего-то еще в этом решении.
Честно говоря, это красивые ответы.
😘
Циклоиды в физике
Полезны ли циклоиды помимо их элегантности? Встречаются ли они где-нибудь в природе? Хотя циклоиды не достигают высот некоторых своих геометрических родственников, они все же поражают воображение своим появлением в мире природы.
Вернемся к математическому заданию Бернулли 1696 года. Вот как он поставил свою задачу перед ведущими математиками того времени:
Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам мира. Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, возможное решение которой принесет славу и останется памятником на века. Следуя примеру Паскаля, Ферма и др., я надеюсь получить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-нибудь сообщит мне решение предложенной задачи, я публично объявлю его достойным похвалы.
Этот человек не боялся говорить о крупной игре — хотя все «Я публично объявлю его достойным похвалы» кажется менее интересным, чем испанское золото, и более чем сексистским.
Затем Бернулли задал свой вопрос:
Если даны две точки А и В на вертикальной плоскости, какую кривую описывает точка, на которую действует только сила тяжести, которая начинается в А и достигает В за кратчайшее время.
Другими словами, если шарик перемещается из более высокой точки в более низкую по кривой (при условии, что точки не расположены непосредственно друг под другом), какой путь должен пройти шарик, чтобы завершить путешествие за кратчайшее время ? Это предполагает, что шарик движется в плоскости без трения с однородным гравитационным полем.
Приз Бернулли в виде «похвалы» еще более забавен, учитывая, что он неправильно вывел правильное решение этой задачи, а затем заимствовал правильный вывод у своего брата. Угу.
Бернулли дал шесть месяцев на то, чтобы люди представили решения, но никто этого не сделал. Лейбниц выступал за продление срока представления на полтора года. Именно в этот продолжительный период Исаак Ньютон услышал об этой проблеме.
Сообщается, что он нашел вызов в письме Иоганна Бернулли в 16:00. когда он вернулся домой с Королевского монетного двора 29 января, 1697. Он не спал всю ночь и на следующий день анонимно отправил правильное решение. Решение было, по-видимому, настолько хорошим и настолько явно принадлежало Ньютону, что Бернулли определил его как человека, «узнавающего льва по следу его когтя». 🐅
Решение Ньютона за один вечер превзошло две недели, которые понадобились Бернулли для решения задачи. Затем, в манере математического микрофона, Ньютон добавил в свое письмо немного пикантности: «Я не люблю, когда иностранцы ругают меня [пристают] и дразнят меня математическими вещами…» Ньютон никогда не был известен как самый приятный человек. Дикий.
Ньютон, самый проницательный циклоидный математик. Источник: Какая культура. Это самое быстрое решение, найденное Ньютоном и Бернулли, называется кривой брахистохроны, что в переводе с греческого означает «кратчайшее время». Как вы могли догадаться по теме этого блога, кривая брахистохроны является частью пути циклоиды.
Ниже видео, которое я нашел в Instagram, показывающее эту кривую в действии. Так же я столкнулся с циклоидами:
Это невероятно круто. Всегда интересно видеть силу форм в природе.
Еще одна забавная кривая, которая является частью репертуара циклоиды, — это кривая таутохрона, что в переводе с греческого означает «одно и то же время». Вы можете поместить шарик в любое место на этой кривой, и ему потребуется столько же времени, чтобы скатиться на дно. Он также основан на половине циклоиды. Вот эта кривая в действии:
Таутохронная кривая, еще одна удивительная циклоидальная форма. Неважно, куда вы поместите цветной шар на этой кривой, все они одновременно покатятся вниз. Есть еще нечто, называемое циклоидальным маятником. Представьте, что вы поместили конец маятника в точку встречи двух перевернутых циклоид.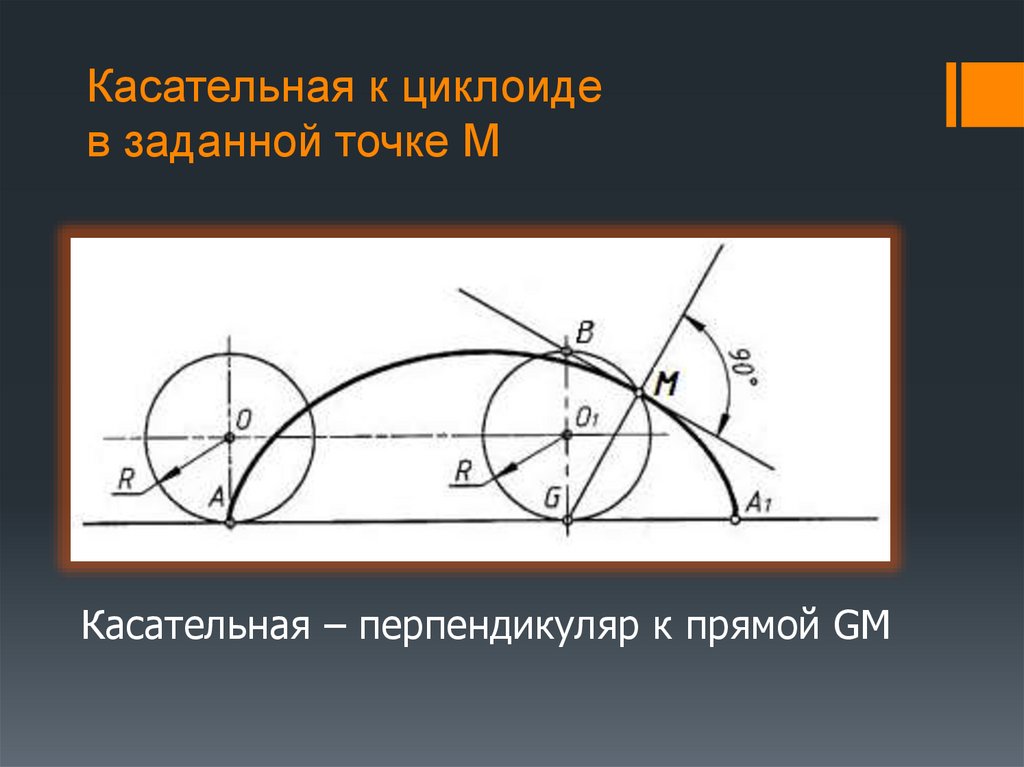
Если вы раскачаете маятник, струна будет изгибаться против циклоид на всем своем пути. Форма конца следов маятника — ЕЩЕ ОДИН ЧЕРТОВЫЙ ЦИКЛОИД. 🤯
Есть множество вариаций, которые вы можете сделать с циклоидами катящегося круга. Вы можете перекатывать круг вперед, но вместо этого отслеживать точку внутри или снаружи периметра круга, чтобы создать более завитые или плоские кривые. Визуализация каждого представлена на изображении ниже:
Вариации циклоидной кривой из ResearchGate.Вы также можете накатывать круги и фигуры на другие круги и фигуры, чтобы расширить семейство циклоидов, как мы увидим позже.
Наконец-то можно создать циклоиду в физике прямо сейчас, бросив что-нибудь с любой высоты. Движение объекта к земле будет прямой линией вниз. Поскольку земля (круг) немного вращается на пути вниз, путь, по которому будет двигаться падающий объект, будет очень слегка перевернутой циклоидой (хотя и очень маленькой)!²
Мы, циклоиды в литературе
Циклоиды, должно быть, были в моде, потому что они время от времени появлялись в литературе в предыдущие века.
Хотя я не буду документировать все случаи, вот один из классического романа Германа Мелвилла 1851 года «Моби Дик »: косвенно бросается в глаза тот замечательный факт, что в геометрии все тела, скользящие по циклоиде , например, мой мыльный камень спустится из любой точки в одно и то же время.
Циклоиды в архитектуре
Теперь, когда мы все согласились, что циклоиды невероятно круты, я начал задаваться вопросом, пропускал ли я циклоиды где-нибудь еще в повседневной жизни.
Архитектура полна геометрических форм. Многие из самых известных типов арок основаны на кругах (римская арка), эллипсе (полуэллиптическая арка), параболах (параболическая арка) и контактных сетях (цепная арка). Существует множество примеров каждого из них, но я привел несколько наиболее известных из них ниже:
Триумфальная арка в Париже, Франция, представляет собой полукруглую арку, также известную как римская арка. Мост Кью через реку Темзу в Лондоне, Великобритания, представляет собой полуэллиптическую арку.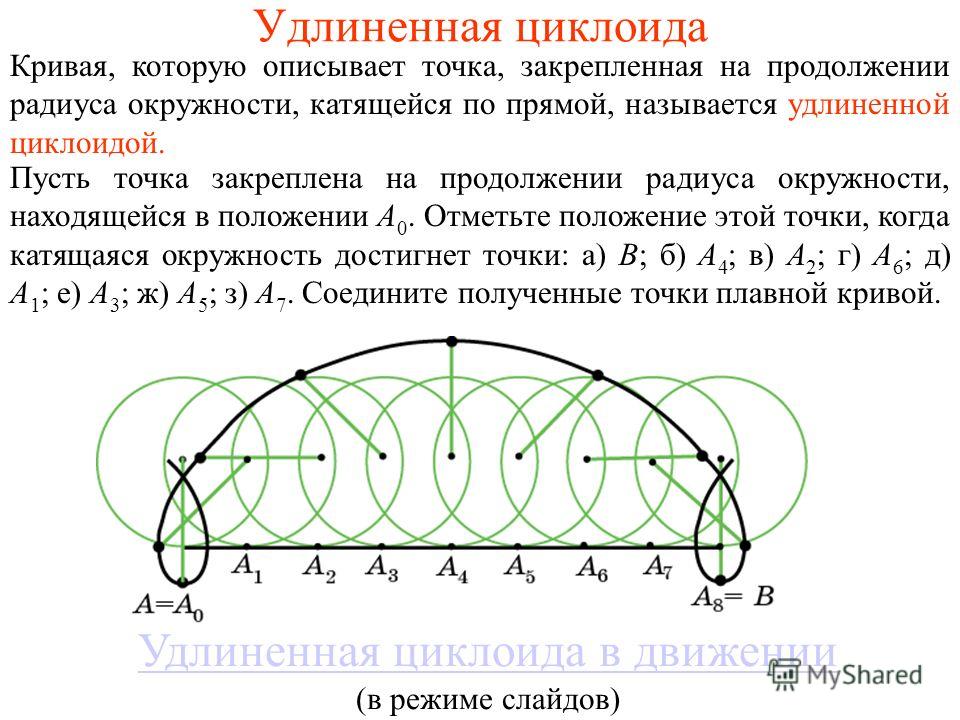
Полуэллиптические арки особенно хороши для создания более широких пролетов арок для таких вещей, как движение лодок и поездов. Мост Биксби-Крик на американском маршруте 1 в Биг-Суре, Калифорния, представляет собой параболическую арку. Фото: Alamy. The Gateway Arch в Сент-Луисе, штат Мичиган, представляет собой цепную арку. Цепные арки являются самыми прочными из всех форм арок, учитывая их равномерное распределение веса.Циклоида очень похожа на арку. Так используются ли циклоидные арки в архитектуре? Согласно моим интернет-исследованиям, они есть, но редко. Есть два ярких примера, которые постоянно появляются (в основном из-за их включения в Википедию, посвященную циклоидам).
Первый — это крыша Художественного музея Кимбелла в Форт-Уэрте, штат Техас. Многочисленные арки этой крыши представляют собой серию циклоидов с небольшим пространством между ними. Это дает успокаивающий вид колеса катящегося. Я копаю это. Отличный выбор для художественного музея.
Циклоидные арки в Художественном музее Кимбелла в Форт-Уэрте, штат Техас.
Второй пример циклоидной арки в архитектурном дизайне заставил меня задуматься. На фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, штат Нью-Хэмпшир, есть циклоидные арки. Дартмут — это место, где я учился на бакалавриате, поэтому я буквально видел эту форму каждый день в течение 4 лет. Может поэтому меня так тянет?
Циклоидные арки на фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, Нью-Хэмпшир.Оказывается, в 2016 году наш журнал для выпускников назвал циклоидные арки Хопа одной из 101 причины полюбить Дартмут. Я не мог удержаться и обратился за дополнительной информацией. Пока ничего существенного в ответ не услышал :
Циклоиды в искусстве и досуге
Вы, наверное, тоже играли с циклоидами в детстве. Игрушка Hasbro Spirograph, которая производится с середины 1960-х годов, основана на модифицированной форме циклоидов, называемых гипоциклоидами. Вместо того, чтобы катить круг по линии, гипоциклоида представляет собой «особую плоскую кривую, образованную следом фиксированной точки на маленьком круге, который катится внутри большего круга».
Двумя особыми формами гипоциклоиды являются дельтовидная и астроидная. Вы можете сделать эти формы, ввернув круг внутри другого большого круга с трехкратным и четырехкратным радиусом соответственно:
Дельтовидная (слева) и астроидная (справа) — две особые формы гипоциклоиды.Вероятно, вы уже видели форму астроида. В логотипе футбольной команды Pittsburgh Steelers три астроида разного цвета. Циклоиды продолжают бить меня близко к дому.
Логотип Pittsburgh Steelers состоит из 3 астроидов, которые представляют собой особый тип гипоциклоиды.Если вы находите эти формы успокаивающими, есть ряд художников, которые создают циклоидные рисунки, подобные показанному ниже, включая в свой дизайн несколько вращающихся кругов разных размеров:
Циклоидная художественная машина, которую я нашел на Pinterest.Циклоидная графика для продажи на Kickstarter.Циклоиды в оптике
Вы также можете катить круги снаружи других кругов и отслеживать их путь, чтобы получить дополнительные производные циклоиды.
Одним из частных случаев этой категории является кардиоида. Это форма, созданная путем отслеживания точки на краю круга, катящегося по снаружи другого круга с таким же радиусом. Путь этой циклоиды имеет ровно один пик, как показано ниже, и напоминает сердце (отсюда и название):
Кардиоиды постоянно появляются в природе, особенно в каустиках, созданных из двух круглых поверхностей. В оптике каустика определяется как «оболочка световых лучей, отраженных или преломленных искривленной поверхностью или объектом, или проекция этой оболочки лучей на другую поверхность. Каустика — это кривая или поверхность, к которой касается каждый световой луч, определяющая границу огибающей лучей как кривую концентрированного света».
Мы видим кардиоиды в каустике, созданной множеством круглых объектов, от кофейных чашек до часов.
Кардиоида в каустике кофейной чашки. Кардиоида в каустике часов.Следите за этой формой, когда в следующий раз будете садиться за чашку чая утром! ☕️
Граница центральной области множества Мандельброта (известного фрактальной геометрией и теорией хаоса) также является точной кардиоидой.
Я действительно не понимаю, как и почему, но это кардиоида, которая выглядит иначе. Шум. 👍
Циклоидные формы не ограничиваются только кругами. Вы также можете накатывать некруглые формы на другие фигуры и знакомиться с целым рядом новых форм, называемых циклогонами. Например, вот циклогон для качения треугольника и квадрата по прямой:
Одна арка циклогона, образованная равносторонним треугольником, катящимся по прямой без проскальзывания. Источник: Википедия. Одна арка циклогона, образованная квадратом, катящимся по прямой без проскальзывания. Источник: Википедия.Циклоиды в космосе
Наблюдение за явлением циклоиды не ограничивается микромасштабом вращающихся колес, часов, чашек и спирографов. Они также видны на планетарном уровне. Поскольку спутник Юпитера Европа (меньший круг) вращается вокруг большой планеты (больший круг), гравитационные силы (линия), действующие на поверхность Луны, имеют циклоидальный характер.
Циклоидная форма видна на растрескивающихся ледяных поверхностях Европы на спутниковых снимках. Трещина соответствует орбитальному пути Луны вокруг Юпитера и возникающему в результате гравитационному давлению.
Резюме
Был ли это очередной гик-фестиваль поста в блоге? Конечно. Но, надеюсь, вы узнали кое-что о новой форме, которую либо открываете для себя впервые, как я, либо узнаете о ней больше. На самом деле, поскольку циклоиды на самом деле представляют собой целую группу интересных форм, я в итоге узнал около 20 новых форм, начиная от брахистохронных кривых и заканчивая дельтоидами и циклогонами.
Насколько круто открывать новые формы, когда тебе за тридцать?
Заставляет меня смотреть на вселенную вокруг меня с большим любопытством и удивлением…
¹ Эли, Маор и Ойген Йост. «Искривленная математика и красивая геометрия».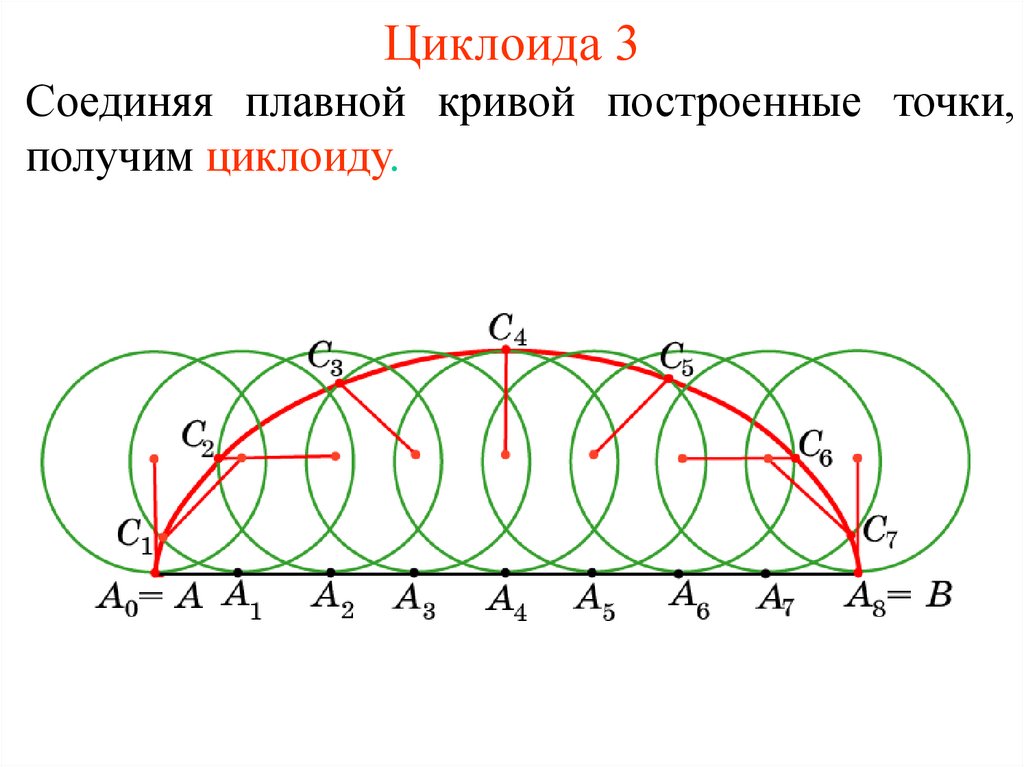
Американский ученый.
² Линч, Питер. «Изогнутая история циклоидов, от Галилея до велосипедных передач». Айриш Таймс . 17 сентября 2015 г.
Циклоид — Матонлайн
Циклоид
Сгиб Содержание Параметрическое уравнение циклоиды X-координаты циклоиды Y-координаты циклоиды Анализ циклоиды |
Циклоида представляет собой параметрическую кривую особого типа, которая очерчивается точкой на окружности окружности, катящейся по прямой линии. Граф циклоиды выглядит так:
Сначала определим центр окружности. Что касается координаты x, обратите внимание, что дуга, образованная при вращении точки P вдоль оси x, равна расстоянию между началом координат и центром окружности (это более подробно описано в следующем разделе), а также обратите внимание, что y -координата окружности никогда не меняется и остается равной длине r. Таким образом, мы получаем, что поскольку длина дуги равна rΘ, то центр окружности равен C(rΘ, r)
x-Координаты циклоиды
Чтобы определить параметрическое уравнение для циклоиды, воспользуемся углом тета, образованным перпендикуляром, опущенным из центра круга, и положением некоторой точки P, очерчивающей окружность по мере увеличения тета.
Сначала давайте найдем функцию x(t), чтобы описать, как координата x циклоиды изменяется при изменении тета. Обратите внимание, что точка P начинается в начале координат и удаляется на расстояние, равное длине отрезка OC. Однако заметьте также, что дуга окружности, образованная тета, также равна отрезку ОС, потому что она катилась по оси абсцисс. Напомним, что дуга окружности равна:
(1)
\begin{align} s = r \theta \end{align}
Нам не нужно знать точное измерение радиуса, а тета варьируется. Так просто:
(2)
\begin{align} OC = r \theta \end{align}
Однако мы ищем не только длину OC. Нам нужно вычесть длину отрезка PC, чтобы получить длину OP = x. Мы можем использовать тригонометрию в этом случае:
(3)
\begin{align} \sin \theta = \frac{PC}{r} \\ r \sin \theta = PC \end{align}
Таким образом, координаты x при изменении теты:
(4)
\begin{align} OC — PC \\ = r \theta — r \sin \theta \\ = r(\theta — \sin \theta) \end{align}
y-координаты циклоиды
Мы будем использовать аналогичные методы для определения координаты y при изменении теты.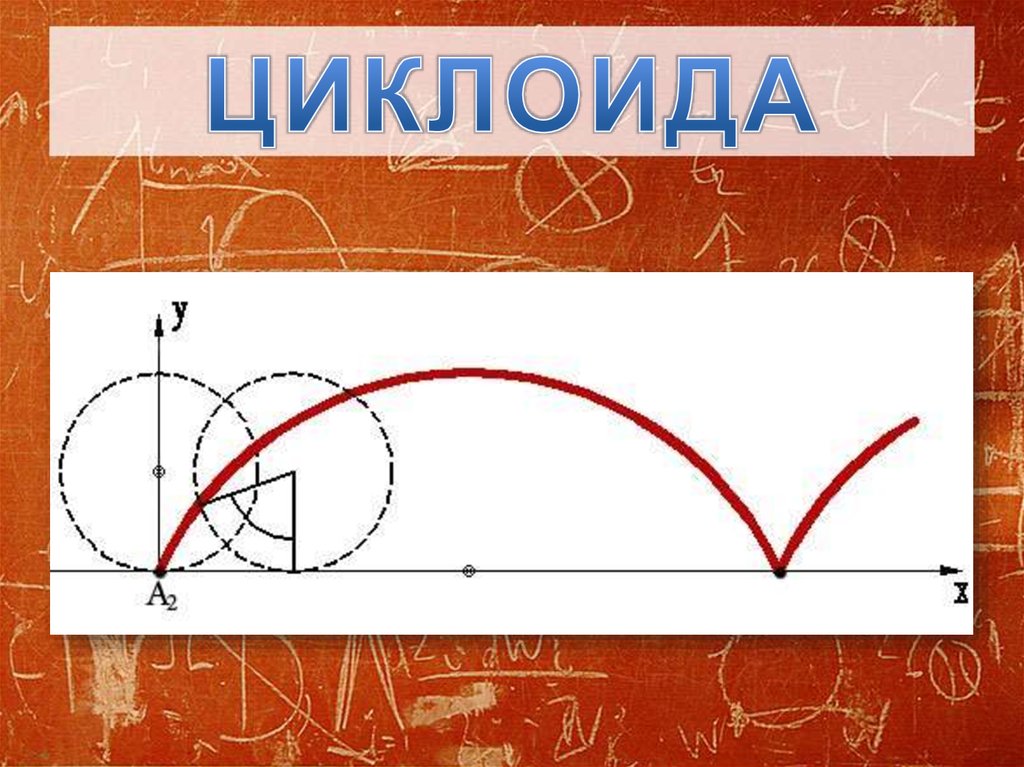
Сначала признаем, что длина опущенного перпендикуляра из центра окружности на ось абсцисс равна r, так как это всего лишь радиус окружности. Теперь мы хотим вычесть расстояние от центра до координаты y. Опять же, мы можем использовать тригонометрию, чтобы получить его длину равной rcosΘ. Таким образом, получаем, что координата y равна:
(5)
\begin{align} y = r — r \cos \theta \\ y = r(1 — \cos \theta) \end{align}
Мы узнали, что циклоида может быть определена двумя параметрическими уравнениями, а именно :
(6)
\begin{align} x = r(\theta — \sin \theta) \quad , \quad y = r(1 — \cos \theta) \end{align}
Поскольку точка, очерчивающая циклоиду, P, начинается с оси x и катится от оси x, имеет смысл, что циклоиде требуется расстояние 2πr, чтобы снова пересечь ось x. Таким образом, одна дуга циклоиды возникает после того, как происходит расстояние в 2πr витков цикла.
Давайте теперь проверим, являются ли эти арки полукругами.