Что такое формальная логика: Логика формальная – Гуманитарный портал

Логика формальная – Гуманитарный портал

Формальная логика — это широкая область логических исследований, изучающая идеализированные рассуждения и их системы посредством логических исчислений на основе метода формализации (см. Формализация). Метод формализации подразумевает, что логические рассуждения изучаются в отвлечении от их конкретного содержания; при этом сами логические рассуждения формулируются на некотором точном (формализованном) языке при помощи специального аппарата символов (см. Язык формализованный). Такие точные языки имеют две составляющие: синтаксис (см. Синтактика) и семантику (см. Семантика). Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет. Формализованный язык позволяет избежать двусмысленной и логической неясности естественного языка, которым пользовалась при описании рассуждений традиционная логика (см.  Логика), развивавшаяся в рамках философии (см. Философия). Методы формализации дали логике такие преимущества, как высокая точность формулировок, возможность изучения более сложных, с точки зрения логической формы, объектов. Определение «формальная логика» было введено И. Кантом с намерением подчеркнуть её ведущую особенность в подходе к изучаемым объектам и отграничить её тем самым от других возможных логик. Способность человеческого мышления к конструктивной языковой деятельности порождает возможность оперировать следующими логическими формами: понятиями, суждениями, умозаключениями, которые представляют собой пространство логических исследований. В качестве наиболее сложного вида логических форм иногда выделяют и теории (см. Теория). Часто эту последовательность воспринимают как некую структурную иерархию. Понятие объявляется наиболее простой из форм мышления, суждение представляется как система понятий, умозаключение как система суждений, а теория как система умозаключений. Эта иерархия недостаточно ясна, и её обоснования порой легко подвергаются критике, однако она часто используется в качестве удобной схемы изложения предметной области формальной логики, что, собственно, подкрепляется многовековой традицией преподавания этой дисциплины. Эти логические формы и лежащие в основе операций с ними законы и принципы, то есть так называемый логический аппарат, составляют основную область исследований формальной логики, а выработка самих эффективных логических аппаратов — её основную цель. В связи с различием логических форм выделяют два основных направления формальной логики: Концептуальный анализ, то есть исследование процедур определения языковых терминов (понятий) и формулировка принципов отношений между ними. Это направление включает в себя широкий спектр теорий, от классификации родо-видовых отношений до конструирования концептуальных «полей». Теория вывода, то есть анализ рассуждений, формализация законов и принципов связи высказываний (суждений) в умозаключениях. Здесь формулируются способы корректного получения суждения, называющегося заключением, из некоторых исходных суждений, называющихся посылками, посредством рассуждения. В рамках теории вывода выделяют логику, рассматривающую дедуктивные рассуждения (см. Дедукция), то есть определённые способы доказательств, и логику, занимающуюся правдоподобными рассуждениями: индукция, аналогия и другие. Кроме того, формальная логика затрагивает и такие вопросы, например, как формализация содержательных теорий, проблема смысла и значения, логические ошибки и парадоксы и многие другие. Самостоятельное выделение этих вопросов достаточно условно, все они погружаются в проблематику основных направлений и тесно переплетены друг с другом. Логика возникла в Древней Греции в рамках философии (см. Философия). История её развития насчитывает около двух с половиной тысячелетий и делится на два основных периода: Традиционная формальная логика (IV век до новой эры — середина XIX века). В развитии традиционной логики, в свою очередь, выделяются три периода: Античная логика (V век до новой эры — середина V века). Схоластическая (Средневековая) логика (середина V века — XV век). Логика Нового времени (XV–XVIII века). Современная (символическая, или математическая) логика (с середины XIX века). Античную и схоластическую логику сейчас объединяет общее название «традиционной логики». Она, кроме историко-философского, по-прежнему имеет важное пропедевтическое значение и, будучи своеобразным стержнем интеллектуальной культуры человека, признается неотъемлемым элементом широкого гуманитарного образования. Новый этап в развитии логики (со второй половины XIX века) был связан с её формализацией и последующей математизацией. В связи с этим новая логика получила название математической (или символической) логики (см. Логика символическая, Логика математическая). Современные логические системы в большинстве своём полностью опираются на формальные математические методы и являются логически интерпретированными исчислениями. Основные разделы математической логики — классические логика высказываний (см. Логика высказываний) и  логика предикатов (см. Логика предикатов). Широкое распространение получили исследования модальной логики (см. Логика модальная). Системы логики, отрицающие те или иные фундаментальные законы логики, образовали спектр неклассических логик (см. Логики неклассические). Значительное число различных систем формальной логики обусловлено широкой сферой их приложения. Теоретическая математика, пожалуй, потеряла абсолютно лидирующее место в этом смысле, поскольку не менее интересные приложения осуществляются в областях теоретической физики (квантовая логика), прикладной математики (вычислительная математика и теория алгоритмов), информатики (компьютерные технологии, сети, программирование и исследования в области искусственного интеллекта), гуманитарного знания (лингвистика, юриспруденция, этика) и других. Важным разделом современной формальной логики является металогика (см.  Металогика), в которой исследуются различные проблемы, относящиеся к логическим теориям. Основными здесь являются вопросы о тех свойствах, которыми обладают логические теории: о непротиворечивости, полноте, наличии разрешающих процедур, независимости исходных дедуктивных принципов, а также о различных отношениях между теориями и так далее. В этом смысле металогика является своего рода саморефлексией логики относительно своих построений. Все метатеоретические исследования проводятся на специальном метаязыке, в качестве которого используется естественный язык, обогащённый специальной терминологией и метатеоретическими дедуктивными средствами.

Асмус В. Ф. Логика. 2-е издание. — М., 2001. Бирюков Б. В. Жар холодных чисел и пафос бесстрастной логики. Формализация мышления от античных времён до эпохи кибернетики. — М., 1985. Бочаров В. А., Маркин В. И. Введение в логику. — М., 2008. Гилберт Д., Бернайс П. Основания математики. Логические исчисления и формализация арифметики. — М., 1979. Гладкий А. В. Введение в современную логику. — М., 2001. Непейвода Н. Н. Прикладная логика. 2-е издание, испр. и доп. — Новосибирск, 2000. Смирнов В. А. Формальный вывод и логические исчисления. — М., 1972. Смирнова Е. Д. Формализованные языки и проблемы логической семантики. — М., 1982. Справочная книга по математической логике. В 4-х частях. Ред. Дж. Барвайс. — М., 1982–1983. Тарский А. Введение в логику и методологию дедуктивных наук. — М., 1948 (2-е издание в 2000). Формальная логика. Ред. И. Я. Чупахин, И. Н. Бродский. — Л., 1977. Фрейденталь Х. Язык логики. — М., 1969. Щедровицкий Г. П. О различии исходных понятий «формальной» и «содержательной» логик. — Методология и логика наук. Учёные записки Томского университета. № 41. — Томск, 1962.

ФОРМАЛЬНАЯ ЛОГИКА | это… Что такое ФОРМАЛЬНАЯ ЛОГИКА?

наука о мышлении, предметом к-рой является исследование умозаключений и доказательств с т. зр. их формы (формы логической) и в отвлечении от их конкретного содержания. Ф. л. является базисной наукой – ее идеи и методы используются как в повседневной практике, напр.

в качестве средства от логич. ошибок, так и в особенности в теории для логического анализа науч. знания и для дедуктивного (синтетического) построения на базе логических исчислений любых «нелогических» науч. дисциплин.

Историч. основу Ф. л. образует т.н. т р а д и ц и о н н а я Ф. л., к к-рой относят обычно учение о понятии, учение о мышления законах, учение о суждении и теорию силлогистич. вывода – учение о силлогизме, или силлогистику, учения о непосредственных умозаключениях и несиллогистических умозаключениях, учение о логических ошибках и, наконец, традиц. логику индуктивную. Основоположником традиц. Ф. л. является Аристотель: обобщив опыт повседневного и отчасти науч. мышления тогда только формировавшейся науки, Аристотель создал учение о силлогизме и дал первые примеры анализа рассуждений с т. зр. их формы. Однако уже сам Аристотель сознавал, что в силлогистич. схемы нельзя уложить многие рассуждения, в особенности математические. Это побудило мегариков и ранних стоиков исследовать др.

формы дедукции (см. Древнегреческая логика). Частично в том же направлении шло развитие логики и в средние века (см. раздел Схоластическая логика в ст. Схоластика), и в эпоху Возрождения (Галилей, Валла, Раме). Развитие опытного естествознания и математики, усилившееся в 17 в., поставило вопрос о прикладной роли Ф. л., о дальнейшем развитии несиллогистич. форм вывода, характерных для логики науки. (В этой области работали с большим или меньшим успехом Ф. Бэкон, Декарт, Паскаль, авторы Пор-Рояля логики, И. Юнг, Лейбниц и их последователи.) Одна из осн. «логистических» идей Лейбница состояла в том, чтобы свести к «вычислению» не только математические, но и любые умозаключения. Лишь ко 2-й пол. 19 в. относятся ощутимые шаги в реализации этой идеи, когда работами Буля, де Моргана, Джевонса, Шрёдера, Порецкого, Пирса, Фреге, Пеано и др. были заложены основы первых совр. логико-матем. исчислений. «Principia Mathematica» Б. Рассела и А. Уайтхеда открывает совр. этап в развитии Ф. л.

С о в р е м е н н а я Ф.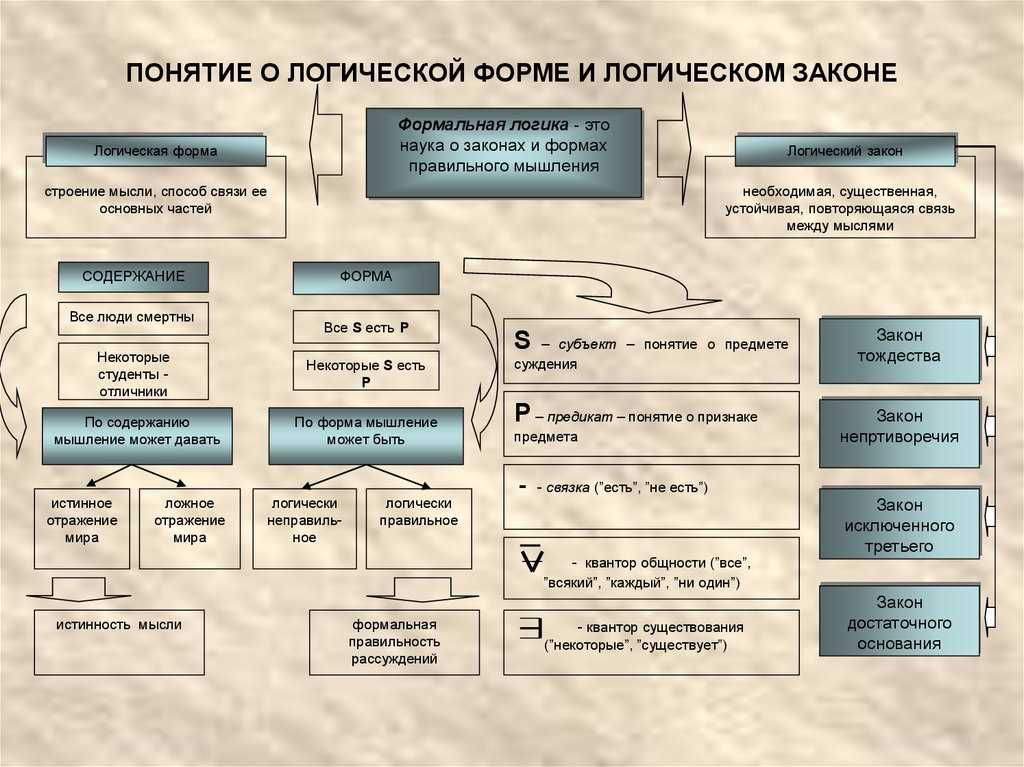 л. является историч. преемником традиц. Ф. л. и в ряде случаев ее прямым продолжением. Расширение и обогащение языка Ф. л., ее осн. понятий в известной мере служат указанием на то, в каком направлении шло развитие Ф. л. от традиционной к современной. В частности, в логич. словаре появились такие понятия, как исчисление и логическое исчисление, математическая индукция, формализация и формализованный язык, независимость, непротиворечивость и полнота, алгоритм и разрешения проблемы, область предметов и переменная, операция и функция и др. неизвестные традиц. Ф. л. понятия. С др. стороны, определ. связь с традицией сохранили такие понятия совр. Ф. л., как аксиома, посылка и постулат, вывод и правило вывода, квантор, следствие и следование (импликация), теорема о дедукции и др., хотя в совр. трактовке этих понятий не сразу узнаются их историч. прообразы.

На протяжении более чем двухтысячелетней истории Ф. л. основную ее цель видели в том, чтобы исследовать, каким образом можно выводить одни высказывания из других. Для совр. Ф. л. характерно построение формальных теорий логич. вывода (см. Вывод в математической логике) в рамках тех или иных логич. «формализмов» (исчислений), а следовательно, и особое внимание к построению самих этих формализмов и применяемых при этом формально-дедуктивных методов. В зависимости от того, какие осн. понятия и методы используются для построения формальных теорий логич. вывода [в том числе и в зависимости от того, как интерпретируются осн. логич. константы: дизъюнкция, конъюнкция, импликация, отрицание (в логике), эквиваленция] различают: классическую (иначе двузначную) логику, интуиционистскую логику, конструктивную логику, модальную логику, многозначную логику и др. Каковы бы ни были различия в построении этих теорий, каждая теория состоит из двух осн. разделов: логики высказываний и логики предикатов. Классич. вариант последней непосредственно примыкает к традиц. силлогистике (логике «одноместных» предикатов), хотя в многочисленных и различных предикатов исчислениях (см. также ст. Натуральное исчисление, Секвенций исчисление) формализуется субъектно-предикатная структура предложений, понимаемая в более широком, чем в традиц. Ф. л., смысле: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты), что делает излишней особую логику отношений в ее традиц. филос. истолковании.

Каждая из указанных выше формальных теорий имеет определ. филос. смысл, являясь логической реализацие й тех или иных методологич. подходов в науке. Связь совр. Ф. л. и философии стимулируется прежде всего актуальной задачей обоснования математики – науч. направлением, имеющим как логический, так и филос. характер (см. ст. Алгоритм, Интуиционизм, Исчисление задач, Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализм в философии математики, Положительная логика, Принцип исключенного третьего, Проверяемость, Теория множеств, формализм, Эффективизм). Примером обогащения и углубления логич. исследований, вызванных стимулирующим влиянием проблем обоснования математики, может служить возникновение металогики – в узком (гильбертовском) смысле как теории формальных систем, ограниченной рамками финитизма, и в широком смысле как метатеории Ф. л. вообще, включающей логический синтаксис (см. Синтаксис в логике, Метаязык), логическую семантику (см. такжеСемантика в логике и примыкающие к ней ст. Взаимозаменимости отношение, Знак, Значение, Имя, Интерпретация, Контрфактические предложения, Логическая истинность, Модель, Название, Описания операторы, Реализуемость, Синтетические и аналитические суждения, Тавтология, Тождественная истинность, Фактическая истинность, Экстенсиональные и неэкстенсиональные языки), теории определения и определимости и теорию тождества (см. А=А, Правило замены равного равным, Принцип замещения, Равенство в логике и математике). Дальнейшим расширением металогич. проблематики явилось выделение в особую дисциплину прагматики, развивавшейся первоначально в рамках логико-семантич. и психологич. анализа (см. Психологизм в логике), и, наконец, появление семиотики. Т.о., связь между мышлением и языком как «практической действительностью мысли» (К. Маркс) нашла отражение во взаимосвязи философии, психологии, лингвистики и логики.

В развитии совр. Ф. л. особую роль играют вопросы ее приложений, особенно в вычислит. математике и технике, кибернетике и теории информации, лингвистике математической и пр. (см., напр., ст. Логические машины, Логические схемы автоматов). Связующим звеном между Ф. л. и вычислит. математикой исторически явилась логика классов, к-рая развилась в результате попыток свести силлогистич. методы решения логич. задач к алгебраич. методам их решения, образовав, т.о., первое алгебраич. направление в совр. Ф. л. – алгебру логики (см. также Теоретико-множественная логика). Дальнейшим развитием алгебраич. направления явилось объединение алгебры логики и логики предикатов в теории конечных автоматов, расширение алгебры логики в сторону «алгебраизации» логики предикатов – теория моделей и математич. теория структур. Другую – «арифметическую» – ветвь, связавшую Ф. л. и вычислит. математику, образуют теория рекурсивных функций и предикатов (см. также ст. Алгоритм, Массовая проблема, Разрешимое и перечислимое множества, Сводимость), исчисление λ-конверсии (см. Оператор абстракции, Функция), логика комбинаторная и др. Из общих науч. приложений Ф. л. следует отметить вопросы, связанные с задачами уточнения понятия науч. закона (см. Диспозициональный предикат, Каузальная импликация, Номологические высказывания, Связь), с попытками применения логики в биологии и физике (см. Логика квантовой механики), в этике и юриспруденции (см. Нормативная логика). Успехи, достигнутые в формальной теории дедукции, способствовали применению точных методов в разработке широкого комплекса проблем теории индукции и индуктивной логики (см. ст. Логика индуктивная, раздел Современная логика индуктивная, ст. Научная индукция, Неполная индукция, Популярная индукция), и вероятностной логики.

Т.о., ответ на вопрос «Что такое Ф. л.?» можно дать, лишь опираясь на историч. анализ ведущих тенденций развития логики, а также принимая во внимание, что термин «Ф. л.» употребляется неоднозначно, что в рамках Ф. л. в широком смысле можно говорить о различных разделах и дисциплинах, к-рые также носят имя «Ф. л.». Такая дифференциация Ф. л., с др. стороны, дополняется интеграцией, появлением новых теорий и концепций, в к-рых Ф. л. рассматривается с к.-л. единой, общей т. зр.

М. Новосёлов, Г. Рузавин, П. Таванец. Москва.

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.

О роли и значении формальной логики в образовательном процессе Текст научной статьи по специальности «Философия, этика, религиоведение»

УДК 160.1/37.025.7

А. А. ИСАЕВ, начальник кафедры социально-гуманитарных и экономических дисциплин Уфимского юридического института МВД России, кандидат философских наук, доцент (г. Уфа)

A. A. ISAEV, head of the department of social, humanitarian and economic disciplines Ufa law Institute of the Ministry of Internal Affairs of the Russia, сandidate of philosophical sciences, associate professor (Ufa)

О РОЛИ И ЗНАЧЕНИИ ФОРМАЛЬНОЙ ЛОГИКИ В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ

ABOUT THE ROLE AND VALUE OF FORMAL LOGIC IN THE EDUCATIONAL PROCESS

Аннотация. В статье рассматривается специфика формальной логики с учетом ее достоинств и недостатков. Определяется область применения и действия формально-логических законов и правил. Делается вывод, что жизнь человека не может быть подвержена абсолютному влиянию требований логики, что и делает ее прекрасной и оригинальной.

Ключевые слова и словосочетания: формальная логика, формально-логические законы, форма мысли, иррациональное, жизнь человека, образовательный процесс.

Annotation. The article discloses the specifics of formal logics, taking into account its advantages and disadvantages. The scope and actions of formal-logical laws and rules are determined. It is concluded that human life cannot be subject to the absolute influence of the requirements of logics, which makes it beautiful and original.

Keywords and phrases: formal logics, formal-logical laws, form of thought, irrational, human life, educational process.

В современном образовательном процессе свое достойное место занимает учебная дисциплина «Логика». К сожалению, она не является обязательной для изучения обучающимися, получающими высшее образование. Однако в юридическом образовании ее важность и ценность признается, поэтому она включается в учебные планы по юридическим специальностям и направлениям подготовки. Не являются исключением и образовательные организации системы МВД России.

Логическая культура мышления важна не только для юриста-теоретика,

но и, безусловно, важное значение имеет в юридической практической деятельности, в том числе в профессиональной деятельности сотрудника органов внутренних дел. Это обусловлено спецификой работы юриста, заключающейся в постоянном применении всего арсенала логических средств: определений, классификаций (вида деления), версий (вида гипотезы), доказательств (аргументаций), опровержений и т. д. Еще Аристотель, определяя предмет своего исследования и основную функцию логики, писал: «Оно о доказа-

тельстве, и это дело доказывающей науки» [1, с. 119].

При изучении данной дисциплины большее внимание уделяется постижению основ традиционной, или аристотелевской, формальной логики. Поэтому в данной работе мы обратимся именно к ней.

Логика изучает сущность, формы и закономерности нашего мышления. И. Кант делит логику на формальную и трансцендентальную. По мнению немецкого философа, формальная логика отвлекается от содержания знания и занимается только формами мышления [2, с. 216]. Для трансцендентальной логики характерно то, что она изучает формы мысли в связи и зависимости от содержания, субстанции познаваемой области. И только в ней достигается синтез формы и содержания [2, с. 157].

Правильно заметив достоинства трансцендентальной логики, Кант принизил познавательные возможности формальной логики, на что справедливо указывает С. Л. Франк: «Кант не только правомерно различал «трансцендентальную» логику от «формальной», но и неправомерно думал, что можно построить первую, совсем не затрагивая последней. В отношении «формальной» логики он, как известно, полагал с величайшей наивностью, что со времени Аристотеля она «не смела сделать ни шагу назад и не могла сделать ни шагу вперед»» [3, с. 305].

Вот как объясняет смысл формальной логики автор учебного пособия по логике Е. И. Бесхлебный: «Формальная — значит, связанная с формой, изучающая ее как нечто отдельное, обособленное от содержания, насколько это возможно. В этом отношении формальная логика подобна геометрии, которая является наукой о формах физических тел и совершенно отвлекается, изучая эти формы, от того, что могло бы быть их содержанием» [4, с. 7] .

Мы попытаемся разобраться в достоинствах и недостатках формальной логики. Эта логика потому и называется формальной, что изучает формы нашего мышления, не интересуясь содержанием самих мыслей. Не только не интересуясь, но и целенаправленно отвлекаясь от него, «отбрасывая его в сторону». Для чего ей это нужно? И почему содержание мыслей только ей мешает? Объяснение здесь достаточно простое. Чтобы выработать формальнологические требования к грамотному построению наших мыслей, формальная логика выделяет лишь их структуру, то есть их формальную сторону. Отвлекаясь от содержательной стороны, она более четко расставляет по своим местам отдельные элементы мысли, тем самым связывая их в единую структуру. Не стоит элемент на своем месте, значит, структурная целостность нарушена. А это и есть нарушение формальнологического закона или правила.

Изучая формальную логику, мы учимся применять эти законы и правила к структурному (формальному) построению наших мыслей. Облекая эти структуры в содержание, мы тем самым будем логически грамотно говорить и писать, поскольку, как хорошо известно, устная и письменная речь есть материальное отображение (выражение) наших мыслей. Такая речь называется правильной (потому что она построена по правилам логики). Но правильность еще не означает ее истинность! Поэтому софисты так искусно владели логикой, преподнося своим собеседникам правильные мысли, не заботясь об их истинности.

Приведем пример простого категорического силлогизма: «Все люди имеют четыре глаза. Вася — человек. Значит, Вася имеет четыре глаза». С точки зрения формальной логики это умозаключение отвечает всем правилам. Так как оно построено по первой фигуре простого категорического силлогиз-

ма, его большая посылка должна быть общим суждением, каковым оно и является: «Все люди имеют четыре глаза». А меньшая посылка должна быть утвердительным суждением: «Вася — человек», оно утвердительное. Однако мы с вами прекрасно понимаем, что этот вывод не является истинным. То есть наше заключение ложное. Как же так? Мы строго соблюдаем правила логики, а приходим к ложному знанию? Все дело в том, что формальная логика, как было сказано выше, не интересуется содержанием мыслей. Для нее не важно, истинную мы мысль используем или ложную (в нашем примере силлогизма мы применили ложную посылку: «Все люди имеют четыре глаза»). Главное, чтобы она отвечала формально-логическим требованиям по своей структуре, то есть по форме. А установление истинности или ложности мысли невозможно без учета ее содержания.

Классическое определение истины гласит: «Истина — это знание, соответствующее действительности». Мы не сможем проверить это соответствие, если будем знать только структуру мысли без ее содержания. Мы никогда не сможем определить, является ли форма мысли «Б есть Р» истинной или ложной. Суждение «Сосна есть дерево», соответствующее данной структуре, вполне соотносимо с данным определением. Мы с уверенностью можем сказать, что данное суждение истинно. С другой стороны, применяя истинные суждения в умозаключениях, нарушая требования формальной логики, мы также приходим к ложному знанию. Классический в логике пример хорошо иллюстрирует эту ситуацию. «Все кошки смертны. Сократ смертен. Значит, Сократ — кошка». Исходные наши суждения (посылки) являются истинными. Действительно, мы не знаем ни одной бессмертной кошки. Ну а то, что Сократ смертен -это исторический факт. Однако наше заключение — ложно. Мы прекрасно

знаем, что Сократ человек, а не кошка. Все объясняется правилами формальной логики, а если точнее, простого категорического силлогизма. Наше умозаключение построено по второй фигуре. Второе правило данной фигуры гласит: «Одна из посылок должна быть отрицательным суждением». Обе посылки в нашем примере являются утвердительными суждениями. Мы утверждаем: «Все кошки смертны» и «Сократ смертен». Таким образом, это правило нарушено, и, как следствие, это ложное заключение.

Деятельность древнегреческих философов-софистов была основана на хорошем знании формально-логических требований, что позволяло им «грамотно» их нарушать и вызывать у людей абсолютную уверенность в обоснованности и доказательстве, в том числе ложных знаний. Такой прием получил в формальной логике название «софизм» и является нарушением ее законов. Эту ошибку можно разобрать на примере известного «софизма»: «То, что я не терял, я имею. Я не терял рогов. Следовательно, я их имею». На первый взгляд -все логично. Но хитрость заключается в подмене понятий, выражаясь языком формальной логики: в нарушении закона тождества.

В первом суждении я веду речь о том, что у меня было, я это не потерял и, следовательно, продолжаю это иметь. Но в следующих суждениях я расширяю мысль, высказанную в первом суждении, практически на все, что существует в мире. Вместо «рогов» я могу сказать о «самом крупном бриллианте в мире», «слитках золота», «миллионе долларов» и т. д. Софисты пользовались логической неграмотностью своих собеседников, т. е. сознательно совершали ошибку, которую в логической теории аргументации называют «аргумент к невежеству». Свою подобную деятельность они осуществляли за плату, что и послужило основанием негативного от-

ношения к репутации данной школы в истории философии.

Итак, мы разобрались в истинности и правильности наших мыслей. Несложно сделать заключение, что логически грамотное рассуждение, приводящее к истинным знаниям, возможно построить только при строгом соблюдении формально-логических требований, применяя лишь однозначно истинные исходные знания-суждения. Формализация помогает вычленить общую структуру мысли, а знание закономерностей этой структуры помогает найти ошибку и определить правильную линию вывода.

Указанная функция является, пожалуй, самой главной функцией логики как науки о формах правильного мышления. Вот что писал по этому поводу известный русский логик Г. И. Челпа-нов: «Логика не поставляет своей целью открытие истин, а ставит своей целью доказательство уже открытых истин. Логика указывает правила, при помощи которых могут быть открыты ошибки. Вследствие этого, благодаря логике можно избежать ошибок. Поэтому становится понятным утверждение английского философа Дж. С. Милля, что «польза логики главным образом отрицательная. Ее задача заключается в том, чтобы предостеречь от возможных ошибок. Вследствие этого практическая важность логики чрезвычайно велика» [5, с. 7].

Изучение логики развивает четкость и ясность мысли, уверенность в уточнении предмета мысли, уравновешенность, внимательность, надежность и убедительность в суждениях. Тот, кто овладевает навыками формально-логического мышления, всегда понятен окружающим его людям. Он способен оценивать доказательную силу высказываний в дискуссии, находить правильные пути исправления ошибок. Не случайно логику считают орудием истины и незаменимым средством разо-

блачения дезинформации, лжи и заблуждения.

Но, признавая важность знания и правильного применения формальнологических требований к нашей мысли, следует сказать, что все эти правила и законы действуют в рациональном поле. Как только мы переходим в область иррационального, логические механизмы не работают, в лучшем случае выступая иногда вспомогательным средством. Поэтому «безумно» влюбленному человеку друзья, пытаясь спасти его от несчастной для него, на их взгляд, любви, советуют: «Остановись! Отключи сердце! Включи разум!». Они подходят к сложившейся ситуации с «холодным» рациональным расчетом: «Она ему не пара, так как …». Далее следует цепочка логических умозаключений, обосновывающая такую точку зрения. И если этот сложный силлогизм будет построен по всем правилам логики и из истинных суждений, можно сказать, что друзья правы и желают своему товарищу только добра. Но так ли это на самом деле? Всегда ли добро логично? Думается, что ответ на этот вопрос однозначно отрицательный.

Наша жизнь не всегда логична и рациональна. Очень часто она бывает алогичной, иррациональной. В этом ее сущность и ее красота. И не случайно искусство в отличие от науки отражает нам окружающую реальность чувственно-эмоциональными, а не рациональными средствами. Возвращаясь к нашему «влюбленному», мы можем вспомнить множество примеров из истории, художественных произведений, да и просто из жизни, когда такая «алогичная любовь» приводила к созданию крепкой, здоровой семьи, воспитывающей своих детей в духе традиционных нравственных ценностей на основе Добра, Любви и Красоты.

Огромным преимуществом современной логики перед более старыми формами науки является тот факт, что

математическая логика способна анализировать структуры, которые традиционная логика никогда не поднимала, и разрешить проблемы, о существовании которых более старая логика никогда не знала. Как будто бы вытекает вывод о необходимости тотальной формализации знания. Но это не так.

Замена традиционной логики, пользующейся естественным языком, математической равносильна замене обычного языка искусственным. Конечно, искусственный язык имеет определенные преимущества перед естественным при решении некоторых проблем. Но как нельзя заменить человеческий глаз микроскопом, так нельзя заменить естественный язык с его обширными функциями искусственным языком, имеющим весьма ограниченные возможности. Применение математической логики вместо традиционной равносильно рассматриванию художественной картины при помощи микроскопа или телескопа.

Признавая величие фигуры Г. В. Лейбница как философа, логика и математика, все же позволим себе не согласиться с его пророческой мечтой о том, что наступит время, когда можно

будет воскликнуть: «Зачем спорить? Давайте вычислять!». Немецкий мыслитель верил, что все человеческие споры возможно будет решить логическими, математическими средствами. Поэтому его справедливо называют предвестником математической (символической) логики. Но жизнь доказала и доказывает ошибочность его пророчества.

Формализация приводит к формализму в человеческих отношениях, а формализм — к черствости и равнодушию. Все эти процессы могут привести к стандартизации человеческих отношений. К счастью, как бы не развивалась научно-техническая мысль, она до сих пор не способна рационально-логическими средствами и новейшими технологиями объяснить «вечные вопросы бытия человека»: что такое любовь, озарение, интуиция, непоколебимая вера и т. д.? А значит, у человечества есть будущее! Оно будет жить до тех пор, пока искусственный интеллект или строгие логико-математические рассуждения не завоюют все пространство нашей жизни и не проникнут в самые сокровенные и интимные уголки нашей души!

***

ЛИТЕРАТУРА

1. Аристотель. Сочинение в 4-х т. Т. 2. М.: Мысль, 1978.

2. Кант И. Сочинения. Т. 3. М.: Мысль, 1964.

3. Франк С. Л. Сочинения. М.: Правда, 1990.

4. Бесхлебный Е. И. Логика: учебное пособие. М.: ДКО МВД России, 2008.

5. Челпанов Г. И. Учебник логики. М.: Прогресс, 1994.

© Исаев А. А.

Основы формальной логики: как не дать собой манипулировать

Мы начинаем серию материалов о манипулятивных техниках, автором которой выступил известный журналист, редактор (и преподаватель философии) Дмитрий Шишкин. В первой части разберёмся, как связаны казахстанские медийные скандалы последнего времени с древними греками Протагором и Аристотелем.

А связаны они очень даже явно — через приёмы словесного мошенничества, названного 2500 лет назад «софизмом». Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам. 

Искусство манипуляции людьми появилось вместе с речью. Правильно подобранными словами можно отправлять в атаку на врага или обращать в бегство, ввергать в депрессию или мотивировать к свершениям. Но в целом смысл манипуляции всегда один — заставлять делать или думать что-то, что мы делать и думать не собирались — то есть, использовать нас.

Что не так в противостоянии людей, желающих сохранить урочище Кок-Жайляу диким местом, и теми, кто хочет его застроить? На первый взгляд обычный гражданский конфликт — урбанистов и экологов. Но если обратить внимание на нюансы: когда «экологи» приводят аргументы против застройки, а их в ответ называют «экологическим талибаном», и взглянуть на список логических уловок, составленный древними, становится понятно, что это классический пример применения уловки Argumentum ad hominem («аргумент к человеку/личности» или «атака на человека»).

Или, например, когда вся страна была взбудоражена новостями о распространении менингита, на одном из ресурсов вышла статья «Кто заказал министра здравоохранения Елжана Биртанова?». Это – классическая уловка Ignoratio elenchi («невежественное опровержение» или подмена тезиса). (Подробно об этом во второй части материала).Со

Такие примеры встречаются ежедневно. И мы предлагаем вам учиться разбираться в них не по наитию, а научно.

Немного истории

Софистика

Более 2500 лет назад в Древней Греции активно распространились школы софистики. Там давали уроки начинающим политикам: как при помощи ораторского искусства добиваться своих целей. От философов, также процветавших в древних полисах, софисты отличались в основном тем, что не считали важными какие-то универсальные задачи и теоретические размышления, а главным признавали достижение практической цели.

Интересно, что софистика появилась раньше логики как оформленной науки, и, скорее всего, именно софисты подтолкнули философов к её созданию (в качестве инструмента противодействия демагогам, вводившим народ в заблуждение ради собственных целей).  

«Он (Протагор, живший примерно в период 485 – 410 годов до нашей эры, за сто лет до Аристотеля – прим. авт.) первый заявил, что о всяком предмете можно сказать двояко и противоположным образом… о мысли он не заботился, спорил о словах, и повсеместное нынешнее племя спорщиков берёт своё начало от него», – писал о самом ярком представителе софистов Диоген Лаэртский в своей книге «О жизни, учениях и изречениях знаменитых философов». 

Аристотель побеждает всех

Софистов ругал ещё Платон, а его ученик Аристотель решил положить конец одурачиванию народа (по крайней мере, попытался — мы и сейчас попадаемся на те же самые уловки, что были известны ещё 2500 лет назад). Он создал научную базу формальной логики (которую сам он называл «Аналитикой») и классифицировал логические ошибки, используемые софистами.

В принципе, логическая ошибка и логическая уловка — это одно и то же, просто ошибка допускается несознательно, а уловка специально вводится в речь.  

Аристотель в своём труде «О софистических опровержениях» наглядно показал, что если разложить любой софизм, будет видна специально внедрённая в него ошибка, благодаря которой выводы софиста кажутся логичными. 

После Аристотеля немало в развитие формальной логики внесли римляне Цицерон и Квинтилиан, а затем и средневековые схоласты – мы будем в дальнейшем пользоваться их типологией логических ошибок, так что пусть вас не удивляют латинские термины.

Немного теории

Теория — это самая скучная часть формальной логики, и передо мной стоит трудная задача: уложить в рамки современного «лонгрида» курс, который в институте преподаётся в течение года. Поэтому отсечём всё ненужное современному человеку, имеющему интернет и способному самостоятельно найти недостающие фрагменты. 

Главное, что есть в формальной логике — это её четыре основных закона

Три из них сформулировал ещё Аристотель:

— закон тождества,
— закон противоречия,
— закон исключённого третьего.

А четвертый закон – достаточного основания — был добавлен немецким математиком и философом Лейбницем в начале XVIII века. 

Закон тождества

«…иметь не одно значение — значит не иметь ни одного значения», писал по этому поводу Аристотель в своей «Метафизике». 

То есть каждая мысль и каждый термин в процессе рассуждения должны иметь одно и то же значение. Подмена понятия в ходе рассуждения — это классическая логическая ошибка (или уловка).

Например: 

– Гражданин N хороший человек, скромный и любит ездить на велосипеде.
– Из него получится хороший аким города!

Здесь мы видим, как в первой части утверждения говорится о личных качествах человека, а вывод делается о его профессиональных качествах — что далеко не тождественно.  

Закон противоречия

Два противоречащих друг другу суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно. 

… невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель, «Метафизика»)

Например:

Мы часто встречаем заявления от официальных лиц и даже целых институтов о том, что:

– Народ Казахстана неоднократно демонстрировал свою политическую зрелость, отдавая голоса на выборах президента и депутатов парламента за стабильность!
– Вместе с тем, наш народ не готов пока к выборности акимов и прочим демократическим преобразованиям.

Налицо явное противоречие: получается, народ Казахстана с одной стороны политически подкован, а с другой — настолько дремуч, что не готов к такому элементарному процессу, как выборы акима. 

Закон исключённого третьего

Два противоречащих друг другу суждения не могут быть одновременно оба истинными или оба ложными.

…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать (Аристотель, «Метафизика»)

Противоречащими называют такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается. 

Например:

– Цензура запрещена!
– Если в интересах общества, то цензура разрешена.

Оба эти утверждения об одном и том же явлении не могут быть одновременно правдивыми или ложными. Если делается исключение, то первое утверждение ложное – «третьего не дано». 

Закон достаточного основания

Всякая правильная мысль должна быть обусловлена другими мыслями, истинность которых доказана.  

…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны (Готфрид Вильгельм Лейбниц, «Монадология»)

Это, в общем — именно то, чем занимается «Фактчек в Казахстане» — поиском достаточных оснований для публикаций. В отличие от первых трёх законов, которые можно применять формальными методами, просто соотнося какие-то утверждения с правилами, для установки достаточности основания необходимо включать критическое мышление и затем прилагать усилия для проверки суждений, в которых вы засомневались.

Например, самые яркие примеры мы встречаем довольно часто в виде панических слухов, распространяемых через мессенджеры и социальные сети.

В случае со скандалом вокруг заболеваемости менингитом: неверными оказались как утверждения об эпидемии, так и «рецепт», в котором утверждалось, что для профилактики менингита всем необходимо пропить курс антибиотиков (что, как пояснили затем врачи, назначается только людям, контактировавшим с больными).  

На законе достаточного основания также базируется важный юридический принцип: «презумпция невиновности», гласящий, что никто не виновен, пока его вина не была доказана.

В соцсетях и даже СМИ он нарушается настолько часто, практически ежедневно, что примеры вы легко найдёте сами. Людей называют ворами и убийцами до судов, друг друга лжецами безо всяких доказательств и опровержений и т.д.

В следующей части читайте о логических уловках, построенных на нарушении этих законов логики:

• Ignoratio elenchi или «подмена тезиса»
• Argumentum Ad Hominem или «переход на личности»

Внесите свой вклад в борьбу с дезинформацией!

Философские идеи В.И.Ленина и логика

Страница 1 из 8

В книге излагается учение В. И. Ленина о материалистической диалектике как теории познания и логике; диалектика как наука, совпадение диалектики, логики и теории познания; диалектика как обобщение истории познания; место диалектики в марксистской философии. Автор рассматривает структуру материалистической диалектики, характер взаимоотношения диалектики и формальной логики, место диалектики в изучении мышления, диалектику форм мышления. В заключительной части книги анализируются такие проблемы, как диалектика и процесс научного исследования, логико-гносеологические основы практической реализации знания.

Книга является обобщением и дальнейшим продолжением ранее изданных трудов автора: «Диалектика как логика» (Киев, 1961), «Гипотеза и познание действительности» (Киев, 1962), «Идея как форма мышления» (Киев, 1963) и другие публикации, связанные с разработкой диалектической логики.

 

ПРЕДИСЛОВИЕ

Наука и общественная жизнь в целом ставят перед философией нашего времени множество актуальных задач, среди которых одной из важнейших является совершенствование метода научно-теоретического мышления, т. е. Логики с большой буквы.

Плодотворная разработка логических проблем предполагает изучение истории развития человеческого знания, в частности его современных форм. В качестве отправных посылок, выполняющих функцию метода анализа, выступает философское наследие прошлого, идеи выдающихся мыслителей, среди которых особое место занимает В. И. Ленин.

Концепции В. И. Ленина впитали в себя достижения мировой культуры и послужили исходным пунктом для развития всех областей современного философского знания, в том числе и логики.

Разработка философского наследства В. И. Ленина составляет важнейшую задачу, которую поставила партия перед советскими философами. Наш долг состоит не только в том, чтобы выявить все богатство философского мышления В. И. Ленина, но и развивать ленинские мысли применительно к новым историческим условиям на базе новых достижений общественных и естественных наук.

Ленинское философское наследство весьма многогранно, его разработка предполагает всесторонний подход к нему. Большое значение имеет дальнейшее развитие ленинских положений о диалектике как логике и теории познания марксизма.

Советские философы и философы-марксисты зарубежных стран в последнее время стали больше уделять внимания проблемам диалектической логики, о чем свидетельствуют вышедшие в свет работы (статьи и монографии). От дискуссий о предмете логики и ее отношении к диалектике. они перешли к разработке конкретных вопросов как формальной, так и диалектической логики. Но это еще только начало большой и серьезной работы в этой области. Развитие науки, в частности естествознания, ставит задачу дальнейшей и более углубленной разработки проблем диалектической логики.

Некоторые зарубежные естествоиспытатели и философы считают, что все проблемы, которые ставит современная наука перед философией, могут быть решены путем совершенствования аппарата формальной логики. По их мнению, возник конфликт между современным уровнем естествознания и аппаратом классической, традиционной логики. Создание нового аппарата формальной логики рассматривается как средство для решения всех вопросов, которые ставит естествознание перед философией, всех реальных трудностей, возникающих в науке.

Конечно, совершенствовать аппарат формальной логики необходимо, его развитие способствует прогрессу в науке (достаточно вспомнить значение аппарата математической логики для кибернетики). Аппарат современной формальной логики довольно развит, созданы многочисленные формальные системы исчисления, которые плодотворно работают в науке и технике. Однако совершенствование аппарата формальной логики — это только одна сторона. Развитие современного естествознания неминуемо подводит нас к диалектике, которая является теорией познания и логикой современной науки. Какими способами, с помощью каких форм мышление приходит к результатам, дающим объективную истину,— проблема, которую ставит перед логикой наука. Эта проблема — предмет не формальной логики, а диалектики.

Как бы ни был совершенен аппарат формальной логики, он не может служить научным методом для философского обобщения результатов естествознания. Ученые-естественники ожидают от философов разработки таких актуальных вопросов, как процесс образования и развития научных понятий, принципы построения и развития гипотез, научных теорий, различные методы современного научного мышления, гносеологическая природа эксперимента и его связь с теоретическим мышлением.

Философия оказывает действенную помощь естествоиспытателям не тем, что сама решает специальные вопросы развития науки с какой-то общей, натурфилософской точки зрения. Этот путь связи философии и современного естествознания бесплоден. Философия не должна и не может заменить ни физики, ни биологии, ни какой-либо другой отрасли научного знания. У каждой науки есть свой предмет, свои специфические приемы исследования. Но философия очень поможет всем другим отраслям научного знания, если она будет правильно и своевременно давать ответы на те методологические вопросы, неразрешенность которых мешает естествоиспытателям успешно преодолеть трудности, стоящие на их пути.

Философия учит правильно мыслить, правильно связывать факты природы. Постижение предмета мыслью возможно лишь по законам диалектики, в категориях и формах диалектической логики. Вот почему Ф. Энгельс и В. И. Ленин придавали огромное значение категориям и формам мышления, считая их анализ благодарной и трудной задачей.

Разработка диалектической логики включает создание трудов как по отдельным проблемам, так и по системе диалектической логики в целом. Причем одно предполагает и дополняет другое. Трудно разрабатывать какую-либо проблему, не зная ее места в общей системе; с другой стороны, невозможно выяснить значение той или иной проблемы, ее место в науке, не раскрыв достаточно полно ее содержание.

В данной книге автор пытается соединить эти два способа исследований, а именно, на основе идей В. И. Ленина рассмотреть целую совокупность проблем диалектической логики, одни из которых будут проанализированы более детально, а другие с меньшей полнотой. Большое внимание обращено на вопросы логики, занимавшие видное место в движении философской мысли В. И. Ленина, разработка которых выдвигается ходом развития современного научного познания.

Большое место при анализе проблем диалектической логики будет занимать анализ историко-философского материала. И это вполне закономерно и соответствует методу В. И. Ленина, который подчеркивал связь истории мысли с ее логикой. Без истории философии нельзя выявить содержания ни одного понятия логики, уяснить необходимость его выдвижения и тенденцию дальнейшего развития. Причем в данном случае историко-философский анализ является не просто историческим, но и логическим. Путем изучения историко-философского материала выделяются основные моменты содержания понятий в их взаимной связи. Иной путь трудно было бы найти. Например, вне истории философии трудно, а может быть, просто невозможно, обосновать необходимость идеи как особой формы мышления. Философия выработала это понятие исходя не из конкретного анализа результатов познания какого-либо предмета, а из потребностей объяснения общего хода движения познания к истине. А если это так, то, следовательно, нужно проанализировать не только конкретные результаты научного знания, а и закономерности его развития вообще, что мы и находим в философских системах прошлого, рассматривая их в историко-логической последовательности.

Ф. Энгельс ставил вопрос о необходимости для естествоиспытателя научно-теоретического мышления, которое «…является прирожденным свойством только в виде способности. Эта способность должна быть развита, усовершенствована, а для этого не существует до сих пор никакого иного средства, кроме изучения всей предшествующей философии»*. Исследование формирования и развития понятий философии необходимо для понимания их роли в современном научном мышлении.

При этом анализ движения мысли в истории философии не должен быть изолирован от современной науки, тенденций ее развития и потребностей. Только синтез истории философии и истории науки, включая ее новейшие теоретические построения, может послужить основой для логических обобщений.

Разработка логической проблематики в марксистской философии показала, что ленинские идеи правильно отразили основные тенденции в развитии логики XX столетия.

Автор благодарен всем товарищам, принявшим участие в обсуждении и подготовке книги к печати.

* К. Маркс и Ф. Энгельс. Сочинения, т. 20, стр. 366.

• Вперед

IV. Формальная логика и диалектика

О полном непонимании природы диалектики свидетельствует уже один тот факт, что г. Дюринг признает ее орудием простого доказательства, подобно тому как, при ограниченном понимании, можно считать таковым формальную логику или элементарную математику. Даже формальная логика представляет, прежде всего, метод для отыскивания новых результатов, для перехода от известного к неизвестному, и то же самое, только в гораздо более высоком смысле, представляет диалектика, которая к тому же содержит в себе зародыш более широкого мировоззрения, так как она прорывает тесный горизонт формальной логики. В математике существует такое же отношение. Элементарная математика, математика постоянных величин, движется, по крайней мере в целом и общем, в границах формальной логики; математика переменных величин, существеннейший отдел которой составляет исчисление бесконечно малых, есть в сущности не что иное, как применение диалектики к математическим отношениям. Простое доказательство отступает здесь совершенно на задний план в сравнении с многообразными применениями метода к новым областям исследования. И почти все доказательства высшей математики, начиная с первых доказательств дифференциального исчисления, являются, с точки зрения элементарной математики, строго говоря, неверными. Это и не может быть иначе, если добытые в диалектической области данные хотят доказать посредством формальной логики. Пытаться доказать такому заядлому метафизику, как г. Дюринг, что-либо посредством одной диалектики было бы таким же даром потраченным трудом, каким был труд Лейбница и его учеников, доказывавших тогдашним математикам теоремы исчисления бесконечно-малых. Дифференциал вызывал в них такие же судороги, какие вызывает в Дюринге отрицание отрицания, в котором, впрочем, дифференциал тоже, как мы увидим, играет некоторую роль. В конце концов, эти господа, поскольку они не умерли тем временем, ворча сдались, — не потому, что были убеждены, а потому, что даваемые дифференциальным исчислением решения были всегда верны. Г-н Дюринг, как сам он рассказывает, достиг только 40 лет, и если — чего мы ему желаем — он доживет до глубокой старости, то еще, может быть, переживет то же самое. (Энгельс, Анти-Дюринг, стр. 95 — 96, 1932 г.)

 

Закон абстрактного тожества

 

Закон тожества в старометафизическом смысле есть основной закон старого мировоззрения: а = а. Каждая вещь равна самой себе. Все было постоянным — солнечная система, звезды, организмы. Естествознание опровергло этот закон в каждом отдельном случае, шаг за шагом; но теоретически он все еще продолжает существовать, и приверженцы старого все еще противопоставляют его новому. Вещь не может быть одновременно сама собой и чем-то другим. И, однако, естествознание в последнее время доказало в подробностях (см. выше [стр. 8 — 9]) тот факт, что истинное, конкретное тожество содержит в себе различие, перемену. — Как и все метафизические категории, абстрактное тожество годится лишь для домашнего употребления, где рассматриваются незначительные отношения или короткие промежутки времени; границы, в рамках которых оно пригодно, различны почти в каждом случае и обусловливаются природой того объекта, к которому его применяют, — в планетной системе, где для обыкновенных астрономических выкладок можно без чувствительной погрешности принимать эллипсис за основную форму, эти границы значительно шире, чем в случае какого-нибудь насекомого, проделывающего свои превращения в течение нескольких недель (привести другие примеры, например, изменение видов, происходящее в течение многих тысячелетий). Но для синтетического естествознания абстрактное тожество совершенно недостаточно даже в любой отдельной области, и хотя в целом идея о таком тожестве практически теперь отвергнута, но теоретически она все еще властвует над умами, и большинство естествоиспытателей все еще воображает, что тожество и различие являются непримиримыми противоположностями, а не односторонними полюсами, имеющими значение только в своем взаимодействии, во включении различия в тожество. (Энгельс, Диалектика природы, стр. 21, 1932 г.)

 

Неприменимость абстрактного тожества

 

В органической природе также неприменимо абстрактное тожество а = а, и отрицательное а равно и неравно а одновременно. Растение, животное, каждая клетка в каждое мгновение своей жизни тожественны сами с собой и в то же время отличаются от самих себя, благодаря усвоению и выделению веществ, благодаря дыханию, образованию и умиранию клеток, благодаря процессу циркуляции, — словом, благодаря сумме непрерывных молекулярных изменений, которые составляют жизнь, и итог которых выступает наглядно в разных фазах жизни — эмбриональной жизни, молодости, половой зрелости, процессе размножения, старости, смерти. Мы оставляем в стороне развитие видов. Чем больше развивается физиология, тем важнее становятся для нее эти непрерывные, бесконечно малые изменения, тем важнее также становится для нее рассмотрение различия внутри тожества, и старая, абстрактная, формальная точка зрения тожества, согласно которой органическое существо рассматривается как нечто просто тожественное с собой, постоянное, оказывается устарелой. Несмотря на это, основывающийся на ней образ мышления продолжает существовать вместе со своими категориями. Но уже в неорганической природе тожество, как таковое, в действительности не существует. Каждое тело подвержено постоянно механическим, физическим воздействиям, которые производят в нем непрерывные изменения, модифицируют его тожество. Абстрактное тожество и его антитеза, различие, уместны только в математике — абстрактной науке, занимающейся умственными построениями, хотя бы и являющимися отражениями реальности, — но и здесь оно постоянно снимается. Hegel, Enz. I, стр. 235. Факт, что тожество содержит в себе различие, выражен в каждом предложении, где сказуемое неизбежно отлично от подлежащего. Лилия есть растение, роза красна; здесь либо в подлежащем, либо в сказуемом имеется (различие) нечто такое, что не покрывается сказуемым или подлежащим. Hegel, Enz. I, стр. 231. Само собой разумеется, что тожество с собою имеет уже заранее необходимым дополнением отличие от всего прочего.

Постоянное изменение, т. е. снимание абстрактного тожества с собой, имеется также в так называемой неорганической природе. Геология является историей этого. На поверхности механические изменения (размывание, мороз), химические (выветривание), внутри земли механические (давление), теплота (вулканическая), химические (вода, кислота, связывающие вещества) в большом масштабе — поднятия почвы, землетрясения и т. д. Современный сланец радикально отличен от ила, из которого он образовался, мел — от не связанных между собой микроскопических раковин, которые его составили; еще более известняк, который, по мнению некоторых ученых, совершенно органического происхождения, песчаник — от не связанного морского песка, который, в свою очередь, возник из размельченного гранита, и т. д., не говоря уже об угле. (Энгельс, Диалектика природы, стр. 8 — 9, 1932 г.)

 

Противоположность формальной логики и логики диалектической

 

Тов. Бухарин говорит о «логических» основаниях. Все его рассуждение показывает, что он — может быть, бессознательно — стоит здесь на точке зрения логики формальной или схоластической, а не логики диалектической или марксистской. Чтобы пояснить это, начну с простейшего примера, взятого самим т. Бухариным. На дискуссии 30 декабря он говорил:

«Товарищи, может быть, на многих из вас споры, которые здесь происходят, производят впечатление, примерно, такого характера: приходят два человека и спрашивают друг у друга, что такое стакан, который стоит на кафедре. Один говорит: «Это стеклянный цилиндр, и да будет предан анафеме всякий, кто говорит, что это не так». Второй говорит: «Стакан, это — инструмент для питья, и да будет предан анафеме тот, кто говорит, что это не так» (стр. 46).

Этим примером Бухарин хотел, как видит читатель, популярно объяснить мне вред односторонности. Я принимаю это пояснение с благодарностью и, чтобы доказать делом мою благодарность, я отвечаю популярным объяснением того, что такое эклектицизм в отличие от диалектики.

Стакан есть, бесспорно, и стеклянный цилиндр, и инструмент для питья. Но стакан имеет не только эти два свойства, или качества, или стороны, а бесконечное количество других свойств, качеств, сторон, взаимоотношений и «опосредствований» со всем остальным миром. Стакан есть тяжелый предмет, который может быть инструментом для бросания. Стакан может служить как пресс-папье, как помещение для пойманной бабочки, стакан может иметь ценность, как предмет с художественной резьбой или рисунком, совершенно независимо от того, годен ли он для питья, сделан ли он из стекла, является ли форма его цилиндрической или не совсем, и так далее и тому подобное.

Далее. Если мне нужен стакан сейчас как инструмент для питья, то мне совершенно не важно знать, вполне ли цилиндрическая его форма и действительно ли он сделан из стекла, но зато важно, чтобы в дне не было трещины, чтобы нельзя было поранить себе губы, употребляя этот стакан, и т. п. Если же мне нужен стакан не для питья, а для такого употребления, для которого годен всякий стеклянный цилиндр, тогда для меня годится и стакан с трещиной в дне или даже вовсе без дна и т. д.

Логика формальная, которой ограничиваются в школах (и должны ограничиваться — с поправками — для низших классов школы), берет формальные определения, руководясь тем, что наиболее обычно или что чаще всего бросается в глаза, и ограничивается этим. Если при этом берутся два или более различных определения и соединяются вместе совершенно случайно (и стеклянный цилиндр и инструмент для питья), то мы получаем эклектическое определение, указывающее на разные стороны предмета — и только.

Логика диалектическая требует того, чтобы мы шли дальше. Чтобы действительно знать предмет, надо охватить, изучить все его стороны, все связи и «опосредствования». Мы никогда не достигнем этого полностью, но требование всесторонности предостережет нас от ошибок и от омертвения. Это, во-первых. Во-вторых, диалектическая логика требует, чтобы брать предмет в его развитии, «самодвижении» (как говорит иногда Гегель), изменении. По отношению к стакану это не сразу ясно, но и стакан не остается неизменным, а в особенности меняется назначение стакана, употребление его, связь его с окружающим миром. В-третьих, вся человеческая практика должна войти в полное «определение» предмета и как критерий истины и как практический определитель связи предмета с тем, что нужно человеку. В-четвертых, диалектическая логика учит, что «абстрактной истины нет, истина всегда конкретна», как любил говорить, вслед за Гегелем, покойный Плеханов (в скобках уместным, мне кажется, заметить для молодых членов партии, что нельзя стать сознательным, настоящим коммунистом без того, чтобы изучать — именно изучать — все, написанное Плехановым по философии, ибо это лучшее во всей международной литературе марксизма) [Кстати, нельзя не пожелать, во-первых, чтобы выходящее теперь в свет издание сочинений Плеханова выделило все статьи по философии в особый том или особые томы с подробнейшим указателем и пр. Ибо это должно войти в серию обязательных учебников коммунизма. Во-вторых, рабочему государству, по-моему, следует требовать от профессоров философии, чтобы они знали изложение марксистской философии Плехановым и умели передать учащимся это знание. Но это все уже есть отступление от «пропаганды» к «администрированию».].

Я, разумеется, не исчерпал понятия диалектической логики. Но пока довольно и этого. (Ленин, Еще раз о профсоюзах (1921 г.), Соч., т. XXVI, стр. 133 — 135, изд. 3-е.)

 

Плеханов придает формальной логике самостоятельное значение

 

«Все течет, все изменяется», — говорит древний эфесский мыслитель. Сочетания, называемые нами предметами, находятся в состоянии постоянного, — более или менее быстрого, — изменения. Поскольку данные сочетания остаются данными сочетаниями, мы обязаны судить о них по формуле: «да — да и нет — нет». А поскольку они изменяются и перестают существовать, как таковые, мы обязаны апеллировать к логике противоречия; мы должны говорить, — рискуя навлечь неудовольствие гг. Бернштейнов, Н. Г. и прочей метафизической братии: «и да, и нет, и существуют, и не существуют».

Как покой есть частный случай движения, так и мышление по правилам формальной логики (согласно «основным законам» мысли) — есть частный случай диалектического мышления. (Плеханов, Предисловие к книге Ф. Энгельса «Л. Фейербах», стр. 22, 1931 г.)

 

Когда мы стоим перед вопросом о переходе одного вида движения в другой, — скажем, механического движения в теплоту, — нам тоже приходится рассуждать согласно основному правилу Ибервега. Этот вид движения есть или теплота, или механическое движение, или и т. д. Это ясно. Но если это так, то основные законы формальной логики в известных пределах применимы также и к движению. А отсюда еще раз следует, что диалектика не отменяет формальной логики, а только лишает ее законы приписываемого им метафизиками абсолютного значения. (Плеханов, Предисловие к книге Энгельса «Л. Фейербах», стр. 24, 1931 г.)

 

Диалектика и эклектицизм

 

Сообразно этому своему стремлению теоретически углубить вопрос, т. Бухарин, начиная с дискуссии 30 декабря, если не раньше, переводит спор именно в указанную область.

«Я считаю абсолютно необходимым, — говорил тов. Бухарин 30 декабря, — в этом состоит теоретическая сущность того, что здесь называется «буферной» фракцией или ее идеологией, — и мне представляется совершенно бесспорным, что нельзя отбросить ни этот политический, ни этот хозяйственный момент…» (стр. 47).

Теоретическая сущность той ошибки, которую здесь делает т. Бухарин, состоит в том, что он диалектическое соотношение между политикой и экономикой (которому учит нас марксизм) подменяет эклектицизмом. «И то, и другое», «с одной стороны, с другой стороны» — вот теоретическая позиция Бухарина. Это и есть эклектицизм. Диалектика требует всестороннего учета соотношений в их конкретном развитии, а не выдергивания кусочка одного, кусочка другого. На примере политики и экономики я уже это показал…

В той же петроградской речи Бухарина на стр. 7 читаем:

«Ошибка т. Троцкого состоит в том, что он недостаточно защищает момент школы коммунизма».

На дискуссии 30 декабря Бухарин рассуждает так:

«Тов. Зиновьев говорил, что профсоюзы — школа коммунизма, а Троцкий говорил, что это — административно-технический аппарат управления производством. Я не вижу никаких логических оснований, которые бы доказывали, что верно не первое и не второе; верны оба эти положения и соединение этих обоих положений» (стр. 48).

Та же мысль в 6-м тезисе Бухарина и его «группы» или «фракции»: …«с одной стороны, они (профсоюзы) — «школа коммунизма»… с другой стороны, они — и притом в возрастающей степени — составная часть хозяйственного аппарата и аппарата государственной власти вообще…» («Правда», 16 января).

Вот тут-то и заключается основная теоретическая ошибка т. Бухарина, подмен диалектики марксизма эклектицизмом (особенно распространенным у авторов разных «модных» и реакционных философских систем). ..

«С одной стороны, школа, с другой, аппарат», — говорит Бухарин и пишет в своих тезисах. У Троцкого ошибка в том, что он «недостаточно защищает момент школы…» у Зиновьева — недостаток насчет «момента» аппарата.

Почему это рассуждение Бухарина есть мертвый и бессодержательный эклектицизм? Потому, что у Бухарина нет и тени попытки самостоятельно, с своей точки зрения, проанализировать как всю историю данного спора (марксизм, то есть диалектическая логика, требует этого безусловно), так и весь подход к вопросу, всю постановку — или, если хотите, все направление постановки — вопроса в данное время, при данных конкретных обстоятельствах. Ни тени попытки у Бухарина сделать это! Он подходит без малейшего конкретного изучения с голыми абстракциями и берет кусочек у Зиновьева, кусочек у Троцкого. Это есть эклектицизм.

Чтобы еще нагляднее пояснить это, возьму пример. Я ровно ничего не знаю о повстанцах и революционерах Южного Китая (кроме 2 — 3 статей Сун Ят-сена, и нескольких книг и газетных статей, которые я читал много лет тому назад). Раз там идут восстания, вероятно, есть и споры между китайцем № 1, который говорит, что восстание есть продукт обостреннейшей и захватившей всю нацию классовой борьбы, и китайцем № 2, который говорит, что восстание есть искусство. Тезисы, подобные тезисам Бухарина, я могу написать, ничего больше не зная: «с одной стороны… с другой стороны». Один недостаточно учел «момент» искусства, другой — «момент обострения» и т. д. Это будет мертвый и бессодержательный эклектицизм, ибо нет конкретного изучения данного спора, данного вопроса, данного подхода к нему и т. д.

Профсоюзы, с одной стороны, школа; с другой — аппарат; с третьей — организация трудящихся; с четвертой — организация почти только промышленных рабочих; с пятой — организация по производствам и т. д. и т. д. Никакого обоснования, никакого самостоятельного анализа у Бухарина нет и тени, чтобы доказать, почему надо взять первые две «стороны» вопроса или предмета, а не третью, четвертую, пятую и т. д. Поэтому и тезисы бухаринской группы — сплошь эклектическая пустышка. Бухарин в корне неверно, эклектически, ставит весь вопрос о соотношении «школы» и «аппарата».

Чтобы поставить этот вопрос правильно, надо от пустых абстракций перейти к конкретному, т. е. данному спору. Берите этот спор, как хотите: так ли, как он возник на V Всероссийской конференции профсоюзов, или так, как его поставил и направил сам Троцкий своей брошюрой-платформой 25 декабря — вы увидите, что весь подход Троцкого, все направление у него неверно. Он не понял того, что надо и можно подойти к профсоюзам, как к школе, и тогда, когда ставишь тему о «советском тред-юнионизме», и тогда, когда говоришь о производственной пропаганде вообще, и тогда, когда так ставишь вопрос, как Троцкий, о «сращивании», об участии профсоюзов в управлении производством. И в этом последнем вопросе, так, как он поставлен во всей брошюре-платформе Троцкого, неправильность состоит в непонимании того, что профсоюзы являются школой административно-технического управления производством. Не «с одной стороны — школа, с другой — нечто иное», a со всех сторон — при данном споре, при данной постановке вопроса Троцким, профсоюзы суть школа, школа объединения, школа солидарности, школа защиты своих интересов, школа хозяйничанья, школа управления. Вместо того, чтобы понять и исправить эту коренную ошибку т. Троцкого, т. Бухарин дал смешную поправочку: «с одной стороны, с другой стороны». (Ленин, Еше раз о профсоюзах (1921 г.), Соч., т. XXVI, стр. 131 — 132, 133, 135 — 136, изд. 3-е.)

формальная логика | Определение, примеры, символы и факты

Альфред Норт Уайтхед

Смотреть все СМИ

Ключевые люди:

Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано

Похожие темы:

теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод

См. весь связанный контент →

формальная логика , абстрактное изучение предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.

Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдения. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии. Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.

Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивное. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают вывод.

Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.

Дедуктивные выводы, с которыми имеет дело формальная логика, — это, как следует из названия, выводы, достоверность которых зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .

Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. такими, которые имеют смысл в контексте) и при этом делается единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.

С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода. На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.

Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны. В качестве примера можно взять аксиоматическую систему логики, т. е. такую ​​систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и от того, каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области. мысли; но, среди прочего, по указанным выше причинам, он обычно позаботится о том, чтобы описать формулы и установить правила системы без ссылки на интерпретацию и указать как отдельный вопрос интерпретацию, которую он имеет в виду.

Многие идеи, используемые при изложении формальной логики, в том числе упомянутые выше, поднимают проблемы, принадлежащие скорее философии, чем самой логике. Примеры: Каков правильный анализ понятия истины? Что такое предложение и как оно связано с предложением, которым оно выражено? Существуют ли какие-то виды здравого рассуждения, которые не являются ни дедуктивными, ни индуктивными? К счастью, можно научиться заниматься формальной логикой, не имея удовлетворительных ответов на такие вопросы, точно так же, как можно заниматься математикой, не отвечая на вопросы, относящиеся к философии математики, например: числа являются реальными объектами или мысленными построениями?

Формальная логика была разработана для понимания природы дедукции

Даже если мы согласимся со всем, что мы только что сделали в отношении логической структуры языка, скептически настроенный специалист по лингвистике все же может возразить, что большая часть того, чему его на самом деле учат на вводном курсе класс символической логики не имеет прямого отношения к пониманию естественного языка.

Это разумное возражение. Многие студенты заканчивают полный курс символической логики и уходят, не зная, какое отношение этот курс имеет к пониманию языка.

У такого замешательства есть причина, это не просто признак плохого обучения.

Причина в том, что вопросы, для ответа на которые была разработана формальная логика, касаются не только логической структуры естественного языка.

Давайте подробнее об этом.

В типичном первом курсе символической логики вы познакомитесь с тремя различными системами логики: категорической (или аристотелевской) логикой, пропозициональной логикой и предикат логика.

В каждой системе вы научитесь переводить утверждения естественного языка на формальный символический язык и (среди прочего) узнаете, как представлять аргументы и проверять их правильность в рамках данного языка.

Например, высказывание на естественном языке, такое как «коровы — это млекопитающие», будет представлено как «Все C являются M» в категориальной логике.

В логике высказываний вы просто использовали бы одну заглавную букву для представления утверждения «коровы — это млекопитающие», потому что логика высказываний безразлична к субъектно-предикатной структуре языка — она имеет дело только с логическими отношениями между предложениями, взятыми как единое целое.

В логике предикатов выражение «коровы — это млекопитающие» будет представлено как «(x)(Cx ⊃ Mx)». Вы можете прочитать это как «для любого индивидуума x, если x — корова, то x — млекопитающее».

Большая часть вашего времени в символическом классе будет посвящена изучению методов ответов на следующие виды вопросов, работающих в рамках каждой из этих логических систем:

• Как бы вы записали следующее утверждение на естественном языке в символической форме?
• Является ли следующий набор утверждений последовательным или противоречивым?
• Выражает ли следующее утверждение тавтологию (необходимая истина), противоречие (необходимая ложь) или случайный факт (возможная истина, возможная ложь)?
• Является ли следующий аргумент допустимым или недопустимым?
• Можете ли вы построить действительное дедуктивное доказательство данного вывода, исходя из следующих предпосылок и стандартных правил вывода?

Большинство страниц учебника по символической логике посвящено методам обучения ответам на эти вопросы.

Но эти вопросы отражают исторические интересы философов и логиков, а не лингвистов.

Вот реальность: формальная логика была разработана как инструмент для понимания природы дедуктивных рассуждений и дедуктивных доказательств . Его предметом является природа логической истины и логический вывод , а не структура естественного языка.

Чтобы быть более конкретным, вот вопросы, которые стимулировали развитие формальной логики (особенно за последние пару сотен лет):

1. Как мы можем определить, является ли часть рассуждения действительным дедуктивным аргументом?
2. Как мы можем определить, является ли вывод необходимым набором предпосылок? Как мы можем найти действительный дедуктивный аргумент, демонстрирующий эту необходимую связь — т.е. е. это показывает почему вывод следует с необходимостью?
3. Что такого в структуре мира, структуре языка и отношениях между словами, мыслями и вещами, что делает возможным дедуктивное умозаключение ?

Мы видим связь с языком в этом последнем вопросе, но связь эта косвенная, движимая главной философской целью — достичь глубокого понимания природы дедуктивных рассуждений.

Теперь оказывается, что формальная логика очень полезна для исследования логической структуры естественного языка. Но эту удачу лучше всего рассматривать как побочный продукт или приложение формальной логики.

Намеренное использование формальных методов для моделирования семантики естественного языка — формальная логика на службе лингвистики — на самом деле относится к середине и концу ^-го -го века. Большинство философов, которые преподают вводную символическую логику, не знакомы с формальной семантикой в ​​​​лингвистике, и во вводных учебниках эти разработки отсутствуют. В философии она рассматривается как специализированная область, пересекающаяся с философией языка и лингвистикой. Более продвинутые курсы по логике иногда охватывают темы в этой области, но формальная семантика обычно преподается только на уровне выпускников по более специализированным программам.

Теперь давайте обратимся к третьему и последнему пункту, который я хотел сделать об отношениях между логикой и языком.

Формальная логика: Символизация аргументов в сентенциальной логике – Философия на 1000 слов: Вводная антология

Автор: Томас Меткалф
Категория: Логика и рассуждение
Количество слов: 1000 предоставить доказательства или доказать какой-либо вывод.[1] Формальная логика — это инструмент, который мы можем использовать для представления и оценки аргументов. Некоторые аргументы лучше других, и формальная логика может помочь нам понять, как именно должен работать тот или иной аргумент, и является ли он хорошим или плохим аргументом (и почему).

Чтобы использовать формальную логику, мы символизируем аргументы: мы представляем аргументы на английском (или другом естественном языке) в некотором другом наборе символов. Эти символические представления могут значительно облегчить определение того, является ли определенный аргумент действительным (т. е. обязательно, если его посылки верны, его вывод верен), а также определить другие важные свойства аргументов.

Здесь мы рассмотрим простейшую разновидность формальной логики: сентенциальную логику. ^[2]

Розеттский камень.

1. Буквы предложений и константы

В логике предложений, ^[3] стандартно обозначать отдельные декларативные предложения , т. е. высказывания, заглавными латинскими буквами, например:

• приносим извинения за опрокидывание мотоциклов». ты.’

Обратите внимание, что ни один из A-C не содержит слов «не», «и», «или», «если» или «тогда». Это потому, что эти слова (иногда называемые «логическими константами») очень важны в формальной логике. . Мы резервируем для них специальные символы, перечисленные ниже. ^[4] Напротив, мы могли бы использовать букву «А» для обозначения «Я прошу прощения за то, что опрокинул ваши мотоциклы» в одном аргументе, и ту же букву «А» для «Счеты хуже цифрового калькулятора». в другой.

Если предложение содержит одно из этих слов «и», «не» и т. д., мы разбиваем его на составные части, разделенные этими словами. Например, если бы мое предложение было:

• Прошу прощения за то, что опрокинул ваши мотоциклы и бобы не полезны для сердца

тогда я мог бы написать:

• A & ¬B.

Если отдельное предложение не содержит никаких логических констант, мы можем назвать его «атомарным» предложением: его больше нельзя разделить.

Вот набор символов для констант, наряду с английскими словами, которые мы используем для приблизительного обозначения этих констант для любых предложений φ, ψ и т. д. В разных языках логики иногда используются разные символы, поэтому я включу все самые общие с их стандартными именами и значениями. ^[5]

2 9026 2 9026 2 9026 2 9026 2 9026 2 9026. видите, еще один важный набор символов, которые мы можем использовать, — это строчные греческие буквы. Мы используем их как переменные, а не сокращения определенных предложений: они заменяют то или иное предложение . Это предложение не обязательно должно быть атомарным; он может сам содержать логические константы.

Заглавные буквы обозначают конкретные предложения, которые мы уже определили, а строчные буквы обозначают любое предложение вообще. Вот несколько примеров:

Название	Символ	Альтернативные символы	Английский прибл.
‘Negation’	¬φ	~φ	‘not φ’ [6]
‘Conjunction’	φ & ψ	φ ∧ ψ, φ ● ψ	‘ φ и ψ’
‘Дизъюнкция’	φ ∨ ψ		‘φ или ψ’ [7]
‘Conditalal’	φ → ψ	φ ⊃ ψ	‘if φ, тогда ψ’ или ‘φ [8]
‘. ↔ ψ	φ ≡ ψ	‘φ if and only if ψ’ (sometimes written ‘φ iff ψ’)
‘Conclusion’	∴ φ		‘therefore φ’
‘ Противоречие’	⊥		[какое-то ложное предложение] [9]
‘Entailment’	φ, ψ ⊢ χ		‘φ и ψ Совместно въезжает χ в системе логики в использовании’ ‘φ и ψ

	Символизация
Я не сплю или если я слон, то огонь горяч.	¬D ∨ (E → F)
Если деньги в конверте, а в конверте нет, то верно противоречие.	(М и ¬М) → ⊥
Ворота открыты тогда и только тогда, когда: вертолет приземлился и либо лед растаял, либо вы не шутите.	G ↔ (H & (I ∨ ¬J))

Мы также можем использовать круглые скобки, чтобы наши предложения было легче читать, а их смысл был понятен. Например, во втором предложении чуть выше, если бы я расставил скобки по-другому, значение изменилось бы:

Ворота открыты тогда и только тогда, когда вертолет приземлился. И то ли лед растаял, то ли вы не шутите.

(G ↔ H) & (I ∨ ¬J)

2. Доказательства

Обратите внимание, что мы использовали английские слова для аппроксимации наших символов. Это не случайно. Например, в сентенциальной логике, если вы знаете, что А истинно, и вы знаете, что Б истинно, вы можете заключить, что «А и В» истинны. И именно так мы используем наше английское слово «и». У вас не может быть и Acura , и линкора, если это правда, что у вас есть Acura и это правда, что у вас есть линкор.

Обратите внимание, что если вы знаете, что у вас есть Acura и линкор, вы можете сделать вывод, что у вас есть Acura. Чтобы символизировать это, мы бы сказали, что если вы знаете «А и В», вы можете заключить «А». Можно считать, что если у вас Акура, то у вас машина. Мы могли бы символизировать это с помощью «A → C». В свою очередь, мы можем, Предполагая , что у вас есть Acura и линкор, докажите , что у вас есть машина. Это может выглядеть так:

Номер	Предложение	Обоснование
1.	А и Б	Предположение.
2.	A → C	Успение.
3.	A	Следует из 1.
4.	∴ C	Следует из 2 и 3.

Как видите, мы идем шаг за шагом, нумеруя наши шаги и указывая, как мы получили наше новое предложение.

Это всего лишь быстрый пример, но вы, вероятно, можете себе представить, как мы можем использовать эти символы для построения более интересных доказательств. Тема доказательств вообще достаточно важна и сложна, чтобы иметь отдельную запись.

3. За пределами сентенциальной логики

Когда мы знаем правила сентенциальной логики и логические константы, несложно символизировать более сложные предложения. Например, мы можем захотеть поговорить о том, какие объекты обладают какими свойствами, или о том, является ли некоторое предложение обязательно истинным или вероятно истинным. Но это темы для других статей.

Примечания

^[1] В этом эссе мы не говорим явно ни о дедукции, ни о индукции, потому что сентенциальная логика может использоваться и для того, и для другого. Однако сентенциальная логика обычно вводится дедуктивными аргументами.

^[2] Здесь мы следуем стандартному способу обозначения аргументов. См., например, Huber 2019 и Sider 2010.

^[3] Иногда это называют «пропозициональной» логикой. Но «сентенциал» более нейтрален. Он лишь обязывает нас к существованию предложений, т. е. грамматических цепочек слов в некотором языке. Это не обязывает нас к существованию пропозиций, которые, если они существуют, являются (грубо говоря) значениями предложений, или содержанием мысли, или тем, что «это» является «истинным», когда я говорю: «Это верно, что электроны меньше, чем протоны.» Сказать «сентенциальный» также, строго говоря, более точно: то, что мы в основном делаем в формальной логике, является синтаксическим, а не семантическим. То есть мы рассматриваем строки из символов , а не значений, стоящих за символами, и предложения (если они существуют) являются значениями предложений.

^[4] Мы называем специальные символы «логическими константами», потому что, в отличие от букв-предложений, они всегда означают одно и то же, где бы они ни встречались.

^[5] Есть несколько других английских слов или терминов, которые также соответствуют этим символам. Например, строка «p, только если q» оказывается эквивалентной «если p, то q». И в стандартной логике «но» и «и» подчиняются одним и тем же правилам; мы не упоминаем коннотацию контраста, присущую «но».

^[6] Конечно, в английском языке мы обычно не говорим о том, является ли «не р» истинным или ложным; мы говорим о том, является ли «не [некоторое предложение]» истинным или ложным. То есть мы не упоминаем саму букву «р»; мы заполняем его любым предложением, о котором говорим. Чтобы упомянуть фразу, содержащую переменную, но указать, что вы собираетесь упомянуть значение переменной, а не имя самой переменной, вы можете использовать угловые кавычки (например, ‘⌜’ и ‘⌝’) для того, что иногда называют «квазицитированием» (Quine 1981 [1940]: 33-37). Однако, чтобы избежать путаницы, я решил сохранить одинарные кавычки.

^[7] Обратите внимание, что в английском языке наше слово «или» может означать включающее или исключающее «или», то есть иногда мы используем «или», чтобы подразумевать, что одно или оба могут быть истинными, в то время как мы иногда используйте его, чтобы подразумевать, что только одно может быть правдой. Например, если я спрашиваю: «Вы когда-нибудь ездили на скутере или мотоцикле?», я, вероятно, повышаю голос в конце предложения, подразумевая, что ответ «да» или «нет», и вы бы скажите «да», если вы ездили на одном из них, но также, если вы когда-то ездили на обоих. Но если я спрошу «Хочешь суп или салат?» в ресторане, я могу понизить голос в конце предложения, подразумевая, что вы должны выбрать, а «и то, и другое» — не вариант. В стандартной логике наш символ дизъюнкции означает включающее «или», то есть он оказывается истинным, даже если оба p и q истинны. Если мы хотим указать исключающее или, мы можем использовать символ отрицания. Например: ‘(A ∨ B) & ¬(A & B)’

^[8] Это приближение может быть особенно запутанным. Строго говоря, «условные» символы (иногда называемые также «материальными условными» символами) в стандартной логике говорят, что ложно, что: p истинно, а не-q истинно . В реальной жизни мы почти всегда можем прочитать это как «если p, то q», но бывают и несколько запутанные случаи. О них мы еще поговорим в записях о таблицах истинности. Но на данный момент, в стандартной сентенциальной логике, условное утверждение будет считаться истинным всякий раз, когда антецедент (часть «если») ложна, и всякий раз, когда антецедент и следствие (часть «тогда») оба истинны. Как я уже сказал, это может немного сбивать с толку.

^[9] Символ обычно используется для обозначения противоречия, но для целей доказательства обычно достаточно, чтобы предложение было ложным. Мы вернемся к этой теме, когда будем рассматривать фактические доказательства.

^[10] Последняя строка в таблице не об истинности предложений, а о выводимости в нашей системе логики. Это может сбивать с толку, пока мы не узнаем о фактических доказательствах, использующих эти символы, поэтому не беспокойтесь об этом слишком сильно, но я хотел включить их для полноты картины. По сути, он говорит, что если у вас есть p в строке и у вас есть q в строке, вы можете добраться до r, используя правила логики.

Ссылки

Хубер, Франц. 2019. Логическое введение в теорию вероятности и индукции . Нью-Йорк, штат Нью-Йорк, и Оксфорд, Великобритания: Издательство Оксфордского университета.

Куайн, В. В. 1981 [1940]. Математическая логика , исправленное издание. Кембридж, Массачусетс: Издательство Гарвардского университета.

Сайдер, Тед. 2010. Логика для философии . Нью-Йорк, штат Нью-Йорк, и Оксфорд, Великобритания: Издательство Оксфордского университета.

Благодарности

Автор выражает благодарность редакции 1000-Word Philosophy , а также Майклу Ферри, Эндрю Лавину и Дэниелу Мэсси за полезные комментарии к этому эссе.

Formal Logic: Symbolizing Arguments in Quantificational or Predicate Logic by Timothy Eshing

The Probability Calculus by Thomas Metcalf

Bayesianism by Thomas Metcalf

Quantum Mechanics and Philosophy III: Implications by Thomas Metcalf

About the Author

Tom Metcalf является адъюнкт-профессором Колледжа Спринг-Хилл в Мобиле, Алабама. Он получил степень доктора философии в Колорадском университете в Боулдере. Он специализируется на этике, метаэтике, эпистемологии и философии религии. У Тома есть две кошки, которых зовут Геспер и Фосфорус. http://shc.academia.edu/ThomasMetcalf

Следуйте философии 1000 слов по телефону Facebook и Twitter и подписки на получение уведомлений по электронной почте новых эссе на 1000wordPhiloshophy.com

Нравится этот:

, подобно нагрузке,

000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.com. Формальная логика — Broadview Press

• Автор: Пол А. Грегори

• Дата публикации: 24 августа 2017 г.
• ISBN: 9781554812721 / 1554812720
• 472 страницы; 5″ х 6″

• Описание
• Содержание
• Авторы/редакторы
• Сопутствующий веб-сайт
• Образец главы

Формальная логика — это текст для студентов, подходящий для вводных, средних и продвинутых курсов по символической логике. Девять глав книги предлагают всестороннее освещение функциональной и количественной логики истинности, а также основы более сложных тем, таких как теория множеств и модальная логика. Сложные идеи объясняются простым языком, не требующим знания логики или математики, а стратегии вывода иллюстрируются многочисленными примерами. Переводы, таблицы, деревья, естественная дедукция и простые метадоказательства преподаются с помощью более 400 упражнений. Сопутствующий веб-сайт предлагает дополнительное программное обеспечение для практики и обучающие видео.

Комментарии

“ Формальная логика ясна, доступна и интуитивно понятна, но она также точна, явна и основательна. Сложные и часто запутанные концепции излагаются без излишеств и напрямую, с забавной и демистифицирующей терминологией и полезными аналогиями. Это педагогическая жемчужина». — Мэри Кейт Макгоуэн, Колледж Уэллсли

«Это отличный вводный текст по символической логике. Он доступен, с четкими и краткими объяснениями ключевых понятий, а также множеством полезных примеров и практических задач, но при этом достаточно строг, чтобы подготовить студентов ко второму курсу логики; действительно, я не знаю ни одной книги, которая лучше сочетала бы эти достоинства. Я с нетерпением жду возможности использовать Формальная логика на моих курсах». — Кевин Моррис, Тулейнский университет

«Эта книга делает идеи сентенциальной логики, логики предикатов и формального доказательства легко доступными, поскольку они непосредственно переходят к сути каждого из них на естественном, нетехническом языке. Это лаконично, но никогда не торопится. Он правильно улавливает детали, не сосредотачиваясь на них как на деталях, а благодаря ясному пониманию того, почему они такие, какие они есть». — Колин Макларти, Университет Кейс Вестерн Резерв

«Паул Грегори Формальная логика заслуживает тщательного изучения для всех, кто принимает новый логический текст. Включение глав по теории множеств и модальной логике делает его ценным ресурсом для студентов, желающих выйти за рамки стандартного введения в логику». — Майкл Хикс, Университет Майами

I: Неформальные понятия
1: Неформальное введение

II: Функциональная логика истинности
2: Язык S

3: Формальная семантика для

2

• 3. 1 Присвоения значений истинности и таблицы истинности
  3.2 Семантические свойства отдельных Wffs
  3.2.1 Упражнения

  3.3 Семантические свойства наборов Wffs

  3.3.1 Упражнения

  3.4 Семантические свойства, их взаимосвязь и простая металогика

  3.4.1 Упражнения

  3.5 Деревья правды

  3.5.1 Тесты с деревьями истинности
  3.5.2 Упражнения

  3.6 Глоссарий глав

4: SD: Натуральная дедукция в С

• 4.1 Основная идея
  4.1.1 Повторение 90–195 4.1.2 Правила клина 90–195 4.1.3 Правила стрелы 90–195 4.1.4 Правила крюка 90–195 4.1.5 Правила Vee 90–195 4.1.6 Правила двойной стрелы 90–195 4.1.7 Упражнения

  4.2 Выводы: стратегии и примечания
  4.3 Теория доказательств в SD

  4.3.1 Упражнения

  4.4 SDE , расширение до SD

  4. 4.1 Правила вывода СДУ
  4.4.2 Упражнения
  4.4.3 Правила замены СДУ
  4.4.4 Упражнения

  4.5 Глоссарий глав

III: Количественная логика
5: Язык P

• 5.1 Введение P
  5.1.1 Логика квантификации
  5.1.2 Предикаты и термины в единственном числе
  5.1.3 Буквы сказуемых и отдельные константы в P
  5.1.4 Местоимения и кванторы
  5.1.5 Переменные и кванторы в P

  5.2 Синтаксис P

  5.2.1 Определение языка
  5.2.2 Синтаксические понятия и соглашения
  5.2.3 Упражнения

  5.3 Простые символы

  5.3.1 Некатегориальные утверждения
  5.3.2 Упражнения
  5.3.3 Категориальные утверждения
  5.3.4 Упражнения

  5.4 Сложные символы

  5.4.1 Основы перекрывающихся квантификаторов 90–195 5.4.2 Упражнения 90–195 5.4.3 Идентичность, численная количественная оценка и определенные описания 90–195 5. 4.4 Упражнения

  5.5 Глава Глоссарий

6: формальная семантика для P

• 6.1 Семантика и интерпретации
  6.1.1 Основы интерпретаций
  6.1.2 Интерлюдия: немного теории множеств
  6.1.3 Формальная интерпретация P
  6.1.4 Построение интерпретаций

  6.2 Семантические свойства отдельных Wffs

  6.2.1 Упражнения

  6.3 Семантические свойства наборов Wffs

  6.3.1 Упражнения

  6.4 Объем и распространение квантификатора

  6.4.1 Упражнения

  6.5 Свойства отношений

  6.5.1 Упражнения

  6.6 Глоссарий глав

7: PD: Натуральная дедукция в P

• 7.1 Правила вывода для кванторов
  7.1.1 Универсальное исключение
  7.1.2 Экзистенциальное введение
  7.1.3 Универсальное введение
  7.1.4 Экзистенциальное исключение
  7. 1.5 Упражнения

  7.2 Выводы: стратегии и примечания
  7.3 Теория доказательств в ПД

  7.3.1 Упражнения

  7.4 PDE, расширение для PD

  7.4.1 Отрицание квантификатора
  7.4.2 Упражнения

  7.4 Глоссарий глав

IV: Расширенные темы
8: Базовая теория множеств, парадокс и бесконечность

• 8.1 Основы множеств
  8.2 Парадокс Рассела
  8.3 Схема аксиом разделения, объединения, подмножества
  Раздел 8,4
  8.4.1 Упражнения

  8.5 Пары, упорядоченные пары, наборы мощности, отношения и функции
  8.6 Бесконечные множества и доказательство Кантора

  8.6.1 Упражнения

  8.7 Глоссарий глав

9: Модальная логика

• 9.1 Необходимость, возможность и невозможность
  9.1.1 Модальности
  9.1.2 Логические, метафизические, физические
  9. 1.3 Возможные миры

  9.2 Язык S

  9.2.1 Синтаксис S
  9.2.2 Упражнения

  9.3 Базовая семантика возможных миров для S

  9.3.1 Семантические свойства Wffs и наборов Wffs 90-195 9.3.2 Упражнения 90-195 9.3.3 Возможные миры и деревья 90-195 9.3.4 Упражнения

  9.4 Натуральный вычет в S

  9.4.1 System K
  9.4.2 System D
  9.4.3 System T
  9.4.4 System B
  9.4.5 System S4
  9.4.6 System S5
  9.4. 7 Отношения между модальными системами
  9.4.8 Упражнения

  9.5 Глоссарий глав

V: Приложения
A: Ответы на упражнения
B: Глоссарий
C: Таблицы истинности, древовидные правила и правила вывода

• C.1 Характеристические таблицы истинности
  C.2 Правила дерева истинности для S
  C. 3 Система деривации SD
  C.4 Система деривации SDE
  C.5 Система деривации 9031 9031

Пол А. Грегори — адъюнкт-профессор и руководитель кафедры философии в Университете Вашингтона и Ли.

Formal Logic имеет два сопутствующих веб-сайта: один для студентов и один для преподавателей.

На студенческом веб-сайте размещена программа проверки правильности языка SD, обсуждаемого в книге, а также серия видеоуроков. Бесплатный код доступа к этому веб-сайту прилагается ко всем новым копиям Formal Logic . Если вы приобрели подержанную копию, вы можете получить доступ за символическую плату здесь.

На веб-сайте инструктора размещен банк тестов с дополнительными вопросами, сопоставленными с главами 1–7 из 9.0031 Формальная логика .

Для просмотра образца главы Формальная логика щелкните здесь. (Открывается в формате PDF.)

Введение в символическую логику

Введение в символическую логику

Philosophy. lander.edu
Домашняя страница > Логика > Символика Логика > Язык символической логики
Викторины Тесты Часто задаваемые вопросы Ссылки Поиск Показания Архивы Учебный план		Философия 103: Введение в логику Язык символической логики Реферат: Соглашения для перевод операторов обычного языка в символическую запись изложил. Мы собираемся создать искусственный «язык», чтобы избежать трудности расплывчатости, двусмысленности, амфиболии и путаницы от эмоциональная значимость. Прежде всего, нужно выучить элементы этого «нового языка». Во-вторых, научиться переводить грамматику обычного языка в символическую запись. В-третьих, нужно оценить аргументы на этом «новом языке». Символическая логика, безусловно, самый простой вид логики. экономия времени на аргументацию. Кроме того, это помогает предотвратить логическую путаницу. Современное развитие началось с Джорджа Буля в 19 веке. Символическую логику можно рассматривать как простую и гибкую стенографию: Рассмотрим символы: [(p q) (q р)] (п р). Это правило было хорошо известно стоикам, но они выражали его так: « Если , если первое, то второе, а если второе, то третье, то, если первое, то третье». Мы обнаружим, что все основные манипуляции в символическом логика примерно так же сложна и работает с числами, состоящими из единиц и нулей. Начнем с простейшей части логики высказываний: объединения простых предложений в составные и определения истинностного значения полученных сложных предложений. Предложения или утверждения можно рассматривать как «атомы» логики высказываний. («Предложение» и «утверждение» часто считаются эквивалентными терминами.) Простые предложения — это утверждения, которые нельзя разбить на части без потери смысла. , «Джон и Чарльз — братья» не могут быть разобраны без изменения смысла утверждения. Обратите внимание на изменение значения слов «Джон — брат» и «Чарльз — мой брат». Принимая во внимание, что «Джон и Чарльз усердно работают» можно разбить без изменения значения: «Джон усердно работает». «Чарльз усердно работает». (Предполагается контекстуально, что значение исходного утверждения не что Джон и Чарльз усердно работают вместе, но, возможно, не так отдельно) Традиционно заглавные буквы (обычно в начале алфавита) могут использоваться в качестве сокращений для определенных предложений. Напр. , «Джон и Чарльз — братья» можно представить как B . и «Джон и Чарльз усердно работают» могут быть обозначены как J и C . Логический оператор «и», как мы увидим, будет символизироваться как « «. В дополнение к предложениям логика высказываний содержит еще один элемент: операторы над предложениями. Предложения можно рассматривать как палочки из набора игрушек-мастеров. Операторы подобны соединительным блокам. Добавляя все больше и больше операторов, мы получаем более сложные структуры. Для оценки утверждений нужно выучить только одно условие: » Чтобы узнать истинностное значение предложения, которое получается в результате применения оператора к высказываниям, все, что нужно знать, это определение оператора и истинностное значение предложений использовал. »
		Отправляйте исправления или предложения по адресу [email protected] Прочитайте отказ от ответственности относительно этой страницы. 26.12.04 2004 г. Лицензия GFDL
		Аргументы | Язык | Заблуждения | Предложения  | Силлогизмы | Перевод | Символический
	.

[произошла ошибка при обработке этой директивы]

Формальная логика и диалектика

Формальная логика и диалектика

Значение логики Гегеля

Формальная логика, которая до Гегеля была логикой , увидела свое поле изучения как ограниченного законами, посредством которых истина одно предложение следует из другого.

Например, словами Джона Стюарта Милля:

.

Логика есть наука об операциях рассудка, подчинены оценке доказательств: как процесс само продвижение от известных истин к неизвестным, и все другие интеллектуальные операции в той мере, в какой они вспомогательные. Это включает в себя, следовательно, операция Именования; .. Определение и классификация. [ Система логики , Дж. С. Милль]

Ильенков поясняет в своем сочинении о Гегеле, что революция Гегеля в логике произошло за счет расширения области логики и области наблюдения, на котором можно было бы проверить справедливость логики, от логики, проявляющейся в артикуляции предложений, к проявление логики в всех аспектах человеческой практики.

Формальная логика также выводит за рамки своей компетенции доказательство первичных или аксиоматические истины, или вывод категорий, посредством которых средства которых предложения указали на реальность. Гегель также расширил логика, чтобы включить критику или вывод этих категорий.

В любом случае логика имеет дело только с истиной , то есть с мышлением, которое соответствует или отражает внешний мир мысли, вне индивидуального сознания, и далее, критерием истинности логики является та степень, в которой она обеспечивает адекватное руководство к практике.

Подобно тому, как мысль отражает материальный мир и ничего не может вместить в себя. которого еще нет в материальном мире или, по крайней мере, условия ее формирования, человеческая практика есть практика материальных людей в материальном мире, и может быть ничего в человеческой практике, что фундаментально противоречит природе.

Таким образом, при разработке наиболее общих закономерностей развития социальной практики, Гегель обязательно открыл законы, которые не являются уникальными или специфическими для человеческого состояния, но являются объективными, материальные законы природы. Итак, глядя не только на то, о чем думали думал о себе, но при том, что он делал, Гегель не только и не так много открыли гораздо более богатые средства понимания отдельных научное сознание, но, что более важно, законы, управляющие развитие коллективной духовной, культурной или общественной деятельности и материального мира в целом.

Гегель вовсе не опровергал и не искоренял формальную логику, он просто определил его имманентные пределы и вскрыл его внутренние противоречия, своего происхождения и своих пределов, за которые он обязательно переходил во что-то другое, его жизнь и его смерть; он отрицал это; он снял это: формальное логическое одновременно преодолено и сохранено с диалектической логикой.

Формальная логика наиболее сильна, когда ее рассматривают как что-то малополезное, что можно произвольно нарушать, но на наоборот, когда он используется с максимальной последовательностью и тщательности, но с сознанием ее имманентных пределов и понимание того, когда и как оно вытесняет само себя. Ничего такого более бесполезна, чем некритическая игра с логическим противоречием и несоответствие, оправдываемое бездумной и поверхностной отсылкой к диалектике.

Хотя я думаю, что Джордж Новак совершенно неправ в своем обращении формальной логики в Логика марксизма , его основной начальный Утверждение о справедливости формальной логики глубоко верно:

Какие характеристики материальной реальности отражены и концептуально воспроизводится в этих формальных законах мышления? Закон тождества формулирует тот материальный факт, что определенные вещи и черты вещей, сохранять и сохранять узнаваемое сходство среди все их феноменальные изменения. Везде, где существует существенная преемственность в действительности применим закон тождества. …

Мы не могли бы ни действовать, ни мыслить правильно без сознательного или бессознательно подчиняясь этому закону. Если бы мы не могли узнать себя как один и тот же человек от момента к моменту и изо дня в день — а есть люди, которые не могут, которые в силу амнезии или чего-то другого психические расстройства потеряли сознание самотождественности — мы бы потерялись. Но закон тождества не менее справедлив для остальной вселенной, чем для человеческого сознания. Это относится каждый день и везде к общественной жизни. Если бы мы не могли распознать один и тот же кусок металла во всех его различных операциях, мы не мог продвинуться очень далеко с производством. Если фермер не мог следовать зерно, которое он сеет из семени в колос, а затем в муку, земледелие было бы невозможно. …

Младенец делает большой шаг вперед в понимании природы мира, когда он впервые осознает тот факт, что мать, которая его кормит, остается одним и тем же человеком на протяжении различных акты кормления. Признание этой истины есть не что иное, как частный случай признания закона тождества. [ Логика марксизма , Лекция 1, часть 4]

Закон Тождества

Таким образом, (продолжая нашу тему приближения к гегелевской Логика с точки зрения теории познания) восприятие начинается когда мы узнаем что-то , когда мы что-то воспринимаем как настойчивый в потоке «одна чертовка после другой» непосредственного восприятия, когда мы можем сказать «А = А». Вся формальная логика покоится на этом тождестве вещь сама с собой, с признанием непрерывности чего-либо. Вся формальная логика разваливается, когда «А не = А».

Совершенно очевидно, что тождество есть абстракция , и:

Если это офис сравнения, чтобы уменьшить существующие различия к Идентичности, наука, которая наиболее совершенно выполняет эту цель это математика . Причина этого в том, что количественные разница есть только разница совершенно внешняя. … [ Короткая логика , § 117n] … Если количество не достигнуто действием мысли, но взятые некритически из нашего обобщенное представление о нем, мы склонны преувеличивать диапазон его достоверности или даже возвысить его до абсолютной категория. И что такая опасность реальна, мы видим, когда заголовок из точная наука ограничивается теми науками, объекты из которых могут быть подвергнуты математическому расчету. [ Короткая логика , § 99n]

Но столь же очевидно, что тождество, количество и математика являются абстракциями, которые отражают материальную реальность , а тождество является абстракцией, которая, как указывает Новак, является фундаментальной основе человеческой практики. В то время как в некотором ограниченном смысле мир воссоздается заново каждую минуту, мы действуем, на практике , для большую часть времени , прежде всего на основе преемственности.

Как указано в приведенной выше цитате из The Shorter Logic , наука об идентичности — это математика. Математика это наука в котором формальная логика применяется в особом смысле, и в этом особого смысла, соблюдается непреклонно и с непререкаемым эвристическая ценность.

В собственно математике следует помнить, что «А» указывает абсолютно на что угодно; это довольно бессмысленно (Бытие = Ничто) и в предложении «А = А» рабочий символ — «=». Предложение пустое тавтологией, поскольку считается, что она делает какое-либо утверждение о A. Если мы сделаем нематематическую интерпретацию «=», например, «этот А такой же, как этот А», то утверждение является тавтологией, если мы допускаем, что А относится к одному и тому же. Если мы допустим, что первое А отлично от второго А, то утверждение реально, действительно и диалектично, но не математическо. (Но, конечно, если бы математика была исключена из того, что в конечном счете интерпретируется или применяется «не математически», это быть совершенно лишенным содержания).

Это вовсе не означает, что в математике отсутствует диалектика. Немыслимо. Движение от одного предложения к другому всегда диалектическим и лишь иногда и в известном отношении формальным. Но без формальной логики нет математики. Пока это вздор возводить математику в образец для всех наук (как это было принято в прошлые века), бессмысленно девальвировать математика как наука.

Но формальная логика вовсе не ограничивается математикой. Первый Условием достоверности или релевантности формальной логики является относительная достоверность тождества в отношении точного движения рассматриваемого познания. И Гегель, конечно, здорово повеселился с борьба математики с изобретением исчисления. Лейбниц и Ньютон создал этот фантастически мощный прибор (который среди прочего является основным методом, с помощью которого законы Природа может быть выражена в общей форме, и которая легла в основу за новую революцию в прикладной математике и естествознании), только откровенным блефом над выкрикиванием формальных логических ловкость рук. Только в последние годы математика смог обеспечить формальный логический вывод исчисления от его основ. Лейбниц и Ньютон мыслили диалектически, и пусть потомство позаботится о формальном доказательстве своего открытия.

На практике мы рассматриваем мир не только как подверженный изменениям, но с учетом нашего изменения . В научном мышлении мы рассматриваем объекты критически, как подлежащие анализу и синтезу. К насколько мы критически относимся к объекту, относимся к реальности как к что-то изменить, то мы специально отвергаем закон тождество и утверждают, что «A not = A», и формальная логика делает перерыв. Здесь мы не можем понять букву «А» с направлена ​​на то, чтобы использовать его в других отношениях, но направлена революционизировать его и раскрыть из его одежды новые А, А-, если хочешь.

В главе об отражении в «Логике » Гегель рассматривает с Законом Тождества, Законом Исключенного Середины, Законом Непротиворечия и Закон достаточного основания как ряд предложений или отношений которые разворачиваются, отрицая друг друга в ряде диалектических этапы. Эти моменты обсуждались выше в Значение Отражение. А пока я хотел бы подумать об их статусе в формальной логике, ибо в то время как все читатели Гегеля девятнадцатого века был бы обучен формальной логике, что, вероятно, не дело сегодня.

Закон исключенного третьего

Закон исключенного третьего гласит, что если предложение А не верно, то его отрицание «не-А» истинно. Даже в пределах в узких пределах формальной логики этот «закон» ненадежен, и здравый смысл подтвердит мнение, что эта линия рассуждений ненадежен. Голландский логик Бруувер реконструировал математические логика, исключив из правила закон исключенного третьего книгу и показал, что математика немногим хуже для потеря. Действительно, квантовая логика Вайзекера основана на включение значения истинности «неопределенного».

Закон непротиворечия

Закон непротиворечия гласит, что как предложение А, так и и его отрицание, не-А, не может быть истинным в пределах одного «теория», в сфере действия закона тождество, «А = А». Этот закон действительно является основополагающим для формальная логика.

Общеизвестно, что последовательное применение основных набор формальных логических принципов приводит к «антиномиям», или плоские противоречия. Это открытие помогло Гегелю революция в логике, но и привела к дальнейшему развитию в пределах формальная логика. В настоящее время условия, порождающие такие противоречия хорошо известны, и формальная логика способна действовать при этом надежно избегая таких «плохих» противоречий путем введение ряда запретов на разряды.

На первый взгляд может показаться, что объяснение этих ограничений имело бы большое значение, но мы не будем заниматься вопросом здесь.

Закон достаточного основания

В той мере, в какой можно сказать, что Закон Достаточного Основания существует в формальной логике это так называемый закон разрешимости, который любое утверждение, справедливое в рамках данной теории, может быть доказано или опровергнуто. В 1931 году Курт Гёдель опроверг этот тезис в его знаменитая теорема Гёделя. Это открытие вызвало огромный кризис в мире математики и логики, но он может вряд ли можно сказать, что она сводила формальную логику к нулю.

Тем не менее замечание Гегеля относительно способа действия от недоказанных аксиом очень уместна и существенно отличает диалектическая логика из формальной логики:

Формальная логика просит эти науки не принимать их предмет как это сразу дано; и все же сама устанавливает закон мысль, не выводя ее, иначе говоря, не проявляя его посредничество. [ Короткая логика § 121n]

Далее, абсолютный статус этого закона отвергается в квантовой теории. механики, хотя Эйнштейн до конца своих дней считал, что эта теория не может считаться полным, и поэтому в дальнейшем оснований для поведения квантово-механических систем ждали открытие. Эта тема достойна дальнейшего обсуждения, но преследоваться здесь не будут.

Однако, что более важно, теория сложности продемонстрировала что явления в сложной системе следуют из внутренней структуры системы, которая в принципе не может быть выведена из этого внутреннего структурировать методами формальной логики. Эмпирически установленный ограничение формальной логики более или менее широко признается за пределами профессиональных математиков, и в целом совпадает с общепризнанная ошибочность редукционизма .

Понятие, суждение и силлогизм —

Универсальный, частный и индивидуальный

Другим компонентом формальной логики является силлогизм, который Гегель подвергается критике в учении о понятии.

Силлогизм — это метод вывода, впервые разработанный формальными логика, в которой из двух утверждений выводится третье. Например, «Все А есть В», «С есть А», , следовательно, «С есть Б».

Всеобщее, частное и индивидуальное являются категориями, тесно связанные с силлогизмом:

• Всеобщее есть истина, применимая всегда и везде, такие как «А», «В» (понятия) и «Все А являются B» в приведенном выше примере, поскольку аспекты знания итог длительного периода общественного развития;
• Индивидуум («С» в приведенном выше примере) — это знание как данное в непосредственном восприятии;
• Частное — вид соединения индивидуального и всеобщего, конечная, но обобщенная истина («С есть А» и «С это б»).

Все вышеперечисленные концепции претерпели значительное развитие. в истории философии, и вышеизложенное лишь указывает на общий объем понятий.

Гегелевская критика формально-логического понятия силлогизма очень глубокий. Во-первых, его понимание Понятие («А» и «Б») принципиально противоречит формальной логике, как и его понятие о суждении (« — это »). Принимая во внимание, что для формальной логики Универсальное, Индивидуальное и Частное существуют бок о бок и независимо, во внешнем отношении друг к другу, для Гегеля эти категории моменты развития, существенно и родственно связанные друг с другом.

Во-вторых, его понятие о понятии проявляется в практиковать этот более глубокий подход и обеспечивает архетипическое демонстрация своего метода вывода понятия из собственного имманентная природа, а не по внешнему определению как абстрактное универсальный.

В-третьих, он предвосхищает материалистическую критику логике, показав, что силлогизм и его категории всеобщее, особенное и индивидуальное суть «формы понятия, жизненный дух реального мира».

Логику понятия обычно трактуют как науку о форме. только и понимаются как имеющие дело с формой понятия, суждения, и силлогизм как форму, нисколько не касаясь вопроса правда ли что-нибудь. Ответ на этот вопрос предполагается зависеть только от содержания. …. Наоборот, они действительно являются, как формы понятия, жизненным духом действительного мира. По отношению к действительному верно только то, что истинно в силу этих формы, через них и в них. Однако до сих пор правда о эти формы никогда не рассматривались и не исследовались сами по себе учитывать не более чем их необходимую взаимосвязь. …

Понятие как понятие содержит три следующих «момента» или функциональные части. (1) Первый — Универсальность — значение что оно находится в свободном равенстве с самим собой в своем специфическом характере. (2) Второй — Особенность — то есть конкретное характер, в котором всеобщее остается безмятежно равным сам. (3) Третий — Индивидуальность — означает отражение в себя конкретных признаков универсальности и особенности; это отрицательное самоединство имеет полную и изначальную определенность, без какой-либо потери своей самотождественности или универсальности. [ Короткая логика , § 162]

Понятие и абстрактная универсалия

Для формальной логики форма категории считается лежащей за пределами своего домена, за небольшим исключением в отношении ограничений которые предписаны во избежание антиномий. Ближайшая формальная логика может прийти к пониманию понятия «класс», что указывает с помощью некоторых эффективных средств, лиц, которым можно отнести к «абстрактным универсалиям». «Аннотация универсальное» есть то свойство, которое является общим для многих индивидуумов 9.0003

Понятие обычно ассоциируется в нашем сознании с абстрактным общность, и поэтому его часто называют общим зачатие. Соответственно, мы говорим о понятиях цвета, растения, животных и т. д. Предполагается, что их можно получить, пренебрегая особенности, которые отличают разные цвета, растений и животных друг от друга и сохраняя те общие в торговый центр. … Но универсальность понятия есть не просто сумма признаков, общих для нескольких вещей, с которыми сталкивается конкретный который наслаждается собственным существованием. Это, наоборот, самоопределение или самоопределение, и с непоколебимой ясностью находит себя дома в своей противоположности. Ради обоих познания и нашего практического поведения крайне важно, чтобы реальное всеобщее не следует смешивать с тем, что есть просто проводится совместно. …

Всеобщее в его истинном и всеобъемлющем значении есть мысль которому, как мы знаем, потребовались тысячи лет, чтобы заставить его войти в сознание мужчин. [ Краткая логика , § 163n, Субъективное понятие]

Неудивительно, что Гегель считает логику, основанную на понятии, абстрактной. универсальный как просто «зевок»! Это очень тривиальные вещи, а когда не тривиально обычно ложно. При тщательной разработке до чрезвычайно высокого уровня сложности, как в развитых отраслях математики, она может дать материал, представляющий некоторый интерес, но относится к очень ограниченной области истины, что совпадает с область, отмеченная степенью действия Закона о Идентичность, и широко узнаваемая как то, что известно в математике как теория множеств, теория групп и так далее.

Классы (абстрактные универсалии) в математике ведут своего рода «двойное существование», когда-то как «набор» «элементов» обладающее данным свойством и, во-вторых, как свойство, составляющее понятие класса или множества. Например, «рабочий класс» является (для формалиста), с одной стороны, списком имена сотрудников взяты из записей налоговой инспекции и с другой — определение «люди, которые зарабатывают себе на жизнь заработная плата или жалованье».

Опять же, как неотъемлемая, хотя и далеко не исчерпывающая, составляющая математики абстрактная универсалия имеет свое место. Но в контекст творческой социальной или естественной теории, который является очень небольшим место.

Но опять же, применимы те же комментарии, что и выше. Поскольку «А = А», так как отношения между вещами остаются неизменными, так как вещи, о которых мыслится, остаются отдельными и отчетливыми, а вещи остаются тождественными своему понятию, понятию абстрактно-всеобщего сохраняет актуальность. Все гегелевские Логика составляет более глубокое понятие «понятие», и с точки зрения Гегелевского понятия, легко увидеть, насколько ограничены возможности формальной логики. понятие Абстрактной Универсалии. Эти аспекты формальной логики рассматривается в части III Гегеля Логика , Доктрина Понятие.

Вопрос в том, как понять и распознать границы формальная логика.

Пределы и отрицание формальной логики

Конечно, на этот вопрос нет простого формального ответа. В противном случае формальная логика уже открыла бы его!

Вся гегелевская Логика учит нас, как определять пределы понятия или предложения. Например, в учении Бытия мы изучаем диалектику Меры, которая выражает ограничения количества и качества. Статья Троцкого Азбука Материалистическая диалектика фокусируется на этом ограничении формальных логика, что каждое понятие имеет свои пределы «терпимости». В «Учении о сущности» мы изучаем, среди прочего, диалектику формы и содержания. Короче говоря, Гегель доказывает и учит «искусство обращения с понятиями». Как Гегель не раз жалуется, формальная логика некритически принимает не только то, что он видит в объективном мире, но категории, которые он использует для схватывать реальность.

В раскрытии ограничений формальной логики из ее «зародыша» в законе тождества — «А = А», Гегель доказывает как следует понимать все понятия, а не простыми абстрактными универсальными определения, а как диалектический, внутренне противоречивый субъект-объект отношения, которые представляют собой не что иное, как моменты, отвлеченные или вырванные из из постоянно движущейся и развивающейся реальности. Наши понятия мира может лишь адекватно приблизить мир к насколько наши понятия отражают это существенное движение и жизнь.

Например, легко сказать: «А есть Б», «Все В есть С», поэтому «А есть С», но что такое В? «Артур — полицейский», «Полицейские работают на заработная плата», следовательно, «Артур — рабочий», следовательно, . ..и т.д., и т.п. И вы можете толковать определения сколько угодно как хотите, делая их «точнее», и это делает приблизит вас хоть на йоту к пониманию социальных отношений между отдельными лицами. «Рабочий» — физическое лицо и . социальная категория. Социальные категории имеют существование и законы, которые нельзя отождествлять со многими индивидуальными отношениями. Рабочий класс не может быть вытащен из записей налоговой инспекции список всех тех, кто получил заработную плату в прошлом финансовом году. Всего не равно сумме частей.

Сложность, математика и диалектика

Это первое ограничение формальной логики, что может назвать его «внутренней границей». второй , его «внешняя граница» наложена сложностью. Если система достаточно сложна и «богата», то явления, возникающие в нем, не могут быть сведены к свойствам компонентов подсистем системы. Например, довольно хорошо известно, что попытки макроэкономистов смоделировать мир экономия с использованием, например, до 4000 одновременных дифференциальных уравнений, неизменно не в состоянии предсказать какие-либо существенные явления вне обычных приливов и отливов индикаторов.

За последнее десятилетие появилась новая наука, известная как «Сложность». Эта наука использует компьютерное моделирование для эмпирического исследования исход очень мало, очень простые формальные правила, регулирующие взаимодействие большого количества составных подсистем, или личности, в системе.

Необходимость эмпирической науки для изучения этих явлений объясняется следствием теоремы Гёделя, открытым Алан Тьюринг, основатель компьютерных наук: в любом вычислительном системе существует хотя бы один алгоритм, результаты которого не могут в принципе предсказуемо. Это немного трюизма для всех кто запрограммировал сложную компьютерную систему!

Значение для понимания отношения формального и диалектического логика глубокая. В любой сложной (т.е. реальной) системе явления выставленные возникают из отношений составных систем способом, который в принципе не может быть выведен из формального логический анализ; и это верно даже там, где атомарные отношения абсолютно просты и статичны.

Такие сложные системы первоначально делятся на два типа: те, в которых атомарные отношения приводят к статической или повторяющейся структуре в массе, где механическое применение формальных логических анализ действителен, а те, которые ведут к хаосу, где Закон больших чисел и теории вероятностей. Простая мера полученный из атомарных отношений, указывает, является ли система может быть структурированным или хаотичным. Но есть и третий случай, пограничный или переходный случай, когда атомарные отношения привести к «сложному поведению», богатому по форме, прыжкам, внезапным преобразования и динамические структуры, все в принципе непредсказуемы с точки зрения формальной логики.

Кроме того, эмпирически установлено, что при подсистемы способны воспроизводиться и видоизменяться в некоторых образом (нормальное состояние любого значимого «реального» системы), тем самым изменяя баланс атомарных отношений, система со временем либо «умрет», либо тяготеет к сложная переходная система, из хаотической или структурированной состояние к сложному, от устойчивой, предсказуемой системы к порождая сложные, «революционные» явления. Эмпирический компьютерное моделирование воспроизвело аналоги систем (неврологические или социальные), которые изучают происхождение жизни от «первобытной суп», точечная эволюция и т. д.

Ученые, занимающиеся этой работой, выразили серьезное озабоченность состоянием мировой экономики, особенно после конец относительно стабильного периода холодной войны и, как правило, стать поклонниками Гераклита или даосизма; интересно, ни один из они до сих пор признали, что очень точная наука о логика сложности уже существует в Логике Гегеля.

Формальная логика в природе и обществе

Как отмечалось выше, формальная логика отражает относительную устойчивость в природе. Формальная логика прекрасно работает в физике, пока атомы твердые шарики; но как только квантовое поведение проскальзывает в картинку и частицы «прыгают», превращаются в одну в другую, исчезают и вновь появляются, ведут себя как волны и так далее. на формальная логика попадает в беду.

Но надо заметить, ибо очень уж физика и химия даже сегодня модель атома «жесткий шар» весьма актуальна.