Разное

Дедукция и индукция примеры из жизни: Какие можно привести примеры индукции и дедукции?

ОпубликованоАвторalexxlab

Урок 8. Типы рассуждений

В предыдущих уроках мы поговорили о разных логических операциях, которые составляют важную часть любого рассуждения. Среди них были операции над понятиями, определения, суждения и умозаключения. Значит, на данный момент должно быть ясно, из каких компонентов рассуждения состоят. Однако мы ещё нигде не касались вопросов о том, каким образом может быть организовано рассуждение в целом и какими в принципе бывают типы рассуждений. Это и станет темой последнего урока.

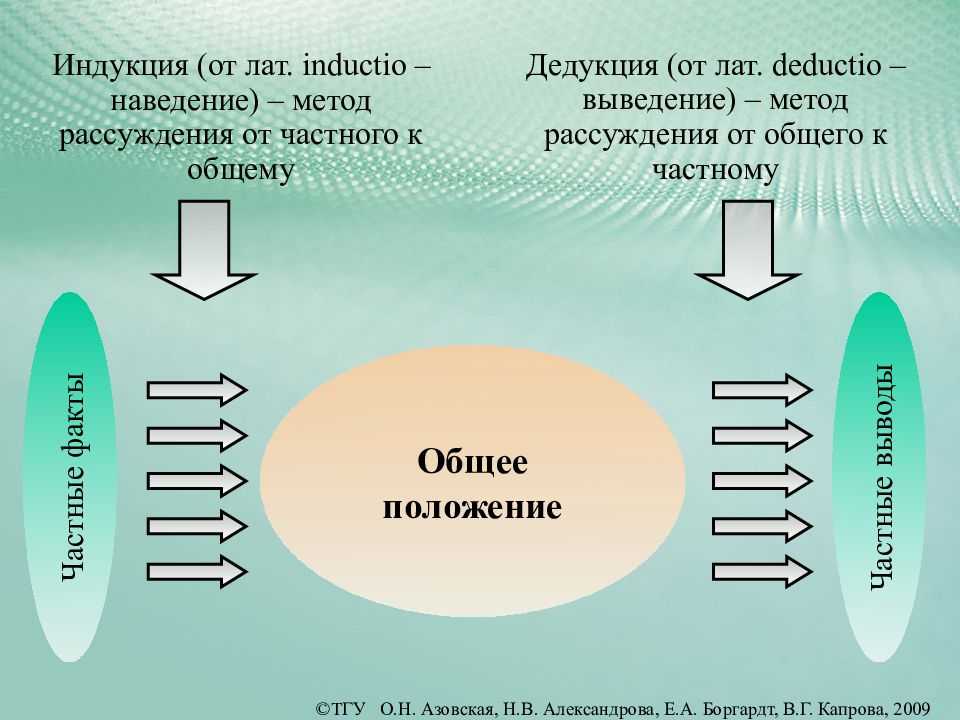
Начнём с того, что рассуждения делятся на дедуктивные и правдоподобные. Все виды умозаключений, рассмотренные в предыдущих уроках: умозаключения по логическому квадрату, обращения, силлогизмы, энтимемы, сориты, – представляют собой именно дедуктивные рассуждения. Их отличительный признак состоит в том, что посылки и заключения в них связаны отношением строгого логического следования, в то время как в случае правдоподобных рассуждений подобная связь отсутствует. Сначала поговорим подобнее о дедуктивных рассуждениях.

Оглавление:

  • Дедукция
  • Правдоподобные рассуждения: индукция и аналогия
  • Индукция
  • Аналогия
  • Проверочные вопросы на усвоение материала

Дедукция

Только что было сказано, что дедукция характеризуется наличием строгого логического следования между посылками и заключением. Что это означает? Прежде всего, нужно сказать, что это формальное отношение – в том смысле, что оно относится к логическим формам посылок и заключения. Логики выявили, что существуют такие комбинации логических форм посылок и заключения, когда при логической истинности посылок невозможно, чтобы заключение оказалось ложным. Это и было названо отношением логического следования. Важно помнить, что в данном случае речь идёт именно о логической, а не фактической истинности высказываний. Мы уже сталкивались с логическим следованием на примере правильных модусов силлогизмов. Модус первой фигуры Barbara является правильным вне зависимости от того, что именно мы подставим на место субъекта, предиката и среднего термина, то есть в нём посылки и заключение связаны отношением логического следования. Другое дело, если мы берём ложные посылки, то, конечно, и заключение будет ложным, но сам модус в этом не виноват: при фактической истинности посылок он всегда гарантирует истинность заключения, просто благодаря определённой комбинации входящих в него логических форм высказываний.

Далее, дедуктивные рассуждения в свою очередь могут быть прямыми и непрямыми. Опять же все рассмотренные нами умозаключения представляли собой примеры прямого способа построения дедукции. Прямые дедуктивные построения строятся таким образом, что мы непосредственно переходим от посылок к заключению. Практически все разновидности простых базовых умозаключений являются прямыми. Однако в более сложных случаях непосредственный переход от посылок к заключению не всегда возможен, поэтому приходится прибегать к различным приёмам, которые косвенным образом всё же позволяют обосновать тезис с помощью имеющихся аргументов.

Прямые дедуктивные рассуждения

Кроме уже описанных в предыдущих уроках умозаключений из силлогистики, существует ещё несколько распространённых типов прямых дедуктивных рассуждений, о которых мы считаем полезным рассказать.

Условно-категорические умозаключения – это умозаключения, в которых одна из посылок представляет собой условное высказывание вида «Если А, то В», а вторая – простое утверждение «А» или отрицание «неверно, что В». Существует два правильных вида условно-категорических умозаключений:

Modus ponens

  • Если А, то В
  • А
  • В

Modus tollens

  • Если А, то В
  • Неверно, что В
  • Неверно, что А
  • Если число делится на 4 без остатка, то оно делится и на 2 без остатка.
  • 8 делится на 4 без остатка.
  • 8 делится на 2 без остатка.
  • Если число делится на 4 без остатка, то оно делится и на 2 без остатка.
  • 5 не делится на 2 без остатка.
  • 5 не делится на 4 без остатка.

Разделительно-категорические умозаключения – умозаключения, где одна посылка представляет собой разделительное (дизъюнктивное) высказывание типа «А или В», вторая посылка – утверждение «А», «В» или отрицание «неверно, что А», «неверно, что В».

Существует несколько типов правильных дизъюнктивных умозаключений.

Modus tollendo ponens

  • А или В
  • Неверно, что А
  • В
  • А или В
  • Неверно, что В
  • А
  • «Ревизора» написал или Пушкин, или Гоголь.
  • Пушкин не писал «Ревизора».
  • Значит, «Ревизора» написал Гоголь
  • Юля читает книги или смотрит телевизор.
  • Юля не смотрит телевизор.
  • Следовательно, Юля читает книги.

Отметим, что modus tollendo ponens будет правильным независимо от того, является ли разделительная посылка строгой или нестрогой дизъюнкцией.

К разделительно-категорическим умозаключениям также относится modus ponendo tollens, однако он корректен только при строгой дизъюнкции:

  • Либо А, либо В
  • А
  • Неверно, что В
  • Либо А, либо В
  • В
  • Неверно, что А
  • Света купила либо красное платье, либо бирюзовое.
  • Света купила красное платье.
  • Тогда Света не покупала бирюзового платья.
  • Петя либо приходит на работу в офис, либо работает удалённо из дома.
  • Петя работает удалённо из дома.
  • Поэтому Петя не ходит на работу в офис

Условно-разделительные умозаключения представляют собой умозаключения, содержащие несколько условных и одну разделительную посылку. В зависимости от количества разделительных посылок, выделяют разные типы условно-разделительных умозаключений. Если умозаключение содержит две разделительные посылки, то его называют дилеммой, если три – трилеммой, но в принципе разделительных посылок может быть и больше. Мы рассмотрим только дилеммы.

Простая конструктивная дилемма

  • Если А, то С
  • Если В, то С
  • А или В
  • С
  • Если Маргарита обладает привлекательной внешностью, то у неё хорошие шансы выйти замуж.
  • Если Маргарита получила большое наследство, то у неё также есть хорошие шансы выйти замуж.
  • Маргарита обладает привлекательной внешностью, либо она получила большое наследство.
  • Маргарита имеет хорошие шансы выйти замуж.

Сложная конструктивная дилемма

  • Если А, то С
  • Если В, то D
  • А или В
  • С или D
  • Если Илья Муромец пойдёт направо, то он потеряет голову.
  • Если Илья Муромец пойдёт налево, то он потеряет коня.
  • Илья Муромец пойдёт направо или налево.
  • Следовательно, он потеряет голову или коня.

Простая деструктивная дилемма

  • Если С, то А
  • Если С, то В
  • Неверно, что А, или неверно, что В
  • Неверно, что С
  • Если Толик глуп, то он вложит всё своё состояние в денежную пирамиду.
  • Если Толик глуп, то он перепишет свою квартиру на мошенников.
  • Толик никогда не вложит всё своё состояние в денежную пирамиду и не перепишет свою квартиру на мошенников.
  • Значит, Толик не глуп.

Сложная деструктивная дилемма

  • Если С, то А
  • Если D, то В
  • Неверно, что А, или неверно, что В
  • Неверно, что С, или неверно, что D
  • Если Виктор дал верные показания, то убийцей должна быть Алина.
  • Если Сергей дал верные показания, то убийцей должен быть Антон.
  • Либо Алина, либо Антон не является убийцей.
  • Поэтому либо Виктор, либо Сергей дал ложные показания.

Непрямые дедуктивные рассуждения

Как уже было сказано непрямые дедуктивные рассуждения, или способы аргументации, задействуются, когда непосредственный переход от имеющихся посылок к заключению невозможен. Это не означает, что посылки и заключение не связаны логически: здесь также невозможна ситуация, когда посылки истинные, а заключение ложно. Просто прямое рассуждение представляет собой очень трудоёмкую задачу. Существует несколько основных способов непрямых дедуктивных рассуждений.

Рассуждение от противного должно быть многим знакомо со школьных уроков геометрии. Строится оно следующим образом: у нас есть тезис, который мы не можем доказать с помощью прямой дедукции, поэтому в качестве исходной посылки берётся его отрицание, далее из этого отрицания дедуктивно выводятся следствия, и на определённом шаге мы приходим к противоречию, то есть, например, на пятом шаге мы имеем высказывание «А», а на десятом – «неверно, что А». Как известно, логика не терпит противоречий, следовательно, можно сделать вывод, что отрицание нашего исходного тезиса было ложным, а сам тезис истинным. Что и требовалось доказать!

Сведение к абсурду очень похоже на рассуждение от противного.

 

Перебор случаев используется, когда нужно вывести некоторый тезис D из дизъюнктивной посылки «А или В или С». В этой ситуации можно сначала вывести D или А, потом вывести D из В, наконец вывести D из С. Если мы можем доказать, что D выводим из А, В и С по отдельности, то на основании этого перебора можно заключить, что D следует из «А или В или С». Нужно отметить, что метод перебора удобен в том случае, если количество альтернатив не очень большое: две, три, четыре. Если их больше, то лучше попробовать поискать другой метод доказательства.

Правдоподобные рассуждения: индукция и аналогия

Очевидно, что в реальной жизни у нас далеко не всегда есть исчерпывающая информация, на основании которой мы можем строить дедуктивные рассуждения. Чаще всего мы обладаем неполными знаниями о тех или иных предметах, явлениях и ситуациях. Поэтому большое значение для аргументации имеют правдоподобные рассуждения. Мы уже сказали, что в правдоподобных рассуждениях между посылками и заключением нет отношения строгого логического следования. Скорее, посылки как бы наталкивают нас на мысль о том, что из них было бы правдоподобно сделать определённый вывод. Переход от посылок к заключению носит не достоверный, а вероятный характер. Наиболее распространёнными типами правдоподобных рассуждений являются индукция и аналогия.

Индукция

Индукция – один из важнейших типов рассуждения, который используется как в повседневной жизни, так и в науках: физике, химии, биологии, социологии, медицине, политологии и т.д. Если бы люди не пользовались индукцией, то им вряд ли удалось бы вообще получить какие бы то ни было знания об окружающем мире. Она строится на том, что, исходя из имеющихся частичных знаний, мы строим выводы о ситуации в целом. Хотя такие выводы обладают лишь вероятной достоверностью, значение их огромно. Поговорим подробнее о разновидностях индукции.

Обобщающая индукция

Обобщающая индукция – это такое рассуждение, в ходе которого мы переходим от знания об отдельных предметах класса к знанию о классе в целом, то есть переходим от единичных утверждений к общим.

В качестве иллюстрации обобщающей индукции рассмотрим следующую ситуацию: представьте, что вам срочно нужно сделать банковский перевод через какой-нибудь банк в воскресенье. Вы приезжаете в одно отделение банка, и оно закрыто. Потом вы приезжаете в другое отделение банка, оно тоже закрыто, в третье, в четвёртое – та же картина. На основании этого вы можете сделать вывод, что ни одно из отделений банка не работает в воскресенье. Это и будет обобщающая индукция. От единичных высказываний «Отделение 1 закрыто в воскресенье», «Отделение 2 закрыто в воскресенье», «Отделение 3 закрыто в воскресенье», «Отделение 4 закрыто в воскресенье» мы перешли к общему утверждению «Все отделения банка закрыты в воскресенье». При этом такой вывод правдоподобен, но не достоверен, так как вполне может обнаружиться, что существует отделение 5, которое как раз было открыто.

Различают полную и неполную обобщающую индукцию. Полная индукция – это рассуждение, в котором вы перебираете все элементы класса и на основании этого перебора делаете вывод обо всём классе предметов. Представьте, что у вас в ящике лежат пять пар носков. Вы проверяете первую пару и обнаруживаете, что она дырявая, потом вторую, опять обнаруживаете, что она дырявая, потом третью, четвертую и пятую, и также обнаруживаете, что они дырявые. В результате вы можете сделать вывод: «Все носки в этом ящике дырявые». Такой вывод будет уже не просто правдоподобным, но достоверным, так как вы действительно проверили все носки в ящике и установили, что каждый из них имеет дырку. Однако далеко не всегда у нас есть возможность проверить все предметы класса, особенно если речь идёт об очень больших классах: люди, звёзды, страны, языки, школьники, рабочие и т.д. Когда строятся обобщающие рассуждения о таких классах, то производится неполная индукция: на основании перебора лишь части объектов класса делается заключение о классе в целом. Предположим, вы собрались продавать деревянные украшения. Вы нашли мастера по дереву, который сделал для вас пять тысяч деревянных браслетов. Очевидно, что вы не можете физически проверить все пять тысяч браслетов. Вы берёте двести произвольных браслетов и проверяете их качество. Если с ними всё в порядке, то вы делаете заключение, что все браслеты соответствуют качеству. Такая индукция будет неполной, но с большой вероятностью ваш вывод будет верным.

Иногда к разновидностям обобщающей индукции также относят так называемую индукцию «к следующему за». Она строится следующим образом: на основании знания о части предметов класса, делается предсказание, что следующий предмет из этого класса, тоже будет обладать выявленным свойством. Предположим, вы звоните в справочную службу аэропорта. На сайте указано пять телефонов. Вы позвонили по первому, вам никто не ответил, по второму, опять никто не ответил, по третьему тоже никто не ответил. Тогда вы делаете заключение: «По ходу дела там вообще сегодня никто не работает, наверное, по четвёртому и пятому телефону мне тоже никто не ответит». Хотя такая индукция широко распространена в повседневной жизни и обладает высокой вероятностью, она не относится к правильным способам рассуждения. Ярким подтверждением этому служит Эвбулидов парадокс кучи: одно зерно – это ещё не куча, два зерна – это тоже не куча, три зерна – не куча, но последовательно прибавляя по одному зерну десять тысяч раз, мы получим, что и десять тысяч зёрен – это не куча, что абсурдно. Поэтому индукции «к следующему за» лучше избегать и не попадаться на её удочку в руках нечестных собеседников.

Исключающая индукция

Исключающая индукция – это индукция, имеющая своей целью установить причинные связи между событиями.

Называется она исключающей, потому что осуществляется следующим образом: предположим, имеется событие А, и мы хотим установить его причину. Допустим, у нас есть пять предшествующих А событий: В, С, D, E, F. С помощью исключающей индукции мы исключаем те из них, которые не подходят на роль причины А, и тем самым находим то единственное событие, которое подходит на роль причины А.

Например, в холодильнике внезапно опустела банка с вареньем. Это будет событием А. Ему предшествовали следующие события: (В) дети играли без присмотра на кухне; (С) муж самостоятельно делал себе завтрак; (D) пёс Бублик научился открывать холодильник; (Е) соседка заходила за солью; (F) в Исландии произошло извержение вулкана Эйяфьятлайокудль.

Соответственно, с помощью исключающей индукции мы можем установить, какое именно из этих событий было причиной А. Как же это сделать? Естественно, если индукция производится путём исключения, то должны быть правила, предписывающие, по каким параметрам то или иное событие отбрасывается. Их называют правилами элиминации:

  1. Если известно, что при отсутствии события В событие А всё же имело место, то событие В не является причиной А.
  2. Если известно, что при наличии события В событие А происходит не всегда, то событие В не является причиной А.
  3. Если известно, что при изменении характеристик события В характеристики события А остаются неизменными, то событие В не является причиной события А.
  4. Если известно, что характеристики события В неизменны, а характеристики события А изменились, то событие В не является причиной события А.

Начнём расследование. Посмотрим на первое правило и событие F: вулкан Эйяфьятлайокудль спал двести лет, а банки с вареньем в это время становились пустыми регулярно во многих семьях мира. Значит, событие F не является причиной. Теперь обратимся ко второму правилу и событию Е: у соседки соль закончилась уже месяц назад, она заходила уже как минимум раз пять, но варенье в предыдущие разы не пропадало. Поэтому событие Е тоже не является причиной пропажи варенья. Возьмём правило три и событие D: на холодильник установили специальное приспособление, не позволяющее псу Бублику туда лазить, но варенье всё равно пропадает. Значит, событие D можно тоже отбросить. Наконец, возьмём четвёртое правило и событие B: дети по-прежнему играют на кухне без присмотра, но варенье после их игр на месте. Следовательно, событие В тоже не подходит на роль причины. Итак, методом исключения остаётся только событие С: муж слопал всё варенье.

Наверное, может возникнуть вопрос: почему подобная индукция является всего лишь правдоподобной, а не достоверной. Дело в том, что обычно в реальных ситуациях существует множество скрытых параметров, которые мы не контролируем, и возможный спектр событий, о которых мы не знаем. Например, в ситуации с вареньем вполне могло иметь место событие H: к нам прилетал Карлсон. Поскольку это событие не было известно, оно даже не попало в круг рассмотрения, но ведь вполне может оказаться, что варенье съел именно он. Поэтому философами и учёными были разработаны дополнительные методы, позволяющие сделать исключающую индукцию более точной:

  1. Метод сходства состоит в том, что наряду с рассматриваемым событием берутся предыдущие похожие ситуации: варенье уже пропадало полгода назад, а у соседки то же самое началось в прошлом месяце, а у пса Бублика пропала колбаса. Затем выявляется, что у них есть общего. Этот общий фактор и объявляется причиной, например: бомж Василий, живущий в подвале нашего дома, нашёл связку запасных ключей, потерянную домоправителем и теперь понемногу ворует из разных квартир еду.
  2. Метод различия строится на поочерёдном изъятии предшествующих событий. Из набора предшествующих событий B, C, D, E, сначала изымается В, потом С, потом D, и, наконец, Е. Выявляется, при отсутствии какого события событие А не происходит. Метод различия сыграл большую роль при открытии реликтового излучения Вселенной. Роберт Вудро Уилсон и Арно Элан Пензиас были астрофизиками и для своих наблюдений они решили использовать специальную антенну. Однако при её тестировании они обнаружили, что антенна даёт шум порядка 3 градусов Кельвина. Соответственно, они стали выяснять, что же было причиной этого шума. Сначала, они подумали, что это излучение нашей Галактики. Это можно было проверить просто с изменением времени наблюдения. Однако выяснилось, что излучение никак не зависит от времени суток и времени года. Значит, это не излучение нашей Галактики. Тогда учёные подумали, что сама антенна может производить этот шум. Дело в том, что в неё поселилась пара голубей. Голубей убрали, но излучение никуда не делось. Однако пока голуби жили в антенне, они успели её хорошенько загадить. Поэтому учёные предположили, что излучение вызвано голубиными экскрементами. Тогда антенну вычистили и оградили специальной сеткой.
    Излучение никуда не делось и на этот раз. В итоге им ничего не оставалось как предположить, что это излучение ранней Вселенной, оставшееся после Большого взрыва. Так они получили Нобелевскую премию.
  3. Метод сходства и различия построен на совмещении двух вышеописанных методов.
  4. Метод сопутствующих изменений заключается в том, что у событий, претендующих на роль причины, начинают варьировать характеристики. В результате определяют, при изменении какой характеристики какого события меняется событие А. Например, у менеджера Николая после новогоднего корпоратива очень болит голова. Предшествующие события: танцевал с Любочкой из отдела продаж, ел оливье, запускал фейерверк, пил водку, играл в фанты. Теперь начинаем варьировать предшествующие события. Если бы Николай станцевал с Любочкой не шесть танцев, а один, прошла бы у него голова? Нет. Если бы он съел не два тазика оливье, а одну тарелку, прошла бы у него голова? Нет, прошёл бы живот. И так далее, пока мы не доходим до водки: если бы Николай выпил не две бутылки водки, а две рюмки, прошла бы у него голова? О да. Значит, именно это и было причиной.

Аналогия

Аналогия – это такой тип рассуждения, в ходе которого в силу сходства двух предметов А и В, заключают о том, что предмет В должен обладать такими же характеристиками, что и А.

К примеру, возьмём племя тумба-юмба. Известно, что перед тем, как стать полноценным членом племени, каждый должен пройти обряд инициации, состоящий из множества испытаний. Теперь возьмём общество студентов какого-нибудь российского вуза. Во многом оно похоже на племя тумба-юмба: оно тоже устроено иерархически, есть молодняк (младшекурсники) и старейшины (пятикурсники, аспиранты), есть вождь (ректор), есть законы (устав) и т.д. Поэтому можно по аналогии предположить, что студенты российского вуза тоже должны проходить инициацию, состоящую из множества испытаний. И это действительно так: вступительные экзамены, посвящение первокурсников и т.д. Можно сказать, что наша аналогия удачна.

Рассуждения по аналогии часто встречаются как в науке, так и в повседневной жизни. Зачастую они, и правда, помогают прояснить какие-то важные вещи, могут выступать как хорошие эвристические приёмы. Однако не стоит увлекаться аналогиями: далеко не всегда они корректны. В частности, в племени тумба-юмба могут быть распространены жертвоприношения, но при всей схожести с устройством сообщества студентов, нет оснований полагать, что студенты тоже занимаются чем-то подобным.

Итак, мы рассмотрели основные типы рассуждений. По большому счёту, если вы знаете, как правильно ими пользоваться, то вы отлично вооружены практически для любой дискуссии и можете без страха пускаться в различные мыслительные построения. Конечно, мы не описали все возможные методы и способы рассуждений, например, мы полностью оставили за рамками повествования тему статистической индукции или гипотетико-дедуктивные рассуждения. Дело в том, что они тесно связаны с конкретными областями научного знания, и их абстрактные описания вряд ли имеют смысл. Также на теме рассуждений мы и завершаем наш курс. Естественно, логика простирается гораздо дальше тех тем, которые были здесь описаны. Мы выбрали только те разделы, которые наиболее полезны и легко применимы в каждодневных ситуациях. Мы надеемся, что, несмотря на это ограничение, уроки всё же помогли вам научиться мыслить и рассуждать логично. 

А теперь проверьте свое понимание рассуждений в нашем кейсе.