Формальная логика является: Логика формальная это

логика тест 2

Вопрос	Ответ	Верно
1.1. Логика – это:	наука о формах и законах правильного мышления	да
1.10. Укажите вид модальности высказывания «Запрещено переходить перекресток на красный сигнал светофора»:	деонтическая модальность	да
1.12. Формальная логика появилась:	в Античности	да
1. 13. Формальная логика является:	аристотелевской	да
1.14. Интуитивная логика – это:	стихийно сформированное в процессе жизненного опыта знание форм и принципов правильного мышления	да
1.16. Создателем логики считается древнегреческий философ:	Аристотель	да
1.17. Математическая или символическая логика появилась:	в XIX в.	да
1.19. Английский ученый конца XVI — начала XVII века, разработавший в произведении «Новый Органон» основы индуктивной логики:	Ф. Бэкон	да
1.2. С точки зрения формальной логики высказывание: «Все Снегурочки – это геометрические фигуры»:	построено по форме: «Все A есть B»	да
1.20. Английский ученый XIX века, развивший теорию научной индукции:	Д.С. Милль	да
1.3. Понятие – это	форма мышления	да
1.4. Истинность в логике означает:	соответствие мысли объекту	да
1. 6. Символическая логика является разделом:	математики	да
1.7.Что означает слово «logos»?	закон, мысль, слово, смысл.	да
1.8. Модальная логика относится к:	неклассической логике	да

Соседние файлы в предмете Логика

• #

  20.01.201912.88 Кб163логика тест 2.docx

• #

  20.01.201915.16 Кб91логика тест.docx

Логика формальная и диалектическая — Новости и политика как она есть! — ЖЖ

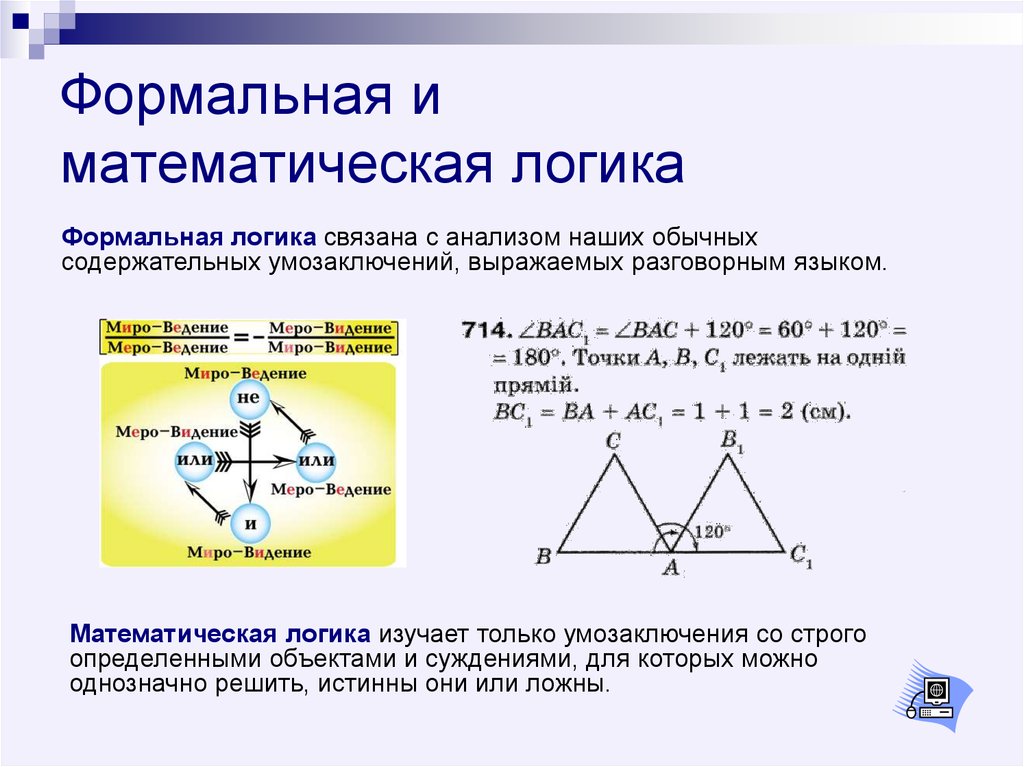
Различают логику формальную и диалектическую. Основателем традиционной формальной логики является, как известно, Аристотель. Термин «диалектическая логика» был введен в науку немецким философом, объективным идеалистом Г. Гегелем (1770 — 1831), впервые на идеалистической основе изложил основные законы и принципы диалектической логики как учения об общем развитии абсолютного духа.
Диалектическая логика — высшая степень в развитии логической науки, но она не отменяет и не поглощает формальную логику, последнюю не следует рассматривать как пройденный этап.
Диалектическая логика, как и формальная, изучает мышление, но с другой стороны и другими методами. Формальная логика — это логика, изучающая структуру мышления, исследует законы строения нашего мнения. Она призвана дать ответ, какой должна быть структура мысли, чтобы она была истинной и правильно воспроизводила действительность. Диалектическая логика исследует то, как в абстрактном мышлении, познает истину, действуют общие законы диалектики. Диалектическая логика изучает природу логических форм, их познавательную суть, раскрывает связь форм и законов мышления с законами объективного мира. Формальная логика исследует структуру готовых, сложившихся логических форм, не интересуясь их генетическими связями и взаимопереход, диалектическая же логика изучает формы мышления в их связях, переходах, в развитии, движении.
Ограниченность формальной логики состоит в том, что соблюдение одних только его законов для познания недостаточно, а не в том, будто она применяется только для познания каких-то элементарных связей и отношений, а при исследовании сложных явлений и связей Ее законы будто не действуют. В процессе познания на ступени абстрактного мышления имеет место постоянное сочетание двух моментов — формального соблюдения в каждом акте мысли и диалектического направления мысли в целом. И формальная, и диалектическая логика действуют повсюду, при познании любых объектов, как простых, так и сложных, при познании как относительно неподвижных предметов, так и предметов, движущихся меняются.
Не существует какой-то особой области элементарных отношений, которые бы узнавались с помощью только формальной логики, а диалектическая логика в них была бы неприменима, как не существует и такой области познания, где мышление подлежит только законам диалектической логики и где необязательно соблюдения требований формальной логики . Там, где соблюдаются законы формальной логики, действительно диалектическое мышление становится невозможным, там диалектика подменяется софистикой и эклектикой. Формальная логика обеспечивает определенность, ясность, последовательность мышления, то, без чего мышление как логический процесс по существу невозможно.
Сложным является вопрос о соотносительность формальной и математической логики. Существуют различные точки зрения. Одни считают, что современной формальной логикой является математическая логика и одной из других (общая, традиционная, классическая), кроме математической, в наши дни не существует. Математическая логика, возникла из потребностей математики, как ветвь традиционной логики, вобрала все ценное, достигнутое последней, и является новым, высшим этапом развития формальной логики.
Другие исходят из того, что существует общая формальная логика и логика математическая, что это хоть и близкие, но разные науки и их нельзя отождествлять. Каждая из этих наук имеет свой предмет, свои задачи и методы. Сторонники этого взгляда считают, что математическая логика не охватывает всех проблем формальной логики, поэтому она не может быть сведенной к математической логики, подменена ней.
Некоторые ученые относят математическую логику к математике и считают ее логике в собственном смысле.
Большинство современных логиков признают первую точку зрения, считают, что формальной логикой на современном этапе развития логической науки является математическая (символическая) логика. Приведем высказывания по этому вопросу отдельных авторов. Б. Рассел, например, отмечает: «Основное положение … состоит в том, что математика и логика тождественны, и я никогда не видел ни одного повода к изменению этой точки зрения» 3.
Этой же точки зрения придерживается и Г. Клаус. Он отмечает, что «существует только одна логика, изъятие математической логики из состава формальной логики невозможно и любая такая попытка связана с полным отрицанием современной логики — все устойчивое, все ценное, имеющееся в традиционной логике, находит себе место в современной логике и именно с ее помощью может быть понят лучше и глубже «4.
Дж. Шенфильд, наоборот, считает, что «логика изучает те типы умозаключений, которыми пользуется математика» 6. Такой же точки зрения придерживается и Б. Мендельсон: «Глубокие и опустошительные результаты Гегеля, Тарского, Рассела, Клини и многих других были богатой наградой за вложенную труд и завоевали для математической логики положения независимой ветви математики». Подобного взгляда на математическую логику придерживается и Р. Л. Гудстеин: «Математическая логика имеет своей целью выражение и систематизацию логических процессов, которые употребляются в математическом рассуждении, а также разъяснения математических понятий. Сама она является ветвью математики, которая использует математическую символику и технику … «7. «Предметом логики как философской науки, — отмечает Б. Фогараши, — является не только математическое, а все человеческое мышление. Но логика имеет математические основы, а математика — логические» 8.
Мышление человека не сводится и не может быть сведено к математическому мышлению, а значит, и логика как наука о мышлении, не может быть сведена к математической логике.

Интересно знать:

А вот если вам нужна пластиковая тара тогда самые выгодные предложения вы найдете на сайте aqua-solutions.ru

4 основных типа рассуждений

Проще говоря, логика — это «изучение правильных рассуждений, особенно в отношении выводов». Логика возникла как философский термин и теперь используется в других дисциплинах, таких как математика и информатика. Хотя определение звучит достаточно просто, понимание логики немного сложнее. Используйте логические примеры, чтобы научиться правильно использовать логику.

Пример формальной логики

Реклама

Определения логики

Логика может включать в себя действие рассуждений людей с целью формирования мыслей и мнений, а также классификаций и суждений. Некоторые формы логики также могут выполняться компьютерами и даже животными.

Логика может быть определена как:

«Изучение истин, полностью основанное на значениях содержащихся в них терминов».

Логика — это способ сделать вывод и инструмент, который вы можете использовать.

• Основой логического аргумента является его предложение или заявление.
• Предложение либо точное (истинное), либо неточное (ложное).
• Посылки — это предложения, используемые для построения аргумента.
• Аргумент затем строится локально.
• Затем из помещения делается вывод .
• Наконец, вывод сделан.

Определение логики в философии

Логика — раздел философии. В философии существуют разные школы логики, но типичная версия называется 9.0003 классическая элементарная логика или классическая логика первого порядка . В этой дисциплине философы пытаются отличить хорошее рассуждение от плохого.

Определение логики в математике

Логика также является областью математики. Математическая логика использует пропозициональных переменных , которые часто являются буквами, для представления пропозиций .

Типы логики с примерами

Вообще говоря, существует четыре типа логики.

Неформальная логика

Неформальная логика обычно используется в повседневных рассуждениях. Это рассуждения и аргументы, которые вы приводите в своем личном обмене мнениями с другими.

• Помещение: Никки увидела черную кошку по дороге на работу. На работе Никки уволили.

  Вывод: Черные кошки — к несчастью.

  Объяснение: Это большое обобщение, которое невозможно проверить.

• Предпосылки: Нет никаких доказательств того, что пенициллин вреден для вас. Я использую пенициллин без каких-либо проблем.

  Вывод: Пенициллин безопасен для всех.

  Объяснение: здесь личный опыт или отсутствие знаний не поддается проверке.

• Помещение: Моя мама знаменитость. Я живу с мамой.

  Вывод: я знаменитость.

  Пояснение: Доказательство славы — это нечто большее, чем предполагать, что она сотрется.

Реклама

Формальная логика

В формальной логике вы используете дедуктивное рассуждение, и посылки должны быть верными. Вы следуете предпосылкам, чтобы прийти к формальному заключению.

• Помещения: Каждый житель Квебека проживает в Канаде. Все жители Канады живут в Северной Америке.

  Вывод: Каждый житель Квебека живет в Северной Америке.

  Пояснение: Здесь представлены только достоверные факты.

• Предпосылки: У всех пауков восемь ног. Черные вдовы — это разновидность пауков.

  Вывод: у черных вдов восемь ног.

  Объяснение: Этот аргумент не вызывает возражений.

• Помещение: У велосипедов два колеса. Ян катается на велосипеде.

  Вывод: Ян едет на двух колесах.

  Объяснение: Посылки верны, как и заключение.

Символическая логика

Символическая логика имеет дело с тем, как символы соотносятся друг с другом. Он присваивает символы словесным рассуждениям, чтобы можно было проверить достоверность утверждений с помощью математического процесса. Обычно вы видите этот тип логики, используемый в исчислении.

Пример символической логики:

• Предложения: Если все млекопитающие кормят своих детенышей молоком матери (A). Если все кошки кормят своих детенышей материнским молоком (Б). Все кошки млекопитающие (С). Ʌ означает «и», а символ ⇒ означает «подразумевает».
• Заключение: A Ʌ B ⇒ C
• Объяснение: Предложения A и B приводят к заключению C. Если все млекопитающие кормят своих детенышей материнским молоком, а все кошки кормят своих детенышей материнским молоком, это означает, что все кошки являются млекопитающими. .

Математическая логика

В математической логике вы применяете формальную логику к математике. Этот тип логики является частью основы логики, используемой в компьютерных науках. Математическая логика и символическая логика часто используются взаимозаменяемо.

Реклама

Типы рассуждений с примерами

Каждый тип логики может включать дедуктивное рассуждение, индуктивное рассуждение или и то, и другое.

Примеры дедуктивных рассуждений

Дедуктивные рассуждения предоставляет полные доказательства истинности своего заключения. Он использует конкретную и точную предпосылку, которая приводит к конкретному и точному заключению. При правильных предпосылках вывод из этого типа аргумента является верифицируемым и правильным.

• Помещения: Все квадраты прямоугольники. Все прямоугольники имеют четыре стороны.

  Вывод: Все квадраты имеют четыре стороны.

• Предпосылки: Все люди смертны. Вы человек.

  Вывод: Вы смертны.

• Помещение: Все деревья имеют стволы. Дуб — это дерево.

  Вывод: У дуба есть ствол.

Примеры индуктивной логики

Индуктивное рассуждение «снизу вверх», что означает, что оно берет конкретную информацию и делает широкое обобщение, которое считается вероятным, учитывая тот факт, что вывод может быть неточным. Этот тип рассуждений обычно включает установление правила на основе серии повторяющихся опытов.

• Помещение: Зонт не даст вам промокнуть под дождем. Эшли взяла свой зонт и не промокла.

  Вывод: В этом случае вы можете использовать индуктивное рассуждение, чтобы высказать мнение, что, вероятно, шел дождь.

  Объяснение: Ваш вывод, однако, не обязательно будет точным, потому что Эшли осталась бы сухой, будь то дождь и у нее был зонтик, или дождя не было вообще.

• Помещение: Каждый трехлетний ребенок, которого вы видите в парке каждый день, большую часть времени плачет и кричит.

  Вывод: все трехлетние дети должны кричать во второй половине дня.

  Объяснение: Это не обязательно будет правильным, потому что вы не видели каждого трехлетнего ребенка в мире днем, чтобы убедиться в этом.

• Помещения: Сгорели 12 из 20 домов квартала. Каждый пожар был вызван неисправной электропроводкой.

  Вывод: Если более чем в половине домов неисправна проводка, значит, неисправна проводка во всех домах квартала.

  Объяснение: Вы не знаете, что этот вывод верен, но он возможен.

• Помещения: Красный свет предотвращает несчастные случаи. Майк не попал в аварию за рулем сегодня.

  Вывод: Майк, должно быть, остановился на красный свет.

  Объяснение: Майк мог вообще не встретить никаких светофоров. Поэтому он мог бы избежать аварий, даже не останавливаясь на красный свет.

Реклама

Следуйте логике

Как показывают эти примеры, вы можете использовать логику, чтобы решать проблемы и делать выводы. Иногда эти выводы являются правильными выводами, а иногда неточными. Когда вы используете дедуктивное рассуждение, вы приходите к правильным логическим аргументам, в то время как индуктивное рассуждение может дать или не дать вам правильный результат. Посмотрите примеры логических ошибок, чтобы увидеть, как выглядят неверные логические рассуждения.

Штатный редактор

Неполнота формальной логики.

Часть I Неполнота формальной логики. Часть I

Философская критика символического исчисления

Дэниел Дж. Кастеллано

(2012)

Часть I: Введение

В англоязычном мире в философии преобладает парадигма, предполагающая, что философская логика идентична символической или математической логике. Многие преподаватели философии имеют опыт работы с логикой, которую преподают в математике или информатике, и именно эта обедненная логика считается философской или истинной логикой. На самом деле математическая логика — это исчисление, независимое от содержания объектов, с которыми оно связано. Поскольку он основан исключительно на форма аргумента или доказательства, независимо от содержания его предпосылок или переменных, она правильно называется формальной логикой. Формальная логика обязательно неполна и неспособна создать систему эпистемологии или метафизики. При всех наших успехах в развитии формальной логики она остается бедной и неадекватной философской логикой, так как не учитывает категориального содержания своих посылок.

Этим объясняется хаотическое состояние современной философии, которая не смогла продемонстрировать каких-либо общепринятых положений метафизики, поскольку формальная логика может доказывать только бесплодные тавтологии.

Следует помнить, что стремление свести философскую логику к формальной логике предполагало, что последняя имплицитно будет содержать все богатство первой. Готтлоб Фреге надеялся доказать, что, поскольку все логические операции следуют набору правил, которые должны применяться к предложениям независимо от их специфического содержания, эту логику можно было бы описать как исчисление. К сожалению, попытки формализовать философскую логику не учитывали должным образом тот факт, что логика действительно зависит от категориального содержания ее переменных, оставляя много пробелов и целые классы метафизических тезисов, которые, хотя и являются безусловно верными, не могут быть доказаны формальной, символической логикой. Только из этих соображений задолго до Гделя должно было быть очевидно, что формальная логика0261 неполный.

Критики формальной логики, прежде всего Бертран Рассел, часто предполагали такое же безразличие к категориальному или семантическому содержанию. Знаменитый парадокс самореферентности Рассела, например, использует неспособность формальной логики адекватно трактовать заместители по отношению к их антецеденту. С философской точки зрения парадокс Рассела не является истинным парадоксом, поскольку любой, кто имеет элементарное представление о том, как анализировать смысл в английском языке, может исправить ошибку. Парадокс не является истинным парадоксом, потому что логика Фреге не является истинной логикой, а представляет собой неполноценное подмножество последней. Это подмножество традиционной логики в смысле типа информации, которую она может доказать. В другом смысле традиционную логику можно рассматривать как подмножество формальной логики, причем последняя слишком широка и не имеет отношения к онтологической реальности. Классическая логика основана на реальности и, как следует из ее названия, основана на

logos , слово , которое, как предполагается, связано с описываемой им реальностью. Без этой связи с реальностью (актуальной или виртуальной) нет причин рассматривать слова как нечто иное, как произвольные ярлыки, и точно так же произвольно определять правила относительно отношений между этими ярлыками (словами или предложениями).

Этот факт не был упущен из виду современными логиками, которые чувствовали себя вправе конструировать небулевы логики, с математически или практически (например, информатика) полезными результатами. Эти успехи лишь доказывают, что эти другие формальные логики полезны 9 .0003 исчисления , но некоторые из их представителей опрометчиво пришли к выводу, что выбор логики произволен, и даже принципы непротиворечия и исключенного среднего подлежат обсуждению. Эта неспособность отличить символическую логику от реальной логики как (в которой самоочевидно, что бытие и небытие исключают друг друга, когда высказываются однозначно) приводит к полной неспособности достичь даже самых элементарных философских истин, поскольку все принципы подлежат обсуждению или произвольны.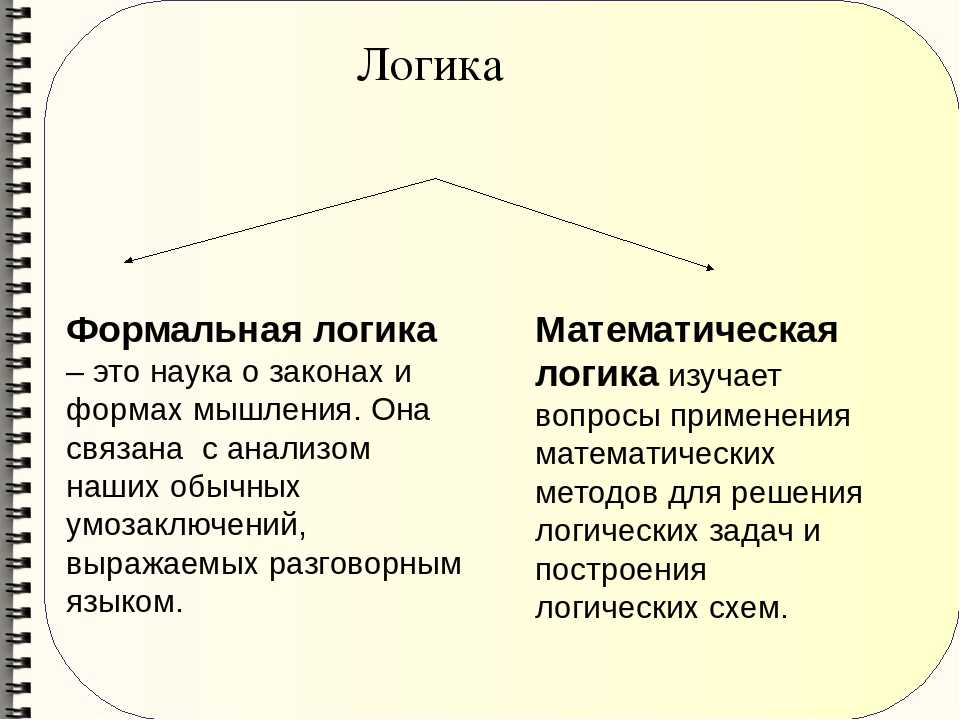 На самом деле неаристотелевские логики (включая булеву логику) — это просто исчисления, неявно основанные на аристотелевской логике бытия. Если бы это было не так, вряд ли можно было бы проводить математические доказательства

о этих логиках (метадоказательствах), показывая, что они внутренне непротиворечивы. При таком сценарии каждый изучающий логику мог бы утверждать, что он заслуживает отличной оценки, поскольку правила математического доказательства произвольны. По сей день все математические доказательства, в том числе доказательства неаристотелевской логики (исчисления), предполагают аристотелевские принципы непротиворечия и исключенного третьего.

Современное предприятие по формализации логики не ставило своей целью выйти за пределы аристотелевской логики, а скорее ограничить ее масштабы, очистив ее от метафизики. Эта цель была четко сформулирована Бертраном Расселом (среди прочих), который стремился свести всю философию к философии естествознания.

Это желание вычеркнуть метафизику из философии само было основано на метафизическом допущении: философском натурализме. С этой точки зрения нет ничего, что можно было бы узнать за пределами естествознания, поэтому не может быть никакой метанауки (метафизики или метафизической логики), которая могла бы быть эталоном истины. Следовательно, единственной логикой является логика науки, предикатами которой являются объекты естествознания. Рассуждения здесь явно цикличны. Мы предполагаем, что нет ничего познаваемого за пределами естествознания, и определяем нашу логику только для рассмотрения объектов естествознания. В нашу логику встраивается чахлая эпистемология, в которой физический эмпиризм является единственным действительным способом познания, который затем используется для показывают , что для метафизики нет логической основы. Это общая черта философского натурализма: от метафизики уклоняются, отказываясь от любых логических или эпистемологических средств достижения ее. Это все равно, что выколоть себе глаза, чтобы отрицать существование цвета. Точно так же философы-аналитики и другие натуралисты практикуют то, что Николас Капальди справедливо назвал усеченным аристотелизмом, отрицая метафизику, просто игнорируя ее. На самом деле все, что они сделали, — это встроили свои эпистемические и метафизические предположения в свою логику, а не позволили логике выносить суждения об этих предположениях, которые не выдерживают такой тщательной проверки.

Если бы действительно было правдой, что ничто не может быть познано за пределами естествознания, а философия была бы лишь логикой науки, не было бы реальной необходимости в философии как отдельной дисциплине. Если философия не является судьей других наук, а является совершенно производной от естественных наук, то зачем ученым философы? Наверняка практикующие каждую науку понимают логику своих дисциплин, включая используемые ими понятия и предписания, которые якобы дают истину обо всем. Если к натурализму относиться серьезно, логика не должна добавлять к естественным наукам никаких знаний, кроме того, что может быть определено в рамках наук. Действительно, в своем рвении прославить наука (как если бы существовала единая эпистемология для всех областей исследования), главным образом для того, чтобы бросить тень на системы метафизики и теологии, аналитические философы и другие натуралисты делают себя неуместными. Гораздо лучше спросить физика, чем философа, о логике физики, если это не что иное, как физика. Нам лучше обратиться к настоящим ученым, а не к их прихлебателям, которые не являются ни философами, ни учеными.

Если бы логицизм преуспел, он мог бы установить интеллектуальную автономию тех наук, которые основаны на математике. Однако символическая логика имеет несколько серьезных недостатков. Поскольку формальная логика абстрагируется от понятийного содержания, имея дело только с формой утверждений, она ограничена в том, что она может доказать, и часто не в состоянии отличить связные утверждения от несвязных, потому что она не основана на здравых априорных понятиях. Даже как формальная логика, символическая логика терпит неудачу, приводя к парадоксам, таким как антиномия Рассела, которые являются результатом пренебрежения априорных онтологических понятий, таких как субстанция. Кроме того, он предполагает онтологию объекта-свойства, поэтому он не способен работать с универсалиями.

Наконец, даже в области математики символическая логика неполна и не может привести ко всем возможным выводам. Искусство математического доказательства не может быть сведено к алгоритму, как доказал Курт Гдель своими 90 261 неполнотой 90 262 теорем, которые показали недостаточность символической логики даже для чисто математических доказательств. Даже в ее собственной области математики нам нужно нечто более сильное, чем символическая логика.

Формальная логика предполагает, что содержание утверждений не имеет значения, а касается только их формы в целях достоверного вывода. Таким образом, он охватывает только те выводы, которые следуют из формы. Тем не менее, даже эти выводы содержат неявные предположения об универсалиях и частностях, а также о том, что значит быть экземпляром универсального, как в 90 261 для каждых 90 262 (∀) и 90 261 существует 90 262 (∃). Таким образом, даже формальная логика имеет концептуальное содержание. В математической логике мы интерпретируем для каждых (∀) и существует (∃) в теоретико-множественном смысле, а не в терминах универсалий и частностей. В аристотелизме, когда всеобщее находится в частном, его сущность находится в частном, так что вы можете сказать, что особенное в известном смысле есть всеобщее. Это отношение инстанцирования отличается от атрибуции, когда вы приписываете субъекту некоторую случайность. Истинная логика должна быть способна трактовать такие отношения, а не отбрасывать их с ходу. Только тогда логика может быть действительно a priori , а не post hoc рационализация существующих наук.

Без здравых онтологических концепций логика — это всего лишь произвольный набор правил, и мы могли бы легко определить другой формализм. Проект логицизма потерпел неудачу, потому что он пытался отбросить онтологию и метафизику, все время контрабандой внося свои собственные специфические онтологические и метафизические предположения, многие из которых не были здравыми. Мы должны сделать нашу онтологию явной и позволить логике охватить все, что может представить разум, не ограничиваясь постоянно меняющимися парадигмами современной науки. Логика должна выйти за пределы теории, а не ограничиваться теорией. Логицизм был сильно нагружен теорией и слеп к ошибочности викторианской идеи о том, что наука может быть целью. Когда логика освобождается от эмпирической смирительной рубашки, она может подвергать эпистемологии и теории физики и метафизики тщательному анализу в соответствии с законами мысли.

Любая попытка восстановить истинную логику из трясины современного формализма должна начинаться с понимания значения символов, стараясь отличать семантику от синтаксиса, подчеркивая при этом важность обоих. Мы сделали это в некоторой степени уже в Логика и язык , но мы подытожим наши результаты чуть позже. Далее мы рассмотрим исторический переход от классической логики терминов к современной логике предикатов и его интеллектуальные мотивы. Затем мы подробно проанализируем логику предикатов первого порядка, постаравшись выявить ее скрытые онтологические предположения. В частности, мы будем иметь дело с проблематичным понятием материальной импликации, а также с упомянутыми выше кванторами ∀ и ∃, показывая, как они смешивают универсалии и партикулярии. Далее мы перейдем к логике более высокого порядка и правилам вывода или доказательства. Это, естественно, приведет к обсуждению утверждений о том, что может доказать символическая логика, и окончательному опровержению этих утверждений Гделем.

Мы подробно рассмотрим теоремы Гделя о неразрешимости и неполноте, прежде чем перейти к обсуждению формальной теории множеств и, в частности, аксиомизации Цермело-Френкеля. Ограниченность логики Рассела сделала необходимым несколько экзистенциальных аксиом, особенно неуклюжую аксиому подстановки, призванную обойти парадокс Рассела. Если бы логика строилась на более прочном семантическом фундаменте, в таких импровизированных средствах не было бы необходимости. Теория множеств не имеет адекватного отношения к универсалиям, как и логика предикатов. Предстоит крупная коррекция.

Эта дискуссия завершится разработкой формальной логики, которая сохраняет большую часть семантического богатства классической логики, сохраняя при этом точность символической логики. Мы начнем с предложенного Джоном Троттером исчисления предикатов, в котором используется обычная языковая обработка заместителей, а затем проверим онтологическую устойчивость. Наконец, мы воспользуемся предложением Троттера построить новую аксиомизацию теории множеств без экзистенциальных аксиом. Мы также проясним загадочные понятия элементности и множественности.

Провалу логицизма уже восемьдесят лет, но лишь немногие сделали очевидный вывод о том, что необходима более надежная логика, восстанавливающая некоторые возможности классической логики. Многие до сих пор считают, что символическая логика была единственной логикой, и видят в Гделе обвинение самой логике. Вместо этого большинство аналитических философов спустились еще глубже в бункер сциентизма, обратившись к лингвистике или нейропсихологии в поисках основы логики. Мы кратко рассмотрим эту школу мысли и укажем на ее эпистемическую непоследовательность. Парадоксально, что аналитические философы, которые были реалистами, противостоявшими кантианскому повороту в философии, теперь прибегают к открытому психологизму, хотя и якобы к психологии.0261 научный материалистический психологизм. Более тщательное опровержение их обожествления эмпиризма ждет работы по эпистемологии, но мы можем, по крайней мере, показать, используя нашу надежную логическую систему, что нет никаких рациональных препятствий для реальности за пределами естественных наук. Что касается предполагаемой интеллектуальной автономии наук, то со временем мы увидим, что каждая из них имеет свои характерные онтологические допущения, подлежащие логическому анализу. Такая философская критика направлена ​​не столько на опровержение наук, сколько на прояснение онтологического и метафизического содержания их притязаний, в исправление грандиозных философских притязаний популяризаторов науки. Те, кто отрицает метафизику, не могут избежать ее, но в конечном итоге делают это плохо, слепо к своим предположениям, которые мы будем разъяснять на протяжении всей этой работы.