Формальной логики: Книга: «Формальная логика» — Валерий Малахов. Купить книгу, читать рецензии | ISBN 5-8291-0051-7

Основы формальной логики: как не дать собой манипулировать

Мы начинаем серию материалов о манипулятивных техниках, автором которой выступил известный журналист, редактор (и преподаватель философии) Дмитрий Шишкин. В первой части разберёмся, как связаны казахстанские медийные скандалы последнего времени с древними греками Протагором и Аристотелем.

А связаны они очень даже явно — через приёмы словесного мошенничества, названного 2500 лет назад «софизмом». Древние греки научились распознавать ложь по формальным признаками, пора бы заново овладеть этим знанием и нам. 

Искусство манипуляции людьми появилось вместе с речью. Правильно подобранными словами можно отправлять в атаку на врага или обращать в бегство, ввергать в депрессию или мотивировать к свершениям. Но в целом смысл манипуляции всегда один — заставлять делать или думать что-то, что мы делать и думать не собирались — то есть, использовать нас.

Что не так в противостоянии людей, желающих сохранить урочище Кок-Жайляу диким местом, и теми, кто хочет его застроить? На первый взгляд обычный гражданский конфликт — урбанистов и экологов. Но если обратить внимание на нюансы: когда «экологи» приводят аргументы против застройки, а их в ответ называют «экологическим талибаном», и взглянуть на список логических уловок, составленный древними, становится понятно, что это классический пример применения уловки Argumentum ad hominem («аргумент к человеку/личности» или «атака на человека»).

Или, например, когда вся страна была взбудоражена новостями о распространении менингита, на одном из ресурсов вышла статья «Кто заказал министра здравоохранения Елжана Биртанова?». Это – классическая уловка Ignoratio elenchi («невежественное опровержение» или подмена тезиса). (Подробно об этом во второй части материала).Со

Такие примеры встречаются ежедневно. И мы предлагаем вам учиться разбираться в них не по наитию, а научно.

Содержание

Немного истории

Софистика

Более 2500 лет назад в Древней Греции активно распространились школы софистики. Там давали уроки начинающим политикам: как при помощи ораторского искусства добиваться своих целей. От философов, также процветавших в древних полисах, софисты отличались в основном тем, что не считали важными какие-то универсальные задачи и теоретические размышления, а главным признавали достижение практической цели.

Интересно, что софистика появилась раньше логики как оформленной науки, и, скорее всего, именно софисты подтолкнули философов к её созданию (в качестве инструмента противодействия демагогам, вводившим народ в заблуждение ради собственных целей). 

«Он (Протагор, живший примерно в период 485 – 410 годов до нашей эры, за сто лет до Аристотеля – прим. авт.) первый заявил, что о всяком предмете можно сказать двояко и противоположным образом… о мысли он не заботился, спорил о словах, и повсеместное нынешнее племя спорщиков берёт своё начало от него», – писал о самом ярком представителе софистов Диоген Лаэртский в своей книге «О жизни, учениях и изречениях знаменитых философов».  

Аристотель побеждает всех

Софистов ругал ещё Платон, а его ученик Аристотель решил положить конец одурачиванию народа (по крайней мере, попытался — мы и сейчас попадаемся на те же самые уловки, что были известны ещё 2500 лет назад). Он создал научную базу формальной логики (которую сам он называл «Аналитикой») и классифицировал логические ошибки, используемые софистами.

В принципе, логическая ошибка и логическая уловка — это одно и то же, просто ошибка допускается несознательно, а уловка специально вводится в речь. 

Аристотель в своём труде «О софистических опровержениях» наглядно показал, что если разложить любой софизм, будет видна специально внедрённая в него ошибка, благодаря которой выводы софиста кажутся логичными. 

После Аристотеля немало в развитие формальной логики внесли римляне Цицерон и Квинтилиан, а затем и средневековые схоласты – мы будем в дальнейшем пользоваться их типологией логических ошибок, так что пусть вас не удивляют латинские термины.

Немного теории

Теория — это самая скучная часть формальной логики, и передо мной стоит трудная задача: уложить в рамки современного «лонгрида» курс, который в институте преподаётся в течение года. Поэтому отсечём всё ненужное современному человеку, имеющему интернет и способному самостоятельно найти недостающие фрагменты. 

Главное, что есть в формальной логике — это её четыре основных закона

Три из них сформулировал ещё Аристотель:

— закон тождества,
— закон противоречия,
— закон исключённого третьего.

А четвертый закон – достаточного основания — был добавлен немецким математиком и философом Лейбницем в начале XVIII века. 

Закон тождества

«…иметь не одно значение — значит не иметь ни одного значения», писал по этому поводу Аристотель в своей «Метафизике». 

То есть каждая мысль и каждый термин в процессе рассуждения должны иметь одно и то же значение. Подмена понятия в ходе рассуждения — это классическая логическая ошибка (или уловка).

Например: 

– Гражданин N хороший человек, скромный и любит ездить на велосипеде.
– Из него получится хороший аким города!

Здесь мы видим, как в первой части утверждения говорится о личных качествах человека, а вывод делается о его профессиональных качествах — что далеко не тождественно.  

Закон противоречия

Два противоречащих друг другу суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно. 

… невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении (Аристотель, «Метафизика»)

Например:

Мы часто встречаем заявления от официальных лиц и даже целых институтов о том, что:

– Народ Казахстана неоднократно демонстрировал свою политическую зрелость, отдавая голоса на выборах президента и депутатов парламента за стабильность!
– Вместе с тем, наш народ не готов пока к выборности акимов и прочим демократическим преобразованиям.

Налицо явное противоречие: получается, народ Казахстана с одной стороны политически подкован, а с другой — настолько дремуч, что не готов к такому элементарному процессу, как выборы акима. 

Закон исключённого третьего

Два противоречащих друг другу суждения не могут быть одновременно оба истинными или оба ложными.

…ничего не может быть посредине между двумя противоречивыми суждениями об одном, каждый отдельный предикат необходимо либо утверждать, либо отрицать (Аристотель, «Метафизика»)

Противоречащими называют такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается. 

Например:

– Цензура запрещена!
– Если в интересах общества, то цензура разрешена.

Оба эти утверждения об одном и том же явлении не могут быть одновременно правдивыми или ложными. Если делается исключение, то первое утверждение ложное – «третьего не дано». 

Закон достаточного основания

Всякая правильная мысль должна быть обусловлена другими мыслями, истинность которых доказана.  

…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны (Готфрид Вильгельм Лейбниц, «Монадология»)

Это, в общем — именно то, чем занимается «Фактчек в Казахстане» — поиском достаточных оснований для публикаций. В отличие от первых трёх законов, которые можно применять формальными методами, просто соотнося какие-то утверждения с правилами, для установки достаточности основания необходимо включать критическое мышление и затем прилагать усилия для проверки суждений, в которых вы засомневались.

Например, самые яркие примеры мы встречаем довольно часто в виде панических слухов, распространяемых через мессенджеры и социальные сети.

В случае со скандалом вокруг заболеваемости менингитом: неверными оказались как утверждения об эпидемии, так и «рецепт», в котором утверждалось, что для профилактики менингита всем необходимо пропить курс антибиотиков (что, как пояснили затем врачи, назначается только людям, контактировавшим с больными).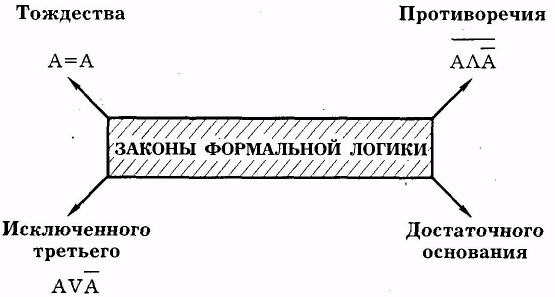  

На законе достаточного основания также базируется важный юридический принцип: «презумпция невиновности», гласящий, что никто не виновен, пока его вина не была доказана.

В соцсетях и даже СМИ он нарушается настолько часто, практически ежедневно, что примеры вы легко найдёте сами. Людей называют ворами и убийцами до судов, друг друга лжецами безо всяких доказательств и опровержений и т.д.

В следующей части читайте о логических уловках, построенных на нарушении этих законов логики:

• Ignoratio elenchi или «подмена тезиса»
• Argumentum Ad Hominem или «переход на личности»

Financial University — Логика. Общий курс формальной логики: учебник. — 3-е изд., перераб. и доп.

 

Record create date: 5/29/2015 Subject: логика; гриф; математическая логика; мышление; суждение; умозаключение; научное знание; учебники; полный текст LBC: 87. 4я73 Collections: Электронные учебники Allowed Actions: – Action ‘Read’ will be available if you login or access site from another network Action ‘Download’ will be available if you login or access site from another network Group: Anonymous Network: Internet

Document access rights

	Network		User group		Action
	Finuniversity Local Network		All
	Internet		Anonymous
	Internet		Readers

Table of Contents

• Оглавление
• Предисловие
• Раздел I. Пропедевтика: предмет логики. Основные понятия и структура логики
  • Введение. Логика как наука
  • Глава 1. Предмет и основные понятия логики
    • 1.1. Основные этапы формирования и развития логики
    • 1.2. Структура формальной логики
    • 1.3. Предмет формальной логики
    • 1.4. Мышление как объект изучения логики
    • 1.5. Основные формы мышления
    • 1.6. Понятие логической формы
    • 1.7. Истинность мысли и формальная правильность рассуждений
    • 1.8. Основные свойства правильного мышления. Понятие логического закона
    • 1.9. Основные принципы (законы) формально-логического мышления
    • 1.10. Понятие логического следования
    • 1.11. Закон логики как отношение логического следования
  • Глава 2. Логический анализ языка
    • 2.1. Мышление и язык
    • 2.2. Естественный и искусственный языки
    • 2.3. Язык, знак, имя
    • 2. 4. Семантическая классификация терминов
    • 2.5. Семантические категории
    • 2.6. Разновидности семантических категорий
    • 2.7. Семиотика: семантика
    • 2.8. Семиотика: синтактика
  • Глава 3. Основные направления и понятия символической (математической) логики
    • 3.1. Классическая логика
    • 3.2. Классическая логика высказываний
    • 3.3. Синтаксис языка логики высказываний
    • 3.4. Семантика языка логики высказываний
    • 3.5. Семантические таблицы логики высказываний
    • 3.6. Семантическая проблема разрешимости
    • 3.7. Табличный способ определения типа формул
    • 3.8. Логические отношения между формулами
    • 3.9. Виды логических отношений между формулами
    • 3.10. Способ приведения формулы к нормальной форме
    • 3.11. Равносильные формулы
    • 3.12. Алгоритм приведения формул к КНФ и ДНФ
    • 3.13. Аксиоматические исчисления
    • 3. 14. Натуральные исчисления
    • 3.15. Секвенциальные исчисления
    • 3.16. Построение секвенции
    • 3.17. Законы логики высказываний
    • 3.18. Классическая логика предикатов
    • 3.19. Основные понятия логики предикатов
    • 3.20. Операции над предикатами. Кванторы
    • 3.21. Синтаксис языка логики предикатов
    • 3.22. Процедура формализации выражений естественного языка в классической логике
    • 3.23. Логическая символика
• Раздел II. Понятие
  • Введение. Понятие — форма мышления
  • Глава 4. Общая характеристика понятия
    • 4.1. Понятие как форма мышления
    • 4.2. Основные семантические характеристики понятия
    • 4.3. Логическая структура понятия
    • 4.4. Классификация видов понятий
    • 4.5. Положительные и отрицательные, относительные и безотносительные понятия
    • 4.6. Пустые и непустые, единичные и общие понятия
    • 4.
      7. Универсальные и неуниверсальные, регистрирующие и нерегистрирующие понятия
    • 4.8. Абстрактные и конкретные, собирательные и несобирательные понятия
  • Глава 5. Отношения между понятиями
    • 5.1. Отношения между понятиями по логическому содержанию
    • 5.2. Отношения между сравнимыми понятиями по содержанию
    • 5.3. Отношения между понятиями по объемам
    • 5.4. Отношения между совместными понятиями по объемам
    • 5.5. Отношения между несовместимыми понятиями по объемам
  • Глава 6. Логические операции с понятиями
    • 6.1. Отношения рода и вида
    • 6.2. Обобщение и ограничение понятий
    • 6.3. Деление понятий
    • 6.4. Таксономическое деление
    • 6.5. Правила деления и возможные ошибки
    • 6.6. Классификация
    • 6.7. Операции с множествами (классами)
    • 6.8. Операция объединения классов
    • 6.9. Операция пересечения классов
    • 6. 10. Законы операций объединения и пересечения
    • 6.11. Операция вычитания
    • 6.12. Дополнение к множеству
    • 6.13. Операции с классами. Диаграмма Венна
  • Глава 7. Определение
    • 7.1. Определение и приемы, сходные с определением
    • 7.2. Виды определений (номинальные и реальные определения)
    • 7.3. Явные и неявные определения
    • 7.4. Виды явных определений
    • 7.5. Виды неявных определений
    • 7.6. Правила определения и возможные ошибки
• Раздел III. Суждение
  • Введение. Суждение (высказывание)
  • Глава 8. Простые суждения
    • 8.1. Структура суждения
    • 8.2. Логическая структура простого суждения
    • 8.3. Логический анализ предложений, выражающих простые суждения
    • 8.4. Виды простых суждений
    • 8.5. Атрибутивные суждения. Деления суждений по качеству и количеству
    • 8. 6. Атрибутивные суждения. Объединеннная классификация суждений по количеству и качеству
    • 8.7. Процедура приведения предложений естественного языка к канонической форме категорических суждений
    • 8.8. Распределенность терминов в общеутвердительных и общеотрицательных суждениях
    • 8.9. Сводная таблица распределенности терминов в категорических суждениях
    • 8.10. Выражение категорических суждений на языке логики предикатов
    • 8.11. Вылеоябшие, исключающие и определенно-частные суждения
    • 8.12. Суждения с отношениями
    • 8.13. Выражение суждений с отношениями на языке логики предикатов
  • Глава 9. Сложные суждения
    • 9.1. Понятие о сложном высказывании и логическом союзе
    • 9.2. Соединительные суждения
    • 9.3. Разделительные суждения
    • 9.4. Условные и импликативные суждения
    • 9.5. Суждения эквивалентности
    • 9.6. Суждение с внешним отрицанием
    • 9. 7. Условия истинности сложных суждений
    • 9.8. Логическая форма сложного суждения
    • 9.9. Выражение одних логических союзов через другие
    • 9.10. Формы сложных суждений
    • 9.11. Логическая вероятность сложных суждений
  • Глава 10. Отрицание суждений
    • 10.1. Отрицание атрибутивных суждений
    • 10.2. Отрицание суждений с отношениями
    • 10.3. Отрицание сложных суждений
  • Глава 11. Отношения между суждениями
    • 11.1. Отношения между суждениями
    • 11.2. Отношения между простыми суждениями
    • 11.3. Условия истинности для простых суждений
    • 11.4. Модельные схемы
    • 11.5. Логический квадрат
    • 11.6. Логический треугольник
    • 11.7. Отношения между сложными суждениями
    • 11.8. Отношение эквивалентности сложных суждений
    • 11.9. Отношение субконтрарности сложных суждений
    • 11. 10. Отношение подчинения сложных суждений
    • 11.11. Отношение противоположности сложных суждений
    • 11.12. Отношение противоречия сложных суждений
  • Глава 12. Модальность суждений
    • 12.1. Структура модальных суждений
    • 12.2. Алетическая модальность
    • 12.3. Эпистемическая модальность
    • 12.4. Деонтическая модальность
    • 12.5. Сводная таблица видов модальностей
    • 12.6. Определения и законы модальной логики. Логические модальные понятия
    • 12.7. Физические модальные понятия
    • 12.8. Законы и определения логики оценок
    • 12.9. Законы и определения логики норм
  • Глава 13. Логические основы вопросно-ответного мышления
    • 13.1. Виды вопросов
    • 13.2. Виды ответов
• Раздел IV. Умозаключение
  • Введение. Умозаключение как форма мышления
  • Глава 14. Общая характеристика и структура умозаключений
    • 14. 1. Структура умозаключения
    • 14.2. Классификация умозаключений по строгости правил вывода
    • 14.3. Классификация умозаключений по направленности логического следования
    • 14.4. Дедуктивные умозаключения
    • 14.5. Обобщенная классификация умозаключений
  • Глава 15. Демонстративные (необходимые) умозаключения
    • 15.1. Выводы из сложных высказываний (выводы на основе свойств логических связок)
    • 15.2. Чисто условное умозаключение
    • 15.3. Условно-категорическое умозаключение (modus ponens)
    • 15.4. Условно-категорическое умозаключение (modus tollens)
    • 15.5. Разделительно-категорическое умозаключение
    • 15.6. Условно-разделительные умозаключения
    • 15.7. Дилемма
    • 15.8. Простая конструктивная дилемма
    • 15.9. Простая деструктивная дилемма
    • 15.10. Сложная конструктивная дилемма
    • 15.11. Сложная деструктивная дилемма
    • 15. 12. Проверка правильности умозаключений из сложных суждений
    • 15.13. Проверка умозаключений методом аналитических таблиц
    • 15.14. Непосредственные умозаключения
    • 15.15. Построение непосредственных умозаключений по логическому квадрату
    • 15.16. Построение непосредственных умозаключений посредством преобразования структуры посылки
    • 15.17. Превращение
    • 15.18. Обращение
    • 15.19. Противопоставление предикату
    • 15.20. Проверка непосредственных умозаключений
    • 15.21. Простой категорический силлогизм
    • 15.22. Структура силлогизма
    • 15.23. Модусы категорического силлогизма
    • 15.24. Правила терминов категорического силлогизма
    • 15.25. Правила посылок категорического силлогизма
    • 15.26. Первая фигура категорического силлогизма
    • 15.27. Вторая фигура категорического силлогизма
    • 15.28. Третья фигура категорического силлогизма
    • 15. 29. Четвертая фигура категорического силлогизма
    • 15.30. Категорический силлогизм с выделяющими суждениями
    • 15.31. Правила логического вывода фигур категорического силлогизма
    • 15.32. Алгоритм анализа силлогизма
    • 15.33. Способ проверки правильности силлогизмов посредством построения схзем для посылок и заключения
    • 15.34. Способы проверки правильности силлогизмов (поиск и предъявление контрпримера)
    • 15.35. Условия неправильности и правильности умозаключения
    • 15.36. Умозаключения из суждений с отношениями
    • 15.37. Сокращенный категорический силлогизм (энтимема)
    • 15.38. Сложные и сложносокращенные силлогизмы (полисиллогизм, сорит, эпихейрема)
    • 15.39. Прогрессивный полисиллогизм
    • 15.40. Регрессивный полисиллогизм
    • 15.41. Прогрессивный сорит
    • 15.42. Регрессивный сорит
    • 15.43. Эпихейрема
  • Глава 16. Недемонстративные (правдоподобные) умозаключения
    • 16.1. Общая характеристика правдоподобных умозаключений
    • 16.2. Отношение подтверждения в правдоподобных умозаключениях
    • 16.3. Установление отношения подтверждения в правдоподобных умозаключениях
    • 16.4. Правдоподобные (индуктивные) умозаключения
    • 16.5. Виды индукции
    • 16.6. Полная индукция
    • 16.7. Математическая индукция
    • 16.8. Неполная индукция (популярная)
    • 16.9. Научная индукция
  • Глава 17. Индуктивные методы установления причинных связей
    • 17.1. Метод единственного сходства
    • 17.2. Метод единственного различия
    • 17.3. Содединенный метод сходства и различия
    • 17.4. Метод сопутствующих изменений
    • 17.5. Метод остатков
    • 17.6. Характеристики причинных связей, делающие возможным применение методов научной индукции
    • 17.7. Ошибки, встречающиеся при обнаружении причинных связей
  • Глава 18. Умозаключения по аналогии
    • 18.1. Аналогия
    • 18.2. Структура аналогии
    • 18.3. Виды умозаключений по аналогии по характеру информации
    • 18.4. Виды умозаключений по аналогии по характеру выводного знания
• Раздел V. Аргументация
  • Введение. Логические основы аргументации
  • Глава 19. Общая характеристика аргументации
    • 19.1. Обоснование как основа аргументации
    • 19.2. Аргументация как способ рассуждения
    • 19.3. Аргументация как рациональный процесс
    • 19.4. Виды аргументации
    • 19.5. Типы аргументированных процессов
    • 19.6. Условия доказательности и недоказательности аргументации
    • 19.7. Структура доказательства
    • 19.8. Способы доказательств
    • 19.9. Виды доказательств
    • 19.10. ÏПрямое обоснование тезиса в аргументированных процессах
    • 19.11. Косвенное обоснование тезиса в аргументированных процессах
    • 19. 12. Критика и опровержение
    • 19.13. Способы опровержения
    • 19.14. Правила по отношению к тезису и возможные ошибки
    • 19.15. Правила по отношению к аргументам и возможные ошибки
    • 19.16. Правила по отношению к форме доказательства и возможные ошибки
• Раздел VI. Формы развития знания
  • Введение. Логика в процессе развития научного знания
  • Глава 20. Проблема
    • 20.1. Общая характеристика проблемы
    • 20.2. Типология проблем
    • 20.3. Обобщенная схема типологии проблем
    • 20.4. Процесс решения проблемы
  • Глава 21. Гипотеза
    • 21.1. Общая характеристика гипотезы
    • 21.2. Построение гипотезы
    • 21.3. Условия состоятельности гипотезы
    • 21.4. Проверка гипотезы
    • 21.5. Логическое доказывание гипотез
  • Глава 22. Теория
    • 22.1. Теория, ее элементы и функции
    • 22. 2. Классификация теорий
• Практикум
  • Раздел 1. Образцы решения типовых задач
  • Раздел 2. Задания для самостоятельной работы студентов очной и заочной формы обучения
  • Приложения
  • Библиографический список

Usage statistics

80-310/610 Формальная логика

80-310/610 Формальная логика

Осень 2018

Стив Авуди

12 турецких лир — 1:20

Бейкер Холл A53

9-12 шт.

Введение в формальную логику с приложениями к информатике. Темы включают индуктивно определенные структуры, синтаксис и семантику. логики первого порядка, полноты, компактности и Лёвенгейма-Скулема. теоремы. Дополнительные темы могут также включать определяемость, нестандартность модели арифметической, высшей, интуиционистской и модальной логики.

Предпосылки: либо 80-210, 80-211, 21-127, 15-251, либо согласие инструктор.

---

Новости

---

Информация о курсе

Лекции	TR 12-1:20, BH A53
Чтения	По вторникам в 18:00 в Baker Hall 150
Учебник	Логика и структура, Дирк ван Дален, Springer 2013. Доступно в кампусе по этой ссылке.
Кредит	9-12 шт.
Оценка	50 % домашнее задание, 25 % промежуточное задание, 25 % итоговое задание
Домашнее задание	Еженедельное домашнее задание размещается здесь по четвергам и должно быть выполнено в следующий четверг в классе. Домашнее задание должно быть сдано лично и не будет принято по электронной почте. Поздняя домашняя работа будет принята только в исключительных случаях.
Среднесрочная	Четверг, 11 октября, в классе. Закрытая книга, разрешен один двусторонний лист для заметок.
Окончательный	Четверг, 6 декабря, в классе. Закрытая книга, разрешен один двусторонний лист для заметок.
Темы	Индуктивные определения и доказательства, Синтаксис и семантика логики высказываний, Синтаксис и семантика логики первого порядка, Теория элементарных моделей, Высший порядок, интуиционистская и модальная логика.
Домашняя страница	http://www.andrew.cmu. edu/course/80-310-610/
Онлайн-обсуждение	piazza.com/cmu/fall2018/80310/home

---

Преподавательский состав

		Офис	Часы работы	Телефон	Электронная почта
Профессор	Стив Авуди	БХ 135F	Ф 11-12	x8-8947	[email protected]
ТП	Мэтью Боуэн	ДХ 4301	Т 3:30-4:30	ххх	[email protected]
ТП	Зесен Цянь	ДХ 4301С	М 3-4	ххх	[email protected]
ТП	Эндрю Уоррен	ДХ 4301D	Ф 3-4	ххх	awarren1@andrew. cmu.edu
Админ. Ассистент	Мэри Грейс Джозеф	БХ 161Н		x8-9459	[email protected]

[email protected]
Стив Аводи

Logic Works: строгое введение в формальную логику — 1-е издание

Logic Works — это критическое и подробное введение в логику. Он задает вопросы о том, почему системы логики такие, какие они есть, как они соотносятся с обычным языком и обычными рассуждениями и какие могут быть альтернативы классическим логическим доктринам.

Книга охватывает классическую логику первого порядка и альтернативы, включая интуиционистскую, свободную и многозначную логику. В нем также рассматривается, как логический анализ может быть применен для тщательного представления рассуждений, используемых в академической и научной работе, лучшего понимания этих рассуждений и выявления их скрытых предпосылок. Стремясь стать таким же справочным пособием и пособием для дальнейшего независимого изучения, как и текст курса, он охватывает больше материала, чем обычно охватывается вступительным курсом. Он также охватывает этот материал более подробно и более подробно, чтобы сделать его доступным для тех, у кого нет предварительной подготовки в области логики или формальных систем.

Вспомогательные онлайн-материалы включают подробное руководство по решениям для учащихся с постоянными комментариями ко всем упражнениям, отмеченным звездочкой, и набор редактируемых слайд-презентаций для курсовых лекций.

Основные характеристики

• Включает необычайно широкий круг тем, что позволяет инструкторам создавать курсы для достижения различных целей
• Принимает критическое отношение к некоторым классическим доктринам, предлагая учащимся альтернативные способы ответа на философские вопросы о логике
• Тщательно рассматривает способы, которыми естественный язык одновременно сопротивляется формализации и поддается формализации
• Упрощает объектную семантику для квантифицированной логики благодаря поэтапному подходу, основанному на правилах, которому помогают многочисленные простые упражнения
• Делает важные метатеоретические результаты доступными для вводных студентов посредством дискурсивного представления этих результатов и использования простых тематических исследований. 0026 1. Введение в изучение логики
  1.1 Демонстрация и интерпретация 1.2 Дедуктивные и индуктивные демонстрации 1.3 Принцип непротиворечия 1.4 Абстракция, переменные и формализация; логические и нелогические элементы; формальное противоречие 1.5 Фундаментальная проблема 1.6 План будущих глав Приложение: Элементы теории доказательной логики

  Часть I. Логика высказываний

  2. Словарь и синтаксис
  2.1: Введение Синтаксис 2.2: Условные обозначения 2.3: Демонстрация синтаксиса с и деревья 2.4: Объем; именованные формы 2.5: Формальные свойства

  3. Семантика
  3.1: Семантика для ⊥ и букв предложения 3.2: Семантика для связок 3.3: Семан тики для сложных предложений 3. 4: Интенсиональные понятия Приложение: Экспрессивная адекватность; дизъюнктивная нормальная форма; бережливый язык

  4. Формализация
  4.1: Слабое соответствие 4.2: Условные предложения английского языка 4.3: Необходимые условия 4.4: Достаточные условия 90 243 4.5: Необходимые и достаточные условия; принцип благотворительности 4.6: Формализация необходимых и достаточных условий 4.7: Исключения и сильные исключения 4.8: Дизъюнкция 4.9: Отрицания и союзы 4.10: Пунктуация 4.11: Пределы формализации 4.12: Формализация демонстрации

  9 0026 5. Работа с семантикой ИЯ
  5.1: Выявление и проверка интерпретаций 5.2: Демонстрация отсутствия интерпретации 5.3: Демонстрация общих принципов 5. 4: Фальсификация общих утверждений 5.5: Отношения между интенсиональными понятиями; модели; следствие Приложение: Альтернативы бивалентности

  А-1. Дополнительные темы, касающиеся семантики ЯЯ
  A-1.1: Математическая индукция A-1.2: Бивалентность A-1.3: Экстенсиональность A-1.4: Компактность

  6 Производные
  6.1: D _L : бережливая система деривации 6.2: Стратегии деривации в D _L  6.3: Ds: система деривации для SL 6 .4: Стратегии вывода в Ds 6.5: Расширения Ds; запись без скобок 6.6: Интуиция и «интуиционизм»; вывод в интуиционистской логике

  А-2. Дополнительные темы, касающиеся надежности и полноты Ds
  A-2.1: Правильность  A-2. 2: Результаты следствия; непротиворечивость и экстенсиональность A-2.3: Полнота Хенкина A-2.4: Доказательство леммы Линденбаума A-2.5: Доказательство леммы 2 A-2.6: Доказательство леммы 3 A-2.7: Результаты следствия A-2.8: Полнота по Посту/Гильберту-Акерману

  7. Деревья редукции
  7.1: 9 0245 Метод и стратегии 7.2: Использование деревьев для определения выводимости 7.3: Теория и определения Приложение: Деревья для трехзначной и паранепротиворечивой логики

  A-3: Дополнительные темы, касающиеся надежности и полноты Ts
  A-3.1: Правильность Ts A-3.2: Полнота Ts A-3.3: Разрешимость Ts A-3.4: Преобразование деревьев в производные; использование T для доказательства полноты Ds 8. 2: Формализация  8.3: Выводы

  9. Семантика и деревья для модальной и интуиционистской сентенциальной логики
  9.1: Семантика для MSL 9.2: Деревья редукции для MSL 9.3: Семантика для ISL 9.4: Деревья редукции для ISL

  A-4: Расширенные темы, касающиеся «надежности» и «полноты» Dm и Tm
  A-4.1: «Надежность» модальных систем вывода A-4.2: Полнота Tm A-4.3: Преобразование дерева A-4.4: Адекватность Dm и Tm

  Часть III: Предикатная сентенциальная логика

  10. Лексика, синтаксис, формализация и производные
  10.1: Английское предикация 10.2: Простые термины 10.3: Сложные термины

  11. Семантика и деревья
  11.1: Интерпретации 11. 2: Правила оценивания 11.3: Работа с семантикой 11.4: Tp 11.5: 9024 5 Семантика функциональных терминов 11.6: Tp f 11.7: Семантика определенных описаний

  A-5: Дополнительные темы для PSL
  A-5.1: Экстенсиональность и дисперсия A-5.2: Правильность Dp A-5.3: Полнота Tp A-5.4: Преобразование дерева; надежность Тп; полнота Dp

  Часть IV: Квантифицированная логика предикатов

  12. Лексика, синтаксис и формализация
  12.1: Неформальная лексика и синтаксис 12.2: Формальный словарь и синтаксис 12.3: Формализация английских предложений в QPL

  13. Производные
  13.1: Dq 13.2: Расширения Dq

  14. Деревья и модель дерева семантика для QPL
  14. 1: Правила 14.2: Метод 14.3: Семантика модели дерева 14.4: Расширения Tq

  15. Семантика для QPL без смешанная множественная количественная оценка
  15.1: Объектная семантика 15.2: Обозначение 15.3: Удовлетворение 15.4: Истина 15.5: Работа с семантикой 15.6: Демонстрация общих принципов

  16. Семантика для QPL со смешанным множественная количественная оценка
  16.1: Варианты присвоения переменных; обозначение переменных 16.2: Условия выполнения квантифицированных формул 16.3: (P) и (=) приложения 16.4: Истина 16.5: Работа с семантикой Приложение: Демонстрация принципа исключительности

  A-6: Дополнительные темы для QPL
  A-6.1: Экстенсиональность и дисперсия A-6. 2: Правильность Dq A-6.3: Полнота Tq A-6.4: Преобразование дерева; надежность Тп; Полнота Dp Приложение: Квантифицированная модальная логика

  17. Логика высшего порядка
  17.1 Словарь и синтаксис 17.2: Формализация; определения предикатов более высокого порядка  17.3: Синтаксис II: примеры 17.4: Производные 17 .5: Семантика 17.6: Деревья и неполнота

  Резюме правил
  1. Основные определения
  2. Интенсиональные понятия
  3. Правила формирования
  4. Правила сентенциального оценивания
  5. Правила формульного и свободного оценивания
  6. Правила вывода
  7. Древовидные правила 900 27

  Биография

  Лорн Фалькенштейн — почетный профессор Западного университета в Лондоне, Канада, где он много лет преподавал символическую логику. Он опубликовал работы по трактовке пространственного представления, временного восприятия и визуального восприятия в работах ряда 17 ^-го -го и 18-го ^-го -го века философов, и продолжает работать в этой области.

  Скотт Стэплфорд — профессор философии Университета Св. Томаса во Фредериктоне, Канада. Он является автором Трансцендентальных аргументов Канта: дисциплинирование чистого разума (2008), соавтором (вместе с Тайроном Гольдшмидтом) Принципов Беркли: расширенные и объясненные (Routledge, 2016) и Исследование Хьюма: расширенное и объясненное (Routledge , 2021), соредактор (вместе с Кевином Маккейном) Epistemic Duties: New Arguments, New Angles (Routledge, 2020) и соредактор (вместе с Кевином Маккейном и Матиасом Стюпом) Epistemic Dilemmas: New Arguments, New Angles (Routledge, 2021).

  Молли Као — доцент кафедры философии Монреальского университета в Монреале, Канада. Ее основной областью исследований является философия науки, она работала над вопросами развития квантовой теории, а также над методологическими вопросами, связанными с объединением и подтверждением.

  No related posts.